Abstract
We investigate a novel nonlinear consensus from the extreme points of doubly stochastic quadratic operators (EDSQO), based on majorization theory and Markov chains for time-varying multi-agent distributed systems. We describe a dynamic system that has a local interaction network among agents. EDSQO has been applied for distributed agent systems, on a finite dimensional stochastic matrix. We prove that multi-agent systems converge at a center (common value) via the extreme waited value of doubly stochastic quadratic operators (DSQO), which are only 1 or 0 or if the exchanges of each agent member has no selfish communication. Applying this rule means that the consensus is nonlinear and low-complexity computational for fast time convergence. The investigated nonlinear model of EDSQO follows the structure of the DeGroot linear (DGL) consensus model. However, EDSQO is nonlinear and faster convergent than the DGL model and is of lower complexity than DSQO and cubic stochastic quadratic operators (CSQO). The simulation result and theoretical proof are illustrated.
1. Introduction
Over the recent years, multi-agent systems have attracted wide-spread research attention, focusing on distributed system problems of autonomous agent groups. The issue of consensus or agreement to a common value appears in several studies [1]. Consensus constitutes a fundamental problem in the study of multi-agent coordination, as it suggests that all agents are required to achieve the same status [2]. To reach consensus, connectivity is required and therefore, multiple connectivity conditions have been created to describe the appropriate switching topologies [2]. The consensus problem indicates the convergence of multiple autonomous agents at a common value through their local interaction. Moreover, a consensus occurs when the states of all agents converge to a common value [3]. Multi-agent systems, driven by manage agents to share their information in wide networks to attain an agreed decision. The consensus problem exists in various scenarios, such as coordinating the direction and velocity in the control of unmanned aerial vehicles or robots [4]. It also applied in other areas such as sensor networks, where consensus is needed to combine various measurements of detection and estimation into a single estimate or into a decision [5], control of formation [6], flocking and swarming [7,8], and controlling communication networks.
The concept of the consensus problem was first discussed by Eisenberg and Gale [9,10,11] in the field of management science.
Vicsek [4] and Jadbabaie [12] presented a consensus model of the behavior of flocks of birds and schools of fish. Consensus protocols have been proposed by [13,14,15,16] to reach an agreement in multi-agent systems with a dynamic topology network for distributed systems. Ren [1] widely surveyed consensus problems, in order to control cooperative multi-agent systems.
A general framework for algorithm distribution in computer science for fixed topology networks is explained in the works of [17,18,19,20] for automata theory and distributed computing. The delay problem and a sub-gradient method in time-varying for consensus problems of multi-agent systems have been provided in the works of [21,22].
Recent empirical and theoretical works on the consensus problem including the use of doubly stochastic matrices are proposed in [14,23].
The application of nonlinear updated rules on the consensus problem has not been widely studied. One of the most challenging issues in mathematics is the design of a nonlinear model for multi nodes of networks [3]. Nonlinear consensus for reaching an agreement is presented by [24,25,26,27,28,29,30,31].
However, most of the recently published nonlinear models are of very high complexity and include restricted conditions such as a cubic triplex stochastic matrix system [32,33], where each member of the agent group has a stochastic interconnection with the others. In addition, the aggregation of these interconnections has to be stochastic, as demonstrated through the QSOs model in [34,35,36,37,38,39,40,41,42,43], and restricted to only the cubic triplex stochastic matrix system.
Accordingly, it is deemed worthwhile to explore a paradigm that includes two features; faster consensus and low computational approach. A number of studies have already been attempted to determine the complexity computation for nonlinear consensus by applying other optimization methods such as a greedy approach [44,45,46,47]. This approach, utilized for stochastic systems optimization, requires restricted rules. However, not all systems can run on these general rules and thus, further effort is required to recover the complexity in optimization. One such research effort resulted in the majorization procedure [48] that entails merging the attitude of majorization with nonlinear control. Even though consuming a straight relative to the greedy technique, it is still bright enough to overawe the simplification settings essential for the greedy way. Owing to the fact that agreement-merged issues are practically equivalent to optimization, stratifying the majorization eventuality to illuminate the intricacy issue in agreement issues is an engaging arrangement.
We can deduce from the previous studies that the consensus models can be classified two categories; linear and nonlinear models. The linear consensus model is easy to compute but slow to reach a consensus, while the nonlinear consensus model is harder to compute but quick to reach a consensus. The first linear consensus models can be traced back to the DeGroot model (DGL), developed in 1974. DGL is considered the easiest mathematical computation structure for the consensus process. The nonlinear consensus model refers to nonlinear consensus under first and second orders, Lyapunov function, fractional-order, and nonlinear stochastic models. It has been found that the nonlinear model performs better than the linear model. From this review, we are proposing a consensus model which is nonlinear, easy to compute, fast to reach a consensus, and generalizes the first liner model for achieving consensus. This proposed model, extreme points of doubly stochastic quadratic operators (EDSQOs), has its own history and background which will be briefly described below.
Quadratic stochastic operators (QSOs), which were first proposed by [49], are nonlinear differential equations that emerged from certain problems pertaining to population genetics. The dynamics systems of the superior QSO class on two-dimensional simplex was studied by [50]. The concept and definition of majorization was first introduced by [51]. The definition of doubly and dissipative QSOs was designed using majorization theory in [52,53]. The findings of [50] were subsequently extended to the entire space finite-dimensional simplex by [54]. Basic properties of majorization and doubly stochastic matrices were studied by [55]. The limit behavior of trajectories of QSOs was exhaustively studied on a one-dimensional simplex, the limit of any initial values being a finite set [17]. The application of QSOs was considered in population genetics where a high-dimensional simplex, even on 2D simplex, continued to be an open complexity problem.
The majorization term is defined according to the fuzzy concept for the vector components, where the vector components of diffuse lesser than, or close to, the components of the vector. In this case, the most effective approach is to stipulate that majorizes or x is majorized by , as . The majorization history has been discussed in [56,57,58,59,60]. Different theories have been developed that are significant from the viewpoint of economics, foremost to failings in income distribution. Various contributions have been made by other researchers, for example by Ando [55], who presented a generalization review from several viewpoints of the doubly stochastic matrix and added majorization. Marshall and Olkin [51] have discussed the theory of majorization and its applications with much scrutiny, and the theory of majorization was included for QSOs by [53,61,62,63,64], for soft nonlinear operators of QSOs and doubly stochastic quadratic operators (DSQOs).
The theories of DSQOs class have been introduced to [61] where it was termed by bio-stochastic quadratic operators [62] and [64]. DSQOs have become closely associated with the majorization system [51] and are discussed in connection with other issues in population genetics [54,61]. DSQOs constitute a sub-class of QSOs; the difference being that the DSQOs are well defined by the majorization concept with doubly stochastic matrices. An equational majorization matrix is also termed the welfare operator used for solving economics problems [51]. In addition, the class of CSQO is referred to QSO and has been introduced in [33] where the elements of the matrices are the permutation of the columns of the DeGroot model matrix.
The difference amongst QSOs and DSQOs is that DSQOs refer to the theory of QSOs, including the concepts of majorization theory, written as . The set of DSQO forms come from a polyhedron in the form of nodes or points in dimensional space. The polyhedron has a vertex point that under typical conditions is called the extreme DSQO. The QSO are called DSQO if , where is the symbolization of the majorization theory [53,63,65]. A more general definition and improvement of a necessary and sufficient condition of EDSQO was offered by [61] in relation to bio-stochastic operators. A description of the results and several open problems of the theory of QSOs are discussed in [62]. The concept of a separate class of EDSQO was introduced by [53], who also studied the sufficient settings for EDSQO. In the same study, 37 operators for the permutation of EDSQO on 2D simplex were revealed. Reference [63] introduced the concept of dissipative stochastic operators and proved sufficient conditions for the dissipation of QSOs. Moreover, [63] proved that the number of extreme points in the set of EDSQO is 37, with a total number of 222 extreme points of permutation matrices. The theory of EDSQO, based on the majorization theory, was discussed by [53,65,66], who also established the conditions necessary for EDSQO. The concept of behavior limitation for the trajectories of extreme EDSQO on 2D simplex was first discussed by [67], followed by [68], that the trajectories of some extreme EDSQO tend to center on a 2D simplex and describe an example of Lyapunov for EDSQO on a finite-dimensional simplex.
This research attempts to provide a nonlinear protocol of EDSQO to solve the consensus problems in multi-agent systems. The rest of the paper is structured as follows: Section 2 provides the study background, methods, and theoretical result, while Section 3 offers the discussion and numerical solution of the proposed nonlinear model of EDSQO. Finally, the paper is concluded in Section 4.
2. Background, Methods and Theoretical Result
Linear protocols of the DGL model for the consensus problem have been proposed by [10]. In general, a multi-agent system is understood as a network system of autonomous agent interactions. Each individual agent is supposed to update its state with regard to the roles of protocols received from its neighbors. Agents update their states based on an algorithm by using protocols, and the local interaction between the agents and their neighbors can either be linear or nonlinear. The context of the agents’ states may include opinions, values, beliefs, positions, and velocity. Therefore, the sense of consensus constitutes a convergence of all agent states on a certain value at the same time. This distributed algorithm for calculating the average of the convergence requires each agent to update its status in the form of a convex combination of the present states of its neighbors and its own state. Various studies have focused on consensus problem study. In biology, a dynamic model for the consensus behavior of a school of fish and a flock of birds is presented in the work of [4]. Consensus processes can be used to analyze, expound, and predict the behavior of a flocking group of animals. In control and robotics, agreement problems are revealed in the management and collaboration of agents in sensors and robots. This problem also constitutes a significant issue in the network applications [5,12]. In the area of economics, agreement is used to decide on a common surety in the price process. In the scope of management science, the consensus problem is used to manage a community [10], while in sociology the consensus is essential for any society to develop a common language and dynamics statuses in social networks [69]. In the computer science domain, consensus has been studied by [70].
The DGL linear model supposes that a formal system must consider n agents, which are numbered from 1 to n. Let state scale agent at time . The algorithm of distributed systems can either be continuous or discrete. A general linear model for distributed discrete time presents:
where is the state of an agent vector at time , and is the chain matrix of the system at time . In this stochastic matrix, all elements are positive, and the sum of each row is equal to 1. Here, the sum of each row in the matrix must be equal to 1, and the non-diagonal elements must be non-negative.
Therefore, consensus describes the convergence of initial values of xi to the same certain value at . In this case, the consensus is achieved by the limit existence of all agents. In fact, it gives room for the study of the entire limit behavior of agents using a local interaction among them. This research focuses on the case of discrete distribution.
The research attempts to modify the linear protocols of the DGL model to nonlinear protocols of EDSQO for multi-agent systems. From our point of view, it is convenient to introduce doubly stochastic operators and the majorization concept.
Definition 1.
The nonlinear stochastic operators are defined on a simplex, and thedimensional of the simplex is [62], as
Definition 2.
The simplex interior is a set where }, while the simplex vertices (extreme points) is a set where, …, 0),. However, the simplex center is a set.
Definition 3.
The evaluation of the nonlinear stochastic operators [62] as
where the is the transaction matrix under the condition [62]:
Definition 4.
The agent can be called selfish if, and only if, all interactions are only with itself, where it has infractions with itself and symmetric interactions with others.
Some definitions and preliminary theories of matrices’ conditions and the QSO are required as given in [36].
EDQSO Protocol: EDSQO is a sub-class of DSQO and defined as and in Equation (2):
where is the succession coefficients [62,71] and satisfies the following conditions:
where and are the row and column of the agent’s statuses respectively, and is a transition matrix.
The logical process of this method for EDSQO is as follows:
The evaluation process of the nonlinear consensus of EDQSO can be as follows:
The algorithm of the EDSQO can be shown as:
- Create n agents.
- Initialize the statuses of the agents with random values [0, 1].
- Create a connection among the agents through a transition matrix for each agent; each matrix should include n*n of agents, and be under the condition of Equation (5).
- Evaluate the new agent statuses via Equation (2).
- If these new statuses are fixed, then proceed to step 7.
- Otherwise, go to step 4 and repeat the evaluation with new statuses until step 5 is complete.
- Stop.
Presented below is the theoretical result of the consensus of the proposed nonlinear model of EDSQO, while the proof of the theorems is shown in the Appendix A section. This research presents the protocols of the nonlinear EDSQO model. The following theorems have demonstrated the performance of the EDSQO consensus using Equations (2) and (5) as follows:
Theorem 1.
Assume that a group of agents have to lead a mission at the same time. Then, the group should meet on an agreed decision according to the rules of EDSQO. The limit of statuses will be updated and converge to a consensus of decision if the discussion of each agent member is not selfish.
Theorem 2.
State Theorem 1; if one agent has a selfish discussion in the communications in the agents’ group, under the EDSQO rule this agent will not change its idea, and will not reach a consensus with the other agents.
Theorem 3.
State Theorem 1; if there are two or more agents who have permuted selfish discussions in the gents’ group, under EDSQO rule these agents will keep on changing each other’s ideas and will not reach a consensus.
3. Discussion and Numerical Solution
In this section, the nonlinear EDSQO is evaluated by considering some cases with a varied numbers of agents, the initial status of the agents, and the interaction weight among agents.
- Considering three (3) agents, the simulation result in this example presents Theorem 1.:
The initial statuses:
The interactions’ weight among agents under the rules of EDSQO:
Using Equation (7):
In this case, the consensus is achieved in Figure 1 and is proved by Theorem 1.
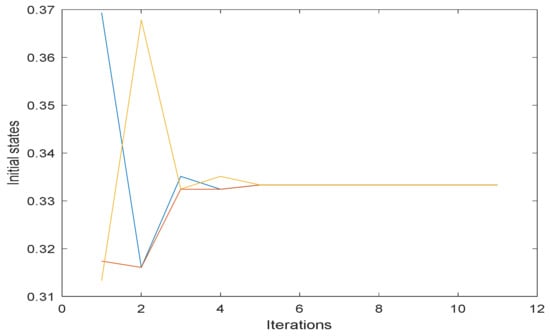
Figure 1.
Extreme points of doubly stochastic quadratic operator (EDSQO) model consensus with three agents.
- 2
- Considering three (3) agents, the simulation result in this example presents Theorems 2 and 3:
The initial statuses:
The interactions’ weight among agents under the rules of EDSQO:
Using Equation (7):
We can see in Figure 2 that the consensus cannot be achieved in this case, as stated in Theorems 2 and 3. The rules that must be applied to avoid this kind of problem will be discussed in Section 3.
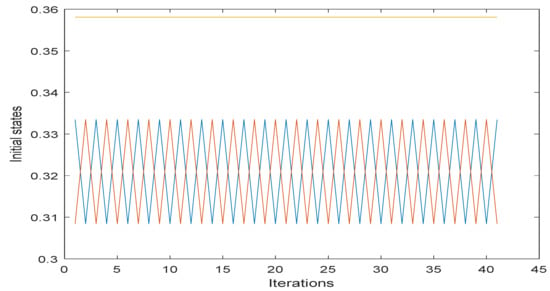
Figure 2.
Selfish and permuted selfish cases of the EDSQO model with three agents.
- 3
- Considering ten (10) agents, the simulation result demonstrates that EDSQO has reached consensus:
In this case, the initial values for ten (10) agents are generated randomly between 0 and 1, where the sum of all initial cases is equal to one. The transition matrices consist of ten (10) distributed matrices under the EDSQO rules, where each matrix is 10 by 10, and the sum of these matrices is a matrix consisting only of ones. In Figure 3, we see that universal consensus is achieved for this number of agents using EDSQO.
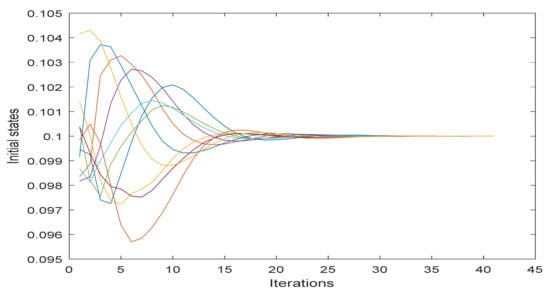
Figure 3.
EDSQO model consensus with 10 agents.
- 4
- Considering 50 agents, the simulation result in this example presents that EDSQO has reached consensus.
In this case, the initial values for 50 agents are generated randomly between 0 and 1, where the sum of all initial cases is equal to one. The transition matrices are also 50 distributed matrices under the EDSQO rules where the size of each matrix is 50 by 50, and the sum of these matrices being a matrix with all elements are equal to one. In Figure 4, we see that universal consensus is also achieved for 50 agents using EDSQO.
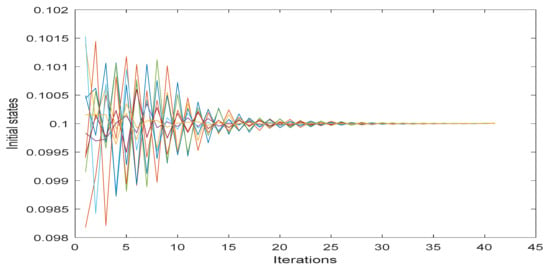
Figure 4.
EDSQO model consensus with 50 agents.
- 5
- Considering 100 agents, the simulation result in this example demonstrates that EDSQO has reached consensus.
In this case, the initial values for 100 agents are generated randomly between 0 and 1, where the sum of all initial cases is equal to one. The transition matrices are also 100 distributed matrices under the EDSQO rules where each matrix is 100 by 100, the sum of these matrices being a matrix with all elements equal to one. In Figure 5, we see that universal consensus is achieved for 100 agents using EDSQO.
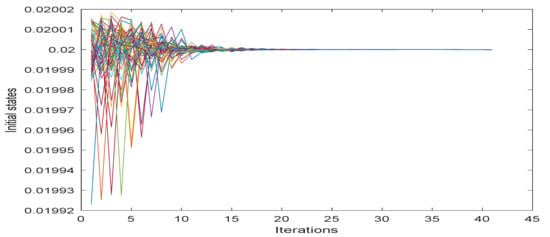
Figure 5.
EDSQO model consensus with 100 agents.
We can observe that there are two priority features that make this model preferable to others. The first priority feature is that the EDSQO model is a nonlinear model, since nonlinear mathematical models are capable of performing highly complex tasks [3]. Thus, researchers are now moving to work with nonlinear models rather than linear models, due to the fact that they perform better and tend to be more robust than the linear model, in addition to the linear consensus displaying certain weaknesses in physical systems [71,72,73]. This prompted the researcher of the present study to create a nonlinear model. The second priority is that most nonlinear models can execute complex and difficult calculations, even though this proposed EDSQO model is less complicated than other nonlinear models when compared to DSQO and CSQO. Here, the transection matrices in EDSQO consists only of 1’s, 0.5’s and 0’s, while in DSQO the transection matrices consists of 0–1. In this study, we have tried to create a mathematical model that acquires two important characteristics for the consensus problem in multi-agent systems.
Using this EDSQO model in all the studied cases, the consensus has been achieved and the central issue for MAS has been signed. The mathematical protocol constitutes the core operation in order to achieve the agreement. In general, a mathematical protocol can be for a nonlinear or a linear model, although the nonlinear model performs more efficiently in realizing the convergence consensus for the network of agents, the point being that designing a nonlinear model constitutes nevertheless a considerable challenge, especially when it comes to soft computation. Furthermore, research into nonlinear models is still a relatively young and unexplored field. In this study, a novel nonlinear consensus model (EDSQO) is built for Mas with low complicity, which refers to quadratic stochastic operators. The proposed nonlinear model of EDSQO will be evaluated in Section 4 where we compare linear and nonlinear consensus models and demonstrate the efficiency of the nonlinear model. It will be concluded that EDSQO achieves the consensus faster than linear models like DGL and has a lower computational complexity than CSQO and DSQO.
In order to prevent MAS from not achieving the consensus through EDSQO, the interaction of each agent should not be selfish, as this would lead to a situation where the transition matrix for this agent has interacted only with itself. This means that the transition matrices should not be the following:
where is the number of columns, is the number of rows, and the number of agents.
In our view, it is better to show the evaluation of the proposed nonlinear consensus model of EDSQ with the same structure theory models of DGL [10], CSQO [33] and DSQO [74]. Each Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 presents the consensus of DGL model, CSQO, DSQO and EDSQO, respectively. It should be noted that each Figure consists of diverse random initial statuses. In addition, the computational complexity of EDSQO is less than CSQO and DSQO, EDSQO being a nonlinear model and DGL being a linear model.
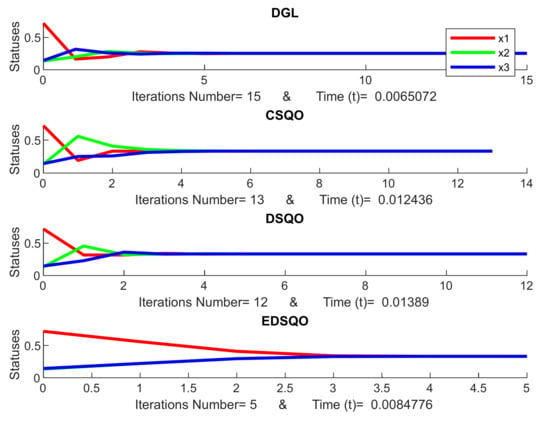
Figure 6.
Consensus of DeGroot linear (DGL), cubic stochastic quadratic operators (CSQO), doubly stochastic quadratic operators (DSQO), and EDSQO.
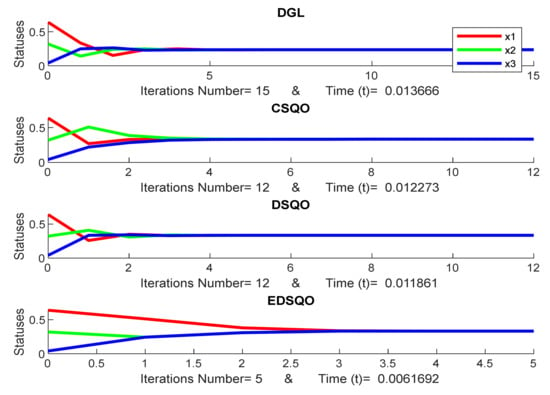
Figure 7.
Consensus of DGL, CSQO, DSQO, and EDSQO.
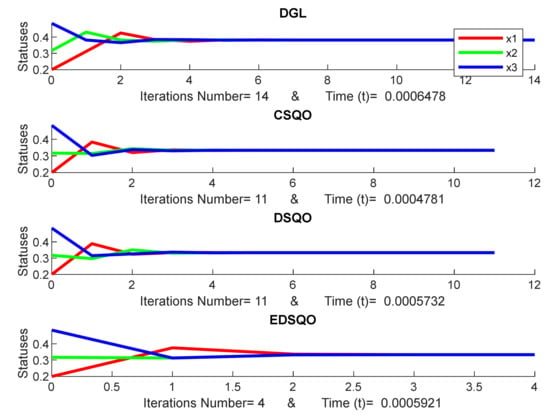
Figure 8.
Consensus of DGL, CSQO, DSQO, and EDSQO.
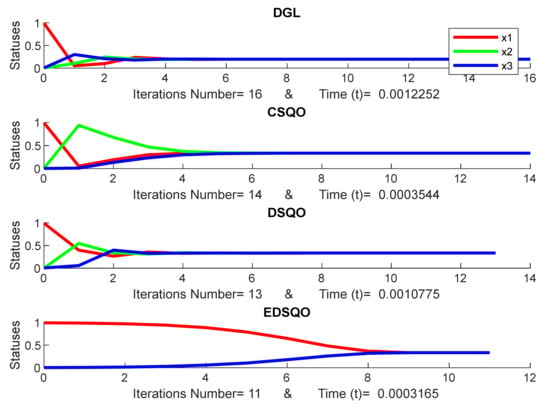
Figure 9.
Consensus of DGL, CSQO, DSQO, and EDSQO.
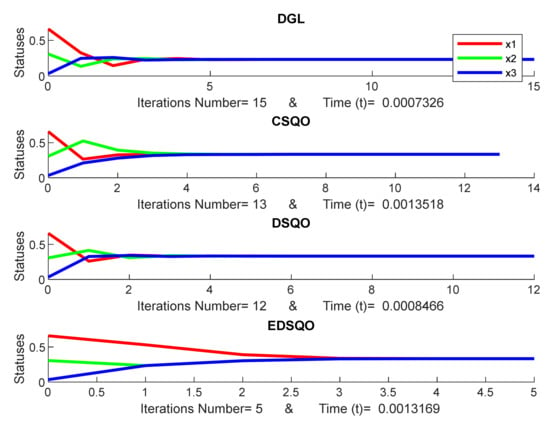
Figure 10.
Consensus of DGL, CSQO, DSQO, and EDSQO.
The initial statuses are the same in each Figure. For example, the initial statuses are the same for the models of DGL, CSQO, DSQO and EDSQO in Figure 6 as well as Figure 7, Figure 8, Figure 9 and Figure 10. However, the initial statuses among Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 are different, while the scale of the number of iterations is based on the model where the consensus can be reached. Therefore, the scale of the iterations number is different for each model. Given their different rules, some models require more iterations, while others require less. Therefore, the proposed model of EDSQO will be evaluated with other consensus models such as DGL, CSQO, and DSQO.
Table 1 and Figure 11 present the evaluation of the iteration number of the proposed consensus models of EDSQO with the consensus models of DGL, CSQO and DSQO. The iteration number of EDSQO is the lowest, with an average of 5.272, while DGL, CSQO, DSQO present an average of 15.885, 12.298, 11.661 iterations respectively. The statistical result has been conducted in Supplementary Materials (Table S2) based on a total of 1000 simulations. Additionally, the evaluation of the computational time of the proposed consensus models of EDSQO in comparison to the consensus models of DGL, CSQO and DSQO is necessary. Here, the result shows that the computation time of EDSQO is the lowest, with an average of 4.73558E-05 seconds, whereas DGL, CSQO, DSQO average at 1.05E-04, 7.1223E-05, 6.81909E-05 seconds, respectively. The computation time required is listed in Supplementary Materials (Table S3). These results are also based on a total of 1000 simulations. Note that if the consensus of EDSQO requires more iterations, the computation time is still less.

Table 1.
Evaluation of DGL, CSQO, DSQO, and EDSQO consensus.
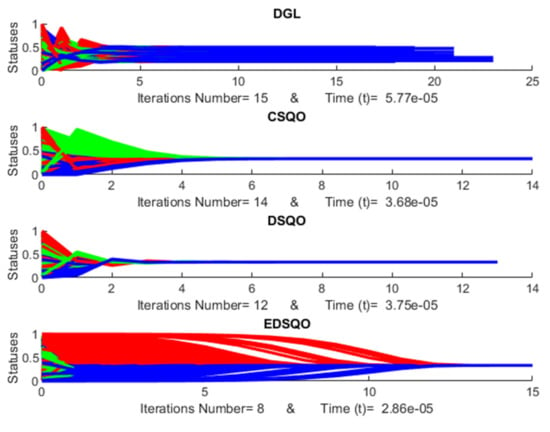
Figure 11.
Consensus of DGL, CSQO, DSQO, and EDSQO for three (3) agents 1000 times with different initial statuses.
From the comparison result, the following evaluation table can be produced:
4. Conclusions
A new nonlinear class protocol of EDSQO for multi-agent systems has been proposed in this paper. In general, the nonlinear EDSQO model is presented as a modification of the DGL linear model. The agents update their information through local interaction and connection by limiting the trajectory of the extreme EDSQO on a finite-dimensional simplex. This study proves that multi-agent systems converge to a consensus using EDSQO, according to the specific majorization condition that the dissection for each agent is not selfish. Furthermore, the numerical solutions have been tested and studied. This work can be used as a reference in modeling a solution to a consensus problem in multi-agent systems.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-8994/12/4/540/s1, Supplementary Materials Table S2: The average of number iterations for 1000 times for the consensus of DGL, CSQO, DSQO, and EDSQO, Table S3: The average of computation time for 1000 times for the consensus of DGL, CSQO, DSQO, and EDSQO.
Author Contributions
Conceptualization, R.A.; methodology, R.A.; software, R.A.; validation, H.A. and B.A.; formal analysis, R.A.; investigation, R.A.; resources, S.A.; writing—original draft preparation, R.A.; writing—review and editing, A.B., and S.S.A., H.A. and B.A.; visualization, S.A.; supervision, R.A.; project administration, S.A.; funding acquisition, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Majmaah University under grant number [RGP-2019-29].
Acknowledgments
First, the authors would like to thank the Faculty of Information and Communication Technology, International Islamic University Malaysia. Additionally, the authors extend their appreciation to the Deanship of Scientific Research at Majmaah University for funding this work under project number NO (RGP-2019-29).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Proof of Theorem 1.
Let be EDSQO, based on majorization condition [53], where
Hence,
The condition of the theorem is that if for and sequences for all meet at the average . On the other hand, let be a cubic stochastic for transaction matrix of heterogeneous individuals based on majorization conditions. Then, is a transition matrix in stochastic case, where
The dynamics’ local interaction among agents in this situation can clear as follows:
If the series of the continued local communications of agents closes and towards to a common value, then will be fixed at this value.
Let be a process of to evaluate the consensus of the agents.
Suppose that for all . If , which, , such that .
Hence, , which means that as is the chains limit of and , thus screening that impossible can be . □
Proof of Theorem 2.
Assume that some agents collaborate to lead a mission at the same time. Consequently, the group should meet and perform local dissection where this communication is considered evolution matrix .
We assign the local communication to a nonlinear evaluator where the weightage communications by as:
where and are the communicated agents, and is the member mission.
Subsequently, the process to evaluate the consensus is defined via the EDSQO protocol, where the weightage of the communications among the agents is only 0 or or 1.
Since the evaluator protocol EDSQ is nonlinear, each member agent has its special communication of transition matrix , where the matrices of all agents form a matrix whose elements are equal to 1. Then, the agents group update their statuses of dissection by
If one agent has a selfish discussion, it follows that
This means that
Refer to Equation (2);
Therefore, we have
which means that the status of this agent does not change.
Therefore, the member agent is selfish and does not change its decision. □
Proof of Theorem 3.
This step is similar to the proof of Theorem 2, but here we assume that the selfish agents are two or more, and that there are interactions among them.
Hence,
This means that
Refer to Equation (2);
After the first iteration we have
After the second iteration we have
After the third iteration we have
Thus, similar results are obtained in all the iterations. The outcomes are found to be similar for further iterations as well. Therefore, and are periodic points.
The members of and keep recycling, and change their decision without fixed negotiation and without converging on a specific decision. □
References
- Ren, W.; Beard, R.W.; Atkins, E.M. A survey of consensus problems in multi-agent coordination. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 1859–1864. [Google Scholar]
- Shi, G.; Johansson, K.H.; Hong, Y. Reaching an optimal consensus: Dynamical systems that compute intersections of convex sets. IEEE Trans. Autom. Control 2013, 58, 610–622. [Google Scholar] [CrossRef]
- Lin, Z.; Francis, B.; Maggiore, M. State agreement for continuous-time coupled nonlinear systems. SIAM J. Control Optim. 2007, 46, 288–307. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 1995, 75, 1226. [Google Scholar] [CrossRef]
- Tsitsiklis, J.; Bertsekas, D.; Athans, M. Distributed asynchronous deterministic and stochastic gradient optimization algorithms. IEEE Trans. Autom. Control 1986, 31, 803–812. [Google Scholar] [CrossRef]
- Fax, J.A.; Murray, R.M. Information flow and cooperative control of vehicle formations. IEEE Trans. Autom. Control 2004, 49, 1465–1476. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Shang, Y.; Bouffanais, R. Influence of the number of topologically interacting neighbors on swarm dynamics. Sci. Rep. 2014, 4, 4184. [Google Scholar] [CrossRef]
- Eisenberg, E.; Gale, D. Consensus of subjective probabilities: The pari-mutuel method. Ann. Math. Stat. 1959, 30, 165–168. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Berger, R.L. A necessary and sufficient condition for reaching a consensus using DeGroot’s method. J. Am. Stat. Assoc. 1981, 76, 415–418. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Saber, R.O.; Murray, R.M. Consensus protocols for networks of dynamic agents. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, USA, 4–6 June 2003; IEEE: Piscatway, NJ, USA, 2003; pp. 951–956. [Google Scholar]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Moreau, L. Stability of multiagent systems with time-dependent communication links. IEEE Trans. Autom. Control 2005, 50, 169–182. [Google Scholar] [CrossRef]
- Lyubich, Y.I.; Vulis, D.; Karpov, A.; Akin, E. Mathematical structures in population genetics. Biomathematics 1992, 22, 373. [Google Scholar]
- Tsitsiklis, J.N. Problems in Decentralized Decision Making and Computation; Massachusetts Inst of Tech Cambridge Lab for Information and Decision Systems: Cambridge, MA, USA, 1984. [Google Scholar]
- Blondel, V.D.; Hendrickx, J.M.; Olshevsky, A.; Tsitsiklis, J.N. Convergence in multiagent coordination, consensus, and flocking. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 2996–3000. [Google Scholar]
- Olshevsky, A.; Tsitsiklis, J.N. Convergence speed in distributed consensus and averaging. SIAM Rev. 2011, 53, 747–772. [Google Scholar] [CrossRef]
- Nedić, A.; Ozdaglar, A. Convergence rate for consensus with delays. J. Glob. Optim. 2010, 47, 437–456. [Google Scholar] [CrossRef]
- Nedic, A.; Ozdaglar, A. Distributed subgradient methods for multi-agent optimization. IEEE Trans. Autom. Control 2009, 54, 48–61. [Google Scholar] [CrossRef]
- Xiao, L.; Boyd, S. Fast linear iterations for distributed averaging. Syst. Control Lett. 2004, 53, 65–78. [Google Scholar] [CrossRef]
- Kokotović, P.; Arcak, M. Constructive nonlinear control: A historical perspective. Automatica 2001, 37, 637–662. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M.; Kurths, J. Second-order consensus for multiagent systems with directed topologies and nonlinear dynamics. IEEE Trans. Syst. Man Cybern. Part B 2010, 40, 881–891. [Google Scholar]
- Bolouki, S. Linear Consensus Algorithms: Structural Properties and Connections with Markov Chains. Ph.D. Thesis, École Polytechnique de Montréal, Montréal, QC, Canada, 2014. [Google Scholar]
- Georgopoulos, L.; Hasler, M. Nonlinear average consensus. In Proceedings of the 2009 International Symposium on Nonlinear Theory and Its Applications, Sapporo, Japan, 19–21 October 2009; pp. 10–13. [Google Scholar]
- Roshanzamir, A.; Piltan, F.; Jahed, A.; Namvarchi, S.; Sulaiman, N.B.; Nazari, I. Research on Nonlinear Automation for First Order Delays System. Int. J. Hybrid Inf. Technol. 2015, 8, 313–328. [Google Scholar] [CrossRef]
- Schwarz, V.; Matz, G. Nonlinear average consensus based on weight morphing. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3129–3132. [Google Scholar]
- Meng, D.; Jia, Y.; Du, J.; Zhang, J. On iterative learning algorithms for the formation control of nonlinear multi-agent systems. Automatica 2014, 50, 291–295. [Google Scholar] [CrossRef]
- Buşoniu, L.; Morărescu, I.C. Consensus for black-box nonlinear agents using optimistic optimization. Automatica 2014, 50, 1201–1208. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Othman, M. An overview of the consensus problem in the control of multi-agent systems. Automatika 2018, 59, 143–157. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Zeki, A.; Al-Shaikhli, I. Linear and nonlinear stochastic distribution for consensus problem in multi-agent systems. Neural Comput. Appl. 2018, 32, 261–277. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Almotairi, S.; Almohamedh, H.; Turaev, S.; Almutairi, B. Nonlinear Consensus Protocol Modified from Doubly Stochastic Quadratic Operators in Networks of Dynamic Agents. Symmetry 2019, 11, 1519. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Shahidi, F.; Zeki, A.; Turaev, S. Dynamics of doubly stochastic quadratic operators on a finite-dimensional simplex. Open Math. 2016, 14, 509–519. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Hassan, R. The nonlinear limit control of EDSQOs on finite dimensional simplex. Automatika 2019, 60, 404–412. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S. Consensus of fractional nonlinear dynamics stochastic operators for multi-agent systems. Inf. Fusion 2018, 44, 1–21. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Zeki, A.; Abubaker, A. Nonlinear convergence algorithm: Structural properties with doubly stochastic quadratic operators for multi-agent systems. J. Artif. Intell. Soft Comput. Res. 2018, 8, 49–61. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Tamrin, M.; Izzuddin, M. Nonlinear consensus for multi-agent systems using positive intractions of doubly stochastic quadratic operators. Int. J. Perceptive Cogn. Comput. 2016, 2, 19–22. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Zeki, A. Necessary and Sufficient Conditions for Complementary Stochastic Quadratic Operators of Finite-Dimensional Simplex. Sukkur IBA J. Comput. Math. Sci. 2017, 1, 22–27. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Abubakar, A.; Zeki, A. The extreme doubly stochastic quadratic operators on two dimensional simplex. In Proceedings of the 2015 4th International Conference on Advanced Computer Science Applications and Technologies (ACSAT), Kuala Lumpur, Malaysia, 8–10 December 2015; pp. 192–197. [Google Scholar]
- Abdulghafor, R.; Turaev, S.; Zeki, A. The Convergence Consensus of Multi-agent Systems Controlled via Doubly Stochastic Quadratic Operators. Int. J. Control 2018, 22, 1–21. [Google Scholar]
- Abdulghafor, R.; Turaev, S.; Izzuddin, M. Nonlinear Models for Distributed Consensus Modified from DSQO in Networks of Dynamic Agents. In Proceedings of the 4th International Conference on Mathematical Sciences, Kuala Lumpur, Malaysia, 8–10 December 2015. [Google Scholar]
- Helman, P.; Moret, B.M.E.; Shapiro, H.D. An exact characterization of greedy structures. SIAM J. Discret. Math. 1993, 6, 274–283. [Google Scholar] [CrossRef]
- Gąsieniec, L.; Wolter, F. Fundamentals of Computation Theory. In Proceedings of the 19th International Symposium, FCT 2013, Liverpool, UK, 19–21 August 2013; Volume 8070, ISBN 3642401643. [Google Scholar]
- Lawler, E.L. Submodular functions and polymatroid optimization. M. O’hEigeartaigh, JK Lenstra Ed. Comb. Optim. Annot. Bibliogr. 1985, 32–38. [Google Scholar]
- Lovász, L. Submodular functions and convexity. Math. Program. State Art 1982, 235–257. [Google Scholar]
- Parker, D.S.; Ram, P. Creed and Majorization; Computer Science Department, University of California. 1994. [Google Scholar]
- Bernstein, S. Solution of a mathematical problem connected with the theory of heredity. Ann. Math. Stat. 1942, 13, 53–61. [Google Scholar] [CrossRef]
- Vallander, S.S. On the limit behavior of iteration sequence of certain quadratic transformations. Soviet Math. Dokl. 1972, 13, 123–126. [Google Scholar]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Shahidi, F. On dissipative quadratic stochastic operators. ArXiv 2007, arXiv:0708.1813. Available online: https://arxiv.org/abs/0708.1813 (accessed on 3 April 2020).
- Ganikhodzhaev, R.; Shahidi, F. Doubly stochastic quadratic operators and Birkhoff’s problem. Linear Algebra Appl. 2010, 432, 24–35. [Google Scholar] [CrossRef][Green Version]
- Ganikhodzhaev, R.N. Quadratic stochastic operators, Lyapunov functions, and tournaments. Russ. Acad. Sci. Sb. Math. 1993, 76, 489. [Google Scholar] [CrossRef]
- Ando, T. Majorization, doubly stochastic matrices, and comparison of eigenvalues. Linear Algebra Appl. 1989, 118, 163–248. [Google Scholar] [CrossRef]
- Muirhead, R.F. Some methods applicable to identities and inequalities of symmetric algebraic functions of n letters. Proc. Edinburgh Math. Soc. 1902, 21, 144–162. [Google Scholar] [CrossRef]
- Lorenz, M.O. Methods of measuring the concentration of wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar] [CrossRef]
- Dalton, H. The measurement of the inequality of incomes. Econ. J. 1920, 30, 348–361. [Google Scholar] [CrossRef]
- Schur, I. Uber eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie. Sitz. Der Berl. Math. Ges. 1923, 22, 9–20. [Google Scholar]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Some simple inequalities satisfied by convex functions. Messenger Math 1929, 58, 310. [Google Scholar]
- Ganikhodzhaev, R.N. On the definition of bistochastic quadratic operators. Russ. Math. Surv. 1993, 48, 244–246. [Google Scholar] [CrossRef]
- Ganikhodzhaev, R.N.; Rozikov, U.A. Quadratic stochastic operators: Results and open problems. ArXiv 2009, arXiv:0902.4207. Available online: https://arxiv.org/abs/0902.4207 (accessed on 3 April 2020). [CrossRef]
- Shahidi, F. On the extreme points of the set of bistochastic operators. Math. Notes 2008, 84, 442–448. [Google Scholar] [CrossRef]
- Mukhamedov, F.; Embong, A.F. On b-bistochastic quadratic stochastic operators. J. Inequal. Appl. 2015, 2015, 226. [Google Scholar] [CrossRef]
- Shahidi, F.A. Doubly stochastic operators on a finite-dimensional simplex. Sib. Math. J. 2009, 50, 368–372. [Google Scholar] [CrossRef]
- Shahidi, F. Necessary and sufficient conditions for doubly stochasticity of infinite-dimensional quadratic operators. Linear Algebra Appl. 2013, 438, 96–110. [Google Scholar] [CrossRef]
- Shahidi, F.; Ganikhodzhaev, R.; Abdulghafor, R. The Dynamics of Some Extreme Doubly Stochastic Quadratic Operators. Middle-East J. Sci. Res. 2013, 13, 59–63. [Google Scholar]
- Abdulghafor, R.; Shahidi, F.; Zeki, A.; Turaev, S. Dynamics classifications of extreme doubly stochastic quadratic operators on 2d simplex. In Advanced Computer and Communication Engineering Technology; Springer: Cham, Switzerland, 2016; pp. 323–335. [Google Scholar]
- Cucker, F.; Smale, S.; Zhou, D.-X. Modeling language evolution. Found. Comput. Math 4. 2004, 3, 315–343. [Google Scholar] [CrossRef]
- Lynch, N.A. Distributed Algorithms; Morgan Kaufmann: Burlington, MA, USA, 1996; ISBN 0080504701. [Google Scholar]
- Cui, G.; Xu, S.; Lewis, F.L.; Zhang, B.; Ma, Q. Distributed consensus tracking for non-linear multi-agent systems with input saturation: A command filtered backstepping approach. IET Control Theory Appl. 2016, 10, 509–516. [Google Scholar] [CrossRef]
- Yu-Mei, L.; Xin-Ping, G. Nonlinear consensus protocols for multi-agent systems based on centre manifold reduction. Chin. Phys. B 2009, 18, 3355. [Google Scholar] [CrossRef]
- Li, Y.; Guan, X.; Hua, C. Nonlinear protocols for output performance value consensus of multi-agent systems. In Proceedings of the 30th Chinese Control Conference (CCC), Yantai, China, 22–24 July 2011; pp. 4831–4834. [Google Scholar]
- Abdulghafor, R.; Turaev, S.; Zeki, A.; Al-Shaikhli, I. Reach a nonlinear consensus for MAS via doubly stochastic quadratic operators. Int. J. Control 2018, 91, 1431–1459. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).