On Symmetry Properties of The Corrugated Graphene System
Abstract
1. Introduction
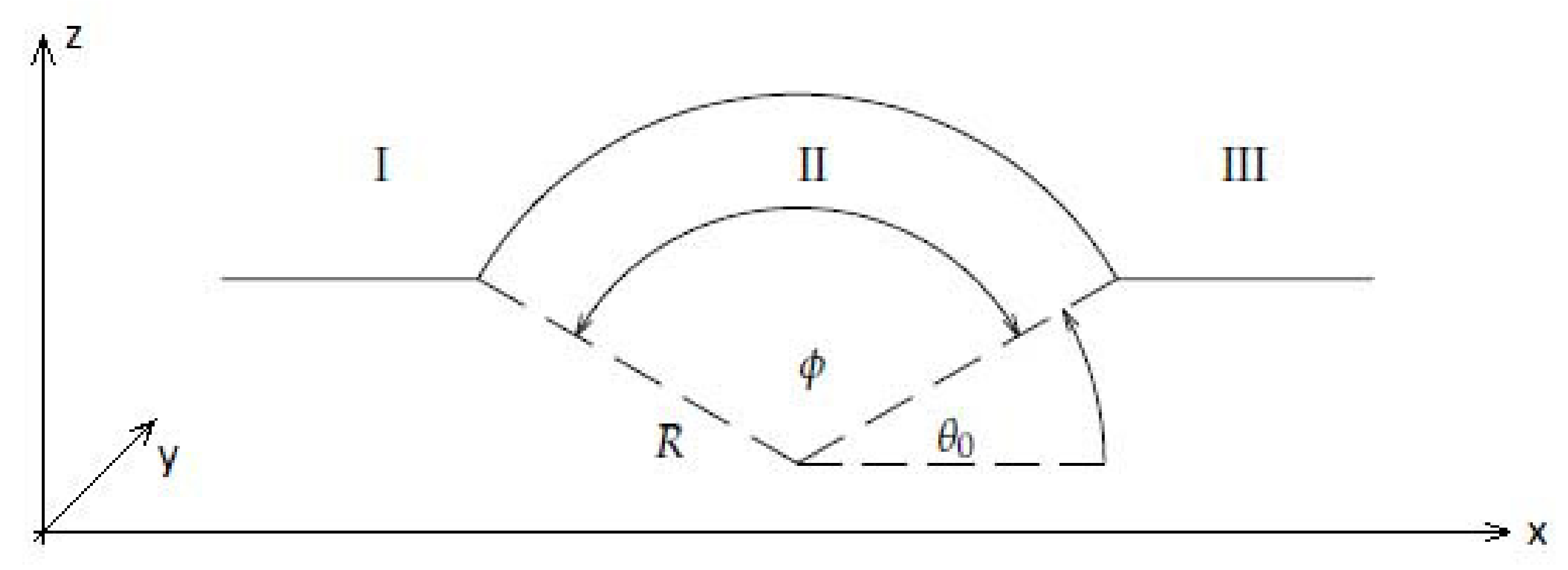
2. Basic Physics of The Corrugated Graphene
3. Symmetries
3.1. The Operator
- at the boundary between Region I and II
- at the boundary between Region II and III
- at the boundary between Regions II and III
- at the boundary between Regions I and II
3.2. The Operator
- 1.
- Quantum numbers: , . These quantum numbers determine the available set of the wave functions: , ,. If the corresponding symmetries are responsible for the transport properties, there are only the following options.
- (a)
- The electron is moving from the left side of our structure (flat graphene sheet) with the spin up polarisation []. In this case, in the rippled graphene region (see Figure 2), there is one open channel, defined by the wave function . The wave function describes the reflection with the electron spin–flip.
- (b)
- The electron is moving from the right side (flat graphene sheet) with the spin down polarisation []. In this case, in the rippled graphene region, there is only the transmission channel, defined by the wave function . The wave function describes the reflection with the electron spin–flip.
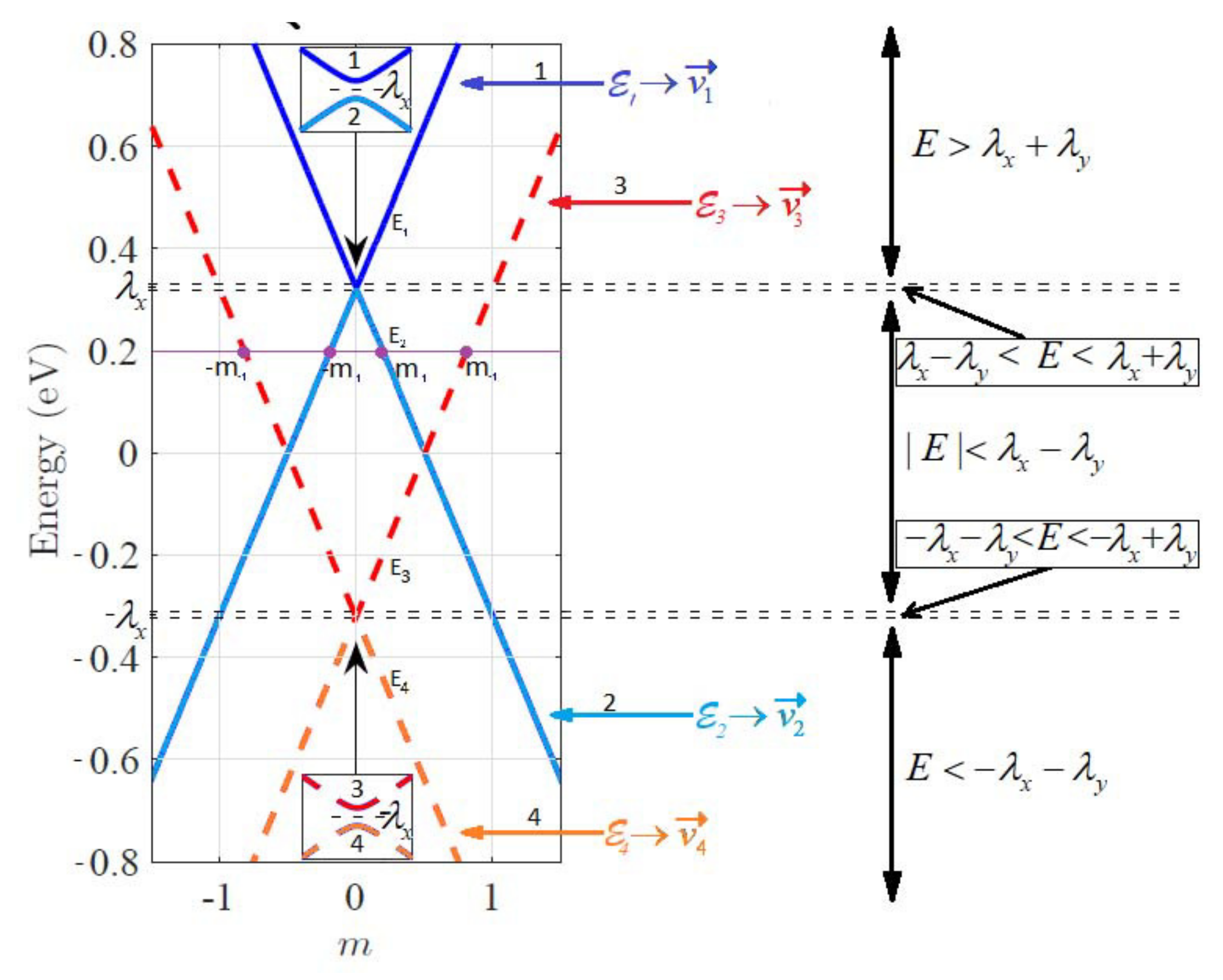
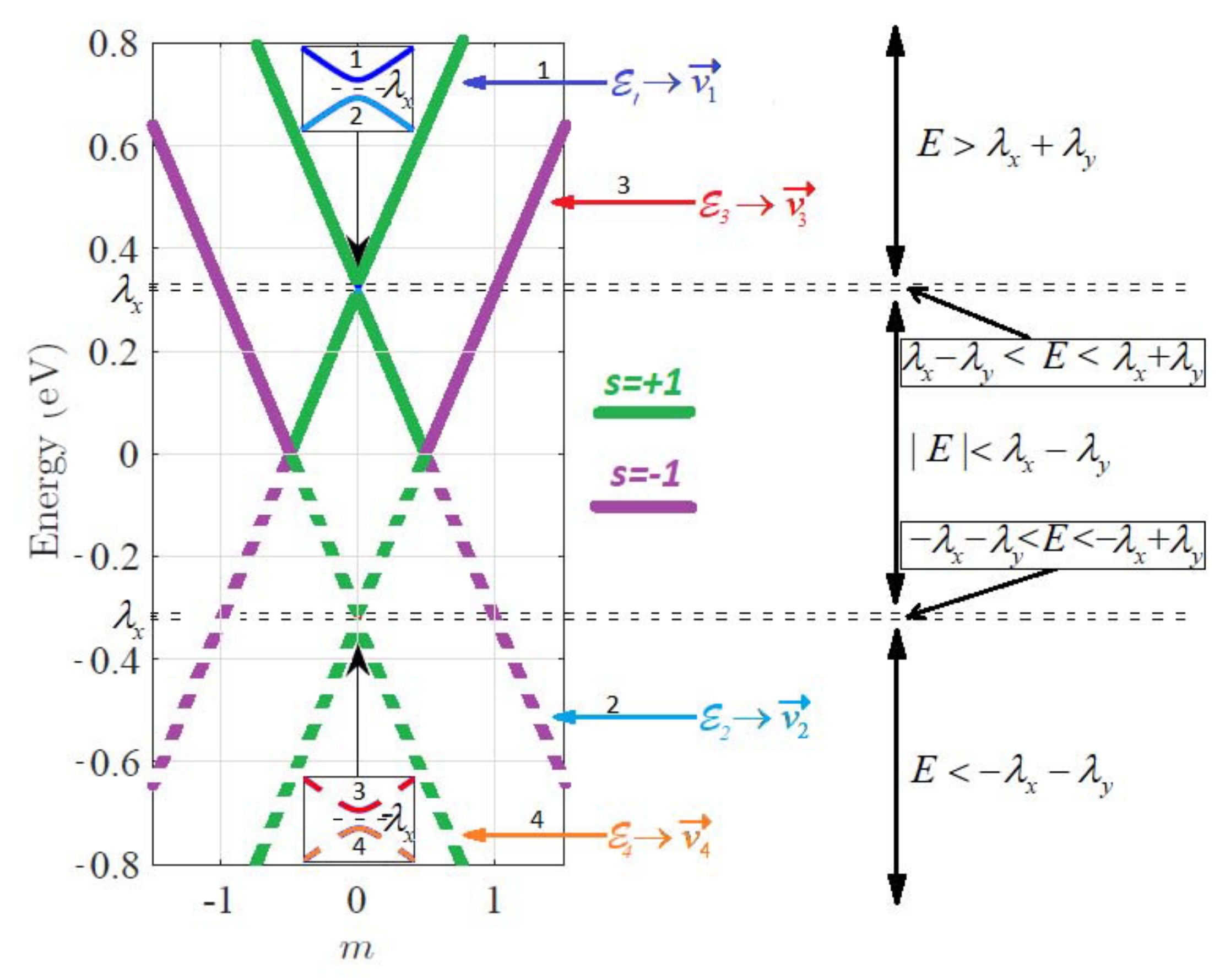
As a result, we expect the equivalence between the left/right transmission probabilities with the opposite spin polarisations. Indeed, this expectation is consistent with Equation (33), obtained from the different arguments at . - 2.
- Quantum numbers: , . The available set of the wave functions: , , . In this case, the symmetries dictate the following options.
- (a)
- The electron is moving from the left side (flat graphene sheet) with the spin down polarisation []. In this case, in the rippled graphene region (see Figure 2), there is one open channel, defined by the wave function . The wave function describes the reflections with the electron spin–flip.
- (b)
- The electron is moving from the right side (flat graphene sheet) with the spin up polarisation []. In this case, in the rippled graphene region for this electron there is only the transmission channel, defined by the wave function . The wave function describes the reflections with the electron spin–flip.
Again, we expect the equivalence between the left/right transmission probabilities with the opposite spin polarisations. Indeed, this expectation is consistent with Equation (35), obtained from different arguments at .
- 1.
- Quantum numbers: , . In this case, the available set includes the following wave functions: , , . The symmetries dictate the following options.
- (a)
- The electron is moving from the left side (flat graphene sheet) with the spin down polarisation []. In the rippled graphene region, there is only the transmission channel, defined by the wave function . The wave function describes the reflections with the electron spin–flip.
- (b)
- The electron is moving from the right side (flat graphene sheet) with the spin up polarisation []. In the rippled graphene region, there is only the transmission channel, defined by the wave function . The wave function describes the reflections with the electron spin–flip.
Again, the expected equivalence between the left/right transmission probabilities with the opposite spin polarisations is consistent with Equation (35), obtained from different arguments at . - 2.
- Quantum numbers: , . In this case, the available set includes the following wave functions: , , . This situation is completely equivalent to the case discussed at , Point 1.
Thus, at , the symmetry, associated with the operator , determines the following transport properties through the rippled graphene piece: (i) at the transmission, it preserves the electron spin polarisation, while forbids the spin–flip; and (ii) the reflection occurs only with the spin–flip.
3.3. The Relation Between the Operators and
4. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, S.; Parks, D.M. Strain Shielding from Mechanically Activated Covalent Bond Formation during Nanoindentation of Graphene Delays the Onset of Failure. Nano Lett. 2015, 15, 1503–1510. [Google Scholar] [CrossRef]
- Cao, K.; Feng, S.; Han, Y.; Gao, L.; Hue, L.T.; Xu, Z.; Lu, Y. Elastic straining of free-standing monolayer graphene. Nat. Commun. 2020, 11, 284. [Google Scholar] [CrossRef]
- Alyobi, M.M.; Barnett, C.J.; Rees, P.; Cobley, R.J. Modifying the electrical properties of graphene by reversible point-ripple formation. Carbon 2019, 143, 762–768. [Google Scholar] [CrossRef]
- Vázquez de Parga, A.L.; Calleja, F.; Borca, B.; Passeggi, M.C.G.; Hinarejos, J.J.; Guinea, F.; Miranda, R. Periodically Rippled Graphene: Growth and Spatially Resolved Electronic Structure. Phys. Rev. Lett. 2008, 100, 056807. [Google Scholar] [CrossRef]
- Maccariello, D.; Al Taleb, A.; Calleja, F.; Vázquez de Parga, A.L.; Perna, P.; Camarero, J.; Gnecco, E.; Farías, D.; Miranda, R. Observation of Localized Vibrational Modes of Graphene Nanodomes by Inelastic Atom Scattering. Nano Lett. 2016, 16, 2–7. [Google Scholar] [CrossRef]
- Politano, A.; Chiarello, G. Plasmon modes in graphene: Status and prospect. Nanoscale 2014, 6, 10927–10940. [Google Scholar] [CrossRef]
- Ni, G.X.; Zheng, Y.; Bae, S.; Kim, H.R.; Pachoud, A.; Kim, Y.S.; Tan, C.L.; Im, D.; Ahn, J.H.; Hong, B.H.; et al. Quasi-Periodic Nanoripples in Graphene Grown by Chemical Vapor Deposition and Its Impact on Charge Transport. ACS Nano 2012, 6, 1158–1164. [Google Scholar] [CrossRef]
- Vasić, B.; Zurutuza, A.; Gajić, R. Spatial variation of wear and electrical properties across wrinkles in chemical vapour deposition graphene. Carbon 2016, 102, 304–310. [Google Scholar] [CrossRef]
- Pudlak, M.; Nazmitdinov, R.G. Klein collimation by rippled graphene superlattice. J. Phys. Cond. Matter 2019, 31, 495301. [Google Scholar] [CrossRef]
- Guinea, F.; Katsnelson, M.I.; Vozmediano, M.A.H. Midgap states and charge inhomogeneities in corrugated graphene. Phys. Rev. B 2008, 77, 075422. [Google Scholar] [CrossRef]
- Katsnelson, M.; Geim, A. Electron scattering on microscopic corrugations in graphene. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 366, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Ando, T. Spin-Orbit Interaction in Carbon Nanotubes. J. Phys. Soc. Jpn. 2000, 69, 1757–1763. [Google Scholar] [CrossRef]
- Pudlak, M.; Pichugin, K.N.; Nazmitdinov, R.G. Cooperative phenomenon in a rippled graphene: Chiral spin guide. Phys. Rev. B 2015, 92, 205432. [Google Scholar] [CrossRef]
- Smotlacha, J.; Pudlak, M.; Nazmitdinov, R.G. Spin transport in a rippled graphene periodic chain. J. Phys. Conf. Ser. 2019, 1416, 012035. [Google Scholar] [CrossRef]
- Izumida, W.; Sato, K.; Saito, R. Spin–Orbit Interaction in Single Wall Carbon Nanotubes: Symmetry Adapted Tight-Binding Calculation and Effective Model Analysis. J. Phys. Soc. Jpn. 2009, 78, 074707. [Google Scholar] [CrossRef]
- Del Valle, M.; Margańska, M.; Grifoni, M. Signatures of spin-orbit interaction in transport properties of finite carbon nanotubes in a parallel magnetic field. Phys. Rev. B 2011, 84, 165427. [Google Scholar] [CrossRef]
- Pichugin, K.N.; Pudlak, M.; Nazmitdinov, R.G. Spin-orbit effects in carbon nanotubes—Analytical results. Eur. Phys. J. B 2014, 87, 124. [Google Scholar] [CrossRef][Green Version]
- Michaeli, K.; Kantor-Uriel, N.; Naaman, R.; Waldeck, D.H. The electron’s spin and molecular chirality—How are they related and how do they affect life processes? Chem. Soc. Rev. 2016, 45, 6478–6487. [Google Scholar] [CrossRef]
- Nazmitdinov, R.G. From Chaos to Order in Mesoscopic Systems. Phys. Part. Nucl. Letts. 2019, 16, 159–169. [Google Scholar] [CrossRef]
- Birman, J.; Nazmitdinov, R.; Yukalov, V. Effects of symmetry breaking in finite quantum systems. Phys. Rep. 2013, 526, 1–91. [Google Scholar] [CrossRef]
- Foa Torres, L.E.F.; Roche, S.; Charlier, J.C. Introduction to Graphene-Based Nanomaterials: From Electronic Structure to Quantum Transport; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Katsnelson, M.I. Graphene: Carbon in Two Dimensions; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Sakurai, J.J. Modern Quantum Mechanics, Revised Edition; Addison-Wesley: Reading, MA, USA, 1994. [Google Scholar]
- Bohr, A.; Mottelson, B. Nuclear Structure; Number v. 1 in Nuclear Structure; World Scientific: Singapore, 1998. [Google Scholar]
- Busa, J.; Pudlak, M.; Nazmitdinov, R.G. On Electron Scattering through a Single Corrugated Graphene Sructure. Phys. Part. Nucl. Lett. 2019, 16, 729–733. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pudlak, M.; Smotlacha, J.; Nazmitdinov, R. On Symmetry Properties of The Corrugated Graphene System. Symmetry 2020, 12, 533. https://doi.org/10.3390/sym12040533
Pudlak M, Smotlacha J, Nazmitdinov R. On Symmetry Properties of The Corrugated Graphene System. Symmetry. 2020; 12(4):533. https://doi.org/10.3390/sym12040533
Chicago/Turabian StylePudlak, Mihal, Jan Smotlacha, and Rashid Nazmitdinov. 2020. "On Symmetry Properties of The Corrugated Graphene System" Symmetry 12, no. 4: 533. https://doi.org/10.3390/sym12040533
APA StylePudlak, M., Smotlacha, J., & Nazmitdinov, R. (2020). On Symmetry Properties of The Corrugated Graphene System. Symmetry, 12(4), 533. https://doi.org/10.3390/sym12040533





