Abstract
Given the fact that the three-qubit symplectic polar space features three different kinds of observables and each of its labeled Fano planes acquires a definite sign, we found that there are 45 distinct types of Mermin pentagrams in this space. A key element of our classification is the fact that any context of such pentagram is associated with a unique (positive or negative) Fano plane. Several intriguing relations between the character of pentagrams’ three-qubit observables and ‘valuedness’ of associated Fano planes are pointed out. In particular, we find two distinct kinds of negative contexts and as many as four positive ones.
1. Introduction
A Mermin pentagram, first introduced by Mermin in 1993 [1] to furnish an observable-based proof of quantum contextuality [2], is a set of ten observables of a three-qubit system with eigenvalues that are arranged into five four-element sets (contexts) that lie along the five edges of a pentagram in such a way that four observables in the same set mutually commute, their product is or , and the number of sets where the latter holds is odd. Some years ago, using a computer, it was shown [3] that the symplectic polar space associated with the three-qubit Pauli group contains as many as 12,096 such pentagrams, forming three distinct families according to the number of negative contexts, that is five (108 members), three (4104 members), or one (7884 members). More recently, Lévay and Szabó [4] analyzed this symplectic polar space in terms of its magic Veldkamp line and discovered that Mermin pentagrams naturally form aggregates of six pairs, each such double-six ‘cell’ being intricately related to six spreads of the core doily (generalized quadrangle of order two). In this short note, we reveal further interesting traits in the structure of Mermin pentagrams by taking into account that the elements of the three-qubit Pauli group (three-qubit observables) are of three different kinds. We also employ an important earlier observation [5] that each edge of a Mermin pentagram corresponds to a unique Fano plane of the associated symplectic polar space with a fixed/prescribed three-qubit labeling of its points.
2. Finite Symplectic Polar Spaces, Fano Plane, and Generalized Pauli Groups
We shall first introduce some necessary details about the most relevant mathematical notions to be employed. A (finite-dimensional) classical polar space (see, e.g., [6]) describes the geometry of a d-dimensional vector space over the Galois field , , carrying a non-degenerate reflexive sesquilinear form . The polar space is called symplectic, and usually denoted as , if this form is bilinear and alternating, i.e., if for all ; such a space exists only if , where N is called its rank. A subspace of is called totally isotropic if vanishes identically on it. can then be regarded as the space of totally isotropic subspaces of , the ordinary -dimensional projective space over , with respect to a symplectic form. Its maximal totally isotropic subspaces, also called generators, have the dimension . For this polar space contains points and generators. contains two different types of non-degenerate quadrics, elliptic and hyperbolic. A hyperbolic quadric is formed by all points of satisfying the standard equation ; for this quadric is also called the Klein quadric.
A projective plane consists of two sets, called lines and points, satisfying the following axioms: there exists a unique line incident with any two given points; there exists a unique point incident with any two given lines; and, there are four points of which no three are on the same line. The projective plane of order two, the Fano plane, is the smallest projective plane. It contains seven points and seven lines, with three points on a line and three lines through a point. Each generator of is isomorphic to the Fano plane. When one removes a line from the Fano plane one gets the affine plane of order two.
The (generalized) N-qubit Pauli group, , is generated by N-fold tensor products of the matrices
Explicitly,
Most interesting, from the physical point of view, is its factored version , where the center consists of and , since its properties are intricately linked to the structure of the symplectic polar space induced by its parent group . The elements of are equivalence classes of the form . For a particular value of N, the elements of can be bijectively identified with the same number of points of in such a way that two collinear points are represented by two equivalence classes, such that each element of one class commutes with each element of the other class and each maximal set of equivalence classes of pairwise commuting representatives corresponds to a generator of . The above correspondence was, in a more general context/setting, studied and worked out in Reference [7] (see also [8]), where the interested reader is referred to for more details and several ( and ) illustrative examples. In what follows, we shall make use of such bijection for the particular case of .
3. Three-Qubit Observables and Positive/Negative Fano Planes
To begin with, we consider the following ‘canonical’ representatives (in what follows, we shall use a shorthand notation for the tensor product: ) of the 63 non-trivial elements of
This choice of representatives is essentially dictated by two facts. The first one is that any physically relevant quantity must be an observable, i.e., a Hermitian matrix; this requirement thus rules out all representatives with factors. The second requirement is simplicity in the sense that all 63 representatives should have the same sign; and all the examples of Mermin pentagrams we have found in the literature available make use of the + sign. Let us therefore assume that has its points labeled by these canonical elements in the way described in Section 2. If we take a coordinate basis of in which the symplectic form is given by
then this labeling acquires the form
with the understanding that
thus, for example, the point of having coordinates corresponds to the element . A line/plane of such a space is then called positive or negative according to the product of the group elements located in it, that is or , respectively. Next, let us call a canonical element to be of type A, B, or C in dependence on whether, respectively, it features two I’s, one I, or no I; obviously, there are nine elements of type A and 27 ones of both type B and type C. With this last notion at hand, we will find that there are four different types of three-qubit-labeled Fano planes: one negative type and three positive ones. A negative Fano plane consists of three concurrent negative lines. If a positive Fano plane contains negative lines (type a), there are always four of them, forming the Pasch configuration. If a positive Fano plane is devoid of negative lines, then it has either one element of type A and three of type C (type b), or vice versa (type c). The situation is schematically illustrated in Figure 1. Out of 135 Fano planes of our ‘labeled’ , there are 54 negative and 81 positive ones, the latter being distributed equally into the three types.
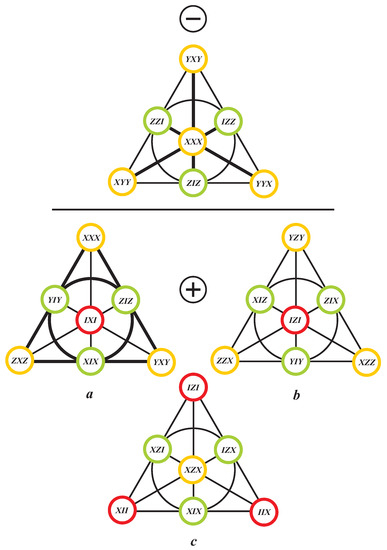
Figure 1.
A representative of the family of negative Fano planes (top) and those of three distinct types of positive Fano planes. Negative lines are shown in bold. An observable of type A, B, and C is colored red, green, and yellow, respectively. Note that the three observables of type B lie always on a line. (We use the traditional picture of the Fano plane where one of its lines is drawn as a circle.)
4. Taxonomy of Mermin Pentagrams
Given a Mermin pentagram, the first parameter of our classification is the number of negative contexts. The next three parameters are the character of three-qubit elements located on it. For example, the pentagram depicted in Figure 2 has three negative contexts and features one observable of type A, five of type B, and four of type C. Next, in Reference [5] it was shown that each edge of a pentagram is isomorphic to an affine plane of order two. As each such plane can uniquely be extended to the projective plane of order two, this also means that each edge is associated with the unique positive- or negative-valued Fano plane. The types of the five associated Fano planes will be the last string of parameters of our classification. Using again the example from Figure 2, we find here two negative and three positive Fano planes, the latter falling into all three types.
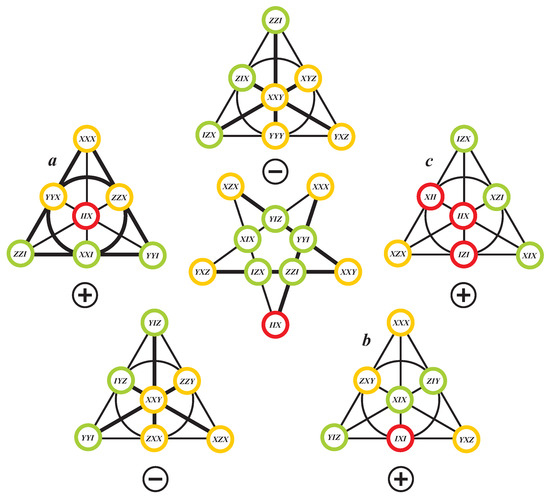
Figure 2.
A Mermin pentagram (drawn in the center) and the associated pentad of labeled Fano planes. The Fano plane at the top corresponds to the horizontal edge of the pentagram; the remaining correspondences follow readily from the rotational symmetry of the figure. Both the negative contexts of the pentagram and the negative lines of three Fano planes are boldfaced. Note that one of the negative contexts corresponds to a positive Fano plane. The Fano planes are labelled by the three-qubit observables in such a way that the closure line of the affine plane (the ‘line at infinity’) is always represented by the circle.
In order to fully classify Mermin pentagrams in this manner, we made use of particular sets of them computed by Michel Planat [9]. One such set comprises all 336 pentagrams located on a particular Klein quadric and another set consists of those pentagrams located (as point-sets) in a particular geometric hyperplane of a copy of the split Cayley hexagon of order two embedded classically into our three-qubit symplectic polar space [3]. To check for completeness, we randomly picked up pentagrams from the whole set, for each of them we looked for those ten pentagrams, each of which shares two edges with the pentagram in question and compared their types with those already found. The results of our analysis are summarized in Table 1; note that our pentagram of Figure 2 belongs to type 15.

Table 1.
Refined geometric classification of Mermin pentagrams. Column one (T) shows the type, column two () the number of negative contexts in a pentagram of the given type, columns three to five ( to ) indicate the number of observables of corresponding types, column six () the number of negative Fano planes and columns seven to nine ( to ) the distribution of types of positive Fano planes. Finally, the last column (K) indicates the number of pentagrams of a given type that lie on the ‘symmetric’ Klein quadric.
Let us highlight some of the most interesting properties of Mermin pentagrams stemming from our analysis. Obviously, there are only two types where all five Fano planes are negative (types 1 and 4) or positive (types 41 and 42). No pentagram possesses less than two observables of type C, or has just eight of them. If a pentagram features observables of type B, there are four or five of them; and if an edge of such a pentagram contains one such observable, it must contain one more. Next, if a pentagram contains just three observables of type A, they are situated on the same edge; the only exception are types 41 and 42, since they feature no negative Fano plane. There are no pentagrams featuring more than six observables of type A. Any pentagram that contains positive Fano planes of type b and c, but none of type a, is that with a single negative context; the only exception to this rule is type 12. One also sees that a pentagram with no observable of type A is also devoid of positive Fano planes of type c. Further, if a pentagram is associated with Fano planes featuring all the three positive types, then this pentagram also exhibits all the three kinds of observables, with a single exception (type 19). It is also worth mentioning that there are three types of pentagrams having positive Fano planes of type c only (types 13, 27, and 45), as well as two types with all positive Fano types being equally represented (types 15 and 32). From the physical point of view, the most important finding is certainly the existence of two different types of negative contexts of Mermin pentagrams and as many as four distinct kinds of positive ones; the former case involves negative Fano planes and positive Fano planes of type a, whereas the latter one entails all the four types of valued Fano planes. A particularly nice example of these properties is furnished by a pentagram of types 28 or 36, whose single negative context is associated with a positive Fano plane and the remaining four positive contexts are all of different characters.
As a particular task, we also analyzed case by case all 336 pentagrams lying on that hyperbolic quadric (Klein quadric) of that accommodates all 35 symmetric canonical elements (i.e., elements featuring two or zero Y’s), and found out that they only fall into 33 distinct types; interestingly enough, the twelve missing types are types 2, 3, 4, 6, 8, 9, 11, 14, 17, 21, 25, and 31, none of them being associated with a positive Fano plane of type c (see the last column of Table 1).
5. Concluding Remarks
We have introduced a remarkable classification of three-qubit Mermin pentagrams that intricately combines the character of three-qubit observables with the properties of positive/negative-valued Fano planes of the associated symplectic polar space and reveals important finer structure of three-qubit (observable-based) quantum contexts, distinguishing between two negative and as many as four positive ones. We believe that such classification can be of relevance in any branch of quantum information theory (quantum protocols) where a Mermin pentagram is an essential element; it can also be helpful in revealing finer traits of the so-called black-hole/qubit correspondence (see, e.g., [10]) in those of its aspects that are linked to the structure of the three-qubit symplectic polar space.
Author Contributions
Conceptualization and analysis, M.S. and F.H.; validation H.J.; writing—original draft preparation, M.S.; funding acquisition, M.S. and F.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Slovak Research and Development Agency under the contract # SK-FR-2017-0002 and the French Ministry of Europe and Foreign Affairs (MEAE) under the project PHC Štefánik 2018/40494ZJ. The financial support of both the Slovak VEGA Grant Agency, Project # 2/0004/20, and the French “Investissements d’Avenir” programme, project ISITE-BFC (contract ANR-15-IDEX-03), are gratefully acknowledged as well.
Acknowledgments
We are indebted to Petr Pracna for the help with the figures. We also thank two anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Mermin, N.D. Hidden variables and the two theorems of John Bell. Rev. Modern Phys. 1993, 65, 803. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59. [Google Scholar] [CrossRef]
- Planat, M.; Saniga, M.; Holweck, F. Distinguished three-qubit ‘magicity’ via automorphisms of the split Cayley hexagon. Quantum Inf. Process. 2013, 12, 2535. [Google Scholar] [CrossRef]
- Lévay, P.; Szabó, Z. Mermin pentagrams arising from Veldkamp lines for three qubits. J. Phys. A Math. Theor. 2017, 50, 95201. [Google Scholar] [CrossRef]
- Saniga, M.; Lévay, P. Mermin’s pentagram as an ovoid of PG(3, 2). EPL Europhys. Lett. 2012, 97, 50006. [Google Scholar] [CrossRef]
- Cameron, P.J. Projective and Polar Spaces. QMW Maths Notes, 13; School of Mathematical Sciences, Queen Mary and Westfield College: London, UK, 1992. [Google Scholar]
- Havlicek, H.; Odehnal, B.; Saniga, M. Factor-group-generated polar spaces and (multi-)qudits. Symmetry Integr. Geom. Methods Appl. 2009, 5, 96. [Google Scholar] [CrossRef]
- Thas, K. The geometry of generalized Pauli operators of N-qudit Hilbert space. EPL Europhys. Lett. 2009, 86, 60005. [Google Scholar] [CrossRef]
- Planat, M.; (Institut FEMTO-ST, Besançon, France). Personal Communication, 2019.
- Borsten, L.; Duff, M.; Lévay, P. The black-hole/qubit correspondence: an up-to-date review. Class. Quantum Gravity 2012, 29, 224008. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).