Use of Determination of the Importance of Criteria in Business-Friendly Certification of Cities as Sustainable Local Economic Development Planning Tool

Abstract

One of the essential activities for sustainable local economic development is continuous improvement of business environment which can be carried out through the business-friendly certification as objective benchmarking process, which is influenced by many factors - criteria that could be analyzed using multi-criteria decision-making methods. Determining criteria weights is the most important task regarding these methods for which a number of methodologies based on different approaches were developed. These methodologies could be generally divided into two groups: subjective and objective. Shortly, these methodologies quantify given preferences using knowledge of experts if they are subjective or using calculations from available data if they are objective. Methodologies from these two groups give different results in a wide range of values. Therefore, it is useful to create composite indicators using aggregation of both approaches in order to reduce the influence of their bad individual characteristics and, therefore, achieve a balanced symmetrical approach. The purpose of this paper is constructing one efficient model that solves a problem of the planning of sustainable local economic development in the Republic of Serbia. Our approach uses the aggregation of the entropy method, as one objective approach, and the analytical hierarchy process, as a subjective approach, in executing business-friendly certification process. The implementation of the proposed approach has been demonstrated as a part of a business-to-government (B2G) platform called “Multi-Criteria Support System for Analysis of the Local Economic Environment” in the City of Niš.

1. Introduction

Business Friendly Certification (BFC) of local self-government units (LSGU) is a process that introduces standards for efficient and transparent governance and allows evaluation of the quality and relevance of services and information for investors and entrepreneurs. This process should be used as one of the most important procedures in the planning of sustainable local economic development. The current application of this procedure in the Republic of Serbia aims to improve the business environment through institutional reforms especially in public administration at the local level with active participation and cooperation of economic subjects, citizens, and municipalities of one local self-government unit. This process involves the determination and evaluation of various criteria on the local self-government level [1,2,3,4,5].

Therefore, the BFC process is complemented with another one carried out by the local self-government BFC (LBFC), which involves the determination and evaluation of various factors-criteria using their impact on the fulfilment of local business environment demands as well as on attracting potential investors. It should be noted that these factors depend on those regulated by the republic and those regulated by local authorities. The BFC process, together with the mentioned LBFC process, must be implemented in accordance with the defined model of one cyclic algorithm of strategic planning of sustainable local economic development (LED), which is framed by year cycles dynamics [6,7].

Multi-criteria decision-making methods (MCDM) of criteria weighting have a significant influence on the final outcome of decision-making and ranking alternatives that participate as a part of the model. That is why it is necessary to determine these weights properly [8,9,10]. Determining the criteria weights can be done using various methods, and all of them can be classified into two groups: the subjective and objective methods. Subjective methods are methods that most respect the subjective preferences of the decision-maker or expert in the process of evaluation of criteria relevance. In this group, the analytic hierarchy process (AHP) and its various forms of improvement and aggregation with some others methods (as for example fuzzy logic, BWM (Best Worst Method), conjoint analysis, Delphi method, according to references [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]) are mostly used in MCDM. The main aim of the paper [11] is a systematic review of possible ways of determining the criteria weights by the decision-maker or by other participants in the decision-making process. In articles [12,13,14,15,16,17,18,19,20,21,22], one can find descriptions of the application of different subjective methods: AHP, IR-AHP-MABAC, AHP-DEMATEL, IRDEMATEL-COPRAS, DEMATEL-MAIRCA, ROUGH DEMATEL-ANP-MAIRCA, FUZZY, ROUGH BWM-WASPAS, BWM-MAIRCA, DELPHI-SWARA-MABAC, WASPAS. In paper [23], the authors propose the novel Full Consistency Method (FUCOM) as more efficient than AHP and BWM. This method implies the definition of two groups of constraints that need to satisfy optimal values of weight coefficients. The first group of constraints are based on the fact that the criteria weight coefficients should be equal to the comparative priorities of the criteria while the second group of constraints are based on the basis of mathematical transitivity conditions. Both of them are solved using the FUCOM model, and in addition to optimal weight values, a deviation from full consistency (DFC) is obtained while its degree is the deviation value of the obtained weight coefficients from the estimated comparative priorities of the criteria. Also, paper [24] is based on the description of the main difference between conceptual and theoretical frameworks as well as on literature review of comparative studies of AHP and conjoint analysis. The authors of article [25] deal with one application of the Delphi method for Iranian medical schools’ ranking purposes. Objective methods, on the other hand, are concerned with weight coefficient assignment on the basis of the analysis of given data, which are used for solving specific mathematical models of selected methods of multi-criteria decision-making, without taking into account the attitude of decision-makers or experts. Mostly used common objective methods are: entropy, CRITIC (Criteria Importance Through Inter-criteria Correlation), FANMA, data envelopment analysis (DEA), correlation analysis, regression analysis, factor analysis, etc. In literature, we can find in [7,26,27,28,29,30,31,32,33] and [34]. The main aim of the paper [26] is one review of possible ways of objective determining of the criteria weights by the algorithms where the relative importance of criteria reflects the amount of information contained in any of them, which is associated with the contrast intensity of each criterion. In paper [27], an analysis of several simpler methods for objective determination of the criteria weight was explained in more details using more complex CRITIC, ENTROPY, and FANMA methods with their advantages and disadvantages in comparison with subjective methods of evaluating criteria, while paper [28] deals with a comparative analysis of two different types of objective techniques for criteria weighting: Entropy and CRITIC (an article [29] considering CRITIC method in detail). In paper [30], authors deal with the entropy method, whereas in paper [31], authors have presented some models to generate the favorable weights from a pairwise comparison matrix combing AHP and DEA models. In addition, paper [32] considers again the usage of the DEA methodology. Papers [7,33,34] present possibilities and results of the implementation of regression, as well as the factor and correlation analysis, respectively, in criteria weighting, which belongs to the objective approach as classical statistics methods.

As mentioned previously, the main aim of this article is to present one aggregated methodology using two mentioned approaches of criteria weighting in MCDM to achieve one balanced-symmetric approach, having higher accuracy by reducing the influence of the disadvantages of each method (which are presented in [7,34,35,36,37,38,39,40,41,42]), and thus make it suitable for the processes of BFC and LBFC. Paper [35] consider obtaining criteria weights in MCDM, from objective and subjective approaches, mainly from the perspective of more participative methods in the construction of composite indicators. In paper [7], the aggregation of AHP and ANOVA on the case study of business-friendly certification processes of five cities in the Republic of Serbia is given. In article [36], a generalized combinative weighting framework is given to show how different types of weightings may be combined to find more reliable rankings of alternatives after the analysis was previously done using different subjective and objective approaches, while paper [37] proposes an integrated approach to determine attribute weights in the MCDM problems, which makes use of the subjective information provided by a decision-maker and the objective information obtained by a two-objective programming model. In papers [38,39], the same case was used to identify and determine the weights of the subjects on the first-year, in order to predict future students’ success related to all of the study programs. In paper [38], the aggregated measure as the combination of weights obtained by DEA as an objective, and AHP as a subjective method is defined for determining the subject’s weight. The paper [39] presents methodology for calculation of an aggregated measure as of arithmetic means for quantitative decision-making with the combination of statistical methodology based on regression and factor analysis on one hand and operational research approaches DEA, as an objective method, and AHP, as a subjective method. Also, in paper [34], authors combine AHP and correlation analysis approaches for determination of weights in a multi-criteria model of a contemporary problem of business-friendly certification in five local self-government units in the Republic of Serbia. In paper [40], we can find the aggregation of AHP and entropy, paper [41] takes a statistical approach for the sensitive analysis of MCDM, and article [42] deals with one aggregation that uses a model of behavior mechanism.

Therefore, the methodology proposed in this paper is applied on the case study in the city of Niš to estimate its quality, i.e., better characteristics in relation with each individual methodology with respect to the basic methodological framework of composite indices, which is described in detail in papers [43,44].

For solving this task, the paper has been organized as follows. After this Introduction as the first section, in Section 2, the proposed method of aggregation is described in individual short sub-sections: AHP as subjective, Entropy as objective, and the proposed method, which aggregate both of them. In Section 3, ‘Brief introduction to the modelling of strategic planning of LED’, the model based on the BFC and LBFC process is proposed in the first subsection while its implementation as the Support System for Analysis of Economic Environment of the Local Self-government in the City of Niš, the Republic of Serbia is presented in the second subsection. In the Results section, the obtained results for the three previously described methods are given. Section 5 presents the discussion about the obtained results, and the ‘Conclusion’ section as the last section of the paper provides the conclusions and underlines the main contributions of this work.

2. Proposed Method of Aggregation in Criteria Weighting one MCDM Method

In order to find the most suitable methodology for MCDM, of which the presence is necessary for the proposed model of strategic planning of LED in Section 2, we are starting from the general multi-criteria analysis model (1) in which it is necessary to evaluate one of the m alternatives (A_i, I = 1, 2, …, m), in accordance with n different criteria that are relevant (C_j, j = 1, 2, …, n). The importance of each of the criterion C_j is determined using the weight coefficients w_j, where criteria values of alternatives could be noted as a_ij. Regardless of the method used for their determination or calculation, all relative weights in the multi-criteria decision-making (MCDM) model must meet the following requirements:

0 ≤ w_j ≤ 1

$${\displaystyle \sum }_{j=1}^n{w}_j = 1$$

$$\begin{array}{ccc}\begin{array}{c} C_1\\ {\omega }_1\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{c}{C}_m\\ {\omega }_m\end{array}\\ \begin{array}{c} A_1 a_{11}\\ ⋮\\ A_n a_{n1}\end{array}& \begin{array}{c}\dots \\ \ddots \\ \dots \end{array}& \begin{array}{c}{a}_{1m}\\ ⋮\\ a_{nm}\end{array}\end{array}$$

(1)

where it is known:

• variants A_i, i = 1, 2, ..., n,
• criteria C_j, j = 1, 2, ..., m,
• criteria values of variants a_ij.

For solving of this model, several taxonomies [45] exist, but as we mentioned in the introduction of this paper, it is very important, after choosing a concrete model, to also choose the appropriate criteria weighting method for the previously chosen method.

The classification of developed criteria of weighting methods can be done in several ways, with the criteria importance irrespective to the classification, which usually implies that the comparison or ranking criteria are applied in determining the weight of the criteria. Thus, for example, methods can be distinguished by the number of participants in the weighting process, when distinct individual or group methods are applied to theoretical concepts or when the statistical and algebraic methods are distinguished based on the concept of compensation or exchange between criteria, where possible methods are divided into a compensatory or no compensative method of combining individual weight criteria like in [13]. Thus, in the literature [46], the method of determining the weight of the criteria was divided into: statistical and algebraic, holistic and decomposed, direct and indirect, compensatory and no compensative. In algebraic methods, the n weight is calculated based on the set of n − 1 judgments by solving the equation system. Statistical procedures use a regression analysis of a redundant set of judgments. The decommissioned procedures are based on the comparison of a one-to-one pair of criteria, while in holistic methods, the decision-maker, when expressing his preferences, considers the criteria and variants and performs the overall assessment of the variants. In direct methods, the decision-maker compares two criteria using a relational scale, while in indirect methods, on the basis of preferences, the decision-makers calculate the weight of the criteria. Compensation methods involve strict compensation between the criterion and the severity of the criteria. They are used to aggregate partial values in the methods of multi attribute theory of values while the no compensative methods are without compensation, and the weight of the criteria are used as coefficients of importance used for aggregation of partial values in higher-order MCDM methods. As we said in the Introduction, basically, most approaches for determination of the weight of criteria can be divided into subjective and objective ones. Subjective approaches are based on determining the severity of the criteria, mainly relying on the information obtained from the decision-maker or from the experts involved in the decision-making process. Subjective approaches reflect the subjective thinking and intuition of the decision-maker, and thus, the decision-maker influences the outcome of the process. Objective approaches are based on determining the severity of the criteria based on the information contained in the decision matrix using certain mathematical models. It is common knowledge that as a result of the need to improve the quality and precision of the criteria, weighting determination is used as one of the methods of composite evaluation of aggregation methods. Namely, aggregation is a unification process and refers to a different combination and merges several, usually numerical, values into one value. Each function that yields one output value using the input value vector is called the aggregation function. The earliest examples of aggregation considered an arithmetic mean, and it was used in all phases of the development of physics, as well as other sciences, based on the experiment. Aggregation plays an important role in optimizing the solution of tasks in various current scientific fields, and especially where there is an intrusion of fusion of data, such as our case of applying the method of multi-criterion decision-making, the choice of location of production capacities, for determining the significance of the determinants of the location of the production facilities in the LBFC process and factors considered from the republic level in the BFC process, which determine the rang of this self-government, i.e., city on the state level, and so, shows the local self-government with how much intensity they must improve the determinants of location in the LBFC process.

In order to get a good aggregation, it is not necessary to use any aggregation operator, but on the basis of an axiomatic approach, it depends on some conditions. These conditions can be values conditioned by nature to be aggregated because of their multidimensionality and inconsistency. In Section 3.1 of this paper, where the algorithm of the double-sided model of strategic planning of LED is described, we proposed the aggregation of the two mostly-used methods for criteria weighting: AHP as subjective, and entropy as one objective method. We have proposed this due to the appropriateness of the aggregation of exactly those two methods for the BFC and LBFC process, which implies a mandatory taking into account of the expert opinion on the significance of particular factor criteria in both BFC and LBFC processes as the initial and obligatory objectification of expert estimates on the data from the decision matrix to eliminate subjectivity and possible errors in the expert assessment. Doing this with the aggregation of these two methods of different approaches, we have obtained a more accurate method than each individual. Authors have in mind that AHP, although an old method, is still the most-used subjective method, having only one important deficiency, which could be inconsistency in the case of more than nine criteria weightings, which we have in the BFC process but not in the LBFC process. In our case study, AHP performs completely consistent pairwise comparisons [23,47,48]. Also, when choosing the entropy method, we must notice that this is because the type of criteria is not important, and it eliminates possible errors in subjective criteria weighting, as it is described in [26,27,29]. AHP-entropy aggregation has been discussed in the literature in many papers [40,49,50,51,52,53,54] where different solutions were proposed in which the application was evaluated to solve different problems. As we still mentioned in the Introduction of this paper, in paper [40], the different criteria for the construction of one agricultural water resources management in the Aras basin in the North West of Iran are integrated using the decision support system to evaluate the performance of nine indicators of structural alternatives. The aggregation of AHP as subjective and entropy method as the objective was used for criteria weighting. This aggregation was also used in [49] to determine the criteria weights in evaluating regional social and economic development in Lithuania, as well as for estimating the strategic potential of enterprises, and for determining the efficiency of economic development and commercial activities of various enterprises. In paper [50], for AHP and entropy aggregation purposes, a simple spreadsheet-based application is developed for deriving criteria weights by synthesizing decision elements and ranking decision alternatives. In [51], the use of an aggregated AHP and entropy method is used for biomass selection in Fischer–Tropsch reactors. One can see that a joint fuzzy comprehensive method and an AHP method have been proposed in paper [52] to demonstrate a variable weighting type for landslide susceptibility evaluation modelling, which combines subjective and objective weights and is tested on the case study with eight influencing factors selected from the study of Zhen’an County, Shanxi Province in the People’s Republic of China. In [53], the aggregation of fuzzy AHP and entropy method is applied for the evaluation of website usability because fuzzy MCDM approaches are widely adapted to measure and rank the website usability as a subjective in nature. Along with these measures, objective design dimension, as well as other support features that encourage the user to reach the desired information in the stipulated time, which is also important, was incorporated in the proposed metric. Finally, in article [54], a smart electricity utilization (SEU), as one of the most important components in a smart grid, which is of crucial importance when evaluating safety, efficiency, and demand response capability of electricity users to achieve the smart use of electricity, is described. For the purpose of taking into account the uncertainty of expert scoring and user data, the authors proposed a hybrid interval analytic hierarchy process and interval entropy method for electricity user evaluation.

2.1. AHP Method

AHP is a multi-criteria analysis method that provides a scientific basis for decision-making problems. It has been widely applied since the 1980 s, when the decision-maker is either an individual or a group [55,56]. Almost all problems related to multi-criteria decision-making were using AHP as a quantitative technique, and its application can include more than 150 different kinds of areas [57]. The AHP method is a method that is used for formulation and analyzing decisions that can measure the influence of many factors relevant to possible outcomes of decisions. It can be used for forecasting, for instance, the performance of relative probability distribution of outcomes.

According to Saaty [58], the AHP algorithm is based on three principles:

i.

Decomposition of the goal-value structure where a hierarchy of criteria, sub-criteria, and alternatives is developed, with the number of levels determined by the problem characteristics;

ii.

Comparative judgments of the criteria on single pair-wise comparisons of such criteria with respect to an upper criteria; and

iii.

Linear-based synthesis of priorities where alternatives are evaluated in pairs with respect to the criteria on the next level of the hierarchy, and criteria can be given a priority expressed as a weight in the AHP matrix.

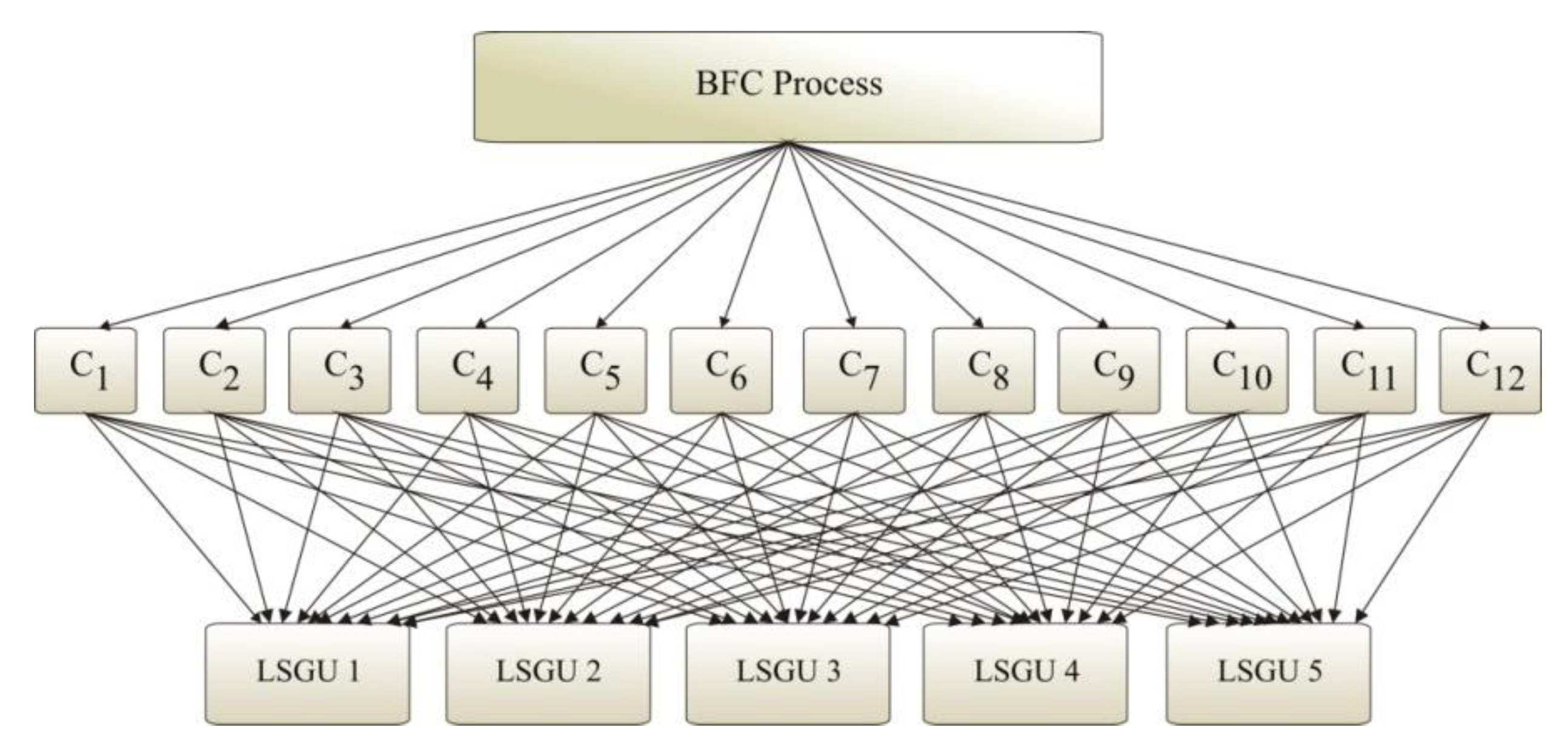
At the first level, the problem is decomposed in hierarchical structure. The goal of the first level is on the top of the structure, while the criteria based on which decision is made are treated at the lower levels within the structure. At the lowest hierarchical level, there are many alternatives for which comparisons must be made. The hierarchical structure of the National Alliance for Local Economic Development (NALED) BFC problem for the evaluation of five LSGU is given in Figure 1.

The next phase involves A pair-wise comparison of criteria, as well as the alternatives at a specific level of the hierarchy, which are also in relation to the criteria of the level directly higher within the hierarchical structure. A pair-wise comparison of alternatives is made in response to the question in which one of the two observed attributes of an alternative to the specific criteria is better in meeting the criteria and contribution to the objective. Strength of preference is expressed with the ratio scale, with increments scaled from 1 to 9. The lowest preferential level 1 shows equality of observed attributes, and the preferential level 9 indicates the highest preference of one attribute over another [59,60].

Such a scale was created by Saaty [58], and it is used in the essential AHP method, as well as for its later advanced variant (Analytic Network Process—ANP) [61]. The defined scale allows comparisons in a limited scope, while the perception is sensitive enough to make a difference in the importance of alternatives.

2.2. Method of Entropy

Following Sanchez and Soyer [62], and also Shannon [63], let us assume, that C_j = (a_1j, a_2j, …, a_mj) denotes a priority vector according to a certain criterion j, j = 1, …, n. Entropy for this vector may be defined as:

$$H(w_j)=-{\displaystyle {\sum }_{i=1}^m{a}_{ij}\ln (a_{ij})}, j=1,\dots ,n$$

(2)

In information theory, the entropy $H(w_j)$ can be defined as a measure of discrete random variable X uncertainty, which can have a value from the finite set (x₁, x₂, …, x_n) in a way that probability that X is going to be equal to x_j is w_j and can be denoted as

P(X = x_j) = w_j

(3)

In the context of multi-criteria, entropy is mainly used to determine the priority of an alternative. The priority p_i, in accordance with the procedure given for weights w_j, can be interpreted as the probability that the i_th alternative will be preferred by the decision-maker (Uden and Kwiesielewicz, [64]). One of the most important entropy characteristics is that H(X) ≥ 0. The entropy of a discrete distribution with finite support always has a non-negative value. It can be equal to zero when all elements in Equation (2) are equal to zero. Such a case is possible only when one value of a discrete random variable has a probability equal to one and, at the same time, all the other values have probabilities equal to zero. The described situation excludes uncertainty.

Entropy achieves the maximum value of the uniform distribution presented by the following equation:

H(1/n, …, 1/n) = ln (n)

(4)

This characteristic of entropy is consistent with the definition of entropy as a measure of uncertainty, which means that the maximum is reached when all values of random variable X have equal probability.

2.3. Aggregation Method

As we said in the introduction of this section, to get a good aggregation, it is possible to use any aggregation operator from several groups of mentioned aggregation, but on the basis of an axiomatic approach, it depends on several conditions. As we said in the introduction of this section, these conditions can be values conditioned by the nature to be aggregated and can also be in solving the multi-criteria problem that is addressed in this paper, where the goal is to obtain a global optimal estimate due to the large range of differences in the values of the criteria obtained. Also, as we concluded in the introduction of this section, because of their suitability to the nature of the considered BFC and LBFC MCDM problems, authors proposed the aggregation of the subjective-AHP and objective-entropy method.

Namely, calculated values of the objective criteria weights actually determine the influence, i.e., the effect of each particular criterion on the rationality of possible alternatives, but subjective criteria weights indicate their importance in terms of the rationality of considered alternatives, and in some cases, these subjective and objective criteria differ considerably, having a negative effect on the accuracy of alternatives determination in considered BFC and LBFC processes of MCDM.

In literature, a variety of constructed methodologies for aggregation of subjective AHP and objective entropy methods are commonly found. The integration of individual preferences of decision-makers using AHP criteria weighting can be performed using various mathematical approaches, which can be categorized into four groups [64].Because, from a mathematical standpoint, unique taxonomy does not exist when aggregation of AHP and entropy methods are used in that sense, the authors try to recognize in literature the three approach groups presented in this paper.

The first approach is simply algebraic aggregation of the individual judgments obtained for each method used in different algebraic form as in [26,49,65,66,67], where, in the paper [26], one of possible ways of algebraic aggregation of objective and subjective determining of the criteria weights is given in the form of a kind of arithmetic mean (same approach of aggregation authors propose in the paper [49], using AHP and entropy methods, and also in [65] in the case of material selection, and in [66], used to select sheet hydroforming process parameters). In contrast, paper [67] has considered two possible ways of algebraic aggregation of objective and subjective determining of the criteria weights in the form of a kind of arithmetic and geometric mean. The second approach is based on using different mathematical programming algorithms to aggregate individually obtained AHP and entropy criteria weights, as in paper [37], which, as we mentioned in the introduction, proposes an integrated approach to determine attribute weights in the MCDM problems using the subjective information that was provided by a decision-maker and the objective information in the form of a two-objective programming model. Paper [68] points out that the objective weight introduced in [37] can be very different from the objective weight obtained by the entropy method. In [69], the authors proposed one programmed model using AHP and entropy to solve a problem of criteria weighting in the process of certifying cities and municipalities in the City of Niš in the Republic of Serbia as favorable to business, while in paper [70], the authors present several versions of a mathematical programming model that determines attribute weights for each consumer. These weights are empirically evaluated using databases of dry cereals and automobiles as an example. The third approach is based on fuzzy logic as one of the most used artificial intelligence techniques in MCDM, which is described in [52,53,54,71,72,73]. In papers [52,53,54] as we presented at the beginning of Section 3 of this paper, a fuzzy comprehensive method and AHP were proposed to demonstrate a variable type of weighting for landslide susceptibility evaluation modelling, then for evaluation of website usability and one hybrid interval analytic hierarchy process and interval entropy method for electricity user evaluation, respectively. In paper [71], it is assumed that in AHP, rankings of factors under particular attributes are given, and after that, based on the entropy, an amount of information associated with each ranking is evaluated and an attribute ranking is fixed. In [72], the authors proposed a new decision-making method using fuzzy AHP based on entropy weight because the traditional method of AHP is mainly used in non-fuzzy (crisp) decision applications with an unbalanced scale of judgements to overcome these problems. For example, in paper [73], the authors apply a fuzzy comprehensive evaluation algorithm to optimize the decision-making process of logistic center location in a way that fuzzy AHP is proposed to determine the rank in logistic center location evaluation. In order to include the domain expertise into the decision-making process and improve evaluation performance, the fuzzy MCDM model is developed with the goal of modifying the fuzzy AHP weights based on the entropy technique by using decision matrix information through the Delphi method. The authors of this paper choose the algebraic approach to decide which of them could be implemented for solving BFC and LBFC processes in the model for LED planning:

• If the aggregated weight of each criterion is obtained one with the AHP method Z_i, i = 1, ..., n and the other weight obtained by using the entropy method, w_i, i = 1, ..., n [65] in the form:

  $${\alpha }_i=\raisebox{1ex}{$z_i{w}_i$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{i=1}^n{z}_i{w}_i}$}\right., i=1,\dots ,n$$
• If the aggregate weight of each criterion is obtained with the weighting entity of the AHP method as Z_i, i = 1, ..., n and the other weight obtained by using the entropy method w_i, i = 1, ..., n [67] in the form:

  $${\alpha }_i = \raisebox{1ex}{$\sqrt{z_i{w}_i}$}\!\left/ \!\raisebox{-1ex}{${{\displaystyle \sum }}_{i=1}^n\sqrt{z_i{w}_i}$}\right. , i = 1, \dots , n$$

3. Brief Introduction to the Modeling of Strategic Planning of LED

Since 2000, LED has been predominantly initiated by international development agencies, which implies changes in organizations, the introduction of new codes of conduct, institutional reform, and the implementation or development of new or existing strategies, etc., making the local community more competitive [74,75]. According to the author’s proposal for strategic planning, the planning of LED, for the time in over five years, is a creative process in which a cyclical algorithm determines the key areas of development and harmonizes stakeholders with the most important goals and assesses the impact of significant factors on LED. Since there are several schools of thought, the authors adhered to one of them, which says that there are three things most important in the LED: location, again location, and finally, location.

The problem of choosing the location of production capacities for sustainable LED is a problem in which it is necessary to compare a large number of locations (alternatives) based on a large number of location determinants (criteria), some of which may be considered locally and some are republican managed, whereas, it should be kept in mind that each individual case, depending on the particular investor, distinguishes preferences, i.e., different criteria have different significance (weight of coefficients), so it is obvious that this problem can be dealt with as a classic MCDM problem [76].

3.1. Double-Sided Model of Strategic Planning of LED

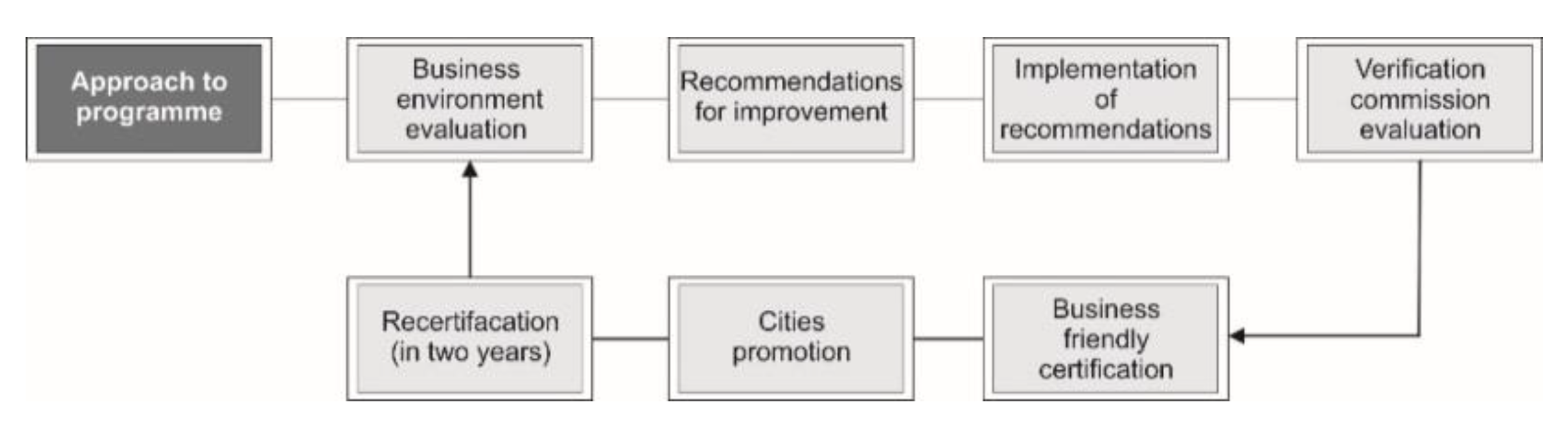
National Alliance for Local Economic Development (NALED) introduced, implemented, and has actively carried out the BFC procedure in Serbia for more than ten years. The results are very concrete and have positive implications on the improvement of the general business climate in Serbia. Almost half of all local self-government units in Serbia participated and improved their business environment through this program of certification. Certification criteria provide unique guidance to LSGUs on the type and quality of services, information they should provide, as well as infrastructure that investors and local business communities think LSGUs should provide. The local self-government, which is a part of the certification process receives specific recommendations for governance reforms that are necessary to be implemented in order to create a favorable and improved business environment and investment climate at the local level. A positive business environment includes transparent local governance, efficient administration, adequate infrastructure, and major strategic development decisions made in partnership with the business community. The BFC process encompasses a wide range of activities, which could be represented as in Figure 2.

The ultimate goal of the certification process is to increase the competitiveness of individual local governments, which contributes to national level competitiveness, as well as investment promotion and attraction, employment generation, and increasing living standards and quality of life in the Republic of Serbia [77]. The certification process has been adjusted, improved, and extended through the years, but mainly, it included 12 criteria and from 80 to more than 100 sub-criteria by which local self-governments and independent NALED-engaged experts could assess whether and to what extent a municipality meets the standards of a friendly business environment [78]: (C1) strategic planning of LED in partnership with businesses; (C2) special department in charge of LED, FDI promotion and business support—LED Office; (C3) business council for economic issues—advisory body to the mayor and local governments; (C4) efficient and transparent system for acquiring construction permits; (C5) economic data and information relevant for starting and developing a business; (C6) multilingual marketing materials and website; (C7) balanced structure of budget revenues/debt management; (C8) investing into the development of local workforce; (C9) cooperation and joint projects with local business on fostering LED; (C10) adequate infrastructure and reliable communal services; (C11) transparent policies on local taxes and incentives for doing business, and (C12) electronic communication and on-line services.

Assessment of the fulfilment of certification criteria methodology and collecting additional information in cooperation with the municipality team and the business community is done through the following set of steps:

i.

Assessment of the existence of certain functions;

ii.

Assessing the quality of services in the municipality;

iii.

Assessing the quality and accuracy of data;

iv.

Assessment of the status of each individual indicator;

v.

Preparation of reports, comments, and recommendations; and

vi.

Define additional requirements that are necessary for a positive evaluation and the fulfilment of the criteria.

According to NALED, the importance of each criterion is defined as the average score of the previous level of evaluation and as such, can be called the relative importance of observed criteria C_j.

Using the given data for self-government of some cities, it is possible to apply different MCDM methods to determine the importance for any city in the Republic of Serbia.

Local self-government can collect data from several subjects of the local business community who assess the location with a few criteria from the local and national level with a similar LBFC procedure using different MCDM methods to determine which type of job must be introduced in order to fulfil the requests of the local business community [79].

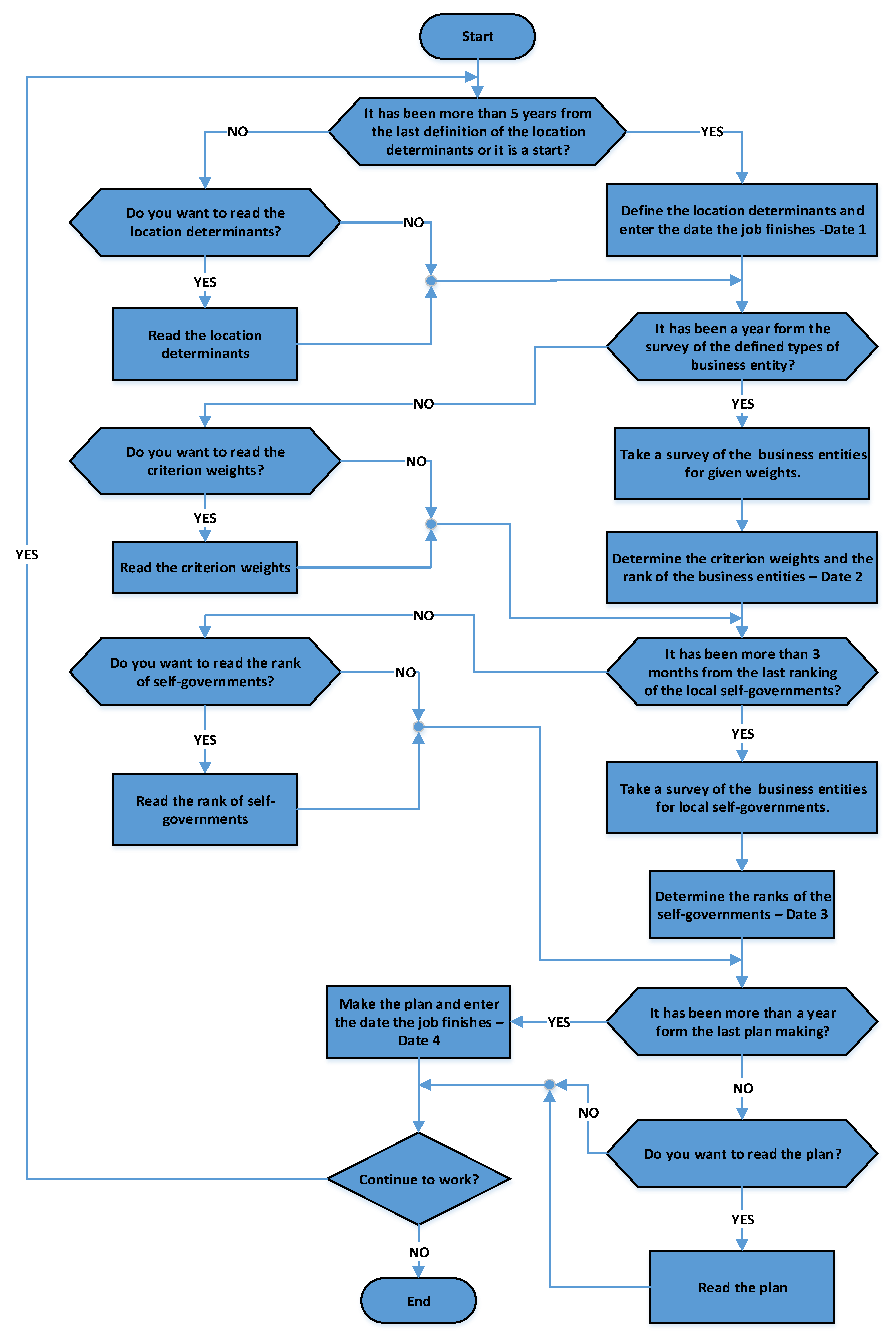
Therefore, in this paper, the authors proposed programmable supported strategic planning of LED using one two-dimensional, i.e., double-sided model, which realizes one cyclic algorithm, as presented in Figure 3.

On the one hand, using the given data from NALED allows to apply different MCDM methods to determine the level of fulfilment of each criterion of a good business environment for considered cities in the Republic of Serbia and to determine the intensity that should be applied to the fulfilment of certain factors in concrete local self-government.

On the other hand, the local government can use some MCDM procedures for solving the mentioned LBFC and collect data from as many local business community members as possible, and so, assess each possible location with several criteria on the local and republic level, determine the significance of each of these criteria, and thus determine which criteria are to be met for better implementation of LED; in addition, it can determine which branches of economic development should be involved because the significance of the criteria that determines the quality of the site that is suitable for the eventual investment depends on the branch [79].

In the proposed model, the strategic plan of LED should be adopted after every five years (this is determined with the date-4), while, each year, the LBFC procedure determines the most important branches of economic development related to the date-1 and the most important factors-criteria of the locations on which the local self-government should work based on the given date-2 and the required intensity of investment determined in the previous step using location factors each three months related to the date-3. The proposed model is valid, regardless of which city will be considered. However, it is used in those that are in the BFC process [67].

For solving criteria weighting that is multidimensional and inconsistent on both mentioned MCDM problems in the proposed model, i.e., for implementation of BFC and LBFC process, we have proposed in this paper the aggregation of the two most-used methods—AHP method from a subjective approach and method of entropy from an objective approach of MCDM in order to improve quality of factors-criteria weighting, which is described in detail in Section 2. The proposed methodology is applied to the case study of the City of Niš in the Republic of Serbia. Having in mind that the authors have already considered one other methodology of such aggregation on a similar case study for the BFC procedure in article [69], in Section 2, we presented only the results obtained by the implementation of the BFC procedure, especially because the implementation of LBFC is principally the same, normally with other criteria factors.

3.2. Multi-Criteria Support System for Analysis Economic Environment of the Local Self-government

The implementation of the above proposed aggregated algorithm is conducted on a business-to-government (B2G) platform called “Multi-Criteria Support System for Analysis of the Local Economic Environment”. Namely, the focus of the technical solution “Multi-Criteria Support System for Analysis of the Local Economic Environment” is associated with the investigation of the business environment in the City of Niš, which is the third-largest local government in the Republic of Serbia, and one of the cities involved in the business-friendly certification process.

The platforms main goal is to deliver feedback from the business community regarding their preferences on the key issues for improving the local business scene. The solution for the MCDM problem may be in the identification of which one of the considered criteria is of the highest importance for making a satisfactory business environment. This analysis is based on the insights and attitudes of the community (several enterprises and entrepreneurs that operate on the territory of the City of Niš). The result of the performed analysis is information for the local authorities on current concerns and observations of those who are doing business under local government. The system was developed in 2015 at the Faculty of Economics, University of Niš, as well as at the Criminalistics and Police Academy, Belgrade, and implemented on the official web page of the Society of Economists of Niš (http://den.org.rs/). This is a decision support system used in the research conducted by the society. Apart from the society, the second beneficiary of this system is the Local Economic Development Office, City of Niš. The main idea is to offer accurate information to the representatives of the Local Economic Development Office in a timely manner and to inform them with the research results so that they would be able to integrate these results into the strategic plans of local economic development. Finally, the system users are business entities that are involved in the research by providing the system with their attitudes on key concerns in order to improve the local business climate. Therefore, they are taking an active part in the creation of local economic policies in this way.

The study consists of two segments:

(1).

The analysis of the importance of certain criteria for creating a favorable business environment

(2).

The analysis of the fulfilment of these criteria in the respective local government, i.e., the City of Niš.

(3).

The implementation of the aggregated weights determination procedure, which is the topic of this paper, refers to both analyses:

In the first analysis, the research is exclusively focused on the criteria in which improvement is in the jurisdiction of the local government—LBFC. The criteria that are within the competence of national institutions (such as tax incentives or subsidies) are not included in the study. By completing the questionnaire, the opinion of the business community is included in the analysis of this important issue. The identity of the participants is anonymous and only visible to researchers. The main goal of the actual research conducted by the Society of Economists of Niš is to recognize the economic policy at the local level, which would allow the local authorities to contribute, regardless of the state institutions, to the enhancement of the business climate and thus contribute to a rise in economic activity. An example of the online questionnaire (anketa.investnis.rs) for collecting the data from clients is given in Figure 4.

The second analysis is research that is exclusively focused on the criteria in which improvement is in the jurisdiction of the state government. The criteria that are listed as relevant are exactly the same as in the BFC process presented in Section 3.1 of this paper. Both researches involve collecting data from many business entities to determine what factors are important (first analysis), and also, for many cities collection of data, to determine the required intensity of improving the specific criteria determined by the first analysis (second analysis), which leads to conclusion that the importance of the criteria is determined on the basis of their collective judgment. Practically, the main problem is determining the relative importance of the criteria in the decision-making multiple criteria model.

4. Results

According to NALED, the importance of the criteria in the process of business-friendly certification of local self-governments in the Republic of Serbia is defined as the average score of the previous level of evaluation, and it can be defined as the relative importance of observed criteria C_j (row named NALED’s evaluation of criteria importance in

Table 1. The level of criteria fulfilment in municipalities surveyed according to the BFC program.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	Average
NALED’s evaluation of criteria	1.250	1.050	0.950	0.900	0.660	1.000	0.800	1.100	1.250	0.850	0.750	1.150
LSGU 1	0.80	1.00	1.00	0.73	0.88	1.00	1.00	0.73	0.64	0.83	1.00	1.00	0.88
LSGU 2	0.63	0.95	0.80	0.94	0.86	1.18	0.90	0.75	0.67	0.94	0.93	1.00	0.88
LSGU 3	0.90	0.82	0.88	1.00	0.95	1.00	1.00	0.70	0.68	0.76	1.00	0.75	0.87
LSGU 4	1.00	0.62	1.00	0.78	0.60	0.67	1.00	0.60	0.59	0.98	0.83	1.00	0.81
LSGU 5	1.00	1.00	0.75	0.94	0.90	0.94	1.00	0.87	0.91	0.79	1.00	1.00	0.93

). The results related to the level of fulfilment for all observed criteria for five specific cities in the Republic of Serbia, which are not named, are given in Table 1. Using these data, we applied two different methods—AHP method as a subjective approach, and entropy as an objective approach—to determine the weights of the criteria.

4.1. Criteria Weights Determination Using AHP

Regarding the particular problems of the case study of business-friendly certification of local self-government in the Republic of Serbia, as discussed in this paper, it is necessary to perform a comparison on the level of criteria in order to determine the weights of the MCDM model using AHP described in Section 2.1.

Using the evaluation of criteria importance defined by NALED [78], shown in the first row of Table 1, on the basis of pair-wise comparison, a reciprocal matrix is formulated (

Table 2. Pair-wise comparison of criteria.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12
C1	1	3	4	4	8	3	6	2	1	5	6	2
C2	1/3	1	2	3	6	1	4	1	1/3	3	4	½
C3	¼	½	1	1	5	1	3	1/2	¼	2	4	1/3
C4	¼	1/3	1	1	4	½	2	1/3	¼	1	3	¼
C5	1/8	1/6	1/5	¼	1	1/5	1/3	1/6	1/8	¼	1/2	1/7
C6	1/3	1	1	2	5	1	3	1/2	1/3	3	4	½
C7	1/6	¼	1/3	½	3	1/3	1	1/4	1/5	1	2	1/5
C8	½	1	2	3	6	2	4	1	½	4	5	1
C9	1	3	4	4	8	3	5	2	1	5	6	2
C10	1/5	1/3	½	1	4	1/3	1	1/4	0.2	1	2	¼
C11	1/6	¼	¼	1/3	2	¼	1/2	1/5	1/6	½	1	1/5
C12	½	2	3	4	7	2	5	1	½	4	5	1

). Based on the pair-wise comparison, reciprocal matrix, and an algorithm from the AHP method, a vector of priorities has been calculated. The rounded values for j = 1, 2, …, 12 are given in

Table 3. Criteria importance of business-friendly certification model obtained using AHP.

Criteria	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12
Importance wjsub	0.191	0.091	0.060	0.046	0.015	0.075	0.030	0.112	0.189	0.036	0.022	0.130

.

4.2. Criteria Weights Determination Using Method of Entropy

Based on the described procedure of entropy calculation in Section 3.2, the weights of criteria are determined. Determining the weight of the criteria w_j j = 1, 2, …, 12 is carried out through three steps using coefficients a_ij i = 1, 2, …, 5; j = 1, 2, …, 12 from Table 1. In the first step, the normalization of the criteria values of the variants is performed using the standard known form:

$$r_{ij}=\frac{a_{ij}}{{\displaystyle \sum _{}^{}{}_{i=1}^n{a}_{ij}}} \mathrm{for} i= 1, 2, \dots , 5;j= 1, 2, \dots , 12$$

(5)

Thus, a normalized decision matrix is obtained for n = 5 and m = 12 as follows:

$$\begin{array}{ccc}\begin{array}{c} C_1\\ {\omega }_1\end{array}& \begin{array}{c}\dots \\ \dots \end{array}& \begin{array}{c}{C}_m\\ {\omega }_m\end{array}\\ \begin{array}{c} A_1 r_{11}\\ ⋮\\ A_n r_{n1}\end{array}& \begin{array}{c}\dots \\ \ddots \\ \dots \end{array}& \begin{array}{c}{r}_{1m}\\ ⋮\\ r_{nm}\end{array}\end{array}$$

(6)

The quantity of information that is contented in a normalized matrix of decision and carried from each criteria C_j could be measured as a value of entropy e_j:

$$e_j=-k{\displaystyle \sum }_{i=1}^5 r_{ij} \ln r_{ij} i = 1,2,\dots ,5; j = 1,2,\dots ,12$$

(7)

By introducing the constant k = 1/ln(n), it is ensured that all values of e_j are in the interval [0,1]. The second step determines the degree of divergence d_j in relation to the average amount of information contained in each criterion:

d_j = 1 − e_j j = 1, 2, …, 12

(8)

where d_j represents the intrinsic contrast intensity of the C_j criterion. The greater the divergence of the initial criterion values of the variant Ai for the given criterion C_j, the value of d_j for the given criterion is higher, and it is concluded that the importance of the criterion C_j for the given decision problem is greater. If all variants have similar values of degree of divergence for a particular criterion, then this criterion is less important for giving the decision problem. Also, if all the values of the diversity variants are the same for a certain criterion, the given criterion may be omitted because it does not bring new information to the decision-maker. Since the value of d_j represents a specific measure of the intensity of the contra-criteria C_j, the final relative weight of the criterion, in the third step of the method, can be obtained by simple additive normalization:

$${\omega }_j=\frac{d_j}{{\displaystyle \sum _{j=1}^n{d}_j}} j=1, 2, \dots , 12$$

(9)

The obtained results for j = 1, 2, …, 12 are presented in

Table 4. The relative importance of criteria determined by the objective approach using the method of entropy.

Criteria	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12
Importance wjobj	0.12	0.10	0.02	0.05	0.14	0.10	0.12	0.07	0.19	0.03	0.02	0.03

.

4.3. Criteria Weights Determination Using Aggregation Method

During this work, as we mentioned in Section 2.3, we have considered the algebraic aggregation operators and two aggregation methods:

If the aggregated weight of each criterion is obtained as the normalized product of the weighting estimator (AHP method) (w_i^sub = Z_i, i = 1, …, n = 12) and the normalized average weight obtained by using the entropy method (w_i^obj = w_i, i = 1, …, n = 12) [65]:

$$w_i{}^{\left(10\right)}={\alpha }_i=\raisebox{1ex}{$z_i{w}_i$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \sum _{i=1}^n{z}_i{w}_i}$}\right., i=1,\dots ,n$$

(10)

The obtained results for aggregation method I are given in

Table 5. The relative importance of criteria determined by the aggregated approach using Equation (10).

Criteria	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12
Importance αi (w(10))	0.23	0.09	0.01	0.03	0.03	0.08	0.04	0.08	0.36	0.01	0.004	0.04

.

If the aggregate weight of each criterion is obtained as a normalized geometric mean of the weighting entity (AHP method) (w_i^sub = Z_i, i = 1, ..., n = 12) and normalized average weights obtained by using the entropy method (w_i^obj = w_i, i = 1, ..., n = 12) [67]

$${w_i}^{\left(11\right)} = {\alpha }_i = \raisebox{1ex}{$\sqrt{z_i{w}_i}$}\!\left/ \!\raisebox{-1ex}{${{\displaystyle \sum }}_{i=1}^n\sqrt{z_i{w}_i}$}\right., i = 1, \dots , n$$

(11)

The obtained results by aggregated approach II using Equation (11) are given in

Table 6. The relative importance of criteria determined by the aggregated approach II using Equation (11).

Criteria	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12
Importance αi (w(11))	0.16	0.10	0.04	0.05	0.06	0.10	0.07	0.09	0.26	0.04	0.02	0.07

.

The results given in Table 3 and Table 4 compared to the results obtained by the aggregated methods given in Table 5 and Table 6 practically indicate that in the BFC process of cities in the Republic of Serbia, an integrated method that uses the normalized geometric mean of one of the possibly weighted subjects and the normalized average weights obtained by another (preferably by the objective method given in Formula (11) because this aggregated weight will always be in the range between ω_i and z_i, i.e., between w_i^sub and w_i^obj [67,80]) should be used.

5. Discussion

The authors have presented the improvements in the theoretical and practical framework for the planning of sustainable local economic development by the application of multi-criteria analysis. The proposed methodology bridges the gap in the literature when we are talking about indicators’ evaluation for sustainable local economic development by using a new approach for the obtaining of criteria weights coefficients. One can see that the new type of aggregation of subjective and objective methodologies for the calculation of criteria weights has been introduced. The efficiency of the proposed approach has been demonstrated experimentally on the web application having the City of Niš, the Republic of Serbia, as an example. Our new aggregation approach proposed here for the obtaining of criteria weights, tested in the process of local economic development, is a required part of the two phases:

(1).

The phase of determination of the criteria importance on a national level

(2).

The phase of determination of the criteria importance on a local level

The results obtained in this work have shown that the proposed approach is a very powerful tool that could notably improve the decision-making process related to sustainable local economic development. To the best knowledge of the authors, this is one of the first papers related to the field of sustainable local economic development that gives a multi-criteria framework practically implemented on the web application we have used for the verification of the proposed methodology.

The significant differences in the results obtained with two different MCDM approaches considered here, AHP and Entropy, observed by comparing results in Table 3 and Table 4, shows that some kind of aggregation of these two methods for obtaining better methodology is necessary.

The difference in the results given in Table 5 and Table 6 indicates:

• That the results of our proposed method (11) are between results of each individual aggregated method (this is not the case for Method (10));
• The need for some kind of their aggregation to finally get a more efficient and rational result that takes advantages of each of them and simultaneously eliminates their weaknesses that are caused by the fact that with the objective entropy method, some insignificant criteria may become crucial in defining the particular decisions as rational, while with the subjective AHP method, determined weighty criteria may practically have a negligible effect on the final result (as in [81]).

Namely, the entropy as the objective approach for weights determination is an adequate method because it is possible to estimate the homogeneity of the individual judgments of all enterprises and entrepreneurs involved in the research. Due to that, the entropy method has been conducted for the determination of individual importance in both analyses while the AHP method has been used as one subjective because it can use subjective knowledge of experts from this field.

As the homogeneity of individual judgments on the observed criterion is higher, the importance of the criterion is lower, assuming that the weights are calculated based on the degree of the diversification of information $H_j^{}$ by the following equation [65]:

$$\overline{H(w_j)}=1-H(w_j), j=1,\dots ,12$$

(12)

Subsequently, the weights are determined as $w_j=\overline{H(w_j)}/{\displaystyle \sum _{j=1}^n\overline{H(w_j)}}$, where $0\le w_j\le 1$ and ${\displaystyle \sum _{j=1}^n{w}_j}=1$.

Finally, we have made one Wilcoxon Signed Ranks Test for the results obtained with Equations (10) and (11).

Using this test we prove that there is no significant difference between these two methodologies and that the proposed methodology could be applicable—

Table 7. The Wilcoxon Signed Ranks Test in SPSS.

Test Statistics
	GeometricAggregatedCriteriaWeights—ArithmeticAggregatedCriteriaWeights
Z	−1.266
Asymp. Sig. (2-tailed).	0.206

.

6. Conclusions

In conclusion, the authors noticed two important facts that are important from the standpoint of sustainable local economic development. The platform of the considered decision support system is based on a proposed double-sided model of strategic planning of LED used in its obligatory BFC and LBFC processes, which ensure the sustainability of the proposed solution. For the realization of these two processes, the MCDM with an approach of aggregation has been used in the form of a geometric mean of results obtained by AHP as subjective and entropy as objective methodology, which provides a balanced approach to the final solution. General limitations of each type of methodology that we have included in the aggregated proposed solutions have been minimized. Using this way, the system creates the favorites of the business community related to the criteria for the assessment of the local business environment (first analysis) and necessary correction estimation of the city in the Republic of Serbia (second analysis on the basis of implementation of the proposed model). This application has been proven as a useful tool for dynamic observing of the local business environment realized as a software tool on a local government website (http://investnis.rs). Results obtained in this article enables that the further work of authors and other researchers who deal with the problem of aggregation of criteria weighting using AHP as subjective and entropy as objective methods could be researched and tested with a more efficient solution of aggregation of one subjective and one objective method. They should have in mind new subjective methods, for example, BMW, SWARA, or FUCOM, and also new objective methods, for example, CRITIC and FANMA, which may have the advantages in enabling better results in solving considered and similar problems in other areas of human life.

The contribution of this paper can be considered from two points of view. The theoretical work has provided a new approach of the aggregation of subjective and objective methods of multi-criteria decision-making, which ensures that the results obtained by its application are always between the results when they are applied individually. This eliminates the possible bad effects of each of the methods from the group of subjective and objective methods. The practical work has dealt with the practical implementation of the proposed method in the concrete system for planning of sustainable local economic development of the City of Niš in the Republic of Serbia.