Study of Entropy Generation with Multi-Slip Effects in MHD Unsteady Flow of Viscous Fluid Past an Exponentially Stretching Surface

Abstract

The current study aims to probe the impacts of entropy in a hydromagnetic unsteady slip flow of viscous fluid past an exponentially stretching sheet. Appurtenant similarity variables are employed to transmute the governing partial differential equations into a system of non-linear differential equations, which are analytically solved by utilizing the homotopy analysis method (HAM). Moreover, a shooting technique with fourth–fifth order Runge–Kutta method is deployed to numerically solve the problem. The impact of the physical parameters that influence the flow and heat transmission phenomena are sketched, tabulated and discussed briefly. Additionally, the impact of these parameters on entropy generation is thoroughly discussed by plotting graphs of the local entropy generation number and the Bejan number.

1. Introduction

Initially, the analytical solution for a boundary layer flow problem over a linearly stretching sheet was explored by Crane [1]. Since then, numerous studies have been carried out on this topic [2,3,4,5]. Such investigations have many diverse applications in crystal growth, polymer extrusion, the spinning of fibers, condensation process, metallic sheet cooling, etc. However, the stretching rate of the surface may not always be linear in practical cases. There may be cases where the sheet may stretch with an exponential order. Motivated by this idea, Magyari and Keller [6] investigated the flow and heat transmission of a Newtonian fluid over an exponentially stretching sheet with an exponential temperature distribution. Elbashbeshy [7] discussed the characteristics of the heat transmission of viscous fluid over a permeable exponentially stretching sheet and attained similarity solutions. Al-Odat et al. [8] examined the impacts of magnetic field on the thermal boundary layer of a viscous fluid past an exponentially stretching surface. El-Aziz [9] assumed the impacts of viscous dissipation on a mixed convective micropolar fluid flow that was induced by an exponentially stretching surface. Bidin and Nazar [10] applied the implicit finite difference scheme to obtain to similarity solutions of radiative boundary layer flow of a Newtonian fluid over an exponentially stretching surface. Ishak [11] numerically investigated the steady hydro magnetic flow of a viscous fluid past a stretching surface in the presence of thermal radiation and found that thermal radiation plays a vital role in the augmentation of fluid temperature. Mukhopadhyay and Gorla [12] assumed the velocity and thermal slip conditions at the surface of a exponentially stretching sheet and explored the flow and heat transmission characteristics. They concluded that velocity and thermal slip parameters have decreasing impact on temperature. Sahoo and Poncet [13] explored the influence of partial slip on the flow and heat transmission of third-grade fluid past a continuously stretching surface. Bhattacharyya and Vajravelu [14] examined the stagnation point flow of a viscous fluid past an exponentially contracting sheet and attained similar solutions. Mukhopadhyay et al. [15] studied a Casson fluid flow that was induced by a stretching of sheet with an exponential order. Jyothi [16] examined the effects of thermophoresis on a dissipative Magneto-hydrodynamics viscous fluid flow due to an exponentially stretching surface and observed that thermophoresis had a decreasing effect on a species concentration profile. Reddy [17] considered a hydromagnetic Casson fluid flow past an inclined exponential surface in the presence of thermal radiation and a chemical reaction, and they carried out a comprehensive parametric analysis of the problem. Patil et al. [18] obtained non-similar solutions of a mixed convective flow of a Newtonian fluid past a stretching surface in an exponential order. Jusoh et al. [19] analyzed the MHD rotating flow of a ferrofluid past a permeable, exponentially stretching/shrinking sheet and obtained dual solutions.

Flow and heat transmission procedures are subjected to energy losses that are irreversible. According to Bejan [20], these energy losses can be measured by using the quantity known as the entropy generation. He remarked that by recognizing the elements that produce entropy, energy losses can be reduced. This idea was adopted by engineers and investigators to explicate entropy impacts in various geometrical configurations. However, Tayamol [21] was the first to examine the entropy generation impacts in a viscous flow past a stretching sheet that was immersed in permeable media. Aiboud and Saouli [22] explored the entropy production in a hydromagnetic viscoelastic fluid past a linearly stretching sheet. Butt et al. [23] investigated the entropy generation effects in a mixed convective flow of a second-grade fluid past a stretching surface and found that the viscoelastic parameter has a significant impact on entropy production. Later on, Butt et al. [24] considered the slip effects on a stretchable surface and studied the entropy effects in the magneto hydrodynamic flow of a viscous fluid. They remarked that the presence of a slip at the surface reduces the production of entropy. The effects of slip and heat generation/absorption effects on a nanofluid flow past a linearly stretching sheet were examined by Noghrehabadi et al. [25]. Butt and Ali [26] carried out a study related to entropy effects in a viscous fluid flow past an unsteady stretching surface. Rashidi et al. [27] considered the stagnation point flow of a Newtonian fluid past a porous stretching sheet that was immersed in spongy media and analyzed the entropy impacts. The entropy effects of a three-dimensional Newtonian fluid over an exponential sheet were considered by Afridi and Qasim [28]. A mathematical investigation of an asymmetrical wavy motion of blood under entropy generation effects was presented by Riaz et al. [29]. Zaib, A. et al. explored the aligned magnetic flow comprising of nanoliquid over a radially stretching surface with entropy generation [30]. Recently, Butt et al. [31] theoretically explored the entropy impacts of a Casson nanofluid flow past an unsteady stretching surface. The found that unsteadiness had an enhancing effect on the generation of entropy effects.

Motivated by the stated facts, efforts have been devoted to scrutinize the impacts of entropy generation in the magnetohydrodynamic unsteady slip flow of a viscous fluid passing over an exponentially stretching sheet. To the best of our knowledge, entropy impacts, with the effect logs of an MHD unsteady slip flow have not been presented yet, and the results that are communicated here are new. The homotopy analysis method (HAM) and the shooting technique with the fourth–fifth order Runge–Kutta method were employed to solve the considered problem. The impact of the pertinent parameters on flow and heat and mass transmission features as well as on entropy generation are presented via graphs and tables, and they are explained briefly.

2. Mathematical Modeling

Consider the unsteady, two-dimensional incompressible flow of an electrically conducting viscous fluid due to an exponentially stretching surface as shown in Figure 1. It is assumed that the exponentially stretching surface is placed along the x-axis, and the y-axis is situated normal to the surface. The viscous fluid is considered to be confined in the area $y\ge 0$. A variable magnetic field $B\left(x,t\right)=\frac{B_0}{\sqrt{1-ct}}{e}^{\frac{x}{2L}}$ is applied normal to the surface where $B_0$ is the constant. Here, c is the dimensional constant and L represents the characteristics’ length. The effects of the induced magnetic field are neglected as the value of the magnetic Reynolds number is small. The surface is stretched with the exponential velocity $U_w(x,t)=\frac{U_0}{1-ct}{e}^{\frac{x}{L}}$, and the surface temperature is kept at $T_w(x)=T_{\infty }+\frac{T_o}{1-ct}{e}^{\frac{x}{2L}}$. The ambient fluid temperature is assumed to be \$T_{\infty }$. The effects of viscous and joule dissipations are assumed to be present. Under the application of the boundary layer approximation, the governing equations for continuity, momentum and heat are:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\nu \frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma B^2}{\rho }u,$$

(2)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k}{\rho c_p}\frac{{\partial }^{2}T}{\partial y^2}+\frac{\nu }{c_p}{\left(\frac{\partial u}{\partial y}\right)}^2+\frac{\sigma B^2}{\rho c_p}{u}^2,$$

(3)

The appurtenant boundary constraints are

$$\begin{array}{l}u=u_w(x,t)=\frac{U_0}{1-ct}{e}^{\frac{x}{L}}+\alpha \frac{\partial u}{\partial y},v=0,T=T_w(x,t)=T_{\infty }+\frac{T_0}{1-ct}{e}^{\frac{A_{o}x}{2L}}\mathrm{at}y=0,\\ u\to 0,v\to 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}T\to T_{\infty }\mathrm{as}y\to \infty .\end{array}\}$$

(4)

Here, $(u,v)$ are the velocity components in the $(x,y)$ directions, respectively, $T$ is the temperature of the fluid, $T_0$ is the reference temperature, $T_{\infty }$ is the temperature far away from the surface, $\rho$ represents the fluid density, $\nu$ is the kinematic viscosity, $k$ is the thermal conductivity, $\sigma$ is the electrical conductivity, $c_p$ represents the specific heat at constant pressure, $U_o$ is the reference velocity, $\alpha$ is the hydrodynamic slip parameter, $T_o$ denotes the reference temperature, $A_0$ is the dimensional constant temperature, and $c$ is the constant with $ct<1$.

The following set of similarity transformation is used to non-dimensionalized Equations (1)–(3):

$$\begin{array}{l}u=\frac{U_0}{1-ct}{e}^{\frac{x}{L}}\hspace{0.17em}{f}^{\prime }(\xi ),v=-\sqrt{\frac{U_0\nu }{2L(1-ct)}}\hspace{0.17em}\hspace{0.17em}{e}^{\frac{x}{2L}}\hspace{0.17em}\left[f(\xi )+\xi f^{\prime }(\xi )\right],\\ \xi =\sqrt{\frac{U_0\nu }{2\nu (1-ct)}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{e}^{\frac{x}{2L}}y,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\theta (\xi )=\frac{T-T_{\infty }}{T_w-T_{\infty }}.\end{array}\}$$

(5)

By substituting Equation (5) into Equations (1)–(3), the continuity Equation (1) is identically satisfied, and Equations (2) and (3) take the form:

$$f^{‴}+f{f}^{″}-2f^{{\prime }^2}-A(\xi f^{″}+2f^{\prime })-M{f}^{\prime }=0,$$

(6)

$${\theta }^{″}+\mathrm{Pr}f{\theta }^{\prime }-A_0\mathrm{Pr}{f}^{\prime }\theta -A\mathrm{Pr}(4\theta +\xi {\theta }^{\prime })+\mathrm{Pr}Ec{f^{″}}^2+M\mathrm{Pr}Ec{f^{\prime }}^2=0.$$

(7)

The associated boundary conditions after applying Equation (5) take the form

$$\begin{array}{l}f\left(0\right)=0,f^{\prime }\left(0\right)=1+\gamma f^{″}\left(0\right),\theta \left(0\right)=1,\\ f^{\prime }\left(\xi \right)\to 0,\theta \left(\xi \right)\to 0\hspace{1em}\hspace{1em}\mathrm{as}\hspace{1em}\hspace{1em}\xi \to \infty .\end{array}\}$$

(8)

Here, $M=\frac{2\sigma B_0^{2}L}{\rho U_0}$ represents the magnetic field parameter, $A=\frac{cL{e}^{-X}}{U_0}$ is the unsteadiness parameter, $\gamma =\alpha \sqrt{\frac{U_0{e}^X}{2\nu L(1-ct)}}$ is the slip parameter, $X=\frac{x}{L}$ is the dimensionless parameter, $\mathrm{Pr}=\frac{\mu c_p}{k}$ is the Prandtl number, and $Ec=\frac{U_w^2}{c_p(T_w-T_{\infty })}$ is the Eckert number. The skin friction coefficient $C_{fx}$ and the local Nusselt number $N{u}_x$ are defined as:

$$C_{f_x}=\frac{{{\tau }_w|}_{y=0}}{\rho u_w^2},\hspace{1em}\hspace{1em}\hspace{1em}N{u}_x=\frac{x{q_w|}_{y=0}}{k\left(T_w-T_{\infty }\right)},$$

(9)

where the shear stress ${\tau }_w$ and the heat flux $q_w$ at the surface are given as:

$${\tau }_w={\mu \left(\frac{\partial u}{\partial y}\right)|}_{y=0},\hspace{1em}\hspace{1em}\hspace{1em}{q}_w=-{k\left(\frac{\partial T}{\partial y}\right)|}_{y=0}.$$

(10)

By substituting Equation (10) into Equation (9) and by using Equation (5), the dimensionless form of the skin friction coefficient $C_{fx}$ and the local Nusselt number $N{u}_x$ are:

$${\mathrm{Re}}_x^{1/2}{C}_{fx}=f^{″}(0),\hspace{1em}\hspace{1em}\hspace{1em}\sqrt{\frac{2}{X}}{\mathrm{Re}}_x^{-1/2}N{u}_x=-{\theta }^{\prime }(0),$$

(11)

where ${\mathrm{Re}}_x=\frac{U_{w}x}{\nu }$ is the local Reynolds number.

3. Entropy Analysis

After the application of the boundary layer approximation, the expression for the local volumetric rate of entropy generation $S_G$ for the viscous fluid in the presence of a magnetic field is defined as:

$$S_G=\underset{\begin{array}{l}\mathrm{Entropy}\mathrm{due}\mathrm{to}\\ \mathrm{Heat}\mathrm{Transfer}\end{array}}{\underbrace{\frac{k}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2}}+\underset{\begin{array}{l}\mathrm{Entropy}\mathrm{due}\mathrm{to}\\ \mathrm{viscous}\mathrm{dissipation}\end{array}}{\underbrace{{\left(\frac{\partial u}{\partial y}\right)}^2}}+\underset{\begin{array}{l}\mathrm{Entropy}\mathrm{due}\\ \mathrm{to}\mathrm{magnetic}\mathrm{field}\end{array}}{\underbrace{\frac{\sigma B_o^2}{T_{\infty }}{u}^2.}}$$

(12)

The above expression shows that the key factors that are responsible for the production of entropy effects are heat transfer, viscous dissipation, and the presence of a magnetic field.

The dimensionless form of the expression for the local entropy generation defined in Equation (12) can be obtained by using Equation (5) as:

$$N_G=\frac{S_G}{S_{Go}}={\mathrm{Re}}_L{\theta }^{{\prime }^2}+{\mathrm{Re}}_L\frac{Br}{\Omega }{f}^{{″}^2}+{\mathrm{Re}}_L\frac{Br}{\Omega }M{f}^{{\prime }^2},$$

(13)

where $N_G$ is the ratio of the local entropy generation rate to the characteristic entropy generation rate and is called the local entropy generation number. Here, $S_{Go}=\frac{k{\left(T_w-T_{\infty }\right)}^2}{T_{\infty }{}^2{L}^2}$ is the characteristic entropy generation rate, $\Omega =\frac{T_w-T_{\infty }}{T_w}$ denotes the dimensionless temperature difference, ${\mathrm{Re}}_L=\frac{U_{L}L}{v}$ is the local Reynolds number, and $Br=\mathrm{Pr}Ec$ is the Brinkman number. Equation (13) can also be written in the form:

$$N_G=N_{G_H}+N_{G_F}+N_{G_M},$$

(14)

where

$$\begin{array}{l}{N}_{G_H}={\mathrm{Re}}_L{{\theta }^{\prime }}^2,\\ N_{G_F}={\mathrm{Re}}_L\frac{Br}{\Omega }{f}^{{″}^2},\\ N_{G_M}={\mathrm{Re}}_L\frac{Br}{\Omega }M{f}^{{\prime }^2}.\end{array}\}$$

(15)

Here, $N_{G_H}$ denotes the entropy generation number due to heat transfer, $N_{G_F}$ represents the entropy generation number due to viscous dissipation, and $N_{G_M}$ is the entropy generation number due to the presence of the magnetic field.

Another useful quantity is the Bejan number, which is given as:

$$Be=\frac{\mathrm{Entropy}\mathrm{due}\mathrm{to}\mathrm{heat}\mathrm{transfer}}{\mathrm{Local}\mathrm{entropy}\mathrm{generation}}=\frac{N_{G_H}}{N_{G_H}+N_{G_F}+N_{G_M}}.$$

(16)

This expression helps to identify whether the heat transfer entropy effects dominate the viscous dissipation and magnetic field or vice versa. It can be seen that the value of the Bejan number varies between 0 and 1. When the value of $Be$ is greater than 0.5, the entropy effects that are caused by heat transfer dominate the fluid friction and magnetic field effects. On the other hand, if the value of the Bejan number is less than 0.5, the entropy effects due to fluid friction and magnetic field dominate the transfer entropy effects. When $Be=0.5$, the contributions of both the entropy effects are equal.

4. Solution to the Problem

4.1. Homotopy Analysis Method

The analytical method known as the homotopy analysis method (HAM) is a powerful technique that is helpful in solving highly nonlinear equations. This method has been employed to obtain the solution of the problems related to fluid dynamics and heat transmission (see [23,24,26,27]). In this article, Equations (6) and (7) with the boundary conditions of Equation (8) were solved by the HAM by considering the following linear operators and linear guesses:

$$\begin{array}{l}{f}_0\left(\xi \right)=\frac{1}{1+\gamma }\left(1-e^{-\xi }\right),\\ {\theta }_0\left(\xi \right)=e^{-\xi }.\end{array}\}$$

(17)

$$\begin{array}{l}{ℒ}_f(f)=\frac{d^{3}f}{d{\xi }^3}-\frac{df}{d\xi },\\ {ℒ}_{\theta }(\theta )=\frac{d^2\theta }{d{\xi }^2}-\theta .\end{array}\}$$

(18)

The above operator possesses the following properties:

$$\begin{array}{l}{ℒ}_f\left(C_1+C_2{e}^{\xi }+C_3{e}^{-\hspace{0.17em}\xi }\right)=0,\\ {ℒ}_{\theta }\left(C_4{e}^{\xi }+C_5{e}^{-\xi }\right)=0,\end{array}\}$$

(19)

where ${C_j}^{\prime }s,(j=1,2,\mathrm{...5})$ are arbitrary constants.

The zeroth order deformation problem can be written as:

$$(1-q){ℒ}_f\left[\overline{F}(\xi ;q)-f_0(\xi )\right]={\hslash }_{f}q{\mathcal{N}}_f\left[\overline{F}(\xi ;q)\right],$$

(20)

$$(1-q){ℒ}_{\theta }\left[\overline{\Theta }(\xi ;q)-{\theta }_0(\xi )\right]={\hslash }_{\theta }q{\mathcal{N}}_{\theta }\left[\overline{F}(\xi ;q),\overline{\Theta }(\xi ;q)\right],$$

(21)

$$\begin{array}{l}\overline{F}(0;q)=0,\frac{\partial \overline{F}(0;q)}{\partial \xi }=1+\gamma \frac{{\partial }^2\overline{F}}{\partial {\xi }^2}\left(0;q\right),\overline{\Theta }(0;q)=1,\\ \frac{\partial \overline{F}(\infty ;q)}{\partial \xi }=0,\overline{\Theta }(\infty ;q)=0.\end{array}\}$$

(22)

Here, ${\hslash }_f\mathrm{and}{\hslash }_{\theta }$ are the convergence control parameters and $q\in [0,1]$ denotes the embedding parameter that is related to the deformation mappings $\overline{F}(\xi ;q),\overline{\Theta }(\xi ;q)$ that continuously deform from $f_0(\xi ),{\theta }_0(\xi )$ to $f(\xi ),\theta (\xi )$ when $q$ varies from 0 to 1.

The non-linear operators are defined as:

$$\begin{array}{l}{\mathcal{N}}_f\left[\overline{F}(\xi ;q)\right]=\frac{{\partial }^3\overline{F}(\xi ;q)}{\partial {\xi }^3}+\overline{F}(\xi ;q)\frac{{\partial }^2\overline{F}(\xi ;q)}{\partial {\xi }^2}-2{\left(\frac{\partial \overline{F}(\xi ;q)}{\partial \xi }\right)}^2\\ -A\left(\xi \frac{{\partial }^2\overline{F}(\xi ;q)}{\partial {\xi }^2}+2\frac{\partial \overline{F}(\xi ;q)}{\partial \xi }\right)-M\frac{\partial \overline{F}(\xi ;q)}{\partial \xi },\end{array}\}$$

(23)

$$\begin{array}{l}{\mathcal{N}}_{\theta }\left[\overline{F}(\xi ;q),\overline{\Theta }(\xi ;q)\right]=\frac{{\partial }^2\overline{\Theta }(\xi ;q)}{\partial {\xi }^2}+\mathrm{Pr}\overline{F}(\xi ;q)\frac{\partial \overline{\Theta }(\xi ;q)}{\partial \xi }-A_o\mathrm{Pr}\frac{\partial \overline{F}(\xi ;q)}{\partial \xi }\overline{\Theta }(\xi ;q)\\ -A\mathrm{Pr}\left(4\overline{\Theta }(\xi ;q)+\xi \frac{\partial \overline{\Theta }(\xi ;q)}{\partial \xi }\right)+\mathrm{Pr}Ec{\left(\frac{{\partial }^2\overline{F}(\xi ;q)}{\partial {\xi }^2}\right)}^2+M\mathrm{Pr}Ec{\left(\frac{\partial \overline{F}(\xi ;q)}{\partial \xi }\right)}^2,\end{array}\}$$

(24)

The rest of the details of the method can be seen in the literature (see [23,24,26]). The solution of the differential Equations (6) and (7) with the boundary conditions of Equation (8) can be written in the form of infinite series as:

$$\begin{array}{l}f(\xi )=f_0(\xi )+{\displaystyle \sum _{m=1}^{\infty }{f}_m(\xi )},\\ \theta (\xi )={\theta }_0(\xi )+{\displaystyle \sum _{m=1}^{\infty }{\theta }_m(\xi )}.\end{array}\}$$

(25)

From the above procedure, it can be noted that the series solutions that are mentioned in Equation (25) contain the convergence control parameters ${\hslash }_f\mathrm{and}{\hslash }_{\theta }$, which can be adjusted to control the convergence rate of the series solutions. In order to ensure the fast convergence of these series solutions, optimal values of ${\hslash }_f\mathrm{and}{\hslash }_{\theta }$ were used. In order to obtain the optimal values of ${\hslash }_f\mathrm{and}{\hslash }_{\theta }$, the averaged root mean square errors were calculated as follows:

$$\begin{array}{l}{E}_{m,f}=\sqrt{\frac{1}{N+1}{\displaystyle \sum _{j=0}^k{\left[{\mathcal{N}}_f\left({\displaystyle \sum _{i=0}^m{f}_i(j\Delta \zeta )}\right)\right]}^2}},\\ E_{m,\theta }=\sqrt{\frac{1}{N+1}{\displaystyle \sum _{j=0}^k{\left[{\mathcal{N}}_f\left({\displaystyle \sum _{i=0}^m{f}_i(j\Delta \zeta )},{\displaystyle \sum _{i=0}^m{\theta }_i(j\Delta \zeta )}\right)\right]}^2}},\end{array}\}$$

(26)

where $f_i(j\Delta \zeta )\mathrm{and}{\theta }_i(j\Delta \zeta )$ are the discretization of the continuous functions $f(\xi )\mathrm{and}\theta (\xi )$ into $N$ pieces by selecting $\Delta \zeta =0.2$ and $N=20$. The optimal values of ${\hslash }_f\mathrm{and}{\hslash }_{\theta }$ were computed by minimizing the values of $E_{m,f}$ and $E_{m,\theta }$ by employing the first derivative law of calculus.

Table 1. Optimal values of ${\hslash }_f$ and ${\hslash }_{\theta }$, as well as their corresponding averaged root mean squared residual errors $E_{m,f}$ and $E_{m,\theta }$ at different orders of approximation when $M=1.0,\gamma =0.5,A=1.0,A_0=0.5,$ $\mathrm{Pr}=1.0,Ec=0.2$.

$\mathit{O}\mathit{r}\mathit{d}\mathit{e}\mathit{r} \mathit{o}\mathit{f} \mathit{A}\mathit{p}\mathit{p}\mathit{r}\mathit{o}\mathit{x}\mathit{i}\mathit{m}\mathit{a}\mathit{t}\mathit{i}\mathit{o}\mathit{n} \mathit{m}$	${\mathit{\hslash }}_{\mathit{f}}$	${\mathit{\hslash }}_{\mathit{\theta }}$	${\mathit{E}}_{\mathit{m},\mathit{\theta }}$	${\mathit{E}}_{\mathit{m},\mathit{\theta }}$
$3$	$-0.464353$	$-0.396157$	$1.05905\times {10}^{-2}$	$2.69482\times {10}^{-3}$
$6$	$-0.405309$	$-0.424927$	$1.81301\times {10}^{-5}$	$1.25275\times {10}^{-4}$
$9$	$-0.382564$	$-0.413877$	$1.49644\times {10}^{-5}$	$2.93299\times {10}^{-5}$
$12$	$-0.369398$	$-0.368290$	$8.38391\times {10}^{-7}$	$9.89133\times {10}^{-6}$
$15$	$-0.314784$	$-0.326304$	$2.48338\times {10}^{-6}$	$3.91650\times {10}^{-6}$

displays the optimal values of ${\hslash }_f\mathrm{and}{\hslash }_{\theta }$ with their corresponding averaged root mean square errors $E_{m,f}$ and $E_{m,\theta }$ at different orders of approximation. It was noticed that the values of ${\hslash }_f\mathrm{and}{\hslash }_{\theta }$ improved with the simultaneous decrease in $E_{m,f}$ and $E_{m,\theta }$ as the order of approximation increased. The convergence rate was further accelerated by employing a Padé approximation on the series solutions that were attained by the homotopy method.

Table 2. Convergence table for the $[m/m]$ homotopy Padé approximation of $-f^{″}(0)\mathrm{and}-{\theta }^{\prime }(0)$ when ${\hslash }_f=-0.314784,{\hslash }_{\theta }=-0.398461,$ $M=1.0,\gamma =0.5,A=1.0,A_0=0.5,$ $\mathrm{Pr}=1.0,Ec=0.2$.

$[\mathit{m}/\mathit{m}]$	$-{\mathit{f}}^{″}(0)$	$-{\mathit{\theta }}^{\prime }(0)$
$\left[5/5\right]$	$0.95890$	$1.93308$
$\left[10/10\right]$	$0.95923$	$1.92904$
$\left[15/15\right]$	$0.95921$	$1.92905$
$\left[20/20\right]$	$0.95921$	$1.92905$
$\left[25/25\right]$	$0.95921$	$1.92905$
$\left[30/30\right]$	$0.95921$	$1.92905$
$\left[35/35\right]$	$0.95921$	$1.92905$

shows the convergence of the numerical values of $-f^{″}(0)\mathrm{and}-{\theta }^{\prime }(0)$ for the $[m/m]$ homotopy Padé approximation when ${\hslash }_f=-0.314784,{\hslash }_{\theta }=-0.398461,$ $M=1.0,\gamma =0.5,A=1.0,A_0=0.5,$ $\mathrm{Pr}=1.0,Ec=0.2$. It can be seen that the convergence of the series solutions of Equation (25) was attained up to 5 decimal places at the $[15/15]$ homotopy Padé approximation.

4.2. Numerical Method

In order to counter check the results that were computed by the HAM, the nonlinear differential Equations (6) and (7) were numerically solved by applying shooting technique with fourth–fifth order Runge–Kutta–Fehlberg method. For this, Equations (6) and (7) were transformed in to a set of first order differential equations. For this purpose, let $f=y_1,f^{\prime }=y_2,f^{″}=y_3,\theta =y_4,{\theta }^{\prime }=y_5$. Thus,

$$\begin{array}{l}{y_1}^{\prime }=y_2,\\ {y_2}^{\prime }=y_3,\\ {y_3}^{\prime }=\left(-y_1{y}_3+2y_2{}^2+A(\xi y_3+2y_2)+M{y}_2\right),\\ {y_4}^{\prime }=y_5,\\ {y_5}^{\prime }=-\mathrm{Pr}{y}_1{y}_5+A_o\mathrm{Pr}{y}_2{y}_4+A\mathrm{Pr}(4y_4+\xi y_5)-\mathrm{Pr}Ec{y}_3{}^2-M\mathrm{Pr}Ec{y}_2{}^2.\end{array}\}$$

(27)

and the associated initial conditions are

$$\begin{array}{l}{y}_1(0)=0,\\ y_2(0)=1+\gamma r_1,\\ y_3(0)=r_1,\\ y_4(0)=1,\\ y_5(0)=r_2,\end{array}\}$$

(28)

where $r_1\mathrm{and}{r}_2$ are the unknown values. In order to solve the above system of Equations (27) and (28) the values of $r_1\mathrm{and}{r}_2$ were to be determined. In the beginning, these values were guessed, and the solution of the system of Equations (27) and (28) was achieved by applying the fourth–fifth-order Runge–Kutta–Fehlberg method. The Secant method is then employed to improve the guessed values of $r_1\mathrm{and}{r}_2$ and the procedure was iteratively repeated. To obtain the solution of the system, the semi-infinite domain $[0,\infty [$ was truncated to a finite domain, $[0,{\xi }_{\infty }[$ where ${\xi }_{\infty }$ was so chosen that the boundary conditions defined in Equations (8) were asymptotically satisfied by the numerical solution. The value of ${\xi }_{\infty }$ was set at 20 for all values of parameters, and the calculations were done. The convergence criterion was taken to be ${10}^{-5}$, and a step size of 0.001 was selected.

5. Results and Discussion

The solutions of non-linear Ordinary differential Equations (6) and (7) with the boundary constraints of Equation (8) were compared with existing literature under limiting conditions.

Table 3. Comparison of present values of $-{\theta }^{\prime }\left(0\right)$ with those reported by Magyari and Keller [6], El-Aziz [9], Nazar [10] and Ishak [11] for variation in the Prandtl number $\mathrm{Pr}$ and the magnetic field parameter $M$ when $\gamma =0.0,A=0.0,A_o=1.0,Ec=0.0$.

$\mathit{M}$	$\mathbf{Pr}$	$-{\mathit{\theta }}^{\prime }(0)$ Magyari and Keller [6]	$-{\mathit{\theta }}^{\prime }(0)$ E1-Aziz [9]	$-{\mathit{\theta }}^{\prime }(0)$ Bidin and Nazar [10]	$-{\mathit{\theta }}^{\prime }(0)$ Anuar Ishak [11]	Present
						$-{\mathit{\theta }}^{\prime }(0)$ HAM	$-{\mathit{\theta }}^{\prime }(0)$ Numerical
$\mathbf{0.0}$	$\mathbf{1.0}$	$\mathbf{0.954782}$	$\mathbf{0.954785}$	$\mathbf{0.9548}$	$0.9548$	$0.95478$	$0.95478$
	$2.0$	$----$	$----$	$1.4714$	$1.4715$	$1.47146$	$1.47146$
	$3.0$	$1.869075$	$1.869072$		$1.8691$	$1.86907$	$1.86907$
	$5.0$	$2.500135$	$2.500132$		$2.5001$	$2.50012$	$2.50012$
	$10.0$	$3.660379$	$3.660372$		$3.6604$	$3.66027$	$3.66027$
$1.0$	$1.0$	$----$	$----$	$----$	$0.8611$	$0.86109$	$0.86109$

was drawn to compare the numerical values of $-{\theta }^{\prime }(0)$ with those mentioned by Magyari and Keller [6], El-Aziz [9], Nazar [10] and Ishak [11] for several values of $\mathrm{Pr}$ and $M$ when $\gamma =0.0,A=0.0,A_o=1.0,Ec=0.0$. It was witnessed that the numerical values of $-{\theta }^{\prime }(0)$ that were obtained by the HAM and the shooting method in the current study were in excellent agreement with the literature.

Table 4. Numerical values of $-f^{″}(0)$ that were obtained by the homotopy analysis method (HAM) and the shooting method for variation in the values of the slip parameter $\gamma$, the magnetic field parameter $M$, and the unsteadiness parameter $A$.

$\mathit{\gamma }$	$\mathit{M}$	$\mathit{A}$	$-{\mathit{f}}^{″}\left(0\right)$$\mathit{H}\mathit{A}\mathit{M}$	$-{\mathit{f}}^{″}\left(0\right)$$\mathit{N}\mathit{u}\mathit{m}\mathit{e}\mathit{r}\mathit{i}\mathit{c}\mathit{a}\mathit{l}$
$0.5$	$1.0$	$0.2$	$0.85691$	$0.85691$
		$0.5$	$0.89946$	$0.89946$
		$1.0$	$0.95920$	$0.95920$
		$1.5$	$1.00841$	$1.00841$
$0.5$	$0.0$	$1.0$	$0.88048$	$0.88048$
	$1.0$		$0.95920$	$0.95920$
	$2.0$		$1.02039$	$1.02039$
	$3.0$		$1.06998$	$1.06998$
$0.0$	$1.0$	$1.0$	$2.04499$	$2.04499$
$0.5$			$0.95920$	$0.95920$
$1.0$			$0.63912$	$0.63912$
$2.0$			$0.38676$	$0.38676$

was constructed to note the impacts of the parameters $\gamma$, $M$ and $A$ on the magnitude of the dimensionless skin friction coefficient $-f^{″}(0)$. This illustrates that rise in the values of $M$ and $A$ enhanced the skin friction at the surface, whereas the slip parameter had a decreasing impact on $-f^{″}(0)$.

Table 5. Numerical values of $-{\theta }^{\prime }(0)$ that were obtained by the HAM and the shooting method for variation in the values of the slip parameter $\gamma$, the magnetic field parameter $M$, the unsteadiness parameter $A$, the temperature exponent $A_o$, the Prandtl number $\mathrm{Pr}$ and the Eckert number $Ec$.

$\mathit{\gamma }$	$\mathit{M}$	$\mathit{A}$	${\mathit{A}}_0$	$\mathbf{Pr}$	$\mathit{E}\mathit{c}$	$-{\mathit{\theta }}^{\prime }\left(0\right) \mathit{H}\mathit{A}\mathit{M}$	$-{\mathit{\theta }}^{\prime }\left(0\right)$$\mathit{N}\mathit{u}\mathit{m}\mathit{e}\mathit{r}\mathit{i}\mathit{c}\mathit{a}\mathit{l}$
$0.5$	$1.0$	$1.0$	$0.5$	$1.0$	$0.2$	$1.92905$	$1.92905$
					$0.5$	$1.86944$	$1.86944$
					$0.7$	$1.82970$	$1.82970$
					$0.9$	$1.78996$	$1.78996$
$0.5$	$1.0$	$1.0$	$0.5$	$0.7$	$0.2$	$1.61368$	$1.61368$
				$1.0$		$1.92905$	$1.92905$
				$2.0$		$2.72687$	$2.72687$
				$3.0$		$3.33743$	$3.33743$
$0.5$	$1.0$	$1.0$	$0.5$	$1.0$	$0.2$	$1.92905$	$1.92905$
			$1.0$			$1.97510$	$1.97510$
			$1.5$			$2.02057$	$2.02057$
			$2.0$			$2.06548$	$2.06548$
$0.5$	$1.0$	$0.2$	$0.5$	$1.0$	$0.2$	$0.96247$	$0.96247$
		$0.5$				$1.40692$	$1.40692$
		$1.0$				$1.92905$	$1.92905$
		$1.5$				$2.33731$	$2.33731$
$0.5$	$0.0$	$1.0$	$0.5$	$1.0$	$0.2$	$1.95329$	$1.95329$
	$1.0$					$1.92905$	$1.92905$
	$2.0$					$1.91235$	$1.91235$
	$3.0$					$1.90015$	$1.90015$
$0.0$	$1.0$	$1.0$	$0.5$	$1.0$	$0.2$	$1.88525$	$1.88525$
$0.5$						$1.92905$	$1.92905$
$1.0$						$1.92378$	$1.92378$
$2.0$						$1.91240$	1.91240

shows the values of $-{\theta }^{\prime }(0)$ that were obtained by both the HAM and the shooting technique for various values of the different parameters $\gamma$, $M$, $A$, $\mathrm{Pr}$, $Ec$ and temperature exponent $A_0$. An increase in the value of $-{\theta }^{\prime }(0)$ was noticed with the rise in the slip parameter $\gamma$, the unsteadiness parameter $A$, the temperature exponent $A_0$, and the Prandtl number $\mathrm{Pr}$. On the other hand, increasing the values of the parameters $M$ and $Ec$ had a decreasing impact on $-{\theta }^{\prime }(0)$.

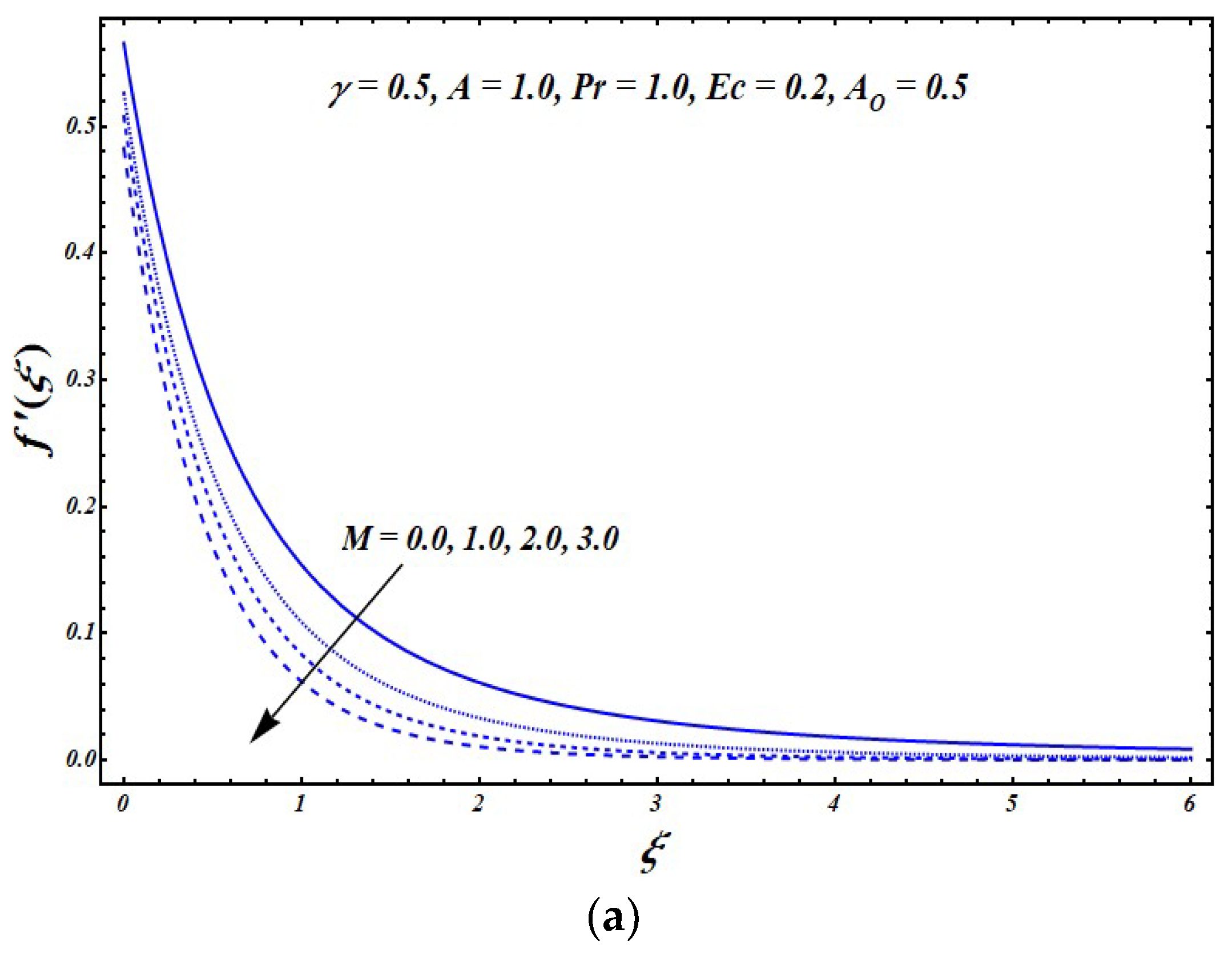
Figure 2a–c explicates the impact of the parameter $M$, $\gamma$ and $A$ on the velocity profile $f^{\prime }(\xi )$. As the value of the magnetic field parameter $M$ increased, the Lorentz force became strong, thus resisting the fluid movement and causing a decline in velocity $f^{\prime }(\xi )$. Additionally, for fixed $M$, the velocity $f^{\prime }(\xi )$ achieved a maximal value at the exponentially stretching surface and reduced with rise in distance $\xi$. In the far away regime, the velocity was asymptotically zero. The impacts of the slip parameter $\gamma$ on fluid velocity $f^{\prime }(\xi )$ are sketched in Figure 2b. A decline in velocity was observed with an increase in the value of the slip parameter $\gamma$, which was quite compatible with the physical fact. In Figure 2c, the velocity profile $f^{\prime }(\xi )$ is drawn versus $\xi$ for variation in the unsteadiness parameter $A$. It is quite evident from the graph that increasing the unsteadiness parameter $A$ results in decreasing the velocity $f^{\prime }(\xi )$. Thus, the unsteadiness parameter $A$ had a decreasing impact on the momentum boundary layer thickness.

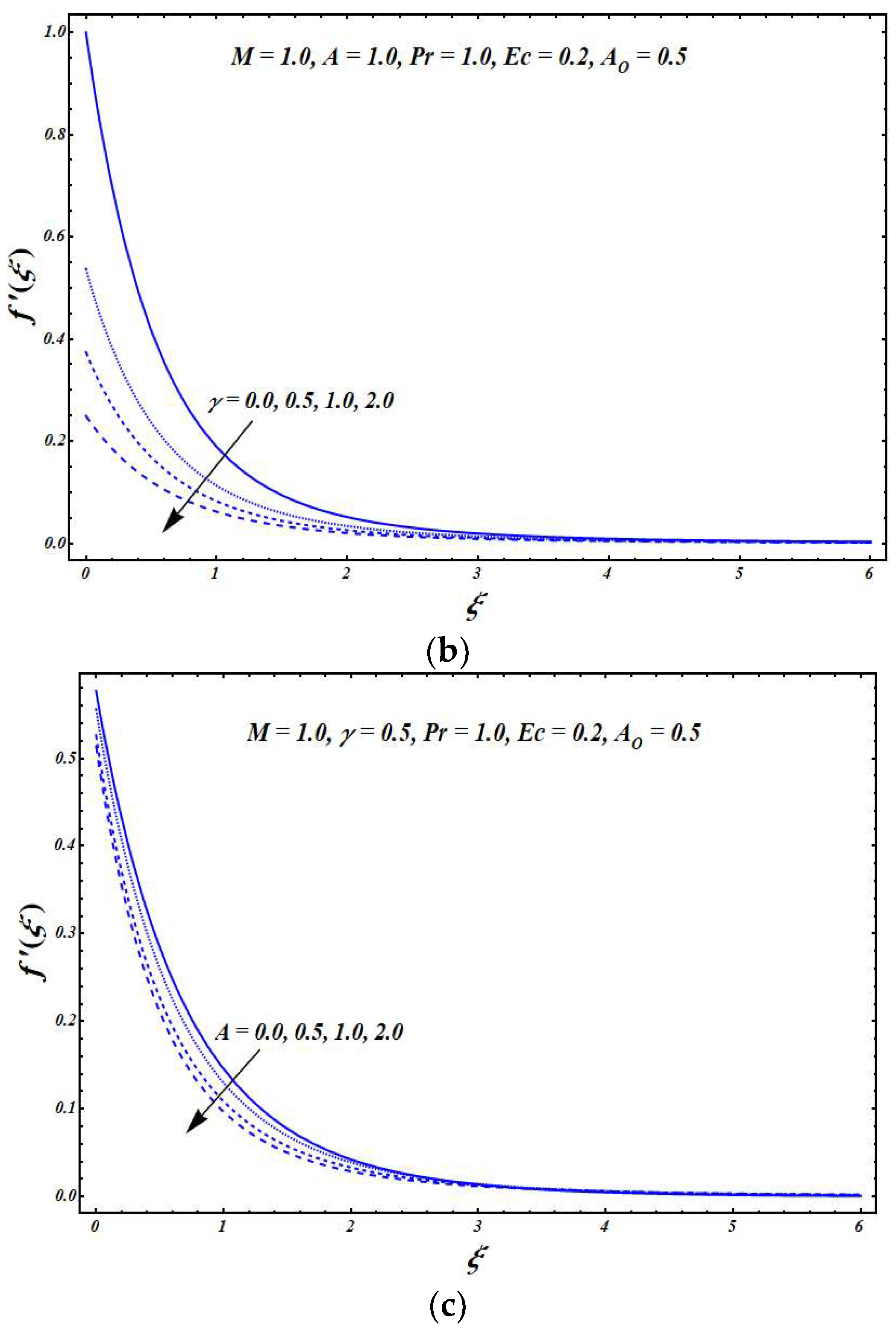
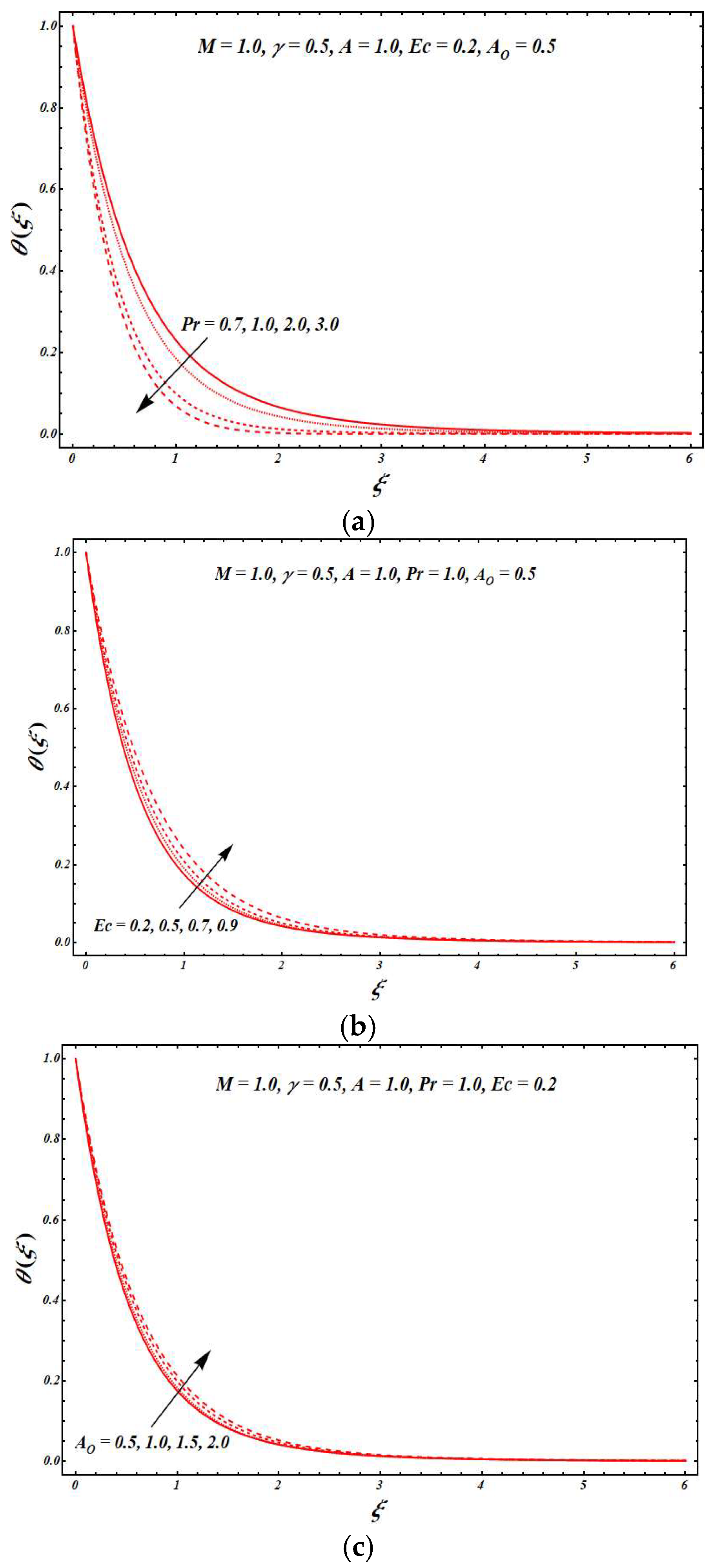
Figure 3 and Figure 4 are plotted to demonstrate the impacts of various flow parameters on temperature distribution $\theta (\xi )$. Figure 3a describes the impact of variation in the magnetic field parameter $M$ on $\theta (\xi )$. The resistive force becomes strong with an increase in the value of $M$, which ultimately results in a rise in the temperature $\theta (\xi )$. The temperature distribution $\theta (\xi )$ is plotted in Figure 3b for various values of the slip parameter $\gamma$. It can be seen that the fluid temperature was augmented with increasing values of $\gamma$. Figure 3c illustrates the behavior of the fluid temperature by varying the values of the unsteadiness parameter $A$. A significant reduction in the temperature was seen by increasing the values of $A$. The impact of the temperature exponent $A_o$ on $\theta (\xi )$ is presented in Figure 4a. A minute boost in the fluid temperature was seen as the value of $A_o$ increased. However, this boost was very miniature as compared to the variation in temperature for other flow parameters. Figure 4b presents the effects of $\mathrm{Pr}$ on the temperature distribution $\theta (\xi )$. A decline in the thermal boundary layer thickness was seen with a rising $\mathrm{Pr}$ value. On the other hand, Figure 4c shows that with the rise in values of $Ec$, the viscous dissipation effects were augmented, which caused an increase in the fluid temperature.

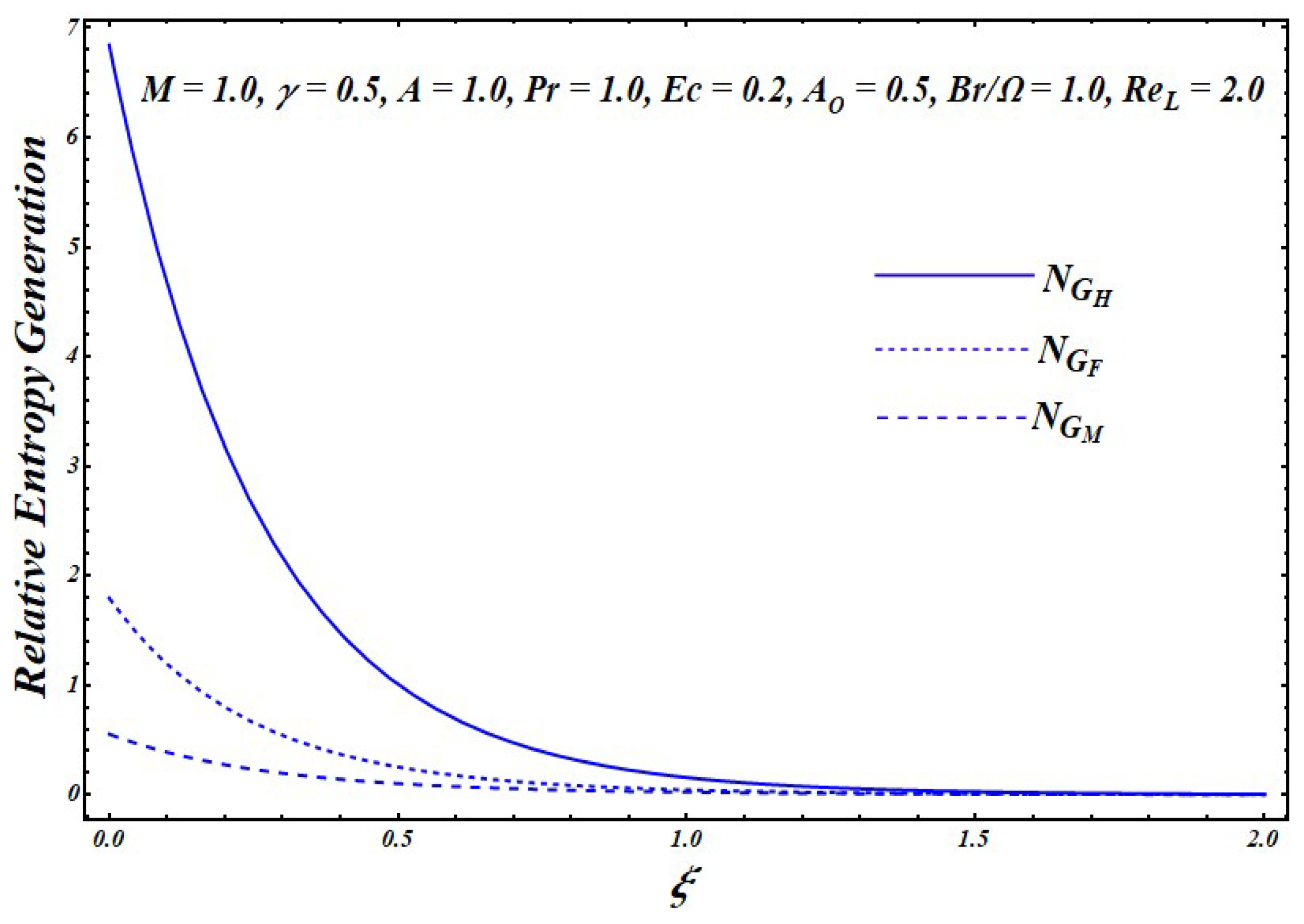
As indicated in Equation (15), there are three sources of entropy generation, i.e., entropy production due to heat transfer $N_{G_H}$, entropy due to viscous dissipation $N_{G_F}$, and the entropy effects caused by an applied magnetic field $N_{G_M}$. Figure 5 shows the contribution of each type of entropy source within the boundary layer thickness. It is quite evident from the figure that entropy production was maximum at the surface of the exponentially stretching sheet. Furthermore, the contribution of the heat transfer entropy effects was maximum as compared to the entropy impacts due to viscous dissipation and the magnetic field. These entropy effects were quite significant within the boundary layer region. However, in the far away regime, these effects were insignificant.

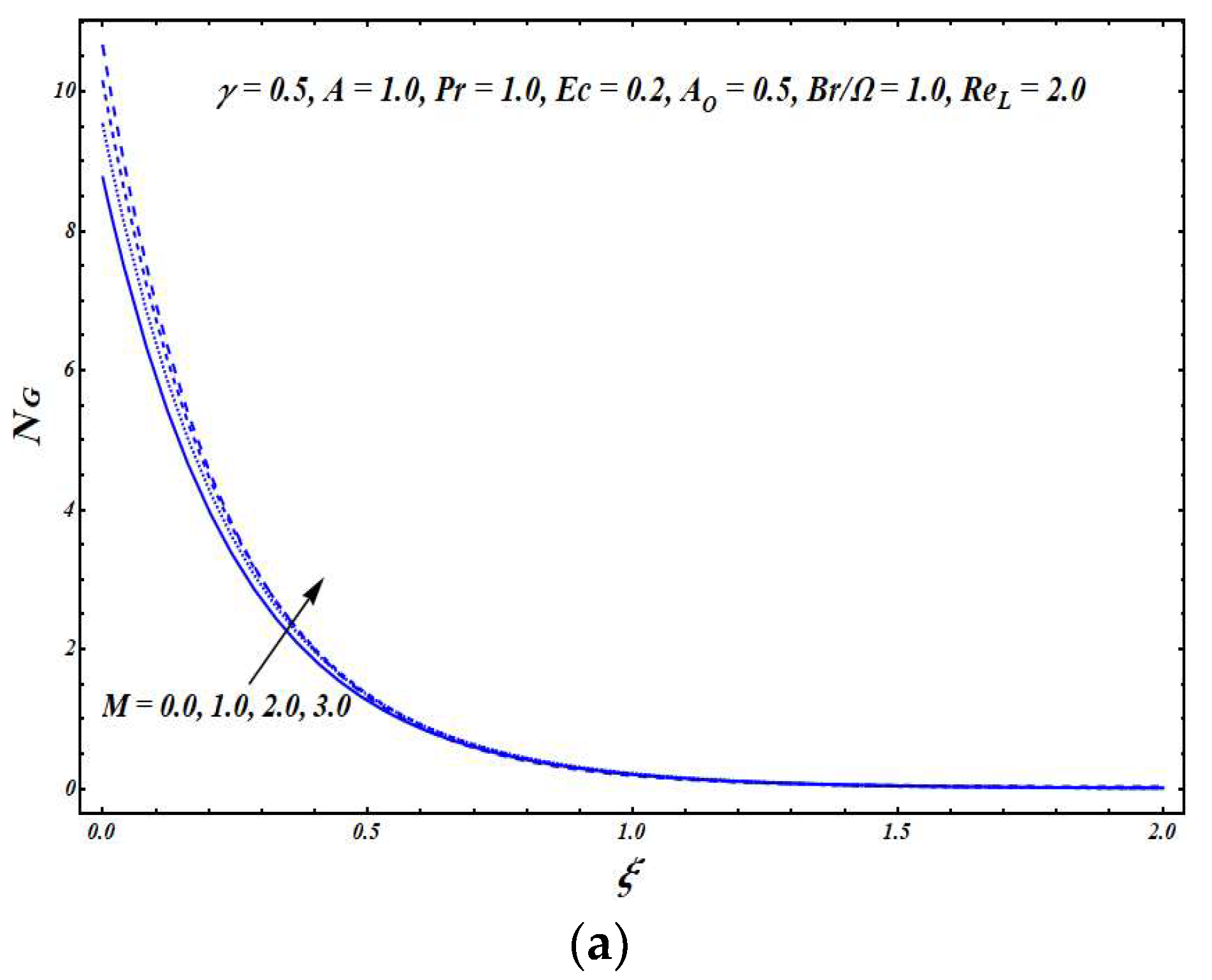
Figure 6 and Figure 7 present the impacts of several flow parameters on the local entropy generation number $N_G$. In Figure 6a, the graph of $N_G$ is plotted against $\xi$ to illustrate the effects of $M$. It was noticed from the figure that in the absence of a magnetic field, the entropy effects were not so significant. However, as the value of $M$ started to increase, $N_G$ increased near the exponentially stretching surface. Thus, the presence of a magnetic field plays a notable role in the production of entropy effects. Figure 6b elucidates the impacts of the slip parameter $\gamma$ on $N_G$. As the value of $\gamma$ increased, the value of $N_G$ reduced, which indicates that the slip phenomena at the surface reduced the impacts of entropy. The influence of $A$ on $N_G$ is illustrated in Figure 6c. A boost in the value of $N_G$ was noticed near the surface with a rise in value of the unsteadiness parameter $A$ increased. However, the situation was reversed within the boundary layer, and the local entropy generation number decreased with an increase in the unsteadiness parameter $A$. 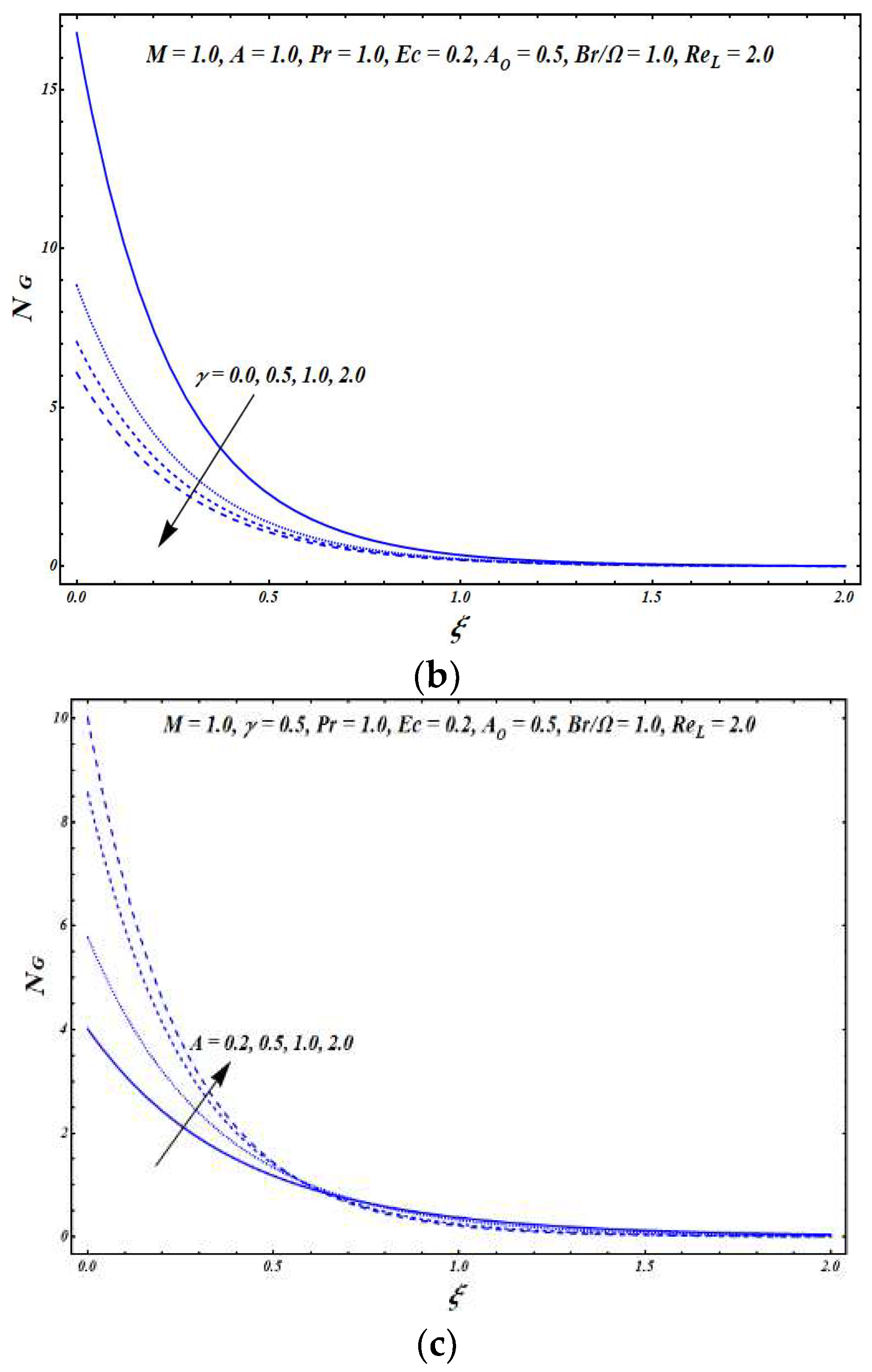Figure 7a demonstrates that the temperature exponent $A_o$ had a decreasing impact on $N_G$ near the exponentially stretching surface where the value of $N_G$ was augmented with an increase in $A_o$ within the boundary layer region. The impact of the group parameter $Br/\Omega$ on $N_G$ is depicted in Figure 7b. As the group parameter got higher values, the viscous dissipation effects were augmented, which resulted in increase in the value of $N_G$. Figure 7c reveals that the effects of the Reynolds number on $N_G$ were increasing.

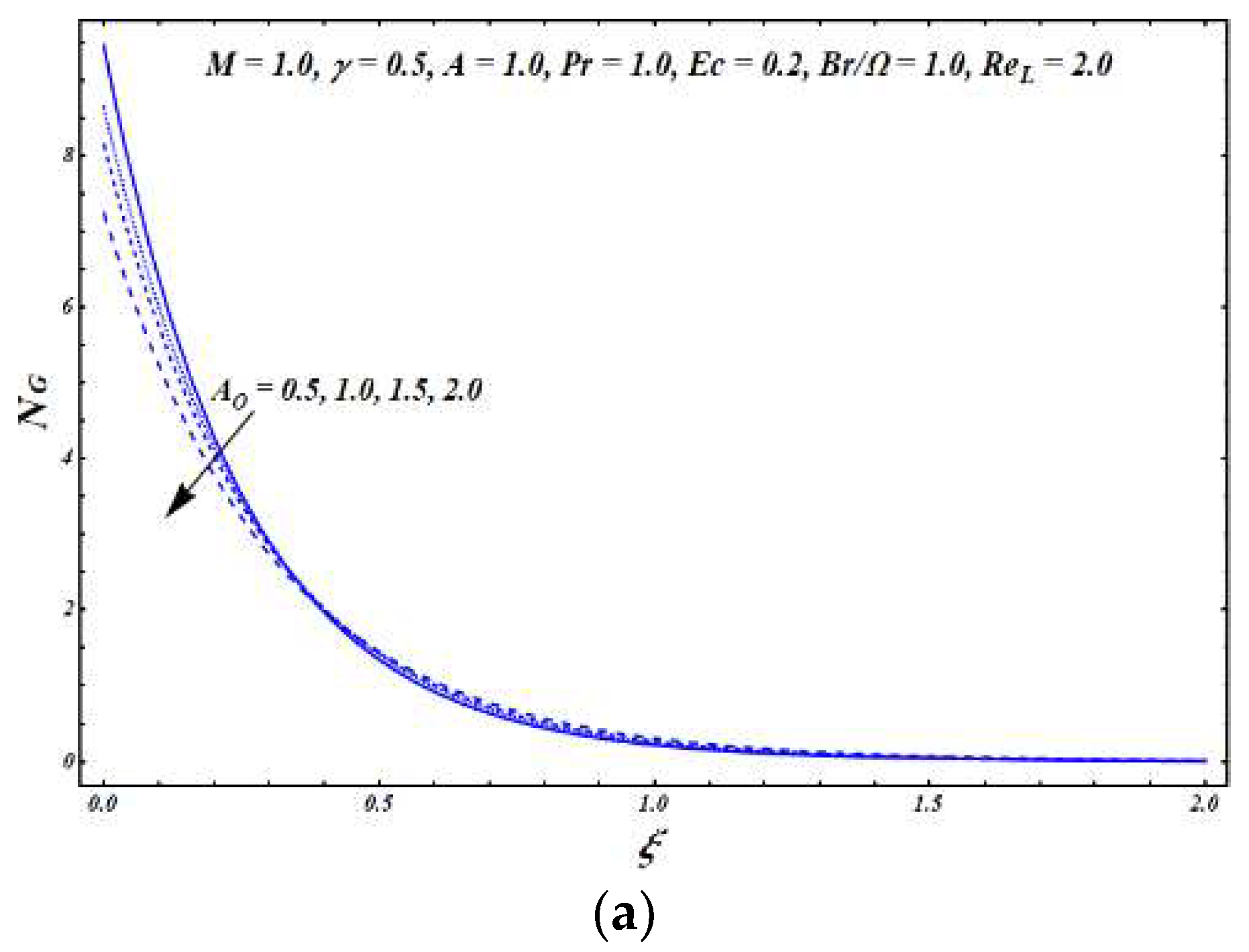
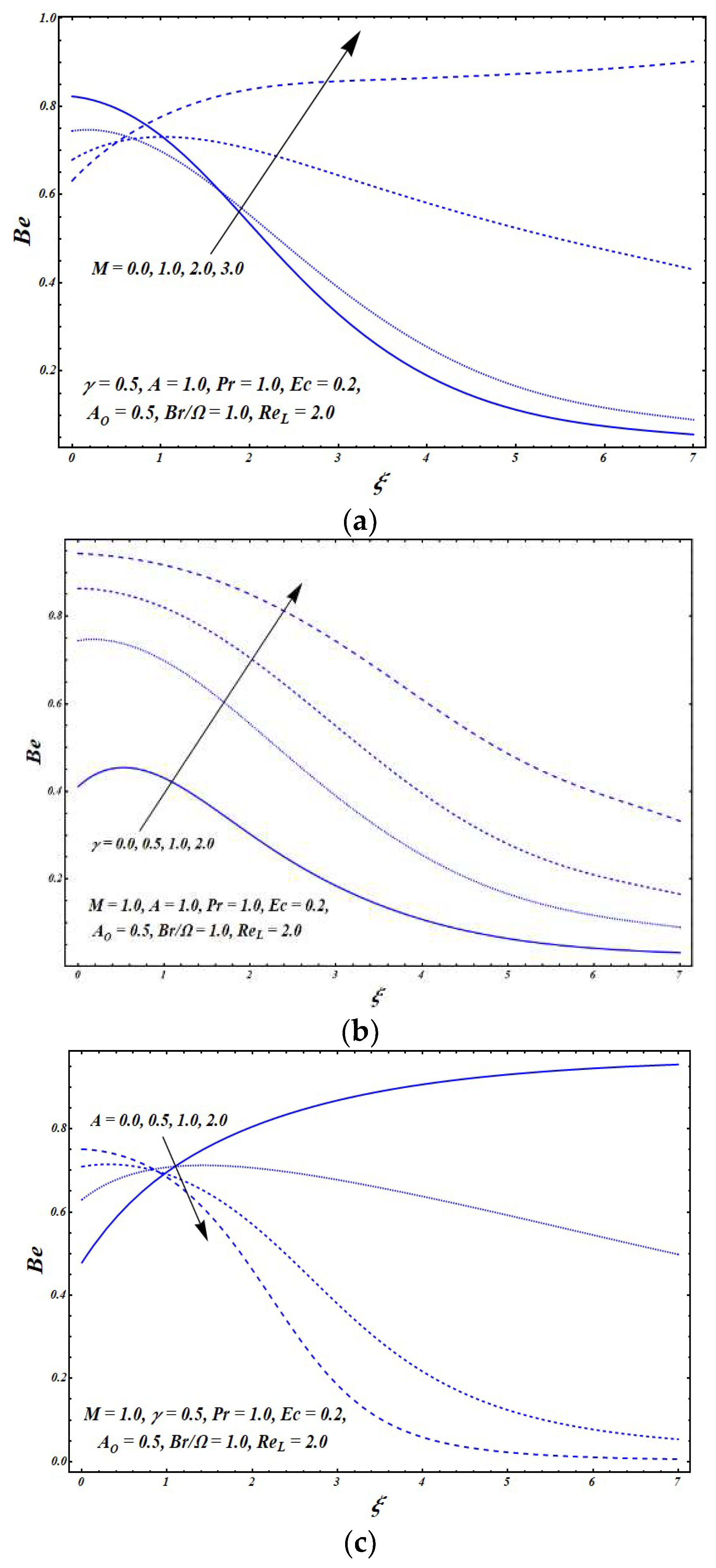
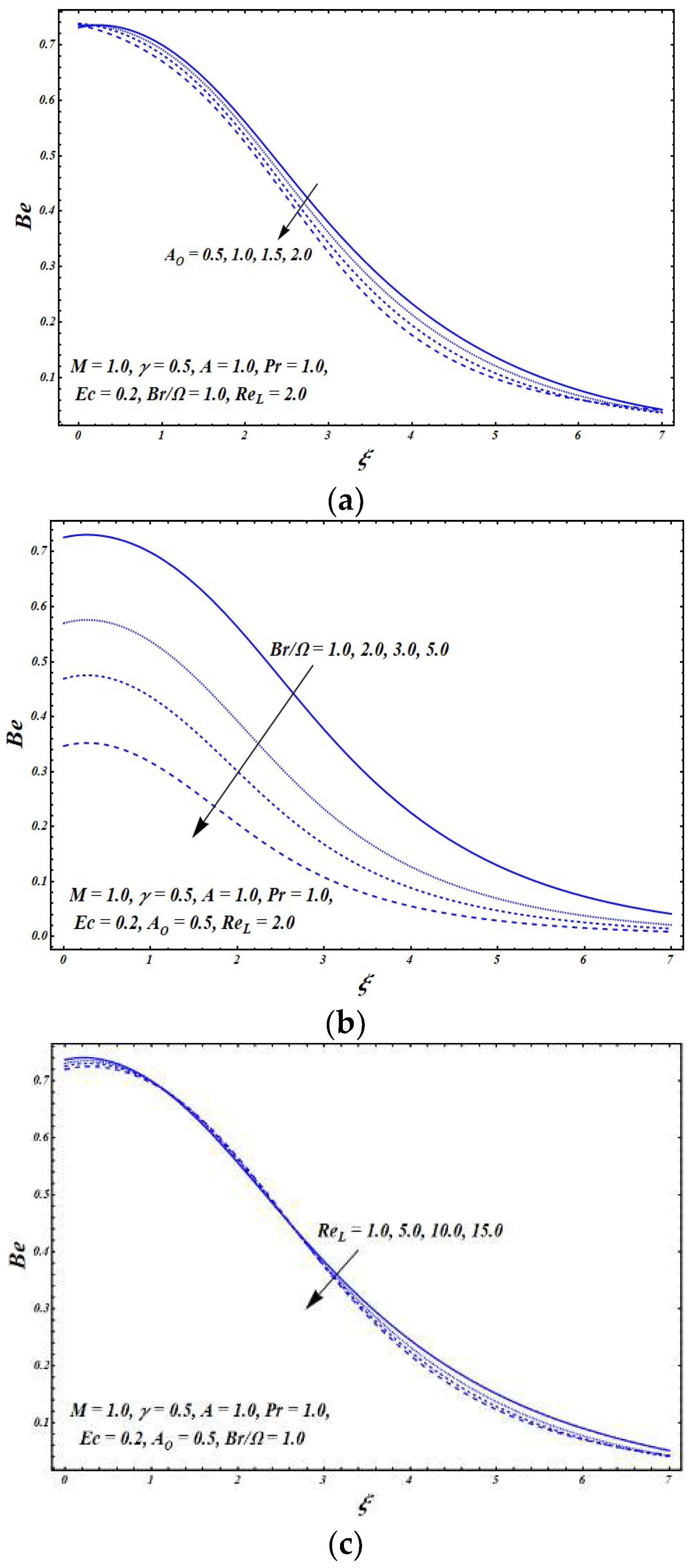
The impacts of several flow parameters on the Bejan number $Be$ are presented in Figure 8 and Figure 9. Figure 8a presents the effects of $M$ on $Be$. It can be seen that the entropy effects due to heat transfer were significant near the vicinity of the exponentially stretching sheet. With a rise in the value of $M$, the heat transfer entropy effects started to decrease a bit. However, within the boundary layer region and the far away regime, the entropy effects due to heat transfer became significantly dominant over the entropy effects due to the viscous dissipation and the magnetic field with an increase in $M$. Figure 8b shows that in the absence of slip effects (i.e., when $\gamma =0$), the impacts of entropy because of the viscous dissipation and the magnetic field were prominent. As the value of the slip parameter $\gamma$ increased, the value of the Bejan number increased. This indicates that the entropy effects due to heat transfer started to become dominant over the viscous dissipation and magnetic field entropy effects, as illustrated in the figure. The impact of $A$ on $Be$ is displayed in Figure 8c. It can be seen that the value of $Be$ lied within the range $0.5<Be\le 1$ in the neighborhood of the exponentially stretching surface. This shows that the heat transfer entropy effects were prominent in this region, and these effects became stronger with increase in the value of $A$. Moreover, it was observed that the entropy effects due to the viscous dissipation and the magnetic field became significantly stronger within the boundary layer and the far away region as the value of $A$ increased. Thus, there was a dominance of the viscous dissipation and magnetic field entropy effects over the heat transfer entropy effects in these regions. 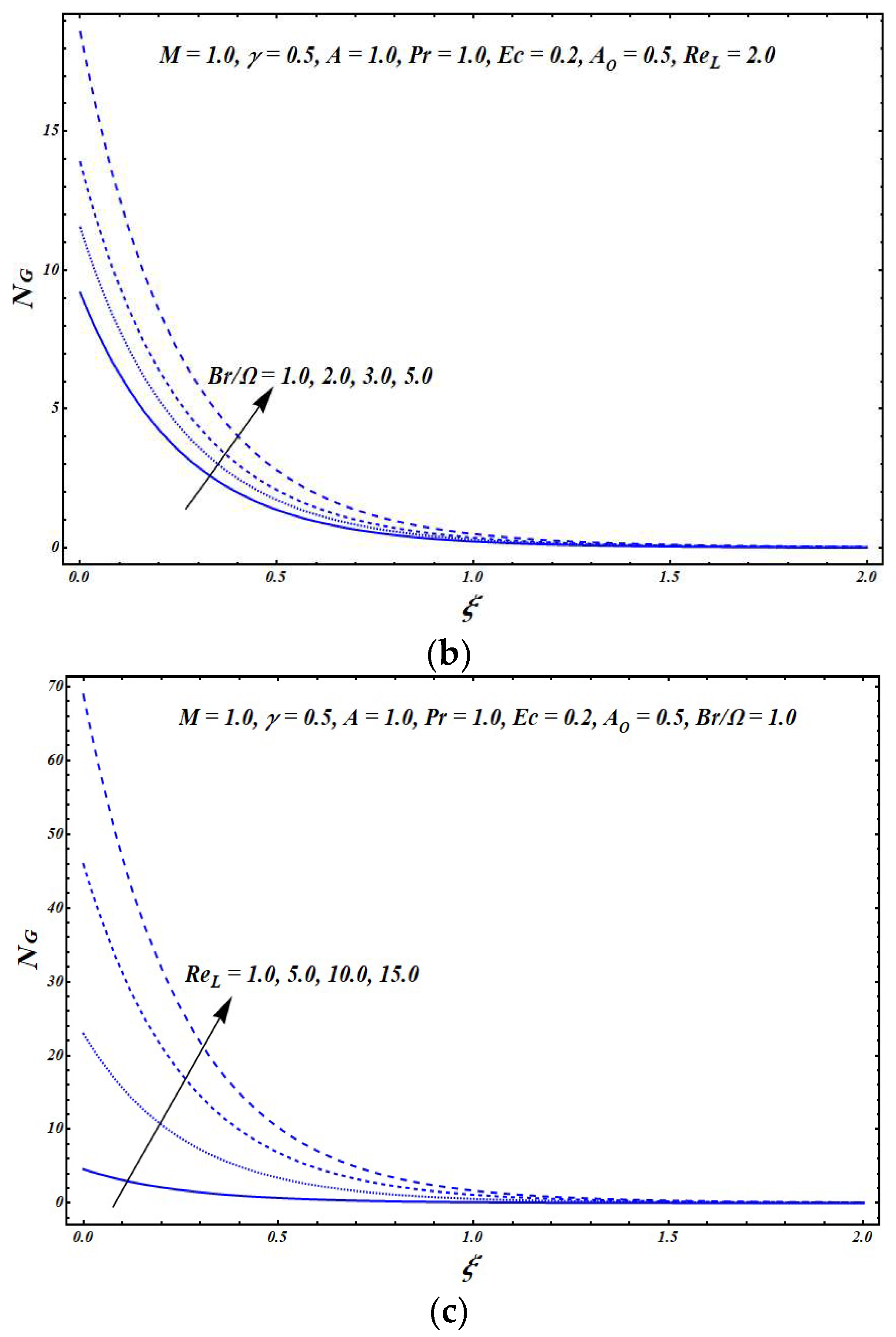Figure 9a depicts the impact of $A_o$ on $Be$. This shows that rise in the value of $A_o$ resulted a slight boost in the value of $Be$. Additionally, it was seen that the heat transfer entropy effects were prominent at the surface of the exponentially stretching sheet, and the viscous dissipation and magnetic field entropy effects were significant in the faraway region. Figure 9b indicates that the entropy effects due to the viscous dissipation and the magnetic field became dominant over the heat transfer entropy effects with an increase in the value of the group parameter $Br/\Omega$. Figure 9c reveals the impact of increasing ${\mathrm{Re}}_L$ on $Be$. The value of $Be$ decreased very slightly near the exponentially stretching sheet with an increase in the Reynolds number ${\mathrm{Re}}_L$. Within the boundary layer, a slight increasing behavior was observed as the value of ${\mathrm{Re}}_L$ increased. Again, a decreasing effect was seen on $Be$ in the far away regime with rise in the value of ${\mathrm{Re}}_L$. Moreover, it was witnessed that heat transfer entropy effects were prominent at the surface, whereas the entropy due to the viscous dissipation and the magnetic field was significant in the faraway region.

6. Conclusions

In this study, the impacts of entropy generation in an MHD unsteady slip flow over an exponentially stretching sheet were explored. The problem was solved by employing both the HAM and the shooting method, and the outcomes were briefly discussed. It was observed that the resistive force reduced the fluid velocity with the rise in the magnetic field parameter $M$ and caused the temperature to augment. Consequently, an increase in entropy was witnessed, as it significantly depended upon the fluid friction. Thus, the presence of magnetic field plays a notable role in the production of entropy effects. Moreover, as the value of the magnetic field parameter $M$ increased, the Lorentz force became strong, which resisted the fluid movement and caused the decline in velocity $f^{\prime }(\xi )$. The heat transfer rate from the exponentially stretching surface increased with a rise in the slip parameter $\gamma$, the unsteadiness parameter $A$, the temperature exponent $A_0$, and the Prandtl number $\mathrm{Pr}$. On the contrary, reverse impacts were observed in the case of $M$ and $Ec$. It can be deduced that the presence of a slip at the surface of exponentially stretching sheet depreciates the entropy effect, whereas the application of an externally applied magnetic field augments the entropy effects. Moreover, unsteady flow also has an increasing effect on entropy production. The heat transmission entropy effects are dominant at the exponentially stretching sheet, whereas the viscous dissipation and magnetic field entropy impacts dominate the heat transmission entropy impacts in the faraway region. The value of $N_G$ rises with an increase in the unsteadiness parameter $A$ near the surface and declines within the boundary layer regime. In the case of the temperature exponent $A_o$, an opposite behavior was observed as compared to the unsteadiness parameter. The heat transmission entropy effects are dominant at the exponentially stretching sheet, whereas the viscous dissipation and magnetic field entropy impacts dominate the heat transmission entropy impacts in the faraway region. Finally, we conclude that the heat transmission entropy impacts are the major cause of entropy production.