A Robust Hybrid Iterative Linear Detector for Massive MIMO Uplink Systems
Abstract
1. Introduction
2. Background
3. Methods
3.1. System Model
3.2. Neumann Series
3.3. Gauss–Seidel
3.4. Jacobi
3.5. A Stair Matrix
- -
- where
- -
- where
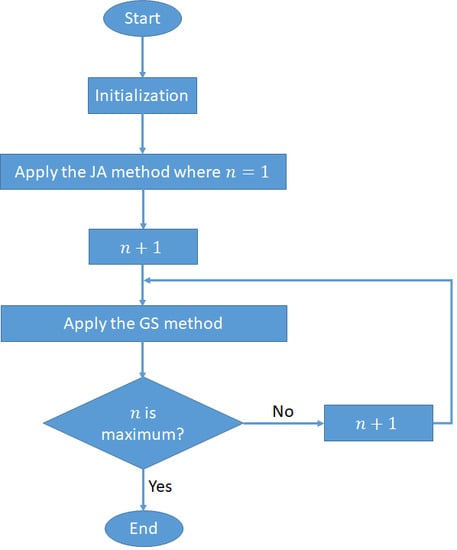
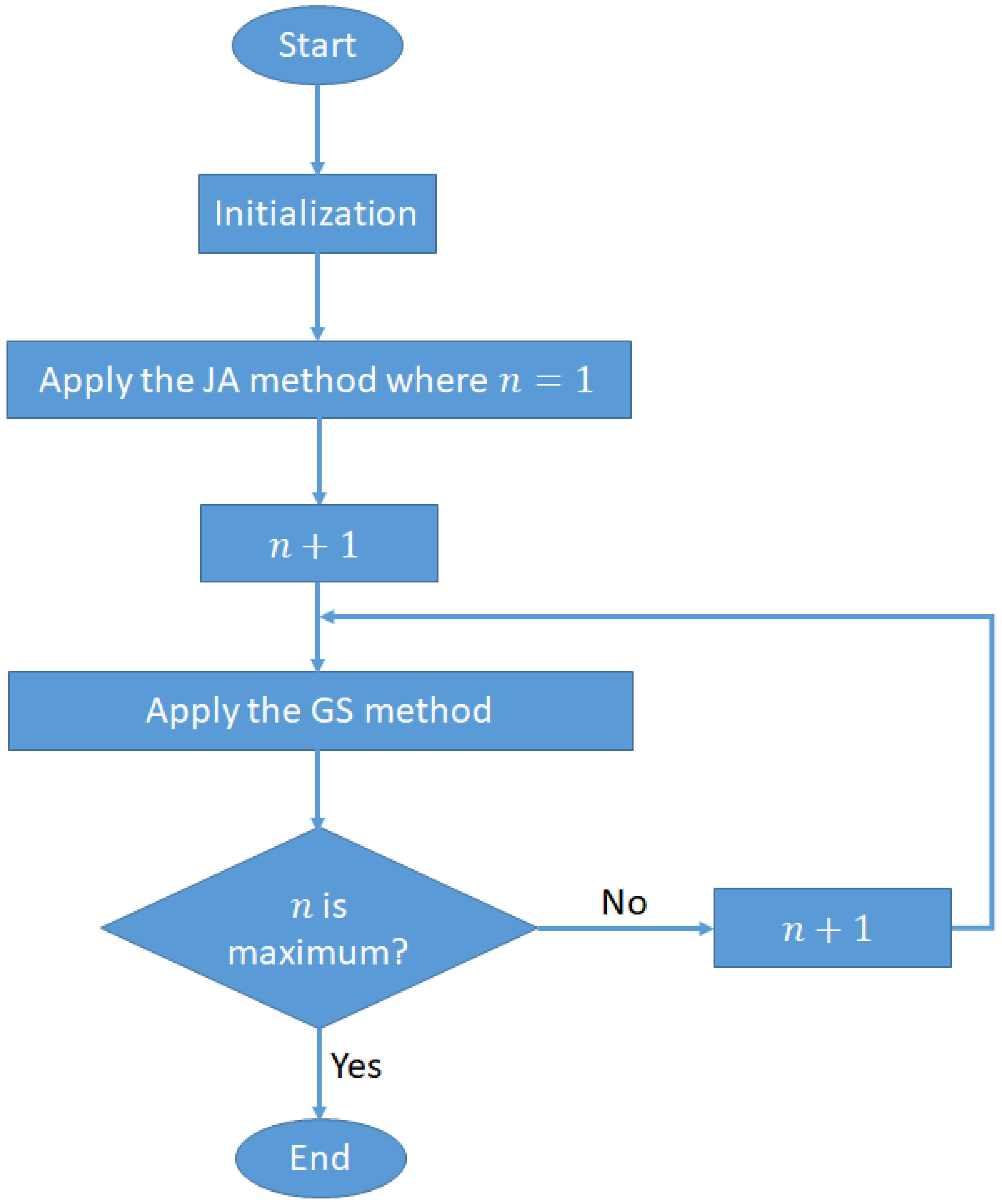
3.6. Proposed Method
| Algorithm 1: Detection method based on joint JA, GS, and a stair matrix |
| Input: Output: Estimated signal Initialization: , , Initial estimations: Iteration: for j = 2:1:n Apply the GS method using (7) end Return . |
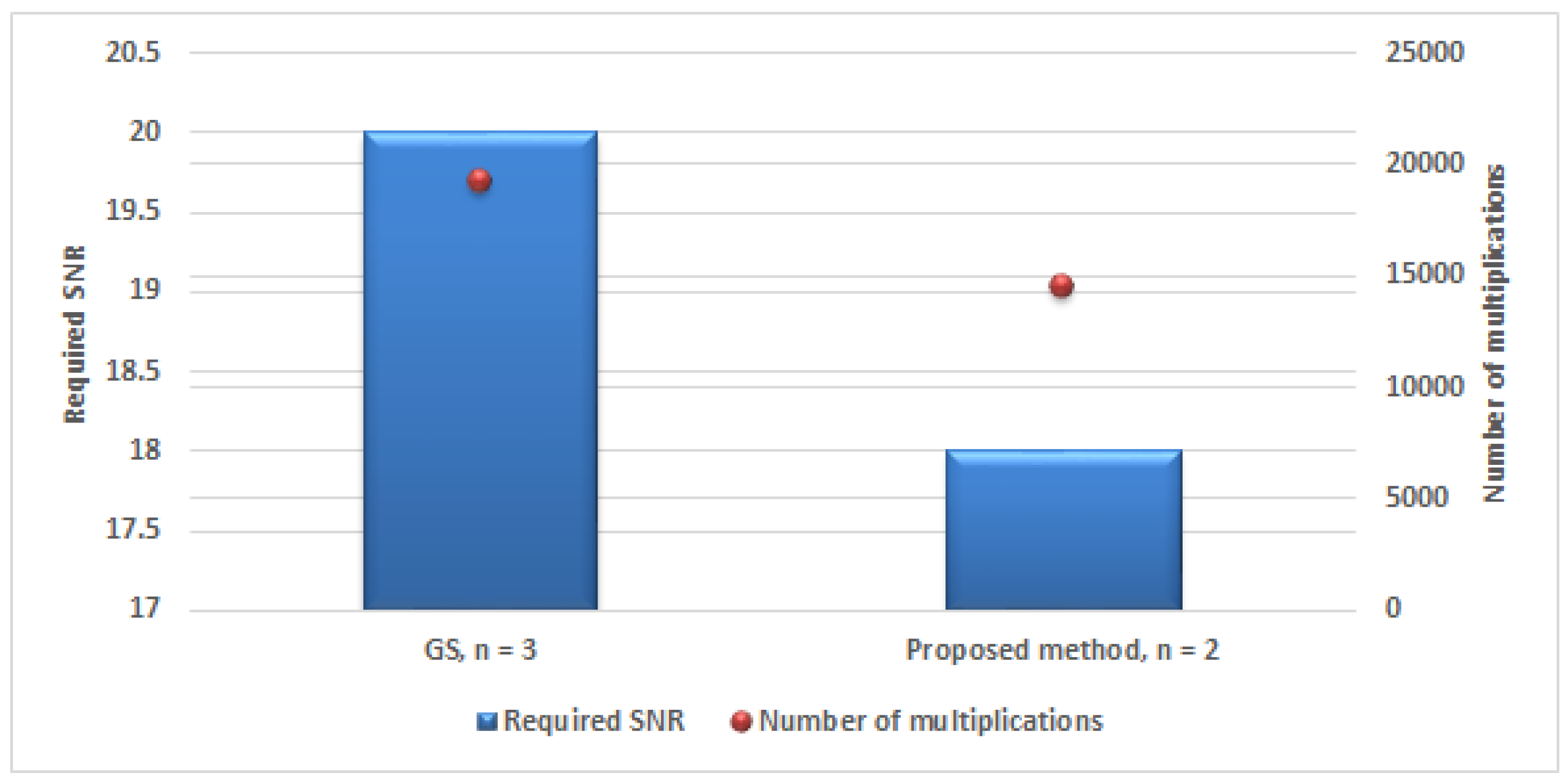
4. Complexity Analysis
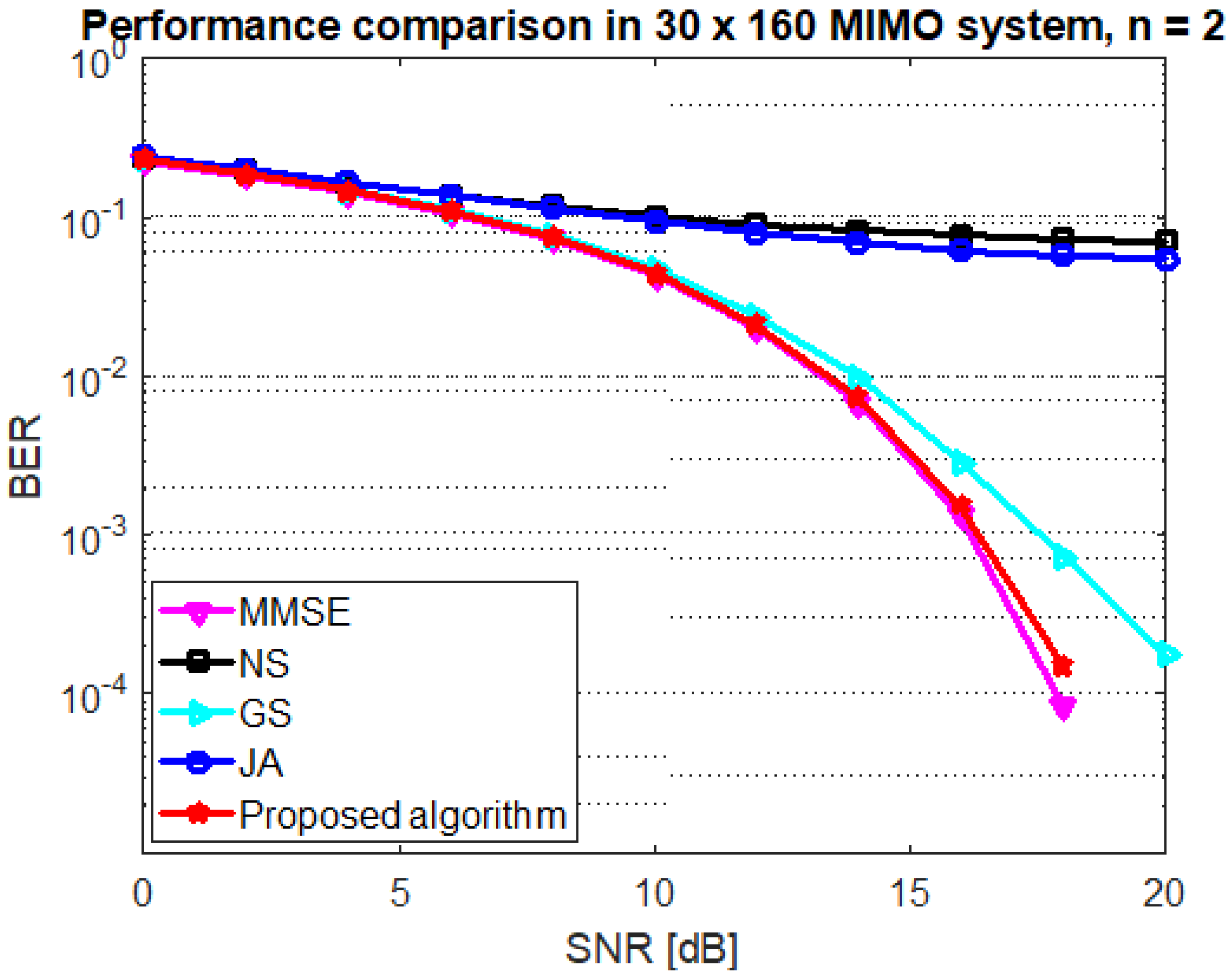
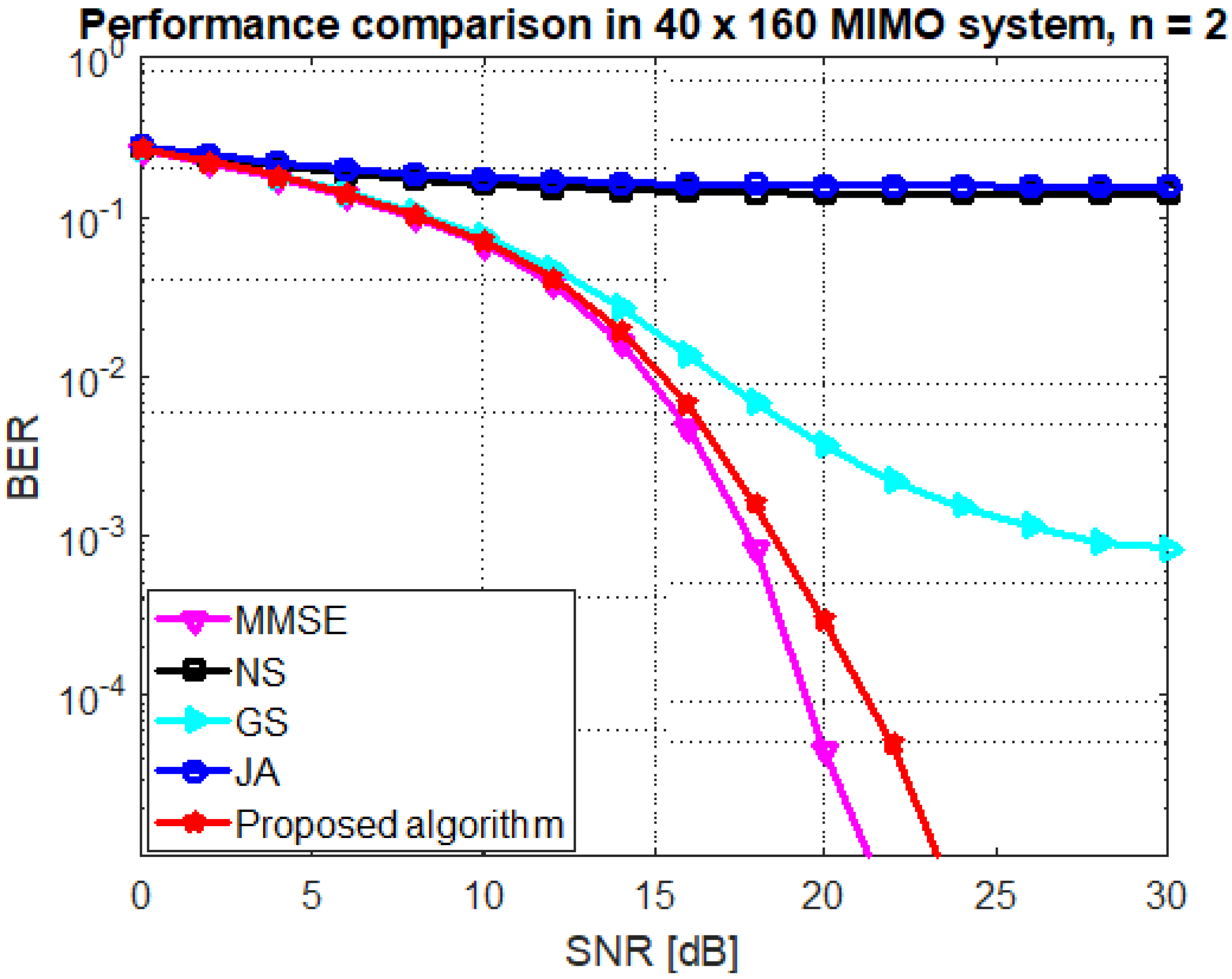
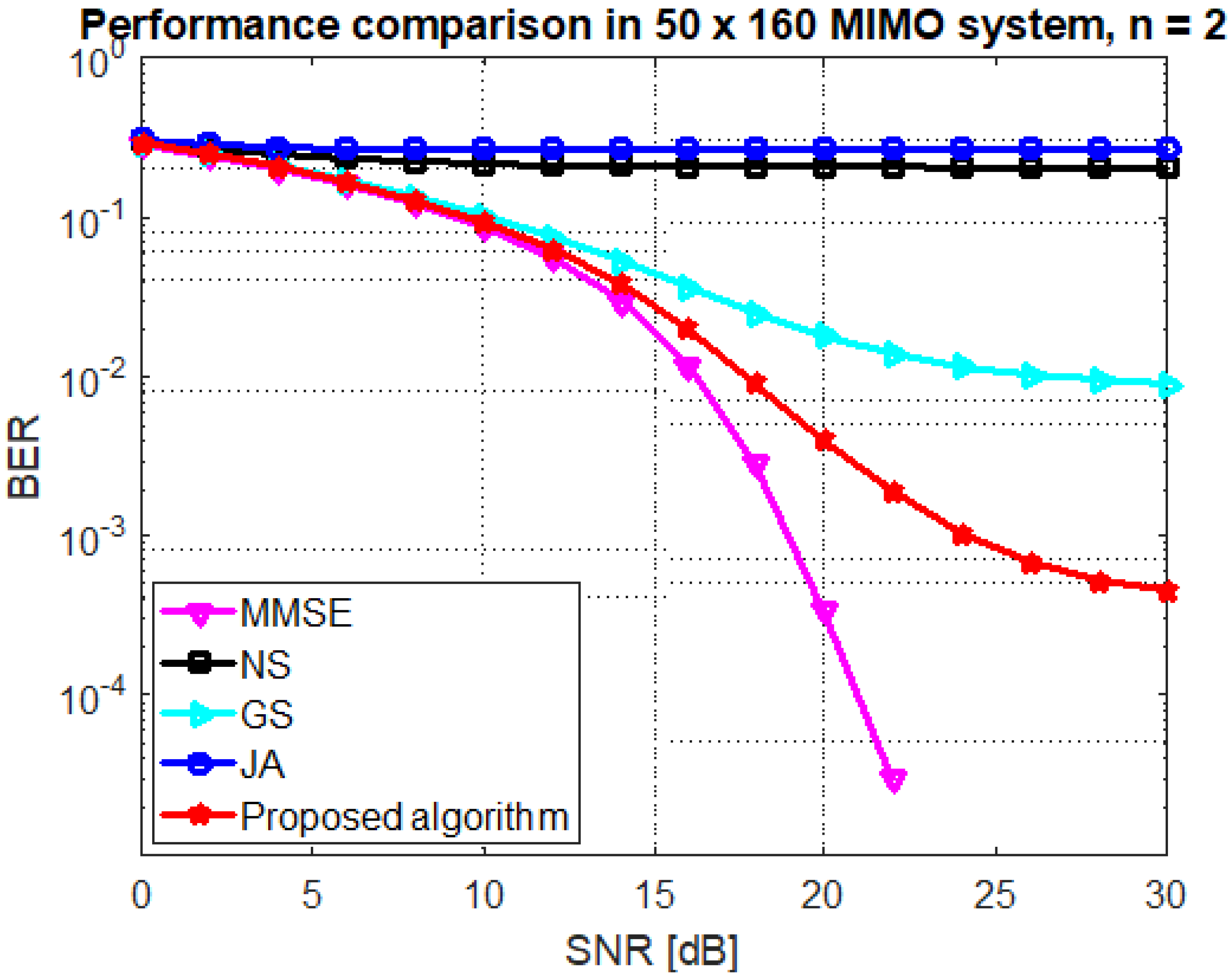
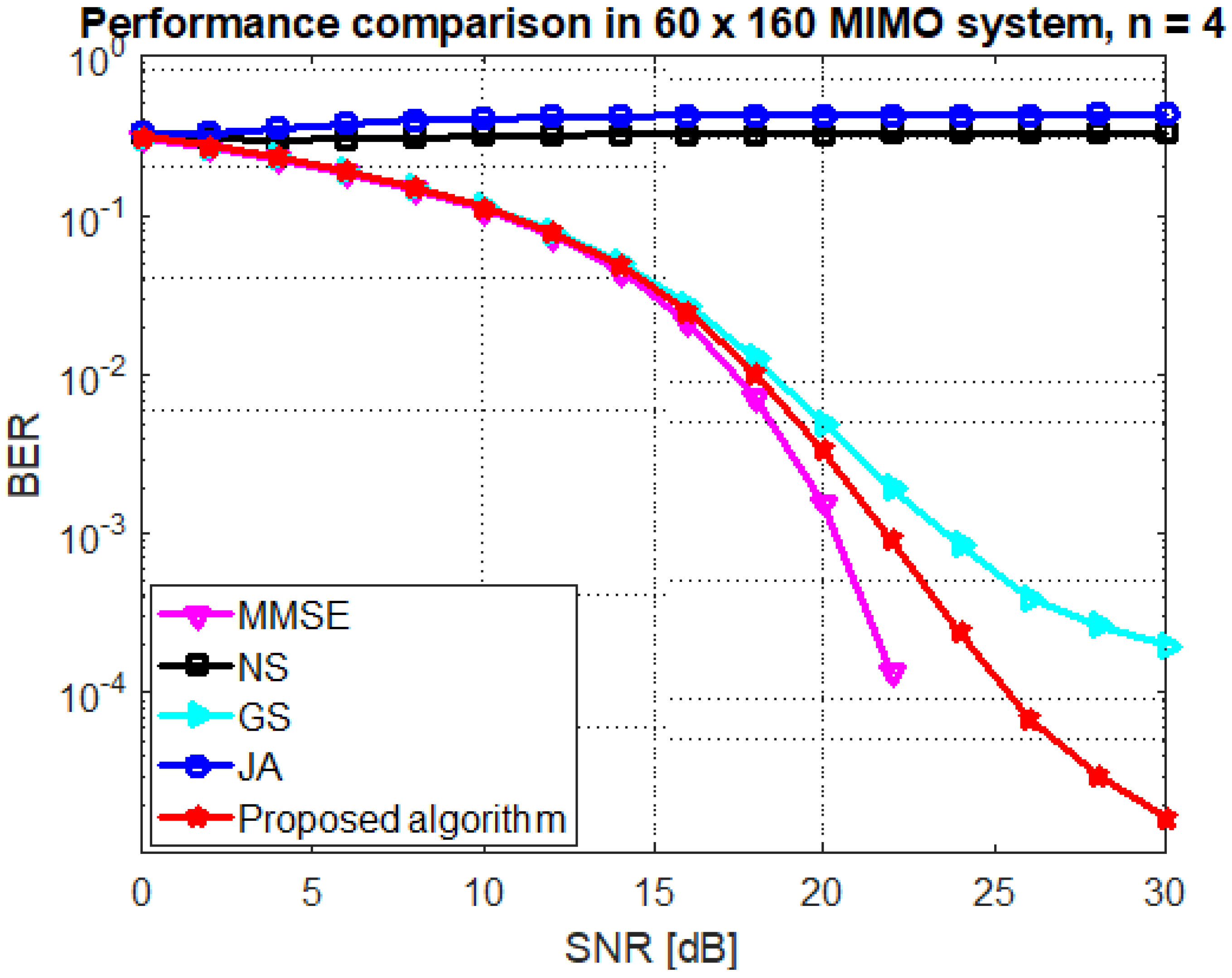
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, L.; Peng, G.; Wang, P.; Zhou, S.; Wei, Q.; Yin, S.; Wei, S. Energy- and Area-Efficient Recursive-Conjugate-Gradient-Based MMSE Detector for Massive MIMO Systems. IEEE Trans. Signal Process. 2020. [Google Scholar] [CrossRef]
- Akhlaghpasand, H.; Björnson, E.; Razavizadeh, S.M. Jamming Suppression in Massive MIMO Systems. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 182–186. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Nordin, R.; Abdullah, N.F.; Kelechi, A.H. How to make key 5G wireless technologies environmental friendly: A review. Trans. Emerg. Telecommun. Technol. 2018, 29, e3254. [Google Scholar] [CrossRef]
- Mohammed, S.L.; Alsharif, M.H.; Gharghan, S.K.; Khan, I.; Albreem, M. Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry 2019, 11, 1424. [Google Scholar] [CrossRef]
- Jia, Z.; Cheng, W.; Zhang, H. A Partial Learning-Based Detection Scheme for Massive MIMO. IEEE Wirel. Commun. Lett. 2019, 8, 1137–1140. [Google Scholar] [CrossRef]
- Guo, Z.; Nilsson, P. Algorithm and implementation of the K-best sphere decoding for MIMO detection. IEEE J. Sel. Areas Commun. 2006, 24, 491–503. [Google Scholar] [CrossRef]
- Larsson, E.G.; Jalden, J. Fixed-Complexity Soft MIMO Detection via Partial Marginalization. IEEE Trans. Signal Process. 2008, 56, 3397–3407. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, C.; Tsai, T.; Sun, W.; Ueng, Y.; Yang, C. A 501mW 7.6lGb/s integrated message-passing detector and decoder for polar-coded massive MIMO systems. In Proceedings of the 2017 Symposium on VLSI Circuits, Kyoto, Japan, 5–8 June 2017; pp. C330–C331. [Google Scholar] [CrossRef]
- Tan, X.; Ueng, Y.; Zhang, Z.; You, X.; Zhang, C. A Low-Complexity Massive MIMO Detection Based on Approximate Expectation Propagation. IEEE Trans. Veh. Technol. 2019, 68, 7260–7272. [Google Scholar] [CrossRef]
- Jeon, Y.; Hong, S.; Lee, N. Blind detection for MIMO systems with low-resolution ADCs using supervised learning. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, X.; Jin, S.; Wen, C. Symbol Detection of Phase Noise-Impaired Massive MIMO Using Approximate Bayesian Inference. IEEE Signal Process. Lett. 2019, 26, 607–611. [Google Scholar] [CrossRef]
- Fang, L.; Xu, L.; Huang, D.D. Low Complexity Iterative MMSE-PIC Detection for Medium-Size Massive MIMO. IEEE Wirel. Commun. Lett. 2016, 5, 108–111. [Google Scholar] [CrossRef]
- Wu, M.; Yin, B.; Wang, G.; Dick, C.; Cavallaro, J.R.; Studer, C. Large-Scale MIMO Detection for 3GPP LTE: Algorithms and FPGA Implementations. IEEE J. Sel. Top. Signal Process. 2014, 8, 916–929. [Google Scholar] [CrossRef]
- Albreem, M. Efficient initialisation of iterative linear massive MIMO detectors using a stair matrix. Electron. Lett. 2020, 56, 50–52. [Google Scholar] [CrossRef]
- Jiang, F.; Li, C.; Gong, Z.; Su, R. Stair Matrix and its Applications to Massive MIMO Uplink Data Detection. IEEE Trans. Commun. 2018. [Google Scholar] [CrossRef]
- Albreem, M.A.; Alsharif, M.H.; Kim, S. Impact of Stair and Diagonal Matrices in Iterative Linear Massive MIMO Uplink Detectors for 5G Wireless Networks. Symmetry 2020, 12, 71. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Wang, X.; Lian, J.; Dai, X. A Low Complexity High Performance Weighted Neumann Series-based Massive MIMO Detection. In Proceedings of the 2019 28th Wireless and Optical Communications Conference (WOCC), Beijing, China, 9–10 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Jin, F.; Liu, Q.; Liu, H.; Wu, P. A Low Complexity Signal Detection Scheme Based on Improved Newton Iteration for Massive MIMO Systems. IEEE Commun. Lett. 2019, 23, 748–751. [Google Scholar] [CrossRef]
- Zhang, C.; Liang, X.; Wu, Z.; Wang, F.; Zhang, S.; Zhang, Z.; You, X. On the Low-Complexity, Hardware-Friendly Tridiagonal Matrix Inversion for Correlated Massive MIMO Systems. IEEE Trans. Veh. Technol. 2019, 68, 6272–6285. [Google Scholar] [CrossRef]
- Ren, W.; Zhou, Y.; Ji, W.; Li, T.; Liang, Y.; Li, F. Matrix Approximate Inversion Based Signal Detection in Large-scale 3D-MIMO Systems. In Proceedings of the 2019 15th International Wireless Communications Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 830–835. [Google Scholar] [CrossRef]
- Albreem, M.A.M.; El-Saleh, A.A.; Juntti, M. On Approximate Matrix Inversion Methods for Massive MIMO Detectors. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakech, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Albreem, M.A.M. Approximate Matrix Inversion Methods for Massive MIMO Detectors. In Proceedings of the 2019 IEEE 23rd International Symposium on Consumer Technologies (ISCT), Ancona, Italy, 19–21 June 2019; pp. 87–92. [Google Scholar] [CrossRef]
- Nhat Cuong, C.; Thi Hong, T.; Duc Khai, L. Hardware Implementation of the Efficient SOR-Based Massive MIMO Detection for Uplink. In Proceedings of the 2019 IEEE-RIVF International Conference on Computing and Communication Technologies (RIVF), Danang, Vietnam, 20–22 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Yu, A.; Jing, S.; Tan, X.; Wu, Z.; Yan, Z.; Zhang, Z.; You, X.; Zhang, C. Efficient Successive Over Relaxation Detectors for Massive MIMO. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 1–12. [Google Scholar] [CrossRef]
- Seidel, P.; Gregorek, D.; Paul, S.; Rust, J. Efficient Initialization of Iterative Linear Massive MIMO Uplink Detectors by Binary Jacobi Synthesis. In Proceedings of the WSA 2019; 23rd International ITG Workshop on Smart Antennas, Vienna, Austria, 24–26 April 2019. [Google Scholar]



| Method | Complexity |
|---|---|
| NS | |
| GS | |
| JA | |
| Proposed Algorithm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albreem, M.A.; Alsharif, M.H.; Kim, S. A Robust Hybrid Iterative Linear Detector for Massive MIMO Uplink Systems. Symmetry 2020, 12, 306. https://doi.org/10.3390/sym12020306
Albreem MA, Alsharif MH, Kim S. A Robust Hybrid Iterative Linear Detector for Massive MIMO Uplink Systems. Symmetry. 2020; 12(2):306. https://doi.org/10.3390/sym12020306
Chicago/Turabian StyleAlbreem, Mahmoud A., Mohammed H. Alsharif, and Sunghwan Kim. 2020. "A Robust Hybrid Iterative Linear Detector for Massive MIMO Uplink Systems" Symmetry 12, no. 2: 306. https://doi.org/10.3390/sym12020306
APA StyleAlbreem, M. A., Alsharif, M. H., & Kim, S. (2020). A Robust Hybrid Iterative Linear Detector for Massive MIMO Uplink Systems. Symmetry, 12(2), 306. https://doi.org/10.3390/sym12020306