A Privacy Preserving Authentication Scheme for Roaming in IoT-Based Wireless Mobile Networks
Abstract
1. Introduction
1.1. The Contributions
- The scheme provides provable security under the hardness of ECDLP (elliptic-curve discrete logarithm and elliptic-cure deffie-Hellman problems.
- The scheme provides security and anonymity under automated security model of ProVerif.
- The scheme provides authentication among user and foreign network with the help of home network.
- The scheme achieves low computation power as compared with baseline scheme presented in Reference [26].
1.2. Security Requirements
- The mobile roaming user should have facility to change his password credentials in an easy manner and he should be facilitated not to memorize a complicated and/or long password.
- Along with traditional security requirements, The scheme should ensure user privacy and anonymity. Any insider/outsider, including foreign agents, should remain unaware regarding the original identity of the roaming user. Moreover, current location of the user should not be exposed to anyone with some previous knowledge.
- Home network should facilitate the authentication process between user and foreign network.
- The authentication should result into a shared secret key among user and foreign network for subsequent confidential communication over insecure link.
- The scheme should at least resist all known attacks.
1.3. Adversarial Model
- Adversary () fully controls the link and can listen, modify, replay a message from all the legal communicating parties. is also able to inject a self created false message.
- can easily get identity related information.
- knows all public parameters.
- Being an insider, can extract verifier table stored in home network database.
- Home Network’s private key is considered as secret and no other entity can extract the key.
- The pre-shared key between home and foreign networks is assumed to be secure.
2. Review of the Scheme of Lu et al.
2.1. Home Network Agent Setup Phase
2.2. Registration Phase
- Step LRP1:
- The mobile user selects identity/password pair , along with (generated randomly), and computes . sends the pair to .
- Step LRP2:
- Upon reception of to pair from , generates random and and stores and a sequence number against registration request of . then computes , , , and . then sends a smart-card containing to . stores in a verifier table maintained by .
- Step LRP3:
- Upon reception of smart-card, inserts . Finally, the smart-card contains: .
2.3. Login & Authentication Phase
- Step LLA1:
- After inserting smart-card, inputs and , the smart-card computes and verifies . Terminates the session if verification is unsuccessful. Otherwise, generates time-stamp , random and computes , , and . sends to .
- Step LLA2:
- upon reception of request, checks freshness of and generates fresh time-stamp , random . then computes , and sends to .
- Step LLA3:
- verifies freshness of after receiving message from . Rejects the message, if is not fresh. Otherwise, based on extracts corresponding shared key from verifier database and decrypts to get . verifies originality of by comparing with the once stored in verifier in a tuple consisting of , and . Upon successful verification, computes and verifies whether . Upon successful verification, computes and then checks . On success, updates and computes , . also updates and computes , . HA then sends to and increments .
- Step LLA4:
- checks freshness of after receiving response of . On success, computes . then verifies validity of and on success, computes .The session key is computed as . Then, sends to .
- Step LLA5:
- Upon reception, verifies freshness of and and on success, computes . further checks validity of and , if both holds, computes session key , and sends to .
- Step LLA6:
- verifies freshness of and checks validity of . If it holds, treats as legitimate user and now further communication between and may be carried out using the shared key .
3. Cryptanalysis of the Scheme of Lu et al.
3.1. Stolen Verifier Attack
- Step IA1:
- generates time-stamp , random , and computes:sends to .
- Step IA2:
- upon reception of request, checks freshness of , as well as generates fresh time-stamp and random . then computes:sends to .
- Step IA3:
- verifies freshness of after receiving message from and accepts the message as is fresh. based on extracts and from the verifier table and computes:compares the decrypted from Equation (6) with the one extracted from verifier table. The attacker will pass this test as both values are same. Now, computes:checks:authenticates on the basis of equality of Equation (8). will also pass this test, as all parameters in computation of were in access to and were correctly calculated at the time of computation of by . Now, computes:then checks:As is legitimate; therefore, it will pass the check of Equation (10). Hence, computes:then updates:Finally, HA sends to and increments .
- Step IA4:
- checks freshness of and computes:then verifies validity of and, on success, computes:Then, sends to .
- Step IA5:
- intercepts the message and computes:sends to .
- Step IA6:
- verifies freshness of and checks validity of . As is freshly generated, so it will pass the test. Similarly, has access to all parameters used for computation of , so it will also pass the test. Therefore, has also deceived the and passed the authentication. Now, can easily communicate with on behalf of using the shared key .
3.2. Traceability
3.3. Incorrectness
3.4. Scalability Problem
4. Proposed scheme
4.1. System Setup Phase
4.2. Proposed Registration Phase
- Step PRP1:
- The mobile user selects identity/password pair , along with (generated randomly), and computes . sends the pair to .
- Step PRP2:
- Upon reception of to pair from , . then computes , , and . then sends a smart-card containing to .
- Step PRP3:
- Upon reception of smart-card, computes inserts . Finally, the smart-card contains: .
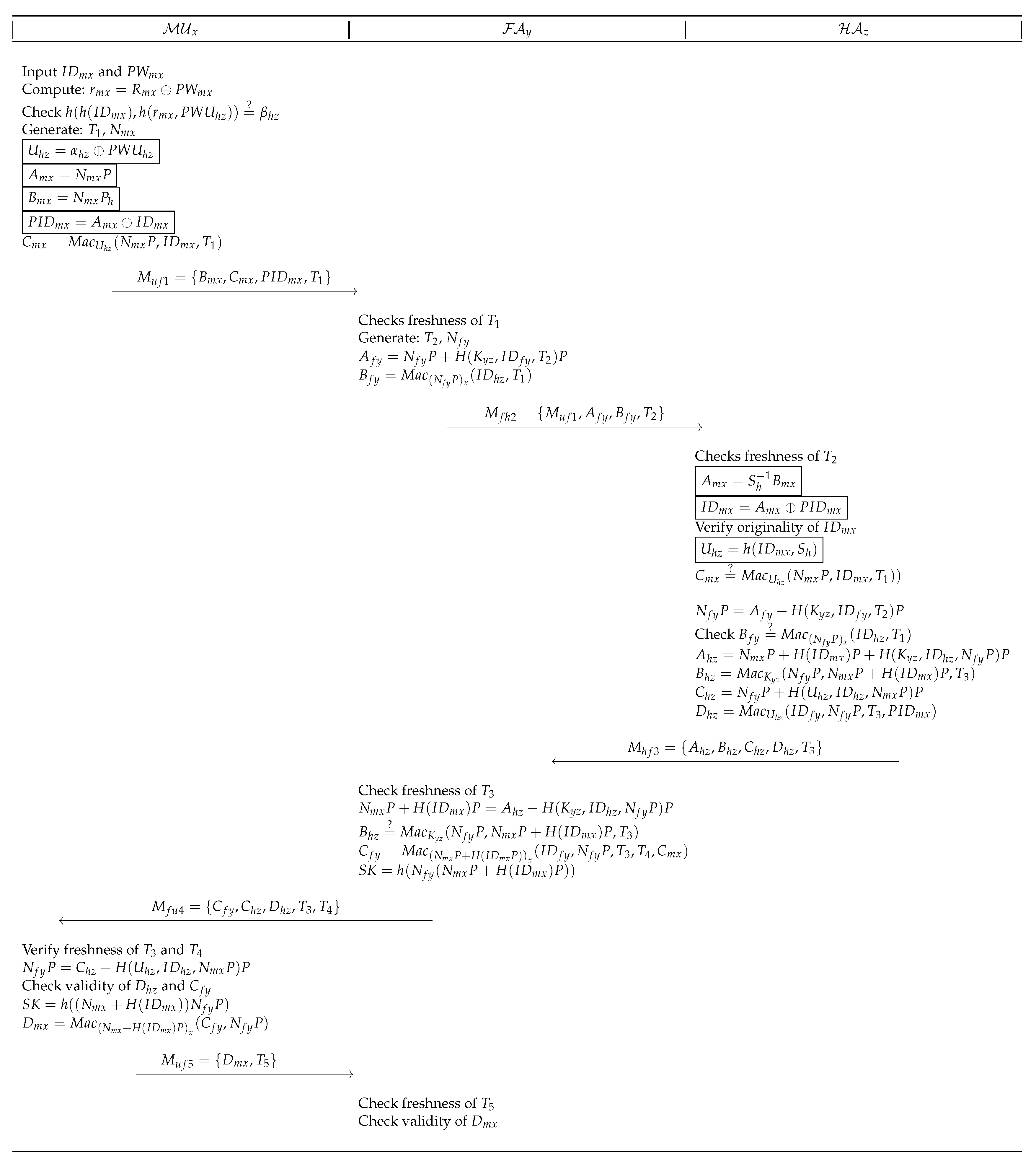
4.3. Login & Authentication Phase
- Step PLA1:
- After inserting smart-card, inputs and ,the smart-card computes and . The smart-card then verifies . Terminates the session if verification is unsuccessful. Otherwise, generates time-stamp , random and computes , , , and . sends to .
- Step PLA2:
- upon reception of request, checks freshness of and generates fresh time-stamp , random . then computes , and sends to .
- Step PLA3:
- verifies freshness of after receiving message from . Rejects the message, if is not fresh. Otherwise, computes and . verifies originality of stored in subscribers identity table. Upon successful verification, computes and verifies . Upon successful verification, computes and then checks . On success, computes , . computes , . HA then sends to .
- Step PLA4:
- checks freshness of after receiving response of . On success, computes . then verifies validity of and on success, computes .The session key is computed as . Then, sends to .
- Step PLA5:
- Upon reception, verifies freshness of and and on success, computes . further checks validity of and , if both holds, computes session key , and sends to .
- Step PLA6:
- verifies freshness of and checks validity of . If it holds, treats as legitimate user and now further communication between and may be carried out using the shared key .
5. Security Analysis
5.1. Formal Security Analysis
- : This oracle will output plain-text k unconditionally from cipher-text that is given.
- : This oracle will output integer y unconditionally from and P that are publicly given values.
- : This oracle will output the input y from O that is the corresponding value of hash.


5.2. Automated Security Analysis with ProVerif
5.3. Security Requirements
5.3.1. Mutual Authentication
5.3.2. Correctness
5.3.3. User Anonymity/Untraceability
5.3.4. Perfect Forward Secrecy:
5.3.5. User Forgery Attack
5.3.6. Stolen Verifier and Insider Attack
5.3.7. Stolen Smart-Card Attack
5.3.8. Known Session-Specific Parameters Attack
6. Performance Comparisons
- : Computation time for hash/mac operations
- : Computation time for Symmetric Enc/Dec
- : Computation time for scalar multiplication of point over
- : Computation time for addition of points over
- : Computation time for modular exponentiation
- : Computation time for bilinear pairing
- : Computation time for map to point hash
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- He, D.; Kumar, N.; Khan, M.K.; Lee, J. Anonymous two-factor authentication for consumer roaming service in global mobility networks. IEEE Trans. Consum. Electron. 2013, 59, 811–817. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Wu, F.; Kumari, S.; Rodrigues, J.J.P.C. Privacy Preserving Data Aggregation Scheme for Mobile Edge Computing Assisted IoT Applications. IEEE Internet Things J. 2019, 6, 4755–4763. [Google Scholar] [CrossRef]
- Wei, F.; Vijayakumar, P.; Jiang, Q.; Zhang, R. A Mobile Intelligent Terminal Based Anonymous Authenticated Key Exchange Protocol for Roaming Service in Global Mobility Networks. IEEE Trans. Sustain. Comput. 2018, 1-1. [Google Scholar] [CrossRef]
- Jiang, Y.; Lin, C.; Shen, X.; Shi, M. Mutual Authentication and Key Exchange Protocols for Roaming Services in Wireless Mobile Networks. IEEE Trans. Wirel. Commun. 2006, 5, 2569–2577. [Google Scholar] [CrossRef]
- Jo, H.J.; Paik, J.H.; Lee, D.H. Efficient Privacy-Preserving Authentication in Wireless Mobile Networks. IEEE Trans. Mob. Comput. 2014, 13, 1469–1481. [Google Scholar] [CrossRef]
- Hsu, R.; Lee, J.; Quek, T.Q.S.; Chen, J. GRAAD: Group Anonymous and Accountable D2D Communication in Mobile Networks. IEEE Trans. Inf. Forensics Secur. 2018, 13, 449–464. [Google Scholar] [CrossRef]
- Alezabi, K.A.; Hashim, F.; Hashim, S.J.; Ali, B.M. An efficient authentication and key agreement protocol for 4G (LTE) networks. In Proceedings of the 2014 IEEE REGION 10 SYMPOSIUM, Kuala Lumpur, Malaysia, 14–16 April 2014; pp. 502–507. [Google Scholar]
- Mun, H.; Han, K.; Lee, Y.S.; Yeun, C.Y.; Choi, H.H. Enhanced secure anonymous authentication scheme for roaming service in global mobility networks. Math. Comput. Model. 2012, 55, 214–222. [Google Scholar] [CrossRef]
- Goutham Reddy, A.; Yoon, E.; Das, A.K.; Yoo, K. Lightweight authentication with key-agreement protocol for mobile network environment using smart cards. IET Inf. Secur. 2016, 10, 272–282. [Google Scholar] [CrossRef]
- El Idrissi, Y.E.H.; Zahid, N.; Jedra, M. An Efficient Authentication Protocol for 5G Heterogeneous Networks. In Ubiquitous Networking; Sabir, E., García Armada, A., Ghogho, M., Debbah, M., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 496–508. [Google Scholar]
- Su, C.; Santoso, B.; Li, Y.; Deng, R.H.; Huang, X. Universally Composable RFID Mutual Authentication. IEEE Trans. Dependable Secur. Comput. 2017, 14, 83–94. [Google Scholar] [CrossRef]
- Li, X.; Niu, J.; Kumari, S.; Wu, F.; Choo, K.K.R. A robust biometrics based three-factor authentication scheme for Global Mobility Networks in smart city. Future Gener. Comput. Syst. 2018, 83, 607–618. [Google Scholar] [CrossRef]
- He, D.; Chen, C.; Chan, S.; Bu, J. Secure and Efficient Handover Authentication Based on Bilinear Pairing Functions. IEEE Trans. Wirel. Commun. 2012, 11, 48–53. [Google Scholar] [CrossRef]
- Jiang, Q.; Ma, J.; Li, G.; Yang, L. An enhanced authentication scheme with privacy preservation for roaming service in global mobility networks. Wirel. Pers. Commun. 2013, 68, 1477–1491. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, J. A new authentication scheme with anonymity for wireless environments. IEEE Trans. Consum. Electron. 2004, 50, 231–235. [Google Scholar]
- Tsai, J.L.; Lo, N.W.; Wu, T.C. Secure Handover Authentication Protocol Based on Bilinear Pairings. Wirel. Pers. Commun. 2013, 73, 1037–1047. [Google Scholar] [CrossRef]
- Chang, C.C.; Lee, C.Y.; Chiu, Y.C. Enhanced authentication scheme with anonymity for roaming service in global mobility networks. Comput. Commun. 2009, 32, 611–618. [Google Scholar] [CrossRef]
- Chaudhry, S.A.; Albeshri, A.; Xiong, N.; Lee, C.; Shon, T. A privacy preserving authentication scheme for roaming in ubiquitous networks. Clust. Comput. 2017, 20, 1223–1236. [Google Scholar] [CrossRef]
- Chen, C.M.; Xiang, B.; Liu, Y.; Wang, K.H. A secure authentication protocol for internet of vehicles. IEEE Access 2019, 7, 12047–12057. [Google Scholar] [CrossRef]
- Chen, C.M.; Wang, K.H.; Yeh, K.H.; Xiang, B.; Wu, T.Y. Attacks and solutions on a three-party password-based authenticated key exchange protocol for wireless communications. J. Ambient Intell. Humaniz. Comput. 2019, 10, 3133–3142. [Google Scholar] [CrossRef]
- Wang, D.; Wang, P. On the anonymity of two-factor authentication schemes for wireless sensor networks: Attacks, principle and solutions. Comput. Netw. 2014, 73, 41–57. [Google Scholar] [CrossRef]
- Youn, T.; Park, Y.; Lim, J. Weaknesses in an Anonymous Authentication Scheme for Roaming Service in Global Mobility Networks. IEEE Commun. Lett. 2009, 13, 471–473. [Google Scholar] [CrossRef]
- Kim, J.S.; Kwak, J. Improved secure anonymous authentication scheme for roaming service in global mobility networks. Int. J. Secur. Its Appl. 2012, 6, 45–54. [Google Scholar]
- Lee, H.; Lee, D.; Moon, J.; Jung, J.; Kang, D.; Kim, H.; Won, D. An improved anonymous authentication scheme for roaming in ubiquitous networks. PLoS ONE 2018, 13, e0193366. [Google Scholar] [CrossRef] [PubMed]
- Gope, P.; Hwang, T. Lightweight and energy-efficient mutual authentication and key agreement scheme with user anonymity for secure communication in global mobility networks. IEEE Syst. J. 2015, 10, 1370–1379. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, G.; Li, L.; Yang, Y. Robust Privacy-Preserving Mutual Authenticated Key Agreement Scheme in Roaming Service for Global Mobility Networks. IEEE Syst. J. 2019, 1–12. [Google Scholar] [CrossRef]
- Eisenbarth, T.; Kasper, T.; Moradi, A.; Paar, C.; Salmasizadeh, M.; Shalmani, M. On the Power of Power Analysis in the Real World: A Complete Break of the KeeLoq Code Hopping Scheme. In Advances in Cryptology, CRYPTO 2008; Wagner, D., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5157, pp. 203–220. [Google Scholar]
- Dolev, D.; Yao, A.C. On the security of public key protocols. Inf. Theory, IEEE Trans. 1983, 29, 198–208. [Google Scholar] [CrossRef]
- He, D.; Zeadally, S.; Kumar, N.; Lee, J.H. Anonymous Authentication for Wireless Body Area Networks With Provable Security. IEEE Syst. J. 2016, 11, 2590–2601. [Google Scholar] [CrossRef]
- He, D.; Kumar, N.; Shen, H.; Lee, J.H. One-to-many authentication for access control in mobile pay-TV systems. Sci. China Inf. Sci. 2016, 59, 052108. [Google Scholar] [CrossRef][Green Version]
- Kumari, S.; Li, X.; Wu, F.; Das, A.K.; Arshad, H.; Khan, M.K. A user friendly mutual authentication and key agreement scheme for wireless sensor networks using chaotic maps. Future Gener. Comput. Syst. 2016, 63, 56–75. [Google Scholar] [CrossRef]
- Hoffstein, J. An introduction to cryptography. In An Introduction to Mathematical Cryptography; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–523. [Google Scholar]
- Bellare, M.; Rogaway, P. Random oracles are practical: A paradigm for designing efficient protocols. In Proceedings of the 1st ACM Conference on Computer and Communications Security, CCS93, Fairfax, VA, USA, 3–5 November 1993; pp. 62–73. [Google Scholar]
- Xie, Q.; Hwang, L. Security enhancement of an anonymous roaming authentication scheme with two-factor security in smart city. Neurocomputing 2019, 347, 131–138. [Google Scholar] [CrossRef]
- Mansoor, K.; Ghani, A.; Chaudhry, S.A.; Shamshirband, S.; Ghayyur, S.A.K.; Mosavi, A. Securing IoT-Based RFID Systems: A Robust Authentication Protocol Using Symmetric Cryptography. Sensors 2019, 19, 4752. [Google Scholar] [CrossRef]
- Ghani, A.; Mansoor, K.; Mehmood, S.; Chaudhry, S.A.; Rahman, A.U.; Najmus Saqib, M. Security and key management in IoT-based wireless sensor networks: An authentication protocol using symmetric key. Int. J. Commun. Syst. 2019, 32, e4139. [Google Scholar] [CrossRef]
- Kilinc, H.; Yanik, T. A Survey of SIP Authentication and Key Agreement Schemes. Commun. Surv. Tutorials IEEE 2014, 16, 1005–1023. [Google Scholar] [CrossRef]


| Notation | Definition |
|---|---|
| ,, | Mobile Node, Home Network, foreign Network |
| , | Identities of , and |
| , | Password and concealed password of |
| , | Shared keys between , and , |
| , P | Elliptic curve and a base point over curve |
| , | Private and public key pair of |
| Symmetric Encryption/decryption | |
| , | Two one-way hash Functions |
| , ⊕ | x-coordinate of a EC point, Exclusive-OR |
| Key based Mac |
| ↓ Features/Scheme → | [9] | [12] | [14] | [25] | [26] | Our |
|---|---|---|---|---|---|---|
| Mutual Authentication | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Correctness | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ |
| User Anonymity/Untraceability | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ |
| Perfect Forward Secrecy | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ |
| Resists User Forgery | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ |
| Resists Stolen Verifier | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ |
| Resists Insiders | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ |
| Resists Stolen Smart-Card | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ |
| Resists Known Session parameters | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, B.A.; Chaudhry, S.A.; Barnawi, A.; Al-Barakati, A.; Alsharif, M.H. A Privacy Preserving Authentication Scheme for Roaming in IoT-Based Wireless Mobile Networks. Symmetry 2020, 12, 287. https://doi.org/10.3390/sym12020287
Alzahrani BA, Chaudhry SA, Barnawi A, Al-Barakati A, Alsharif MH. A Privacy Preserving Authentication Scheme for Roaming in IoT-Based Wireless Mobile Networks. Symmetry. 2020; 12(2):287. https://doi.org/10.3390/sym12020287
Chicago/Turabian StyleAlzahrani, Bander A., Shehzad Ashraf Chaudhry, Ahmed Barnawi, Abdullah Al-Barakati, and Mohammed H. Alsharif. 2020. "A Privacy Preserving Authentication Scheme for Roaming in IoT-Based Wireless Mobile Networks" Symmetry 12, no. 2: 287. https://doi.org/10.3390/sym12020287
APA StyleAlzahrani, B. A., Chaudhry, S. A., Barnawi, A., Al-Barakati, A., & Alsharif, M. H. (2020). A Privacy Preserving Authentication Scheme for Roaming in IoT-Based Wireless Mobile Networks. Symmetry, 12(2), 287. https://doi.org/10.3390/sym12020287






