Abstract
Fifth-generation (5G) communications system is commercially introduced by several mobile operators where sub-6 GHz bands are the backbone of the 5G networks. A large-scale multiple-input multiple-output (MIMO), or massive MIMO (mMIMO), technology has a major impact to secure high data rate, high spectral efficiency, and quality of service (QoS). It could also have a major role in the beyond-5G systems. A massive number of antennas seek advanced signal processing to detect and equalize the signal. However, optimal detectors, such as the maximum likelihood (ML) and maximum posterior (MAP), are not desirable in implementation due to extremely high complexity. Therefore, sub-optimum solutions have been introduced to obtain and guarantee enough balance between the performance and the computational complexity. In this paper, a robust and joint low complexity detection algorithm is proposed based on the Jacobi (JA) and Gauss–Seidel (GS) methods. In such iterative methods, the performance, complexity, and convergence rate are highly dependent on the initial vector. In this paper, initial solution is proposed by exploiting the benefits of a stair matrix to obtain a fast convergence rate, high performance, and low complexity. Numerical results show that proposed algorithm achieves high accuracy and relieve the computational complexity even when the BS-to-user-antenna ratio (BUAR) is small.
1. Introduction
In last few years, a vast development in telecommunication systems has been witnessed to offer data-oriented services. In fifth-generation (5G) wireless communication systems, massive multiple-input multiple-output (mMIMO) is utilized to attain high data rate, reliability, robustness, energy efficiency, and spectral efficiency [1,2,3]. The mMIMO technology is also a strong candidate to be used in beyond-5G systems. However, computational complexity is remaining a challenge in implementation of the mMIMO system where large number of antennas are deployed at the base station (BS) to serve many users in a single cell [4]. The complexity is exponentially increases as the number of antenna elements increases. Therefore, a design of efficient low complexity detector for mMIMO uplink (UL) system requires a sophisticated signal processing. It is well known that the maximum likelihood (ML) obtains the lowest bit-error-rate (BER), but requires a very high computational complexity, which is not desirable in implementation. For instance, in a mMIMO system with 64 transmit antennas, ML detector exhaustively searches solutions to find the optimal result which is not practical [5]. In addition, computational complexity of the ML detector remarkably increases as the number of users increases. Sub-optimum detectors have been proposed to attain a considerable performance and complexity trade-off where a comprehensive survey can be found in [6].
Nonlinear algorithms like the K-best [6] and sphere decoding (SD) [7] are proposed for MIMO, but they include a QR decomposition which increases required signal processing operations, and therefore the computational complexity increases unfavorably with the system’s size. The case of utilizing the K-best and the SD algorithms in mMIMO system is being worse because of the large system’s size. The successive interference cancellation (SIC) cannot achieve a quasi-optimum performance close to the ML based detector [5]. Other nonlinear algorithms are also proposed such as the expectation propagation detector and the message passing detector [8]. However, myriad area and high power are required for real implementation in case of nonlinear algorithms. In addition, the belief propagation (BP)-based detector achieves low performance when the ratio between the BS-to-user-antenna ratio (BUAR) is close to 1 [9]. It is also hard to obtain the optimal damping factor. However, the convergence may not be achievable under certain circumstances. In [10], a detection algorithm based on the BP and neural networks have been proposed. Unfortunately, the computational complexity is greatly increased as the number of layers and neurons increased. The approximate message passing (AMP) and generalized approximate message passing (GAMP) algorithms are not robust and they obtain a poor performance outside the situation of the zero-mean independent and identically distributed (i.i.d) sub-Gaussian matrix [11].
Linear detection methods have been proposed to achieve a quasi-optimal performance and relieve some of the burden of the computational complexity in mMIMO systems. They work properly when the number of users is small. For instance, a minimum mean square error (MMSE) achieves a near-optimal performance when the BUAR is large enough [1]. Unfortunately, the MMSE algorithm includes undesirable and complicated matrix inversion, which is a critical task in the computational complexity, particularly when the number of antennas is large. The complexity of utilizing the MMSE algorithm is , where K is the number of users. Alternative detection algorithms have been illustrated such as the MMSE-parallel-interference-cancellation (MMSE-PIC) to achieve a satisfactory performance. However, complexity of the MMSE-PIC algorithm is still for computing the matrix inversion [12]. The channel hardening property of the mMIMO channel can be exploited to relatively relieve the computational complexity by replacing the matrix inversion challenge by matrix-vector multiplications. The truncated Neumann series expansion (NSE) approach is an example of such replacement where it achieves a significant performance enhancement when the BUAR is large. The convergence rate of the NSE method is slow. Therefore, another method, namely, the Newton iteration (NI), is proposed and it has faster convergence rate than the NSE method. Performance of the NSE and NI methods decays significantly when the BUAR is small, i.e., BUAR [13]. In other words, the NSE and NI methods are limited to the mMIMO system when the number of user terminals is comparatively small. Therefore, iterative methods have been proposed to avoid the matrix inversion by representing and solving the detection problem as a set of linear equations, and then refinements are performed iteratively over the solutions. It is well known that iterative methods, such as the successive over relaxation (SOR), the Gauss–Seidel (GS), the Jacobi (JA), the Richardson (RI), and etc., approach the MMSE performance with low complexity, i.e., . The performance and the complexity of RI and SOR methods depend on a relaxation parameter (). If , we obtain the GS method from the SOR method. The GS method achieves the MMSE performance when the BUAR is small. The JA method can be implemented in a parallel pattern. However, the performance–complexity profile and the convergence rate of iterative methods are highly dependent on the initial solution. Therefore, initial solution has to be selected carefully. In the literature, the initial solution is usually selected based on the diagonal property of the equalization matrix. In recent literature, a stair matrix have been utilized to initiate the initial solution which shows a considerable performance enhancement as well as a fast convergence rate [14,15,16].
In this paper, a robust low complexity joint detection algorithm is proposed based on the JA and GS methods to achieve the MMSE performance where the initial solution is selected based on properties of the stair matrix. The convergence rate of proposed algorithm is fast even when the BUAR is small. This paper is organized as follows. Section 2 presents the fundamentals and the background of proposed detection algorithm. Section 3 illustrates the iterative methods, whereas Section 3.6 presents the proposed hybrid low complexity detection algorithm. Section 4 presents the complexity analysis of the proposed algorithm. Section 5 illustrates the performance and complexity profiles of the proposed algorithm as well as a comparison with up-to-date methods is presented. Finally, Section 6 concludes the paper.
2. Background
The matrix inversion operation is undesirable in mMIMO systems and will greatly inflate the computational complexity. To reduce the complexity, iterative matrix inversions methods are proposed to estimate iteratively the signal. However, iterative methods can be categorized into two groups: approximate matrix inversion methods and avoid matrix inversion methods. Approximate matrix inversion methods, such as the NS method and the NI method, are alternative approach to approximate the inverse of equalization matrix before estimating the received signal. In the NS method, the matrix inversion is converted into a matrix-vector multiplication, which reduces the performance. In [17], weighted NS (WNS) detection technique is proposed to minimize the error between the exact matrix inversion and the WNS-based matrix inversion where online learning basis is used to obtain the optimal weights. Proposed technique improves the performance when the BUAR is large, i.e., and BUAR = . However, approximate matrix inversion methods require where K is the number of user terminals. In [18], modified detection algorithms are proposed based on the NI method where the computational complexity is reduced to , where N is the number of antennas at the BS side. In [19], tridiagonal matrix and a modified NSE are used to reduce the complexity of detection algorithm. The proposed algorithm performance is investigated on a Xilinx Virtex-7 XC7VX690T FPGA. It achieves a high performance when the BUAR is large, i.e., . However, approximate matrix inversion methods require a large number of iterations to achieve a satisfactory performance which increases the computational complexity. On the other hand, avoid matrix inversion methods, such as the GS, SOR, JA, and RI, refine the signal through iterations until the best estimation is obtained. This approach is usually achieving higher performance and lower complexity in comparison with the first approach where the complexity is usually [20]. In [21,22], it is illustrated that a detector based on the GS, SOR, JA, and RI methods achieve high performance and low complexity if the BUAR is large. However, they suffered from a considerable performance loss when the BUAR is small. In [23], a detector based on the SOR method has been implemented as on XILINX VIRTEX-7 XC7V690T FPGA for mMIMO system (BUAR = ). Two adaptive and non-adaptive SOR detectors have been proposed where the relaxation parameter has been selected based on different approaches [24]. Proposed detectors attained a satisfactory performance and low complexity for mMIMO system. In [25], a detector based on the JA method has been proposed based on the concept of a decentralized feedforward initialization approach where the mMIMO system is decomposed into multiple smaller subsystems. Proposed algorithm obtained a good performance when the BUAR is large, i.e., BUAR = and BUAR = . The RI method and Chebyshev acceleration technique are exploited in the detection approach for mMIMO system. Proposed techniques achieved acceptable performance when the BUAR is large, i.e., BUAR = and BUAR = [25]. It is also well known that initialization has a great impact in achieving a high performance and low complexity [15]. In [16], the impact of a stair matrix in algorithms based on iterative methods has been investigated and a compared with diagonal matrix based detection algorithms. It is shown that the utilization of a stair matrix contributes in obtaining a satisfactory performance within a small number of iterations (low complexity). In [14], a stair matrix is exploited in initializing the GS, the SOR, the NI, and the RI methods and a high performance is achieved when the BUAR is large (BUAR = ). It is also shown that the utilization of a stair matrix contributes positively in obtaining a high convergence rate.
In the literature, most of the existing detection techniques have been tested and investigated when BUAR is large, and thus they achieve high performance. In [16], several detectors have been studied based on a stair matrix, the GS, SOR, JA, NI, and RI methods. However, they achieved a good performance–complexity profile when the BUAR is large (BUAR = ). However, this is not the case when the BUAR is small. In such case, a sophisticated signal processing is required to select the optimal solution.
3. Methods
3.1. System Model
We consider an uncoded mMIMO system where the BS is furnished with N antennas to serve K single antenna users simultaneously in a single cell where . The vector presents the transmitted data by all users and the symbol vector presents received data at the BS where and are and , respectively. The received vector is usually corrupted by channel effects and the noise (). The channel matrix () entries are independent and identically distributed (i.i.d) with zero mean and unit variance. The mMIMO model is given as
In the MMSE algorithm, the equalization matrix () plays a role in estimating the signal as
and
and
where is the noise variance and is the identity matrix. The Gram matrix (G) is . However, a direct computation of requires . However, literature is rich with methods to avoid the direct and exact matrix inversion which relieves a burden of high computational complexity.
3.2. Neumann Series
The NS method approximates iteratively the matrix inversion where the problem is represented as a sum of infinite number of terms. However, the computational complexity increases as the number of iterations (n) and terms increase. In such approximation method, the equalization matrix is decomposed into a diagonal matrix () and a non-diagonal matrix , where can be iteratively approximated and refined as
The initial vector of the matrix inversion () is usually selected as and refined iteratively [14]. However, it converges to if . After that, the estimated signal () is written as .
3.3. Gauss–Seidel
The GS method is an efficient iterative method and it is a special scenario of the SOR method. Signal estimation using the SOR depends on the lower triangular matrix () and upper triangular matrix () as
where is the relaxation parameter, the lower triangular matrix. When in Equation (6), the GS iterative method is obtained and the estimated signal can be written as
Generally, the GS method has a fast convergence rate. The initial estimation is sit as and can be refined iteratively.
3.4. Jacobi
The JA method is another iterative method where estimation of the signal is written as
The rate of convergence of the JA method is slower than the GS method. However, computational complexity of the JA method is lower than the GS method and it is easy to implement in parallel manner.
3.5. A Stair Matrix
A stair matrix has one of the formulas listed below.
- -
- where
- -
- where
In the stair matrix, off-diagonal elements on either the odd or the even row are zeros [15]. For instance, a stair matrix of size can be written as
3.6. Proposed Method
Initialization of detection methods impacts the performance–complexity profile as well as the convergence rate. Proposed method exploits the benefits of low complexity JA and GS methods. In addition, a stair matrix () is also utilized to guarantee a fast convergence rate. In the literature, most methods are using the diagonal matrix where there is no guarantee of achieving a satisfactory convergence rate. Figure 1 illustrates the block diagram of the proposed detector, and Figure 2 presents the flowchart of the two stages proposed detector, the initialization, and the final estimation. Unlike the work in [16], where a detector is proposed based on individual GS, individual SOR, individual JA, individual NI, and individual RI methods, this paper proposes a hybrid JA-GS detector which initialized using a stair matrix. Proposed detector obtained a satisfactory balance between the performance and the complexity even when the BUAR is small (BUAR ).

Figure 1.
Block diagram of the proposed detector based on the JA and GS methods and a stair matrix.
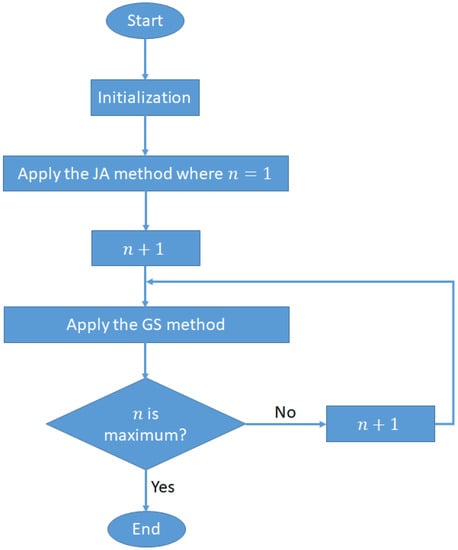
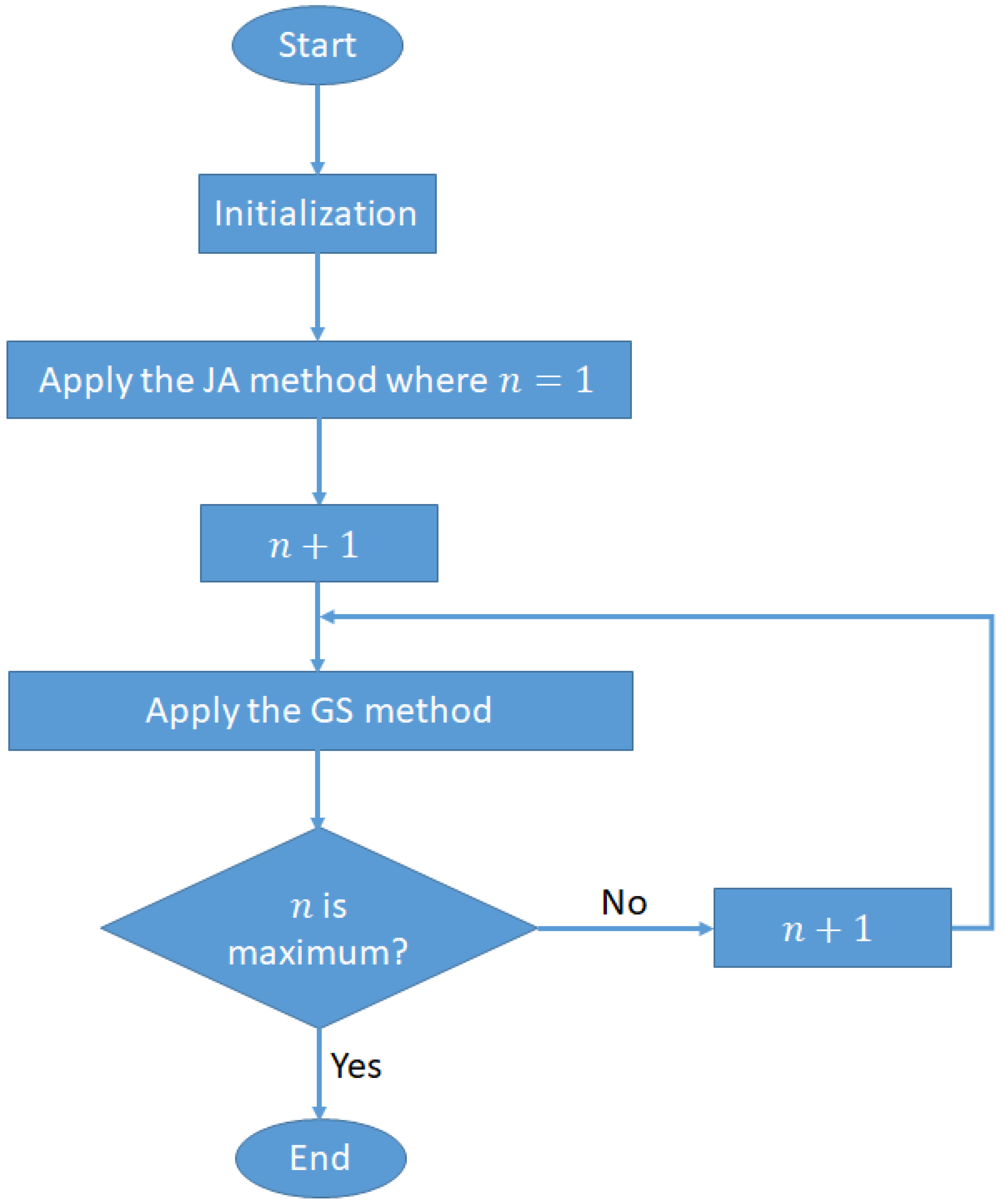
Figure 2.
Flowchart of the proposed detector based on the JA and GS methods and a stair matrix.
The initial solution is first computed based on the stair matrix as
Then, the first iteration of the JA method is conducted as
In the next step, the estimation is conducted and iteratively refined based on the GS method as shown in (7), where . Algorithm 1 illustrates the proposed detection algorithm using the JA, GS methods, and the stair matrix.
| Algorithm 1: Detection method based on joint JA, GS, and a stair matrix |
| Input: Output: Estimated signal Initialization: , , Initial estimations: Iteration: for j = 2:1:n Apply the GS method using (7) end Return . |
4. Complexity Analysis
It is well known that the complexity is greatly controlled by the number of performed mathematical operations, such as multiplications and divisions. In addition, large number of iterations contributes in elevating the computational complexity. Also, note that the selection of initial vector affect the computational complexity. Inverse of a stair matrix () requires a K real number of divisions as well as real number of multiplications. The JA method initialized based on a stair matrix requires real number of multiplications. The GS method requires real number of multiplications. Therefore, the proposed algorithm imposes real number of multiplications. However, the proposed algorithm avails a small number of iterations which reduces the computational complexity. The number of multiplications is illustrated in Table 1.

Table 1.
Complexity of the NS, GS, JA, and proposed algorithm.
5. Numerical Results
Simulation results are presented in this section as well as a comparison between the proposed algorithm and recently introduced mMIMO UL detectors to show the veracity of proposed algorithm. Simulation results are obtained using MATLAB for various iterations and BUAR = , , , . Results and comparisons are provided in bit-error-rate (BER) with the signal-to-noise ratio (SNR). In addition, the computational complexity comparison is also provided in the number of multiplications. A modulation scheme of 64QAM and the i.i.d Gaussain channels are utilized.
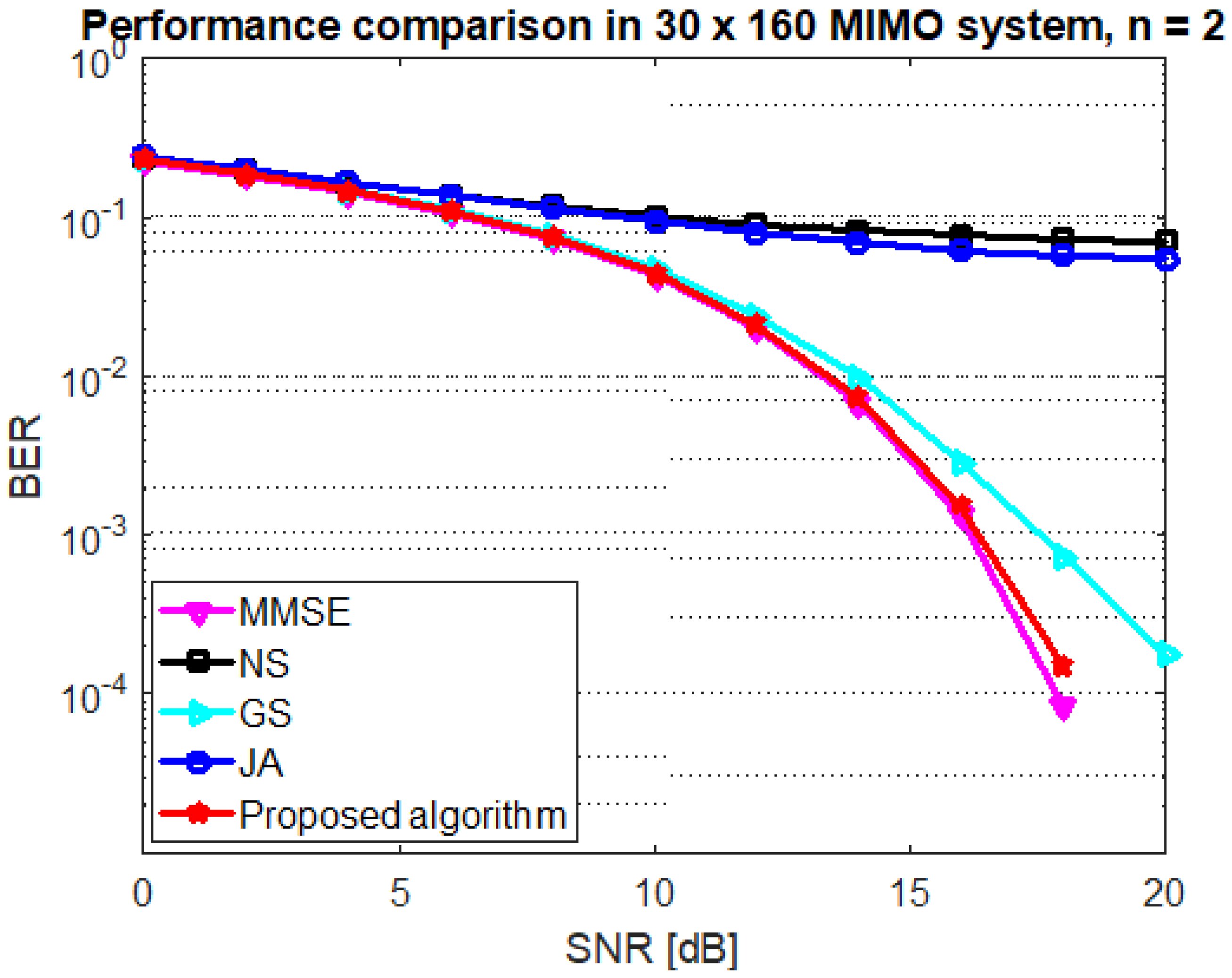
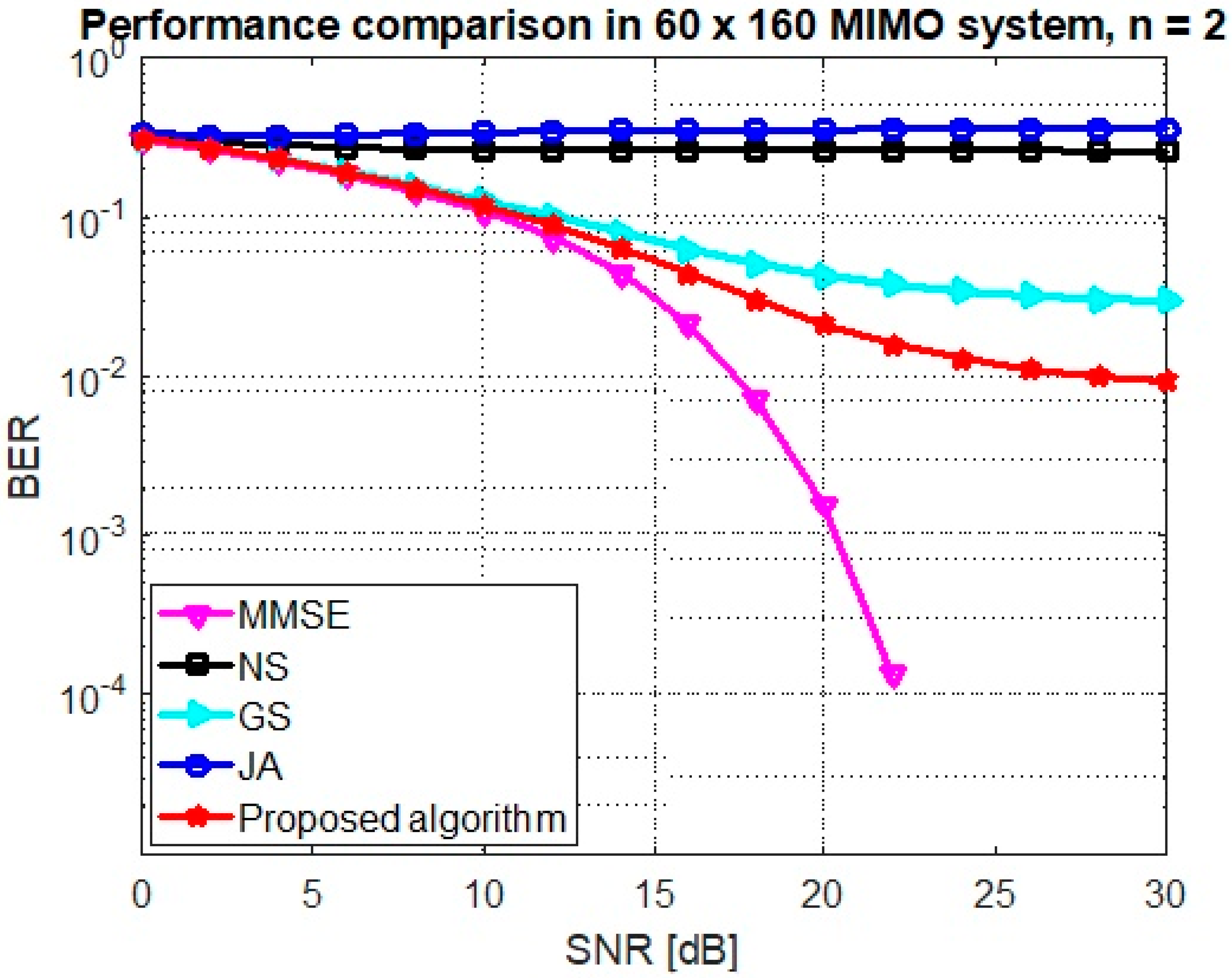
Figure 3 shows the BER comparison of proposed algorithm using joint JA and GS with initialization of the stair matrix and other up-to-date methods for antenna configuration (BUAR ). It is clear that the proposed algorithm can considerably speed up the convergence rate compared with existing methods. The proposed algorithm achieved the MMSE performance at , whereas the traditional GS, JA, and NS methods require extra iterations which increases the computational complexity. It is illustrated that the proposed algorithm achieved a BER = at SNR dB, whereas the GS method can achieve the target performance at SNR dB.
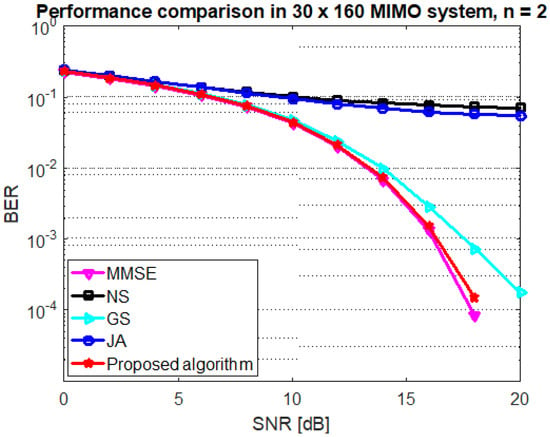
Figure 3.
Performance of the GS, JA, NS, and proposed algorithm at mMIMO size and .
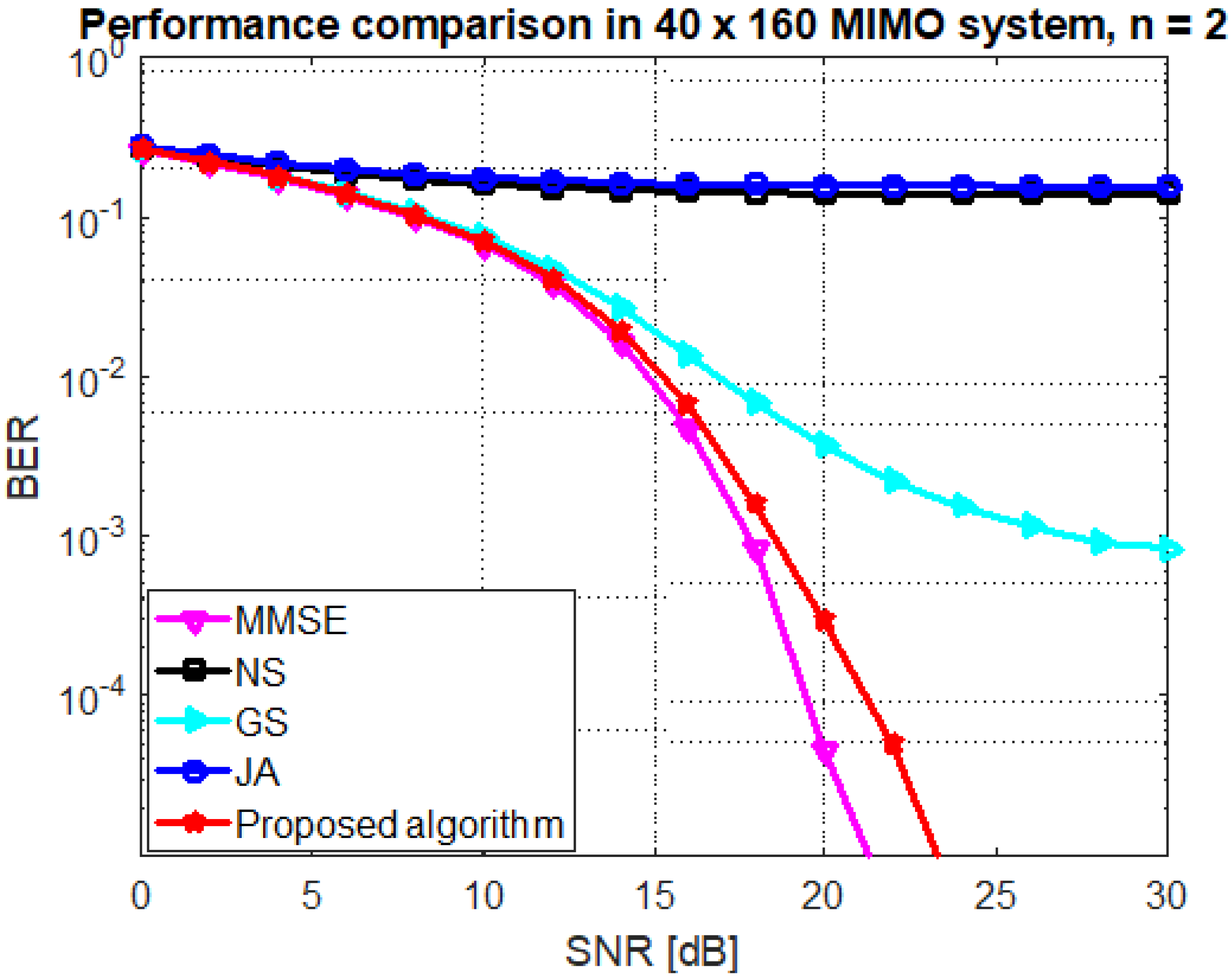
Figure 4 illustrates the BER comparison of proposed algorithm and other methods for antenna configuration (BUAR ). It is illustrated that the proposed algorithm achieved a quasi-MMSE performance at , whereas other methods require high number of iterations. For instance, the proposed algorithm achieved a BER = at SNR dB while the GS method achieved the same performance at dB. The performance of the NS and JA methods is very disappointed when BUAR .
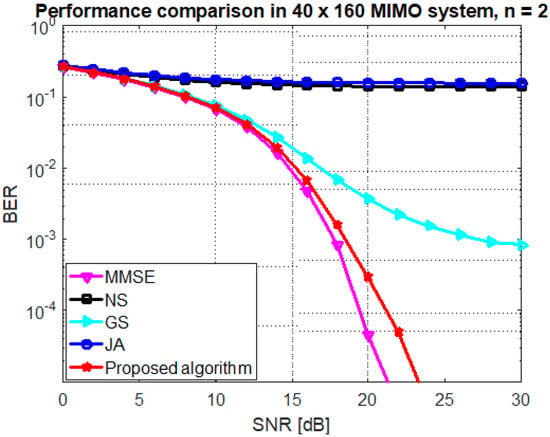
Figure 4.
Performance of the GS, JA, NS, and proposed algorithm at mMIMO size and
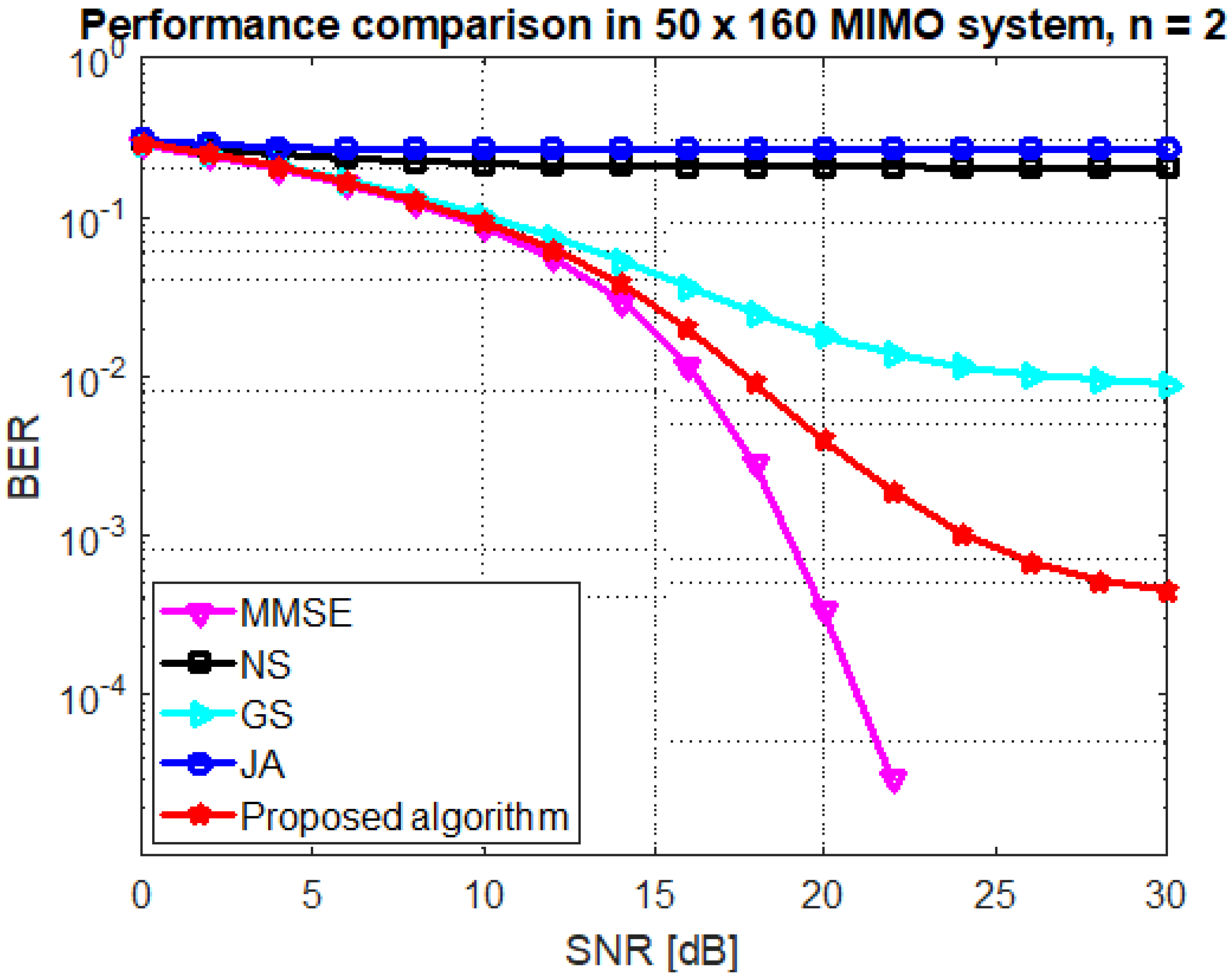
Figure 5 shows the performance comparison for antenna configuration (BUAR ). It is illustrated that the performance of proposed algorithm is better than the GS method. For instance, at SNR dB, the BER and for the proposed algorithm and the GS method, respectively. It is also clear that the JA and NS methods are not desirable when BUAR is small.
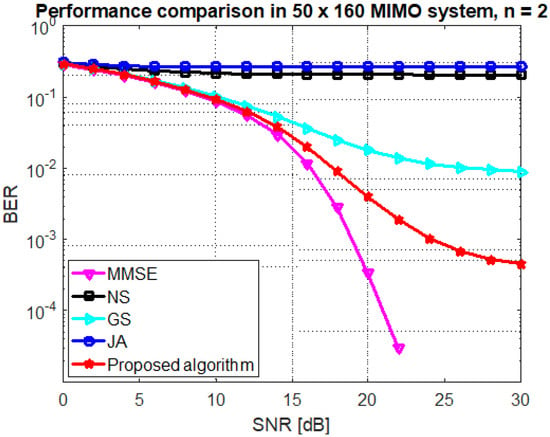
Figure 5.
Performance of the GS, JA, NS, and proposed algorithm at mMIMO size and .
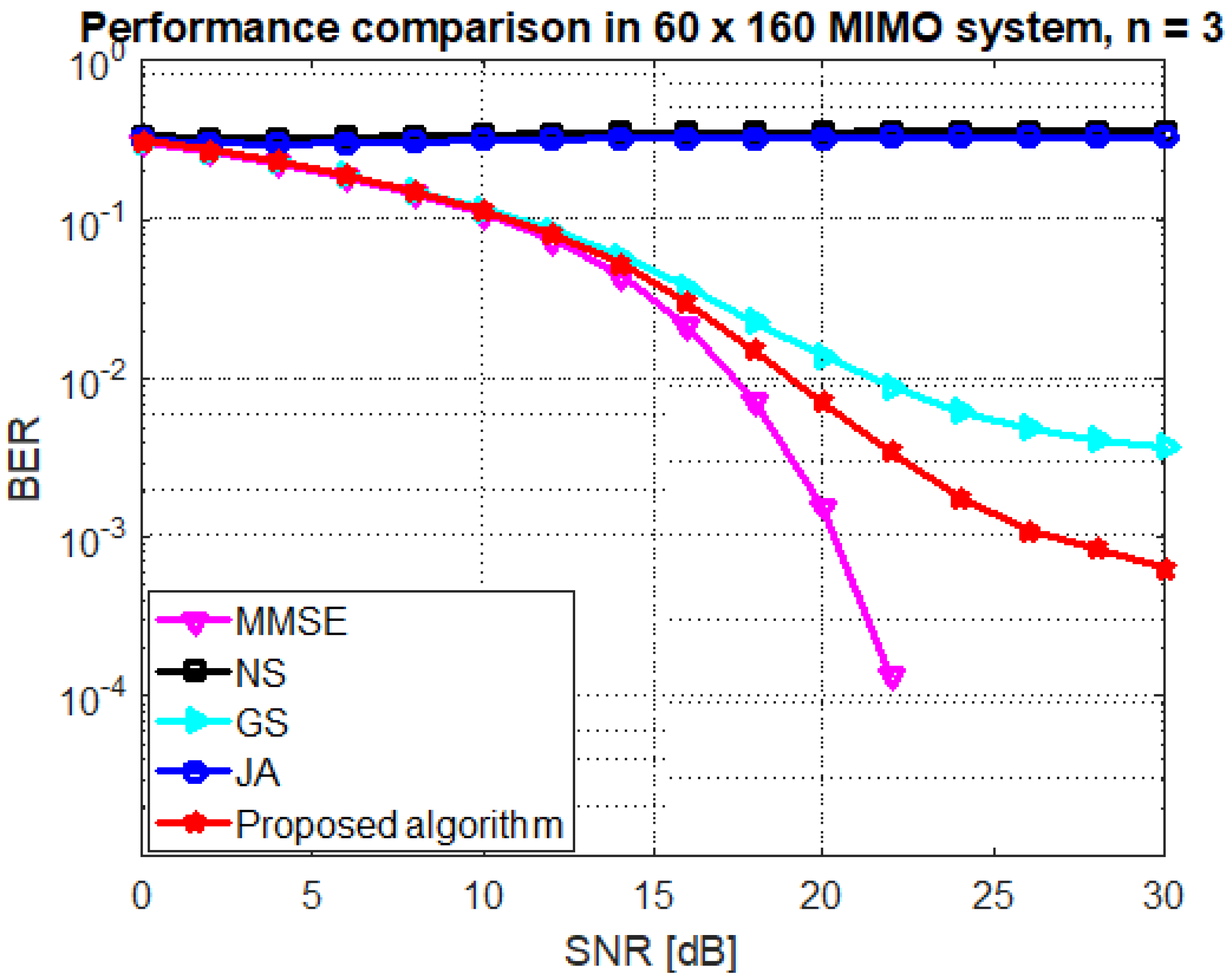
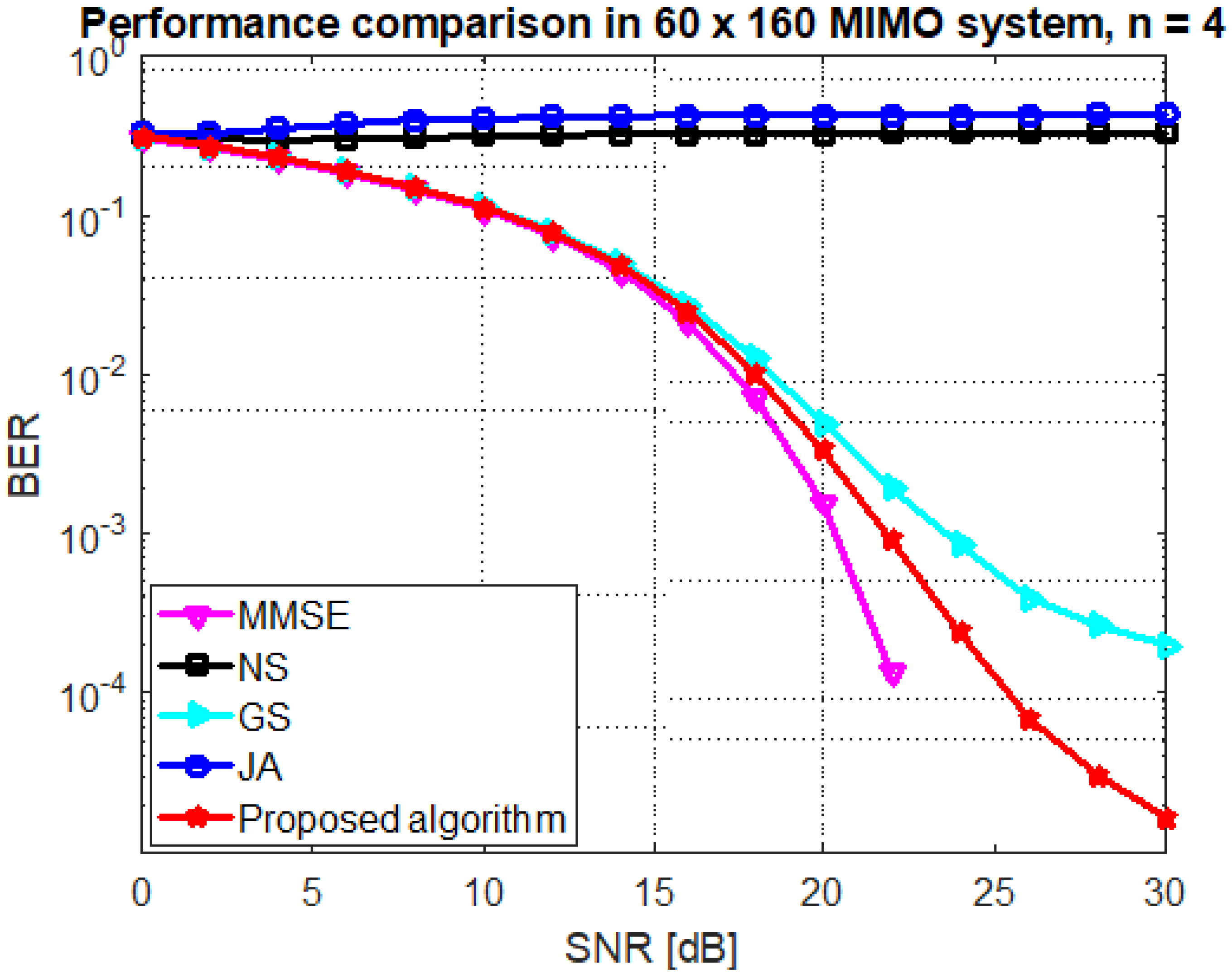
Figure 6, Figure 7 and Figure 8 show the performance comparison for antenna configuration (BUAR ) and and 4, respectively. It is illustrated that the proposed algorithm outperforms the others over all iterations within a few number of iterations. For instance, The proposed algorithm achieved the BER at SNR dB and , whereas the GS method achieved the target performance at .
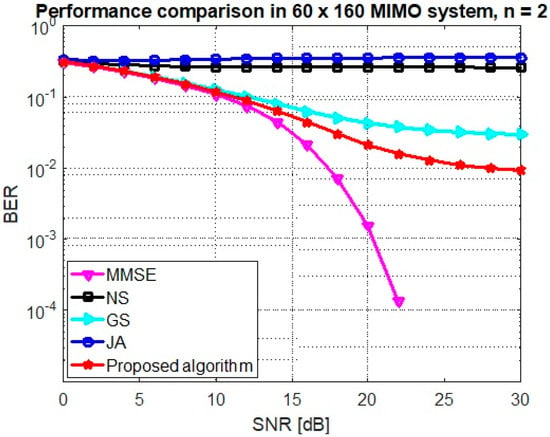
Figure 6.
Performance of the GS, JA, NS, and proposed algorithm at mMIMO size and .
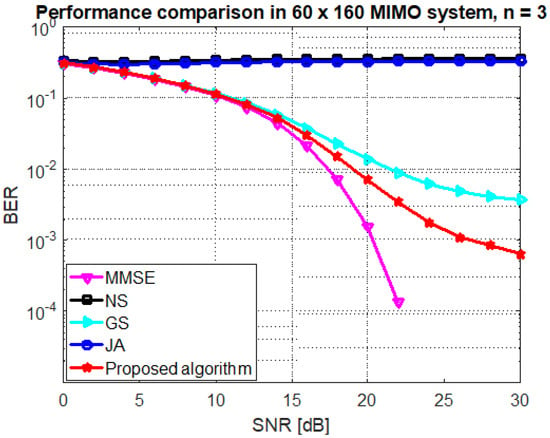
Figure 7.
Performance of the GS, JA, NS, and proposed algorithm at mMIMO size and .
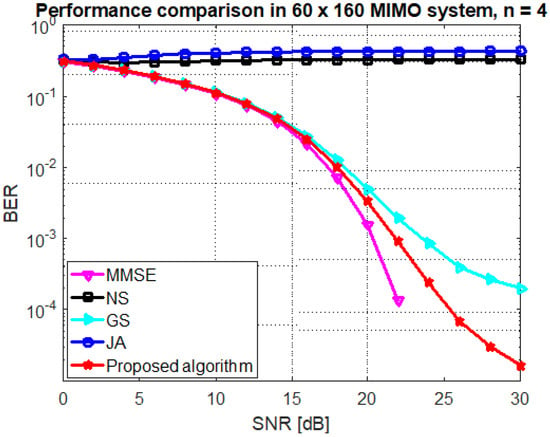
Figure 8.
Performance of the GS, JA, NS, and proposed algorithm at mMIMO size and .
Unlike the GS method, the proposed algorithm can achieve the target performance within a small number of iterations. The JA and NS method are not practical when BUAR .
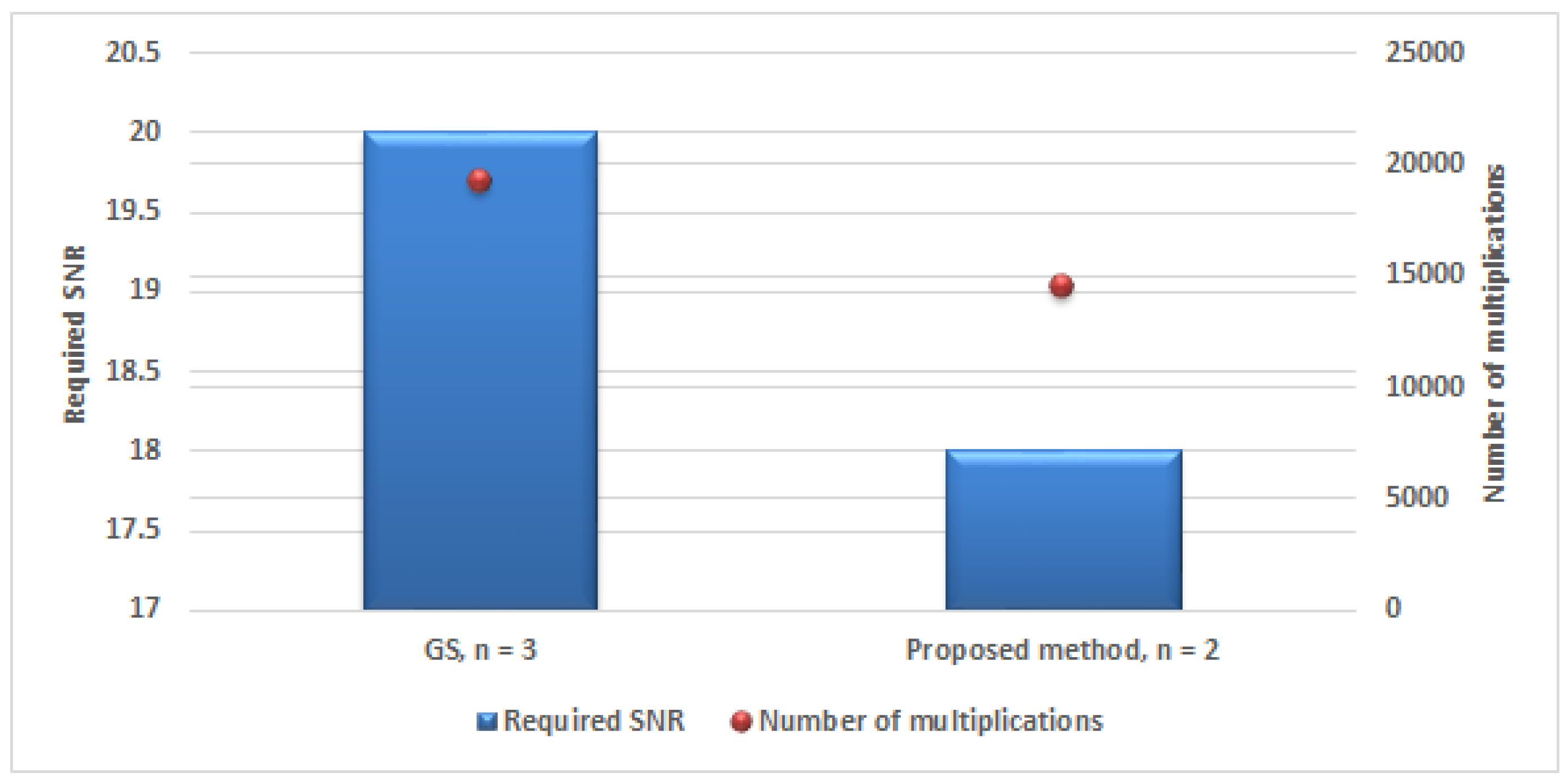
The target performance can be achieved within a small number of iterations when we utilize the proposed algorithm. For instance, BER = can be achieved when and using the proposed algorithm and the GS method, respectively. In case of the proposed algorithm, the number of multiplications is 32,457, whereas it is 43,200 when the GS method is used. This shows the advantage of utilizing the proposed algorithm over the traditional iterative method.
Figure 9 illustrates a comparison between the proposed method and the GS method to achieve BER = . It is clear that the GS method requires a large number of iterations, and therefore a high number of multiplications and high complexity.
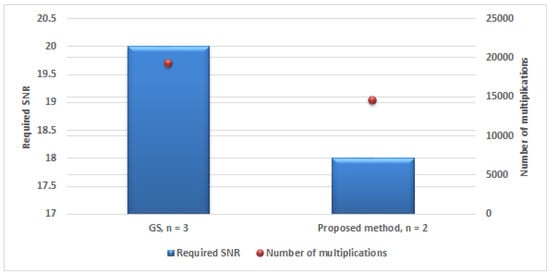
Figure 9.
A comparison between a detector based on the GS method and the proposed method in 40 mMIMO system to obtain BER = .
6. Conclusions
This paper proposes a robust hybrid iterative linear detector for mMIMO systems when BUAR is relatively small. Proposed detector utilizes the advantages of iterative methods such as the JA and the GS methods. In addition, a stair matrix structure is also exploited to initialize the proposed detector. Numerical results show that the proposed detector obtained the target performance with the lowest complexity. The JA and the NS methods are not suiting the detector design when the BUAR is small.
Utilization of hybrid iterative methods could be extended to propose efficient hybrid detectors such as the JA-SOR, JA-RI, GS-RI, and RI-SOR. In addition, early mentioned hybrid detectors could be initialized based on the stair matrix structure. The performance–complexity profile of such detectors has to be tested in realistic radio channels, i.e., the QUAsi Deterministic RadIo channel GenerAtor (QuaDRiGa) package.
Author Contributions
Conceptualization, M.A.A.; methodology, M.A.A.; software, M.A.A.; validation, M.H.A.; formal analysis, M.A.A.; project administration, M.A.A. and S.K.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results has received funding from the Research Council (TRC) of the Sultanate of Oman under the Block Funding Program. TRC Block Funding Agreement No. BFP/RGP/ICT/18/079). This work was supported by the Research Program through the National Research Foundation of Korea (NRF-2019R1A2C1005920).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, L.; Peng, G.; Wang, P.; Zhou, S.; Wei, Q.; Yin, S.; Wei, S. Energy- and Area-Efficient Recursive-Conjugate-Gradient-Based MMSE Detector for Massive MIMO Systems. IEEE Trans. Signal Process. 2020. [Google Scholar] [CrossRef]
- Akhlaghpasand, H.; Björnson, E.; Razavizadeh, S.M. Jamming Suppression in Massive MIMO Systems. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 182–186. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Nordin, R.; Abdullah, N.F.; Kelechi, A.H. How to make key 5G wireless technologies environmental friendly: A review. Trans. Emerg. Telecommun. Technol. 2018, 29, e3254. [Google Scholar] [CrossRef]
- Mohammed, S.L.; Alsharif, M.H.; Gharghan, S.K.; Khan, I.; Albreem, M. Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry 2019, 11, 1424. [Google Scholar] [CrossRef]
- Jia, Z.; Cheng, W.; Zhang, H. A Partial Learning-Based Detection Scheme for Massive MIMO. IEEE Wirel. Commun. Lett. 2019, 8, 1137–1140. [Google Scholar] [CrossRef]
- Guo, Z.; Nilsson, P. Algorithm and implementation of the K-best sphere decoding for MIMO detection. IEEE J. Sel. Areas Commun. 2006, 24, 491–503. [Google Scholar] [CrossRef]
- Larsson, E.G.; Jalden, J. Fixed-Complexity Soft MIMO Detection via Partial Marginalization. IEEE Trans. Signal Process. 2008, 56, 3397–3407. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, C.; Tsai, T.; Sun, W.; Ueng, Y.; Yang, C. A 501mW 7.6lGb/s integrated message-passing detector and decoder for polar-coded massive MIMO systems. In Proceedings of the 2017 Symposium on VLSI Circuits, Kyoto, Japan, 5–8 June 2017; pp. C330–C331. [Google Scholar] [CrossRef]
- Tan, X.; Ueng, Y.; Zhang, Z.; You, X.; Zhang, C. A Low-Complexity Massive MIMO Detection Based on Approximate Expectation Propagation. IEEE Trans. Veh. Technol. 2019, 68, 7260–7272. [Google Scholar] [CrossRef]
- Jeon, Y.; Hong, S.; Lee, N. Blind detection for MIMO systems with low-resolution ADCs using supervised learning. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, X.; Jin, S.; Wen, C. Symbol Detection of Phase Noise-Impaired Massive MIMO Using Approximate Bayesian Inference. IEEE Signal Process. Lett. 2019, 26, 607–611. [Google Scholar] [CrossRef]
- Fang, L.; Xu, L.; Huang, D.D. Low Complexity Iterative MMSE-PIC Detection for Medium-Size Massive MIMO. IEEE Wirel. Commun. Lett. 2016, 5, 108–111. [Google Scholar] [CrossRef]
- Wu, M.; Yin, B.; Wang, G.; Dick, C.; Cavallaro, J.R.; Studer, C. Large-Scale MIMO Detection for 3GPP LTE: Algorithms and FPGA Implementations. IEEE J. Sel. Top. Signal Process. 2014, 8, 916–929. [Google Scholar] [CrossRef]
- Albreem, M. Efficient initialisation of iterative linear massive MIMO detectors using a stair matrix. Electron. Lett. 2020, 56, 50–52. [Google Scholar] [CrossRef]
- Jiang, F.; Li, C.; Gong, Z.; Su, R. Stair Matrix and its Applications to Massive MIMO Uplink Data Detection. IEEE Trans. Commun. 2018. [Google Scholar] [CrossRef]
- Albreem, M.A.; Alsharif, M.H.; Kim, S. Impact of Stair and Diagonal Matrices in Iterative Linear Massive MIMO Uplink Detectors for 5G Wireless Networks. Symmetry 2020, 12, 71. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Wang, X.; Lian, J.; Dai, X. A Low Complexity High Performance Weighted Neumann Series-based Massive MIMO Detection. In Proceedings of the 2019 28th Wireless and Optical Communications Conference (WOCC), Beijing, China, 9–10 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Jin, F.; Liu, Q.; Liu, H.; Wu, P. A Low Complexity Signal Detection Scheme Based on Improved Newton Iteration for Massive MIMO Systems. IEEE Commun. Lett. 2019, 23, 748–751. [Google Scholar] [CrossRef]
- Zhang, C.; Liang, X.; Wu, Z.; Wang, F.; Zhang, S.; Zhang, Z.; You, X. On the Low-Complexity, Hardware-Friendly Tridiagonal Matrix Inversion for Correlated Massive MIMO Systems. IEEE Trans. Veh. Technol. 2019, 68, 6272–6285. [Google Scholar] [CrossRef]
- Ren, W.; Zhou, Y.; Ji, W.; Li, T.; Liang, Y.; Li, F. Matrix Approximate Inversion Based Signal Detection in Large-scale 3D-MIMO Systems. In Proceedings of the 2019 15th International Wireless Communications Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 830–835. [Google Scholar] [CrossRef]
- Albreem, M.A.M.; El-Saleh, A.A.; Juntti, M. On Approximate Matrix Inversion Methods for Massive MIMO Detectors. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakech, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Albreem, M.A.M. Approximate Matrix Inversion Methods for Massive MIMO Detectors. In Proceedings of the 2019 IEEE 23rd International Symposium on Consumer Technologies (ISCT), Ancona, Italy, 19–21 June 2019; pp. 87–92. [Google Scholar] [CrossRef]
- Nhat Cuong, C.; Thi Hong, T.; Duc Khai, L. Hardware Implementation of the Efficient SOR-Based Massive MIMO Detection for Uplink. In Proceedings of the 2019 IEEE-RIVF International Conference on Computing and Communication Technologies (RIVF), Danang, Vietnam, 20–22 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Yu, A.; Jing, S.; Tan, X.; Wu, Z.; Yan, Z.; Zhang, Z.; You, X.; Zhang, C. Efficient Successive Over Relaxation Detectors for Massive MIMO. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 1–12. [Google Scholar] [CrossRef]
- Seidel, P.; Gregorek, D.; Paul, S.; Rust, J. Efficient Initialization of Iterative Linear Massive MIMO Uplink Detectors by Binary Jacobi Synthesis. In Proceedings of the WSA 2019; 23rd International ITG Workshop on Smart Antennas, Vienna, Austria, 24–26 April 2019. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).