Abstract
In massive multiple-input multiple-output (M-MIMO) systems, a detector based on maximum likelihood (ML) algorithm attains optimum performance, but it exhaustively searches all possible solutions, hence, it has a very high complexity and realization is denied. Linear detectors are an alternative solution because of low complexity and simplicity in implementation. Unfortunately, they culminate in a matrix inversion that increases the computational complexity in high loaded systems. Therefore, several iterative methods have been proposed to approximate or avoid the matrix inversion, such as the Neuamnn series (NS), Newton iterations (NI), successive overrelaxation (SOR), Gauss–Siedel (GS), Jacobi (JA), and Richardson (RI) methods. However, a detector based on iterative methods requires a pre-processing and initialization where good initialization impresses the convergence, the performance, and the complexity. Most of the existing iterative linear detectors are using a diagonal matrix () in initialization because the equalization matrix is almost diagonal. This paper studies the impact of utilizing a stair matrix () instead of in initializing the linear M-MIMO uplink (UL) detector. A comparison between iterative linear M-MIMO UL detectors with and is presented in performance and computational complexity. Numerical Results show that utilization of achieves the target performance within few iterations, and, hence, the computational complexity is reduced. A detector based on the GS and achieved a satisfactory bit-error-rate (BER) with the lowest complexity.
1. Introduction
Nowadays, fifth generation (5G) wireless communications systems have been introduced by several mobile companies to meet user demands for high data rates (up to 10 Gbps) and quality of service (QoS). The main target is to obtain an enhanced mobile broadband (eMBB), massive machine type communications (mMTC), and ultra-reliable and low-latency communications. In 5G, several technologies are utilized such as the millimeter-wave (mmWave), the Internet of Things (IoT), the visible light communication (VLC), and the massive multiple-input multiple-output (M-MIMO) [1]. In mmWave, a wide spectral resource can be exploited to support a wide signal bandwidth and high data throughput. The electromagnetic wave at mmWave band is highly attenuated because of the path loss and shadowing. However, high antenna gain can be obtained when the mmWave band is utilized [2]. In the IoT, a large number of devices are connected to process huge data rates, make classifications and decisions, and solve problems. It would exploit the artificial intelligence and linked to cloud networks [3]. In the VLC, a light emitting diode (LED) is utilized in an indoor scenario for simultaneous wireless communications. In addition, the VLC provides high energy efficiency, high security, and free of interference [4]. The M-MIMO system is an extension of a small scale MIMO where a large number of antennas at the base-station (BS) are deployed to serve multiple user terminals [5]. It contributes positively in spectrum efficiency (SE) and energy efficiency (EE), increases the degree of freedom, and reduces the latency. However, a large number of antennas requires advanced signal processing techniques to equalize and estimate the signal. Although a detector based on the maximum likelihood (ML) obtains the optimum performance, it is banned in implementation because of the exponential computational complexity [6]. Sphere decoding (SD) is a possible solution to achieve a quasi-optimum performance. However, it depends on the sphere radius selection and the complexity increases as the radius increased [7]. Other detectors are also proposed such as detectors based on successive interference cancellation (SIC) [8], local search [9], and belief propagation (BP) [10]. The computational complexity of the SIC based detector is high. The local search based detector depends on the size of the neighborhood. In the BP, the damping factor is required, and it is very hard to find it. In addition, the convergence is not guaranteed. However, a large number of antennas at the BS leads to an interesting phenomena called channel hardening where the columns of the channel matrix are being orthogonal or nearly orthogonal. Thus, a simple linear detector can achieve a satisfactory performance. Linear minimum mean square error (MMSE) is a possible solution, but it sustains a significant performance loss in highly loaded systems [11]. It also contains an exact matrix inversion that increases the computational complexity. In order to avoid the exact matrix inversion, a plethora of iterative linear M-MIMO detection algorithms have been proposed such as the Neumann series (NS) [12], Newton iteration (NI) [13], successive over relaxation (SOR) [14], Gauss–Seidel (GS) [15], Jacobi (JA) [16], and Richardson (RI) [17]. A detector based on the NS and NI methods approximates the matrix inversion of the Gram matrix instead of computing it. A detector based on the SOR, GS, JA, and RI methods estimates the signal () by avoid a matrix inversion. However, the behavior of a detector based on iterative methods is greatly influenced by selection of the initial solution () where an inappropriate initial solution could increase the number of iterations, and hence increases the complexity. In contrast, good initialization reduces the number of iterations and hence reduces the computational complexity.
Most of the existing iterative linear detectors are utilizing the diagonal matrix () in estimating the initial vector because the equalization matrix is diagonally dominant. In some cases, the diagonal matrix has a slow convergence, or it may not converge. In [18], a stair matrix () is proposed as an alternative solution to replace in initializing iterative linear detectors based on the NS and JA methods. This paper aims to study the impact of and in initialization of iterative linear M-MIMO UL detectors where iterative methods are utilized such as the SOR, GS, JA, and RI methods. In addition, a comparison between the performance-complexity profiles of and will be presented. Therefore, thousands of random channel matrices have been generated to examine the convergence rate using both and .
This paper is organized as follows: Section 2 presents the system model and the definition of a stair matrix and a diagonal matrix. Section 3 presents the NS, NI, SOR, GS, JA, and RI methods with the initialization using stair and diagonal matrices. Section 4 provides a comprehensive analysis of the computational complexity required by each detector. In Section 5, results and discussion are presented. Section 6 concludes the paper.
2. Background
2.1. System Model
Consider N antennas at the BS are serving simultaneously K user terminals where . The symbol vector is transmitted by users and the symbol vector is received at the BS side. However, it is corrupted by the noise and effects of the channel. indicates the channel matrix which is decisive in the input–output relationship as
where w is the additive white Gaussian noise (AWGN). In the MMSE detector, the transmitted signal can be estimated based on the equalization matrix () as
and
and
where and are the noise variance and the identity matrix, respectively. is the Gram matrix. Recently, several methods have been proposed to reduce the complexity of a linear MMSE detector by iterative estimation of the signal without exact computation of as shown in Equation (2). The diagonal property is predominant in the equalization matrix . Thus, most of the existing iterative linear MMSE detectors are employing the diagonal matrix to estimate the signal. However, limited research shows the utilization of a stair matrix in iterative detectors based M-MIMO [18].
2.2. Definition of a Diagonal Matrix and a Stair Matrix
In linear algebra, a matrix is called a diagonal matrix if elements outside the main diagonal are all zero [19]. For instance, a diagonal matrix can be expressed as:
In order to call a matrix a stair matrix, one of the following expressions has to be obtained:
- -
- , where ,
- -
- , where .
From the definition, a stair matrix is a tri-diagonal matrix where the off-diagonal entries on either the odd or the even row are zeros [18]. For example, a stair matrix can be presented as:
3. Diagonal and Stair Matrices in Iterative Linear M-MIMO UL Detectors
3.1. Linear Detectors Based on Neumann Series and Newton Iteration
The Neumann series (NS) and Newton iteration (NI) methods approximate iteratively the matrix inversion instead of computing it. They depend on the concept of polynomial expansion where the matrix inversion is expanded as a sum of infinite number of terms. The computational complexity increases when the number of terms and iterations (n) increases. In the NS method, () is decomposed into a diagonal matrix () and a non-diagonal matrix . In the NS method, can be iteratively approximated as:
In the NI method, can be presented as
Selection of the initial inversion is crucial. In this paper, we investigate the selection of in the NS and NI methods as:
- , where is the diagonal matrix,
- , where is the stair matrix.
is the initial solution to iterations shown in Equations (5) and (6), which converge quadratically to if
is refined iteratively. In order to investigate the condition in Equation (7), channel matrices are generated where D and S are extracted from each H. Figure 1 shows that the condition in Equation (7) is always valid for both diagonal and stair matrices.
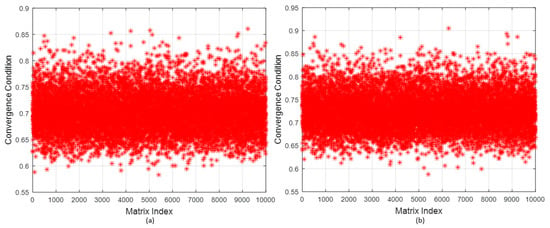
Figure 1.
in Equation (7) for channel realizations using (a) a stair matrix and (b) a diagonal matrix.
The signal can be estimated as
3.2. Linear Detectors Based on Iterative Methods
In this subsection, the signal is equalized by avoiding inverse of the matrix using several iterative methods such as the SOR, the GS, the JA, and the RI. The concept of an iterative method depends on two major procedures: initial solution and iterative updates. The concept of iterative methods is that the initial solution is refined iteratively for few iterations to obtain a better and modified estimation. The iterations are repeated until the best performance is achieved.
The SOR iterative method depends on the relaxation parameter (). The estimated signal is expressed as
where and are the upper and the lower triangular matrices, respectively. Appropriate selection of impacts positively the performance and the computational complexity. If , the SOR method is called the GS iterative method where the estimated signal is given as
In general, the SOR and GS methods have a good convergence rate.
In the RI iterative method, is utilized to find the estimated signal as
It requires a large number of iterations to converge. Thus, high computational complexity is required.
In the JA iterative method, the received signal is given as:
In general, the JA method has a low convergence rate in comparison with the SOR and GS methods.
In this paper, the initial solution depends on D and S and is expressed as one of the following solutions:
- Using a stair matrix: ,
- Using a diagonal matrix: .
is refined iteratively and the new solution is updated until the best performance is obtained.
4. Complexity Analysis
Complexity is highly affected by the number of multiplications, divisions, and number of iterations. An inappropriate number of iterations increases or decreases the number of multiplications and divisions. Therefore, the computational complexity and the performance are greatly affected by the initial estimation. In order to compute and , K real number of divisions is required. However, the computation of requires an additional real number of multiplications. However, this increment is a small. For instance, in the GS based MIMO and , 8192 and 8285 number of multiplications are required if D and S are exploited, respectively. In order to obtain a good performance, a detector based on S requires a small number of iterations in comparison with a detector based on D matrix. The required number of multiplications are listed in Table 1.

Table 1.
Complexity comparison among initialized detectors based on Diagonal and Stair Matrices.
5. Numerical Results
In this section, we investigate the impact of using the diagonal and stair matrices in the performance and the computational complexity of a detector based on the NI, NS, SOR, GS, JA, and RI methods. It will be presented in the bit-error-rate (BER), the signal-to-noise ratio (SNR), and number of multiplications. In simulations, independent and identically distributed (i.i.d) Gaussian channels are considered, the MIMO sizes is , the modulation scheme is 64QAM, and several iterations are conducted.
Table 2 shows that the convergence condition in Equation (7) is satisfied for all random S and . However, statistical values are smaller in the case of S than the values in the case of D. For instance, the mean values of the convergence condition are 0.7027 and 0.7255 when using S and D, respectively.

Table 2.
Statistics of in Equation (7) for channel realizations for M-MIMO system.
Figure 2 presents the performance of the NI, the NS, the SOR, the GS, the JA, and the RI based detector using both S and D matrices. Detectors initialized by S outperform detectors initialized by D in each iteration. For example, at , the BER is obtained at SNR dB and SNR dB for the GS based detector using S and D, respectively. In the SOR based detector, the target performance is achieved at and using S and D, respectively. The worst performance is occurred when a detector based on the RI and the NS is initialized by D. In other words, all detectors can achieve the target performance when the number of iterations is large (i.e., ), but the best detector achieves the target performance with the smallest number of iterations (lowest complexity).
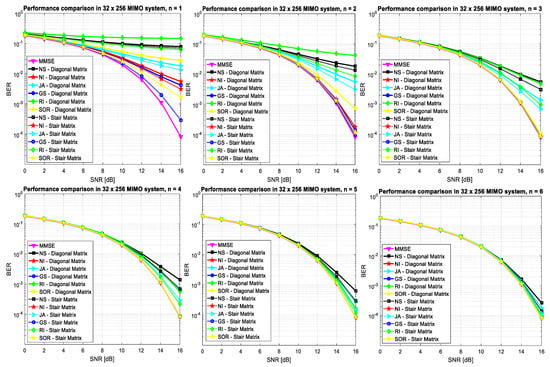
Figure 2.
Performance of a detector based on iterative matrix inversion methods with D and S for M-MIMO system.
Figure 3 illustrates the relationship between the performance and the computational complexity to obtain BER . The lowest computational complexity is achieved by a detector based on the GS and initialized by S when SNR dB. In contrast, a detector based on the NS method and initialized by D requires the highest computational complexity to achieve the target BER performance.
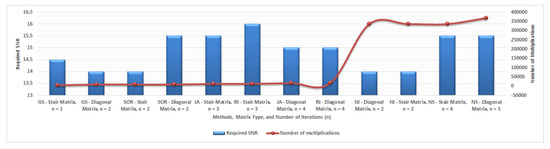
Figure 3.
Performance-complexity trade-off to achieve BER = .
6. Conclusions
In this paper, the impact of D and S has been studied in M-MIMO UL detectors. It is shown that the initialization of a detector based on S achieves a good balance between the performance and the computational complexity. A detector based on the GS method and initialized by S obtained the best performance–complexity profile. However, a detector based on the NS method and D requires a high number of iterations to achieve the target performance and hence it has the highest computational complexity.
Detection techniques for M-MIMO are a hot research topic and utilization of S could be extended to nonlinear detectors such as the sphere decoding (SD) and successive interference cancellation (SIC) detectors. In addition, the performance-complexity profile of detectors based on local research and belief propagation (BP) could be developed by the usage of S. However, the utilization of S should be investigated in realistic radio channels such as the QUAsi Deterministic RadIo channel GenerAtor (QuaDRiGa) package.
Author Contributions
Conceptualization, M.A.A.; methodology, M.A.A.; software, M.A.A.; validation, M.H.A.; formal analysis, M.A.A.; project administration, M.A.A. and S.K.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results has received funding from the Research Council (TRC) of the Sultanate of Oman under the Block Funding Program—TRC Block Funding Agreement No. BFP/RGP/ICT/18/079). This work (S2666095) was also supported by the project for Cooperative R&D between Industry, Academy, and the Research Institute funded Korea Ministry of SMEs and Startups in 20.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Albreem, M.A.M. 5G wireless communication systems: Vision and challenges. In Proceedings of the 2015 International Conference on Computer, Communications, and Control Technology (I4CT) 2015, Kuching, Malaysia, 21–23 April 2015; pp. 493–497. [Google Scholar] [CrossRef]
- Mohammed, S.; Alsharif, M.; Gharghan, S.; Albreem, M. Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry 2019, 11, 1424. [Google Scholar] [CrossRef]
- Alsharif, M.; Kim, S.; Kuruoğlu, N. Energy Harvesting Techniques for Wireless Sensor Networks/Radio-Frequency Identification: A Review. Symmetry 2019, 11, 865. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Yang, S.; Son, Y.; Han, S. Mitigation of Inter-Cell Interference Utilizing Carrier Allocation in Visible Light Communication System. IEEE Commun. Lett. 2012, 16, 526–529. [Google Scholar] [CrossRef]
- Albreem, M.A.; Juntti, M.; Shahabuddin, S. Massive MIMO Detection Techniques: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 3109–3132. [Google Scholar] [CrossRef]
- Thian, B.S.; Goldsmith, A. Decoding for MIMO Systems with imperfect channel state information. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM, Miami, FL, USA, 6–10 December 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Albreem, M.; Salleh, M. Lattice Sphere Decoding for Block Data Transmission Systems. Wirel. Person. Commun. 2015, 82, 1833–1850. [Google Scholar] [CrossRef]
- Albreem, M.; Ismail, N. A Review: Detection Techniques For LTE System. Telecommun. Syst. 2015, 63, 153–168. [Google Scholar] [CrossRef]
- Chaudhary, M.; Meena, N.K.; Kshetrimayum, R.S. Local search based near optimal low complexity detection for large MIMO System. In Proceedings of the 2016 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Bangalore, India, 6–9 November 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Takahashi, T.; Ibi, S.; Sampei, S. On Normalization of Matched Filter Belief in GaBP for Large MIMO Detection. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Xie, T.; Han, Q.; Xu, H.; Qi, Z.; Shen, W. A Low-Complexity Linear Precoding Scheme Based on SOR Method for Massive MIMO Systems. In Proceedings of the IEEE Vehicular Technology Conference, Glasgow, Scotland, 11–14 May 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Costa, H.; Roda, V. A Scalable Soft Richardson Method for Detection in a Massive MIMO System. Prz. Elektrotechniczny 2016, 92, 199–203. [Google Scholar] [CrossRef]
- Minango, J.; de Almeida, C. Optimum and quasi-optimum relaxation parameters for low-complexity massive MIMO detector based on Richardson method. IEE Electron. Lett. 2017, 53, 1114–1115. [Google Scholar] [CrossRef]
- Kong, B.Y.; Park, I.C. Low-complexity symbol detection for massive MIMO uplink based on Jacobi method. In Proceedings of the IEEE International Symposium on Personal, Indoor, and Mobile Radio Communications, Valencia, Spain, 4–8 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, C.; Liang, X.; Wu, Z.; Xu, S.; You, X. Efficient iterative soft detection based on polynomial approximation for massive MIMO. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing, Nanjing, China, 15–17 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Dai, L.; Gao, X.; Su, X.; Han, S.; I, C.L.; Wang, Z. Low-Complexity Soft-Output Signal Detection Based on Gauss Seidel Method for Uplink Multiuser Large-Scale MIMO Systems. IEEE Trans. Veh. Technol. 2015, 64, 4839–4845. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, J.; Chen, J.; He, S. Biased MMSE soft-output detection based on conjugate gradient in massive MIMO. In Proceedings of the 2015 IEEE 11th International Conference on ASIC, Chengdu, China, 3–6 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Jiang, F.; Li, C.; Gong, Z.; Su, R. Stair Matrix and its Applications to Massive MIMO Uplink Data Detection. IEEE Trans. Commun. 2018, 66, 2437–2455. [Google Scholar] [CrossRef]
- Prabhu, H.; Edfors, O.; Rodrigues, J.; Liu, L.; Rusek, F. Hardware efficient approximative matrix inversion for linear pre-coding in massive MIMO. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems, Melbourne, Australia, 1–5 June 2014; pp. 1700–1703. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).