Dual Solutions and Stability Analysis of a Hybrid Nanofluid over a Stretching/Shrinking Sheet Executing MHD Flow
Abstract
1. Introduction
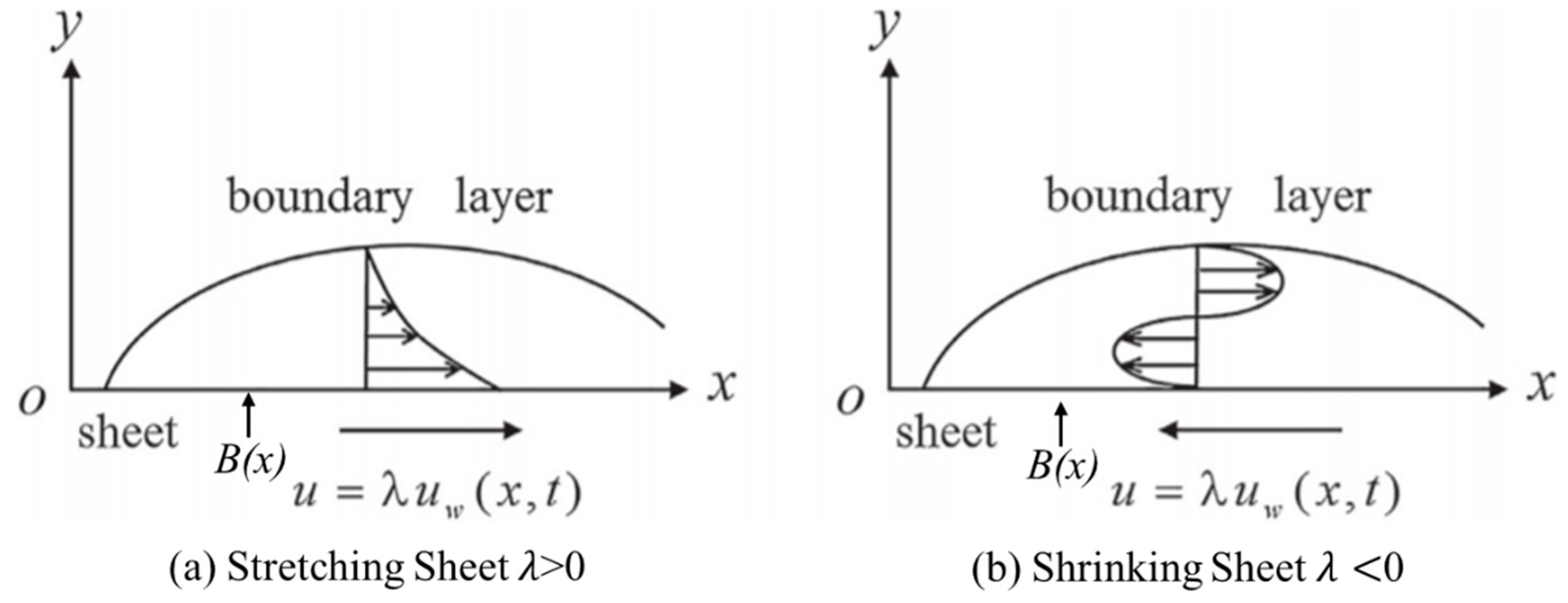
2. Problem Formulation
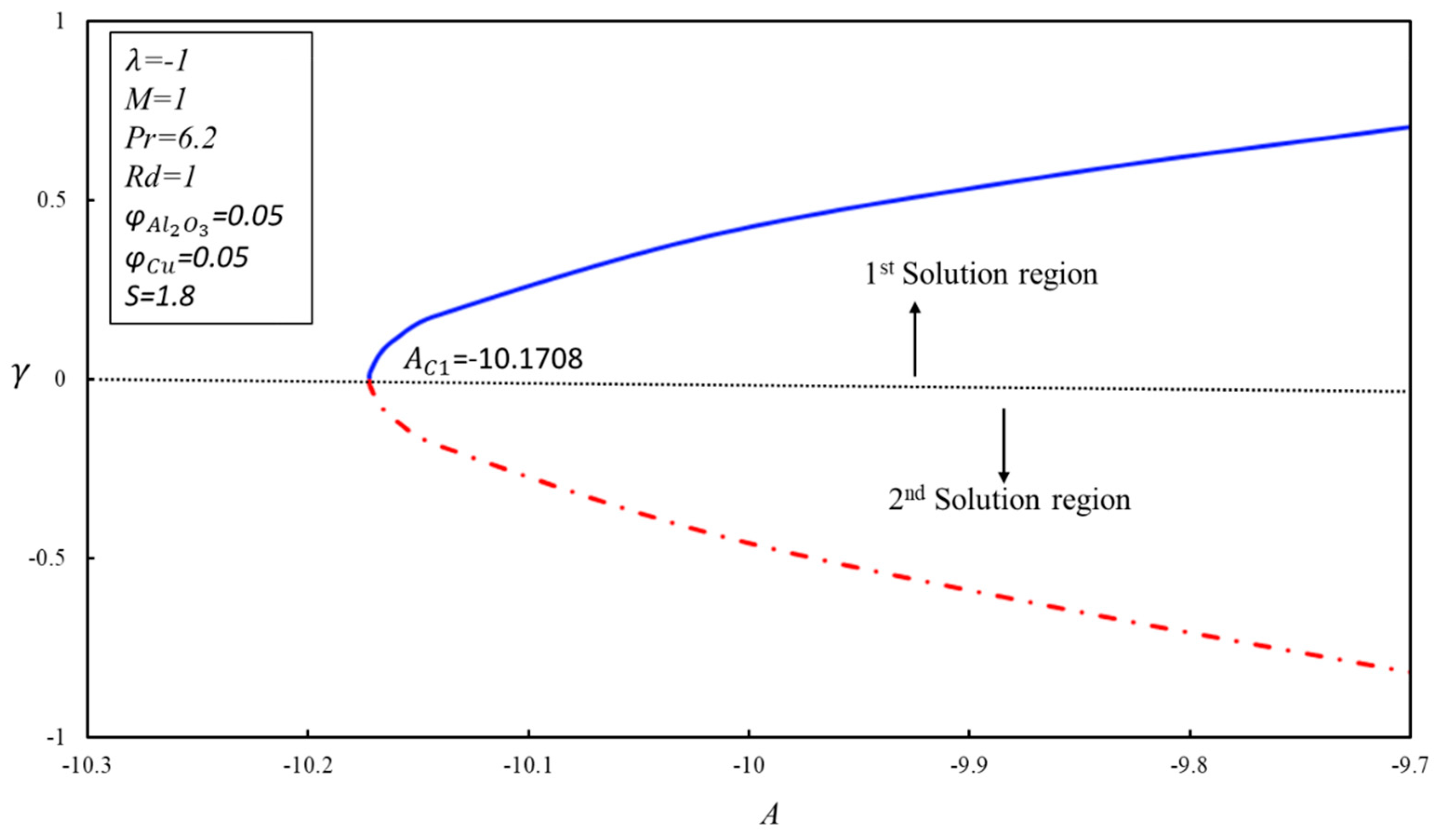
3. Stability Analysis
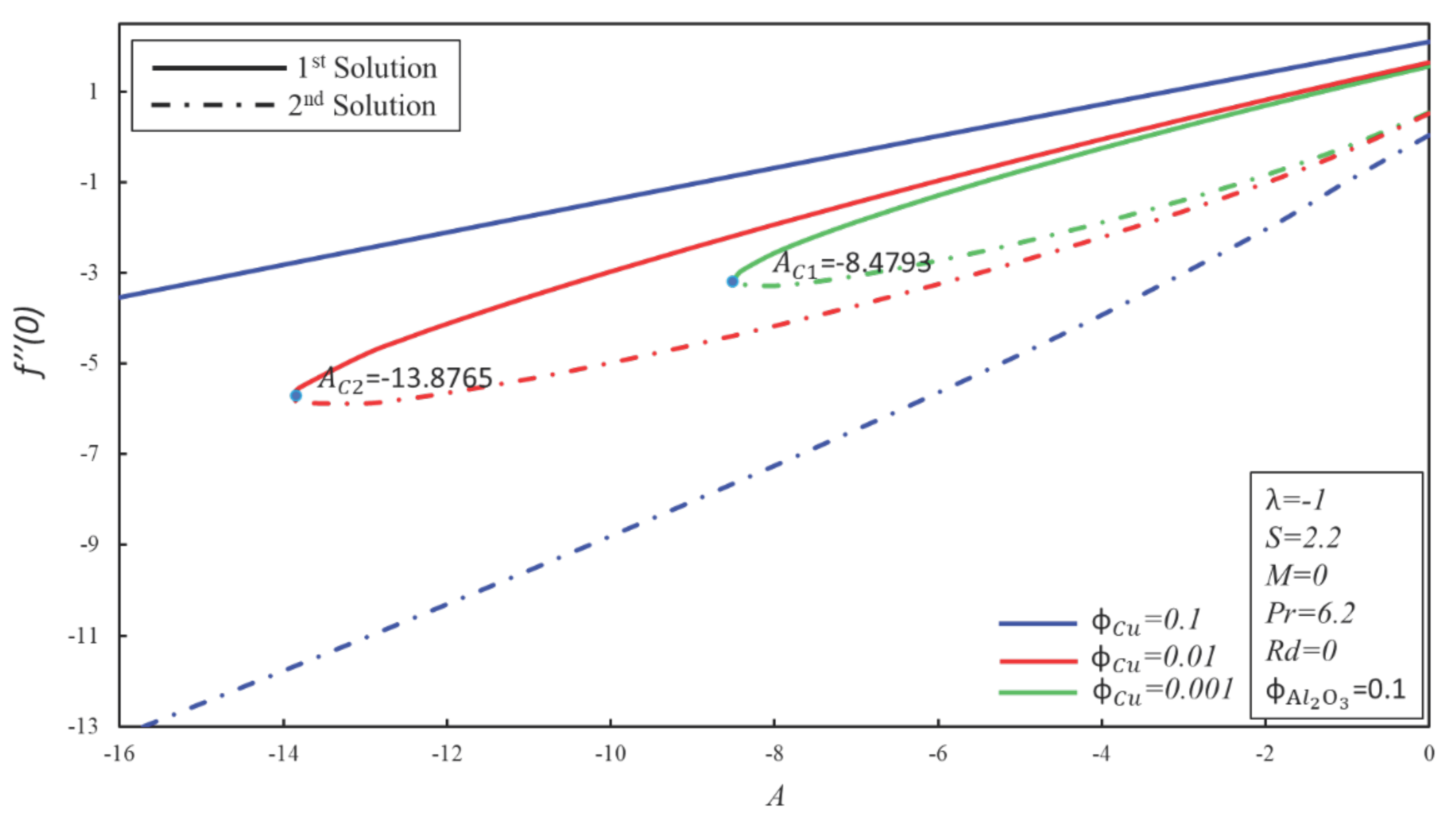
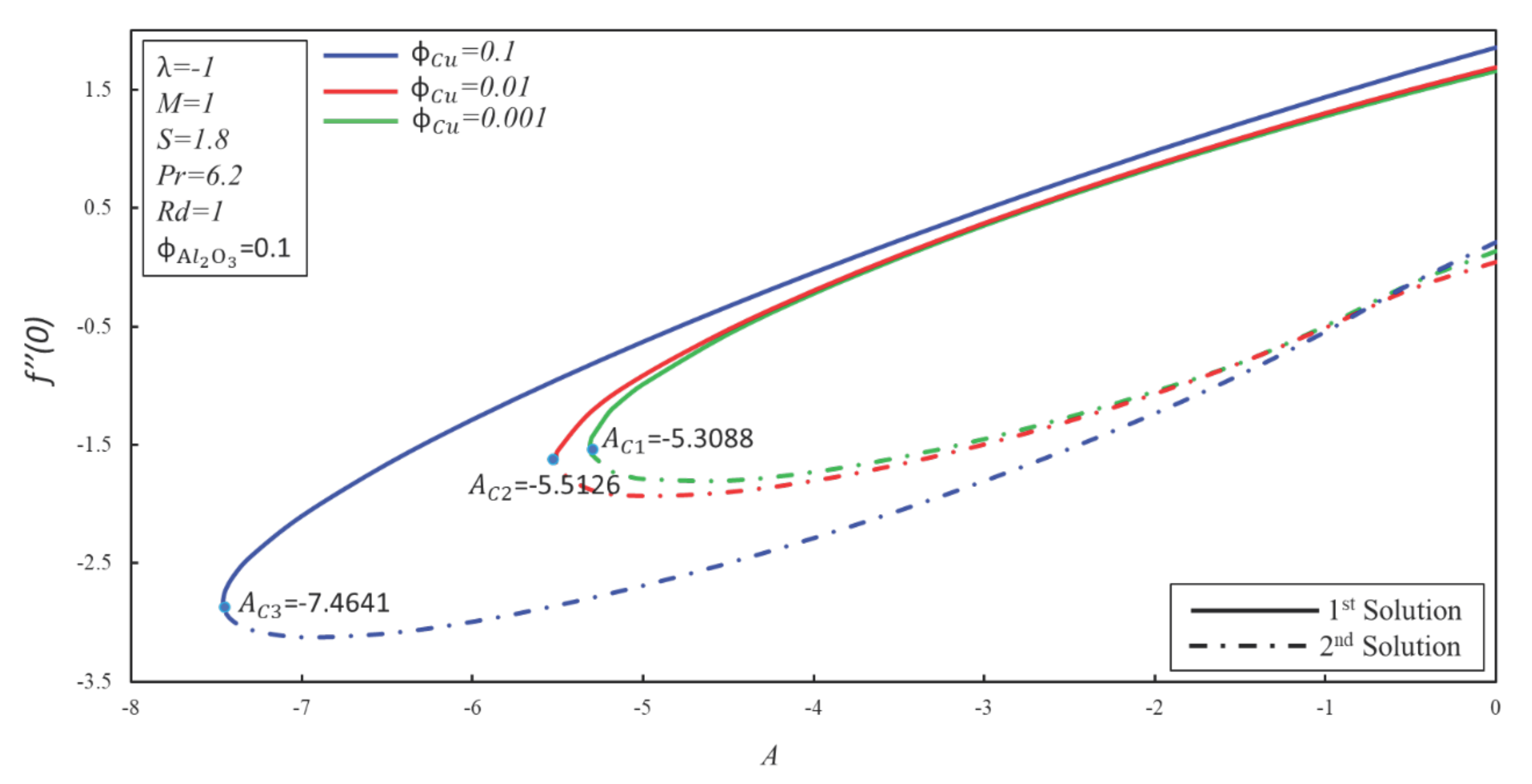
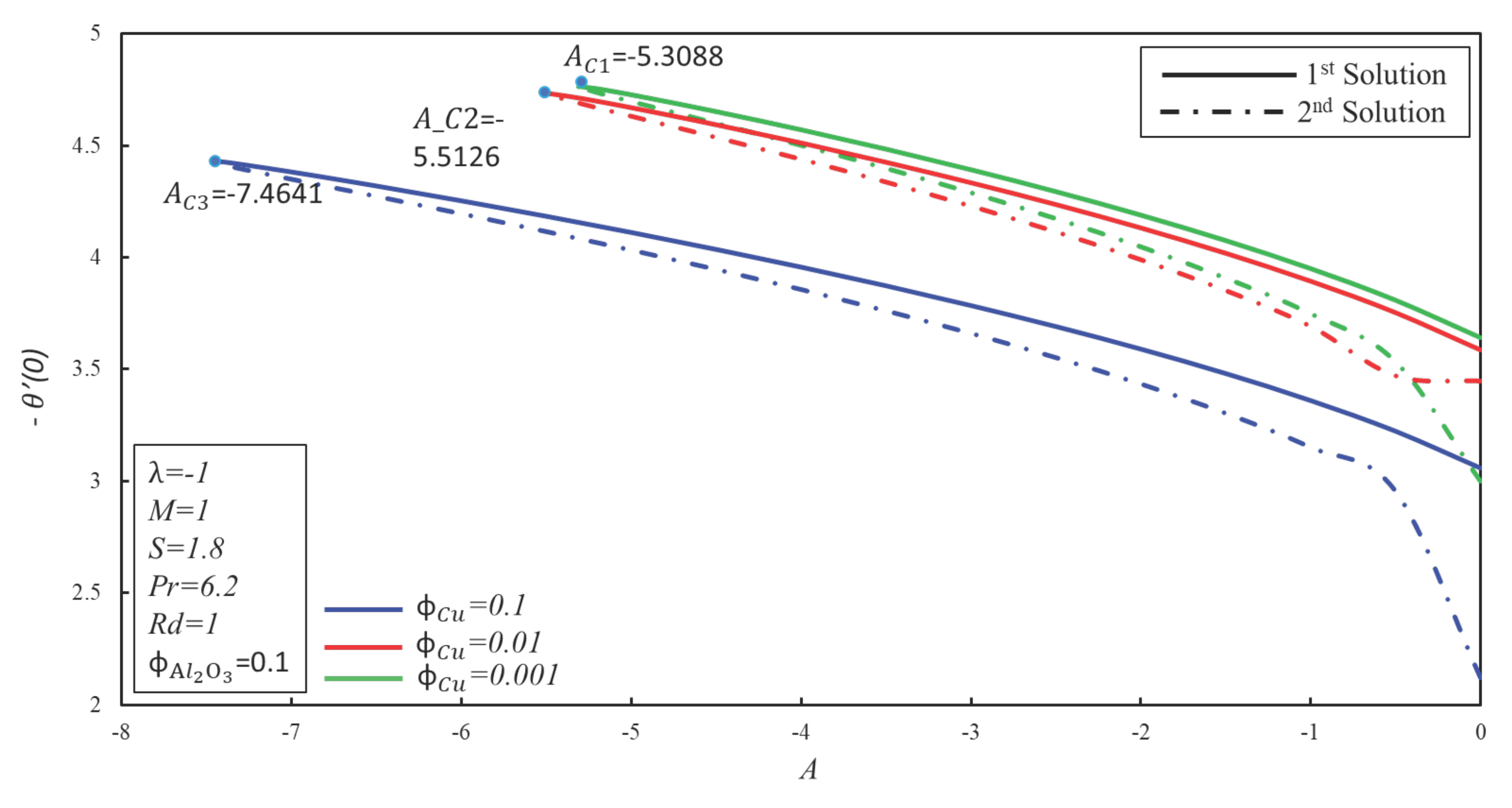
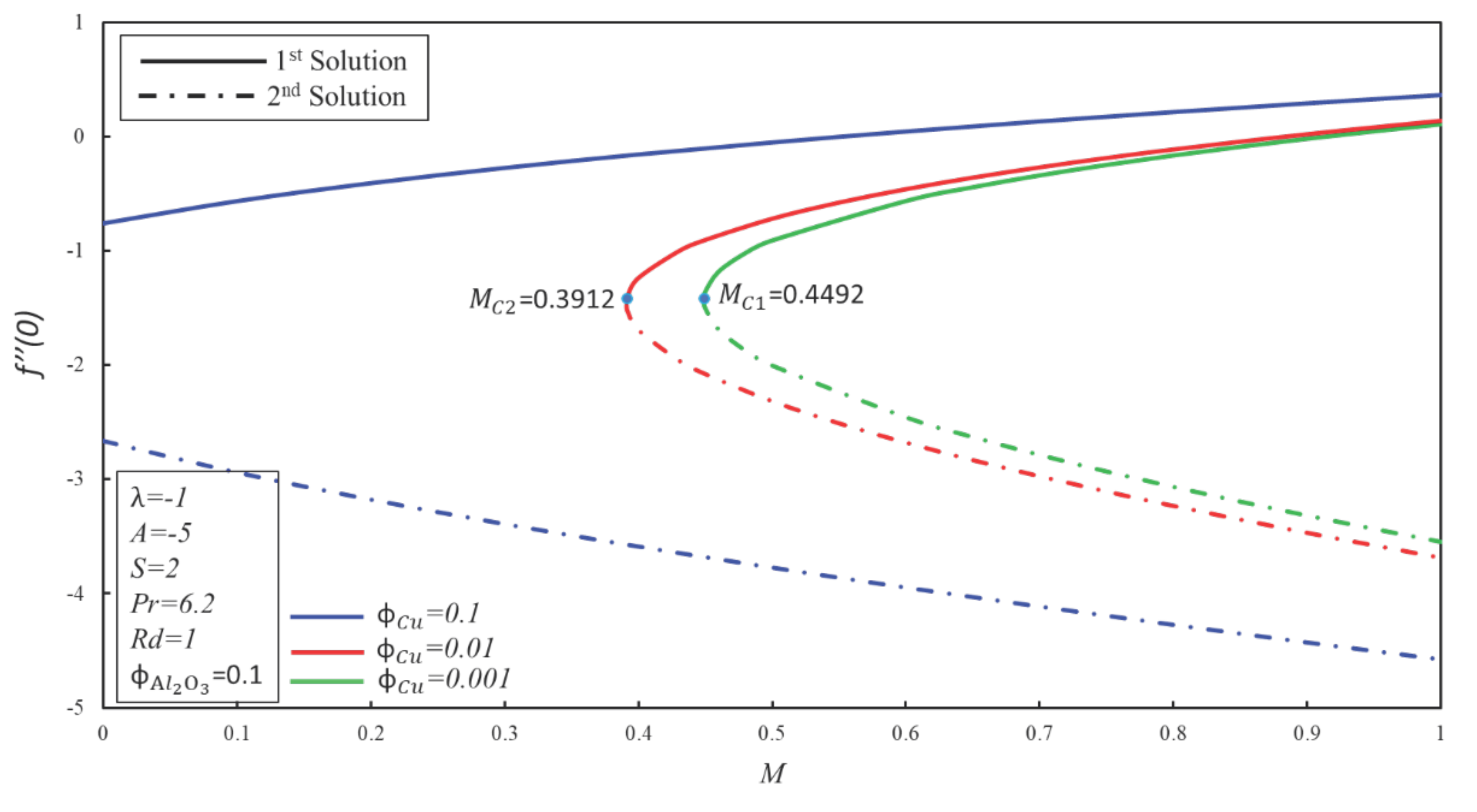
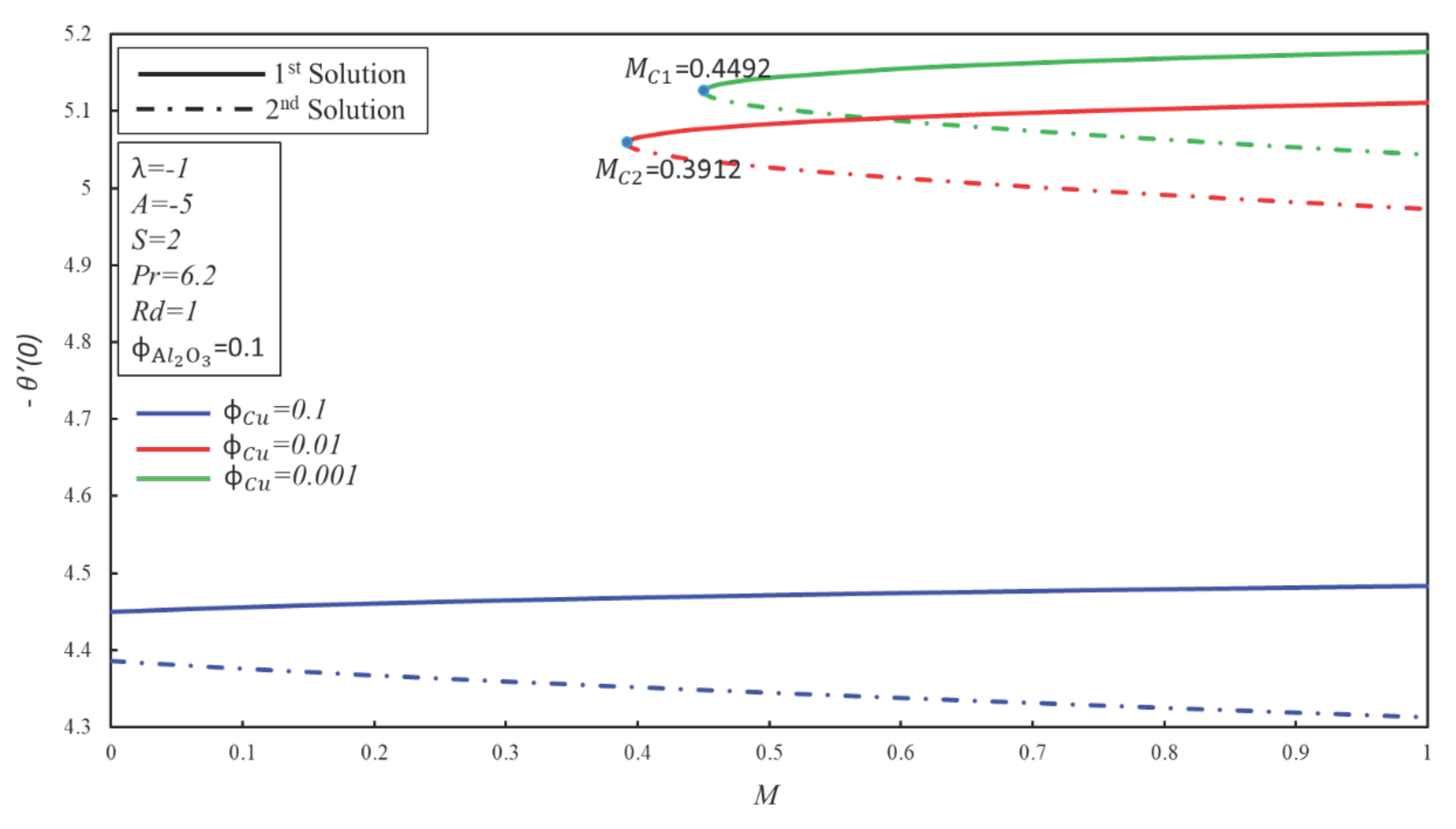
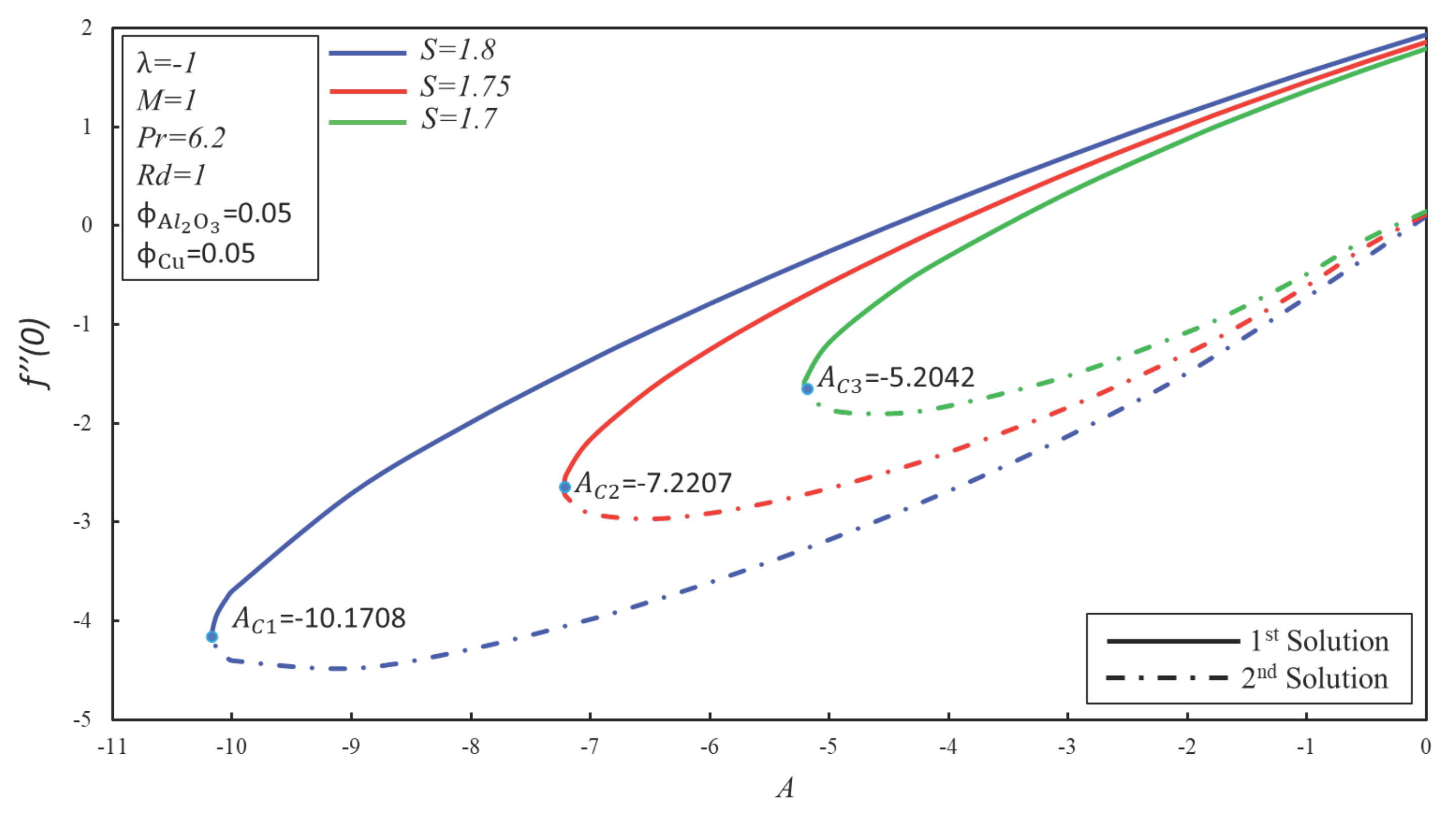
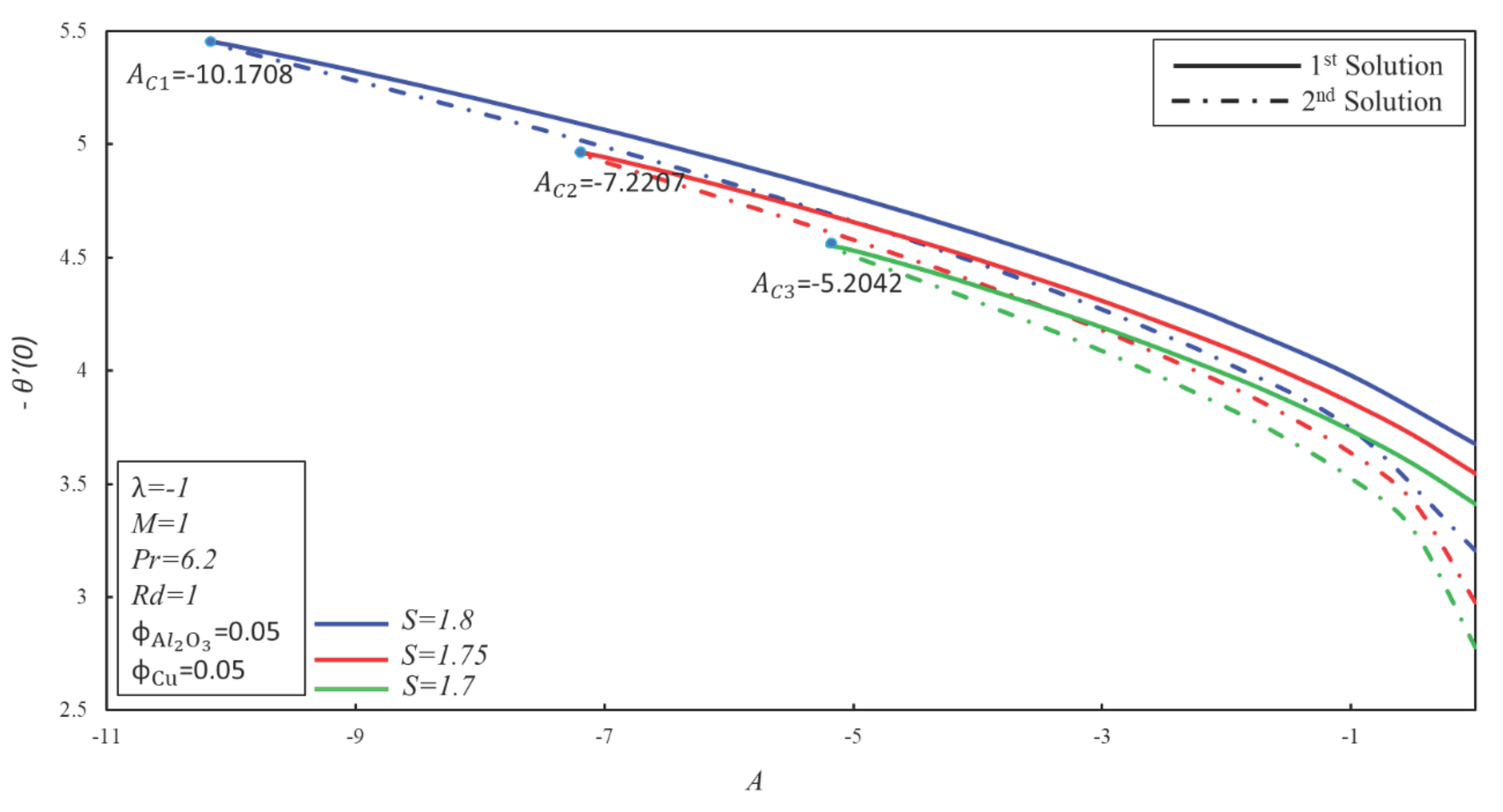
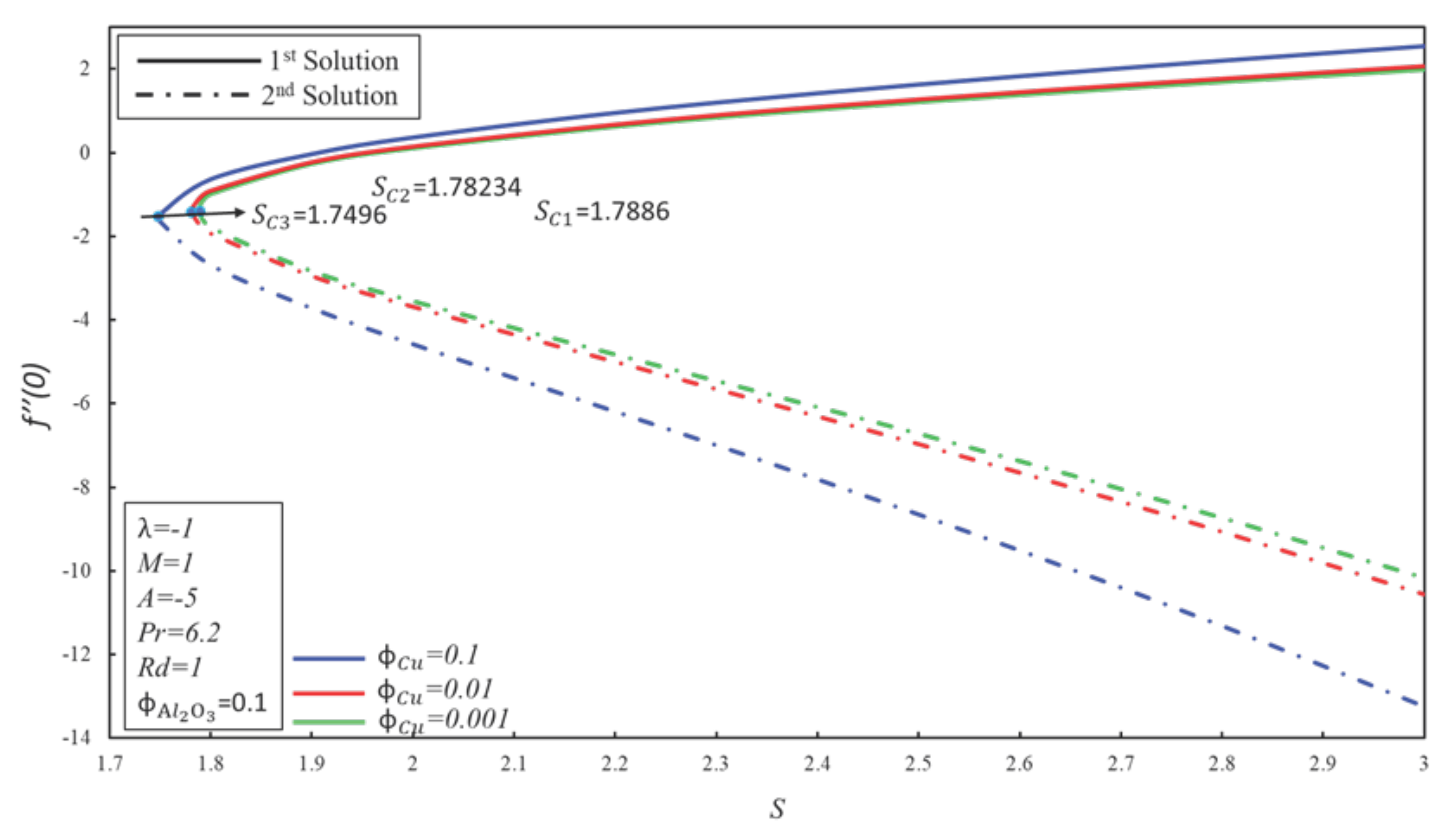
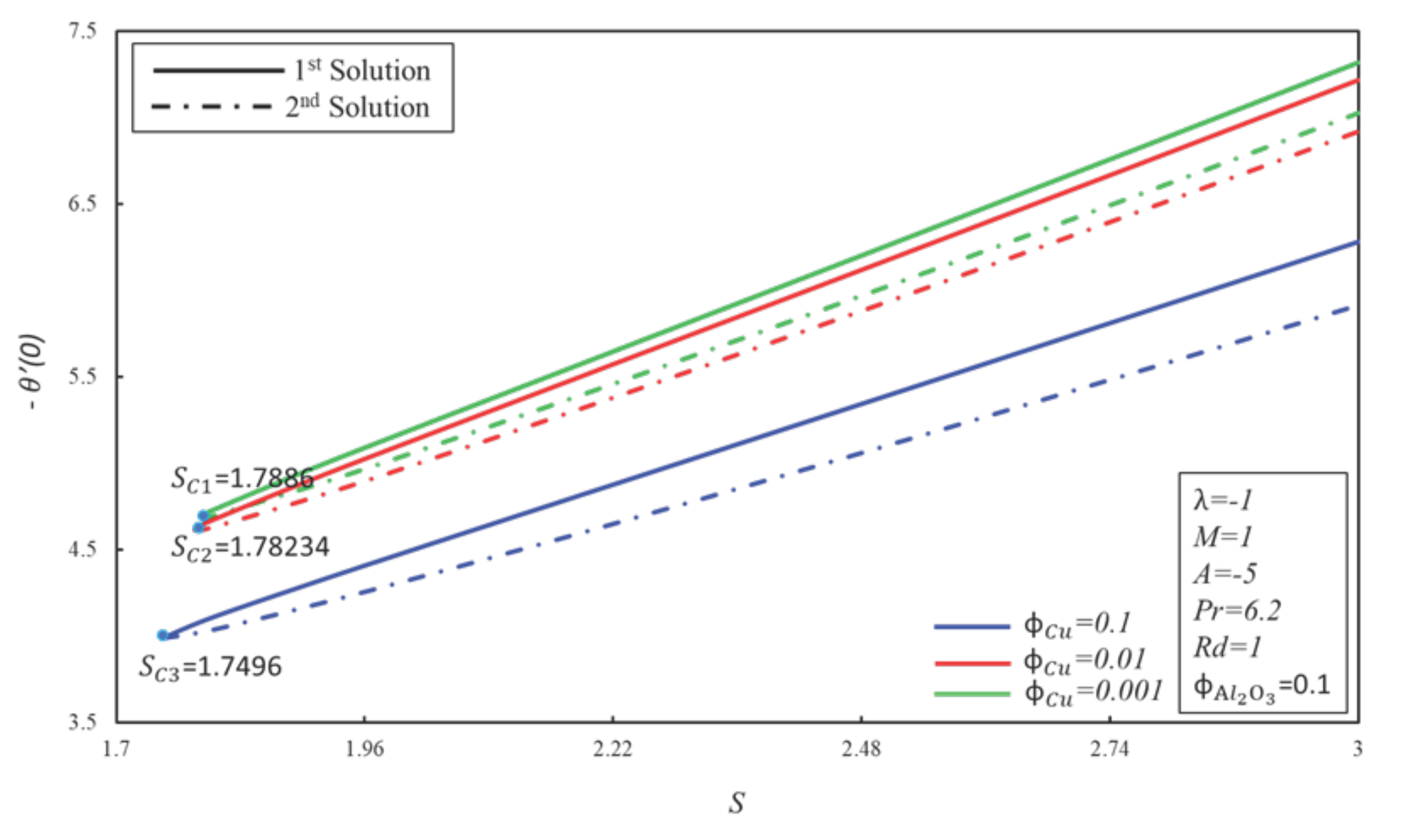
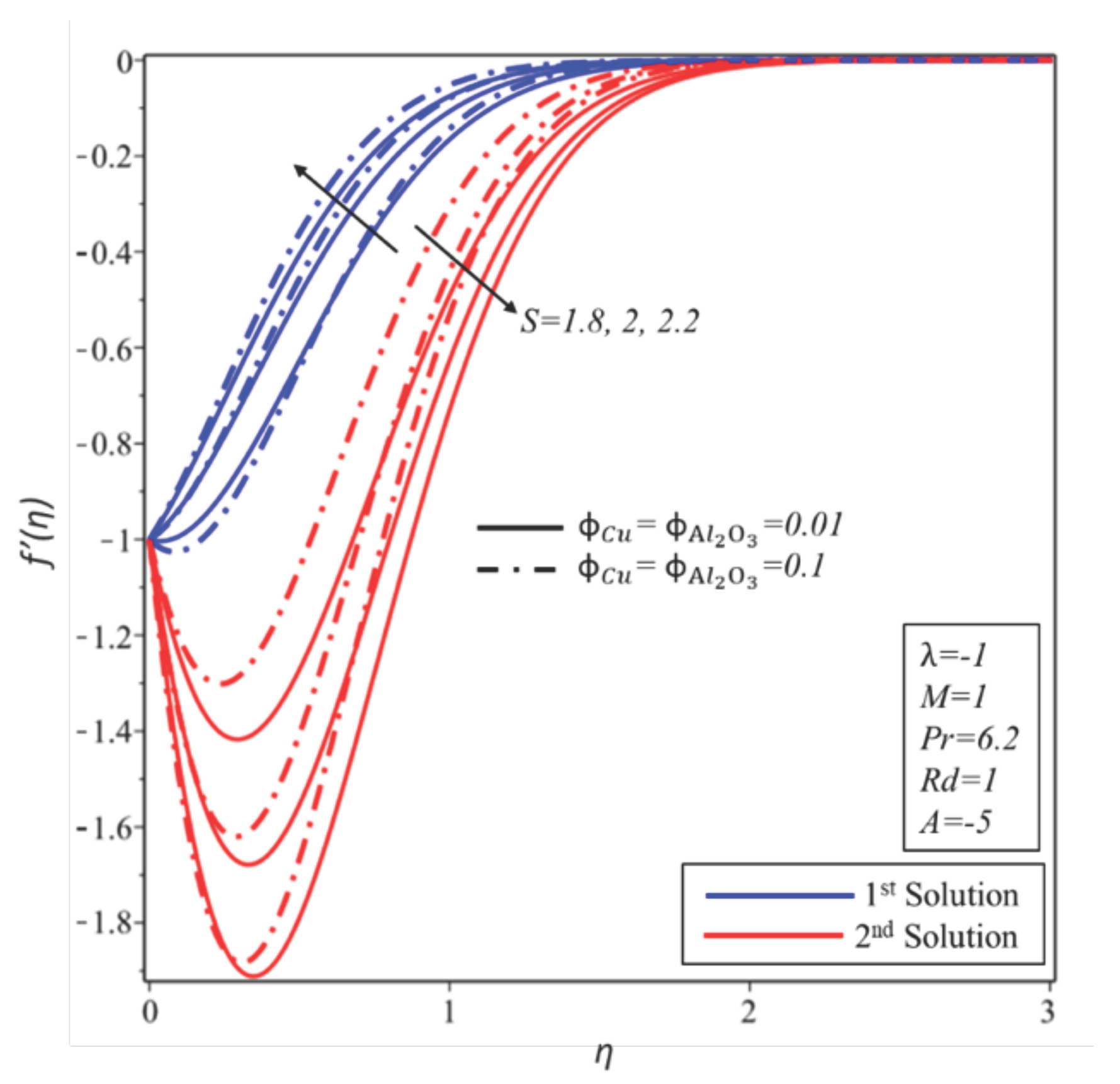
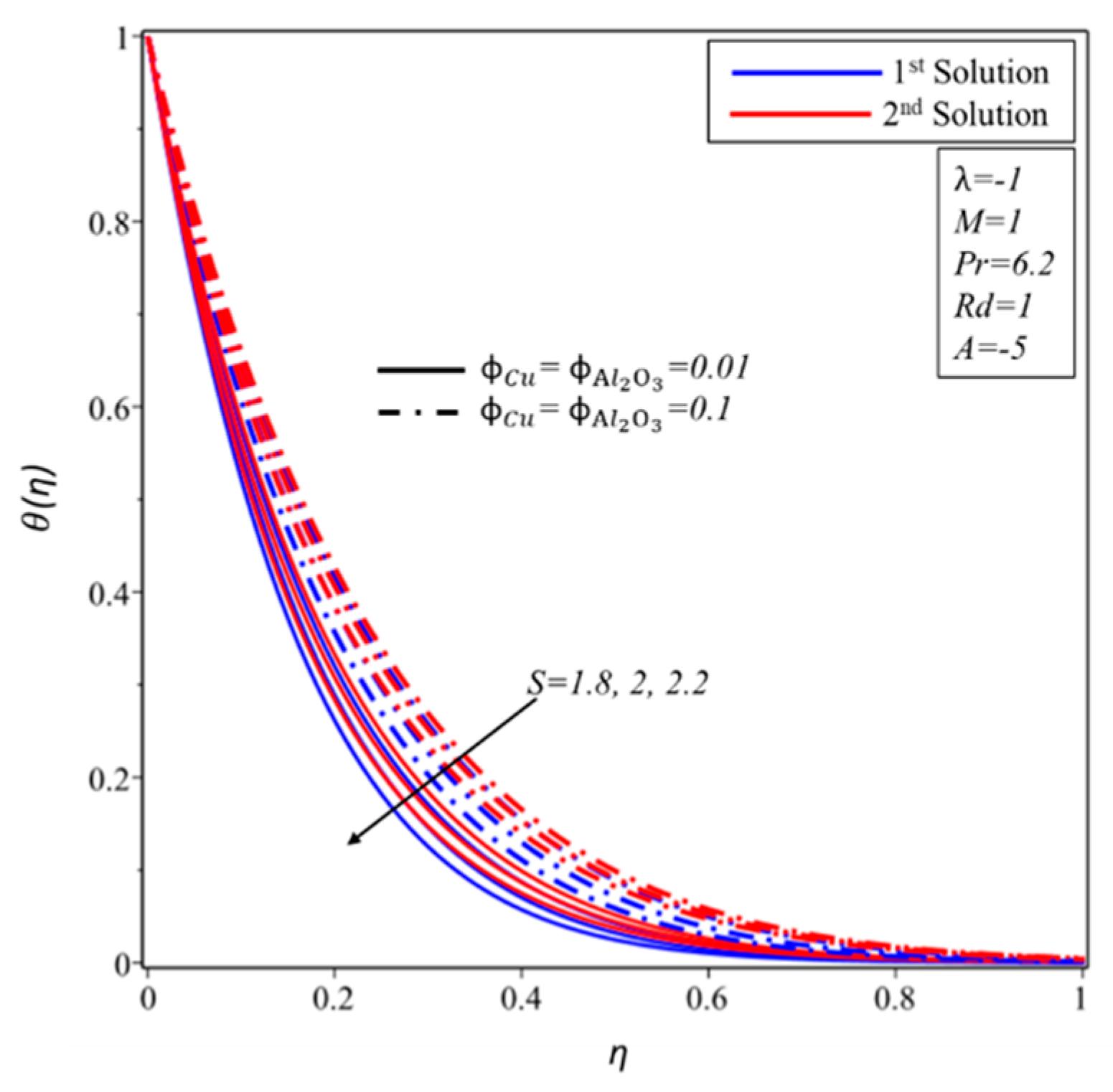
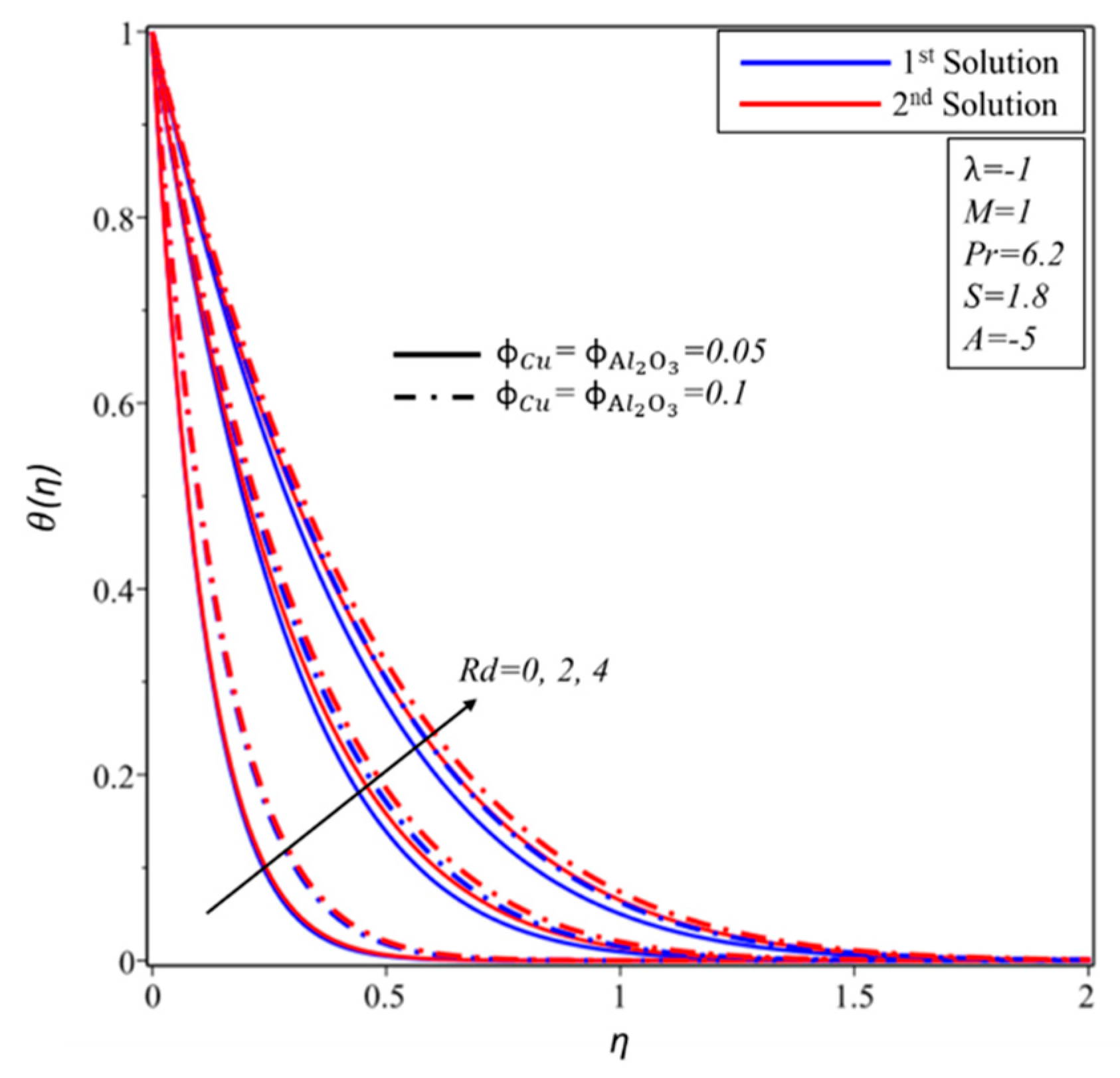
4. Result and Discussion
| Properties | Hybrid Nanofluid |
|---|---|
| Dynamic viscosity | |
| Density | |
| Thermal conductivity | where |
| Heat capacity |
| Fluids | k (W/m K) | ||
|---|---|---|---|
| Alumina () | 3970 | 765 | 40 |
| Copper (Cu) | 8933 | 385 | 400 |
| Water () | 997.1 | 4179 | 0.613 |
| Waini | [31] | Present | Results | Waini | [31] | Present | Results | ||
|---|---|---|---|---|---|---|---|---|---|
| 1st Soln | 2nd Soln | 1st Soln | 2nd Soln | 1st Soln | 2nd Soln | 1st Soln | 2nd Soln | ||
| −1 | 0 | 2.194247 | −1.491281 | 2.19424658 | −1.49128119 | 7.073680 | 6.884548 | 7.0736798 | 6.88454793 |
| −1 | 0.1 | -- | -- | 1.60888878 | −0.69818494 | -- | -- | 5.2238150 | 5.0737595 |
| −3 | 0 | 1.521197 | −4.144746 | 1.52119229 | −4.14474572 | 7.497151 | 7.296176 | 7.4971508 | 7.2961762 |
| −3 | 0.1 | -- | -- | 0.83697819 | −2.53135605 | -- | -- | 5.6316794 | 5.4925121 |
| −5 | 0 | 0.844435 | −6.431507 | 0.84443506 | −6.43150738 | 7.858446 | 7.657801 | 7.8584457 | 7.6578012 |
| −5 | 0.01 | -- | -- | 0.77597819 | −6.20435575 | -- | -- | 7.6375695 | 7.4426329 |
| −9 | 0 | −0.517287 | −10.58983 | −0.51728551 | −10.5898303 | 8.473316 | 8.277676 | 8.4733163 | 8.27767616 |
| −9 | 0.01 | -- | -- | −0.60021181 | −10.2417356 | -- | -- | 8.24709639 | 8.05819003 |
5. Conclusions
Abbreviation
| Nomenclature | |||
| a constant | nanoparticle volume fraction of the iron oxide. | ||
| ambient temperature | M | magnetic parameter | |
| differentiation with respect to | Porous parameter | ||
| Thermal radiation | c | constant | |
| effective density of hybrid nanofluid | Prandtl number | ||
| effective density of nanofluid | skin friction coefficient | ||
| effective dynamic viscosity of hybrid nanofluid | smallest eigen value | ||
| effective dynamic viscosity of nanofluid | Stability transformed variable | ||
| electrical conductivity | suction/injection velocity | ||
| fluid fraction | T | Temperature | |
| M | Hartmann/magnetic number | thermal conductivity of the hybrid nanofluid | |
| heat capacitance of the hybrid nanofluid | thermal conductivity of the nanofluid | ||
| heat capacitance of the nanofluid | t | time | |
| hnf | Hybrid nanofluid | transformed variable | |
| local Nusselt number | Unsteadiness parameter | ||
| local Reynolds number | variable temperature at the sheet | ||
| B | Magnetic field | u, v | velocity components |
| nanofluid fraction | shrinking/stretching parameter | ||
| mean absorption coefficient | Stefan–Boltzmann constant | ||
| nanoparticle volume fraction of the copper | for suction parameter and for blowing parameter |
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab: Lemont, IL, USA, 1995. [Google Scholar]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Benzema, M.; Benkahla, Y.K.; Labsi, N.; Ouyahia, S.E.; El Ganaoui, M. Second law analysis of MHD mixed convection heat transfer in a vented irregular cavity filled with Ag-MgO/water hybrid nanofluid. J. Therm. Anal. Calorim. 2019, 137, 1113–1132. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A. The dual solutions and stability analysis of nanofluid flow using tiwari-das modelover a permeable exponentially shrinking surface with partial slip conditions. J. Eng. Appl. Sci. 2019, 14, 4569–4582. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Dero, S. Multiple solutions of Cu-C6H9NaO7 and Ag-C6H9NaO7 nanofluids flow over nonlinear shrinking surface. J. Cent. South Univ. 2019, 26, 1283–1293. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, U.; Khan, I.; Baleanu, D.; Nisar, K.S. Stability analysis and dual solutions of micropolar nanofluid over the inclined stretching/shrinking surface with convective boundary condition. Symmetry 2020, 12, 74. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Chamkha, A.J.; Hashemi-Tilehnoee, M.; Seyyedi, S.M.; Ganji, D.D. Effects of homogeneous-heterogeneous reactions and thermal radiation on magneto-hydrodynamic Cu-water nanofluid flow over an expanding flat plate with non-uniform heat source. J. Cent. South Univ. 2019, 26, 1161–1171. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Ismael, M.A.; Chamkha, A.J.; Ganji, D.D. Numerical analysis of natural convection of Cu-water nanofluid filling triangular cavity with semicircular bottom wall. J. Therm. Anal. Calorim. 2019, 135, 3485–3497. [Google Scholar] [CrossRef]
- Amini, Y.; Akhavan, S.; Izadpanah, E. Vortex-induced vibration of a cylinder in pulsating nanofluid flow. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Zaib, A.; Khan, M.; Shafie, S. Boundary-layer flow of a cu-water nanofluid over a permeable shrinking cylinder with homogenous-hetrogenous reactions: Dual solutions. Therm. Sci. 2019, 23, 295–306. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z.; Awais, M. Heat and mass transfer analysis of MHD nanofluid flow in a rotating channel with slip effects. J. Mol. Liq. 2016, 219, 703–708. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Shafiq, A. Marangoni effect in second grade forced convective flow of water based nanofluid. J. Adv. Nanotechnol. 2019, 1, 50. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Khalique, C.M.; Zhang, T. Magneto-hydrodynamic Darcy-Forchheimer nanofluid flow over nonlinear stretching sheet. Phys. Scr. 2019, 94, 10. [Google Scholar] [CrossRef]
- Dinarvand, S. Nodal/saddle stagnation-point boundary layer flow of CuO-Ag/water hybrid nanofluid: A novel hybridity model. Microsyst. Technol. 2019, 25, 2609–2623. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Pop, I. Unsteady separated stagnation-point flow and heat transfer past a stretching/shrinking sheet in a copper-water nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Ahmed, N.; Saba, F.; Khan, U.; Mohyud-Din, S.T.; Sherif, E.S.M.; Khan, I. Nonlinear thermal radiation and chemical reaction effects on a Cu-CuO/NaAlg hybrid nanofluid flow past a stretching curved surface. Processes 2019, 7, 962. [Google Scholar] [CrossRef]
- Devi, S.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3-Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surf. A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Toghraie, D.; Chaharsoghi, V.A.; Afrand, M. Measurement of thermal conductivity of ZnO-TiO2/EG hybrid nanofluid. J. Therm. Anal. Calorim. 2016, 125, 527–535. [Google Scholar] [CrossRef]
- Moghadassi, A.; Ghomi, E.; Parvizian, F. A numerical study of water based Al2O3 and Al2O3-Cu hybrid nanofluid effect on forced convective heat transfer. Int. J. Therm. Sci. 2015, 92, 50–57. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S.; Khan, A.U. Rotating flow of Ag-CuO/H2O hybrid nanofluid with radiation and partial slip boundary effects. Eur. Phys. J. E 2018, 41, 75. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Khan, U.; Waheed, A.; Rafiq, M.; Mohyud-Din, S. Thermophysical analysis of water based (Cu-Al2O3) hybrid nanofluid in an asymmetric channel with dilating/squeezing walls considering different shapes of nanoparticles. Appl. Sci. 2018, 8, 1549. [Google Scholar] [CrossRef]
- Acharya, N.; Bag, R.; Kundu, P.K. Influence of hall current on radiative nanofluid flow over a spinning disk: A hybrid approach. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 111, 103–112. [Google Scholar] [CrossRef]
- Afridi, M.I.; Alkanhal, T.A.; Qasim, M.; Tlili, I. Entropy Generation in Cu-Al2O3-H2O Hybrid Nanofluid Flow over a Curved Surface with Thermal Dissipation. Entropy 2019, 21, 941. [Google Scholar] [CrossRef]
- Shafiq, A.; Khan, I.; Rasool, G.; Sherif, E.S.M.; Sheikh, A.H. Influence of single-and multi-wall carbon nanotubes on magnetohydrodynamic stagnation point nanofluid flow over variable thicker surface with concave and convex effects. Mathematics 2020, 8, 104. [Google Scholar] [CrossRef]
- Shafiq, A.; Zari, I.; Rasool, G.; Tlili, I.; Khan, T.S. On the MHD casson axisymmetric marangoni forced convective flow of nanofluids. Mathematics 2019, 7, 1087. [Google Scholar] [CrossRef]
- Manh, T.D.; Nam, N.D.; Abdulrahman, G.K.; Moradi, R.; Babazadeh, H. Impact of MHD on hybrid nanomaterial free convective flow within a permeable region. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. Magnetohydrodynamics (MHD) axisymmetric flow and heat transfer of a hybrid nanofluid past a radially permeable stretching/shrinking sheet with joule heating. Chin. J. Phys. 2019. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Seikh, A.H.; Sherif, E.S.M.; Nisar, K.S. Stability analysis and multiple solution of Cu-Al2O3/H2O nanofluid contains hybrid nanomaterials over a shrinking surface in the presence of viscous dissipation. J. Mater. Res. Technol. 2019, 9, 421–432. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow and heat transfer past a vertical thin needle with prescribed surface heat flux. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A.; Khan, I. Dual solutions and stability analysis of micropolar nanofluid flow with slip effect on stretching/shrinking surfaces. Energies 2019, 12, 4529. [Google Scholar] [CrossRef]
- Dero, S.; Uddin, M.J.; Rohni, A.M. Stefan blowing and slip effects on unsteady nanofluid transport past a shrinking sheet: Multiple solutions. Heat Transf. Asian Res. 2019, 6, 2047–2066. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I. Mathematical analysis of magnetohydrodynamic (MHD) flow of micropolar nanofluid under buoyancy effects past a vertical shrinking surface: Dual solutions. Heliyon 2019, 5, e02432. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Dero, S.; Khan, I. Linear stability analysis of MHD flow of micropolar fluid with thermal radiation and convective boundary condition: Exact solution. Heat Transf. Asian Res. 2019. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Kadry, S.; Rho, S.; Mari, I.A.; Nisar, K.S. Effect of viscous dissipation in heat transfer of MHD flow of micropolar fluid partial slip conditions: Dual solutions and stability analysis. Energies 2019, 12, 4617. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Sherif, E.S.M.; Seikh, A.H. Magnetohydrodynamic (MHD) flow of micropolar fluid with effects of viscous dissipation and joule heating over an exponential shrinking sheet: Triple solutions and stability analysis. Symmetry 2020, 12, 142. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Rashidi, M.M.; Hafidzuddin, E.H.; Wahi, N. Magnetohydrodynamics (MHD) stagnation point flow past a shrinking/stretching surface with double stratification effect in a porous medium. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Transpiration effects on hybrid nanofluid flow and heat transfer over a stretching/shrinking sheet with uniform shear flow. Alex. Eng. J. 2019. [Google Scholar] [CrossRef]
- Asma, M.; Othman, W.A.M.; Muhammad, T. Numerical study for darcy-forchheimer flow of nanofluid due to a rotating disk with binary chemical reaction and arrhenius activation energy. Mathematics 2019, 7, 921. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Basir, M.F.M.; Kumar, R.; Ismail, A.I.M.; Sarojamma, G.; Narayana, P.S.; Raza, J.; Mahmood, A. Exploration of thermal-diffusion and diffusion-thermal effects on the motion of temperature-dependent viscous fluid conveying microorganism. Arab. J. Sci. Eng. 2019, 44, 8023–8033. [Google Scholar] [CrossRef]
- Wang, Q. Optimal strokes of low Reynolds number linked-sphere swimmers. Appl. Sci. 2019, 9, 4023. [Google Scholar] [CrossRef]
- Iqbal, Z.; Akbar, N.S.; Azhar, E.; Maraj, E.N. Performance of hybrid nanofluid (Cu-CuO/water) on MHD rotating transport in oscillating vertical channel inspired by Hall current and thermal radiation. Alex. Eng. J. 2018, 57, 1943–1954. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Hafidzuddin, E.H.; Wahi, N. Thermally stratified flow of Cu-Al2O3/water hybrid nanofluid past a permeable stretching/shrinking circular cylinder. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 63, 154–163. [Google Scholar]
- Rahman, A.N.H.; Bachok, N.; Rosali, H. Numerical solutions of MHD stagnation-point flow over an exponentially stretching/shrinking sheet in a nanofluid. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1366. [Google Scholar]
- Zaib, A.; Khan, U.; Shah, Z.; Kumam, P.; Thounthong, P. Optimization of entropy generation in flow of micropolar mixed convective magnetite (Fe3O4) ferroparticle over a vertical plate. Alex. Eng. J. 2019, 58, 1461–1470. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lund, L.A.; Omar, Z.; Khan, I.; Sherif, E.-S.M. Dual Solutions and Stability Analysis of a Hybrid Nanofluid over a Stretching/Shrinking Sheet Executing MHD Flow. Symmetry 2020, 12, 276. https://doi.org/10.3390/sym12020276
Lund LA, Omar Z, Khan I, Sherif E-SM. Dual Solutions and Stability Analysis of a Hybrid Nanofluid over a Stretching/Shrinking Sheet Executing MHD Flow. Symmetry. 2020; 12(2):276. https://doi.org/10.3390/sym12020276
Chicago/Turabian StyleLund, Liaquat Ali, Zurni Omar, Ilyas Khan, and El-Sayed M. Sherif. 2020. "Dual Solutions and Stability Analysis of a Hybrid Nanofluid over a Stretching/Shrinking Sheet Executing MHD Flow" Symmetry 12, no. 2: 276. https://doi.org/10.3390/sym12020276
APA StyleLund, L. A., Omar, Z., Khan, I., & Sherif, E.-S. M. (2020). Dual Solutions and Stability Analysis of a Hybrid Nanofluid over a Stretching/Shrinking Sheet Executing MHD Flow. Symmetry, 12(2), 276. https://doi.org/10.3390/sym12020276







