Abstract
Nowadays, real world problems are complicated because they deal with uncertainty and incomplete information. Obviously, such problems cannot be solved by a single technique because of the multiple perspectives that may arise. Currently, the combination of DEMATEL and the neutrosophic environment are still new and not fully explored. Previous studies of DEMATEL and this neutrosophic environment have been carried out based on numerical values to represent a new scale. Until now, little importance has been placed on the development of a linguistic variable for DEMATEL. It is important to develop a new linguistic variable to represent opinions based on human experience. Therefore, to fill this gap, the concept of Interval Neutrosophic Vague Sets (INVS) has been extended to the linguistic variable that can be used in the decision-making process. The INVS is useful tool to deal with uncertainty and incomplete information. Additionally, the advantages of the linguistic variable of INVS allows the greater range of value for membership functions. This study proposes a new framework for INVS and DEMATEL. In addition, a case study on the quality of hospital service has been evaluated to demonstrate the proposed approach. Finally, a comparative analysis to check the feasibility of the proposed method is presented. It demonstrates that different methods produce different relations and levels of importance. This is due to the inclusion of the INVS linguistic variable.
1. Introduction
Multi Criteria Decision Making (MCDM) was introduced in the mid-1960s, and is still a hot topic in decision making. The application fields of the MCDM include in-system engineering [1], energy planning [2,3], supply chain-selection [4], risk management [5], water resources management [6], and so on. Besides that, Pamučar et al. [7] used the MCDM method to select of the optimal type of hotel for investment. MCDM can be defined as a systematic and standardized method of decision making to resolve complex problems [8]. This method requires decision makers to choose the best among a set of alternatives by comparing them according to the relevant criteria. Today, the Trial Evolution Laboratory (DEMATEL) method approach is one of the widely known MCDM methods. In the 1970s, the DEMATEL method was developed to solve complex problems in the identifying relationships between cause–effect [9]. In DEMATEL, there are formally four basic steps: the development of a direct influence matrix, establishing the direct influence matrix, constructing the total influence matrix and producing the influential relation map. DEMATEL’s strengths are as a systematic tool for constructing and evaluating the structure of complex causal relationships between matrix or diagram variable.
Generally, crisp numbers are used to represent the existing scale in classical DEMATEL in order to reflect the ambiguity and vagueness that occur in the decision-making problems. However, several studies have criticized classical DEMATEL, which is insufficient to resolve ambiguity due to the input of linguistic experts into the information [10,11,12,13]. Thus, the DEMATEL method is extended by integrating with fuzzy set theory. The combination is called Fuzzy DEMATEL.
Zadeh [14] introduced Fuzzy Sets to overcome the confusion in decision making. Fuzzy DEMATEL has been successfully applied in various applications. Most of the linguistic variables in DEMATEL are constructed based on Fuzzy Set. This model has been applied in green supply chain management practices by [15,16,17]. Meanwhile Akyuz and Celik [18] used Fuzzy DEMATEL to evaluate critical operational hazards during the gas freeing process. Atanassov [19] extended the concept of the fuzzy set to the intuitionistic fuzzy set (IFS). An IFS consists of membership and non-membership to deal with uncertain information. A study by Govindan et al. [20] applied IFS with DEMATEL to handle the linguistic impression and ambiguity of human judgment. Another study by Li et al. [21] used IFS as a linguistic variable with a DEMATEL to identify critical success factors in emergency management. Hosseini et al. [22] proposed a fuzzy extension of the DAMATEL. In this study, the linguistic variable is in form of a type 2 fuzzy set to obtain the weight of criteria based on word. Later, research by Dalalah et al. [23] developed a modified fuzzy DEMATEL where the fuzzy distance measure is presented. The FPIS and FNIS are used to find similarities of the available alternatives. There was an attempt made by Abdullah and Zulkifli [24] to propose the integration of fuzzy AHP and interval type 2 fuzzy DEMATEL. The authors focus on linguistic variables in interval type-2 fuzzy sets (IT2FS) and the expected value for normalizing the upper and lower membership of IT2FS. Authors in [25] developed an interval type-2 fuzzy set based hierarchical MADM model by combining DEMATEL and TOPSIS. The inherent complexity that arises in the decision-making problem is solved using a hierarchical decomposition approach. The interval type-2 fuzzy DEMATEL is used to solve interdependencies among problem attributes. Baykasoğlu et al. [26] proposed fuzzy DEMATEL for the assessment of criteria, weight of criteria and the hierarchical fuzzy TOPSIS method for the assessment of alternatives by criteria.
Gray system theory is a good theory that combines with MCDM, and this set is being used with DEMATEL. Julong [27] implemented the gray system to solve uncertainties and incomplete information [28,29,30,31]. Besides that, the combination between gray–fuzzy and DEMATEL in expert judgment to evaluate interrelationship of service quality has been done by Tseng [32]. In short, several kinds of extensions of DEMATEL are used to model uncertainty inherent in the assessment. Nevertheless, some sources of uncertainty are partially or completely overlooked in the previous literature [28].
The neutrosophic set is a powerful tool for dealing with uncertainty-related issues, and consists of the level of truth, indeterminate and false degrees. In recent years, the theory extensions of neutrosophic have made rapid progress among scholars, such as [33,34,35,36,37,38]. A considerable amount of literature has been published on neutrosophic and MCDM, such as Dung et al. [39], who used interval neutrosophic set with TOPSIS to evaluate personnel selection. In addition, one work [40] suggested the TOPSIS method for MCDM under a single-valued neutrosophic set, and illustrated it by example. Abdel-Basset et al. [41] implemented the combination in the neutrosophic context of the Analytic Hierarchy Process (AHP) and Delphi Method. The authors have highlighted different techniques for monitoring consistency and evaluating the consensus level of expert opinions. Pamučar et al. [42] developed a new model which combines linguistic neutrosophic numbers (LNNs) and the weighted aggregated sum product assessment (WASPAS) for evaluating consultants’ work in hazardous goods transport. In addition, Abdel-Basset et al. [43] developed a combination of the neutrosophic ANP and VIKOR method to achieve sustainable supplier choice. The triangular neutrosophic numbers (TriNs) are used in this study to represent a linguistic variable based on opinion experts and decision makers. However, a combination of neutrosophic, particularly with DEMATEL, has not yet been fully explored [44]. The literature published related to DEMATEL and the neutrosophic environment, such as Abdel-Basset et al. [45] simply represents numerical values without focusing on the linguistic variable.
Most experts cannot give accurate numerical values to represent opinions based on human experience and rather use linguistic assessments as opposed to numerical values to be more practical [10,46]. This method seems to lack information on the linguistic parameter, since the key shortcoming of DEMATEL is that it relies on the input of linguistic experts [12,47]. Hence to fill this gap, we develop a new linguistic variable under the neutrosophic environment. Our proposed method can be seen as a DEMATEL framework in which interval neutrosophic vague sets are used as the linguistic variable. The benefits of our new linguistic variable allow greater range of values for the membership functions, since a new parameter is added to the interval neutrosophic set. It considers more range of values while handling the uncertainty that arises in decision-making problems. The insertion of INVS in DEMATEL gives a new representation of the model.
The remainder of the paper is organized as follows: In Section 2, some fundamental concepts of interval neutrosophic vague sets is presented. Section 3 discusses the proposed method, and Section 4 introduces an implementation of the proposed method. Finally, Section 5 describes the findings and proposal for future study.
2. Preliminaries
This section introduces the basic definitions related to the interval neutrosophic vague set (INVS).
Definition 1.
[48] Let be a universe discourse and the interval-valued neutrosophic set is defined as follows:
where , , satisfies . When the upper and lower limits of , , in INS are equal, the INS is reduced to SVNS. For notational convenience, we use to represent the element in INS, while the element refers to an interval-valued neutrosophic number (INN).
Definition 2.
[49] Let be a universe discourse . Then an interval neutrosophic vague set denoted as is written as:
Whose truth membership, indeterminacy membership and falsity-membership functions are defined as:
where
Definition 3.
[49] Let be an INVS of the universe where ,
Then, a unit INVS is denoted as where .
Definition 4.
[49] Let be an INVS of the universe where ,
Hence, a zero INVS is denoted as where .
3. Proposed Method
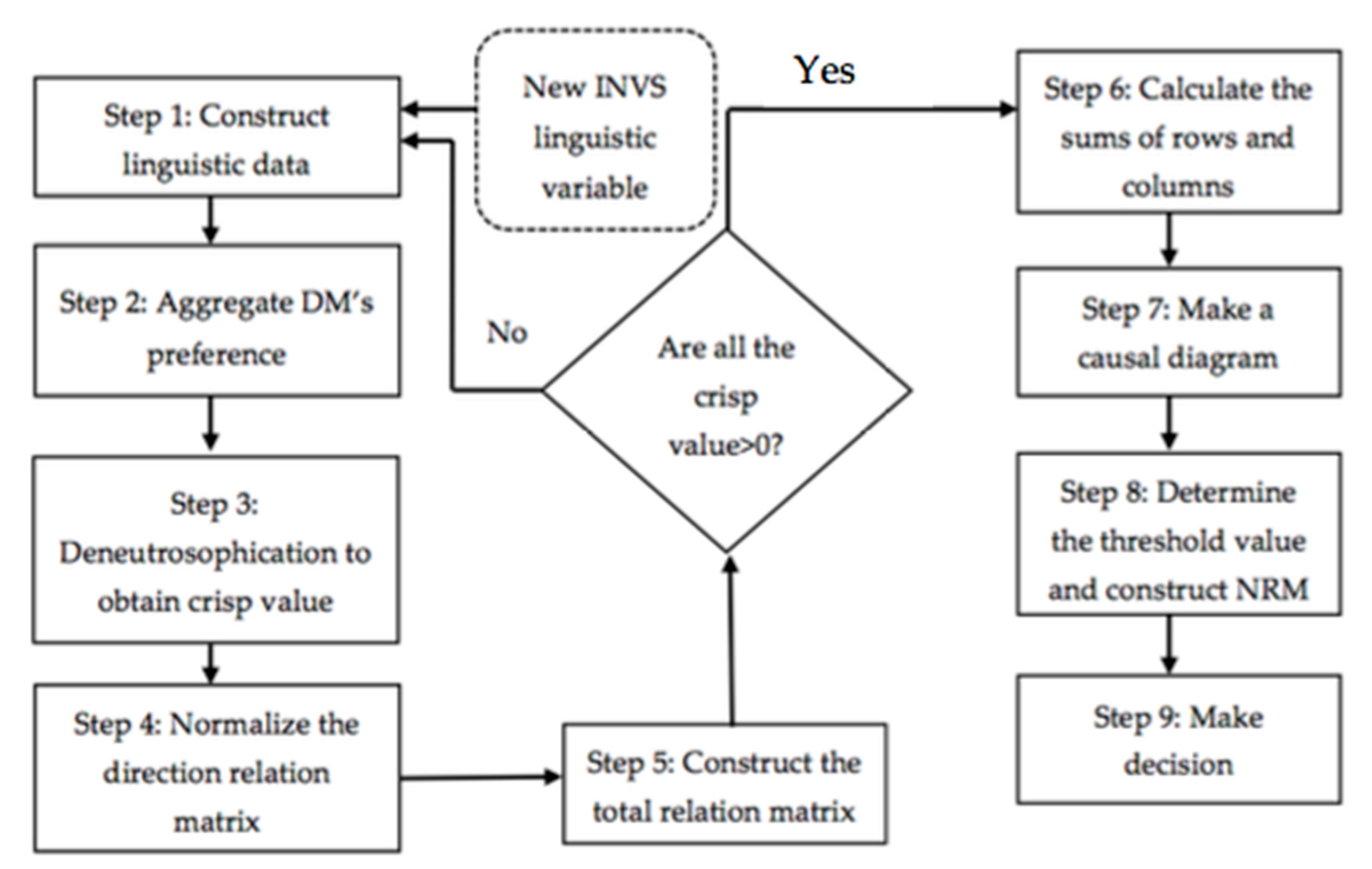
This section is presented mainly to discuss the development of the INVS-DEMATEL. In this study, a new linguistic variable for INVS DEMATEL is constructed, and some changes have been made to DEMATEL without the loss of originality of the DEMATEL method. Figure 1 demonstrates the overall structure of the proposed method.
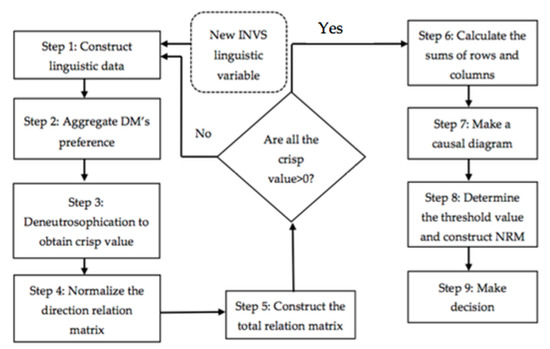
Figure 1.
Algorithm of the proposed method.
The proposed method consists of nine steps, and is basically similar with the concept of DEMATEL. However, the difference in the proposed method is especially in the development of the linguistic variable. The proposed method INVS-DEMATEL uses the linguistic variable developed from the interval neutrosophic set. Definition of INS in [49] is extended to the new linguistic variable in the form of IVNS. The aggregation operator is used to aggregate all the experts’ opinion. The important step is, the total relation matrix should be greater than zero before the casual diagram is obtained. The threshold value is setup and the degree of importance and net impact is obtained from the NRM.
3.1. Construction of Linguistic Variable
Gabus et al. [9] introduced a 4-degree scale in the classical DEMATEL. The most commonly used are: the original 4-degree scale and a 3-degree scale, but other scales such as a 5-degree scale or even an 8-degree scale are also available [50]. The linguistic variable under neutrosophic environment SVNS and INS have been developed by [39,40]. In this study, we have constructed a new linguistic variable for INVS based on Equation (1). The linguistic variable INVS consists of a 5-degree scale. Table 1 shows the linguistic variables for INS:

Table 1.
Linguistic variable [39].
In order to illustrate this conversion, the linguistic variable of “No Influence” from Table 1 is considered and calculated as follows:
- Step 1: Convert linguistic variable of INS to INVS.
Using the definition of the interval neutrosophic set Equation (1), we have , where , and . Therefore, it is represented as .
Using definition of INVS Equation (2) , therefore we obtain .
- Step 2: Calculation of is obtained by condition of INVS.
Using Equations (3) and (4) and restated , , and . Therefore, we get:
In the definition of INVS, the indeterminate value is free since vague set do not handle indeterminacy. Therefore, we can assign any value (if possible) for indeterminacy interval. Therefore, we reach:
- Step 3: verify the linguistic variable for INVS.
Using condition , therefore, we have and .
Therefore, we have .
The rest of calculation for the linguistic variable INVS is calculated similarly. Finally, we propose the linguistic variables that are defined in INVS, as presented in Table 2.

Table 2.
The new linguistic variable under the Interval Neutrosophic Vague Sets (INVS) concept.
3.2. The INVS DEMATEL Procedures
The procedures of INVS DEMATEL with the new linguistic variable are described as follows:
- Step 1: Construct linguistic data using the new linguistic variable.
The decision makers (DMs) constructs a decision matrix based on the proposed INVS linguistic variable. DMs were asked to determine a score using five linguistic variables that ranged from no influence to absolute influence based on criteria. The DM gave the INVS score and the notation of shows the degree to which DM believes criteria affects criteria . The diagonal components are set to zero for decision making, where:
The matrix contains INVSs in the form of
- Step 2: Aggregate DM’s preferences using the mean operator of INVS.
The membership degrees obtained from the DMs are combined using mean operators of INVS as follows:
where is the total number of DMs and .
- Step 3: Deneutrosophication process to obtain crisp value.
Deneutrosophication is the method by which a crisp number is collected. The deneutrosophication formula is as follows:
- Step 4: Normalizing the direct relation matrix.
The initial direct-relation is normalized using where
- Step 5: Constructing the INVS total relation matrix.
In this step, from the normalized matrix , the INVS total relation matrix is computed using Equation (9), where denotes the identity matrix.
- Step 6: Calculating the sum of the rows and columns.
The sum of rows denoted as and the sum of columns denoted as are both calculated as using Equations (10) and (11) as follows:
- Step 7: Construct a causal diagram.
The graph is constructed by plotting the (, ) data set. The on the horizontal axis characterizes as “Prominence” and the vertical axis represents as “Relation”. Generally, when is positive, the criterion belongs to the cause group. Otherwise, the criterion belongs to the effect group if is negative. This diagraph is very useful as a decision-making aid.
- Step 8: Set up the threshold value and the network relationship map.
In this step, the threshold value referred as is calculated by measuring the average of the component in matrix . Matrix elements are considered to be zero if they are lower than , which means their effect is lower than other criteria. The network relationship map’s advantages can reflect the MCDM flow. Each graph node represents the object examined, while the arc between two nodes shows the direction and strength of the influence relationship [50].
4. Illustrative Example: Hospital Service Quality
The proposed INVS DEMATEL with a new linguistic variable has been tested using a numerical example provided by [51].
- Step 1: Construct the decision matrix with proposed INVS linguistic variable.
Three decision makers are selected to define key success factors for the performance of hospital service. There are seven criteria involved, which are: : well-equipped medical facilities, : service personnel with good communication skills, : trusted medical staff with professional competence of health care, : service personnel with immediate-solving abilities, : detailed description of the patient’s condition by the medical doctor, : medical staff with professional skills and : pharmacist’s advice for taking medicine. Table 3 shows DMs analysis based on 7 criteria.

Table 3.
Decision makers’ (DMs) analysis of the criteria.
- Step 2: Aggregate DM’s preferences using mean operator of INVS.
Equation (6) is used to aggregate the DM’s opinion; for instance the element of can be obtained as follows:
The rest of the elements are calculated similarly.
- Step 3: Deneutrosophication process to obtain crisp value.
Equation (7) is used to obtain crisp value and the result is presented in Table 4.

Table 4.
The crisp values of matrix.
Step 4: Normalizing the INVS direct relation matrix.
Normalizing the direct relation matrix denoted as can be achieved using Equation (8). The sum for each row is calculated, and the largest value is obtained by row 7 (see Table 4). Each element in Table 4 is divided by 7.5244. The result is shown in Table 5.

Table 5.
The normalize direct relation matrix.
- Step 5: Construct the INVS total relation matrix.
The total relation matrix can be computed using Equation (9), where is denoted as the identity matrix. Since we have 7 criteria, then identity matrix should be size of 7 × 7. In this step, Maple software is used to calculate total relation matrix. Table 6 shows total relation matrix.

Table 6.
The Interval Neutrosophic Vague Sets (INVS) total relation matrix.
- Step 6: Calculating the sum of the rows and columns.
The sums of rows are represented by and sums of columns represented by is calculated by Equations (10) and (11). The and values are calculated in which these values reflect the importance and relation values, respectively. Based on the information in Table 7, the importance degree of criteria towards hospital service quality is identified as . The most important criteria that influence the hospital service quality are and . Meanwhile, and are the least important. The details results are presented in Table 7.

Table 7.
The total of rows and columns.
- Step 7: Construct a causal diagram.
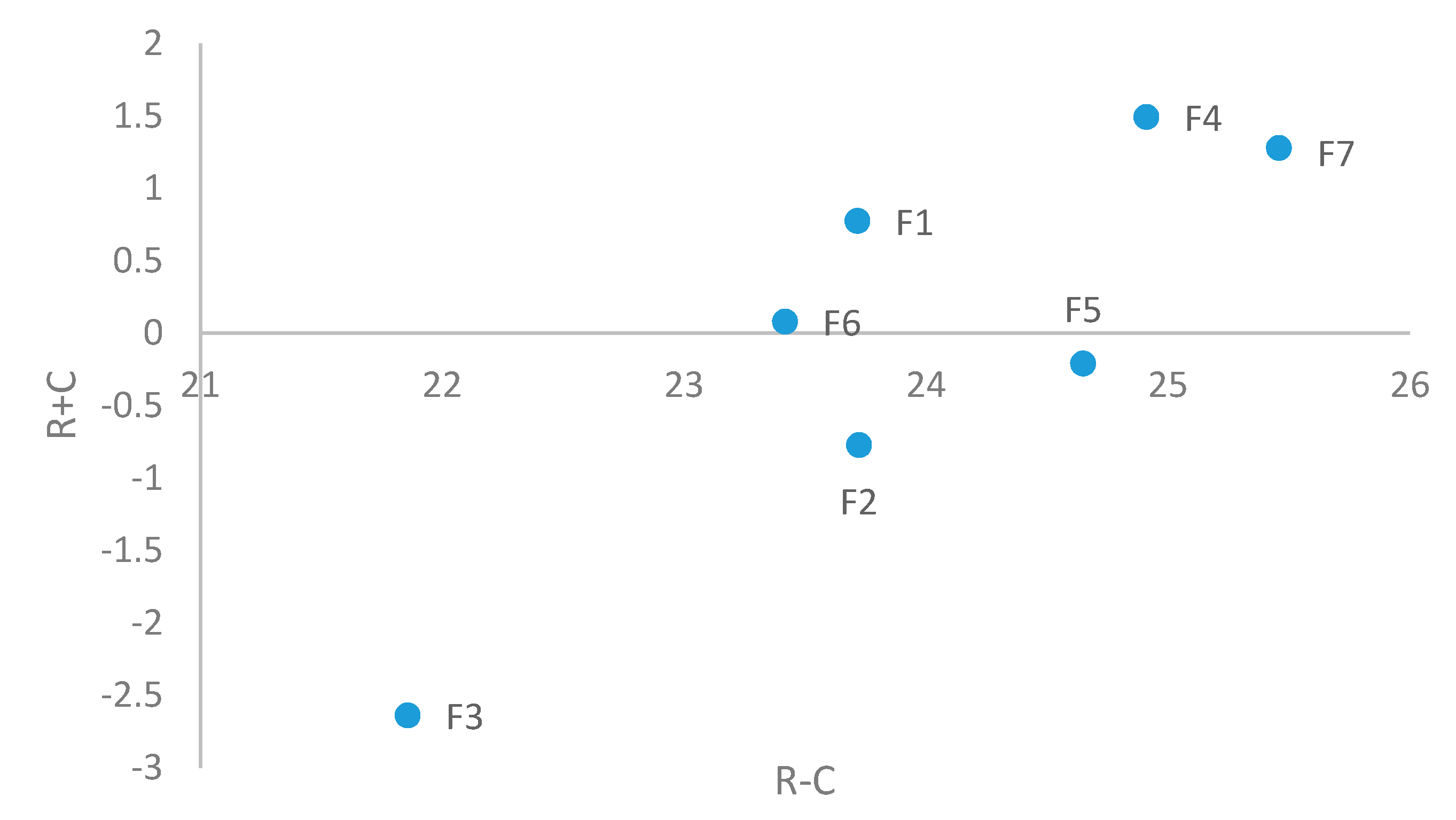
The complex causal relationships of criteria can be seen in the causal diagram illustrated in Figure 2. In addition, it provides valuable insight into solving problems. The horizontal in this diagram reflects the level of importance of each criterion, while the vertical axis classifies the criteria into the category of causes and effects.
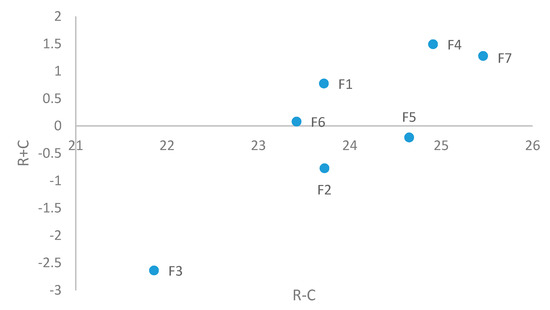
Figure 2.
Causal diagram.
Figure 2 shows that the criteria with positive values of are ; these criteria are categorized into a cause group. On the other hand, and are categorized into the effect group.
- Step 8: Setup a threshold value and construct the network relationship map.
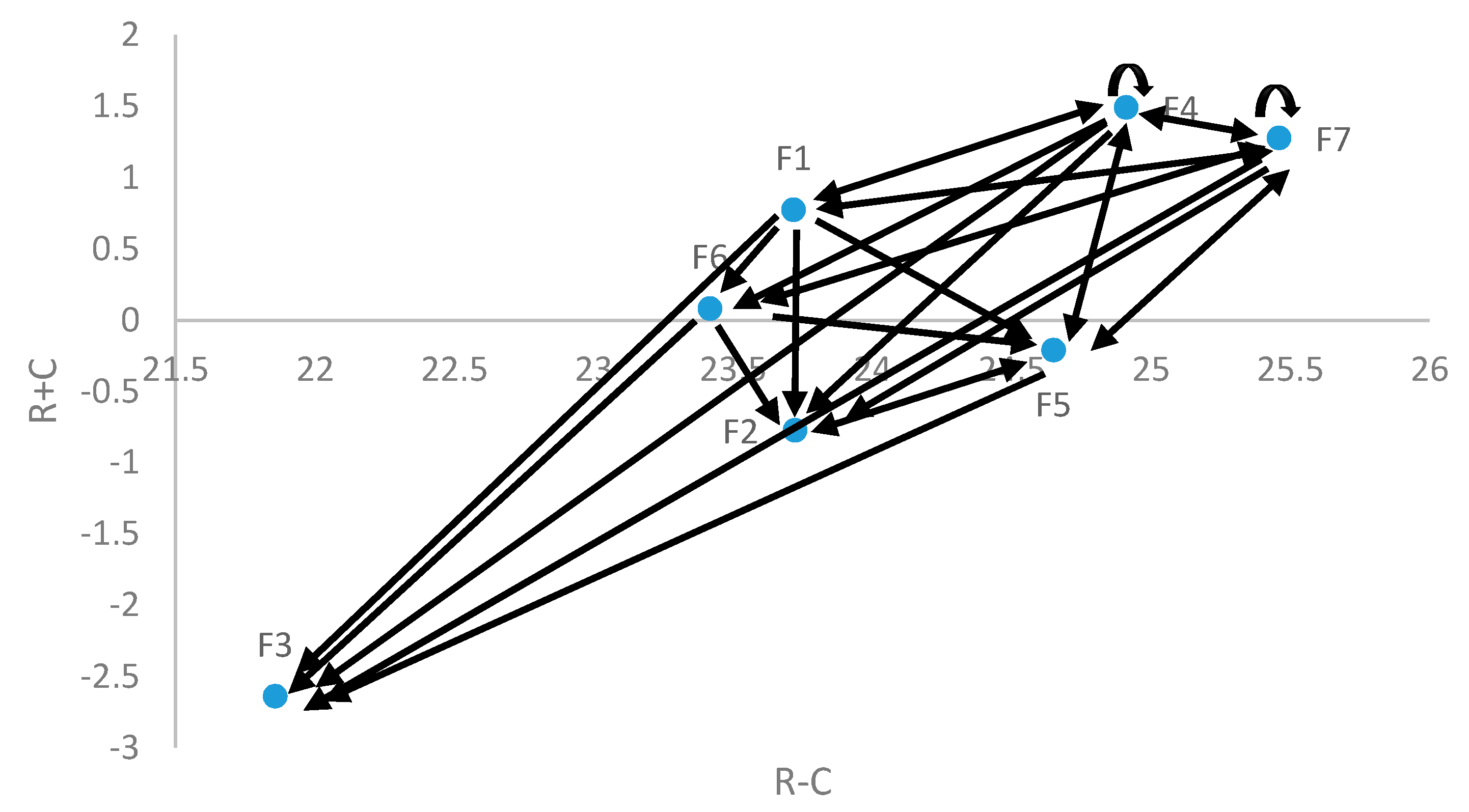
The threshold value is obtained by taking the average of the INVS total relation matrix, . The values below the are set by 0, and the values above the are set by 1. Table 8 shows the new total relation matrix denoted as . Figure 3 displays the graph of the network relationship map to visualize the existent of mutual influence among the criteria. This map is constructed based on new total influence in Table 8. It can be seen that (well-equipped medical equipment) has arrows pointing toward the other criteria, which indicates that it has an influence on them. On the other hand, there are arrows pointing toward (well-equipped medical equipment), which indicates that this criterion is affected by some other criteria.

Table 8.
New total influence.
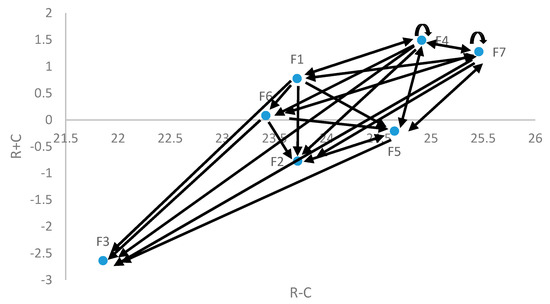
Figure 3.
Network relationship map.
5. Comparison Analysis
In this section, comparison analysis is performed in order to validate the proposed method. For this purpose, firstly we present comparative analysis between DEMATEL, Neutrosophic DEMATEL and the proposed method INVS-DEMATEL. In second section, we compare the INVS-DEMATEL with two other existing models which are interval-valued hesitant fuzzy sets and Neutrosophic DEMATEL.
5.1. Comparative Analysis
Comparative analysis is performed in this study to observe the accuracy of the DEMATEL’s modification. Table 9 represents comparative findings of the INVS-DEMATEL method against DEMATEL and Neutrosophic DEMATEL methods. It can be seen that INVS-DEMATEL reveals an obvious difference degree of importance and net impact. For example, by using the proposed method, is the most important criterion. The main reason is that the new linguistic variable is included. Even though a new linguistic variable is suggested, the proposed method was implemented without losing the originality of the DEMATEL method. In addition, INVS-DEMATEL introduces a new linguistic variable that consists of truth, falsity and indeterminacy degrees which are not limited to a single interval. This set provides interval-based membership when dealing with incomplete and inconsistent information. Meanwhile, classical DEMATEL uses crisp value to solve the uncertainty problems. The classical DEMATEL cannot represent the better decision under uncertainty. Besides that, Neutrosophic DEMATEL is characterized by truth membership, indeterminacy membership and falsity membership. In real life, some complicated problems cannot be solved by SVNS, but need to use several possible values. Therefore, INVS is blended with DEMATEL to accurately assess the relationship between the factors.

Table 9.
Comparative results of the different models.
5.2. Comparison between INVS-DEMATEL and the Existing Models
In this study, we have used INVSs as a linguistic variable accompanied with DEMATEL. The development of a new linguistic variable is important to better represent the opinions of experts. The INVS-DEMATEL is applied in the case study of hospital service quality to represent the effectiveness of this model. The findings are in the form of a cause and effect group. In this section, we will compare our proposed INVS-DEMATEL with two other existing models which are interval-valued hesitant fuzzy sets DEMATEL [28] and Neutrosophic DEMATEL [45].
Umut et al. [28] integrate interval-valued hesitant fuzzy sets and DEMATEL to better represent the uncertainty and vagueness in the decision-making problem. The concept of interval-valued hesitant fuzzy set is a generalization of fuzzy set and hesitant fuzzy set [52]. It consists of the membership degrees of an element in the form of several possible interval values. However, the interval-valued hesitant fuzzy set is unable to solve problems that involved indeterminacy. Considering the complexity of the decision-making process, it is difficult to insert the indeterminacy degree during the process of collection data in the decision making. This is beyond the scope of interval-valued hesitant fuzzy sets. Therefore, this integration may lead to incomplete information and results.
Abdel-Baset et al. [45], developed a combination of Neutrosophic and DEMATEL. Neutrosophic sets involve an indeterminacy degree that helps experts to express their opinions more accurately. The authors examine the proposed model for selection of supplier. The Neutrosophic DEMATEL method represents a new scale from 0 to 1 and employs the maximum truth membership degree , the minimum indeterminacy membership degree and the minimum falsity membership degree of a single value neutrosophic number. Nevertheless, in this analysis, authors focused on the numerical values in order to convey the opinion of the experts without emphasizing linguistic variable growth. The DEMATEL method requires qualitative evaluation by experts as data input. Therefore, it is better to represent the experts’ opinion in the form of a linguistic variable.
INVS is able to overcome the classical challenges of DEMATEL methods. INVS is characterized by multiple intervals instead of a single interval. INVS allows a greater range of value when dealing with an uncertain and incomplete environment. The use of simple a linguistic variable is not suitable to express the real preferences of the expert. For this reason, our approach is more focused towards defining a new linguistic variable in the entire framework INVS-DEMATEL, and without losing the originality of DEMATEL.
6. Conclusions
A new INVS-DEMATEL has been successfully proposed. We have constructed a new linguistic variable for INVS based on the definition of INS from previous study. The proposed approach is used for identifying the key success factors of hospital service quality. The results show that is the most important criterion and the most influential criterion among these seven criteria, because it has the highest strength of relation to other criteria. The management should give attention on this criterion so that the hospital service quality is guaranteed. In addition, ,, and are categorized as a cause criteria group. Meanwhile, the effect criterion group were , and . A comparative analysis between the proposed methods and the other existing method has been performed. The results show that different methods produce difference results. This research contributes to the literature by filling in the gap of linguistic variable in a neutrosophic environment.
In summary, this research’s main results are as follows:
- In this research, the neutrosophic environment was used to establish the linguistic variable of the DEMATEL. The new INVS linguistic variable considers more range of value while handling uncertainty, since a new parameter is added to INS. This is accordance with recommendations by Rodríguez et al. [53]. It is useful to include the complex linguistic variable to capture information in different forms and to manage uncertainties of different types within a single framework.
- The combination of INVS and DEMATEL can manage the complex interactions between criteria.
- The insertion of a vague set with a neutrosophic set gives a new result on the degree of importance and net impact.
As an extension of this study, different types of threshold value should be explored [44]. Additionally, future studies can be extended to another types of aggregation operator. The sensitivity analysis is recommended for the future studies to show the robustness of INVS DEMATEL and its results by changing the criteria weights in different situations. Additionally, the weighted super-matrix should be computed to become a long-term stable super-matrix.
Author Contributions
Conceptualization, H.H. and A.A.-Q.; formal analysis, H.H., A.A.-Q. and L.A.; investigation, A.A.-Q.; methodology, A.A.-Q. and H.H.; writing-original draft, H.H.; writing-review and editing, A.A.-Q., supervision, L.A. and A.A.-Q.; funding acquisition, A.A.-Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work was fully supported by the Deanship of Scientific Research, King Faisal University through the Nasher track under Grant 186311.
Acknowledgments
The authors acknowledge the Deanship of Scientific Research at King Faisal University for the financial support under Nasher Track (Grant No.186311).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gou, X.; Xu, Z.; Liao, H. Hesitant fuzzy linguistic entropy and cross-entropy measures and alternative queuing method for multiple criteria decision making. Inf. Sci. 2017, 388–389, 225–246. [Google Scholar] [CrossRef]
- Ekel, P.; Kokshenev, I.; Parreiras, R.; Pedrycz, W.; Pereira, J., Jr. Multiobjective and multiattribute decision making in a fuzzy environment and their power engineering applications. Inf. Sci. 2016, 361–362, 100–119. [Google Scholar] [CrossRef]
- Wang, J.-J.; Jing, Y.-Y.; Zhang, C.-F.; Zhao, J.-H. Review on multi-criteria decision analysis aid in sustainable energy decision-making. Renew. Sustain. Energy Rev. 2009, 13, 2263–2278. [Google Scholar] [CrossRef]
- Wan, S.; Xu, G.; Dong, J. Supplier selection using ANP and ELECTRE II in interval 2-tuple linguistic environment. Inf. Sci. 2017, 385–386, 19–38. [Google Scholar] [CrossRef]
- Rodríguez, A.; Ortega, F.; Concepción, R. An intuitionistic method for the selection of a risk management approach to information technology projects. Inf. Sci. 2017, 375, 202–218. [Google Scholar] [CrossRef]
- Kuang, H.; Kilgour, D.M.; Hipel, K.W. Grey-based PROMETHEE II with application to evaluation of source water protection strategies. Inf. Sci. 2015, 294, 376–389. [Google Scholar] [CrossRef]
- Karabasevic, D.; Popovic, G.; Stanujkic, D.; Maksimovic, M.; Sava, C. An approach for hotel type selection based on the single-valued intuitionistic fuzzy numbers. Int. Rev. 2019, 1–2, 7–14. [Google Scholar] [CrossRef]
- Smarandache, F. α-Discounting Method for Multi-Criteria Decision Making (α-D MCDM). In Proceedings of the 2010 13th Conference on Information Fusion (FUSION), Edinburgh, UK, 26–29 July 2010. [Google Scholar] [CrossRef]
- Gabus, A.; Fontella, E. Perceptions of the World Problematique; Battelle Institute, Geneva Research Center: Geneva, Switzerland, 1975. [Google Scholar]
- Lin, C.-J.; Wu, W.-W. A causal analytical method for group decision-making under fuzzy environment. Expert Syst. Appl. 2008, 34, 205–213. [Google Scholar] [CrossRef]
- Bai, C.; Sarkis, J. A grey-based DEMATEL model for evaluating business process management critical success factors. Int. J. Prod. Econ. 2013, 146, 281–292. [Google Scholar] [CrossRef]
- Haleem, A.; Khan, S.; Khan, M.I. Traceability implementation in food supply chain: A grey-DEMATEL approach. Inf. Process. Agric. 2019, 6, 335–348. [Google Scholar] [CrossRef]
- Cui, L.; Chan, H.K.; Zhou, Y.; Dai, J.; Lim, J.J. Exploring critical factors of green business failure based on grey-decision making trial and evaluation laboratory (DEMATEL). J. Bus. Res. 2019, 98, 450–461. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Lin, R.-J. Using fuzzy DEMATEL to evaluate the green supply chain management practices. J. Clean. Prod. 2013, 40, 32–39. [Google Scholar] [CrossRef]
- Malviya, R.K.; Kant, R. Identifying Critical Success Factors for Green Supply Chain Management Implementation Using Fuzzy DEMATEL Method. In Proceedings of the 2014 IEEE International Conference on Industrial Engineering and Engineering Management, Selangor, Malaysia, 9–12 December 2014; pp. 214–218. [Google Scholar] [CrossRef]
- Lin, K.-P.; Hung, K.-C.; Lin, R.-J. Developing Tω Fuzzy DEMATEL Method for Evaluating Green Supply Chain Management Practices. In Proceedings of the 2014 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Beijing, China, 6–11 July 2014; pp. 1422–1427. [Google Scholar] [CrossRef]
- Akyuz, E.; Celik, E. A fuzzy DEMATEL method to evaluate critical operational hazards during gas freeing process in crude oil tankers. J. Loss Prev. Process Ind. 2015, 38, 243–253. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Govindan, K.; Khodaverdi, R.; Vafadarnikjoo, A. Intuitionistic fuzzy based DEMATEL method for developing green practices and performances in a green supply chain. Expert Syst. Appl. 2015, 42, 7207–7220. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Y.; Zhang, X.; Deng, Y.; Mahadevan, S. An evidential DEMATEL method to identify critical success factors in emergency management. Appl. Soft Comput. 2014, 22, 504–510. [Google Scholar] [CrossRef]
- Hosseini, M.B.; Tarokh, M.J. Type-2 fuzzy set extension of DEMATEL method combined with perceptual computing for decision making. J. Ind. Eng. Int. 2013, 9, 10. [Google Scholar] [CrossRef]
- Dalalah, D.; Hayajneh, M.; Batieha, F. A fuzzy multi-criteria decision making model for supplier selection. Expert Syst. Appl. 2011, 38, 8384–8391. [Google Scholar] [CrossRef]
- Abdullah, L.; Zulkifli, N. Integration of fuzzy AHP and interval Type-2 fuzzy DEMATEL: An application to human resource management. Expert Syst. Appl. 2015, 42, 4397–4409. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Gölcük, İ. Development of an interval Type-2 fuzzy sets based hierarchical MADM model by combining DEMATEL and TOPSIS. Expert Syst. Appl. 2017, 191, 194–206. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Kaplanoğlu, V.; Du, Z.D.; Şahin, C. Integrating fuzzy DEMATEL and fuzzy hierarchical TOPSIS methods for truck selection. Expert Syst. Appl. 2013, 40, 899–907. [Google Scholar] [CrossRef]
- Julong Deynrt, D. Introduction to grey system theory. Introd. Grey Syst. Theory 1989, 1, 1–24. [Google Scholar]
- Asan, U.; Kadaifci, C.; Bozdag, E.; Soyer, A.; Serdarasan, S. A new approach to DEMATEL based on interval-valued hesitant fuzzy sets. Appl. Soft Comput. 2018, 66, 34–49. [Google Scholar] [CrossRef]
- Çelikbilek, Y.; Tüysüz, F. An integrated grey based multi-criteria decision making approach for the evaluation of renewable energy sources. Energy 2016, 115, 1246–1258. [Google Scholar] [CrossRef]
- Moktadir, M.A.; Ali, S.M.; Rajesh, R.; Paul, S.K. Modeling the interrelationships among barriers to sustainable supply chain management in leather industry. J. Clean. Prod. 2018, 181, 631–651. [Google Scholar] [CrossRef]
- Bouzon, M.; Govindan, K.; Taboada, C.M. Resources, conservation and recycling evaluating barriers for reverse logistics implementation under a multiple stakeholders’ perspective analysis using grey decision making approach. Resour. Conserv. Recycl. 2018, 128, 315–335. [Google Scholar] [CrossRef]
- Tseng, M.-L.; Lin, Y.H. Application of fuzzy DEMATEL to develop a cause and effect model of municipal solid waste management in metro manila. Environ. Monit. Assess. 2009, 158, 519–533. [Google Scholar] [CrossRef]
- Ali, M.; Smarandache, F. Complex neutrosophic set. Neural Comput. Appl. 2017, 28, 1817–1834. [Google Scholar] [CrossRef]
- Alias, S.; Mohamad, D.; Shuib, A. Rough neutrosophic multisets relation with application in marketing strategy. Neutrosophic Sets Syst. 2018, 21, 36–55. [Google Scholar]
- Al-Quran, A.; Hassan, N. Neutrosophic vague soft set and its applications. Malays. J. Math. Sci. 2017, 11, 141–163. [Google Scholar]
- Al-Quran, A.; Hassan, N. Neutrosophic vague soft multiset for decision under uncertainty. Songklanakarin J. Sci. Technol. 2018, 40, 290–305. [Google Scholar]
- Alkhazaleh, S. Neutrosophic vague set theory. Crit. Rev. 2015, X, 29–39. [Google Scholar]
- Kumar Maji, P. Neutrosophic soft set. Ann. Fuzzy Math. Inform. 2013, 5, 157–168. [Google Scholar]
- Dung, V.; Thu Thuy, L.; Quynh Mai, P.; Van Dan, N.; Thi Mai La, N. TOPSIS approach using interval neutrosophic sets for personnel selection. Asian J. Sci. Res. 2018, 11, 434–440. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. TOPSIS method for multi-attribute group decision-making under single-valued neutrosophic environment. Neural Comput. Appl. 2016, 27, 727–737. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, M.; Sangaiah, A.K. Neutrosophic AHP-delphi group decision making model based on trapezoidal neutrosophic numbers. J. Ambient Intell. Humaniz. Comput. 2018, 9, 1427–1443. [Google Scholar] [CrossRef]
- Pamučar, D.; Sremac, S.; Stević, Ž.; Ćirović, G.; Tomić, D. New multi-criteria LNN WASPAS model for evaluating the work of advisors in the transport of hazardous goods. Neural Comput. Appl. 2019, 31, 5045–5068. [Google Scholar] [CrossRef]
- Abdel-Baset, M.; Chang, V.; Gamal, A.; Smarandache, F. An integrated neutrosophic ANP and VIKOR method for achieving sustainable supplier selection: A case study in importing field. Comput. Ind. 2019, 106, 94–110. [Google Scholar] [CrossRef]
- Si, S.L.; You, X.Y.; Liu, H.C.; Zhang, P. DEMATEL technique: A systematic review of the state-of-the-art literature on methodologies and applications. Math. Probl. Eng. 2018, 2018, 1–33. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Gamal, A.; Smarandache, F. A hybrid approach of neutrosophic sets and DEMATEL method for developing supplier selection criteria. Des. Autom. Embed. Syst. 2018, 22, 257–278. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Martínez, L. A fusion approach for managing multi-granularity linguistic term sets in decision making. Fuzzy Sets Syst. 2000, 114, 43–58. [Google Scholar] [CrossRef]
- Wei, D.; Liu, H.; Shi, K. What are the key barriers for the further development of shale gas in china? A grey-DEMATEL approach. Energy Rep. 2019, 5, 298–304. [Google Scholar] [CrossRef]
- Wang, H.; Smarandache, F.; Zhang, Y.-Q.; Sunderraman, R. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing; HEXIS: Phoenix, AZ, USA, 2005. [Google Scholar]
- Hashim, H.; Abdullah, L.; Al-Quran, A. Interval neutrosophic vague sets. Neutrosophic Sets Syst. 2019, 25, 66–75. [Google Scholar]
- Kobryń, A. DEMATEL as a weighting method in multi-criteria decision analysis. Mult. Criteria Decis. Mak. 2017, 12, 153–167. [Google Scholar] [CrossRef]
- Shieh, J.-I.; Wu, H.-H.; Huang, K.-K. A DEMATEL method in identifying key success factors of hospital service quality. Knowl. Based Syst. 2010, 23, 277–282. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z.; Xia, M. Interval-valued hesitant preference relations and their applications to group decision making. Knowl. Based Syst. 2013, 37, 528–540. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Labella, Á.; Martínez, L. An overview on fuzzy modelling of complex linguistic preferences in decision making. Int. J. Comput. Intell. Syst. 2016, 9, 81–94. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).