Evaluation of the Mass Diffusion Coefficient and Mass Biot Number Using a Nondominated Sorting Genetic Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Moisture Transfer Analysis
- Initial condition: M at any point of the sample is the same at the beginning of drying:
- Boundary conditions of the third kind: The moisture flux from the surface of the sample is described in terms of moisture content difference between the surface and the equilibrium moisture content:
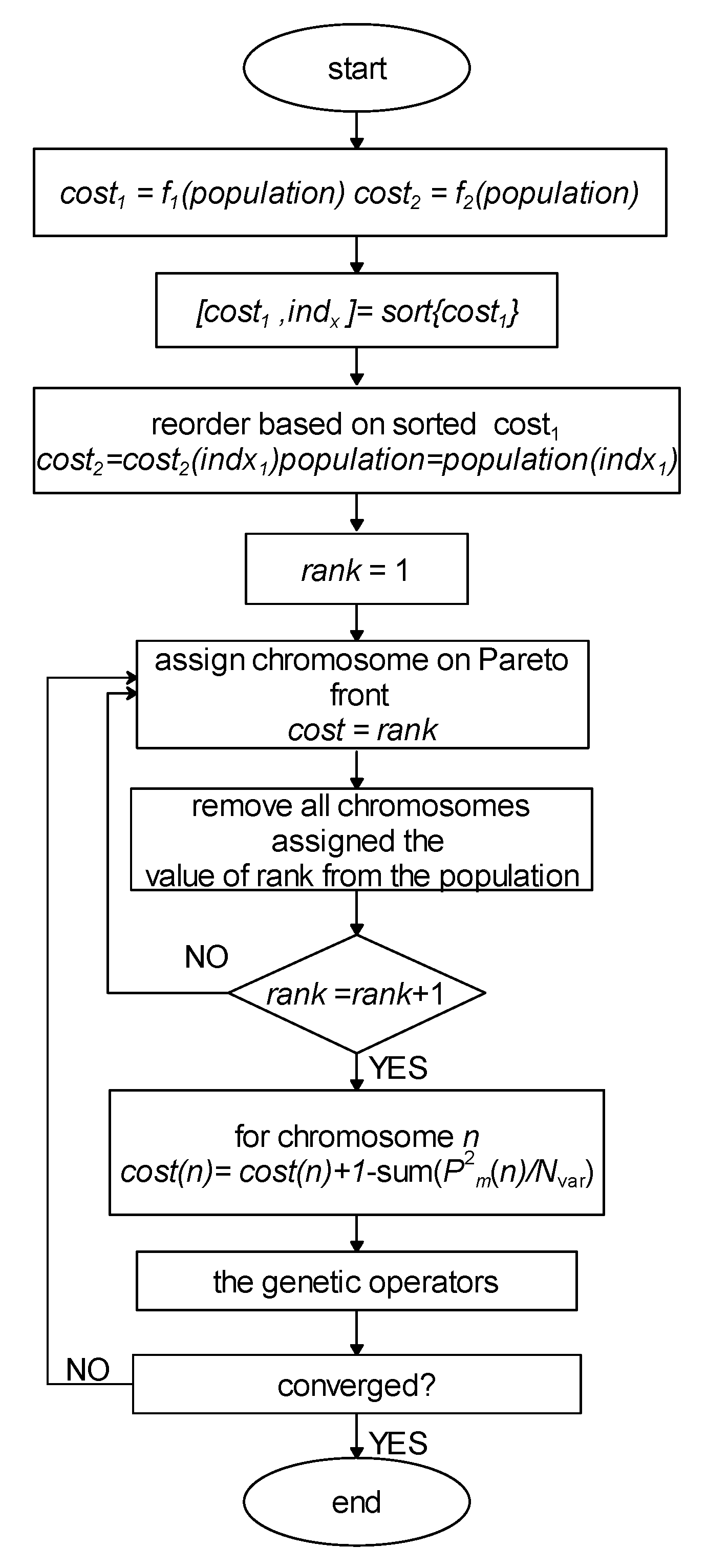
2.3. Multi-Objective Optimization
2.4. The Optimization Tasks
3. Results and Discussion
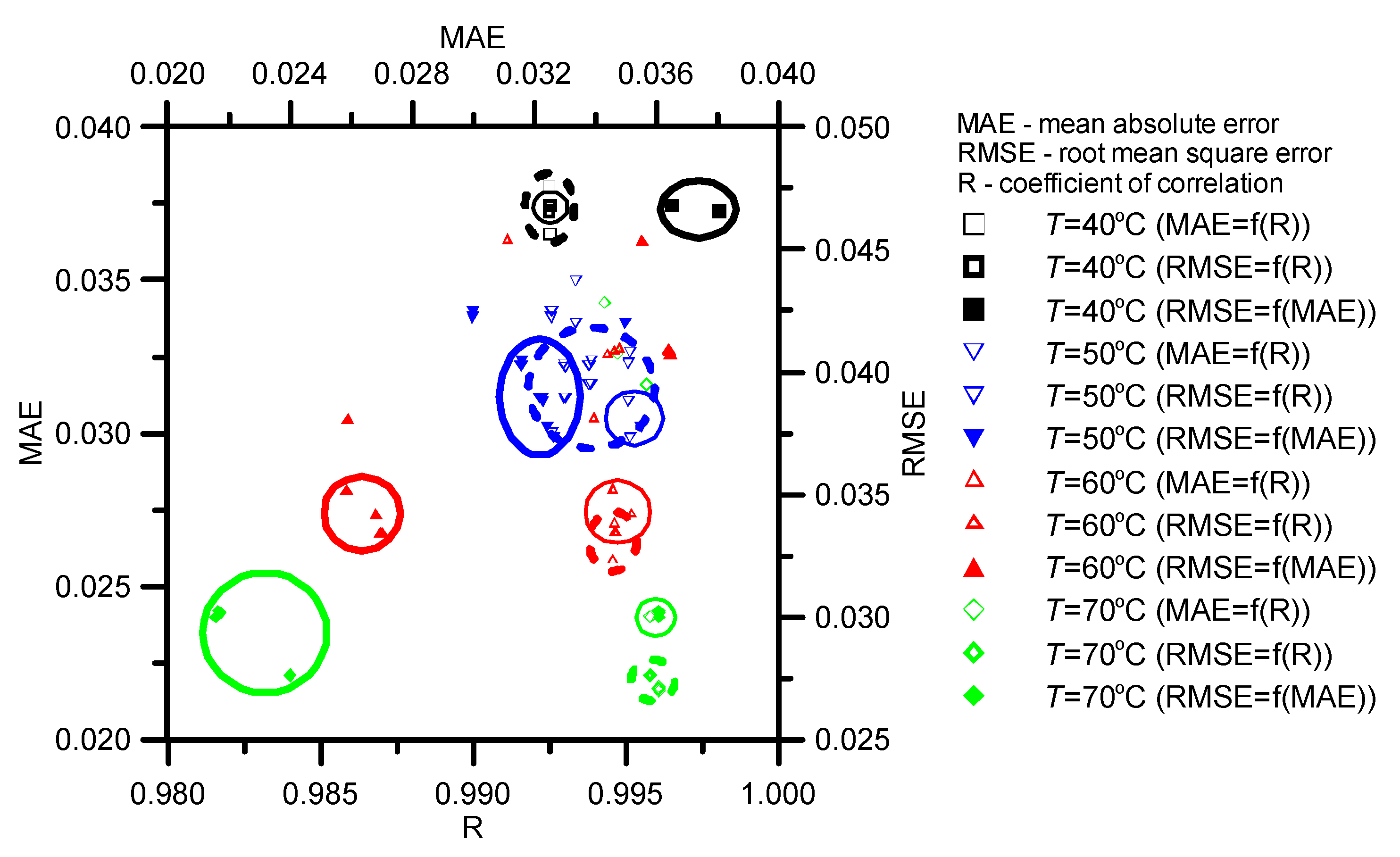
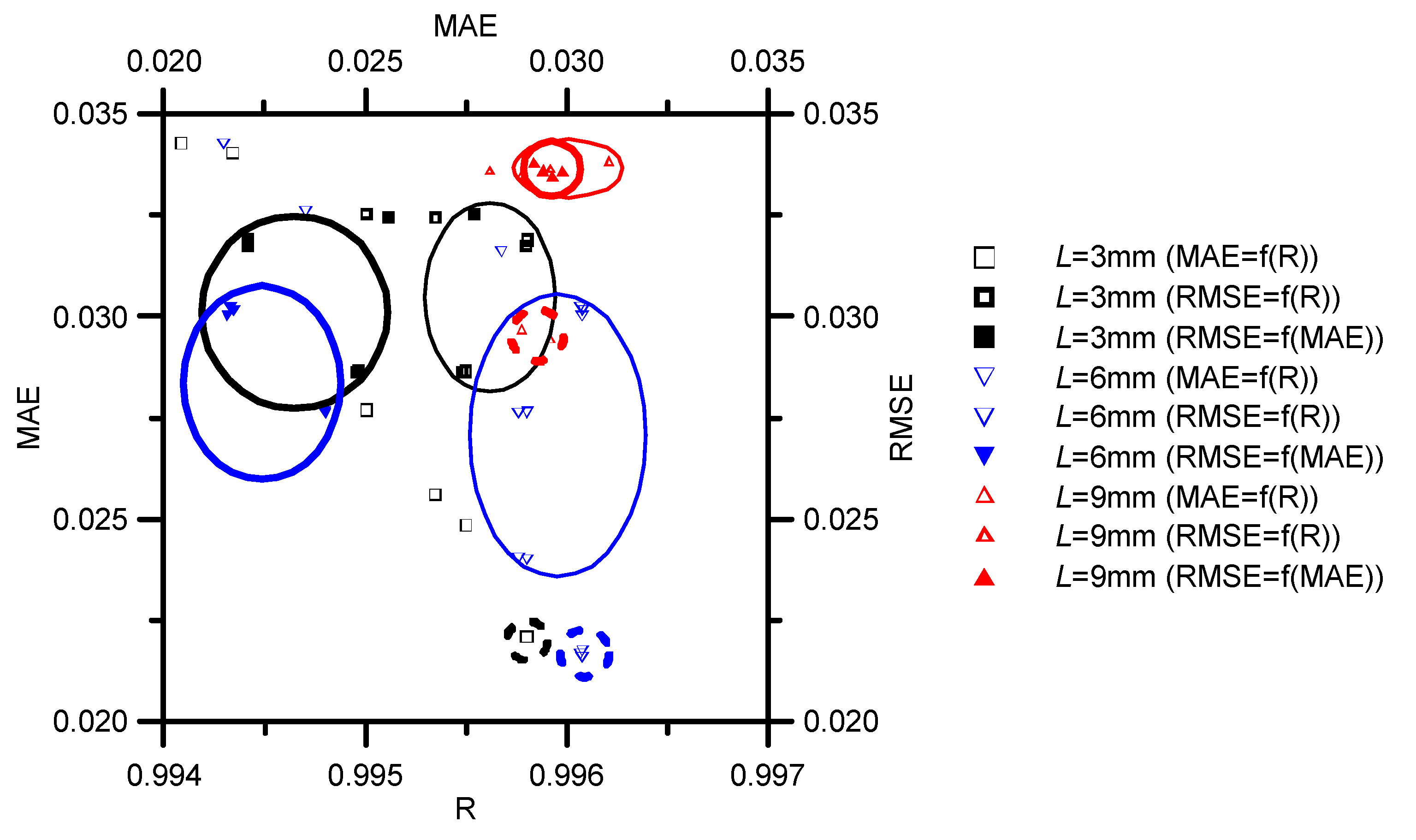
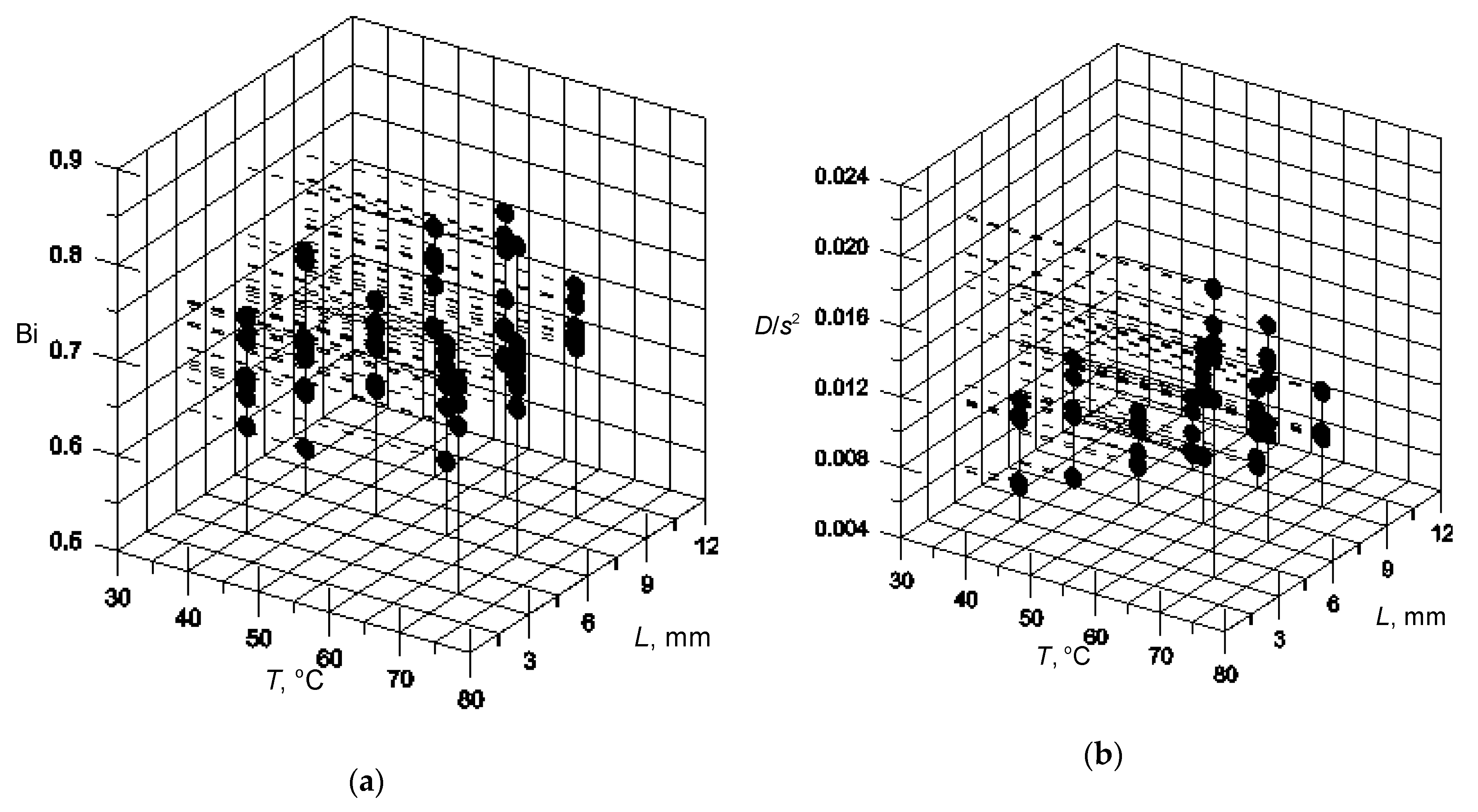
3.1. Optimization of Bi and D
3.2. Optimization of Parameters of the Functions for Determining Bi and D.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| aBi, bBi, cBi, dBi, eBi, fBi | constants in Equation (7) (-) |
| aD, bD, cD, dD, eD, fD | constants in Equation (8) (-) |
| Bi | mass Biot number |
| D | mass diffusion coefficient (m2 s−1) |
| k | mass transfer coefficient (m s−1) |
| L | characteristic dimension (m) |
| M, M0, Me | moisture content, initial moisture content, equilibrium moisture content (kg H2O kg−1 d.m.) |
| MR, MRexp, MRpred | moisture ratio, moisture ratio from experiment, predicted moisture ratio (-) |
| average moisture ratio from experiment | |
| N | number of data (-) |
| s | half of plane (slice) thickness (m) |
| t | time (s) |
| T | temperature (°C) |
References
- Lewicki, P.P. Water as the determinant of food engineering properties. A review. J. Food Eng. 2004, 61, 483–495. [Google Scholar] [CrossRef]
- Doulia, D.; Tzia, K.; Gekas, V. A knowledge base for the apparent mass diffusion coefficient of foods. Int. J. Food Prop. 2000, 3, 1–14. [Google Scholar] [CrossRef]
- Gros, J.B.; Ruegg, M. Physical Properties of Foods-2. In COST 90bis Final Seminar Proceedings; Jowitt, R., Escher, F., Kent, M., McKenna, B., Roques, M., Eds.; Elsevier Applied Science: London, UK, 1987; p. 71. [Google Scholar]
- Warin, F.; Gekas, V.; Voirin, A.; Dejmek, P. Sugar Diffusivity in Agar Gel/Milk Bilayer Systems. J. Food Sci. 1997, 62, 454–456. [Google Scholar] [CrossRef]
- Rattanakijsuntorn, K.; Penkova, A.; Sadha, S.S. Mass diffusion coefficient measurement for vitreous humor using FEM and MRI. IOP Conf. Ser. Mater. Sci. Eng. 2018, 297, 012024. [Google Scholar]
- Efremov, G.; Markowski, M.; Białobrzewski, I.; Zielinska, M. Approach to calculation time-dependent moisture diffusivity for thin layered biological materials. Int. Commun. Heat Mass 2008, 35, 1069–1072. [Google Scholar] [CrossRef]
- Zamel, N.; Astrath, N.G.C.; Li, X.; Shen, J.; Zhou, J.; Astrath, F.B.G.; Wang, H.; Liu, Z.-S. Experimental measurements of effective diffusion coefficient of oxygen–nitrogen mixture in PEM fuel cell diffusion media. Chem. Eng. Sci. 2010, 65, 931–937. [Google Scholar] [CrossRef]
- Chan, C.; Zamel, N.; Li, X.; Shen, J. Experimental measurement of effective diffusion coefficient of gas diffusion layer/microporous layer in PEM fuel cells. Electrochim. Acta 2012, 65, 13–21. [Google Scholar] [CrossRef]
- García-Salaberri, P.A.; Hwang, G.; Vera, M.; Weber, A.Z.; Gostick, J.T. Effective diffusivity in partially-saturated carbon-fiber gas diffusion layers: Effect of through-plane saturation distribution. Int. J. Heat Mass Transf. 2015, 86, 319–333. [Google Scholar] [CrossRef]
- Wang, Y.; Combe, C.; Clark, M.C. The effects of pH and calcium on the diffusion coefficient of humic acid. J. Membr. Sci. 2001, 183, 49–60. [Google Scholar] [CrossRef]
- Stewart, P.S. A Review of Experimental Measurements of Effective Diffusive Permeabilities and Effective Diffusion Coefficients in Biofilms. Biotechnol. Bioeng. 1998, 59, 261–272. [Google Scholar] [CrossRef]
- Perré, P.; Pierre, F.; Casalinho, J.; Ayouz, M. Determination of the Mass Diffusion Coefficient Based on the Relative Humidity Measured at the Back Face of the Sample During Unsteady Regimes. Dry Technol. 2015, 33, 1068–1075. [Google Scholar] [CrossRef]
- Piot, A.; Woloszyn, M.; Brau, J.; Abele, C. Experimental wooden frame house for the validation of whole building heat and moisture transfer numerical models. Energ. Build. 2011, 43, 1322–1328. [Google Scholar] [CrossRef]
- Liu, J.Y.; Simpson, W.T.; Verrill, S.P. An inverse moisture diffusion algorithm for the determination of diffusion coefficient. Dry Technol. 2001, 19, 1555–1568. [Google Scholar] [CrossRef]
- Bruin, S.; Luyben, K.C.A.M. Recent developments in dehydration of food materials. In Food Process Engineering; Food processing Systems; Applied Science Publishers: London, UK, 1980; Volume 1. [Google Scholar]
- Sitompul, J.P.; Istadi; Widiasa, I.N. Modeling and simulation of deep-bed grain dryers. Dry Technol. 2001, 19, 269–280. [Google Scholar] [CrossRef][Green Version]
- Rovedo, C.O.; Suarez, C.; Viollaz, P. Analysis of moisture profiles, mass Biot number and driving forces during drying of potato slabs. J. Food Eng. 1998, 36, 211–231. [Google Scholar] [CrossRef]
- Shi, Q.; Zheng, Y.; Zhao, Y. Mathematical modeling on thin-layer heat pump drying of yacon (Smallanthus sonchifolius) slices. Energy Convers. Manag. 2013, 71, 208–216. [Google Scholar] [CrossRef]
- Zielinska, M.; Markowski, M. Drying behavior of carrots dried in a spout–fluidized bed dryer. Dry Technol. 2007, 25, 261–270. [Google Scholar] [CrossRef]
- Giner, S.A.; Irigoyen, R.M.T.; Cicuttín, S.; Fiorentini, C. The variable nature of Biot numbers in food drying. J. Food Eng. 2010, 101, 214–222. [Google Scholar] [CrossRef]
- Ruiz-López, I.I.; Ruiz-Espinosa, H.; Arellanes-Lozada, P.; Bárcenas-Pozos, M.E.; García-Alvarado, M.A. Analytical model for variable moisture diffusivity estimation and drying simulation of shrinkable food products. J. Food Eng. 2012, 108, 427–435. [Google Scholar] [CrossRef]
- Gigler, J.; van Loon, W.K.P.; van der Berg, J.V. Natural wind drying of willow stems. Biomass Bioenerg. 2000, 19, 153–163. [Google Scholar] [CrossRef]
- Arévalo-Pinedo, A.; Murr, F.E.X. Kinetics of vacuum drying of pumpkin (Cucurbita maxima): Modeling with shrinkage. J. Food Eng. 2006, 76, 562–567. [Google Scholar] [CrossRef]
- Falade, K.O.; Abbo, E.S. Air-drying and rehydration characteristics of date palm (Phoenix dactylifera L.) fruits. J. Food Eng. 2007, 79, 724–730. [Google Scholar] [CrossRef]
- Reyes, A.; Mahn, A.; Vásquez, F. Mushrooms dehydration in a hybrid-solar dryer, using a phase change material. Energy Convers. Manag. 2014, 83, 241–248. [Google Scholar] [CrossRef]
- Kaleta, A.; Górnicki, K.; Winiczenko, R.; Chojnacka, A. Evaluation of drying models of apple (var. Ligol) dried in a fluidized bed dryer. Energy Convers. Manag. 2013, 67, 179–185. [Google Scholar] [CrossRef]
- Saguy, I.S.; Marabi, A.; Wallach, R. New approach to model rehydration of dry food particulates utilizing principles of liquid transport in porous media. Trends Food Sci. Tech. 2005, 16, 495–506. [Google Scholar] [CrossRef]
- Sanjuán, N.; Simal, S.; Bon, J.; Mulet, A. Modelling of broccoli stems rehydration process. J. Food Eng. 1999, 42, 27–31. [Google Scholar] [CrossRef]
- García-Pascual, P.; Sanjuán, N.; Bon, J.; Carreres, J.E.; Mulet, A. Rehydration process of Boletus edulis mushroom: Characteristics and modelling. J. Sci. Food Agric. 2005, 85, 1397–1404. [Google Scholar] [CrossRef]
- García-Pascual, P.; Sanjuán, N.; Melis, R.; Mulet, A. Morchella esculenta (morel) rehydration process modelling. J. Food Eng. 2006, 72, 346–353. [Google Scholar] [CrossRef]
- Resio, A.N.C.; Aguerre, R.J.; Suárez, C. Study of some factors affecting water absorption by amaranth grain during soaking. J. Food Eng. 2003, 60, 391–396. [Google Scholar] [CrossRef]
- Cunningham, S.E.; Mcminn, W.A.M.; Magee, T.R.A.; Richardson, P.S. Effect of processing conditions on the water absorption and texture kinetics of potato. J. Food Eng. 2008, 84, 214–223. [Google Scholar] [CrossRef]
- Maldonado, S.; Arnau, E.; Bertuzzi, M.A. Effect of temperature and pretreatment on water diffusion during rehydration of dehydrated mangoes. J. Food Eng. 2010, 96, 333–341. [Google Scholar] [CrossRef]
- Ramallo, L.A.; Albani, O.A. Water diffusion coefficient and modeling of water uptake in packaged yerba mate. J. Food Process. Preserv. 2007, 31, 406–419. [Google Scholar] [CrossRef]
- Markowski, M. Air drying of vegetables: Evaluation of mass transfer coefficient. J. Food Eng. 1997, 34, 55–62. [Google Scholar] [CrossRef]
- Dincer, I. Moisture transfer analysis during drying of slab woods. Int. J. Heat Mass Transf. 1998, 34, 317–320. [Google Scholar] [CrossRef]
- Miketinac, M.J.; Sokhansanj, S.; Tutek, Z. Determination of Heat and Mass Transfer Coefficients in Thin Layer Drying of Grain. Trans. ASAE 1992, 35, 1853–1858. [Google Scholar] [CrossRef]
- Wang, N.; Brennan, J.G. A mathematical model of simultaneous heat and moisture transfer during drying of potato. J. Food Eng. 1995, 24, 47–60. [Google Scholar] [CrossRef]
- Białobrzewski, I. Determination of the mass transfer coefficient during hot-air-drying of celery root. J. Food Eng. 2007, 78, 1388–1396. [Google Scholar] [CrossRef]
- Górnicki, K.; Kaleta, A. Drying curve modelling of blanched carrot cubes under natural convection condition. J. Food Eng. 2007, 82, 160–170. [Google Scholar] [CrossRef]
- Huang, C.-H.; Yeh, C.-Y. An inverse problem in simultaneous estimating the Biot numbers of heat and moisture transfer for a porous material. Int. J. Heat Mass Transf. 2002, 45, 4643–4653. [Google Scholar] [CrossRef]
- Chen, X.D.; Peng, X. Modified Biot number in the context of air drying of small moist porous objects. Dry Technol. 2005, 23, 83–103. [Google Scholar] [CrossRef]
- Li, Z.X.; Renault, F.L.; Gómez, A.O.C.; Sarafraz, M.M.; Khan, H.; Safaei, M.R.; Filho, E.P.B. Nanofluids as secondary fluid in the refrigeration system: Experimental data, regression, ANFIS, and NN modeling. Int. J. Heat Mass Transf. 2019, 144, 118635. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Tlili, I.; Tian, Z.; Bakouri, M.; Safaei, M.R. Smart optimization of a thermosyphon heat pipe for an evacuated tube solar collector using response surface methodology (RSM). Phys. Stat. Mech. Its Appl. 2019, 534, 122146. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Safaei, M.R.; Goodarzi, M.; Arjomandi, M. Experimental investigation and performance optimisation of a catalytic reforming micro-reactor using response surface methodology. Energy Convers. Manag. 2019, 199, 111983. [Google Scholar] [CrossRef]
- Benyounis, K.Y.; Olabi, A.G. Optimization of different welding processes using statistical and numerical approaches—A reference guide. Adv. Eng. Softw. 2008, 39, 483–496. [Google Scholar] [CrossRef]
- Kopsidas, G. Multiobjective optimization of table olive preparation systems. Eur. J. Oper. Res. 1995, 85, 383. [Google Scholar] [CrossRef]
- Kiranoudis, C.; Markatos, N. Pareto design of conveyor-belt dryers. J. Food. Eng. 2000, 46, 145–155. [Google Scholar] [CrossRef]
- Therdthai, N.; Zhou, W.; Adamczak, T. Optimization of the temperature profile in bread baking. J. Food. Eng. 2002, 55, 41–48. [Google Scholar] [CrossRef]
- Erdogdu, F.; Balaban, M. Complex method for nonlinear constrained optimization of thermal processing multi-criteria. J. Food Process. Eng. 2003, 26, 357–375. [Google Scholar] [CrossRef]
- Gergely, S.; Bekassy-Molnar, E.; Vatai, G. The use of multiobjective optimization to improve wine filtration. J. Food Eng. 2003, 58, 311–316. [Google Scholar] [CrossRef]
- Hadiyanto, M.; Boom, R.; Straten, G.; Boxtel, A.; Esveld, D. Multi-objective optimization to improve the product range of baking systems. J. Food Process. Eng. 2009, 32, 709–729. [Google Scholar] [CrossRef]
- Zhang, Y.; Hidajat, K.; Ray, A.K. Optimal design and operation of SMB bioreactor: Production of high fructose syrup by isomerization of glucose. Biochem. Eng. J. 2004, 21, 111. [Google Scholar] [CrossRef]
- Kawajiri, Y.; Biegler, L.T. Nonlinear programming superstructure for optimal dynamic operations of simulated moving bed processes. Ind. Eng. Chem. Res. 2006, 45, 8503. [Google Scholar] [CrossRef]
- Hakanen, J.; Kawajiri, Y.; Miettinen, K.; Biegler, L.T. Interactive multi-objective optimization for simulated moving bed processes. Control Cybern. 2007, 36, 50. [Google Scholar]
- Abakarov, A.; Sushkov, Y.; Almonacid, S.; Simpson, R. Multiobjective Optimization Approach: Thermal Food Processing. J. Food Sci. 2009, 74, E477–E487. [Google Scholar] [CrossRef] [PubMed]
- Winiczenko, R.; Górnicki, K.; Kaleta, A.; Martynenko, A.; Janaszek-Mańkowska, M.; Trajer, J. Multi-objective optimization of convective drying of apple cubes. Comput. Electron. Agric. 2018, 145, 341–348. [Google Scholar] [CrossRef]
- Winiczenko, R.; Górnicki, K.; Kaleta, A.; Janaszek-Mankowska, M.; Trajer, J. Multi-objective optimization of the apple drying and rehydration processes parameters. EJFA 2018, 30, 1–9. [Google Scholar]
- Seng, C.; Rangaiah, S. Multi-objective optimization in food engineering. In Optimization in Food Engineering; Erdogdu, F., Ed.; Taylor & Francis Book: Abingdon, UK, 2008; Chapter 4; p. 800. [Google Scholar]
- Górnicki, K.; Winiczenko, R.; Kaleta, A. Estimation of the Biot Number Using Genetic Algorithms: Application for the Drying Process. Energies 2019, 12, 2822. [Google Scholar] [CrossRef]
- Górnicki, K.; Kaleta, A. Modelling convection drying of blanched parsley root slices. Biosyst. Eng. 2007, 97, 51–59. [Google Scholar] [CrossRef]
- Luikov, A.V. Analytical Heat Diffusion Theory; Academic Press Inc.: New York, NY, USA, 1970. [Google Scholar]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975; ISBN 978-0-19-853344-3. [Google Scholar]
- Pabis, S.; Jayas, D.S.; Cenkowski, S. Grain Drying: Theory and Practice; John Wiley: New York, NY, USA, 1998; ISBN 978-0-471-57387-6. [Google Scholar]
- Kaleta, A.; Górnicki, K. Some remarks on evaluation of drying models of red beet particles. Energy Convers. Manag. 2010, 51, 2967–2978. [Google Scholar] [CrossRef]
- Kaleta, A.; Górnicki, K. Evaluation of drying models of apple (var. McIntosh) dried in a convective dryer. Int. J. Food Sci. Technol. 2010, 45, 891–898. [Google Scholar] [CrossRef]
- Górnicki, K.; Kaleta, A.; Choińska, A. Suitable model for thin-layer drying of root vegetables and onion. Int. Agrophysics 2020, 1, 79–86. [Google Scholar] [CrossRef]
- Foneseca, C.M.; Flemming, P. Genetic algorithms for multi-objective optimization: Formulation, discussion, and generalization. In Proceedings of the 5th International Conference on Genetic Algorithms, Urbana-Champaign, July 17–21; Morgan Kaufmann: San Francisco, CA, USA, 1993; pp. 416–423. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- MATLAB 7.6 R2008a, Documentation R; MathWorks, Inc.: Natick, MA, USA, 2008.
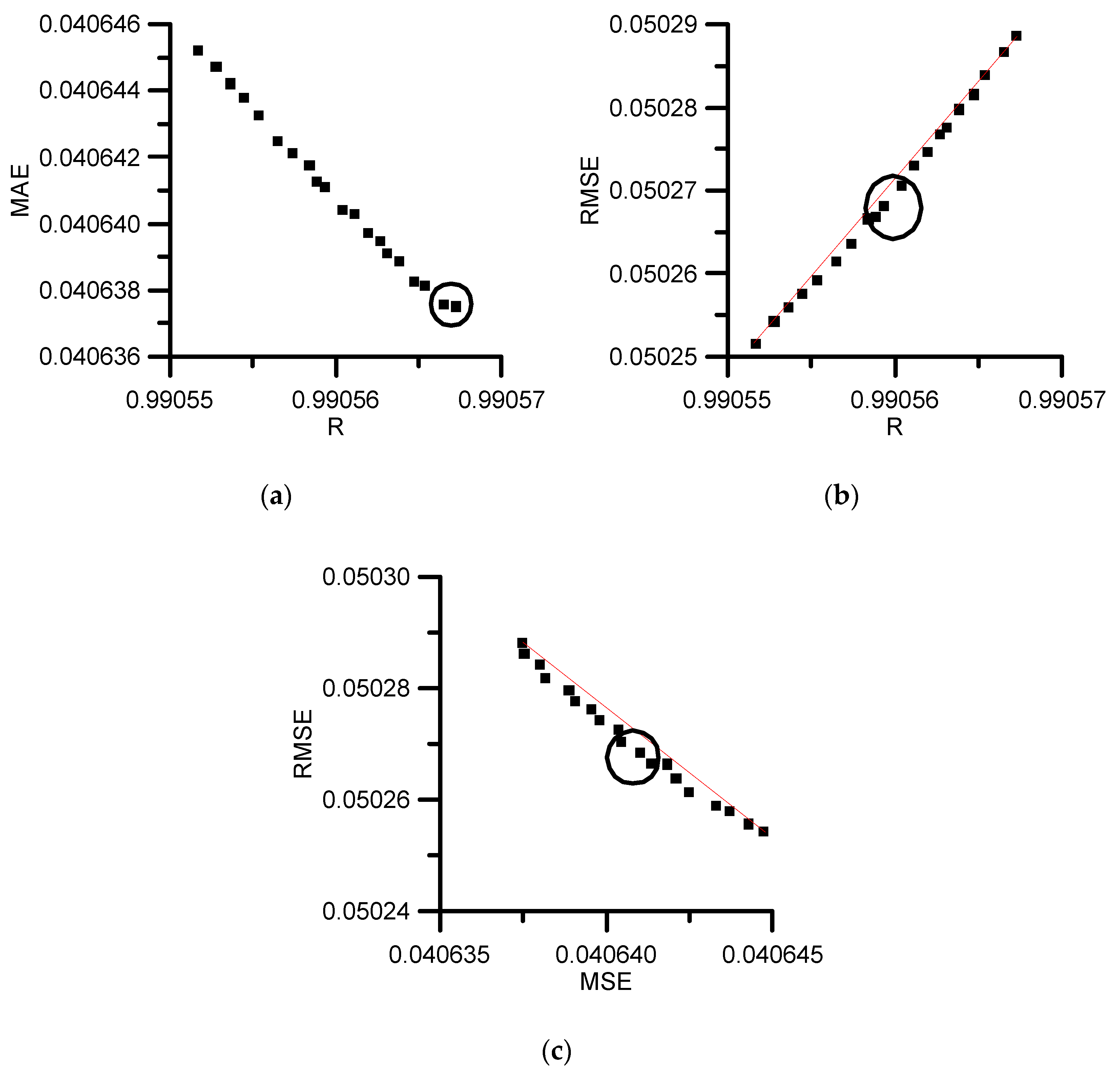
| ID | aBi | bBi | cBi | dBi | eBi | fBi | R | RMSE | MAE |
|---|---|---|---|---|---|---|---|---|---|
| S_1 | 0.7647141 | 10.1689977 | −0.003400086 | 948.715758 | 0.000024316 | −0.12478256 | 0.9905672 | 0.050289 | 0.0406375 |
| S_2 | 0.7647140 | 10.1689891 | −0.003400089 | 948.715738 | 0.000024316 | −0.12478252 | 0.9905665 | 0.050287 | 0.0406376 |
| S_3 | 0.7647142 | 10.1689057 | −0.003400089 | 948.715760 | 0.000024319 | −0.12478129 | 0.9905653 | 0.050284 | 0.0406381 |
| S_4 | 0.7647142 | 10.1689752 | −0.003400082 | 948.715784 | 0.000024316 | −0.12478196 | 0.9905647 | 0.050282 | 0.0406383 |
| S_5 | 0.7647143 | 10.1689954 | −0.003400083 | 948.715759 | 0.000024317 | −0.12478102 | 0.9905638 | 0.050280 | 0.0406389 |
| S_6 | 0.7646614 | 10.1689890 | −0.003400072 | 948.715763 | 0.000024330 | −0.12478277 | 0.9905631 | 0.050278 | 0.0406391 |
| S_7 | 0.7647142 | 10.1689346 | −0.003400066 | 948.715773 | 0.000024316 | −0.12477951 | 0.9905627 | 0.050277 | 0.0406395 |
| S_8 | 0.7646615 | 10.1689980 | −0.003400071 | 948.715758 | 0.000024330 | −0.12478214 | 0.9905619 | 0.050275 | 0.0406397 |
| S_9 | 0.7647164 | 10.1689977 | −0.003400082 | 948.715752 | 0.000024316 | −0.12478000 | 0.9905611 | 0.050273 | 0.0406403 |
| S_10 | 0.7646749 | 10.1689859 | −0.003400075 | 948.715762 | 0.000024323 | −0.12478259 | 0.9905604 | 0.050271 | 0.0406404 |
| S_11 | 0.7647171 | 10.1689683 | −0.003400077 | 948.715759 | 0.000024316 | −0.12478368 | 0.9905593 | 0.050268 | 0.0406411 |
| S_12 | 0.7646708 | 10.1689920 | −0.003400071 | 948.715757 | 0.000024324 | −0.12478274 | 0.9905588 | 0.050267 | 0.0406412 |
| S_13 | 0.7646981 | 10.1689694 | −0.003399883 | 948.715758 | 0.000024320 | −0.12478335 | 0.9905584 | 0.050267 | 0.0406418 |
| S_14 | 0.7647143 | 10.1689797 | −0.003400077 | 948.715764 | 0.000024316 | −0.12478110 | 0.9905574 | 0.050264 | 0.0406421 |
| S_15 | 0.7646723 | 10.1689885 | −0.003400092 | 948.715759 | 0.000024324 | −0.12478362 | 0.9905565 | 0.050261 | 0.0406425 |
| S_16 | 0.7647146 | 10.1689610 | −0.003400070 | 948.715796 | 0.000024316 | −0.12478125 | 0.9905553 | 0.050259 | 0.0406432 |
| S_17 | 0.7647112 | 10.1689946 | −0.003400011 | 948.715761 | 0.000024316 | −0.12478272 | 0.9905544 | 0.050257 | 0.0406438 |
| S_18 | 0.7646966 | 10.1689920 | −0.003400075 | 948.715743 | 0.000024323 | −0.12478189 | 0.9905537 | 0.050256 | 0.0406442 |
| S_19 | 0.7647146 | 10.1689886 | −0.003400073 | 948.715721 | 0.000024317 | −0.12478261 | 0.9905528 | 0.050254 | 0.0406447 |
| S_20 | 0.7647145 | 10.1689228 | −0.003400067 | 948.715776 | 0.000024316 | −0.12478094 | 0.9905517 | 0.050252 | 0.0406452 |
| ID | aD | bD | cD | dD | eD | fD | R | RMSE | MAE |
|---|---|---|---|---|---|---|---|---|---|
| S_1 | 0.000000127547936 | −0.000023808 | −0.00000000508365633 | 0.0030005179 | 0.00000000004266495 | 0.0000008336330 | 0.9905672 | 0.050289 | 0.0406375 |
| S_2 | 0.000000127547948 | −0.000023806 | −0.00000000508365753 | 0.0030005175 | 0.00000000004266493 | 0.0000008336334 | 0.9905665 | 0.050287 | 0.0406376 |
| S_3 | 0.000000127547939 | −0.000023803 | −0.00000000508365666 | 0.0030005216 | 0.00000000004266494 | 0.0000008336333 | 0.9905653 | 0.050284 | 0.0406381 |
| S_4 | 0.000000127547938 | −0.000023801 | −0.00000000508365663 | 0.0030004841 | 0.00000000004266493 | 0.0000008336339 | 0.9905647 | 0.050282 | 0.0406383 |
| S_5 | 0.000000127547934 | −0.000023799 | −0.00000000508365680 | 0.0030005241 | 0.00000000004266493 | 0.0000008336334 | 0.9905638 | 0.050280 | 0.0406389 |
| S_6 | 0.000000127547927 | −0.000023797 | −0.00000000508365755 | 0.0030005275 | 0.00000000004266495 | 0.0000008336336 | 0.9905631 | 0.050278 | 0.0406391 |
| S_7 | 0.000000127547932 | −0.000023796 | −0.00000000508365677 | 0.0030005201 | 0.00000000004266492 | 0.0000008336339 | 0.9905627 | 0.050277 | 0.0406395 |
| S_8 | 0.000000127547934 | −0.000023794 | −0.00000000508365671 | 0.0030005301 | 0.00000000004266494 | 0.0000008336337 | 0.9905619 | 0.050275 | 0.0406397 |
| S_9 | 0.000000127547936 | −0.000023792 | −0.00000000508365669 | 0.0030005201 | 0.00000000004266494 | 0.0000008336338 | 0.9905611 | 0.050273 | 0.0406403 |
| S_10 | 0.000000127547930 | −0.000023790 | −0.00000000508365669 | 0.0030005199 | 0.00000000004266495 | 0.0000008336335 | 0.9905604 | 0.050271 | 0.0406404 |
| S_11 | 0.000000127547935 | −0.000023787 | −0.00000000508365634 | 0.0030004820 | 0.00000000004266493 | 0.0000008336332 | 0.9905593 | 0.050268 | 0.0406411 |
| S_12 | 0.000000127547929 | −0.000023786 | −0.00000000508365667 | 0.0030005267 | 0.00000000004266494 | 0.0000008336337 | 0.9905588 | 0.050267 | 0.0406412 |
| S_13 | 0.000000127547934 | −0.000023785 | −0.00000000508365706 | 0.0030005213 | 0.00000000004266494 | 0.0000008336336 | 0.9905584 | 0.050267 | 0.0406418 |
| S_14 | 0.000000127547935 | −0.000023782 | −0.00000000508365694 | 0.0030004793 | 0.00000000004266493 | 0.0000008336337 | 0.9905574 | 0.050264 | 0.0406421 |
| S_15 | 0.000000127547933 | −0.000023780 | −0.00000000508365703 | 0.0030005265 | 0.00000000004266494 | 0.0000008336336 | 0.9905565 | 0.050261 | 0.0406425 |
| S_16 | 0.000000127547937 | −0.000023777 | −0.00000000508365643 | 0.0030004974 | 0.00000000004266494 | 0.0000008336336 | 0.9905553 | 0.050259 | 0.0406432 |
| S_17 | 0.000000127547934 | −0.000023775 | −0.00000000508365667 | 0.0030005259 | 0.00000000004266494 | 0.0000008336337 | 0.9905544 | 0.050257 | 0.0406438 |
| S_18 | 0.000000127547929 | −0.000023773 | −0.00000000508365675 | 0.0030005227 | 0.00000000004266494 | 0.0000008336335 | 0.9905537 | 0.050256 | 0.0406442 |
| S_19 | 0.000000127547931 | −0.000023771 | −0.00000000508365740 | 0.0030005313 | 0.00000000004266494 | 0.0000008336340 | 0.9905528 | 0.050254 | 0.0406447 |
| S_20 | 0.000000127547938 | −0.000023768 | −0.00000000508365654 | 0.0030005173 | 0.00000000004266493 | 0.0000008336333 | 0.9905517 | 0.050252 | 0.0406452 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winiczenko, R.; Górnicki, K.; Kaleta, A. Evaluation of the Mass Diffusion Coefficient and Mass Biot Number Using a Nondominated Sorting Genetic Algorithm. Symmetry 2020, 12, 260. https://doi.org/10.3390/sym12020260
Winiczenko R, Górnicki K, Kaleta A. Evaluation of the Mass Diffusion Coefficient and Mass Biot Number Using a Nondominated Sorting Genetic Algorithm. Symmetry. 2020; 12(2):260. https://doi.org/10.3390/sym12020260
Chicago/Turabian StyleWiniczenko, Radosław, Krzysztof Górnicki, and Agnieszka Kaleta. 2020. "Evaluation of the Mass Diffusion Coefficient and Mass Biot Number Using a Nondominated Sorting Genetic Algorithm" Symmetry 12, no. 2: 260. https://doi.org/10.3390/sym12020260
APA StyleWiniczenko, R., Górnicki, K., & Kaleta, A. (2020). Evaluation of the Mass Diffusion Coefficient and Mass Biot Number Using a Nondominated Sorting Genetic Algorithm. Symmetry, 12(2), 260. https://doi.org/10.3390/sym12020260







