Artificial Neural Network and Adaptive Neuro-Fuzzy Interface System Modelling to Predict Thermal Performances of Thermoelectric Generator for Waste Heat Recovery
Abstract
1. Introduction
2. Experimental Set-Up
3. Numerical Method
4. Artificial Intelligence Models
4.1. Artificial Neural Network (ANN) Modelling
4.2. Adaptive Neuro-Fuzzy Interface System Modelling (ANFIS)
5. Data Reduction
6. Results and Discussion
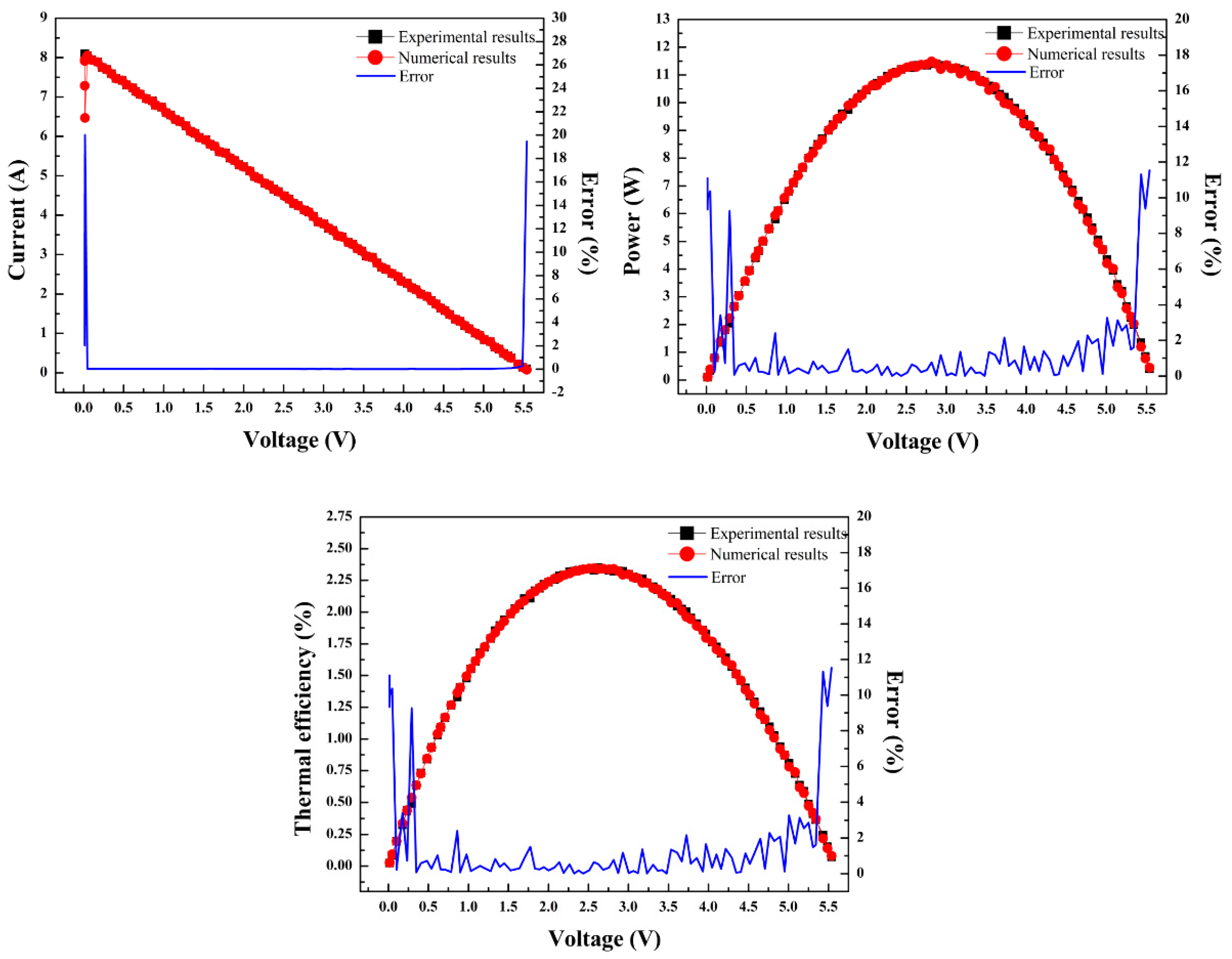
6.1. Experimental Outputs of Current, Power and Thermal Efficiency
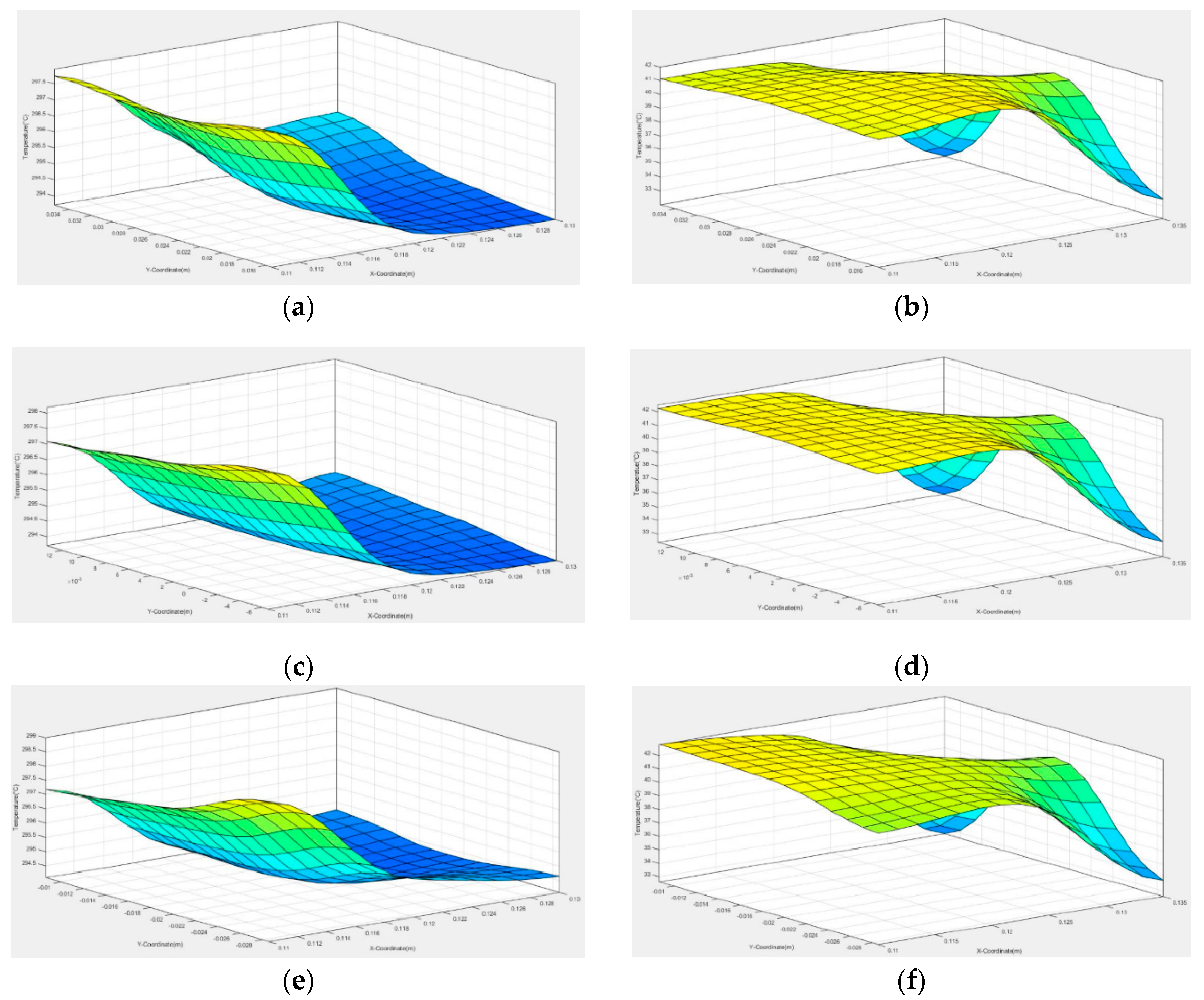
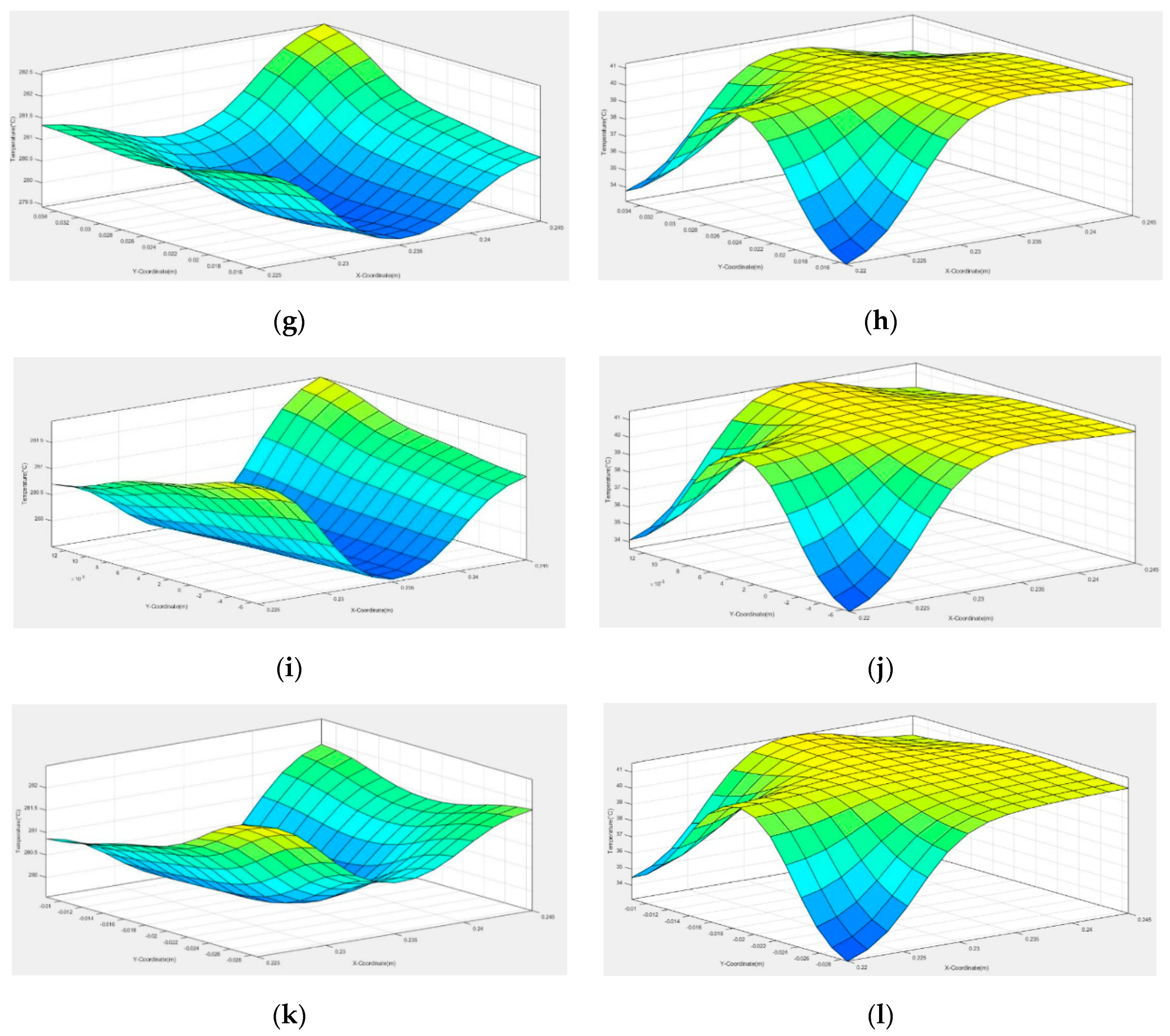
6.2. Prediction Results from the Numerical Method
6.3. Training and Testing Data Sets for ANN and ANFIS Models
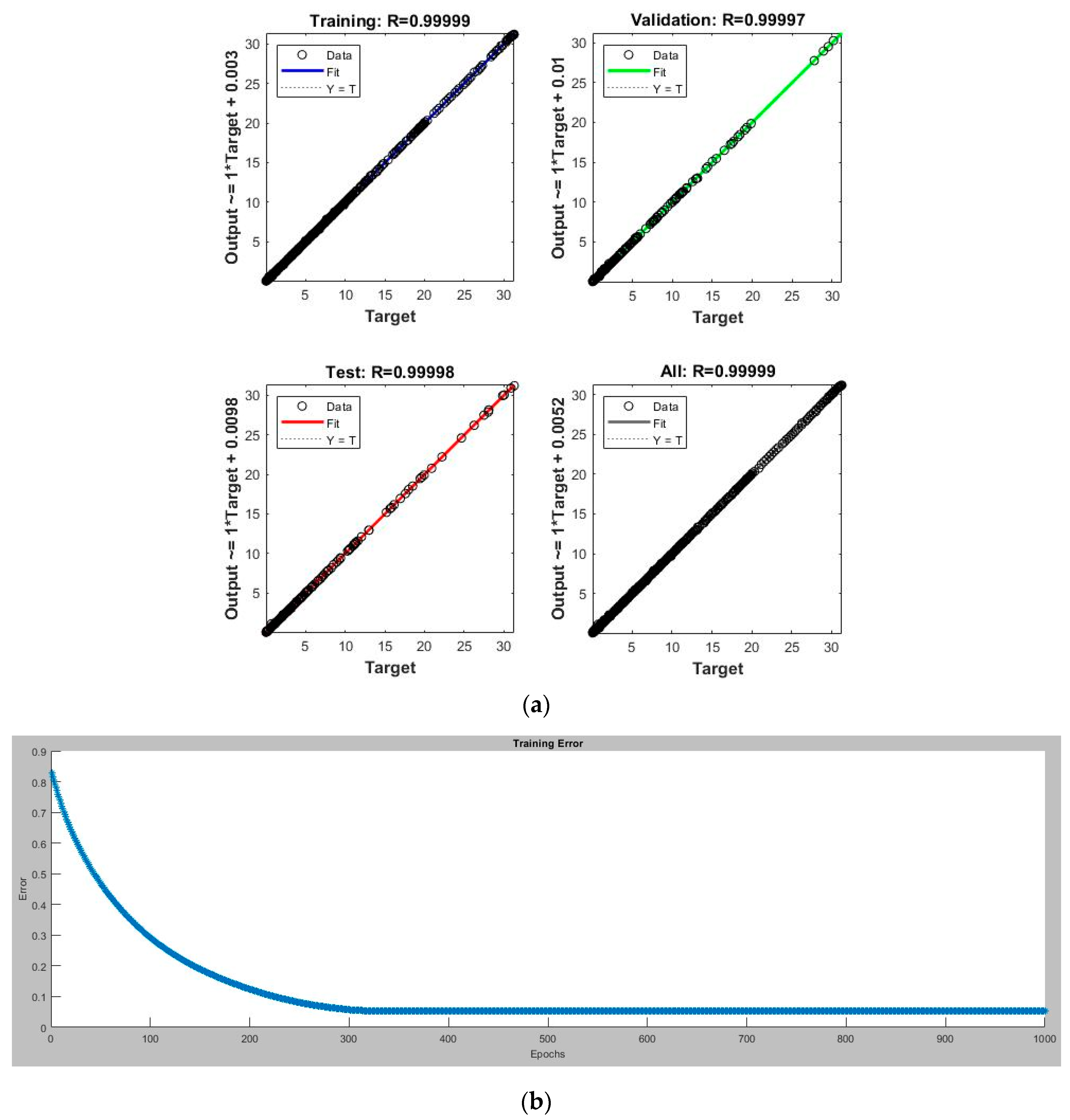
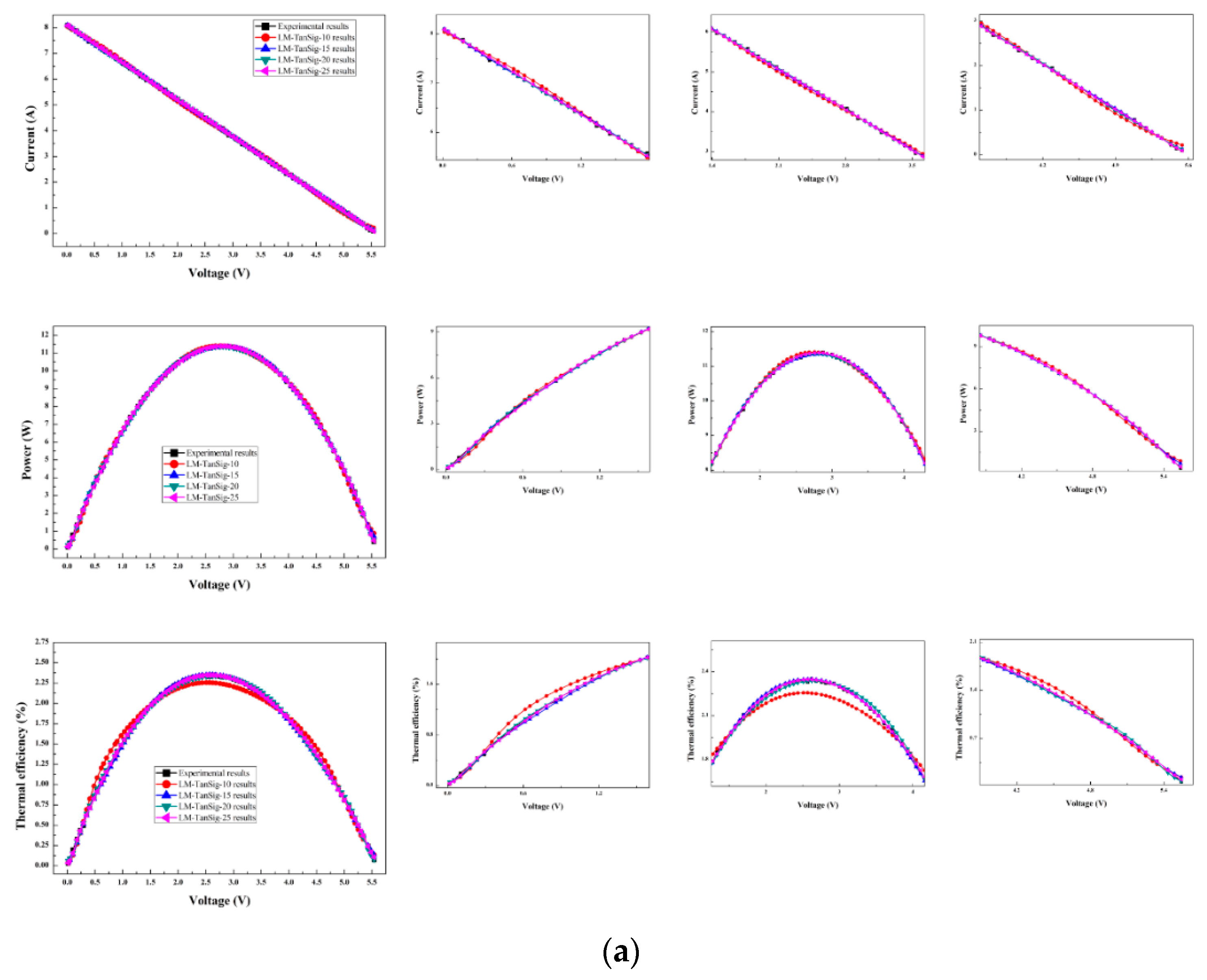
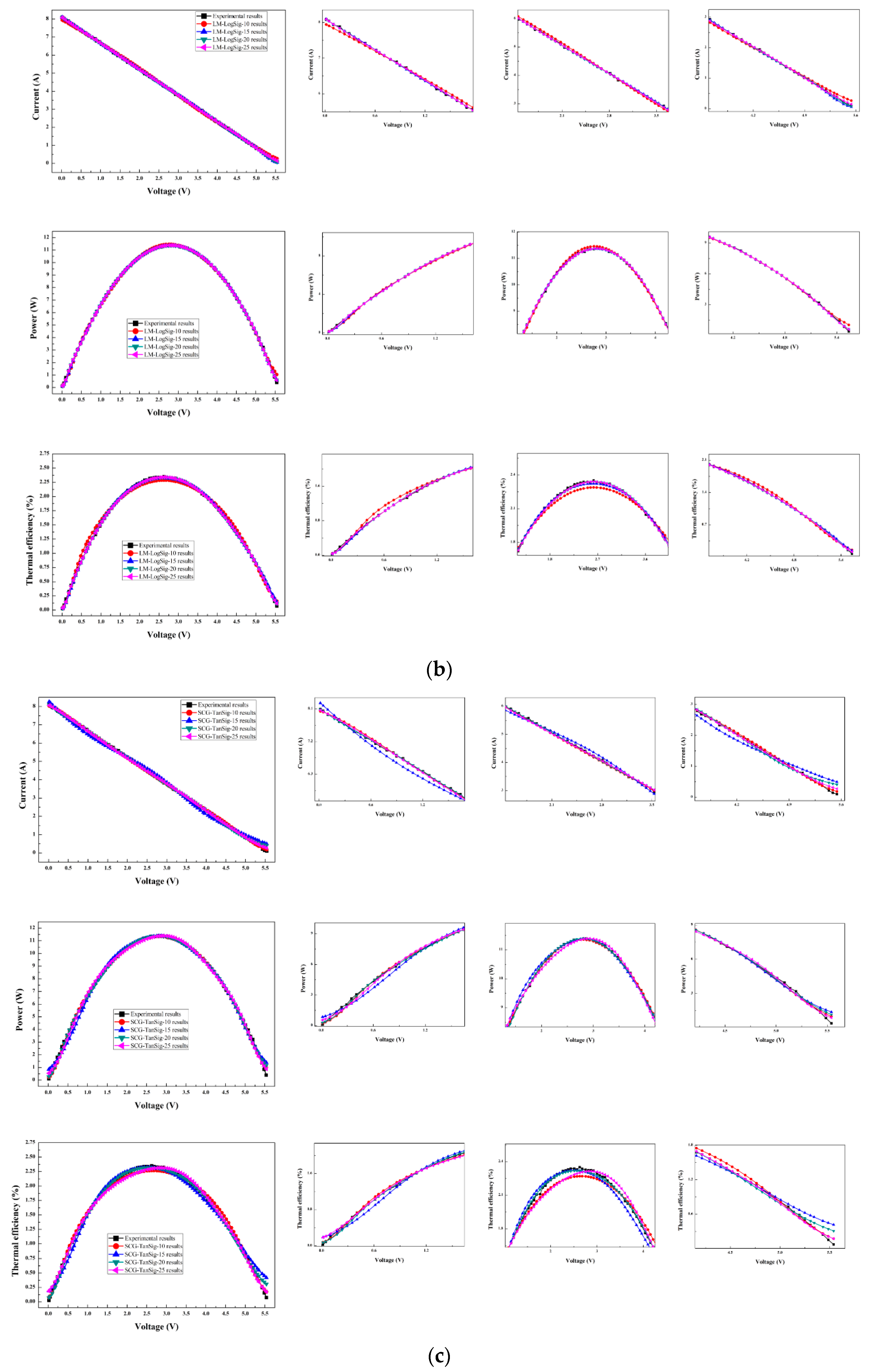
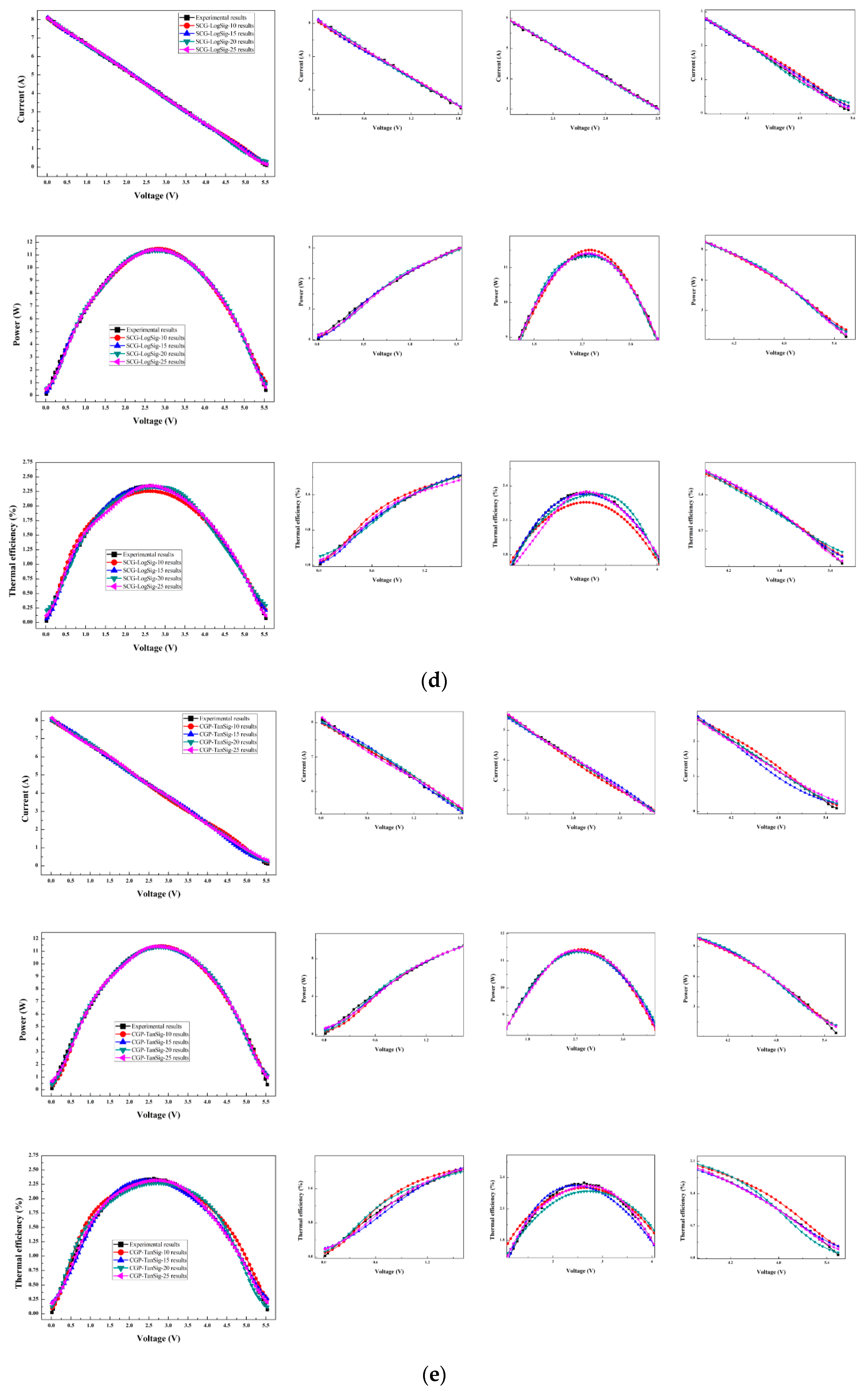
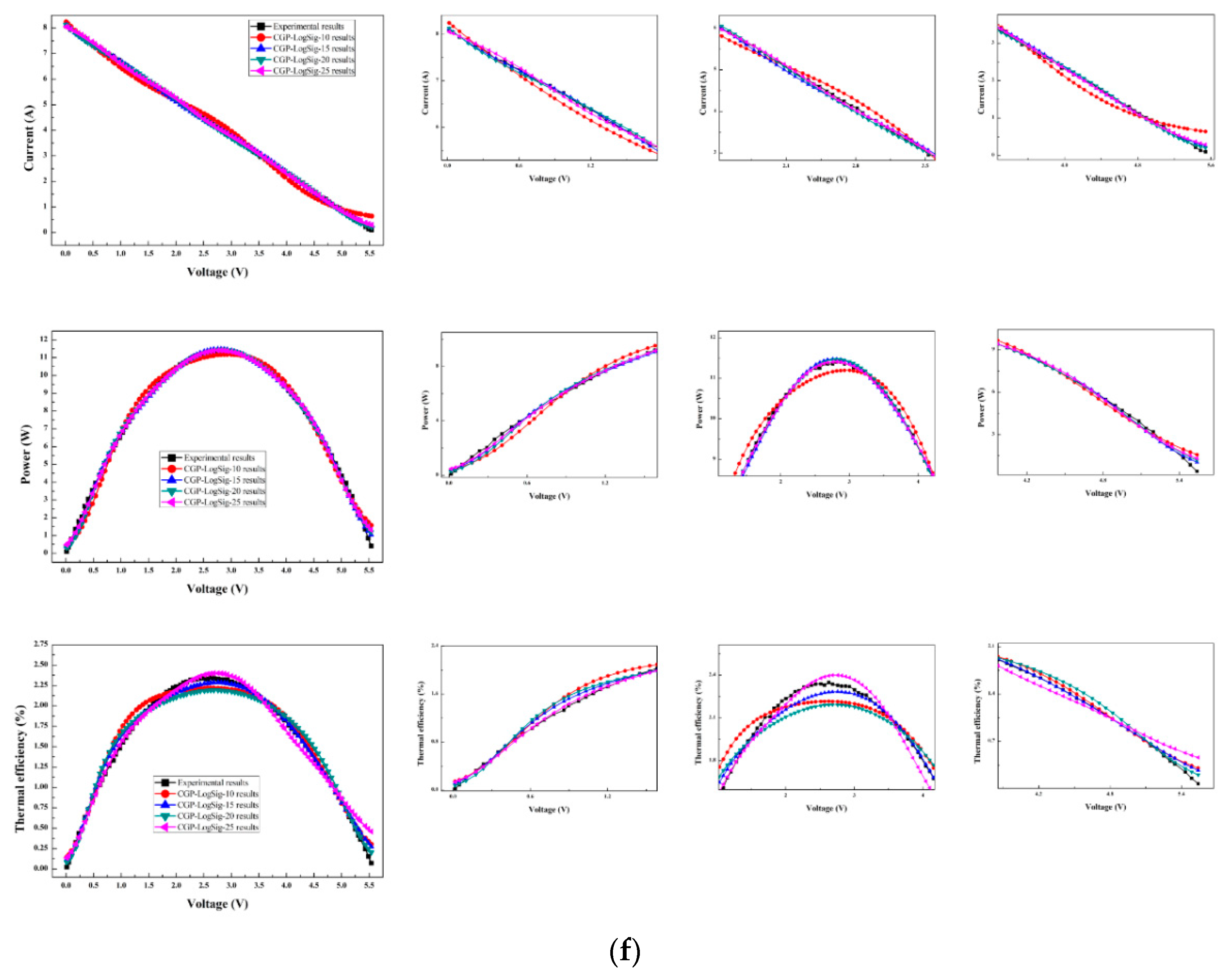
6.4. Prediction Results from ANN Models
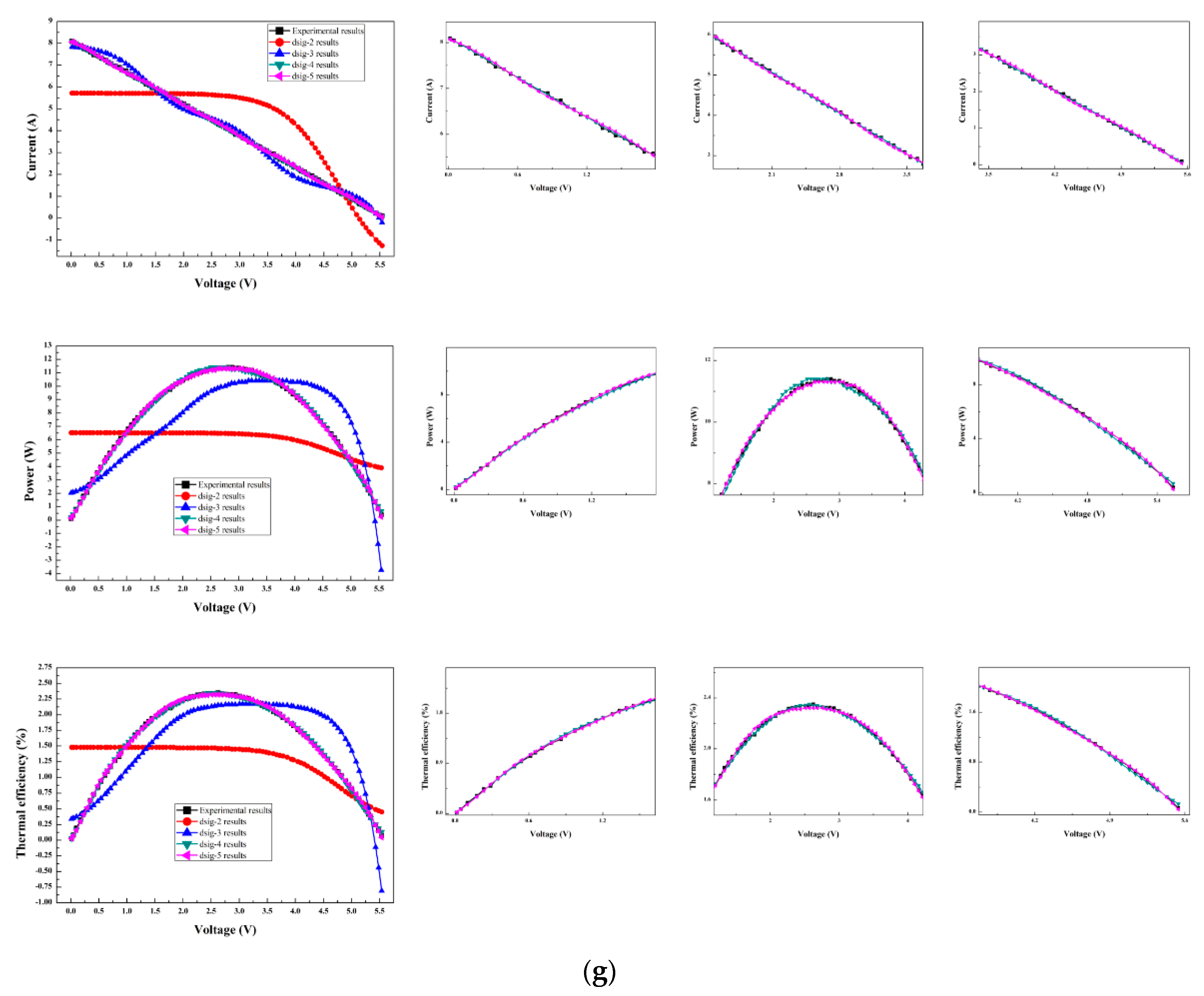
6.5. Prediction Results from ANFIS Models
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Demirel, Y. Energy: Production, Conversion, Storage, Conservation, and Coupling; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Riffat, S.B.; Ma, X. Thermoelectrics: A review of present and potential applications. Appl. Therm. Eng. 2003, 23, 913–935. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Xie, X.; Deng, Y.; Liu, X.; Su, C. Performance evaluation of an automotive thermoelectric generator with inserted fins or dimpled-surface hot heat exchanger. Appl. Energy 2018, 218, 391–401. [Google Scholar] [CrossRef]
- Niu, Z.; Diao, H.; Yu, S.; Jiao, K.; Du, Q.; Shu, G. Investigation and design optimization of exhaust-based thermoelectric generator system for internal combustion engine. Energy Convers. Manag. 2014, 85, 85–101. [Google Scholar] [CrossRef]
- Liu, X.; Deng, Y.D.; Zhang, K.; Xu, M.; Xu, Y.; Su, C.Q. Experiments and simulations on heat exchangers in thermoelectric generator for automotive application. Appl. Therm. Eng. 2014, 71, 364–370. [Google Scholar] [CrossRef]
- Quan, R.; Liu, G.; Wang, C.; Zhou, W.; Huang, L.; Deng, Y. Performance investigation of an exhaust thermoelectric generator for military SUV application. Coatings 2018, 8, 45. [Google Scholar] [CrossRef]
- Luo, D.; Wang, R.; Yu, W.; Sun, Z.; Meng, X. Modelling and simulation study of a converging thermoelectric generator for engine waste heat recovery. Appl. Therm. Eng. 2019, 153, 837–847. [Google Scholar] [CrossRef]
- Nithyanandam, K.; Mahajan, R.L. Evaluation of metal foam based thermoelectric generators for automobile waste heat recovery. Int. J. Heat Mass Transf. 2018, 122, 877–883. [Google Scholar] [CrossRef]
- Cao, Q.; Luan, W.; Wang, T. Performance enhancement of heat pipes assisted thermoelectric generator for automobile exhaust heat recovery. Appl. Therm. Eng. 2018, 130, 1472–1479. [Google Scholar] [CrossRef]
- He, W.; Wang, S. Performance Comparison of Different Exhaust Exchanger Types Considering Peak Net Power and Optimal Dimension in a Thermoelectric Generator System. Adv. Theory Simul. 2018, 1, 1800012. [Google Scholar] [CrossRef]
- Lu, X.; Yu, X.; Qu, Z.; Wang, Q.; Ma, T. Experimental investigation on thermoelectric generator with non-uniform hot-side heat exchanger for waste heat recovery. Energy Convers. Manag. 2017, 150, 403–414. [Google Scholar] [CrossRef]
- Rana, S.; Date, A.; Iqbal, A.; Akbarzadeh, A. Optimization model for power generation using thermoelectric generator. Energy Procedia 2019, 160, 723–730. [Google Scholar] [CrossRef]
- Suter, C.; Jovanovic, Z.R.; Steinfeld, A. A 1 kWe thermoelectric stack for geothermal power generation–Modeling and geometrical optimization. Appl. Energy 2012, 99, 379–385. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Ge, M.; Liang, Z.; Liang, Y.; Li, Y. Performance analysis of automobile exhaust thermoelectric generator system with media fluid. Energy Convers. Manag. 2018, 171, 427–437. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S.; Ge, M.; Liang, Z.; Liang, Y.; Li, Y. Performance investigation of an intermediate fluid thermoelectric generator for automobile exhaust waste heat recovery. Appl. Energy 2019, 239, 425–433. [Google Scholar] [CrossRef]
- Lu, H.; Wu, T.; Bai, S.; Xu, K.; Huang, Y.; Gao, W.; Chen, L. Experiment on thermal uniformity and pressure drop of exhaust heat exchanger for automotive thermoelectric generator. Energy 2013, 54, 372–377. [Google Scholar] [CrossRef]
- Dheenamma, M.; Soman, D.P.; Muthamizhi, K.; Kalaichelvi, P. In pursuit of the best artificial neural network configuration for the prediction of output parameters of corrugated plate heat exchanger. Fuel 2019, 239, 461–470. [Google Scholar] [CrossRef]
- Angeline, A.A. Power generation from combusted “Syngas” using hybrid thermoelectric generator and forecasting the performance with ANN technique. J. Therm. Eng. 2018, 4, 2149–2168. [Google Scholar] [CrossRef]
- Angeline, A.A.; Asirvatham, L.G.; Hemanth, D.J.; Jayakumar, J.; Wongwises, S. Performance prediction of hybrid thermoelectric generator with high accuracy using artificial neural networks. Sustain. Energy Technol. Assess. 2019, 33, 53–60. [Google Scholar] [CrossRef]
- Liu, X.; Deng, Y.D.; Li, Z.; Su, C.Q. Performance analysis of a waste heat recovery thermoelectric generation system for automotive application. Energy Convers. Manag. 2015, 90, 121–127. [Google Scholar] [CrossRef]
- Raj, A.K.; Kunal, G.; Srinivas, M.; Jayaraj, S. Performance analysis of a double-pass solar air heater system with asymmetric channel flow passages. J. Therm. Anal. Calorim. 2019, 136, 21–38. [Google Scholar] [CrossRef]
- Park, S.H.; Jin, Y.; Cha, J.; Hong, K.; Kim, Y.; Yoon, H.; Chung, I. High-Power-Density Skutterudite-Based Thermoelectric Modules with Ultralow Contact Resistivity Using Fe–Ni Metallization Layers. ACS Appl. Energy Mater. 2018, 1, 1603–1611. [Google Scholar] [CrossRef]
- Seo, J.H.; Patil, M.S.; Cho, C.P.; Lee, M.Y. Heat transfer characteristics of the integrated heating system for cabin and battery of an electric vehicle under cold weather conditions. Int. J. Heat Mass Transf. 2018, 117, 80–94. [Google Scholar] [CrossRef]
- Ma, Q.; Fang, H.; Zhang, M. Theoretical analysis and design optimization of thermoelectric generator. Appl. Therm. Eng. 2017, 127, 758–764. [Google Scholar] [CrossRef]
- Yazdani-Chamzini, A.; Zavadskas, E.K.; Antucheviciene, J.; Bausys, R. A model for shovel capital cost estimation, using a hybrid model of multivariate regression and neural networks. Symmetry 2017, 9, 298. [Google Scholar] [CrossRef]
- Mohanraj, M.; Jayaraj, S.; Muraleedharan, C. Performance prediction of a direct expansion solar assisted heat pump using artificial neural networks. Appl. Energy 2009, 86, 1442–1449. [Google Scholar] [CrossRef]
- Islam, K.T.; Raj, R.G.; Mujtaba, G. Recognition of traffic sign based on bag-of-words and artificial neural network. Symmetry 2017, 9, 138. [Google Scholar] [CrossRef]
- Moya-Rico, J.D.; Molina, A.E.; Belmonte, J.F.; Tendero, J.C.; Almendros-Ibanez, J.A. Characterization of a triple concentric-tube heat exchanger with corrugated tubes using Artificial Neural Networks (ANN). Appl. Therm. Eng. 2019, 147, 1036–1046. [Google Scholar] [CrossRef]
- Ullah, I.; Fayaz, M.; Kim, D. Improving accuracy of the kalman filter algorithm in dynamic conditions using ANN-based learning module. Symmetry 2019, 11, 94. [Google Scholar] [CrossRef]
- Şahin, A.Ş. Performance analysis of single-stage refrigeration system with internal heat exchanger using neural network and neuro-fuzzy. Renew. Energy 2011, 36, 2747–2752. [Google Scholar] [CrossRef]
- Bogiatzis, A.; Papadopoulos, B. Global Image Thresholding Adaptive Neuro-Fuzzy Inference System Trained with Fuzzy Inclusion and Entropy Measures. Symmetry 2019, 11, 286. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Zhang, X.; Song, S.; Niu, C.; Shangguan, Y. Using ANFIS and BPNN Methods to Predict the Unfrozen Water Content of Saline Soil in Western Jilin, China. Symmetry 2019, 11, 16. [Google Scholar] [CrossRef]
- Mehrabi, M.; Pesteei, S.M. Modeling of heat transfer and fluid flow characteristics of helicoidal double-pipe heat exchangers using adaptive neuro-fuzzy inference system (ANFIS). Int. Commun. Heat Mass Transf. 2011, 38, 525–532. [Google Scholar] [CrossRef]
- Sarkar, M.; Julai, S.; Wen Tong, C.; Toha, S.F. Effectiveness of Nature-Inspired Algorithms using ANFIS for Blade Design Optimization and Wind Turbine Efficiency. Symmetry 2019, 11, 456. [Google Scholar] [CrossRef]
- Yeom, C.U.; Kwak, K.C. Performance Comparison of ANFIS Models by Input Space Partitioning Methods. Symmetry 2018, 10, 700. [Google Scholar] [CrossRef]
- Erturun, U.; Mossi, K. A feasibility investigation on improving structural integrity of thermoelectric modules with varying geometry. In Proceedings of the ASME 2012 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Stone Mountain, GA, USA, 19–21 September 2012; pp. 939–945. [Google Scholar]
- Phillips, S.S. Characterizing the Thermal Efficiency of Thermoelectric Modules. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Gunasekar, N.; Mohanraj, M.; Velmurugan, V. Artificial neural network modeling of a photovoltaic-thermal evaporator of solar assisted heat pumps. Energy 2015, 93, 908–922. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M. ANN and ANFIS models for performance evaluation of a vertical ground source heat pump system. Expert Syst. Appl. 2010, 37, 8134–8147. [Google Scholar] [CrossRef]
- Belaout, A.; Krim, F.; Mellit, A.; Talbi, B.; Arabi, A. Multiclass adaptive neuro-fuzzy classifier and feature selection techniques for photovoltaic array fault detection and classification. Renew. Energy 2018, 127, 548–558. [Google Scholar] [CrossRef]
- Yaïci, W.; Entchev, E. Adaptive neuro-fuzzy inference system modelling for performance prediction of solar thermal energy system. Renew. Energy 2016, 86, 302–315. [Google Scholar] [CrossRef]
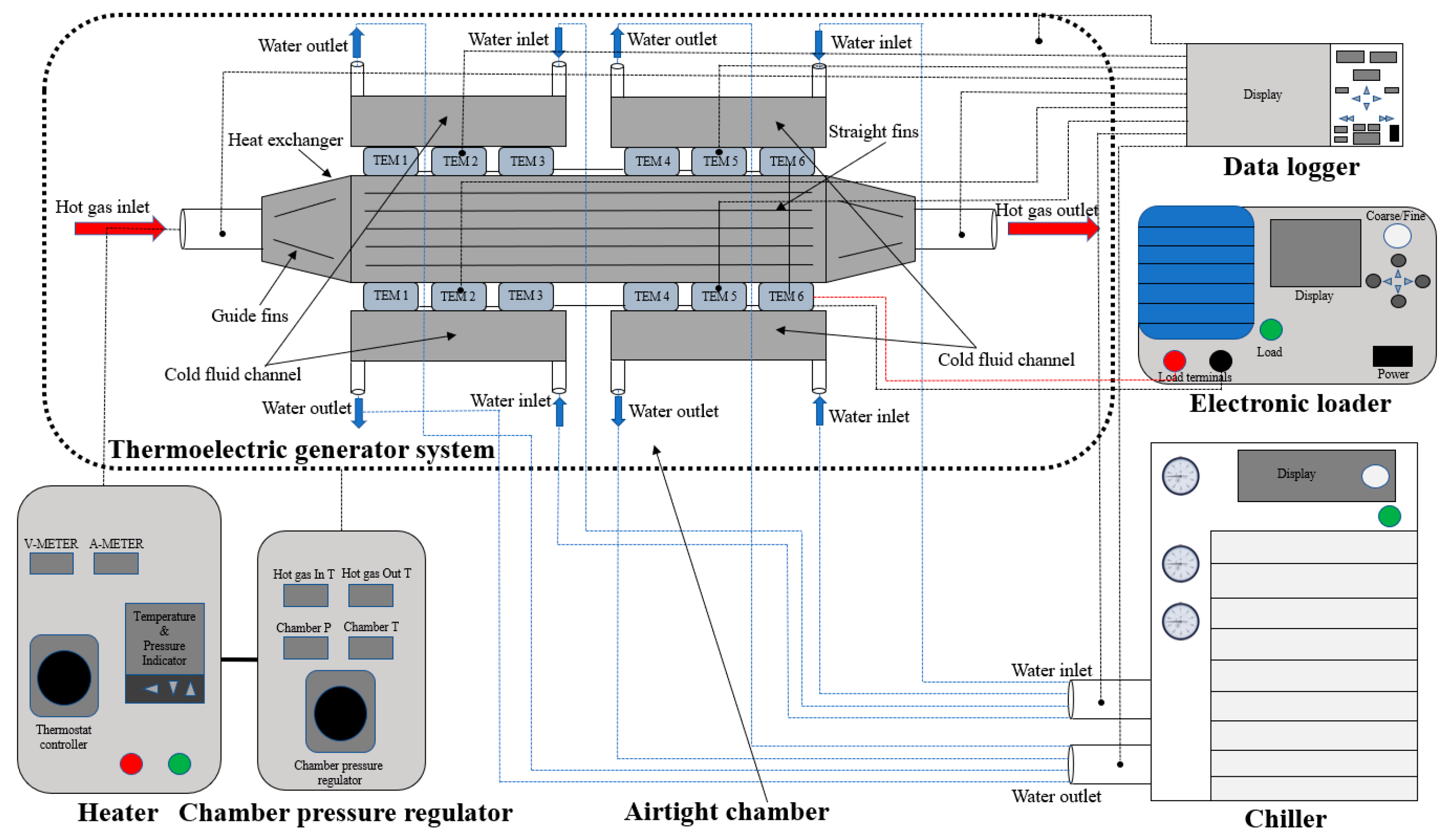
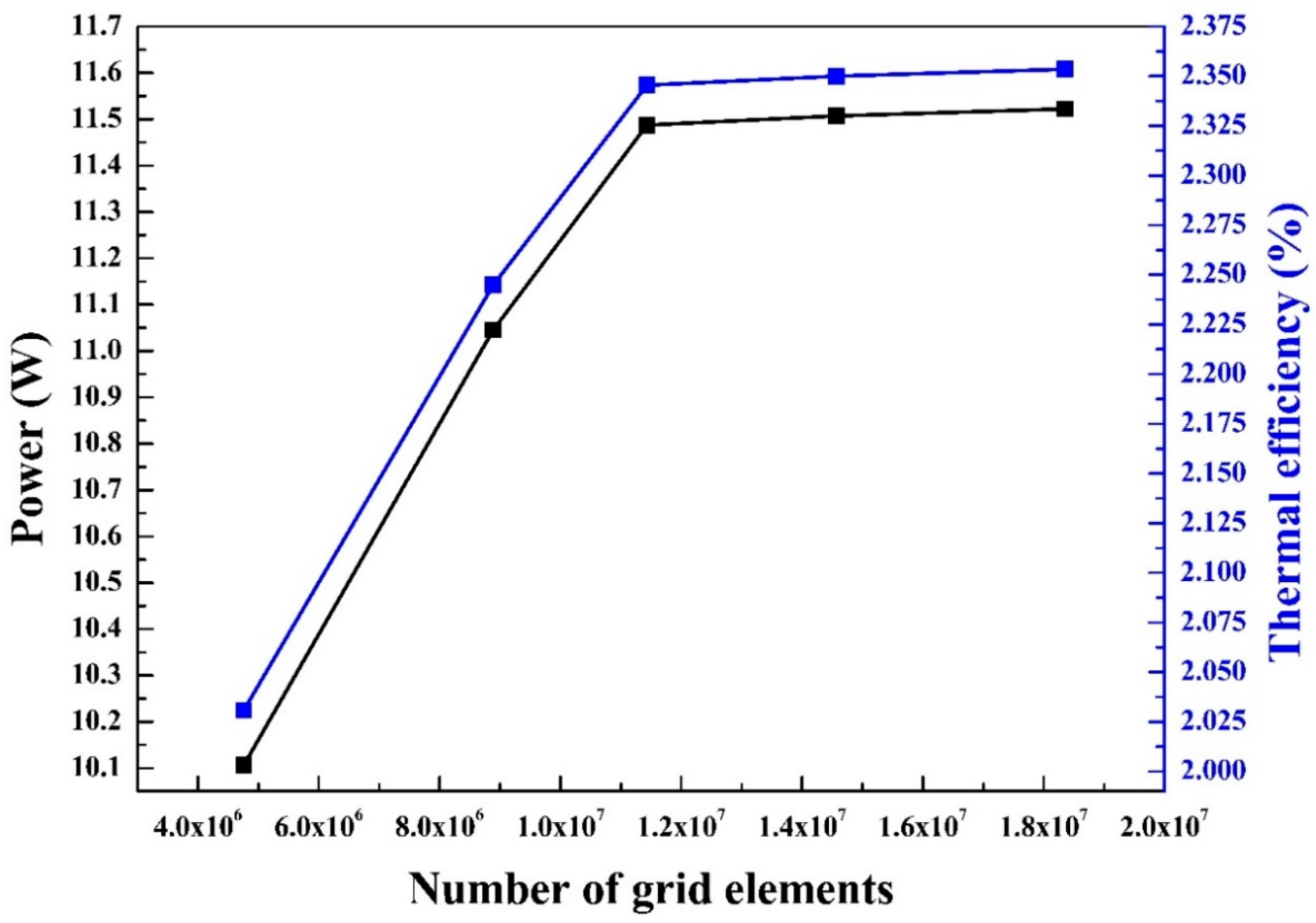
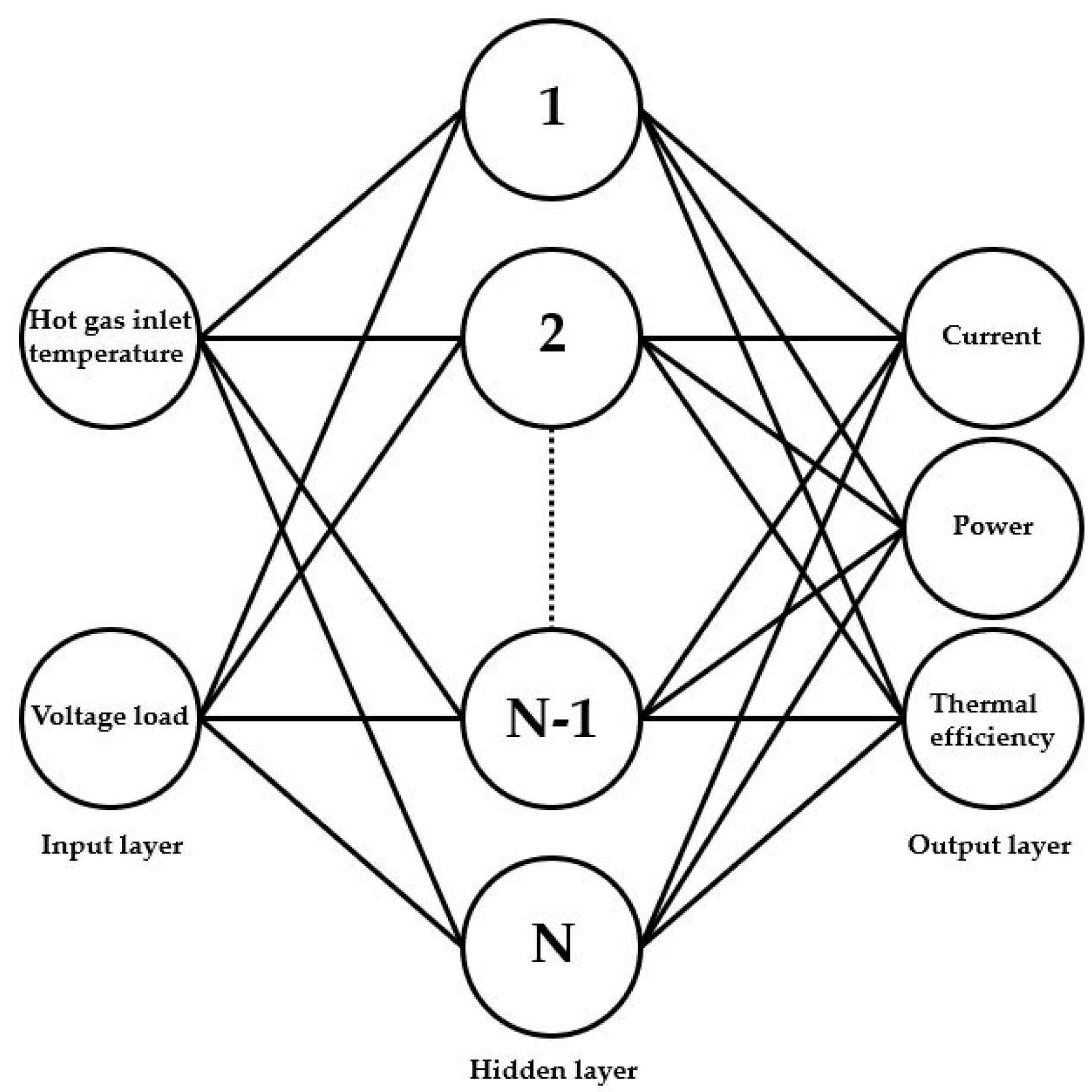
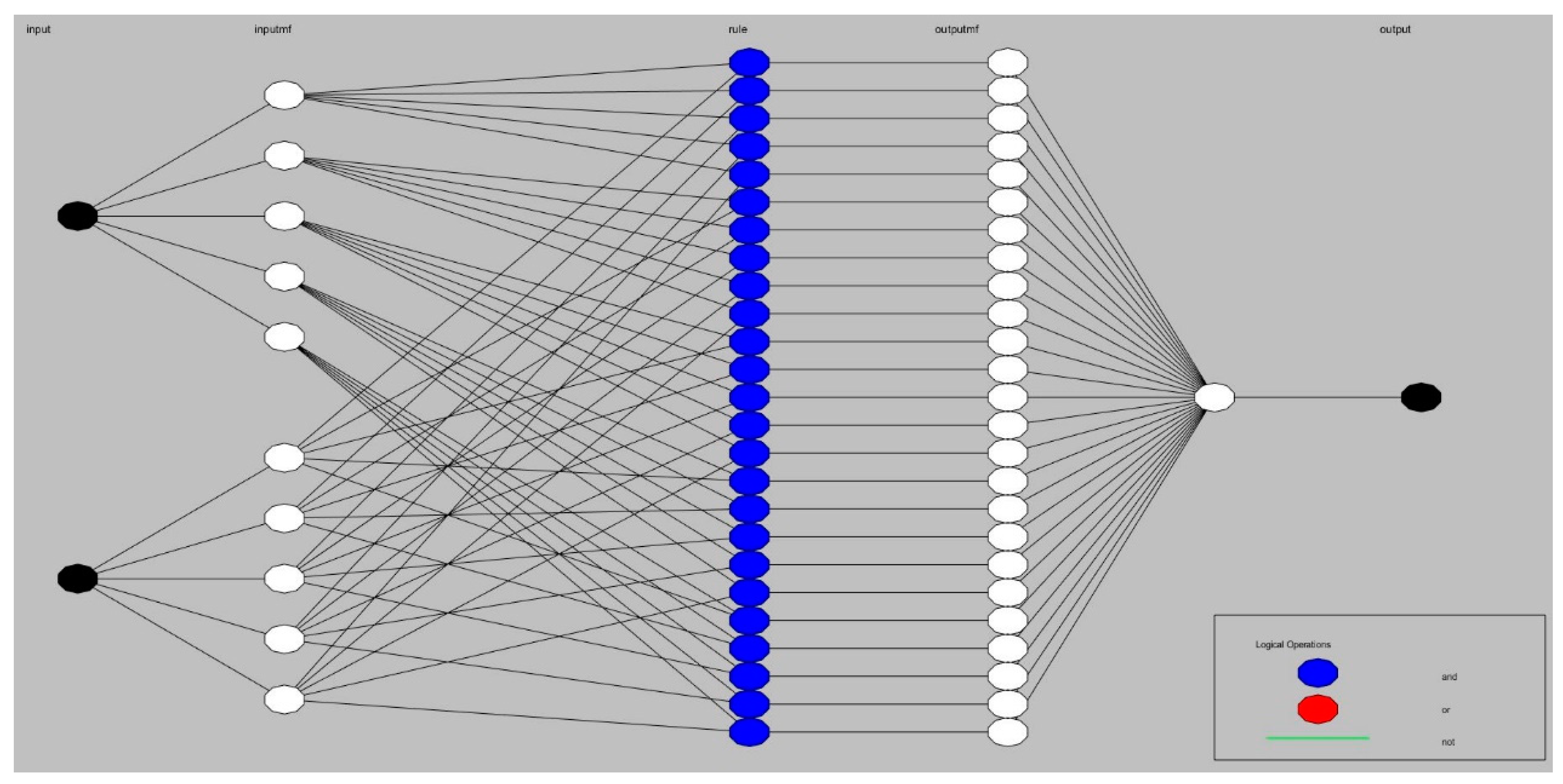

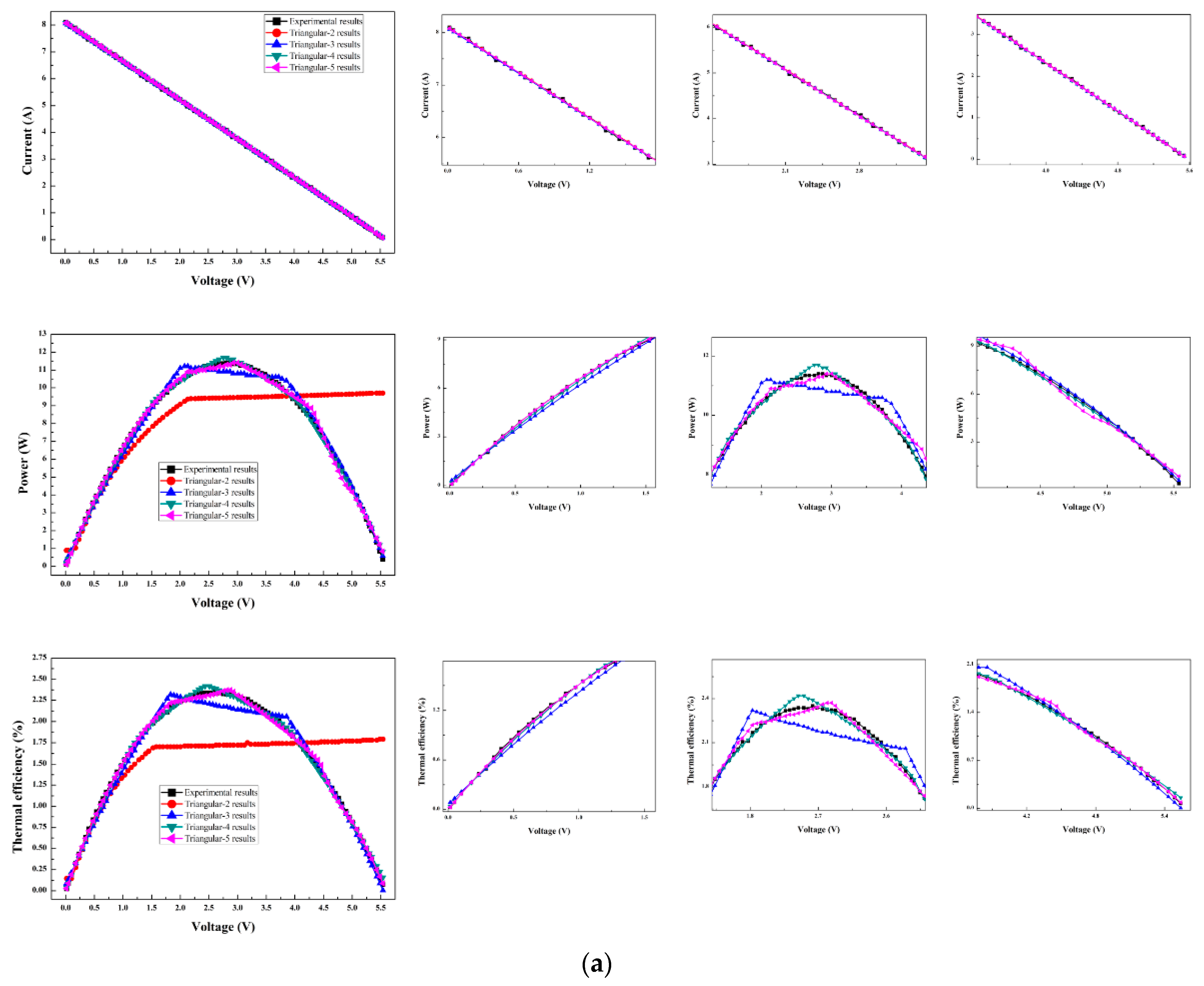
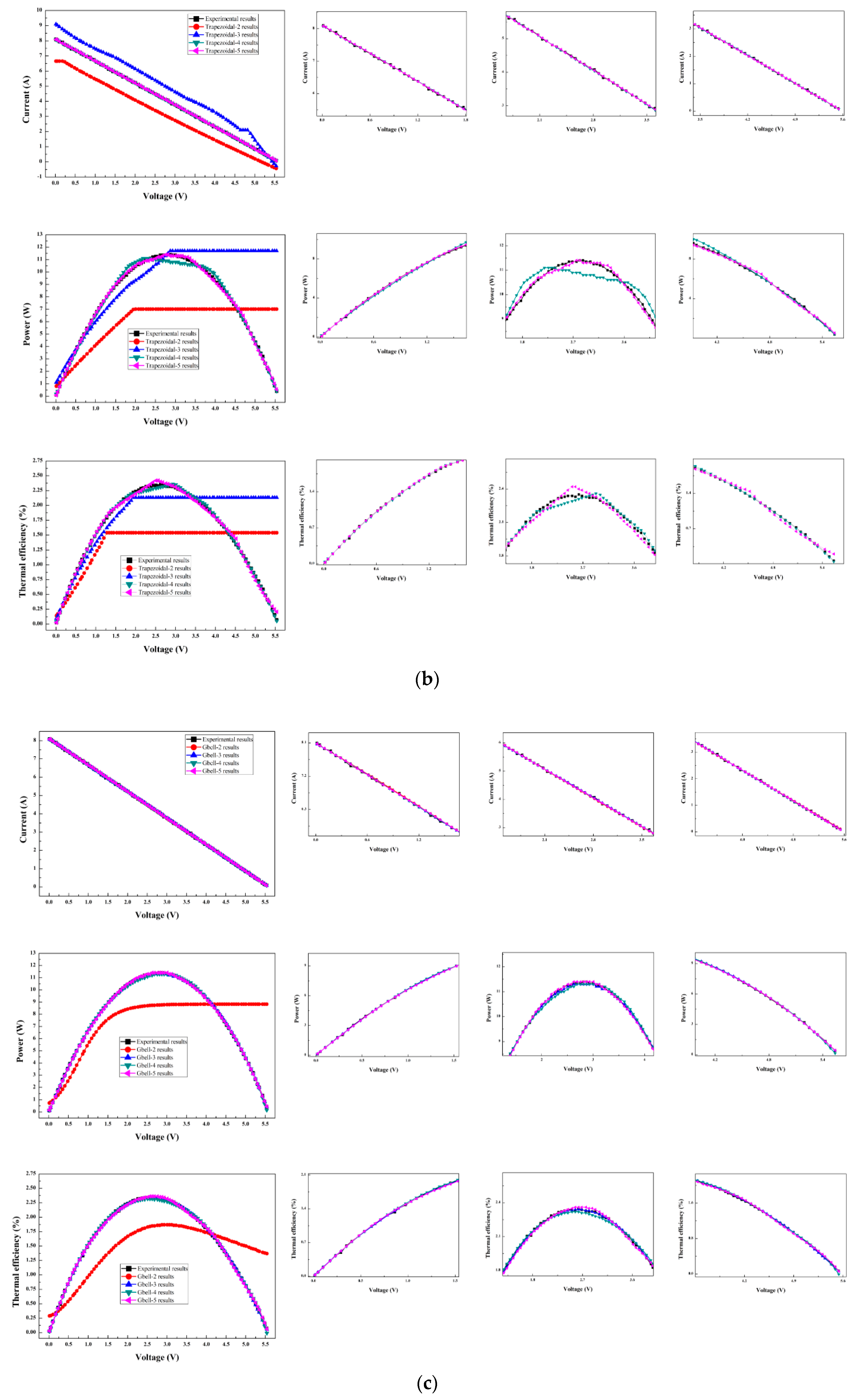
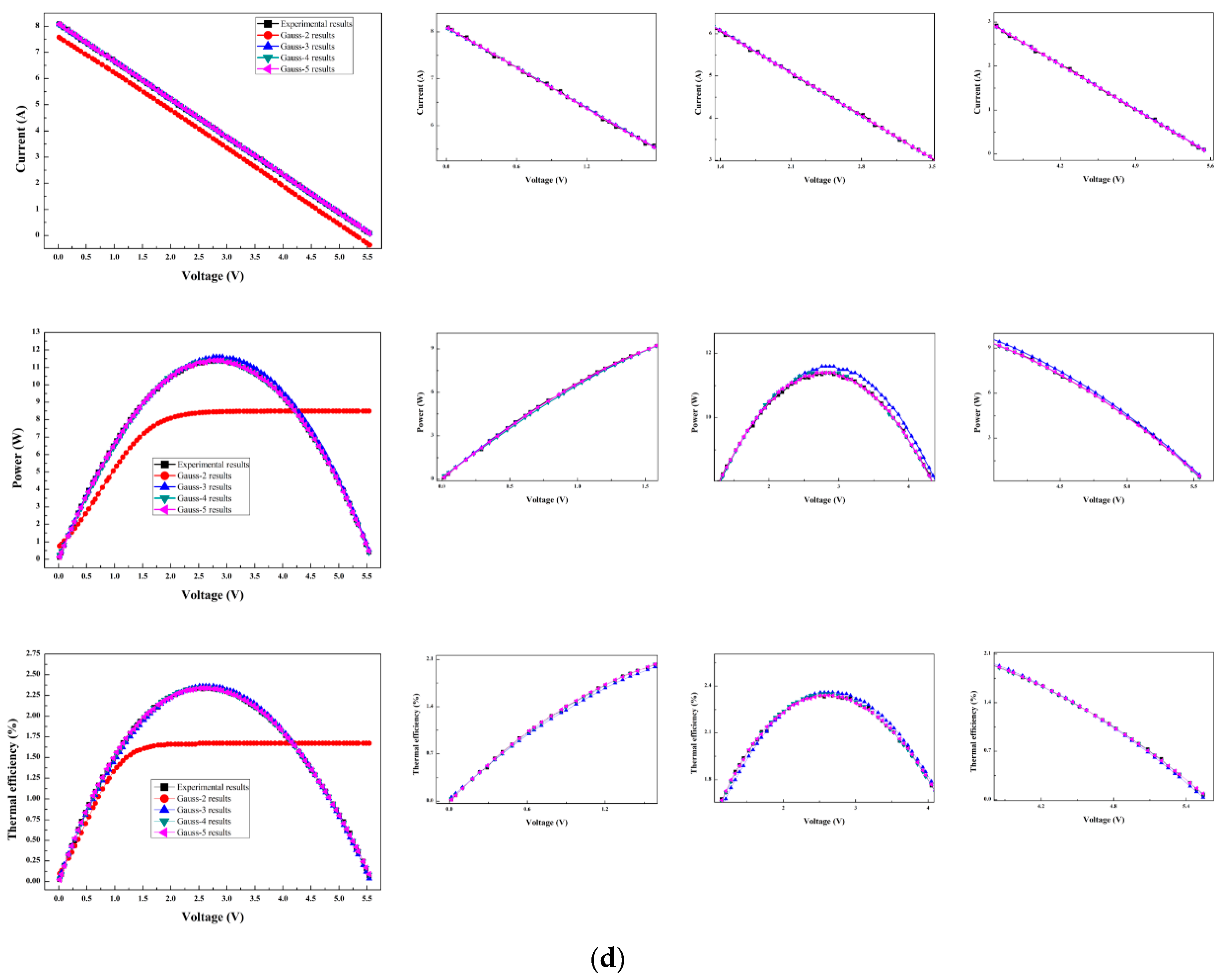
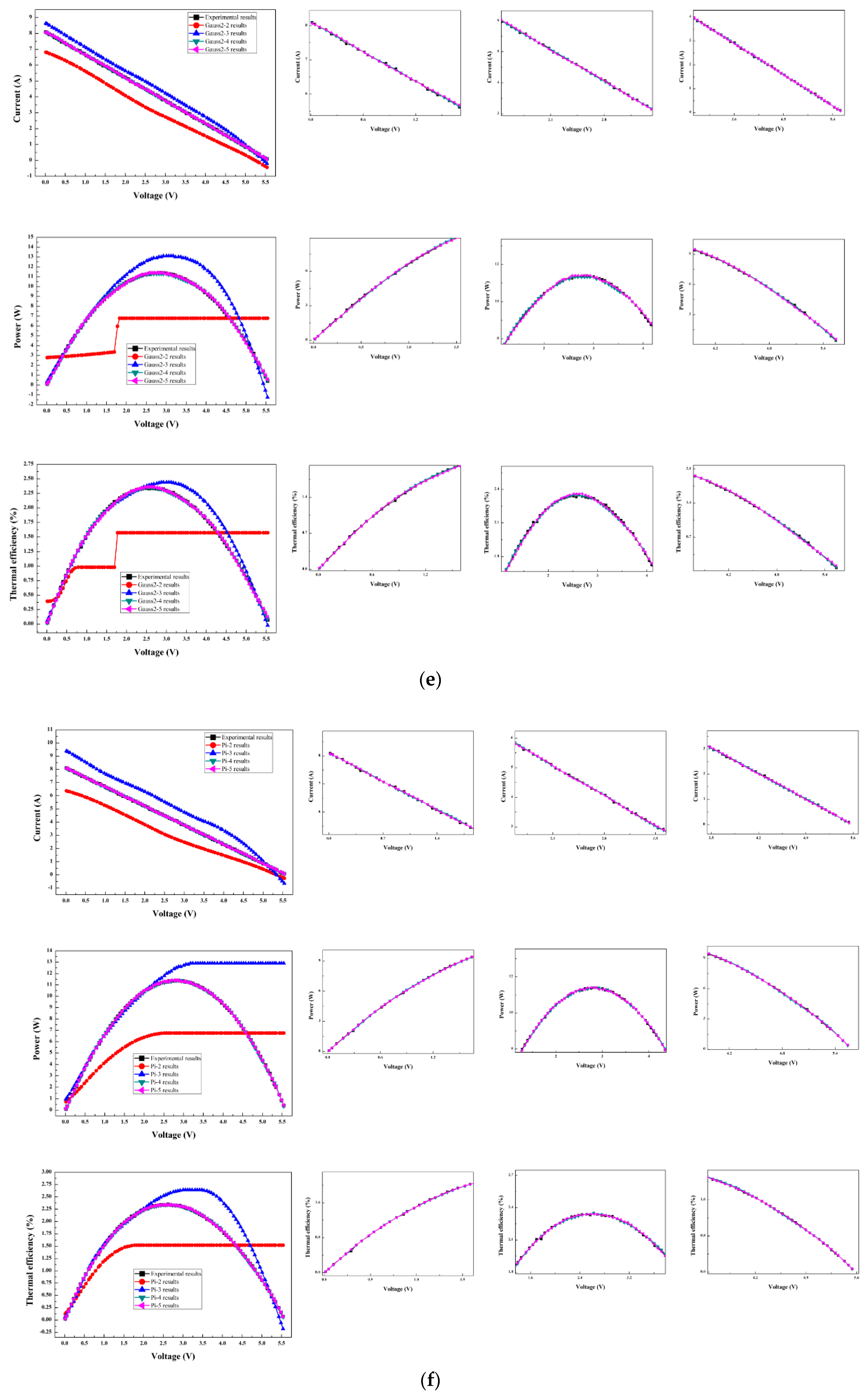
| Parameter | Value |
|---|---|
| Hot gas (air) inlet temperature (°C) | 315.12, 419.26, 521.7, 621.61 |
| Coolant (water) inlet temperature (°C) | 30 |
| Hot gas (air) mass flow rate (kg/s) | 0.018 |
| Coolant (water) mass flow rate (kg/s) | 0.075 |
| High potential voltage (V) | 0 to 10 V |
| Low potential voltage (V) | 0 |
| Parameter | R2 | RMSE | COV |
|---|---|---|---|
| Current | 0.99865 | 0.18633 | 4.22614 |
| Power | 0.99992 | 0.07032 | 1.01243 |
| Thermal efficiency | 0.99992 | 0.01422 | 0.99102 |
| Parameter | Number of Hidden Neurons | R2 | RMSE | COV |
|---|---|---|---|---|
| Current | 10 | 0.99986 | 0.06013 | 1.36373 |
| 15 | 0.99997 | 0.02578 | 0.58476 | |
| 20 | 0.99998 | 0.02507 | 0.56860 | |
| 25 | 0.99998 | 0.02163 | 0.49061 | |
| Power | 10 | 0.99977 | 0.12180 | 1.75370 |
| 15 | 0.99993 | 0.06769 | 0.97459 | |
| 20 | 0.99993 | 0.06609 | 0.95152 | |
| 25 | 0.99997 | 0.04111 | 0.59192 | |
| Thermal efficiency | 10 | 0.99809 | 0.07170 | 4.99773 |
| 15 | 0.99983 | 0.02126 | 1.48165 | |
| 20 | 0.99981 | 0.02277 | 1.58688 | |
| 25 | 0.99996 | 0.01050 | 0.73183 |
| Parameter | Number of Membership Functions | R2 | RMSE | COV |
|---|---|---|---|---|
| Current | 2 | 0.94053 | 1.23658 | 28.0468 |
| 3 | 0.96078 | 1.00416 | 22.7752 | |
| 4 | 0.99997 | 0.02852 | 0.64682 | |
| 5 | 0.99998 | 0.02469 | 0.55991 | |
| Power | 2 | 0.83830 | 3.19468 | 45.9964 |
| 3 | 0.71781 | 4.22023 | 60.7620 | |
| 4 | 0.99994 | 0.05948 | 0.85635 | |
| 5 | 0.99997 | 0.04029 | 0.58006 | |
| Thermal efficiency | 2 | 0.87063 | 0.58791 | 41.1021 |
| 3 | 0.96815 | 0.29262 | 20.3952 | |
| 4 | 0.99994 | 0.01257 | 0.87619 | |
| 5 | 0.99997 | 0.00931 | 0.64890 |
| Parameter | Number of Membership Functions | R2 | RMSE | COV |
|---|---|---|---|---|
| Current | 2 | 0.99250 | 0.43925 | 9.96247 |
| 3 | 0.99998 | 0.02366 | 0.53671 | |
| 4 | 0.99998 | 0.02254 | 0.51116 | |
| 5 | 0.99998 | 0.02165 | 0.49110 | |
| Power | 2 | 0.88660 | 2.67538 | 38.5195 |
| 3 | 0.99957 | 0.16457 | 2.36942 | |
| 4 | 0.99988 | 0.08667 | 1.24784 | |
| 5 | 0.99997 | 0.04429 | 0.63770 | |
| Thermal efficiency | 2 | 0.88430 | 0.55769 | 38.8710 |
| 3 | 0.99967 | 0.03002 | 2.09204 | |
| 4 | 0.99996 | 0.01056 | 0.73603 | |
| 5 | 0.99997 | 0.00911 | 0.63516 |
| Parameter | Number of Membership Functions | R2 | RMSE | COV |
|---|---|---|---|---|
| Current | 2 | 0.99997 | 0.02820 | 0.63965 |
| 3 | 0.99998 | 0.02432 | 0.55166 | |
| 4 | 0.99998 | 0.02266 | 0.51393 | |
| 5 | 0.99998 | 0.02325 | 0.52728 | |
| Power | 2 | 0.88847 | 2.65317 | 38.1999 |
| 3 | 0.99996 | 0.04812 | 0.69281 | |
| 4 | 0.99990 | 0.08003 | 1.15220 | |
| 5 | 0.99996 | 0.04865 | 0.70043 | |
| Thermal efficiency | 2 | 0.90510 | 0.50507 | 35.2033 |
| 3 | 0.99994 | 0.01241 | 0.86506 | |
| 4 | 0.99984 | 0.02086 | 1.45405 | |
| 5 | 0.99987 | 0.01848 | 1.28804 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garud, K.S.; Seo, J.-H.; Cho, C.-P.; Lee, M.-Y. Artificial Neural Network and Adaptive Neuro-Fuzzy Interface System Modelling to Predict Thermal Performances of Thermoelectric Generator for Waste Heat Recovery. Symmetry 2020, 12, 259. https://doi.org/10.3390/sym12020259
Garud KS, Seo J-H, Cho C-P, Lee M-Y. Artificial Neural Network and Adaptive Neuro-Fuzzy Interface System Modelling to Predict Thermal Performances of Thermoelectric Generator for Waste Heat Recovery. Symmetry. 2020; 12(2):259. https://doi.org/10.3390/sym12020259
Chicago/Turabian StyleGarud, Kunal Sandip, Jae-Hyeong Seo, Chong-Pyo Cho, and Moo-Yeon Lee. 2020. "Artificial Neural Network and Adaptive Neuro-Fuzzy Interface System Modelling to Predict Thermal Performances of Thermoelectric Generator for Waste Heat Recovery" Symmetry 12, no. 2: 259. https://doi.org/10.3390/sym12020259
APA StyleGarud, K. S., Seo, J.-H., Cho, C.-P., & Lee, M.-Y. (2020). Artificial Neural Network and Adaptive Neuro-Fuzzy Interface System Modelling to Predict Thermal Performances of Thermoelectric Generator for Waste Heat Recovery. Symmetry, 12(2), 259. https://doi.org/10.3390/sym12020259






