Abstract
Within the earlier developed high-energy--Hamiltonian approach to describe graphene-like materials, the simulations of non-Abelian Zak phases and band structure of the quasi-relativistic graphene model with a number of flavors have been performed in approximations with and without gauge fields (flavors). It has been shown that a Zak-phases set for non-Abelian Majorana-like excitations (modes) in Dirac valleys of the quasi-relativistic graphene model is the cyclic group . This group is deformed into at sufficiently high momenta due to deconfinement of the modes. Since the deconfinement removes the degeneracy of the eightfolding valleys, Weyl nodes and antinodes emerge. We offer that a Majorana-like mass term of the quasi-relativistic model affects the graphene band structure in the following way. Firstly, the inverse symmetry emerges in the graphene model with Majorana-like mass term, and secondly the mass term shifts the location of Weyl nodes and antinodes into the region of higher energies.
PACS:
73.22.-f; 81.05.Bx
1. Introduction
Currently, topological graphene-like materials attract great attention due to possibility of implementing robust quantum computing on quantum devices constructed from such materials. Types of topological defects in the band structure of graphene-like materials are diverse, namely Weyl nodes and antinodes [1], Weyl nodal (antinodal) lines [2], drumhead-like surface flat bands [3,4], and zero-energy Majorana modes [5], even though the crystal structure of all topological materials is either hexagonal or almost hexagonal [6]. Establishing a mechanism of the influence of the degree of symmetry breaking due to spin–orbit coupling (SOC) on the type of the band-structure defectiveness is a challenge, but it is extremely important for applications of topological materials. A hindrance to solving this problem lies in impossibility to construct maximally localized Wannier orbitals in a lattice site i for a band structure with topological defects owing to the presence of the defect in the site i. Majorana end states were implemented as subgap levels of an atomic chain on the surface of a p-wave superconductor. This system is named a Kitaev’s chain [7,8]. These subgap levels are similar to Shockley or Shiba states bound to electric or magnetic end impurities (see [9,10] and references therein) but Shockley or Shiba states do not possess topological stability of vortex states. By connecting three Kitaev’s chains into Y-like form and tuning interactions , of the edge Majorana fermions in that Y-trijunction, it is possible to force two Majorana midgap states from three ones at the ends of the trijunction to alternatively change their positions [11]. The main problem of the Kitaev’s-chain network is the broadening of Majorana chain-end states in the place of contacts between the chains and, respectively, the small lifetime of Majorana quasi-particle excitations in the Kitaev’s chain. As it turns out [12], an interface between a topological isolator (TI) and a s-wave superconductor can be described by the same system of equations as for the Kitaev’s chain. Zero-energy Weyl nodes and anti-nodes (monopoles) in TI-surface band structure play a role of Majorana-vortex cores, and Cooper pairs are a “feathering” of these cores. The advantage of the implementation of motionless Majorane-like excitations on the edge of metallic TI-surfaces is an opportunity to realize an interchanging (one-dimensional braiding) of Majorana particles among themselves on a contactless Y-shaped Josephson junction, which increases the Majorana lifetime [13,14,15,16,17,18].
A chiral massless Dirac fermion (helical state) acquires a phase when bypassing on a closed loop due to its spin (helicity) pointing in the direction of motion. Two Majorana bound states, which form this Dirac fermion, are interchanged at such bypass by Dirac fermion and, respectively, one more interchange of the Majorana fermions is necessary to place them on their original positions. Therefore, at single interchange of Majorana particles, their wave function gains only half of the phase gained by the massless Dirac fermion the particles compose. Accordingly, on every Majorana fermion in the pair, the phase shift is accounted for, signifying that the statistics of the Majorana helical edge states is non-Abelian.
Graphene is a bipolar material for which there exists a diverging contribution of electron–electron interactions leading to a diverging behavior of Fermi velocity near the Dirac point K [19]. Therefore, graphene belongs to strongly correlated many-body systems. The electron is a complex fermion, thus, if one decomposes it into its real and imaginary parts, which would be Majorana fermions, they are rapidly re-mixed by electromagnetic interactions. However, such a decomposition could be reasonable for graphene because of the effective electrostatic screening. An imposition of strong SOC results in the appearance of Majorana-like excitations at the ends of a Fe atom chain on the surface of conventional superconductor composed of Pb atoms [20]. At the present time, there exist experimental signatures of graphene Majorana states in graphene-superconductor junctions without the need for SOC [5]. However, a Dirac-mass Kane–Mele-term [21] originating from non-zero SOC is a negligibly small one of order meV for graphene at K. A model of interacting spins , , of Dirac particles () on a honeycomb lattice may be mapped on free Majorana fermions hopping in a static gauge field W [22]. This model predicts suddenly topological phases of spin metals. However, in the Kitaev approach the problem of redefinition of the Majorana hopping and W of the magnetically ordered system into physical characteristics suitable for the description of pseudo-Dirac massless fermions in diamagnetic graphene was not solved. Another challenge in graphene physics is the problem of dynamical mass of graphene charge carriers that, for example, an Eliashberg self-consistent technique predicted an excitonic pairing in a graphene-like system with a number of physical flavors originating from a dynamic screening at low energy E in K [23]. The ab initio calculations predicted also a gapped band structure of two-dimensional graphite, although for 3D graphite it is known as gapless one [24]. However, in accordance with experimental data [19], although is diverged near K, no insulating phases emerge at E as low as 0.1 meV. Thus, the mass term for graphene cannot be of the Dirac type. Constructions of a mass term preserving chiral symmetry for a graphene model of Majorana type are absent.
In relativistic quantum mechanics, a quasi-relativistic approximation is known (see, e.g., the review in [25]) as the following procedure. In terms of the bispinor composed of two spinor components , the Dirac equation reads
where the operator is written as
with being a vector of Pauli matrixes, the momentum, m the electron mass, c the speed of light, and V some scalar potential. If one is interested in electronic states only, the relation between upper and lower bispinor components can be written in the form , with being a solution of the equation . One can omit the last two terms on the right-hand side of the last equation and obtain . In this case, the lower bispinor () component is of the order of the upper () one, which corresponds to the use of the leading term in series expansion on for the original systems and is known as quasi-relativistic theory or limit.
Our model of graphene originates from the genuine relativistic approach and is derived by this procedure in a self-consistent Dirac–Hartree–Fock field approximation [26,27,28,29,30]. We called this model the quasi-relativistic graphene model. A two-dimensional (2D) graphene model with pseudo-Dirac massless fermions as charge carriers is originated from the Wallace’s model of three-dimensional (3D) graphite [31] derived within non-relativistic quantum mechanics. The projection of the 3D-model into the pseudo-Dirac 2D-model predicts the values of electrical and magnetic characteristics that differ by two orders of magnitude from their experimental values, and in this model there is no universal limit for the low-frequency conductivity of graphene. Moreover, the pseudo-Dirac model does not describe experimental signatures of graphene Majorana states in graphene-superconductor junctions without the need for SOC [5]. It is also known [32] that the usage of non-relativistic approaches fails when applied to ab initio band simulations of solids. This is why all software in this field (see, e.g., [33,34,35]) employs the genuine Dirac equation and appropriate field theory variants. Thus, the pseudo-Dirac model needs substantial extension and generalization. We offer our quasi-relativistic graphene model as such a generalization. An analysis of Majorana-like graphene models becomes relevant in connection with the discovery of an unconventional superconductivity for twisted bilayer graphene at a very small angle of rotation of one monoatomic layer (monolayer) relative to another one [36]. A feature of the unconventional superconductivity is accompanying insulator states such as flat bands being Dirac cone-like bands with zero Fermi velocity at . In the case of graphene monolayer without strain, a phenomenological tight-binding model of the graphene superlattice with interlayer interaction of the graphite type predicts such flat bands at only [37] but unfortunately parameters of this non-realistic model cannot be adapted to experimental data.
In this paper, we investigate a vortex dynamics of charge carriers in the quasi-relativistic graphene model and its approximations using a high-energy Hamiltonian. The Wilson non-closed loop method to characterize band-structure topology through holonomy is used to study the relationship between the topology of the Brillouin zone, the symmetry breaking of the band structure, spin–orbital coupling, and different types of resonances in the graphene model.
2. Theoretical Background
Graphene is a 2D semimetal hexagonal monolayer, which is comprised of two trigonal sublattices . Semi-metallicity of graphene is provided by delocalization of -electron orbitals on a hexagonal crystal cell. Since the energies of relativistic terms and of a hydrogen-like atom are equal to each other [38], there is an indirect exchange through d-electron states to break a dimer. Therefore, a quasi-relativistic model monolayer graphene, besides the configuration with three dimers per the cell, also has a configuration with two dimers and one broken conjugate double bond per the cell. The high-energy Hamiltonian of a quasi-particle in the sublattice, for example A, reads
where is a spinor wave function (vector in the Hilbert space); is the 2D vector of the Pauli matrixes; is the 2D momentum operator; and are relativistic exchange operators for sublattices , respectively; is an unconventional Majorana-like mass term for a quasi-particle in the sublattice A; is a spinor wave function of quasi-particle in the sublattice B; and denotes the graphene Dirac point (valley) () in the Brillouin zone. A small term in Equation (1) is a spin–valley–current coupling. One can see that the term with conventional mass in Equation (1) is absent. Since the exchange operators transform a wave function from sublattice A into B and vice versa in accord with Equation (2), the following expression holds
Since the latter can be written inthe form , one gets the following property of the exchange operator matrix:
with some parameter . Due to the property in Equation (3), one can transform Equation (1) into the following form:
Let us introduce the following notations
Then, Equation (4) can be rewritten as
Here, is the Fermi velocity operator: ,
Equation (6) formally is similar to the massless Dirac fermion equation.
Let us prove that the mass operators remain invariant under the action of exchange interactions in Equation (7), namely, the transformed mass operator in Equation (7) for an electron (hole) in the Majorana mode represents itself the mass operator for a hole (electron) in this mode. Using the property in Equation (3), we transform Equation (1) an another way:
Then, due to the property in Equation (3), and by the following notations
Equation (8) can be rewritten as
Since the operator acts on vectors and , belonging to the same Hilbert space, the operator represents itself a result of the transformation in Equation (7):
Owing to the invariance of the operators with respect to the transformation in Equation (7), their eigenvalues are dynamical masses of the Dirac fermions, which gain in the Majorana-like superposition (Majorana electron–hole pair).
An equation similar to Equation (10) can be also written for the sublattice B. As a result, one gets the equations of motion for a Majorana bispinor [26,28]:
3. Band Structure and Non-Abelian Zak Phase Simulations
The system of Equations (12) and (13) for the stationary case can be approximated by a Dirac-like equation with a “Majorana-force” correction in the following way. The operator in Equation (12) plays a role of Fermi velocity as well: . Then, one can assume that there is the following expansion up to a normalization constant :
where denotes the commutator, . Substituting Equations (2) and (14) into the right-hand side of Equation (13), one gets the Dirac-like equation with a “Majorana-force” correction of an order of energy difference of quantum exchange for two graphene sublattices:
where . The exchange interaction term is determined as [30]
Here, interaction ()-matrices and are gauge fields (or components of a gauge field). Vector-potentials for these gauge fields are determined by the phases and , of -electron wave functions and , , respectively, for which the exchange interaction (Equation (16)) accounting for the nearest lattice neighbors for a tight-binding approximation reads [26,27,30]
where the origin of the reference frame is located at a given site on the sublattice A (B); is the three-dimensional (3D) Coulomb potential; designations , , refer to atomic orbitals of p-electrons with 3D radius-vectors in the neighbor lattice sites ; and nearest to the reference site; is the p-electron 3D-radius-vector. Elements of the matrices and include bilinear combinations of the wave functions so that their phases and , enter into and from Equations () and () in the form
Therefore, an effective number N of flavors in our gauge field theory is equal to 3. Then, owing to translational symmetry, we determine the gauge fields in Equation (21) in the following form:
Substituting the relative phases in Equation (22) of particles and holes into Equation (19), one gets the exchange interaction operator
with following matrix elements:
where , ; , , . There are similar formulas for .
Now, neglecting the mass term, we can find the solution of Equation (15) by the successive approximation technique as:
According to Equation (22), eigenvalues of Equation (27) as well as eigenvalues of the Hamiltonian in Equations (12) and (13) are functionals of . To eliminate arbitrariness in the choice of phase factors , one needs a gauge condition for the gauge fields. The eigenvalues are real because the system of Equations (12) and (13) is transformed to the Klein–Gordon–Fock equation [28]. Therefore, we impose the gauge condition as a requirement on the absence of imaginary parts in the eigenvalues of the Hamiltonian in Equations (12) and (13):
To satisfy the condition in Equation (28) in the momentum space, we minimize a function , the absolute minimum of which coincides with the solution of the system in Equation (28). For the mass case, band structures for the sublattice Hamiltonians are the same. Therefore, neglecting the mass term, the cost function is . For the non-zero mass case, we assume the same form of the function f due to smallness of the mass correction.
Topological defect pushes out a charge carrier from its location. The operator of this non-zero displacement presents a projected position operator with the projection operator for the occupied subspace of states . Here, N is a number of occupied bands, is a momentum. Eigenvalues of are called Zak phase [39]. The Zak phase coincides with a phase
of a Wilson loop being a path-ordered (T) exponential with the integral over a closed contour [40]. Let us discretize the Wilson loop by Wilson lines :
Here, momenta , form a sequence of the points on a curve (ordered path), connecting initial and final points in the Brillouin zone: , and ; , are eigenstates of a model Hamiltonian. We perform the integration by parts and then expand the matrix element , of the Wilson line with Bloch waves for our model hamiltonian into series in terms of :
where is a Dirac -function, is the Kronecker symbol, and . Taking into account that and a band-crossing condition
in Equation (31), one gets
In our calculation of Equations (30) and (32) for the Hamiltonian without the mass term, the number N of bands is equal to four (): two electron and hole valent bands and two electron and hole conduction bands. We consider the parallel transport of filled Bloch waves around momentum loops because the basis of Wannier functions generated only by the occupied Bloch eigenstates. A global characterization of all Dirac touching is possible with a non-Abelian Zak invariant defined over a noncontractible momentum loop [39]. Therefore, instead the closed contour, we take a curve being one side of the equilateral triangle of variable size (defined by the value of component of the wavevector ) with the coordinate system origin in the Dirac -point. A change in the flux of the non-Abelian gauge field along the non-closed oriented loop in the occupied half Brillouin zone of graphene is shown in Figure 1a. The N phases are defined then as arguments of the eigenvalues of the Wilson loop. One chooses () that a “noise” in output data is sufficiently small to observe discrete values of Zak phases.
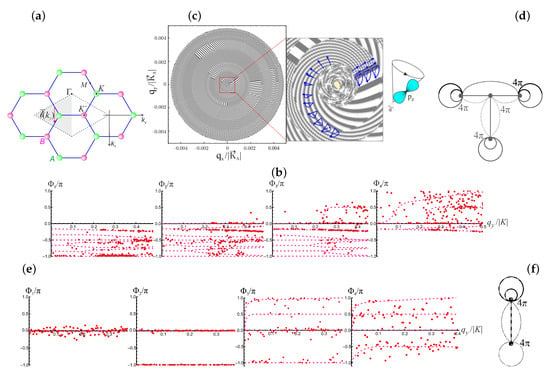
Figure 1.
(a) Definition of a change in the flux of non-Abelian gauge field along the paths to define Wilson loops. A rhombic first Brillouin zone (BZ) of the honeycomb lattice consisting of two triangular sublattices A (green) and B (red) is labelled with a dashed line. High-symmetry points are . Occupied half-BZ is gray shaded. A reference point of coordinates is in . (b,e) Non-Abelian phases of the Wilson-loop eigenvalues in the units of at non-zero (b) and zero (e) gauge fields. (c) A spin–orbit texture of the bands on momentum scales in contour plots and a model vortex of the precessing orbitals in inset to (d). The angle is a variable precession angle of p-orbital. (d,f) Sketch of topological defects for the quasi-relativistic graphene model at non-zero (d) and zero (f) gauge fields; a bypass over each contour in (d,f) gives phase shift value ; .
4. Results and Discussion
Simulation of the Zak phases was performed for three graphene models: the first one is a massless pseudo-Dirac fermion model [8]; the second one is our quasi-relativistic graphene model in an approximation of zero gauge field; and the third model is the same but accounting for the non-zero gauge field. The results are presented in Table 1 and Figure 1b,e.

Table 1.
Topological characterization of the graphene models: Model 1 is the massless pseudo-Dirac fermion model, and Models 2 and 3 are the quasi-relativistic graphene model in the approximations of zero- and nonzero-gauge field, respectively. the second column from the left: arguments of the Wilson-loop eigenvalues .
Up to finite accuracy of the numeric method, we get a discrete set of obtained values of phases for considered models. For the massless pseudo-Dirac model, arguments of the Wilson-loop eigenvalues are equal to and are multipliers of . Hence, due to hexagonal symmetry of the lattice, the first model is a topologically trivial one.
For the second model, there exist two different sets of the Wilson-loop-arguments eigenvalues, namely one set in the vicinity of the Dirac point and a second one at sufficiently high values of wavevectors (see Figure 1e). This testifies the topological non-triviality of the second model. In the vicinity of , the arguments of the Wilson-loop eigenvalues form the same cyclic group as for the case of the massless pseudo-Dirac model. Additional values of the Wilson-loop arguments and two cyclic groups with generators or , respectively, are at values of higher than . The observed deformation of the cyclic group to is a consequence of the increase in spin–orbit coupling at the high . The strong spin–orbital coupling lifts the degeneration on pseudospin. Meanwhile, Weyl node and antinode emerge. Since the cyclic group is , the Weyl node (antinode) should be a double defect (in the form of two singular points). Only in this case, as shown in Figure 1f, bypassing the doubled node (antinode) along a contour with a double rotation on an angle gives the phase shift for the wave function by . Since the Weyl node (antinode), similar to any quantum fermion state, is a Kramers doublet, its doubling is a result of splitting spin degeneration owing to the spin–orbital-coupling breaking of time-reversal symmetry. However, resulting homotopy group protects the electron–hole symmetry for the approximation with zero gauge field.
As simulation results for the third model demonstrate in Figure 1b, paths with the topological Zak phases, multiple to , constitute the cyclic groups in the vicinity of at small momenta and additional Majorana Wilson-loop-arguments eigenvalues, multiple to , appear at high . These results testify that the quasi-relativistic graphene model is a topologically nontrivial one in the entire energy range. A contour plot in Figure 1c displays the vortex distribution of levels of equal energy in the zone. The vorticity of the distribution around defects originates a band dichroism. Simulations discovers eight right- and left-handed vortices on the surfaces of electron and hole bands, as shown in Figure 2a. A rotation is equivalent to a rotation due to hexagonal symmetry and, correspondingly, the electron and hole configurations in the momentum space are orthogonal to each other. A schematic representation of this electron–hole configuration in the form of a T-shaped trijunction of four peculiar points (topological defects) is presented in Figure 1d. An atomic chain with two topological defects at the ends implements a Majorana particle. Therefore, the trijunction is formed by three Majorana particles (modes) produced in flavor states, a number of flavors . The total angular momentum of such a Majorana-like excitation is equal to with the absolute value . Here, is angular momentum of ith Majorana particle, . Majorana and antiMajorana states (excitations) with differ by the projections of the total angular momentum . Therefore, the Majorana and antiMajorana excitations confined in the Dirac point by hexagonal symmetry are fourth-fold degenerated. Fusions and fissions of the configuration of three Majorana modes with are represented in an inset to Figure 1c as precession of the p-electron orbital with a variable procession angle and the total angular momentum . The cyclic group existing at small momenta q, testifies that hexagonal symmetry confines the Majorana mode in the vicinity of the Dirac point owing to small spin–orbital coupling. We associate each component of the Majorana (antiMajorana) excitation with the projection one of these vortex states of the band structure. Then, the coincidence of the four left-handed (right-handed) bands at small q, implies the degeneracy of these vortices in the . We call these vortex states subreplicas.
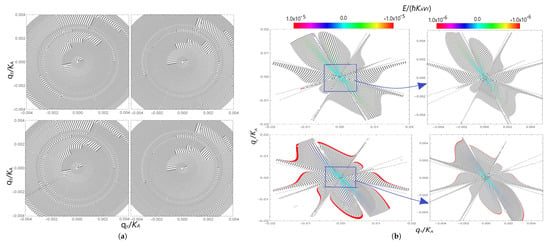
Figure 2.
(a) A vortex texture in contour plots of electron (left) and hole (right) bands calculated without (top) and with (bottom) Majorana-like mass term on momentum scales . (b) A mass correction to the hole (top) and electron (bottom) bands on momentum scales . Contour plots in (b) are displayed in color gradations.
Increasing spin–orbit interaction at high splits the degeneracy of vortex states on and, correspondingly, the degeneracy of the subreplicas. The appearance of eight subreplicas is shown in Figure 2a and Figure 3. This octal splitting of conical bands represents a phenomenon of Majorana particles deconfinement. The deconfinement violates the hexagonal symmetry that SOC deforms the cyclic group with the generator to with the generator . Zak phase values, multiple to , appear at momenta , as shown in Figure 1b. A configuration of four nondegenerate vortices is equivalent to a T-shaped trijunction from three deconfined Majorana modes or anti-modes. As shown in Figure 1d, the bypass of the T-shaped trijunction along a contour with four turns by an angle of gives a phase shift for the wave function by , while at bypass of a single vortex defect the wave function acquires the phase . The deformation is accompanied by subsequent flatting of the bands that the Fermi velocity trends to 0, as Figure 3 demonstrates. Since the Majorana “force” Equation (27) diverges for the flat bands, four vortices in the T-trijunction are always linked at high energies, but they become asymptotically free in the vicinity of the Dirac points (). The splitting of the Dirac cones by strong SOC into the non-coinciding four electron and four hole subreplicas implies the break of electron–hole symmetry. This violation is revealed as an appearance of additional topological Zak phases equal to and, correspondingly, an additional cyclic group at values of momentum . Resonances and antiresonances that are non-invariant with respect to change in sign of the energy band E of the form are observed in the band structure (see Figure 3) as a manifestation of broken electron–hole symmetry due to strong SOC. Vortices are created in pairs. Therefore, one can assume that the observed resonances and anti-resonances are, respectively, the cores (sinks) and anti-cores (sources) of the vortices remaining after the destruction of their pair at the spin–orbital coupling. Such topological defects are monopoles and are called Weyl nodes and antinodes. Since the homotopy group is , the Weyl nodes (antinodes) in the quasi-relativistic graphene model are doubled. Since spin states are Kramers doublets, this doubling can be explained by violation of the symmetry of time reversal, which splits the Kramers degeneracy on spin of Weyl nodes and antinodes.
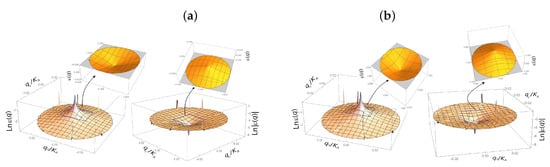
Figure 3.
Band structure calculated with (a) and without (b) Majorana-like mass term on momentum scale for quasi-relativistic model of graphene with non-zero gauge field.
We also investigated effects of the Majorana-like mass mass operator (). Hamiltonian of our graphene model holds the Majorana-like mass term . Therefore, to reveal violations of chiral symmetry by , the band structures for the Hamiltonian of the graphene model are compared with and without the mass term. Direct numerical calculation replacing with the constant near Dirac point showed that the parameter entering Equation (3) depends on the absolute value of the wave vector. Therefore, since , is a small term of order at . It is equal to zero in because in . The Majorana-like mass correction to energy hole and electron bands, presented in Figure 2b, is very small, of the order , and is vanishing in . According to numerical results presented in Figure 2a, band structures are chiral for both graphene models with and without the mass term. As Figure 2b demonstrates, the mass term leads to the appearance of the center of inversion, preserving the Dirac touching in the band structure for the Hamiltonian with . Since vorticity is also observed for the band structure for the Hamiltonian with , at least one of the eigenvalues of the mass term gives a chiral one-particle state. Since chiral and non-chiral one-particle states are mixed by the mass term, this is sufficient for the existence of a band dichroism. Since there is the cyclic group with generator at high energy, the strong spin–orbital coupling lifts the degeneration on pseudospin and time-reversal symmetry is broken. Meanwhile, Weyl node and antinode emerge (Figure 3a). Comparing the band structures calculated with and without in Figure 3, the mass-term shifts the location of Weyl nodes and antinodes into the region of higher energies. Thus, we find that band inversion leads to a class of topological, gapless phases.
5. Conclusions
Our finding is a graphene model with valleys and bands in a vortex state. Four vortex defects form three Majorana fermions confined by the hexagonal symmetry. Deconfinement of the Majorana modes stems from a spin–orbital coupling. We present a new method to construct a mapping between spectra of Wilson non-closed loop over the first Brillouin zone and vortex bands. We prove that is a homotopy group of the momentum space in the Dirac corners with the confined Majorana modes. The spin–orbital coupling deforms into of the deconfined Majorana modes and leads to an emergence of Weyl nodes. We predict that there is a very small nonzero Majorana mass term of the order of in the graphene model. The Majorana mass term keeping Dirac-points chiral symmetry tends to frustrate only one of two pairs of left-handed and right-handed vortex modes. However, mixing the mass term remains the resulting bands in a helical state signifying that this term keeps the chiral symmetry of the model.
Finally, we discuss the possibility to realize a topological Majorana band structure of the diamagnetic honeycomb graphene-like system. An experimental observation of such systems with fine effects that stem from the Majorana nature of quasi-particle excitations demands a new advanced high-accuracy experimental setup.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded within the State Program of Scientific Researches “Convergence-2020” of the Republic of Belarus
Conflicts of Interest
Both authors declare no conflict of interest.
References
- Lu, H.-Z.; Shen, S.-Q. Quantum transport in topological semimetals under magnetic fields. Front. Phys. 2017, 12, 127201. [Google Scholar] [CrossRef]
- Bian, G.; Chang, T.-R.; Sankar, R.; Xu, S.-Y.; Zheng, H.; Neupert, T.; Chiu, C.-K.; Huang, S.-M.; Chang, G.; Belopolski, I.; et al. Topological nodal-line fermions in spin-orbit metal PbTaSe2. Nat. Commun. 2016, 7, 10556. [Google Scholar] [CrossRef]
- Muechler, L.; Alexandradinata, A.; Neupert, T.; Car, R. Topological Nonsymmorphic Metals from Band Inversion. Phys. Rev. X 2016, 6, 041069. [Google Scholar] [CrossRef]
- Lu, J.-L.; Luo, W.; Li, X.-Y.; Yang, S.-Q.; Cao, J.-X.; Gong, X.-G.; Xiang, H.-J. Two-Dimensional Node-Line Semimetals in a Honeycomb-Kagome Lattice. Chin. Phys. Lett. 2017, 34, 057302. [Google Scholar] [CrossRef]
- San-Jose, P.; Lado, J.L.; Aguado, R.; Guinea, F.; Fernández-Rossier, J. Majorana Zero Modes in Graphene. Phys. Rev. X 2015, 5, 041042. [Google Scholar] [CrossRef]
- Sangwan, V.K.; Hersam, M.C. Electronic Transport in Two-Dimensional Materials. Annu. Rev. Phys. Chem. 2018, 69, 299–325. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys. Uspekhi. 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Semenoff, G.W.; Sodano, P. Stretched quantum states emerging from a Majorana medium. J. Phys. B 2007, 40, 1479–1488. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Search for Majorana Fermions in Superconductors. Annu. Rev. Condens. Matt. Phys. 2013, 4, 113–136. [Google Scholar] [CrossRef]
- Peng, Y.; Pientka, F.; Vinkler-Aviv, Y.; Glazman, L.I.; von Oppen, F. Robust Majorana Conductance Peaks for a Superconducting Lead. Phys. Rev. Lett. 2015, 115, 266804. [Google Scholar] [CrossRef]
- Van Heck, B.; Akhmerov, A.R.; Hassler, F.; Burrello, M.; Beenakker, C.W.J. Coulomb-assisted Braiding of Majorana Fermions in a Josephson Junction Array. New J. Phys. 2012, 14, 035019. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed]
- Ge, M.-L.; Yu, L.-W. Yang-Baxter equation, Majorana fermions and three body entangling states. Int. J. Mod. Phys. B 2014, 28, 1450089. [Google Scholar] [CrossRef]
- Nayak, C.; Wilczek, F. 2n-quasihole states realize 2n-1-dimensional spinor braiding statistics in paired quantum Hall states. Nucl. Phys. B 1996, 479, 529–553. [Google Scholar] [CrossRef]
- Ivanov, D. Non-Abelian Statistics of Half-Quantum Vortices in p -Wave Superconductors. Phys. Rev. Lett. 2001, 86, 268. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef]
- Von Oppen, F.; Peng, Y.; Pientka, F. Topological Superconducting Phases in One Dimension; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Elias, D.C.; Gorbachev, R.V.; Mayorov, A.S.; Morozov, S.V.; Zhukov, A.A.; Blake, P.; Ponomarenko, L.A.; Grigorieva, I.V.; Novoselov, K.S.; Guinea, F.; et al. Dirac cones reshaped by interaction effects in suspended graphene. Nat. Phys. 2012, 8, 172. [Google Scholar] [CrossRef]
- Nadj-Perge, S.; Drozdov, I.K.; Li, J.; Chen, H.; Jeon, S.; Seo, J.; MacDonald, A.H.; Bernevig, A.; Yazdani, A. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 2014, 346, 602–607. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef]
- Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006, 321, 2–111. [Google Scholar] [CrossRef]
- Wang, J.-R.; Liu, G.-Z. Eliashberg theory of excitonic insulating transition in graphene. J. Phys. Condens. Matter. 2011, 23, 155602. [Google Scholar] [CrossRef] [PubMed]
- Grushevskaya, G.V.; Komarov, L.I.; Gurskii, L.I. Exchange and correlation interactions and band structure of non-close-packed solids. Phys. Solid State 1998, 40, 1802–1805. [Google Scholar] [CrossRef]
- Kutzelnigg, W.; Liu, W. Quasirelativistic theory I. Theory in terms of a quasi-relativistic operator. Int. Interface Chem. Phys. 2006, 104, 2225–2240. [Google Scholar] [CrossRef]
- Grushevskaya, H.V.; Krylov, G. Semimetals with Fermi Velocity Affected by Exchange Interactions: Two Dimensional Majorana Charge Carriers. Int. J. Nonlinear Phenom. Complex Syst. 2015, 18, 266–283. [Google Scholar]
- Grushevskaya, H.V.; Krylov, G.G. Chapter 9. Electronic Structure and Transport in Graphene: QuasiRelativistic Dirac-Hartree-Fock Self-Consistent Field Approximation. In Graphene Science Handbook: Electrical and Optical Properties; Aliofkhazraei, M., Ali, N., Milne, W.I., Ozkan, C.S., Mitura, S., Gervasoni, J.L., Eds.; CRC Press: Boca Raton, FL, USA, 2016; Volume 3, pp. 117–132. [Google Scholar]
- Grushevskaya, H.V.; Krylov, G.G. Massless Majorana-Like Charged Carriers in Two-Dimensional Semimetals. Symmetry 2016, 8, 60. [Google Scholar] [CrossRef]
- Grushevskaya, H.V.; Krylov, G.G. Non-Abelian Majorana-Like Quasi-Excitation in Dirac Materials. Int. J. Nonlinear Phenom. Complex Syst. 2017, 20, 153–169. [Google Scholar]
- Grushevskaya, H.V.; Krylov, G.G.; Gaisyonok, V.A.; Serow, D.V. Symmetry of Model N = 3 for Graphene with Charged Pseudo-Excitons. Int. J. Nonlinear Phenom. Complex Syst. 2015, 18, 81–98. [Google Scholar]
- Wallace, P.R. The Band Theory of Graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Eschrig, H.; Richter, M.; Opahle, I. Relativistic Solid State Calculations. Theor. Comput. Chem. 2004, 13, 723–776. [Google Scholar]
- Gonze, X.; Beuken, J.-M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.-M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties: The ABINIT software project. Comput. Mat. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S.B. Full-Potential, Linearized Augmented Plane Wave Programs for Crystalline Systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- WIEN2k Package. Available online: http://www.wien2k.at/index.html (accessed on 20 January 2020).
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. [Google Scholar] [CrossRef] [PubMed]
- Bistritzer, R.; MacDonald, A.H. Moiré bands in twisted double-layer graphene. Proc. Natl. Acad. Sci. USA 2011, 108, 12233. [Google Scholar] [CrossRef]
- Fock, V.A. Foundations of Quantum Mechanics; Science Publishing Company: Moscow, Russia, 1976. (In Russian) [Google Scholar]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef]
- Alexandradinata, A.; Dai, X.; Bernevig, B.A. Wilson-loop characterization of inversion-symmetric topological insulators. Phys. Rev. 2014, B89, 155114. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).