Abstract
The objective of this study was to investigate the power generation, efficiency, and thermal stress of a thermoelectric module with leg geometry, material, segmentation, and two-stage arrangement. The effects of leg geometry, material, segmentation, and two-stage arrangement on maximum power, maximum efficiency, and maximum stress under various temperature differences and voltage load conditions were investigated. The performance parameters of the thermoelectric module were evaluated based on a numerical approach using ANSYS 19.1 commercial software. An analytical approach based on theoretical equations of the thermoelectric module was used to verify the accuracy and reliability of the numerical approach. The numerically predicted values for maximum power and maximum efficiency of the thermoelectric module were validated as ±5% and those for the maximum thermal stress of the thermoelectric module as ±7% with the corresponding calculated theoretical values. In addition, the predicted values of maximum power and maximum stress of the thermoelectric module were validated as ±2% and ±5%, respectively, with studies reported by Ma et al. and Al-Merbati et al. Of all the combinations, the single stage segmented arrangement with cylindrical leg geometry and SiGe+Bi2Te3 material was suggested as the best combination with maximum power of 0.73 W, maximum efficiency of 13.2%, and maximum thermal stress of 0.694 GPa.
1. Introduction
The world is currently facing global environmental challenges related to energy crisis, depletion of fossil fuel, and global warming [1,2]. To overcome these challenges, numerous research works have been carried out on high efficiency energy conversion technologies, as well as on the effective utilization of energy resources. One of the major sources of energy waste is automobile vehicles, where more than 50% of fuel energy is exhausted as heat [1]. Hence, the recovery and conversion of automobile exhaust heat using suitable conversion technology is a prerequisite in reducing fuel consumption as well as excessive demand of fossil fuel and natural resources. A thermoelectric generator is the most promising and convenient technology to convert waste heat into electrical energy [3].
Thermoelectric generators convert energy without degrading the environment. In addition, no mechanical moving parts are involved in the operation, and it is hence free of noise and vibration [4]. However, low conversion efficiency restricts their globalization in various application fields [5]. This low conversion efficiency is due to two major challenges: the lower Figure of Merit () of the thermoelectric materials and various equipment-level challenges. Several new materials with higher have been developed or the of existing materials improved to overcome the low conversion efficiency. However, research works on thermoelectric equipment level challenges are comparatively less, especially those that seek to improve the performance of thermoelectric generators.
The thermo-electrical and thermo-mechanical behavior of four thermoelectric leg geometries wer compared by Erturun et al. for the non-segmented and segmented configurations [1]. For effective utilization of heat sources or sinks that are circular in shape, Shen et al. presented the concept and superiority of an annular segmented thermoelectric generator over an annular non-segmented thermoelectric generator [2]. Jin predicted the thermal stresses and deformations induced in a multilayer thin film thermoelectric module by developing the laminate and strength of material models [3]. Ma et al. showed the superiority of the performance of a multifunctional gradient thermoelectric module over a single functional gradient thermoelectric module [4]. Patil et al. investigated the performance characteristics of symmetrical segmented as well as asymmetrical segmented thermoelectric generators for various geometrical parameters and operating conditions [5]. Erturun et al. reported the influence of rectangular and cylindrical leg geometries, leg height, leg width/diameter, and leg spacing on power output, conversion efficiency, and thermal stresses. The predicted power, efficiency, and stress values using statistical models show accuracies of 8.85%, 1.22%, and 6.56%, respectively, with the corresponding simulated values using finite element analysis [6]. Wu et al. numerically investigated the effects of thermoelectric leg spacing, thickness of conducting plate, thickness of soldering layers, and thickness of ceramic plate on the power, efficiency, and thermal stresses of a thermoelectric generator under various heat flux conditions [7]. Erturun et al. proved that, compared to cylindrical legs, cylindrical coaxial legs show 7% higher efficiency and 10% reduced stresses, whereas rotated cylindrical legs showed 1.2% lower stresses and 0.3% higher efficiency [8]. Jia et al. concluded that a linear-shaped thermoelectric generator had superior performance compared to conventional π shaped thermoelectric generators [9]. Yilbas et al. conducted thermal stress analysis on a thermoelectric module with horizontally arranged rectangular as well as tapered leg geometries. The tapered leg geometry showed a lower value of thermal stress compared to the rectangular leg geometry [10]. Merbati et al. proved that thermoelectric legs with the cold side area twice the area of the hot side show lower values of thermal stress with small improvement in thermoelectric performance [11]. Ali et al. investigated the power generation and conversion efficiency of pin-shaped thermoelectric legs for various temperature ratios as well as external load resistance ratios [12]. Erturun et al. compared six different thermoelectric leg geometries and concluded that the cylindrical legs show less thermal stress and deformation with enhancement in thermoelectric power generation [13]. Yilbas et al. showed improvements in the first and second law efficiencies of the thermoelectric generator with double tapered leg geometry under various conditions of external load resistance and temperature ratio [14]. Gao et al. conducted thermal stress analysis on a single stage thermoelectric generator constructed with cubical leg geometry and Bi2Te3 material in order to optimize its mechanical performance [15]. Two-stage and three-stage thermoelectric generators were designed by Zhang et al. [16] and Kanimba et al. [17] in order to achieve high conversion efficiency. Wilbrecht et al. presented a two-stage thermoelectric module with 44.2% higher efficiency and 22.8% lower power output compared to the single stage thermoelectric module for diesel electric locomotives [18]. For a cryogenic nitrogen-based waste cold heat recovery system, Weng et al. presented four two-layer cascaded thermoelectric generators with power generation of 0.93 W [19]. Chen et al. concluded that multistage thermoelectric generators show better performance than single stage thermoelectric generators [20]. Kaibe et al. developed a cascaded thermoelectric generator with conversion efficiency of 12.1% [21]. Thermoelectric generators arranged thermally as well as electrically in three different series/parallel connections were compared by Almeida et al. based on the equivalent [22]. Ibrahim et al. optimized the shape and length size of thermoelectric legs to enhance the power output and conversion efficiency of a thermoelectric generator [23]. Under steady state temperature conditions, Turenne et al. showed that thermal stresses in larger thermoelectric generators consisting of a number of thermoelectric modules were reduced due to the provision of soldering layers [24]. Kunal et al. showed the applicability of thermoelectric modules in waste heat recovery for lower power generation [25].
The comparison of single stage, segmented, and two-stage arrangements of thermoelectric modules with various combinations of leg geometries and materials based on their electrical and structural performances has not been explored yet. Therefore, the objective of this study was to numerically compare single stage, two-stage, and single stage segmented arrangements with three different leg geometries, namely, square prism legs, cylindrical legs, and trapezoidal legs, constructed with SiGe, Bi2Te3, and a combination of SiGe+Bi2Te3 materials in ANSYS 19.1 commercial software under various boundary conditions of temperature difference and voltage load. The comparison was made for maximum power, maximum efficiency, and maximum thermal stress. Additionally, in order to achieve higher power, higher efficiency, and lower thermal stress, an optimum configuration was suggested with leg geometry, material, segmentation, and two-stage arrangement.
2. Methodology
The single stage, two-stage, and single stage segmented arrangements with square prism legs, cylindrical legs, and trapezoidal legs, as well as SiGe, Bi2Te3, and combination of SiGe+Bi2Te3 materials were modelled in order to investigate the behavior of power generation, efficiency, and stress of the thermoelectric module. Modelled configurations of the thermoelectric module were analyzed numerically using the thermal-electric and static structure solvers of ANSYS 19.1 under various temperature difference and voltage load conditions.
2.1. Geometry and Material Specifications
Among the three arrangements of the thermoelectric module, the single stage was baseline and the two-stage and single stage segmented arrangements were considered as modified cases of the single stage arrangement. Figure 1 shows the schematic diagrams of the single stage, two-stage, and single stage segmented arrangements of a thermoelectric module. A thermoelectric module with single stage arrangement comprised of one pair of p- and n-type thermoelectric legs and three conducting plates. The two-stage arrangement comprised of two single stage arrangements, positioned in the form of steps with an intermediate plate between them. The two pairs of thermoelectric legs in the two-stage arrangement were either made up of the same or different materials [17,18], whereas the single stage segmented arrangement was obtained by dividing the thermoelectric legs of the single stage arrangement into two equal halves. The upper half was named Segment 1 and the lower half Segment 2. Both segments were made of different materials [1,4].
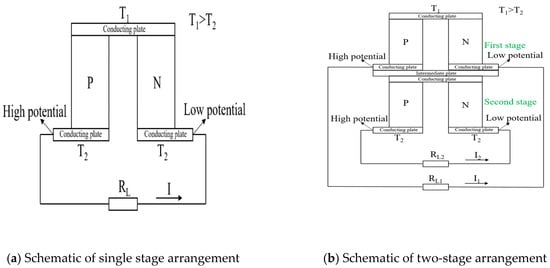
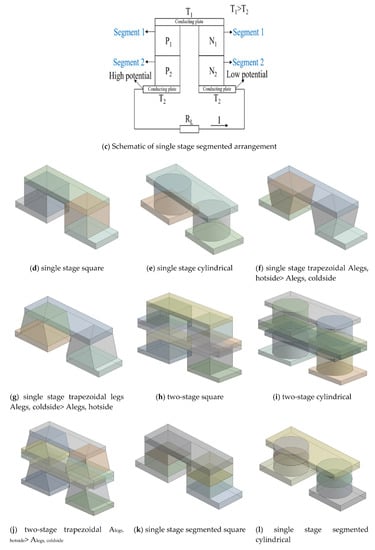
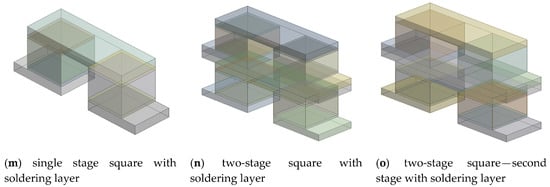
Figure 1.
Various configurations of the thermoelectric module with different combinations of arrangements and leg geometries.
The single stage and two-stage arrangements of the thermoelectric module were modelled with square prism legs, cylindrical legs, and trapezoidal legs; whereas the single stage segmented arrangement of the thermoelectric module was modelled with square prism and cylindrical leg geometries. The square prism legs were modelled with a 1.0 mm × 1.0 mm cross-section area (base area) and 0.96 mm height [4]. The spacing between the legs was kept constant at 0.8 mm [4]. By having the same cross-section area (base area), height, spacing, and volume as the square prism legs, cylindrical legs with 1.13 mm diameter were modelled. Trapezoidal legs with two different leg configurations, Alegs, coldside > Alegs, hotside and Alegs, hotside > Alegs, coldside were also modelled. The larger side area had dimensions of 1.2 mm × 1.0 mm and the smaller side area had dimensions of 0.8 mm × 1.0 mm. The trapezoidal legs were also modelled with same cross-section area, height, spacing, and volume as that of the square prism legs and cylindrical legs. However, the cross-section areas at the base of the square prism and cylindrical legs were identical to the cross-section area at the center of the trapezoidal legs. The spacing in square prism and cylindrical legs was constant for leg height, which varied in the trapezoidal legs with 0.8 mm spacing at the larger side area, continuously increasing toward the smaller side area. Each pair of p- and n- type thermoelectric legs was sandwiched between three copper conducting plates—two at the bottom and one at the top. The bottom two plates had the same dimensions: 1.4 mm × 1.4 mm area and 0.25 mm thickness. In order to construct various leg geometries with the same cross-section area, spacing, and volume, the area of the top conducting plate was kept different in each case. The top conducting plates with square prism legs, cylindrical legs, and trapezoidal legs with Alegs, hotside> Alegs, coldside and Alegs, coldside> Alegs, hotside had areas of 2.8 mm × 1.0 mm [4], 3.06 mm × 1.0 mm, 3.2 mm × 1.0 mm and 2.8 mm × 1.0 mm, respectively. However, the thickness of the top conducting plate was 0.25 mm in each case. The thermoelectric legs in the single stage configuration were either made of SiGe or Bi2Te3 material in the two-stage configurations; the thermoelectric legs of both the stages were made of SiGe or Bi2Te3 or a combination of SiGe+Bi2Te3 materials. For the segmented configuration, the thermoelectric legs were made of a combination of SiGe+Bi2Te3 materials. In the two-stage arrangement with combination of SiGe+Bi2Te3, the upper stage was made of SiGe material and the bottom stage of Bi2Te3 material. Similarly, in the segmented legs, the upper half was made of SiGe material and the lower half of Bi2Te3 material. For a combination of SiGe+Bi2Te3 materials, the SiGe material was used near the hot side and the Bi2Te3 material near the cold side due to their melting point temperatures. The configurations of the thermoelectric module were modelled and compared without considering soldering layers. However, in order to show the effect of soldering layers on the performance characteristics of the thermoelectric module, the single stage and two-stage arrangements with square prism legs and Bi2Te3 material as well as the two-stage arrangements with square prism legs and SiGe+Bi2Te3 material were modelled separately with the soldering layers. Soldering layers were provided between the thermoelectric legs and the hot plate as well as the thermoelectric legs and the cold plates with an area of 1.0 mm × 1.0 mm and thickness of 0.08 mm [4]. Hence, when soldering layers were provided in those cases, the height of the legs reduced to 0.8 mm. The soldering layers were made up of 63Sn-37Pb material. The two-stage configuration carried an intermediate plate between both the stages of the thermoelectric modules. An intermediate plate in each case of the two-stage arrangement was made up of ceramic material having an area of 3.6 mm × 1.0 mm and thickness of 0.25 mm. Figure 1 shows the various configurations of the thermoelectric module with different combinations of arrangements and leg geometries. Table 1 shows the material specifications used in the numerical analysis.

Table 1.
Material specifications used in the numerical analysis [1,4,26,27].
2.2. Mesh Convergence
Mesh dependency of maximum power, maximum efficiency, and maximum stress for the single stage thermoelectric module constructed with square prism legs and SiGe material is shown in Figure 2a–c, respectively. Maximum power and maximum efficiency showed negligible variations within 0.00008% and 0.00002%, respectively, for the selected mesh numbers; however, maximum stress showed a variation within 0.7% above mesh number of 115,401. Hence, the mesh with 115,401 nodes was selected for the single stage thermoelectric module with square prism legs and SiGe material to evaluate maximum power, maximum efficiency, as well as maximum stress. Similarly, mesh dependency was conducted for the thermoelectric module with combinations of leg geometries, materials, and arrangements. The number of nodes for the same arrangement of thermoelectric module with materials and leg geometries are the same, but the number of nodes for varying arrangements are different. Therefore, the number of nodes for various combinations of leg geometries and materials after mesh dependency was selected as 115,401 for the single stage arrangement, 540,706 for the two-stage arrangement, and 242,138 for the single stage segmented arrangement. Maximum power, maximum efficiency, and maximum stress were converged as 1% above 115,401 (number of nodes) for the single stage arrangement, 540,706 for the two-stage arrangement, and 242,138 for the single stage segmented arrangement of the thermoelectric module with leg geometries and materials [28]. Meshing for the single stage, two-stage, and segmented arrangements of the thermoelectric module with square prism leg geometry is shown in Figure 3a–c, respectively.
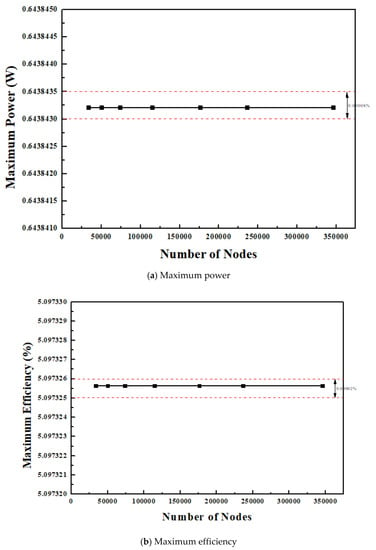
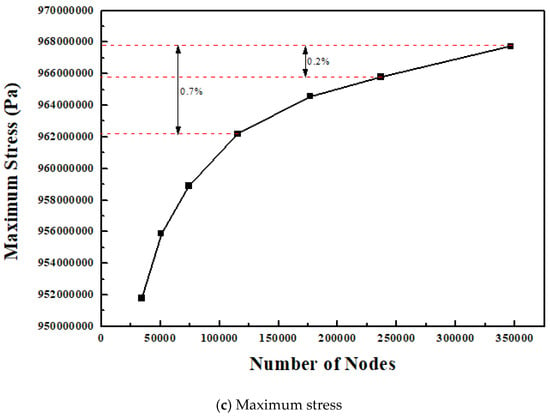
Figure 2.
Mesh independency test for (a) maximum power, (b) maximum efficiency, and (c) maximum stress.
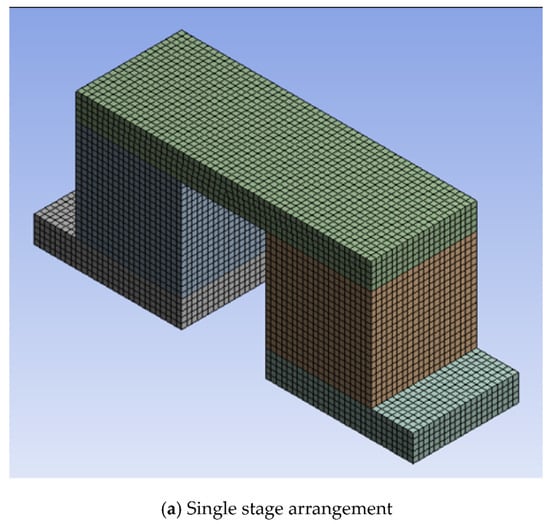
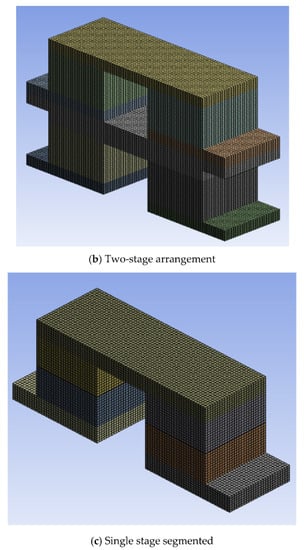
Figure 3.
Meshing for (a) single stage, (b) two-stage, and (c) single stage segmented arrangements with square prism leg geometries.
2.3. Boundary Conditions
In order to predict temperature distribution, power, conversion efficiency, and thermal stress, a thermoelectric module with various configurations was investigated under four boundary conditions, temperatures of hot and cold junctions, and voltage conditions at high and low potential sides. These boundary conditions were applied to the four different faces, as shown in Figure 1a–c. Temperature of the cold junction was kept constant at 20 °C and voltage at the low potential side was fixed at 0 V. Temperature of the hot junction and voltage at the high potential were not constant for the various configurations of the thermoelectric module. The boundary conditions for the hot junction temperature and the high potential voltage of leg geometries, materials, and arrangements were shown in Table 2. The hot side temperature was varied with a step size of 50 °C and the high potential voltage with a step size of 0.001 V. The maximum temperatures for the hot junction of various configurations were decided based on the melting point temperature of the corresponding material of construction. The high potential voltages varied from 0 V to voltage value at which current and power became zero. During variations in high potential voltages, there existed an optimum voltage, which showed maximum power and maximum efficiency. Optimum voltage values were different with different configurations of the thermoelectric module because the variation ranges of the voltage were different for different configurations. In addition, the optimum voltage varied with the temperature difference for each configuration of the thermoelectric module. Maximum power and maximum efficiency were simulated at the optimum voltage for each configuration of the thermoelectric module at different temperature difference conditions. Apart from these four boundary conditions, the convection boundary condition with heat transfer coefficient of 1 × 10−6 W/mm2 °C was applied to all remaining faces of each configuration of the thermoelectric module. The heat transfer from the surfaces with the convection boundary condition to its surroundings was negligible.

Table 2.
Boundary conditions used in the numerical analysis.
2.4. Governing Equations
The thermoelectric module works on the conjugate physics of thermal and electrical effects; hence, the coupled equations related to heat transfer (temperature), and the electric field has to be solved in order to analyze the thermoelectrical characteristics of the thermoelectric modules [4,29].
The thermoelectric coupling equations are presented as:
The term in Equation (1) represents volumetric joule heating.
For all configurations of the thermoelectric module, the thermoelectric coupling equations were solved in the thermal electric solver of ANSYS 19.1 software using the Galerkin finite element method and the corresponding boundary conditions in order to predict their thermoelectric behavior. The dimensionless displacement-strain relation needed to be solved in order to deal with the coupled thermal stress effect [7,30]:
The exact dimensionless relationship between the stress and the strain is presented in terms of the non-dimensional Jacobian matrix, which is deducted from Equations (3) and (4) using Newton’s method [7,30].
The non-symmetrical Jacobian matrix was solved in the static structure solver of ANSYS 19.1 software for all configurations of the thermoelectric module using the corresponding boundary conditions in order to predict the stress and strain generated within them.
2.5. Data Reduction
2.5.1. Physical Assumptions
The heat transfer from the hot side to the cold side of the thermoelectric module was caused by the conduction mode based on Fourier’s law using the inherent thermal properties of thermoelectric materials [4]. In addition, the conduction heat transfer along the thermoelectric legs was assumed to be one-dimensional. Heat transfer by the convection and the radiation modes was neglected [4]. The Seebeck and Peltier effects were taken into consideration in the present study. However, because the properties of materials are independent of temperature, the Thomson effect was neglected [12]. The thermal resistance of the conducting plates was also neglected [17].
2.5.2. Theoretical Analysis
In order to confirm the validity of the numerically predicted values of all performance characteristics of the thermoelectric module, the same performance characteristics were evaluated with a theoretical approach. The voltage at maximum power indicates optimum voltage and is calculated from Equation (6) [1,31,32]. Here, is the Seebeck coefficient, which is measured as the amount of thermoelectric voltage induced in any material due to temperature difference across that material. Each thermoelectric material has its own unique value of Seebeck coefficient. The Seebeck coefficient is also recognized as thermopower, thermoelectric power, and thermoelectric sensitivity:
Current depends on voltage, external load resistance, and internal resistance—Equation (7) [10]. is the condition to obtain optimal current wherein power is maximum [4,31]:
By manipulating the equations of and , the power equation was obtained. To obtain maximum power, constraint of was applied on the power equation, which gave the maximum power condition of . When is used in the power equation, Equation (8) is derived, which calculates the theoretical maximum power of the thermoelectric module [4,33]:
The theoretical maximum efficiency was calculated using Equation (9) under the same condition of in the theoretical efficiency equation of [4].
Resistance for square prism and cylindrical legs was calculated with Equation (10) [1].
Resistance of the trapezoidal legs cannot be calculated using Equation (10) because of the non-uniform cross-sectional area, which varies along the height of the thermoelectric legs. In the trapezoidal legs, an unevenly distributed area along the centerline of leg in height was converted to an evenly distributed area along the same centerline of the leg such that volume of the leg was same in both cases. Using the uniform area approach, the resistance for the trapezoidal legs was calculated with Equation (11) [11].
where RA is the ratio of the top side area of the trapezoidal leg () to the bottom side area of the trapezoidal leg () from Equation (12). is the equivalent uniform cross-section area of the trapezoidal leg:
In order to evaluate the maximum power and maximum efficiency of the thermoelectric module with the two-stage arrangement, it is necessary to derive the intermediate temperature between the two stages. This intermediate temperature can be obtained using voltage and temperature difference correlation equation of or . In the present study, the voltages applied to both the stages were different; hence, the equations were modified to and is the cold side temperature for the first stage, whereas is the hot side temperature of the second stage. The difference of shows the temperature loss due to the thermal resistance of the intermediate plate. The voltage boundary conditions applied to the high potential sides of both the stages were inserted in the corresponding voltage equations, obtaining and temperatures. These temperatures are used in Equations (8) and (9) in order to calculate the maximum power and maximum efficiency of the two-stage arrangement of the thermoelectric module. The segmented thermoelectric module consists of a combination of two materials in a single thermoelectric leg. Hence, the concept of equivalent Seebeck coefficient, equivalent resistivity, equivalent thermal conductivity, and equivalent Figure of Merit was used. Using this equivalent parameter concept, maximum power and maximum efficiency of the segmented thermoelectric module were calculated theoretically from the following equations [22,34]:
Thermal stress induced in the thermoelectric modules due to various temperature conditions, as well as due to mismatch in thermal properties of different materials, were calculated in the form of von Mises stress. This is the equivalent of the second deviatory stresses and computed using the following equation [1,3]:
Normal stress in the longitudinal direction can be calculated using the following equation. In this equation, normal strain = 0 and curvature K = 0 for the present study [3] are:
Thermal stress in the direction of temperature gradient can be calculated using the following equations, which are based on temperature difference and thermal properties.
Thermal strain is the ratio of thermal stress to the Young modulus, which is represented by Equation (21).
2.5.3. Numerical Analysis
Optimum voltage at maximum power and efficiency exists for the given temperature difference condition. The current corresponding to the optimum voltage is called optimum current. Using the simulated optimum current value corresponding to the employed optimum voltage value, the maximum power based on the numerical approach was calculated using Equation (22) [13].
The maximum efficiency was calculated using the numerical maximum power and heat absorbed [13]. The heat absorbed by the thermoelectric module from the hot side was simulated:
Similarly, thermal stress in terms of the equivalent stress or von-Mises stress was simulated from the numerical analysis with the static structure solver of ANSYS under various temperature conditions.
The maximum power and maximum efficiency were taken into consideration with the thermal-electric solver under various boundary conditions for the hot side and cold side temperatures, as well as voltage loads of the low and high potential sides. The thermal stress analysis of various configurations of the thermoelectric module was carried out in the static structure solver using the same temperature boundary conditions as the thermal-electric solver.
3. Results and Discussion
The results and discussion of this study includes the validation of numerically predicted values of maximum power, maximum efficiency, and maximum stress with data published by Ma et al. [4] and Al-Merbati et al. [11], as well as the values calculated using the theoretical approach. The comparison of different configurations of the thermoelectric module based on maximum power, maximum efficiency, and maximum stress is considered and the effect of soldering layers on the performance of the thermoelectric module is discussed.
3.1. Validation
The maximum power and maximum stress predicted in this study using ANSYS codes were validated with the corresponding data published by Ma et al. [4] and Al-Merbati et al. [11]. The validation of codes for maximum power and stress are presented and the comparison between the numerical and theoretical values of the various performance parameters are discussed.
3.1.1. Code Validation
The maximum power values evaluated in the present study using the thermal electric solver were found to be of the corresponding maximum power values reported by Ma et al. [4]. Similarly, the maximum stress and centerline stress values evaluated numerically in the present study using the static structure solver were validated at with the corresponding maximum stress and centerline stress values reported by Al-Merbati et al. [11]. The maximum power and maximum stress evaluated using ANSYS codes in the present study were found to be in the error range of with the corresponding data of Ma et al. [4] and Al-Merbati et al. [11]. Hence, the application of numerical approach using the validated ANSYS codes is justified for the further analysis. Figure 4a,b show the maximum power and stress validation with the corresponding previous studies of Ma et al. [4] and Al-Merbati et al. [11].
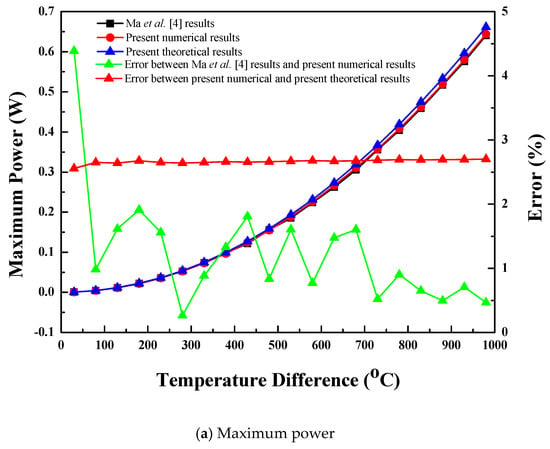
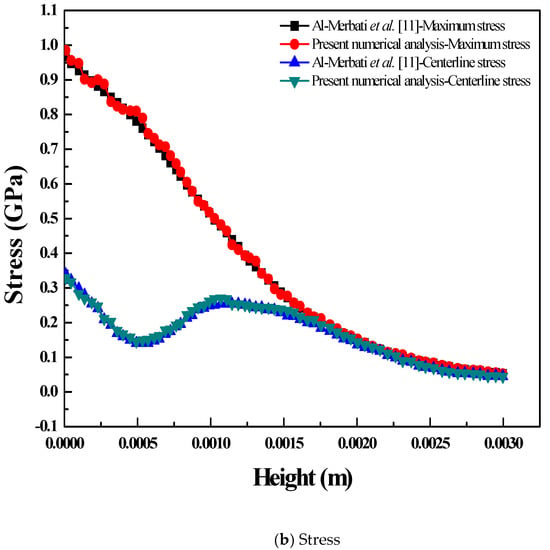
Figure 4.
Validation with previous study for (a) maximum power and (b) stress.
3.1.2. Validation of Numerical Results with Theoretical Results
The theoretical maximum power for the thermoelectric module with leg geometries, materials, and arrangements were calculated using correlations with Table 3. The maximum power for various configurations of the thermoelectric module were calculated using Equations (8) and (13). Similarly, the maximum efficiency for various configurations of the thermoelectric module was calculated theoretically using Equations (9) and (15). The simulated values of maximum power as well as maximum efficiency were calculated using Equations (22) and (23), respectively, which were compared with the corresponding theoretical values of maximum power and maximum efficiency. Figure 5a,b show the comparison between the numerical and theoretical results of maximum power and maximum efficiency, respectively, for the various configurations of the thermoelectric module. The numerical values of maximum power as well as maximum efficiency were validated with the corresponding theoretical values at ±5% with the entire temperature difference range for all configurations of the thermoelectric module.

Table 3.
Maximum power correlations derived for various leg geometries, materials, and arrangements.
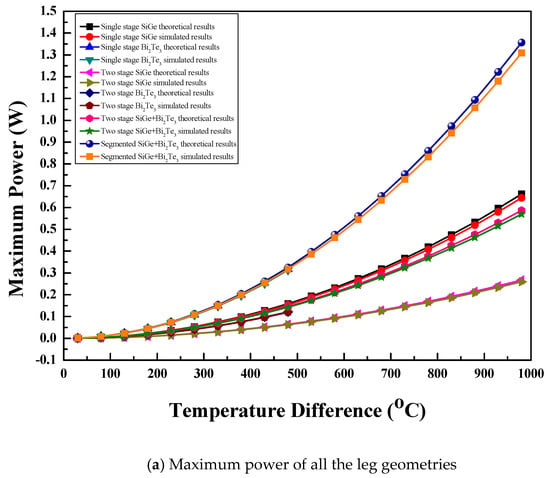
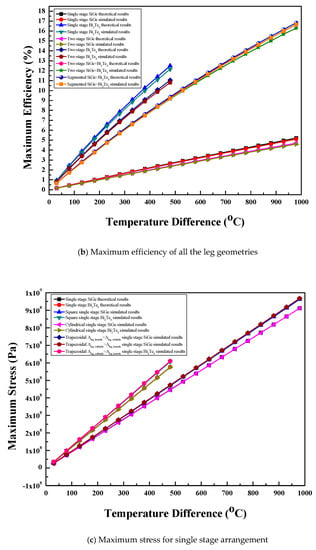
Figure 5.
Comparison of numerical and theoretical results for (a) maximum power, (b) maximum efficiency, and (c) maximum stress.
The maximum stress values were calculated theoretically using Equations (18)–(20). The calculated theoretical values of the maximum stress were compared with the corresponding predicted values. The comparison of theoretical and numerical results of maximum stress for the single stage arrangement of the thermoelectric module with three leg geometries and two materials is shown in Figure 5c. The equations show that the theoretical values of stress are not dependent on leg geometry; hence, the stress values are same for all leg geometries. However, different materials have different theoretical values of maximum stress. For the same material, the numerical stress values for cylindrical legs show closer agreement, whereas square prism legs as well as trapezoidal legs with two-area configurations show almost equal error with the corresponding theoretical stress values. For the same material, the numerically predicted maximum stress for all the leg geometries was found at ±7% with the corresponding theoretical stress with the entire temperature difference range.
3.2. Optimum Temperature
The single stage as well as two-stage arrangements with either SiGe or Bi2Te3 material were operated at maximum temperature differences of 980 °C and 480 °C, respectively, lower than the melting point temperature of SiGe or Bi2Te3 material. If the two-stage and segmented arrangements of the thermoelectric module with SiGe+Bi2Te3 material are operated at the maximum temperature difference of 980 °C, the operating temperature of SiGe material is below its melting point temperature, but the operating temperature of Bi2Te3 material is higher than its melting point temperature limit. Therefore, optimum temperature was introduced for the two-stage and segmented arrangements of the thermoelectric module with SiGe+Bi2Te3 material in order to operate them below the melting point temperature limit without failure. The optimum temperature is the hot junction temperature of the second stage for the two-stage arrangement of the thermoelectric module with SiGe+Bi2Te3 material and the interface temperature between two segments for the segmented arrangement of the thermoelectric module with SiGe+Bi2Te3 material [4,17]. The maximum value of the optimum temperature is the melting point temperature of Bi2Te3 material, which is around 585 °C. Figure 6 shows the optimum temperature values of the two-stage and segmented arrangements of the thermoelectric module with SiGe+Bi2Te3 material at various temperature difference conditions. The optimum temperature increases linearly with the temperature difference, as shown in the figure. As presented in the figure, in order to maintain optimum temperature of 585 °C or below, the two-stage arrangement with square prism legs are operated at the maximum temperature difference of 880 °C or lower, the two-stage arrangement with cylindrical and trapezoidal legs are operated at the maximum temperature difference of 830 °C or lower, and the segmented arrangement with square prism and cylindrical legs are operated at the maximum temperature difference of 730 °C or lower.
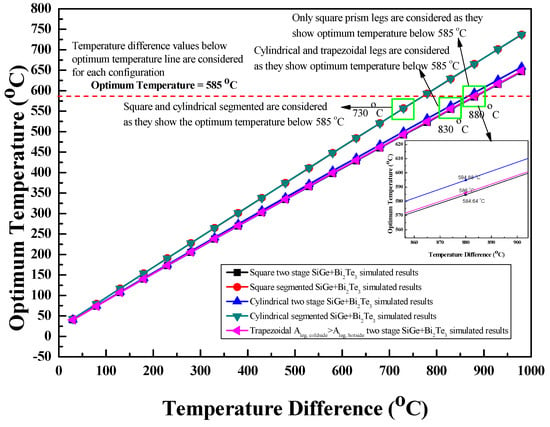
Figure 6.
Optimum temperature variation with respect to temperature difference.
For the single stage arrangement of the thermoelectric module with SiGe material, trapezoidal legs with Alegs, hotside> Alegs, coldside showed higher average stress compared to trapezoidal legs with Alegs, coldside> Alegs, hotside [11], which is discussed in detail in Section 3.5.1. Therefore, out of the two configurations of trapezoidal legs, only trapezoidal legs with Alegs, coldside> Alegs, hotside were considered for maximum power, maximum efficiency, and maximum stress analyses for single stage arrangement with Bi2Te3 material and two-stage arrangement with SiGe, Bi2Te3, and SiGe+Bi2Te3 materials.
3.3. Maximum Power
The comparison of maximum power for the single stage, two-stage, and single stage segmented arrangements of the thermoelectric module with various leg geometries and materials are presented in this section.
3.3.1. Single Stage Arrangement
The comparison of maximum power with temperature difference for the single stage arrangement of the thermoelectric module with three leg geometries and two semiconductor materials is shown in Figure 7a. For the same material, leg geometry had no significant effect on maximum power because of the same internal resistance as well as the same optimum voltage values [1,6,10]. At the same temperature difference, the optimum voltage of the thermoelectric module was the same and leg geometry had the same volume and base area with equal internal resistance for all the legs. However, materials with high showed higher maximum power than those with lower [4,17]. Hence, for the same leg geometry, the Bi2Te3 material showed higher maximum power than the SiGe material at the same temperature difference. This behavior was observed up to a temperature difference of 480 °C as the Bi2Te3 material could not be operated at a higher temperature difference because operation above that temperature difference increased the hot side temperature above its melting point. Hence, beyond the temperature difference of 480 °C, the SiGe material showed an increase in maximum power with the highest value at the temperature difference of 980 °C. For all the materials and leg geometries with the single stage arrangement of the thermoelectric module, the maximum power increased with the temperature difference. All the leg geometries with the SiGe material showed maximum power of 0.65 W at a temperature difference of 980 °C, while all the leg geometries with the Bi2Te3 material showed maximum power of 0.31 W at a temperature difference of 480 °C.
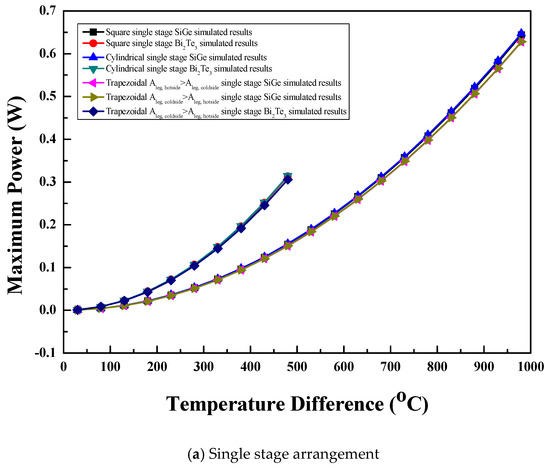
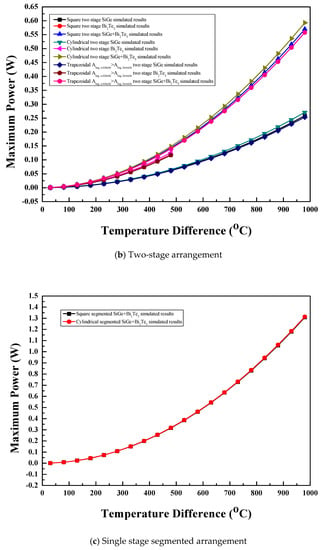
Figure 7.
Maximum power for (a) single stage arrangement, (b) two-stage arrangement, and (c) single stage segmented arrangement.
3.3.2. Two-Stage Arrangement
The variation of maximum power with the temperature difference for the two-stage thermoelectric module with various leg geometries and materials is shown in Figure 7b. In the two-stage arrangement of the thermoelectric module with the same leg geometry, a combination of materials in the first stage made up of SiGe material and the second stage made up of Bi2Te3 material showed significant enhancement in maximum power, compared to both stages either made of SiGe or Bi2Te3 alone [17,18]. In the case of SiGe, Bi2Te3, and SiGe+Bi2Te3 material, the square prism and trapezoidal legs with Alegs, coldside> Alegs, hotside showed similar maximum power with the temperature difference but the cylindrical legs showed enhancement in maximum power at the corresponding same temperature difference, although the degree of increase was less [1,6,10]. In the case of the SiGe+Bi2Te3 material, maximum power of 0.46 W was obtained for square prism legs at a temperature difference of 880 °C, whereas the cylindrical legs showed 0.43 W and trapezoidal legs showed 0.41 W maximum power at a temperature difference of 830 °C. For the SiGe material and temperature difference of 980 °C, the square prism and trapezoidal legs showed maximum power of 0.25 W and the cylindrical legs showed maximum power of 0.27 W. For the Bi2Te3 material and temperature difference of 480 °C, the square prism legs and trapezoidal legs showed maximum power of 0.12 W and the cylindrical legs showed maximum power of 0.13 W. The maximum power increased with the temperature difference in all the cases, as shown in Figure 7b.
3.3.3. Single Stage Segmented Arrangement
The maximum power variation with the temperature difference is shown in Figure 7c for the segmented thermoelectric module constructed with two leg geometries and the SiGe+Bi2Te3 material. Maximum power increased with the temperature difference for both the combinations. The leg geometry had no effect on the maximum power [1,6,10], as shown in Figure 7c, due to same internal resistance and same optimum voltage condition. The square prism as well as the cylindrical legs showed maximum power of 0.73 W at a temperature difference of 730 °C.
3.4. Maximum Efficiency
The comparison of maximum efficiency for the single stage, two-stage, and single stage segmented arrangements of the thermoelectric module with various leg geometries and materials are presented in this section.
3.4.1. Single Stage Arrangement
The variation of maximum efficiency with the temperature difference for the single stage thermoelectric module with three leg geometries and two materials is shown in Figure 8a. Maximum efficiency is the ratio of maximum power to the heat absorbed [13]. Similar to that of maximum power, the leg geometries had no effect on maximum efficiency for the same material [1,6,10]. For all the leg geometries and materials, as the temperature difference increased, the maximum efficiency also increased. For the same leg geometry, the Bi2Te3 material showed superior increase in maximum efficiency compared to the SiGe material over the entire temperature difference range due to high [4]. Although the Bi2Te3 material was operated up to a temperature difference of 480 °C due to its low melting point temperature, it still showed the highest value of maximum efficiency at a temperature difference of 480 °C, compared to the maximum efficiency value for the SiGe material at a temperature difference of 980 °C. At temperature difference of 480 °C, the Bi2Te3 material had a higher maximum power, thus showing higher maximum efficiency than SiGe. From a temperature difference of 480 to 980 °C, the SiGe material showed increase in maximum power and the heat absorbed also increased due to increase in temperature difference, which resulted in lower maximum efficiency for the SiGe material than that of the Bi2Te3 material. Maximum efficiency of 12.2% was observed at a temperature difference of 480 °C for all the leg geometries with the Bi2Te3 material. However, maximum efficiency of 5.1% was obtained for all the leg geometries with the SiGe material at a temperature difference of 980 °C.
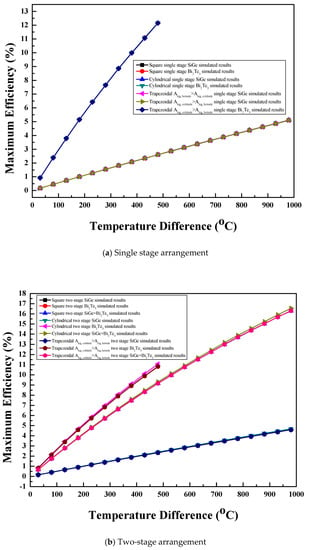
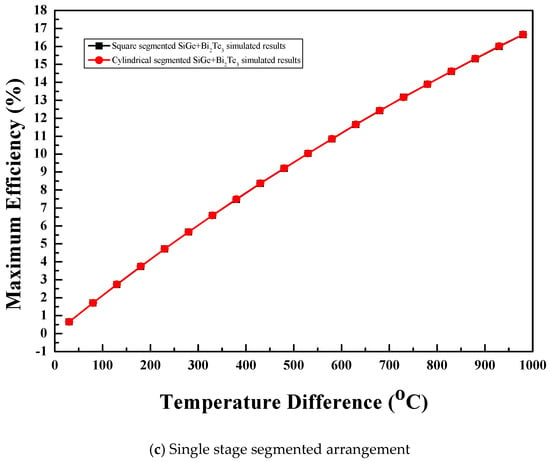
Figure 8.
Maximum efficiency for (a) single stage arrangement (b) two-stage arrangement, and (c) single stage segmented arrangement.
3.4.2. Two-Stage Arrangement
Figure 8b shows maximum efficiency variations with temperature difference for the two-stage arrangement of the thermoelectric module with various leg geometries and materials. For the same leg geometry, the Bi2Te3 material showed the highest values of maximum efficiency with temperature difference, compared to the SiGe+Bi2Te3 and SiGe materials but up to a temperature difference of 480 °C. However, from temperature difference of 480 °C, the SiGe+Bi2Te3 material showed increase in maximum efficiency up to the temperature difference corresponding to the optimum temperature condition. The SiGe material showed the lowest values of maximum efficiency until the temperature difference of 980 °C. Although Bi2Te3 as well as SiGe+Bi2Te3 materials are operated till a particular temperature difference because of the limitation of their melting point temperatures, they still showed comparatively higher values of maximum efficiencies than the SiGe material. For the same material, leg geometry had very less effect on maximum efficiency because of the same optimum voltage load and same internal resistance [1,6,10]. In the case of SiGe, Bi2Te3 and SiGe+Bi2Te3 materials, square prism, cylindrical, and trapezoidal legs showed almost the same maximum efficiency variation with temperature difference. At a temperature difference of 980 °C and for the SiGe material, the square prism legs and cylindrical legs showed maximum efficiency of 4.6% and the cylindrical legs showed maximum efficiency of 4.7%. For the Bi2Te3 material and temperature difference of 480 °C, the square prism legs and cylindrical legs showed maximum efficiency of 10.8% and the cylindrical legs showed maximum efficiency of 11.1%. In the case of the SiGe+Bi2Te3 material, the square prism legs showed maximum efficiency of 15% at a temperature difference of 880 °C and the cylindrical as well as trapezoidal legs showed maximum efficiencies of 14.6% and 14.4%, respectively, at a temperature difference of 830 °C. The maximum efficiency of the two-stage arrangement of the thermoelectric module with leg geometries and materials increased over the entire temperature difference range.
3.4.3. Single Stage Segmented Arrangement
The maximum efficiency of the single stage segmented arrangement of the thermoelectric module with two leg geometries and combination of SiGe+Bi2Te3 material increased with the temperature difference. The maximum efficiency variation with the temperature difference is shown in Figure 8c. Like maximum power, the leg geometries had no effect on the maximum efficiency of the single stage segmented arrangement of the thermoelectric module with two leg geometries and combination of the SiGe+Bi2Te3 material [1,6,10]. At a temperature difference of 730 °C, the square prism and cylindrical legs showed maximum efficiency of 13.2%.
3.5. Maximum Stress
The comparison of maximum stress for the single stage, two-stage, and single stage segmented arrangements of the thermoelectric module with various leg geometries and materials is presented in this section. Stress variation along the height of various thermoelectric legs of different materials and for various arrangements is also presented.
3.5.1. Single Stage Arrangement
The maximum stress variation with temperature difference for the single stage thermoelectric module with various leg geometries and various materials is shown in Figure 9a. For the same leg geometry, the Bi2Te3 material showed higher values of maximum stress compared to the SiGe material till a temperature difference of 480 °C; above that, the SiGe material showed increase in maximum stress with the highest value at a temperature difference of 980 °C due to the increase in temperatures. The coefficient of the thermal expansion of the Bi2Te3 material was higher than that of the SiGe material. Therefore, the thermal stress induced in the Bi2Te3 material was higher than that induced in the SiGe material at the same temperature difference condition. Further, for the same material, the cylindrical legs showed fewer maximum stress than the other two leg geometries [1,10] and square prism legs, trapezoidal legs with Alegs, coldside> Alegs, hotside, and Alegs, hotside> Alegs, coldside showed almost equal values of maximum stress due to the same geometrical structure with sharp corner edges. Square prism and trapezoidal legs have sharp edges, which are absent in cylindrical legs; therefore, the latter show lower thermal stress. Square prism legs, trapezoidal legs with Alegs, coldside> Alegs, hotside and trapezoidal legs with Alegs, hotside> Alegs, coldside with the SiGe material showed average stress of approximately 39 MPa, 38 MPa, and 41 MPa, respectively. The intensity of stress was high near the hot junction plate [1,10,11] and in the case of trapezoidal legs with Alegs, coldside> Alegs, hotside, the area of legs exposed to the hot side plate was less compared to the area of legs exposed to the hot side plate by the square prism legs and trapezoidal legs with Alegs, hotside> Alegs, coldside. Therefore, the average stress induces in the trapezoidal legs with Alegs, coldside> Alegs, hotside was lower than that of the square prism and trapezoidal legs with Alegs, hotside> Alegs, coldside [11]. Based on the area of legs exposed to the hot junction plate and the average stress values, the square prism legs and trapezoidal legs with Alegs, coldside> Alegs, hotside was preferred over the trapezoidal legs with Alegs, hotside> Alegs, coldside. For the SiGe material and at a temperature difference of 980 °C, the square prism legs and trapezoidal legs with Alegs, coldside> Alegs, hotside and Alegs, hotside> Alegs, coldside showed maximum stress of 0.96 GPa and the cylindrical legs showed maximum stress of 0.91 GPa. Similarly, for the Bi2Te3 material and at a temperature difference of 480 °C, the square prism legs and trapezoidal legs with Alegs, coldside> Alegs, hotside showed a maximum stress value of 0.61 GPa, whereas the cylindrical legs showed maximum stress of 0.58 GPa. The maximum stress of the single stage arrangement of the thermoelectric module with all leg geometries and materials increased linearly with the temperature difference.
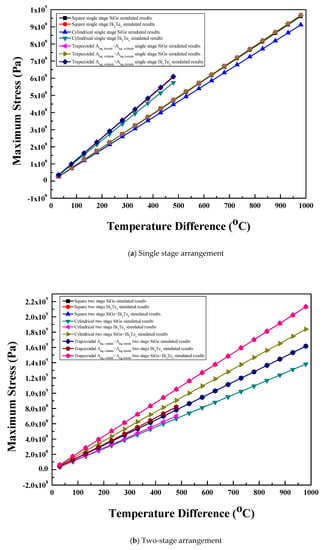
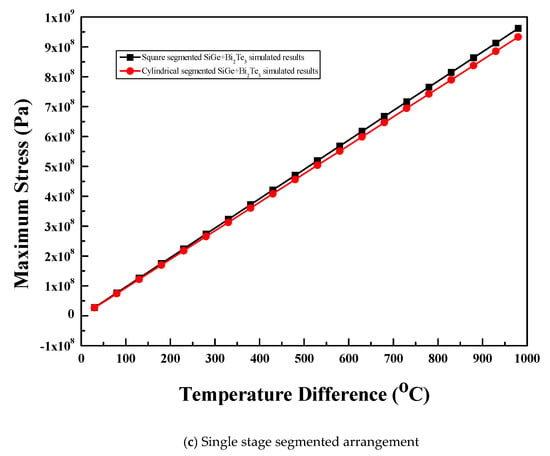
Figure 9.
Maximum stress for (a) single stage arrangement (b) two-stage arrangement, and (c) single stage segmented arrangement.
3.5.2. Two-Stage Arrangement
The maximum stress shows linear variation with the temperature difference for the two-stage thermoelectric module with various leg geometries and materials, as shown in Figure 9b. In the case of SiGe, Bi2Te3 and SiGe+Bi2Te3 materials, the square prism and trapezoidal legs showed almost same maximum stress variation with temperature difference, which were higher than the corresponding maximum stress values for the cylindrical legs [1,10]. The cylindrical legs have a smooth geometrical structure; hence, they presented lower maximum stress compared to the other two leg geometries. For the same leg geometry, the SiGe+Bi2Te3 material showed higher maximum stress, followed by the Bi2Te3 and SiGe materials. The Bi2Te3 material showed higher thermal stress than the SiGe material due to its higher coefficient of thermal expansion. The SiGe+Bi2Te3 material showed higher thermal stress than the Bi2Te3 material because when two different materials with different thermal properties are connected at higher temperature conditions, it results in higher stress generation [1]. For the SiGe material and at temperature difference of 980 °C, the square prism and trapezoidal legs showed maximum stress of 1.62 GPa and the cylindrical legs showed maximum stress of 1.38 GPa. Similarly, for the Bi2Te3 material and at a temperature difference of 480 °C, the square prism and trapezoidal legs showed maximum stress of 0.82 GPa and the cylindrical legs showed maximum stress of 0.7 GPa. For the SiGe+Bi2Te3 material, the square prism legs showed maximum stress of 1.91 GPa at a temperature difference of 880 °C and the cylindrical as well as trapezoidal legs showed maximum stress of 1.56 GPa and 1.81 GPa, respectively, at a temperature difference of 830 °C.
3.5.3. Single Stage Segmented Arrangement
Maximum stress varies linearly with temperature difference for the single stage segmented arrangement of the thermoelectric module with both the leg geometries and the SiGe+Bi2Te3 material, as shown in Figure 9c. The cylindrical leg geometry showed the lowest values of maximum stress, compared to the square prism legs [1,10] over the entire temperature difference range due to no sharp edges and a smooth geometrical structure. At a temperature difference of 730 °C and for the SiGe+Bi2Te3 material, the square prism legs showed maximum stress of 0.72 GPa and the cylindrical legs showed maximum stress of 0.69 GPa.
3.5.4. Stress Variation along Thermoelectric Leg Height
Stress variation along the selected locations of the thermoelectric module with various combinations of leg geometries, materials, and arrangements are discussed here. The selected centerline locations in the vertical direction for various arrangements of the thermoelectric module with square prism legs are shown in Figure 10a–c. In Figure 10a–c, the dotted line of locations on the thermoelectric legs shows the direction from the bottom of the thermoelectric legs to the top. Similar locations are selected in the cylindrical and trapezoidal leg geometries. The variation of stress for the selected locations were considered at the maximum operating temperature difference for each combination.
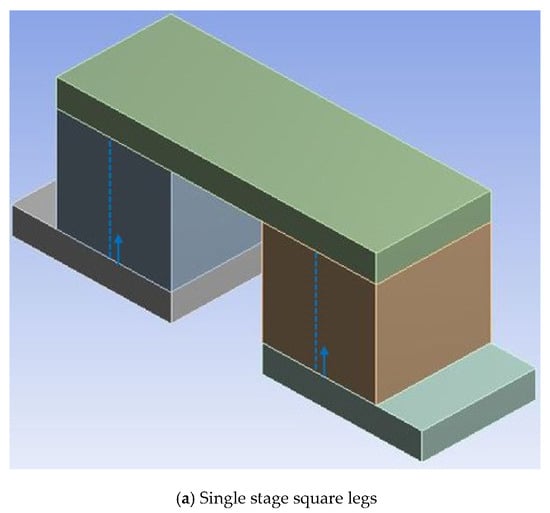
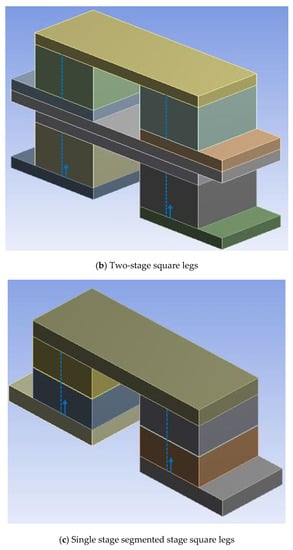
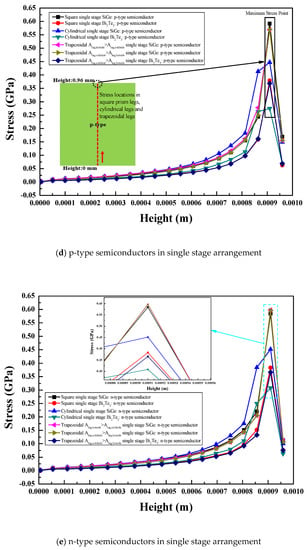
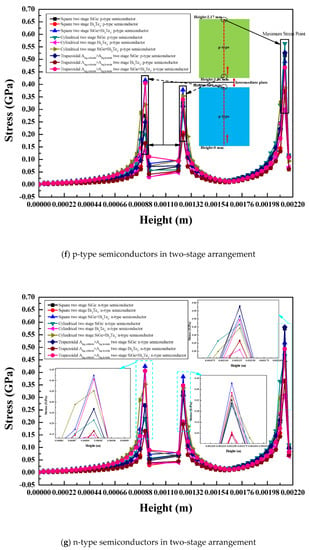
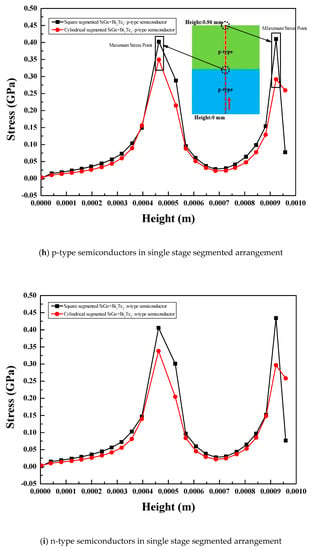
Figure 10.
Selected centerline locations in the vertical direction for (a) single stage square legs (b), two-stage square legs (c), single stage segmented stage square legs and variation of the stress along the selected centerline locations of (d) p type semiconductors in single stage arrangement, (e) n-type semiconductors in single stage arrangement, (f) p type semiconductors in two-stage arrangement, (g) n-type semiconductors in two-stage arrangement, (h) p type semiconductors in single stage segmented arrangement, and (i) n-type semiconductors in single stage segmented arrangement.
Single Stage Arrangement
For the single stage arrangement of the thermoelectric module, the variation of stress along the selected centerline locations of various thermoelectric legs with different materials is shown in Figure 10d,e. Figure 10d shows the variations of stress in different p-type semiconductor materials of various legs geometries and Figure 10e shows the variations of stress in different n-type semiconductor materials of various legs geometries. For each geometry, same p-type and n-type semiconductor material showed similar behavior with small variations in values due to same thermal properties [1]. However, the same p-type and n-type semiconductor material had different electrical properties. The intensity of stress was high at the intersection of the thermoelectric legs and the hot plate (top of the thermoelectric legs) for the single stage arrangement of the thermoelectric module with materials and leg geometries, as shown in Figure 10d,e because the materials of the thermoelectric legs and hot plate were different, and the top of the legs was exposed to a higher temperature. The stress reduced from the hot side of the thermoelectric legs to the cold side of the thermoelectric legs with the minimum value at the bottom of the leg near the cold junction plate because of reduction in temperature [1,10,11]. The materials of the thermoelectric legs and the cold side plate were also different, but the temperature at this location was low to generate lower stress. For the SiGe material, the square and trapezoidal legs showed higher stress compared to the cylindrical legs. Similarly, for the Bi2Te3 material, the cylindrical legs presented lower stress than the other leg geometries. The higher temperature difference showed higher thermal stress. Therefore, the Bi2Te3 material showed lower stress than the SiGe material for all three leg geometries because stress variation along the selected locations was presented at a temperature difference of 480 °C for the Bi2Te3 material and 980 °C for the SiGe material.
Two-Stage Arrangement
Figure 10f,g show the stress variation along the selected center line locations in the two-stage arrangement with various thermoelectric leg geometries and various materials. The variation of stress in various leg geometries with different p-type semiconductor materials is shown in Figure 10f. Figure 10g shows the stress variation in different leg geometries with various n-type semiconductor materials. In the two-stage arrangement of the thermoelectric module, the variation of stress was the same for the same p-type and n-type semiconductor material with a small variation in their values due to same thermal properties [1]. In the second stage of the two-stage arrangement, the variation trend of stress was similar as of the single stage arrangement case, the minimum value of stress was at the bottom of the leg near the cold junction, and increased towards the hot side of the legs. The intensity of stress for the second stage of the two-stage arrangement with various materials and leg geometries was high near the intersection of the thermoelectric legs of the second stage and the intermediate plate. A height of 0.00096 m to 0.001210 m points to the intermediate plate, and stress variation in the intermediate plate is not considered here, as this section deals only with stress variation in the thermoelectric legs. The variation trend of stress in the first stage of the two-stage arrangement is different compared to the second stage of the two-stage arrangement. In the first stage of the two-stage arrangement, higher values of stress occurred at two locations—the first was at the interconnection of the intermediate plate with the thermoelectric legs of the first stage, and the second one was at the interconnection of the thermoelectric legs of the first stage and the hot side plate. When materials with different properties are connected with each other at a higher temperature, it results in higher stress [1]. However, the values of stress in the thermoelectric legs near the hot side plate were higher than that near the intermediate plate because of a higher temperature of the hot side plate than that of the intermediate plate. As shown in Figure 10f,g, the minimum values of stress for the first stage of the two-stage arrangement occurred at the middle of the thermoelectric legs—at a location between 0.00154 m to 0.00176 m. For the same leg geometry, the SiGe+Bi2Te3 and SiGe materials showed higher values of stress than the Bi2Te3 material because the stress variation of the latter for the selected locations was at a temperature difference of 480 °C, which is lower than the temperature difference at which stress variation were presented for the SiGe+Bi2Te3 and SiGe materials. In the case of the second stage of the two-stage arrangement, the square prism and trapezoidal legs showed higher stress than the cylindrical legs for the same material, while in the case of the first stage of the two-stage arrangement, the cylindrical legs showed higher stress than the square prism and trapezoidal legs for the same material. Thus, for the selected centerline locations on the thermoelectric legs, the intensity of stress was high in the cylindrical legs for the first stage of the two-stage arrangement, but it was low in the cylindrical legs for the second stage of the two-stage arrangement. As the stress effect is considered for the whole leg geometry of the two-stage arrangement, the cylindrical legs were found to have lower stress than the other two leg geometries.
Single Stage Segmented Arrangement
For the single stage segmented arrangement of the thermoelectric module with two leg geometries and the SiGe+Bi2Te3 material, the variation of stress along the selected center line locations in the p-type and n-type semiconductors is presented in Figure 10h,i. For the same leg geometry, the same behavior of the stress variation was observed for the p-type and n-type semiconductors [1] with the SiGe+Bi2Te3 material due to same thermal properties. The maximum values of stress occur at the interconnection of both the materials (at the middle height) as well as at the interconnection of the thermoelectric legs and the hot side plate [1] because of the interconnections of different materials at both the locations. The hot side plate and thermoelectric legs with the different materials were interconnected at a higher temperature with a higher stress at the interconnection. In addition, two different materials with different thermal properties are interconnected at the middle height of the thermoelectric legs at a higher temperature with higher stress at the middle height of the legs. The maximum stress at the middle height and the hot side of the thermoelectric legs are almost equal. Minimum stress was observed at the cold side of the thermoelectric legs, as shown in Figure 10h,i, because the temperature in this location was low, resulting in lower stress. The square legs showed higher values of stress compared to the cylindrical legs due to its sharp edges.
Figure 11 shows the stress distribution contours of the thermoelectric legs of different configurations in the thermoelectric module. Figure 11 supports the graphical presentation and discussion of stress described for various configurations of the thermoelectric module in Section 3.5. Figure 11 also describes that the intensity of stress is high at the intersection of the hot side plate and the thermoelectric legs for all configurations of the thermoelectric module. In addition, for various leg geometries and materials, the intensity of stress was high at the interconnection and the intermediate plate of thermoelectric legs for the two-stage arrangement and at the middle height of thermoelectric legs for the single stage segmented arrangement. The strain generated in various configurations of the thermoelectric module, as presented in Equation (21), is a replica of the stress. Namely, the behavior of the strain is same as the stress for various configurations of the thermoelectric module. Therefore, detailed discussions on this strain are not considered further in this study.
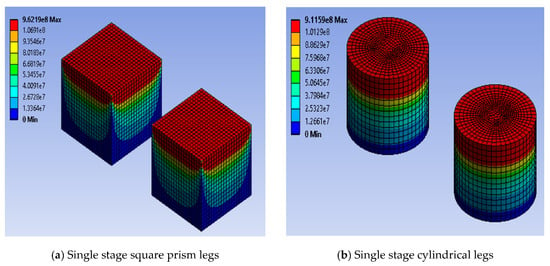
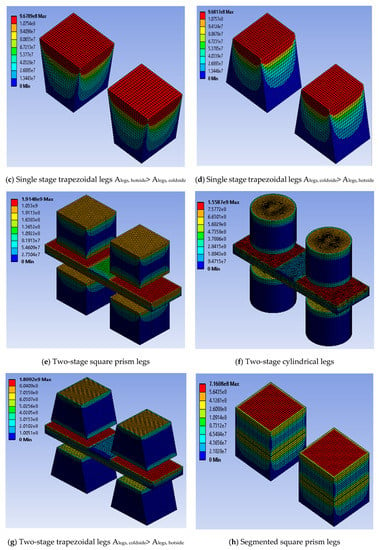

Figure 11.
Maximum thermal stress contours in (a) single stage square prism legs, (b) single stage cylindrical legs, (c) single stage trapezoidal legs Alegs, hotside> Alegs, coldside, (d) single stage trapezoidal legs Alegs, coldside> Alegs, hotside, (e) two-stage square prism legs, (f) two-stage cylindrical legs, (g) two-stage trapezoidal legs Alegs, coldside> Alegs, hotside, (h) single stage segmented square prism legs, and (i) single stage segmented cylindrical legs.
3.6. Selection of Optimum Configuration for the Thermoelectric Module
A comparison of the thermoelectric module with combinations of leg geometry, material, segmentation, and two-stage arrangement based on maximum power, maximum efficiency, and maximum stress at the corresponding maximum operating temperature difference is discussed in this section. Optimum configurations of the thermoelectric module with the combinations of leg geometry, material, segmentation, and two-stage arrangement were selected based on three performance parameters of maximum power, maximum efficiency, and maximum stress. Therefore, higher values of maximum power and maximum efficiency, and lower values of maximum stress of all combinations for the thermoelectric module were suggested as optimum configuration.
A graphical presentation of the comparison of various configurations of the thermoelectric module based on maximum temperature difference, maximum efficiency, maximum power, and maximum stress is shown in Figure 12. In Figure 12 and Table 4, numbers 1 to 18 on the abscissa presents various combinations of the thermoelectric module and the thermoelectric module constructed with the segmented arrangement, cylindrical legs, and combination of the SiGe+Bi2Te3 material show the optimum values of maximum power, maximum efficiency, and maximum stress. The single stage segmented arrangement of the thermoelectric module with the cylindrical leg geometry and the SiGe+Bi2Te3 material showed a combination of higher maximum power, higher maximum efficiency, and lower maximum thermal stress [35]. Therefore, based on the overall effect of power, efficiency, and stress, a thermoelectric module constructed with the segmented arrangement, cylindrical legs, and combination of the SiGe+Bi2Te3 material is suggested as the optimum configuration of the thermoelectric module.
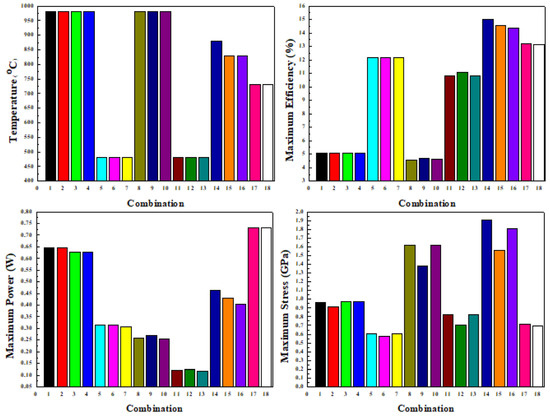
Figure 12.
Comparison of various configurations of thermoelectric module based on maximum temperature difference, maximum efficiency, maximum power, and maximum stress.

Table 4.
Comparison of various combinations of thermoelectric module based on maximum temperature difference, maximum power, maximum efficiency, and maximum stress.
The comparison of all 18 configurations of the thermoelectric module was carried out based on computational time/single case of simulation, which is presented in Table 5. From the table, it can be concluded that the two-stage arrangement has a higher computational time, followed by the segmented arrangement and single stage arrangement, respectively. The computational time for the selected optimum configuration of the thermoelectric module constructed with the segmented arrangement, cylindrical legs, and combination of SiGe+Bi2Te3 materials is 2100 s.

Table 5.
Comparison of various combinations of thermoelectric module based on computational time/single case of simulation.
3.7. Effect of Soldering Layers
Table 6 shows the effect of soldering layers on maximum power, maximum efficiency, and maximum thermal stress of the thermoelectric module. For the same range of operating temperature difference, the Bi2Te3 material showed higher thermal stress compared to the SiGe material. Hence, soldering layers were only provided on the thermoelectric legs constructed with the Bi2Te3 material [4]. In order to investigate the effect of the soldering layers, the single stage arrangement of the thermoelectric module with the square prism legs and the Bi2Te3 material as well as the two-stage arrangement of the thermoelectric module with the square prism legs and the Bi2Te3 material are compared with and without soldering layers. In addition, the two-stage arrangement with square prism legs with the SiGe+Bi2Te3 material is also compared with and without soldering layers. In the case of the SiGe+Bi2Te3 material with the soldering layers, the second stage of the Bi2Te3 material is provided with soldering layers. Addition of the soldering layers reduces the thermal stress compared to the corresponding same configuration without soldering layers. The soldering layers experience most of the deformation compared to the other parts of the thermoelectric module and sometimes undergo plastic deformation. Hence, excessive thermal stress on the thermoelectric legs are reduced because the larger effect of the thermal stress is absorbed by the soldering layers. The thickness of the soldering layers is very small; hence, the resistance offered is a small contribution to the total effective resistance of the thermoelectric module. Therefore, the soldering layers have no significant effect on maximum power or maximum efficiency. The melting point temperature of the soldering layers is 185 °C; hence, various configurations of the thermoelectric module with soldering layers are operated at a maximum hot junction temperature below 185 °C. Therefore, a comparison of configurations of the thermoelectric module provided with and without soldering layers was done for temperature difference of 150 °C. Maximum stress for the various configurations with the soldering layers were considered only for the thermoelectric legs, not the entire thermoelectric module, as is shown in Table 6.

Table 6.
Effect of soldering layers on various performance parameters.
4. Conclusions
The behavior of maximum power, maximum efficiency, and maximum thermal stress was investigated numerically and theoretically for a thermoelectric module with various combinations of leg geometry, material, segmentation, and two-stage arrangement. From the conducted numerical and theoretical analysis, the following critical observations are summarized:
- (a)
- For all configurations of the thermoelectric module, the numerically predicted values of maximum power and maximum efficiency were validated at ±5% error and the numerically predicted values of maximum stress were validated at ±7% error with their theoretical values, respectively.
- (b)
- For the same arrangement and the same material, leg geometries with the same volume and same base area have a negligible effect on maximum power and maximum efficiency. However, the cylindrical legs showed lower values of maximum stress than that of the square prism and trapezoidal legs.
- (c)
- For the same arrangement and leg geometry, the SiGe+Bi2Te3 material for the thermoelectric module showed higher maximum power and maximum efficiency than the other individual materials. The thermal stress of the thermoelectric module with the SiGe+Bi2Te3 material was higher than those of the thermoelectric module with the SiGe and Bi2Te3 materials. In addition, the intensity of stress in the thermoelectric module with the SiGe+Bi2Te3 material could be reduced by using soldering layers without affecting maximum power and maximum efficiency.
- (d)
- The segmented arrangement of the thermoelectric module showed a higher maximum power and maximum efficiency and lower maximum stress in all combinations of the thermoelectric module. Therefore, the segmented arrangement of the thermoelectric module with cylindrical leg geometry and a combination of SiGe+Bi2Te3 materials was selected as the optimum configuration for the thermoelectric module with maximum power of 0.73 W, maximum efficiency of 13.2%, and maximum thermal stress of 0.69 GPa.
Author Contributions
Conceptualization, M.-Y.L.; J.-H.S., and K.S.G.; methodology, M.-Y.L., J.-H.S., H.-S.L., and K.S.G.; software, M.-Y.L., J.-H.S., and K.S.G.; validation, M.-Y.L., J.-H.S., and K.S.G.; formal analysis, M.-Y.L., J.-H.S., H.-S.L., and K.S.G.; investigation, M.-Y.L., J.-H.S., H.-S.L., and K.S.G.; resources, M.-Y.L., J.-H.S., and K.S.G.; data curation, M.-Y.L.; writing—original draft preparation, M.-Y.L., J.-H.S., and K.S.G.; writing—review and editing, M.-Y.L., J.-H.S., and K.S.G.; visualization, M.-Y.L.; supervision, M.-Y.L.; project administration, M.-Y.L.; funding acquisition, M.-Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work was supported by the Dong-A University research fund.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | Leg cross-sectional area (m2) |
| E | Yong modulus (GPa) |
| Electric field intensity (N/C or V/m) | |
| Heat absorbed (W) | |
| Theoretical optimum current (A) | |
| Numerical optimum current (A) | |
| Electric current intensity (A/ m2) | |
| K | Curvature (m−1) |
| Thermal conductivity of segment 1 (W/m °C) | |
| Thermal conductivity of segment 2 (W/m °C) | |
| L | Leg length (m) |
| Theoretical maximum power (W) | |
| Numerical maximum power (W) | |
| p | Peltier coefficient (V) |
| R | Internal resistance ( |
| Equivalent resistance ( | |
| RL | External load resistance ( |
| Hot junction temperature (°C) | |
| Cold junction temperature (°C) | |
| Average temperature (°C) | |
| Temperature difference (°C) | |
| Temperature gradient | |
| Theoretical optimum voltage (V) | |
| Numerical optimum voltage (V) | |
| Figure of Merit | |
| Coordinate (m) | |
| Equivalent Figure of Merit | |
| Seebeck coefficient (V/K) | |
| Theoretical maximum efficiency | |
| Numerical maximum efficiency | |
| Electrical resistivity of p-type (Ω m) | |
| Electrical resistivity of n-type (Ω m) | |
| Electrical conductivity of p-type (Ω−1 m−1) | |
| Electrical conductivity of n-type (Ω−1 m−1) | |
| Equivalent Seebeck coefficient (V/K) | |
| Seebeck coefficient of segment 1 (V/K) | |
| Seebeck coefficient of segment 2 (V/K) | |
| Electrical resistivity of segment 1 (Ω m) | |
| Electrical resistivity of segment 2 (Ω m) | |
| von-Mises stress (GPa) | |
| Thermal stress (i, j = 1,2,3) (GPa) | |
| Normal stress in longitudinal direction (GPa) | |
| Coefficient of thermal expansion (K−1) | |
| Strain | |
| Normal strain | |
| Poisson’s ratio | |
| Electrical potential gradient |
References
- Erturun, U.; Erermis, K.; Mossi, K. Effect of various leg geometries on thermo-mechanical and power generation performance of thermoelectric devices. Appl. Therm. Eng. 2014, 73, 128–141. [Google Scholar] [CrossRef]
- Shen, Z.G.; Liu, X.; Chen, S.; Wu, S.Y.; Xiao, L.; Chen, Z.X. Theoretical analysis on a segmented annular thermoelectric generator. Energy 2018, 157, 297–313. [Google Scholar] [CrossRef]
- Jin, Z.H. Thermal stresses in a multilayered thin film thermoelectric structure. Microelectron. Reliab. 2014, 54, 1363–1368. [Google Scholar] [CrossRef]
- Ma, Q.; Fang, H.; Zhang, M. Theoretical analysis and design optimization of thermoelectric generator. Appl. Therm. Eng. 2017, 127, 758–764. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.H.; Lee, M.Y. Numerical Study on Geometric Parameter effects of Power Generation Performances for Segmented Thermoelectric Generator. Int. J. Air-Cond. Refrig. 2018, 26, 1850004. [Google Scholar] [CrossRef]
- Erturun, U.; Erermis, K.; Mossi, K. Influence of leg sizing and spacing on power generation and thermal stresses of thermoelectric devices. Appl. Energy 2015, 159, 19–27. [Google Scholar] [CrossRef]
- Wu, Y.; Ming, T.; Li, X.; Pan, T.; Peng, K.; Luo, X. Numerical simulations on the temperature gradient and thermal stress of a thermoelectric power generator. Energy Conv. Manag. 2014, 88, 915–927. [Google Scholar] [CrossRef]
- Erturun, U.; Mossi, K. Thermoelectric devices with rotated and coaxial leg configurations: Numerical analysis of performance. Appl. Therm. Eng. 2015, 85, 304–312. [Google Scholar] [CrossRef]
- Jia, X.; Gao, Y. Optimal design of a novel thermoelectric generator with linear-shaped structure under different operating temperature conditions. Appl. Therm. Eng. 2015, 78, 533–542. [Google Scholar] [CrossRef]
- Yilbas, B.S.; Akhtar, S.S.; Sahin, A.Z. Thermal and stress analyses in thermoelectric generator with tapered and rectangular pin configurations. Energy 2016, 114, 52–63. [Google Scholar] [CrossRef]
- Al-Merbati, A.S.; Yilbas, B.S.; Sahin, A.Z. Thermodynamics and thermal stress analysis of thermoelectric power generator: Influence of pin geometry on device performance. Appl. Therm. Eng. 2013, 50, 683–692. [Google Scholar] [CrossRef]
- Ali, H.; Sahin, A.Z.; Yilbas, B.S. Thermodynamic analysis of a thermoelectric power generator in relation to geometric configuration device pins. Energy Conv. Manag. 2014, 78, 634–640. [Google Scholar] [CrossRef]
- Erturun, U.; Mossi, K. A feasibility investigation on improving structural integrity of thermoelectric modules with varying geometry. In Proceedings of the ASME 2012 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Stone Mountain, GA, USA, 19–21 September 2012; American Society of Mechanical Engineers: Stone Mountain, GA, USA; pp. 939–945. [Google Scholar]
- Yilbas, B.S.; Ali, H. Thermoelectric generator performance analysis: Influence of pin tapering on the first and second law efficiencies. Energy Conv. Manag. 2015, 100, 138–146. [Google Scholar] [CrossRef]
- Gao, J.L.; Du, Q.G.; Zhang, X.D.; Jiang, X.Q. Thermal stress analysis and structure parameter selection for a Bi2Te3-based thermoelectric module. J. Electron. Mater. 2011, 40, 884–888. [Google Scholar] [CrossRef]
- Zhang, L.; Tosho, T.; Okinaka, N.; Akiyama, T. Design of cascaded oxide thermoelectric generator. Mater. Trans. 2008, 49, 1675–1680. [Google Scholar] [CrossRef]
- Kanimba, E.; Pearson, M.; Sharp, J.; Stokes, D.; Priya, S.; Tian, Z. A modeling comparison between a two-stage and three-stage cascaded thermoelectric generator. J. Power Sources 2017, 365, 266–272. [Google Scholar] [CrossRef]
- Wilbrecht, S.; Beitelschmidt, M. The Potential of a Cascaded TEG System for Waste Heat Usage in Railway Vehicles. J. Electron. Mater. 2018, 47, 3358–3369. [Google Scholar] [CrossRef]
- Weng, C.C.; Lin, M.C.; Huang, M.J. A waste cold recovery from the exhausted cryogenic nitrogen by using thermoelectric power generator. Energy 2016, 103, 385–396. [Google Scholar] [CrossRef]
- Chen, G.; Mu, Y.; Zhai, P.; Li, G.; Zhang, Q. An investigation on the coupled thermal–mechanical–electrical response of automobile thermoelectric materials and devices. J. Electron. Mater. 2013, 42, 1762–1770. [Google Scholar] [CrossRef]
- Kaibe, H.; Aoyama, I.; Mukoujima, M.; Kanda, T.; Fujimoto, S.; Kurosawa, T.; Ishimabushi, H.; Ishida, K.; Rauscher, L.; Hata, Y.; et al. Development of thermoelectric generating stacked modules aiming for 15% of conversion efficiency. In Proceedings of the ICT 2005. 24th International Conference on Thermoelectrics, Clemson, SC, USA, 19–23 June 2005; pp. 242–247. [Google Scholar]
- Vargas-Almeida, A.; Olivares-Robles, M.A.; Camacho-Medina, P. Thermoelectric system in different thermal and electrical configurations: Its impact in the figure of merit. Entropy 2013, 15, 2162–2180. [Google Scholar] [CrossRef]
- Ibrahim, A.; Rahnamayan, S.; Martin, M.V.; Yilbas, B. Multi-objective thermal analysis of a thermoelectric device: Influence of geometric features on device characteristics. Energy 2014, 77, 305–317. [Google Scholar] [CrossRef]
- Turenne, S.; Clin, T.; Vasilevskiy, D.; Masut, R.A. Finite element thermomechanical modeling of large area thermoelectric generators based on bismuth telluride alloys. J. Electron. Mater. 2010, 39, 1926–1933. [Google Scholar] [CrossRef]
- Garud, K.S.; Seo, J.H.; Patil, M.S.; Bang, Y.M.; Pyo, Y.D.; Cho, C.P.; Lee, M.Y. Thermal-Electrical-Structural Performances of Hot Heat Exchanger with Different Internal Fins of Thermoelectric Generator for Low Power Generation Application. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Jones, M.H.; Jones, S.H. The General Properties of Si, Ge, SiGe, SiO2 and Si3N4; Virginia Semiconductor: Fredericksburg, VA, USA, 2002. [Google Scholar]
- Bennis, A.; Leinenbach, C.; Raudzis, C.; Müller-Fiedler, R.; Kronmüller, S. Measurement technique for elastic and mechanical properties of polycrystalline silicon-germanium films using surface acoustic waves and projection masks. arXiv 2007, arXiv:0711.3305. [Google Scholar]
- Seo, J.H.; Patil, M.S.; Cho, C.P.; Lee, M.Y. Heat transfer characteristics of the integrated heating system for cabin and battery of an electric vehicle under cold weather conditions. Int. J. Heat Mass Transf. 2018, 117, 80–94. [Google Scholar] [CrossRef]
- Garud, K.S.; Seo, J.H.; Cho, C.P.; Lee, M.Y. Artificial Neural Network and Adaptive Neuro-Fuzzy Interface System Modelling to Predict Thermal Performances of Thermoelectric Generator for Waste Heat Recovery. Symmetry 2020, 12, 259. [Google Scholar] [CrossRef]
- Al-Merbati, A.S.; Yilbas, B.S.; Sahin, A.Z. A model study for cyclic thermal loading and thermal performance of a thermoelectric generator. Int. J. Energy Res. 2014, 38, 1351–1360. [Google Scholar] [CrossRef]
- Elzalik, M.; Rezk, H.; Mostafa, R.; Thomas, J.; Shehata, E.G. An experimental investigation on electrical performance and characterization of thermoelectric generator. Int. J. Energy Res. 2020, 44, 128–143. [Google Scholar] [CrossRef]
- Baheta, A.T.; Looi, K.K.; Oumer, A.N.; Habib, K. Thermoelectric Air-Conditioning System: Building Applications and Enhancement Techniques. Int. J. Air-Cond. Refrig. 2019, 27, 1930002. [Google Scholar] [CrossRef]
- Luo, Y.; Kim, C.N. Effects of the cross-sectional area ratios and contact resistance on the performance of a cascaded thermoelectric generator. Int. J. Energy Res. 2019, 43, 2172–2187. [Google Scholar] [CrossRef]
- Tritt, T.M. Thermoelectric phenomena, materials, and applications. Ann. Rev. Mater. Res. 2011, 41, 433–448. [Google Scholar] [CrossRef]
- Ali, H.; Yilbas, B.S. Configuration of segmented leg for the enhanced performance of segmented thermoelectric generator. Int. J. Energy Res. 2017, 41, 274–288. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).