Stability and Convergence Analysis of a Biomagnetic Fluid Flow Over a Stretching Sheet in the Presence of a Magnetic Field
Abstract
1. Introduction
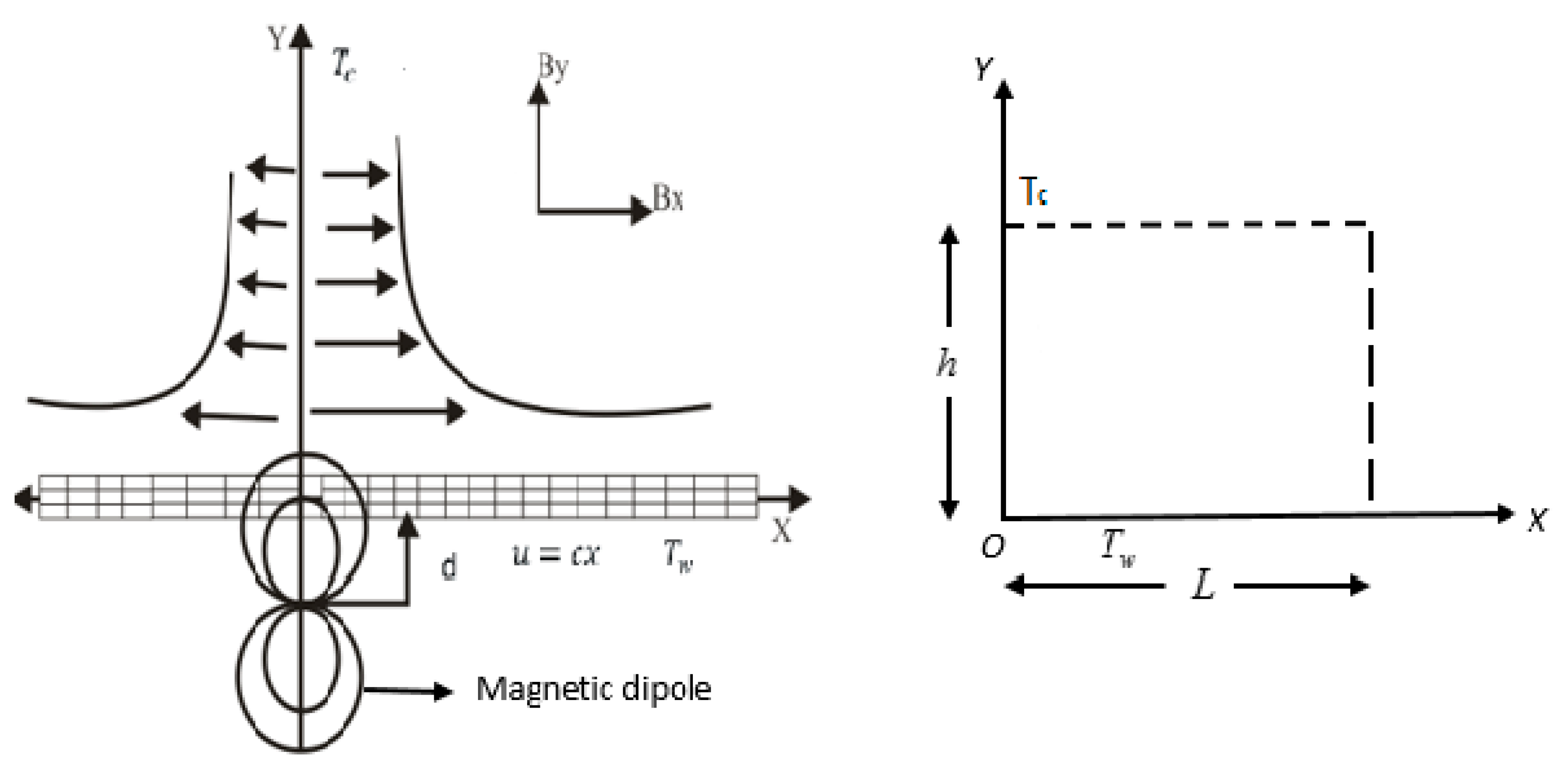
2. Mathematical Model of the Flow
3. Mathematical Formulation
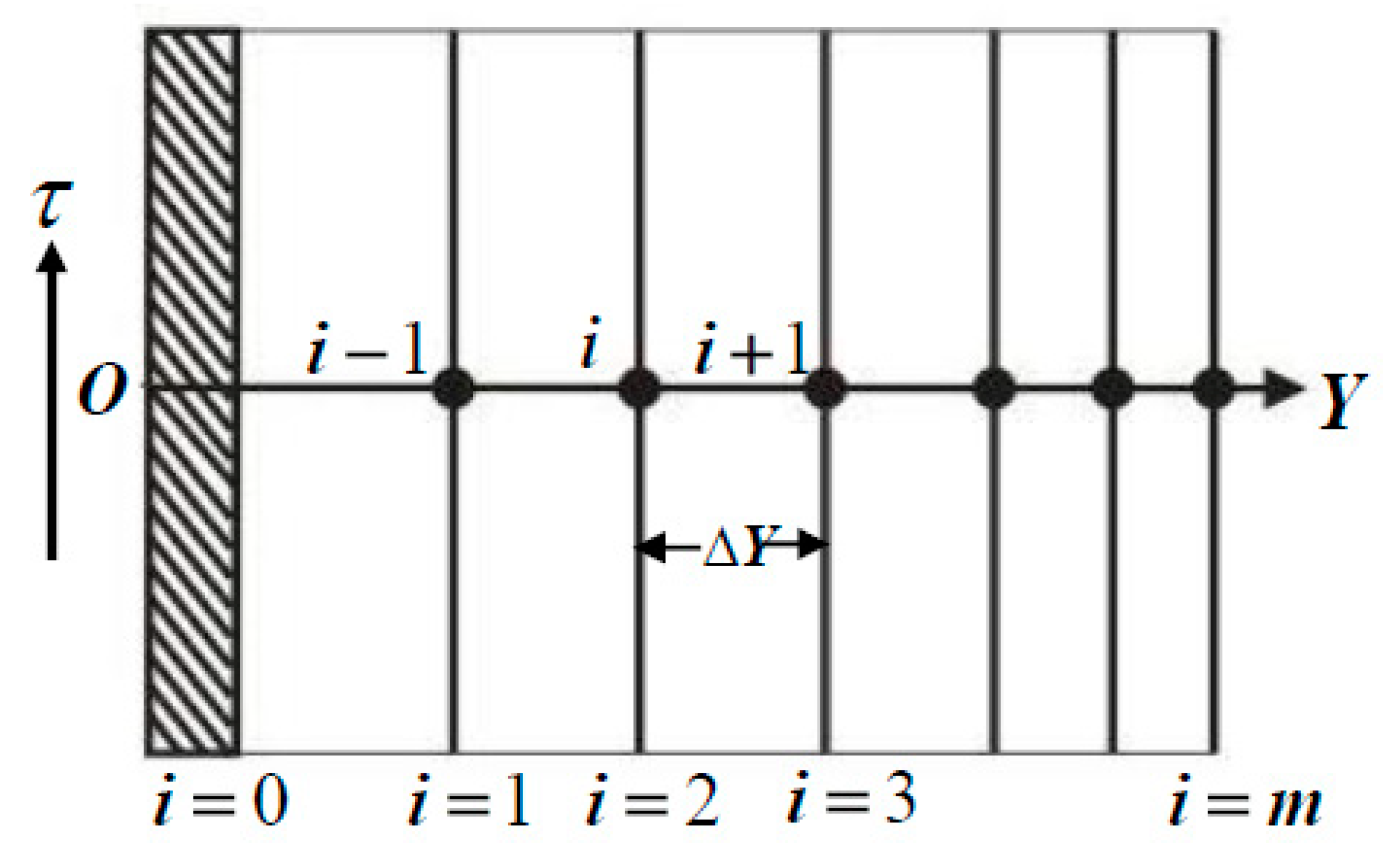
4. Numerical Method
5. Stability and Convergence Analysis
6. Results and Discussion
6.1. Justification of the Grid Space
6.2. Steady-State Solution
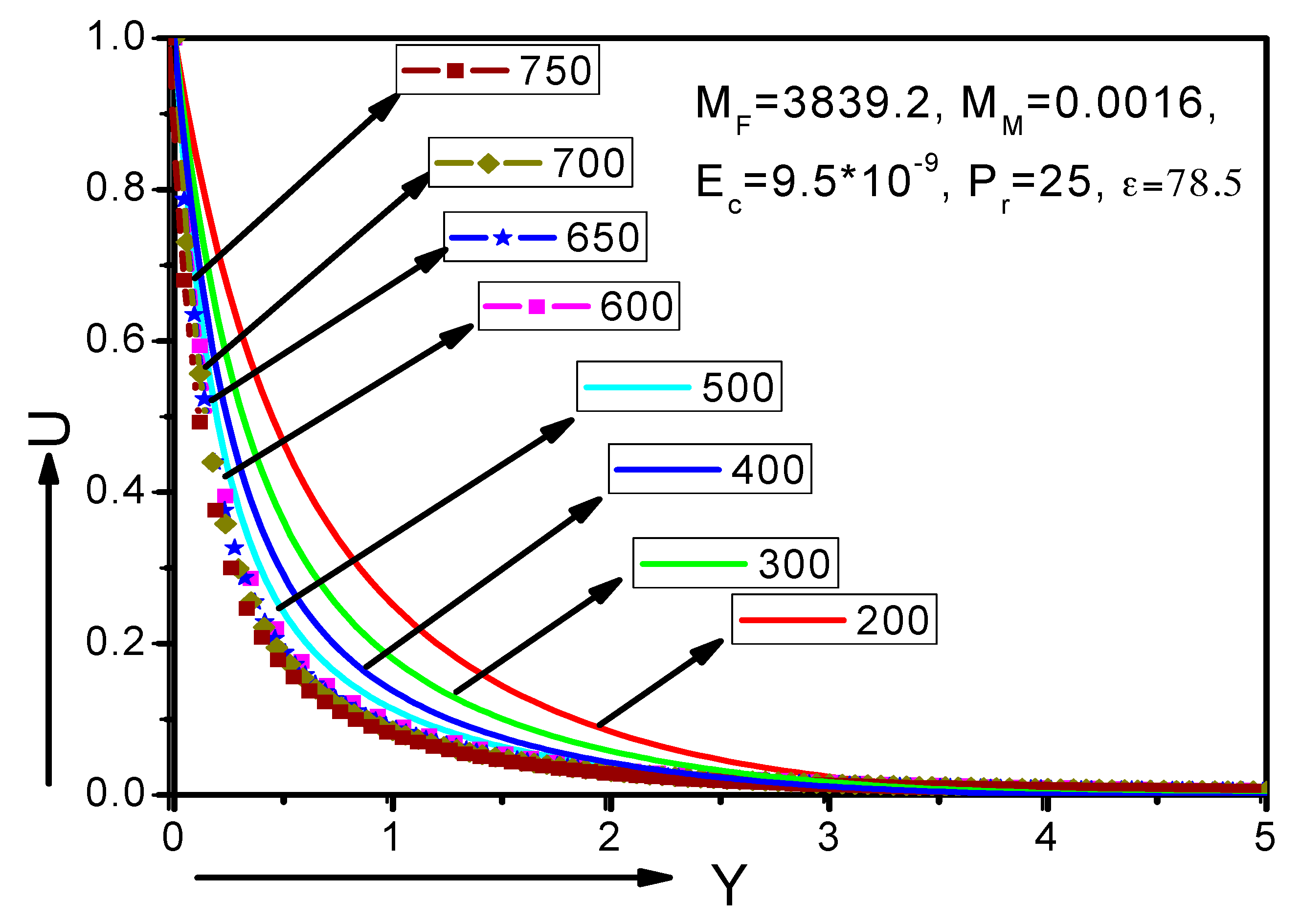
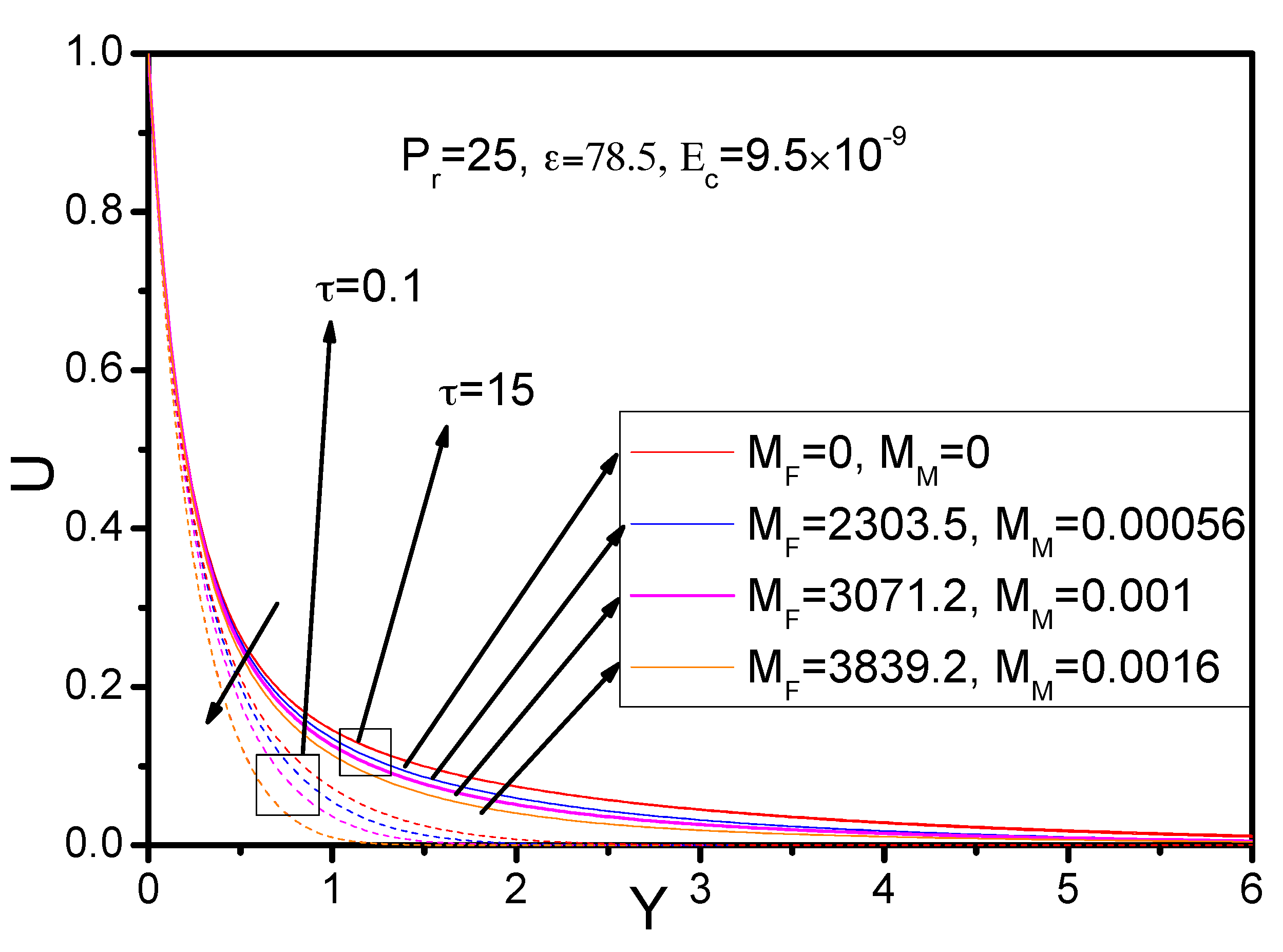
6.3. Estimation of Parameters
7. Conclusions
- The fluid primary velocity and temperature distribution decreased in the area of the boundary layer with the simultaneous increase of the MHD and FHD parameters, whereas the corresponding secondary velocities were increased.
- The increment of the magnetic field resulted in a reduction of the skin friction coefficient on the wall, whereas the heat transfer on the wall was increased.
- With a greater elapsing of time , the velocity and temperature profiles were found to be enhanced.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Velocity components in the direction | |
| Cartesian coordinates | |
| Fluid pressure | |
| Magnetization | |
| Magnetic field intensity | |
| Magnetic induction | |
| Fluid temperature inside the boundary layer | |
| Fluid temperature far away from the sheet | |
| Temperature of the sheet | |
| Dimensionless velocity components in the directions | |
| Dimensionless pressure | |
| Dimensionless temperature | |
| Time | |
| Density of fluid | |
| Kinematic viscosity | |
| Dynamic viscosity | |
| Magnetic permeability | |
| Electrical conductivity | |
| Specific heat constant pressure | |
| Thermal conductivity | |
| Prandtl number (dimensionless) | |
| Eckert number (dimensionless) | |
| Dimensionless Curie temperature | |
| Ferromagnetic interaction parameter (dimensionless) | |
| Magnetohydrodynamic parameter (dimensionless) | |
| Dimensionless time |
Appendix A
References
- Haik, Y.; Pai, V.; Chen, C.J. Development of magnetic device for cell separation. J. Magn. Magn. Mater. 1999, 194, 261. [Google Scholar] [CrossRef]
- Plavins, J.; Lauva, M. Study of colloidal magnetic binding erythrocytes: Prospects for cell separation. J. Magn. Magn. Mater. 1999, 122, 349. [Google Scholar] [CrossRef]
- Voltairas, P.A.; Fotiadis, D.I.; Michalis, L.K. Hydrodynamics of magnetic drug targeting. J. Biomech. 2002, 35, 813–821. [Google Scholar] [CrossRef]
- Ruuge, E.K.; Rusetski, A.N. Magnetic fluid as drug carries: Targeted transport of drugs by a magnetic field. J. Magn. Magn. Mater. 1993, 122, 335. [Google Scholar] [CrossRef]
- Misra, J.C.; Sinha, A.; Shit, G.C. Flow of a biomagnetic viscoelastic fluid: Application to estimation of blood flow in arteries during electromagnetic hyperthermia, a therapeutic procedure for cancer treatment. Appl. Math. Mech. 2011, 13, 1405–1420. [Google Scholar] [CrossRef]
- Lauva, M.; Plavins, J. Study of Colloidal Magnetite Binding Erythrocytes: Prospects for cell separation. J. Magn. Magn. Mater. 1993, 122, 349–353. [Google Scholar] [CrossRef]
- Fiorentini, G.; Szasa, S. Hyperthermia today: Electric energy, a new opportunity in cancer treatment. J. Cancer Res. Ther. 2006, 2, 41–46. [Google Scholar] [CrossRef]
- Haik, Y.; Chen, C.J.; Pai, V.M. Development of biomagnetic fluid dynamics. In Proceedings of the IX International SYMPOSIUM on Transport Properties in Thermal Fluid Engineering, Pacific Center of Thermal Fluid Engineering, Singapore, 25–28 June 1996; pp. 121–126. [Google Scholar]
- Rosensweig, R.E. Ferrohydrodynamics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Bashtovoy, V.G.; Berkovsky, B.M.; Vislovich, A.N. Introduction to Thermomechanics of Magnetic Fluids; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Tzirtzilakis, E.E. A mathematical model for blood flow in magnetic field. Phys. Fluids 2005, 17, 077103-15. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. J. Appl. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Andersson, H.I.; Valnes, O.A. Flow of a heated ferrofluid over a stretching sheet in the presence of a magnetic dipole. Acta Mech. 1998, 128, 39–47. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R. Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J. Mol. Liq. 2016, 215, 549–554. [Google Scholar] [CrossRef]
- Tzirtzilakis, E.E.; Kafoussias, N.G. Biomagnetic fluid flow over a stretching sheet with nonlinear temperature dependent magnetization. Z. Angew. Math. Phys. 2003, 54, 551–565. [Google Scholar]
- Tzirtzilakis, E.E.; Tanoudis, G.B. Numerical study of Biomagnetic fluid flow over a stretching sheet with heat transfer. Int. J. Numer. Methods Heat Fluid Flow 2003, 13, 830–848. [Google Scholar] [CrossRef]
- Murtaza, M.G.; Tzirtzilakis, E.E.; Ferdows, M. Effect of electrical conductivity and magnetization on the biomagnetic fluid flow over a stretching sheet. Z. Angew. Math. Phys. 2017, 68, 93. [Google Scholar] [CrossRef]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. MHD stagnation-point flow and heat transfer towards stretching sheet with induced magnetic field. Appl. Math. Mech. 2011, 32, 409–418. [Google Scholar] [CrossRef]
- Misra, J.C.; Sinha, A. Effect of thermal radiation on MHD flow of blood and heat transfer in a permeable capillary in stretching motion. Heat Mass Transf. 2013, 49, 617–628. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S.; Jana, R.N.; Makinde, O.D. Entropy analysis of unsteady magneto-nanofluid flow past accelerating stretching sheet with convective boundary condition. Appl. Math. Mech. 2015, 36, 1593–1610. [Google Scholar]
- Hayat, T.; Shafiq, A.; Alsaedi, A.; Shahzad, S.A. Unsteady MHD flow over exponentially stretching sheet with slip conditions. Appl. Math. Mech. 2016, 37, 193–208. [Google Scholar] [CrossRef]
- Misra, J.C.; Shit, G.C.; Rath, H.J. Flow and heat transfer of a MHD viscoelastic fluid in a channel with stretching walls: Some applications to haemodynamics. Comput. Fluids 2008, 37, 1–11. [Google Scholar] [CrossRef]
- Carnahan, B.; Luther, H.A.; Wilkes, J.O. Applied Numerical Methods; John Wiley and Sons: New York, NY, USA, 1969. [Google Scholar]
- Tzirtzilakis, E.E.; Xenos, M.A. Biomagnetic fluid flow in a driven cavity. Meccanica 2013, 48, 187–200. [Google Scholar] [CrossRef]
- Matsuki, H.; Yamasawa, K.; Murakami, K. Experimental Considerations on a new Automatic Cooling Device Using Temperature Sensitive Magnetic Fluid. IEEE Trans. Magn. 1977, 13, 1143–1145. [Google Scholar] [CrossRef]
- Davidson, P.A. An Introduction to Magnetohydrodynamics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Callahan, G.D.; Marner, W.J. Transient free convection with mass transfer on an isothermal vertical flat plate. Int. J. Heat Mass Transf. 1976, 19, 165–174. [Google Scholar] [CrossRef]
- Gabriel, C.; Peyman, A.; Grant, E.H. Electrical conductivity of tissue at frequencies below 1 MHz. Phys. Med. Biol. 2009, 54, 4863–4878. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.S.; Wahiduzzaman, M.; Uddin, M.S.; Sazad, M.A.K. Finite difference solution of MHD free convection heat and mass transfer flow of a nanofluid along a stretching sheet with heat generation effects. Indian J. Theor. Phys. 2012, 60, 285–306. [Google Scholar]


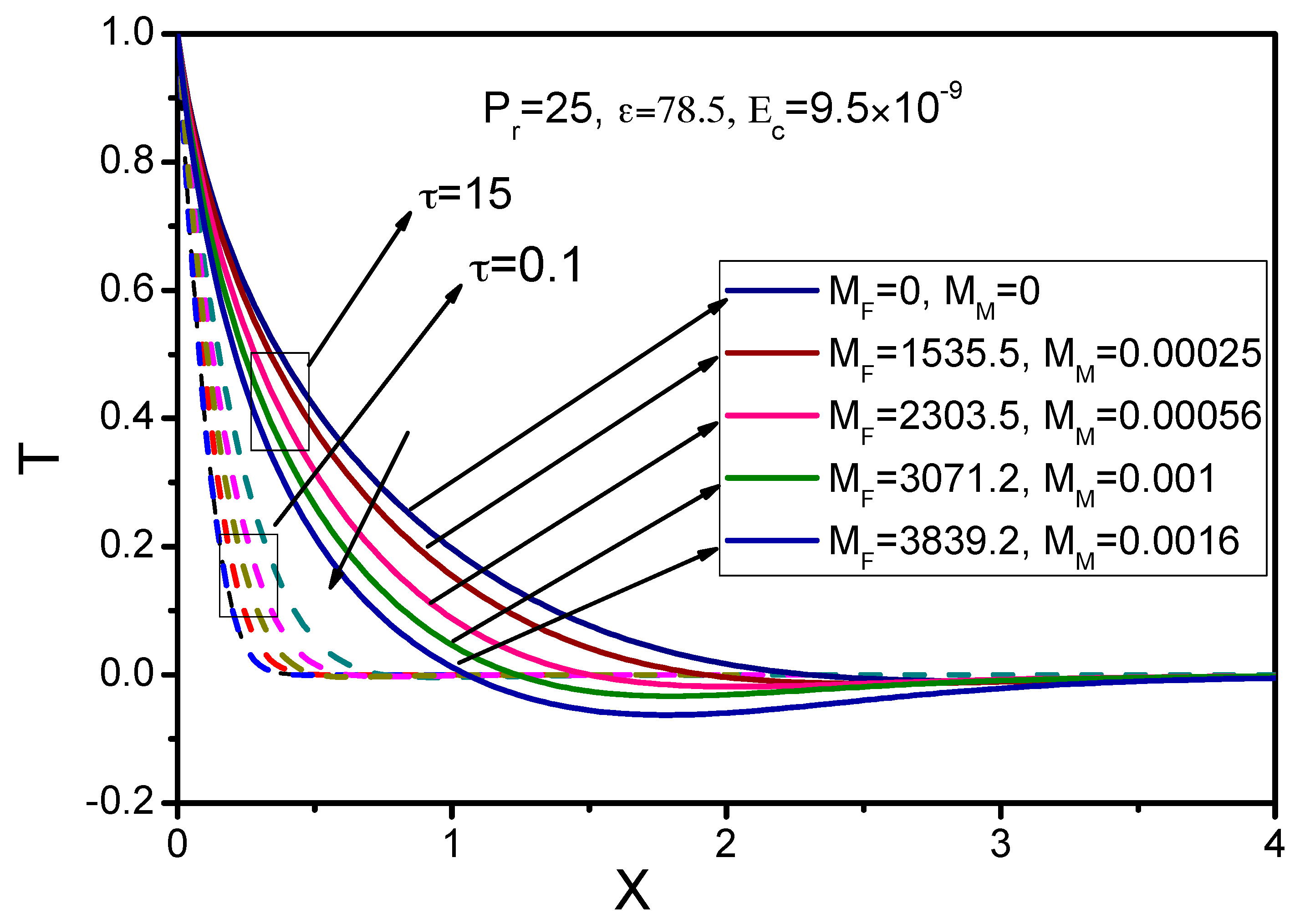

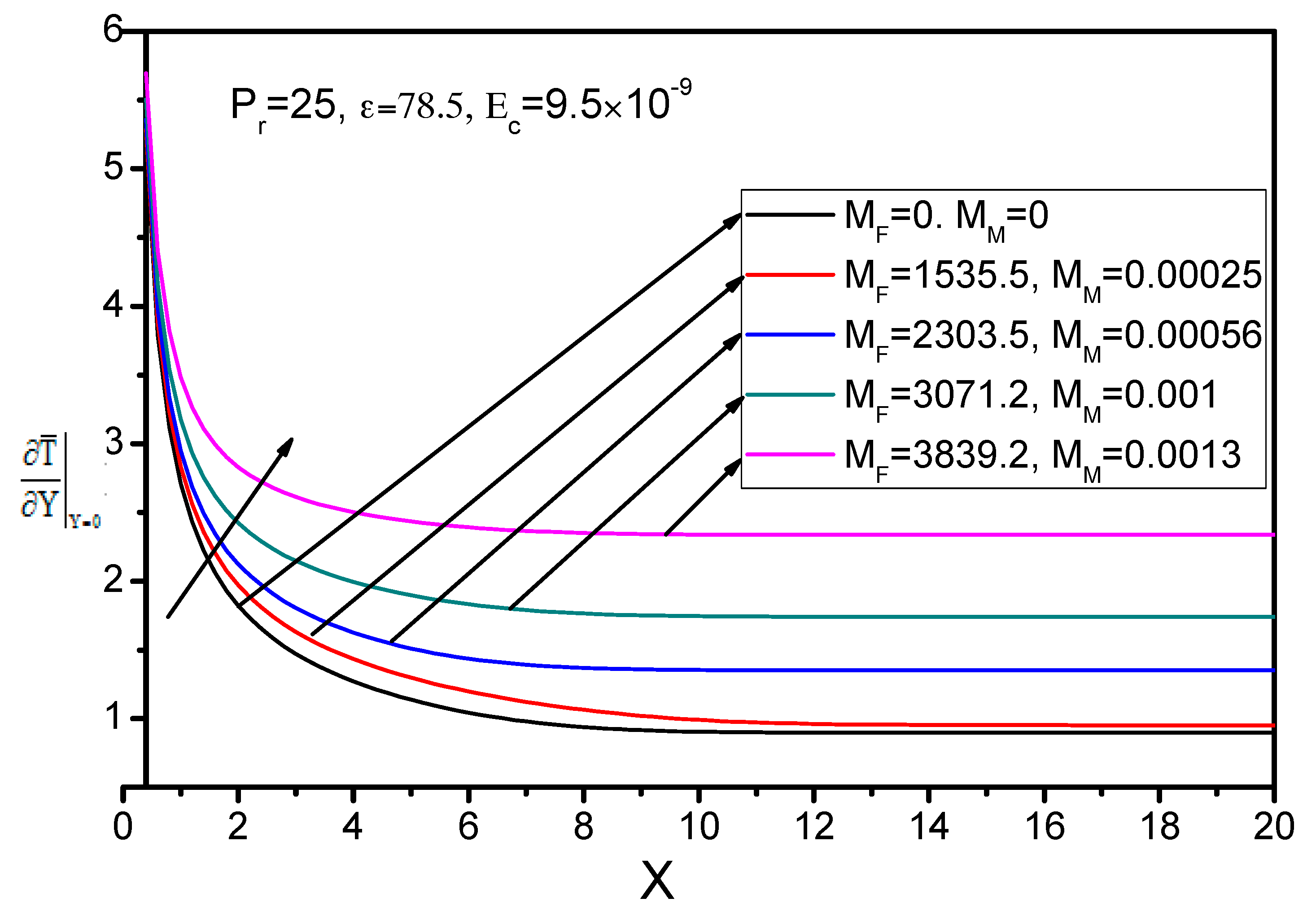
| Magnetohydrodynamic Number (MM) | Ferromagnetic Number (MF) | |
|---|---|---|
| 2 T | 0.000062 | 767.8 |
| 4 T | 0.00025 | 1535.5 |
| 6 T | 0.00056 | 2303.5 |
| 8 T | 0.001 | 3071.2 |
| 9 T | 0.0013 | 3455.1 |
| 10 T | 0.0016 | 3839.2 |
| Present Result | Khan et al. [29] | |
|---|---|---|
| 0.2 | 0.1689 | 0.1694 |
| 0.7 | 0.4524 | 0.4544 |
| 2 | 0.909 | 0.9109 |
| 7 | 1.8930 | 1.8960 |
| 20 | 3.3532 | 3.3541 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murtaza, M.G.; Tzirtzilakis, E.E.; Ferdows, M. Stability and Convergence Analysis of a Biomagnetic Fluid Flow Over a Stretching Sheet in the Presence of a Magnetic Field. Symmetry 2020, 12, 253. https://doi.org/10.3390/sym12020253
Murtaza MG, Tzirtzilakis EE, Ferdows M. Stability and Convergence Analysis of a Biomagnetic Fluid Flow Over a Stretching Sheet in the Presence of a Magnetic Field. Symmetry. 2020; 12(2):253. https://doi.org/10.3390/sym12020253
Chicago/Turabian StyleMurtaza, Md. Ghulam, Efstratios Emmanouil Tzirtzilakis, and Mohammad Ferdows. 2020. "Stability and Convergence Analysis of a Biomagnetic Fluid Flow Over a Stretching Sheet in the Presence of a Magnetic Field" Symmetry 12, no. 2: 253. https://doi.org/10.3390/sym12020253
APA StyleMurtaza, M. G., Tzirtzilakis, E. E., & Ferdows, M. (2020). Stability and Convergence Analysis of a Biomagnetic Fluid Flow Over a Stretching Sheet in the Presence of a Magnetic Field. Symmetry, 12(2), 253. https://doi.org/10.3390/sym12020253




