The Gray-Box Based Modeling Approach Integrating Both Mechanism-Model and Data-Model: The Case of Atmospheric Contaminant Dispersion
Abstract
1. Introduction
2. Materials
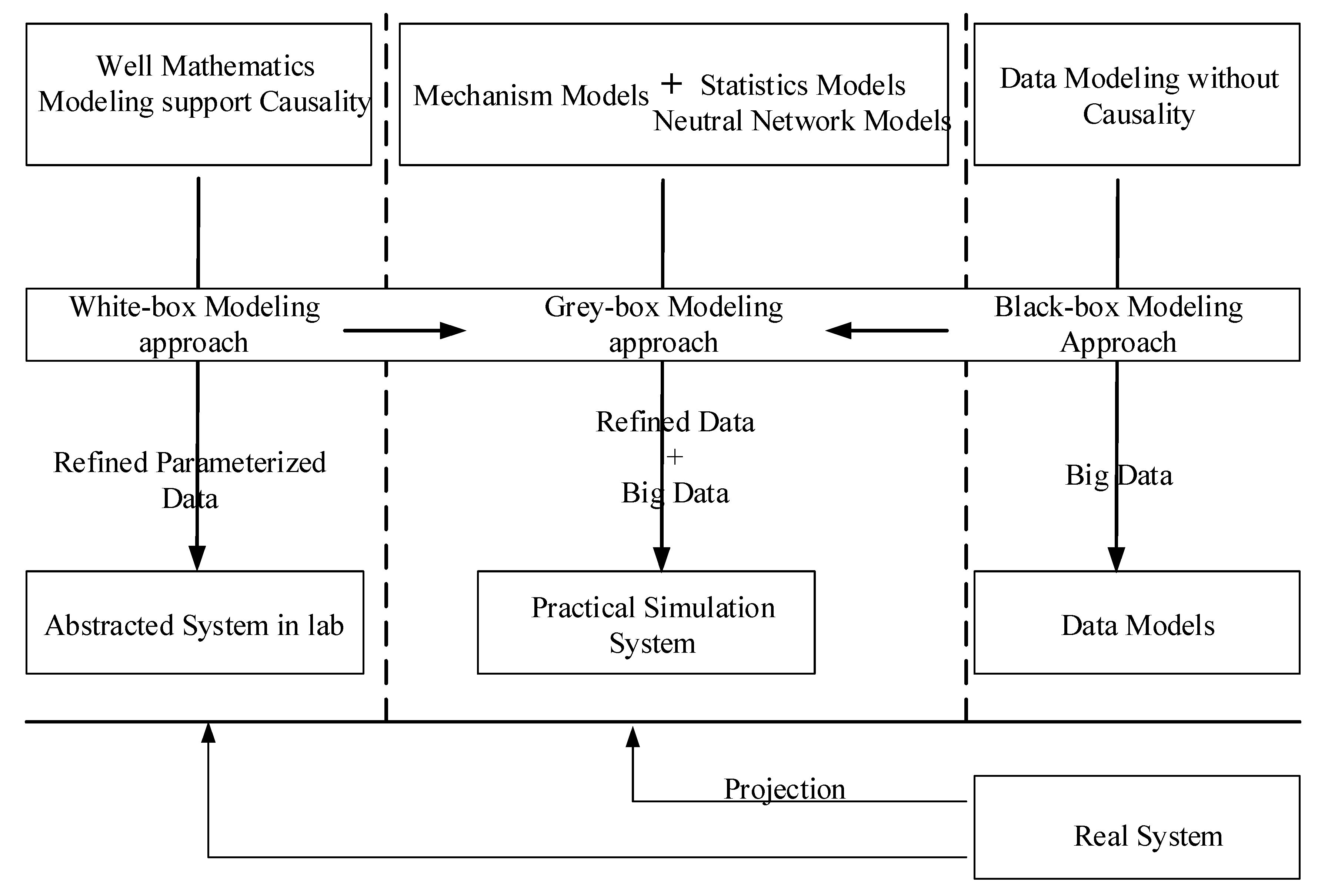
2.1. The Gray-Box Based Modeling Approach
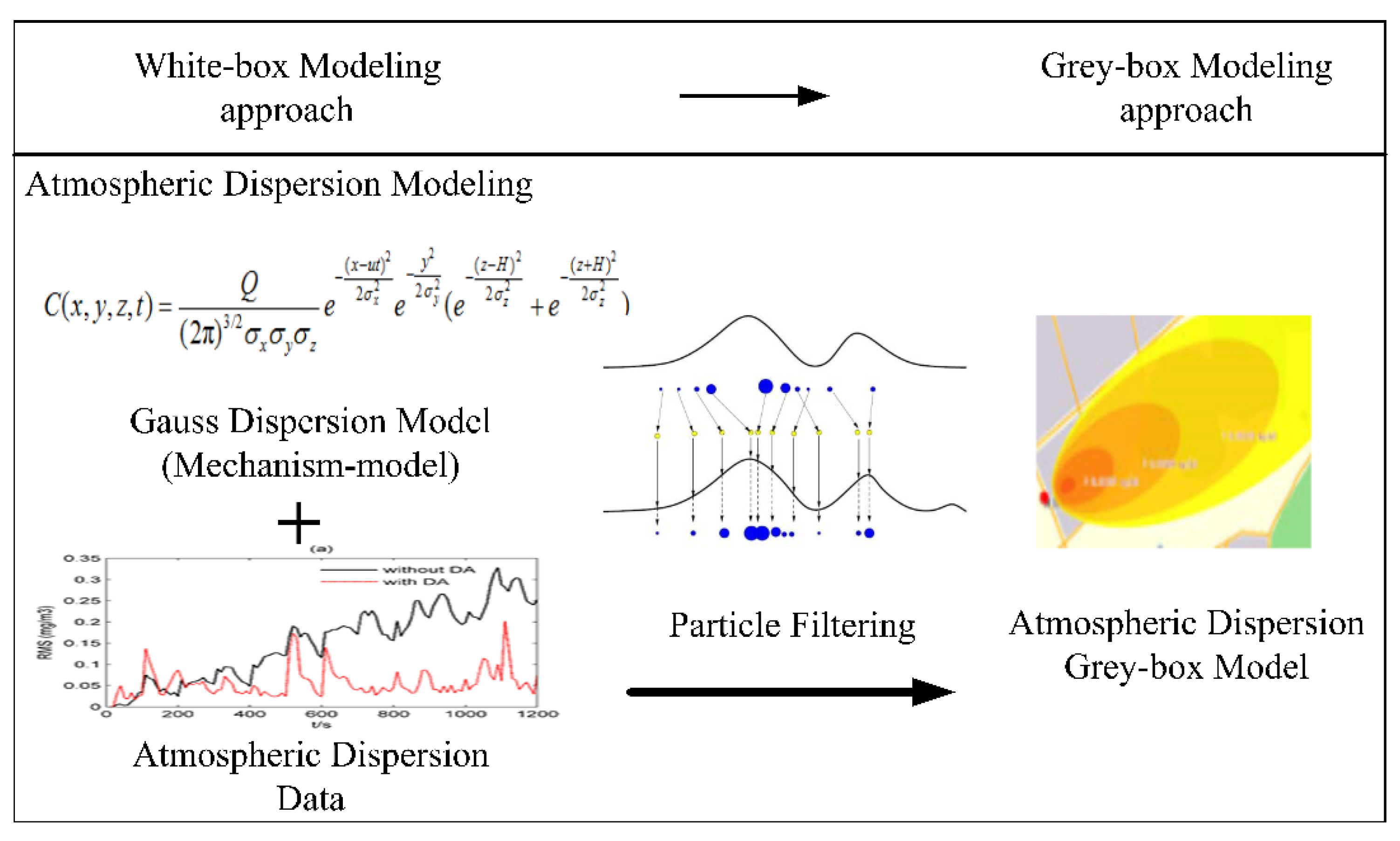
2.2. Dynamic Data Driven Atmospheric Dispersion Modeling Method (from White-Box to Gray-Box)
2.2.1. Gaussian Dispersion Model
2.2.2. Data Assimilation Framework Based on a Particle Filter
2.3. Atmospheric Dispersion Modeling Method Based on Gaussian-Machine Learning (from Black-Box to Gray-Box)
2.3.1. Support Vector Regression
2.3.2. Feature Construction Method Based on Gaussian Model Knowledge
3. Case 1: Dynamic Data Driven Atmospheric Dispersion Modeling Method (from White-Box to Gray-Box)
3.1. Experimental Design
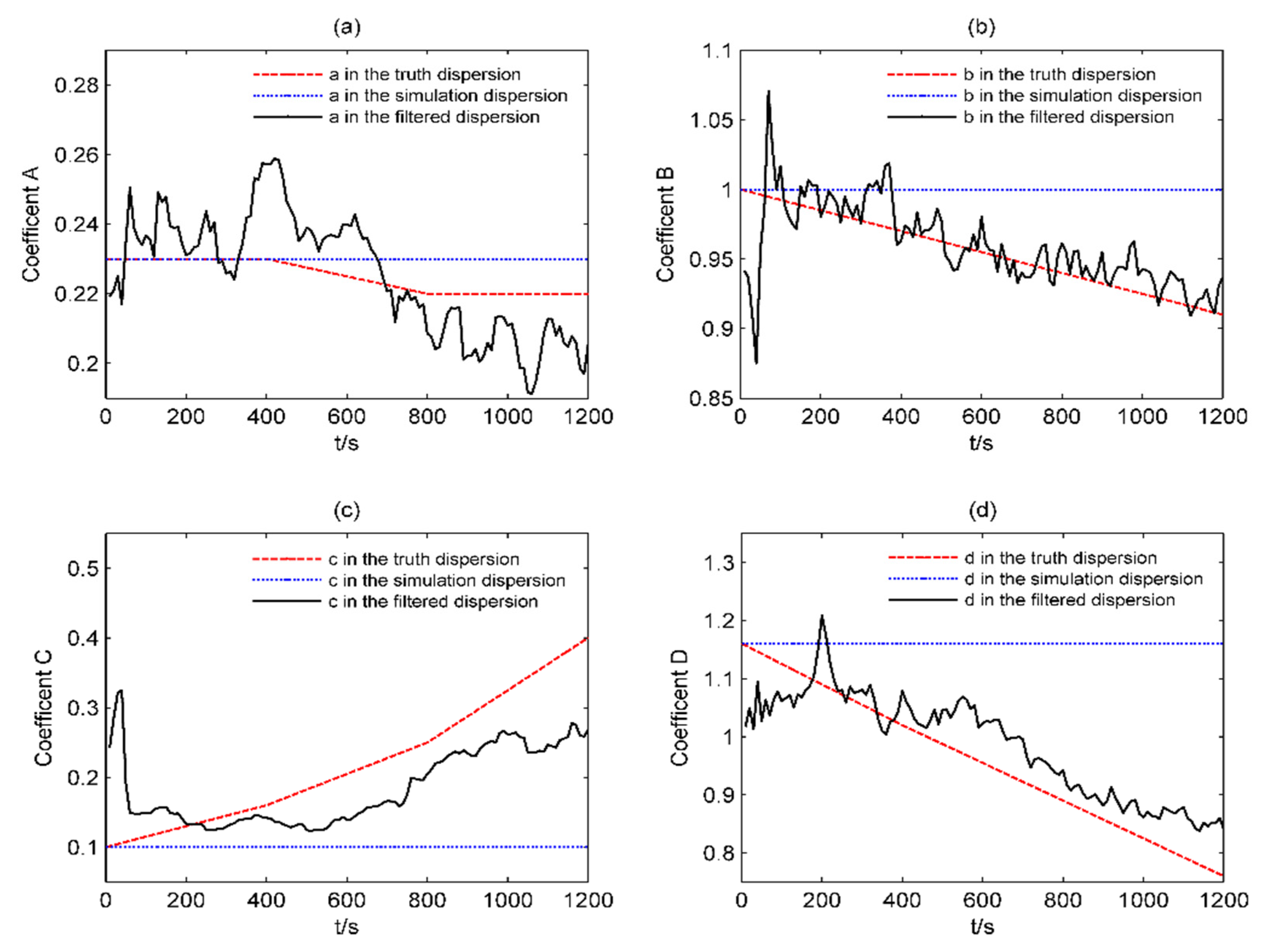
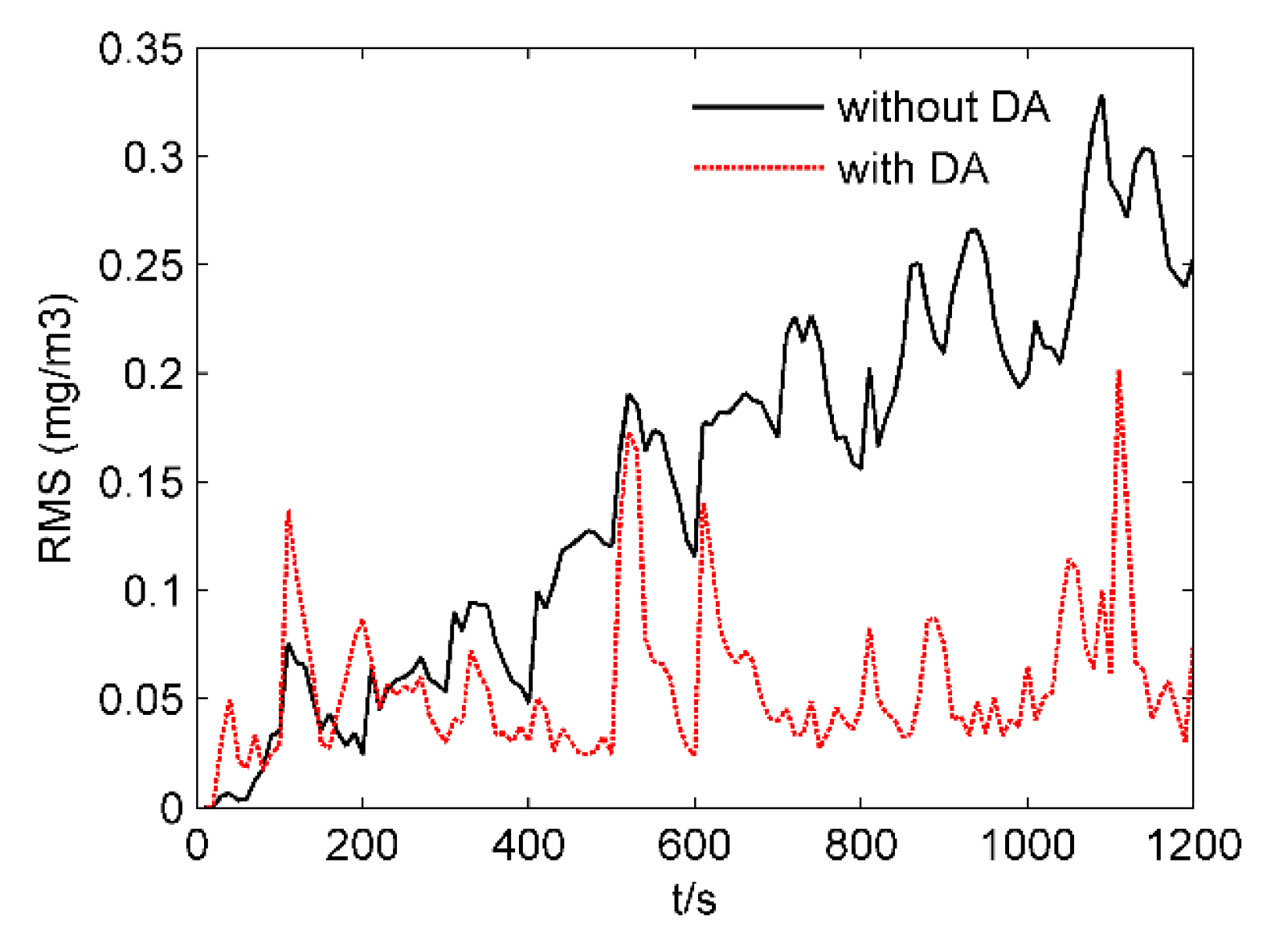
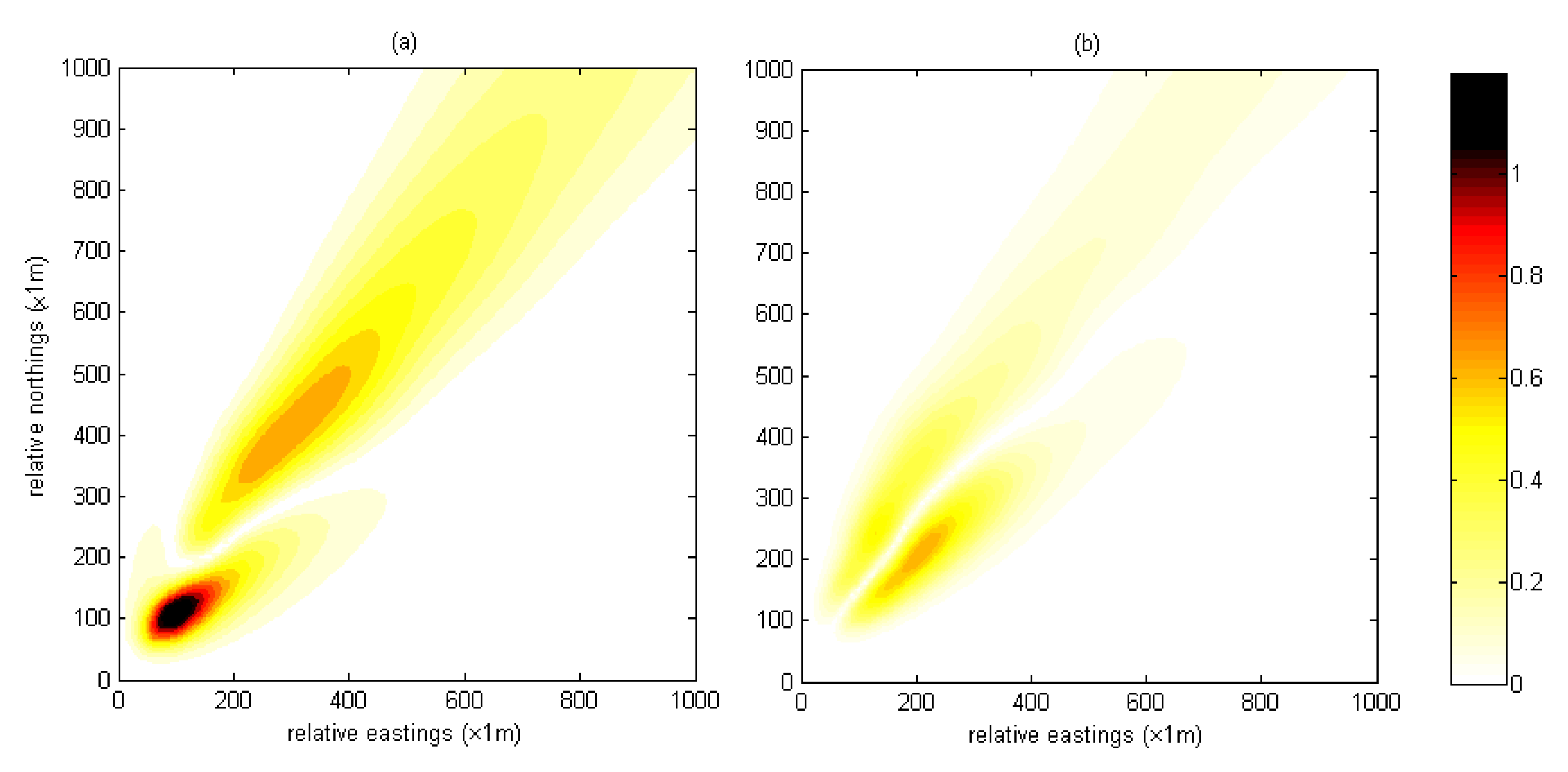
3.2. Experimental Results
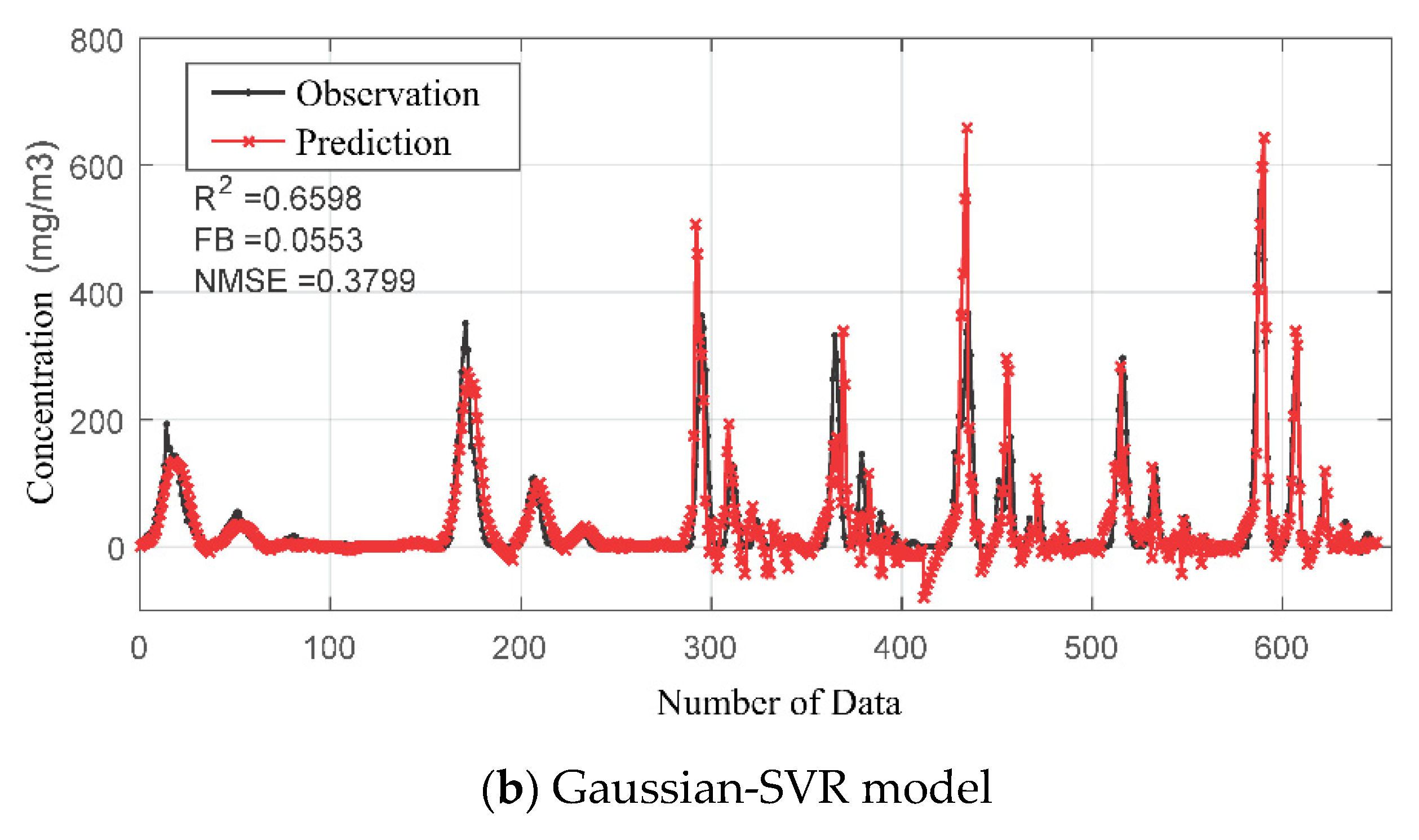
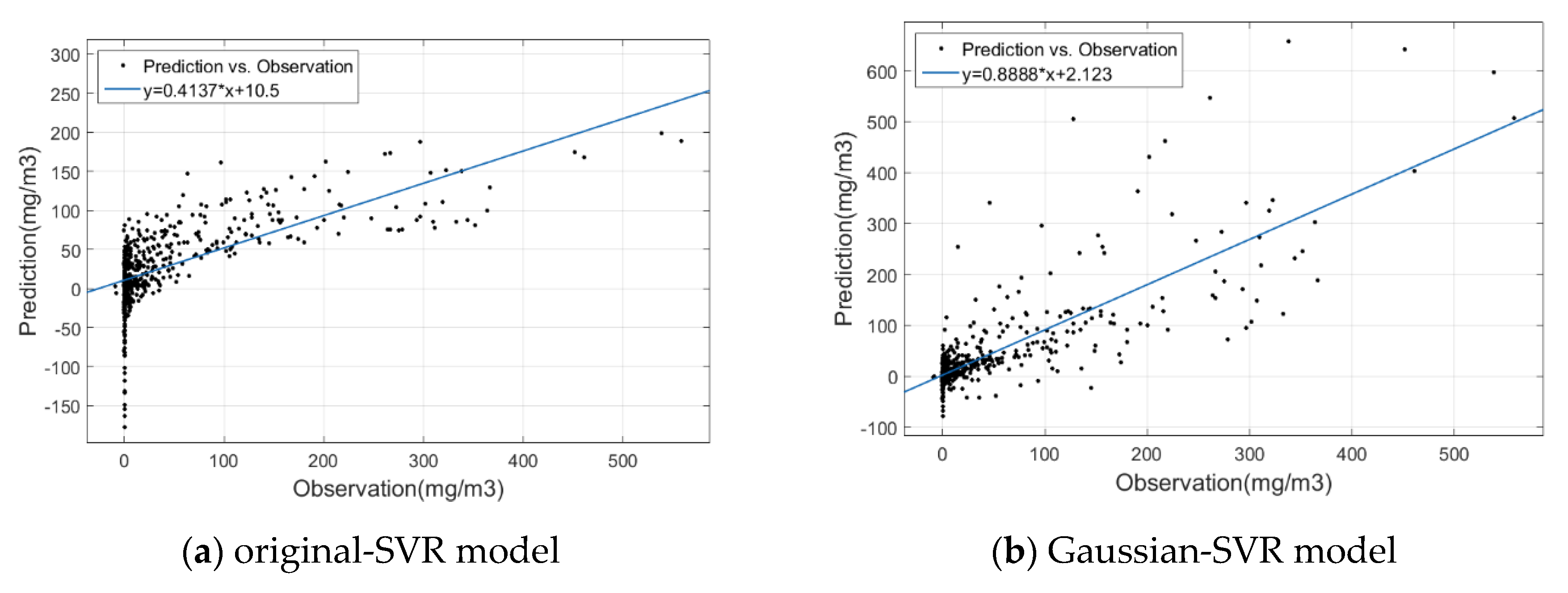
4. Case 2: Atmospheric Dispersion Modeling Method Based on Gaussian-Machine Learning (from Black-Box to Gray-Box)
5. Conclusions and Expectations
Author Contributions
Funding
Conflicts of Interest
References
- Chen, B.; Qiu, X.; Wang, Y. An Intelligent ACP based Experimental Approach. J. Syst. Simul. 2017, 29, 2064–2072. [Google Scholar]
- Kedi, H. System Simulation Techniques; Press of National University of Defense Technology: Changsha, China, 1998. [Google Scholar]
- Gerstlauer, A.; Haubelt, C.; Pimentel, A.D.; Stefanov, T.P.; Gajski, D.D.; Teich, J. Electronic system-level synthesis methodologies. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2009, 28, 1517–1530. [Google Scholar] [CrossRef]
- Builder, C.H.; Bankes, S.C. Artificial Societies: A Concept for Basic Research on the Societal Impacts of Information Technology; RAND Corporation: Santa Monica, CA, USA, 1991. [Google Scholar]
- Yi, L.; Shunjiang, N.; Wenguo, W. Development of the Public Safety System and a Security-Guaranteed Society. Strateg. Study Chin. Acad. Eng. 2017, 19, 118–123. [Google Scholar]
- Bock, H.G.; Carraro, T.; Jäger, W.; Körkel, S.; Rannacher, R.; Schlöder, J.P. Model Based Parameter Estimation: Theory and Applications; Springer Science & Business Media: Berlin, Germany, 2013; Volume 4. [Google Scholar]
- Zhu, Z.; Chen, B.; Qiu, S.; Wang, R.; Wang, Y.; Ma, L.; Qiu, X. A data-driven approach for optimal design of integrated air quality monitoring network in a chemical cluster. R. Soc. Open Sci. 2018, 5, 180889. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.L.; Chen, J.M.; Tung, C.W. A data mining approach for retail knowledge discovery with consideration of the effect of shelf-space adjacency on sales. Decis. Support Syst. 2006, 42, 1503–1520. [Google Scholar] [CrossRef]
- Sagae, K.; Lavie, A. Combining rule-based and data-driven techniques for grammatical relation extraction in spoken language. In Proceedings of the Eighth International Conference on Parsing Technologies, Nancy, France, 23–25 April 2003. [Google Scholar]
- Dahl, N.; Xue, H.; Hu, X.; Xue, M. Coupled fire–atmosphere modeling of wildland fire spread using DEVS-FIRE and ARPS. Nat. Hazards 2015, 77, 1013–1035. [Google Scholar] [CrossRef]
- Wilkie, D.; Sewall, J.; Lin, M.C. Transforming GIS data into functional road models for large-scale traffic simulation. IEEE Trans. Vis. Comput. Graph. 2011, 18, 890–901. [Google Scholar] [CrossRef]
- Varma, D.R.; Guest, I. The Bhopal accident and methyl isocyanate toxicity. J. Toxicol. Environ. Health 1993, 40, 513–529. [Google Scholar] [CrossRef]
- Fernando, H.; Lee, S.; Anderson, J.; Princevac, M.; Pardyjak, E.; Grossman Clarke, S. Urban fluid mechanics: Air circulation and contaminant dispersion in cities. Environ. Fluid Mech. 2001, 1, 107–164. [Google Scholar] [CrossRef]
- Turner, D.B. A diffusion model for an urban area. J. Appl. Meteorol. 1964, 3, 83–91. [Google Scholar] [CrossRef]
- Pontiggia, M.; Derudi, M.; Busini, V.; Rota, R. Hazardous gas dispersion: A CFD model accounting for atmospheric stability classes. J. Hazard. Mater. 2009, 171, 739–747. [Google Scholar] [CrossRef]
- Xing, J.; Liu, Z.; Huang, P.; Feng, C.; Zhou, Y.; Zhang, D.; Wang, F. Experimental and numerical study of the dispersion of carbon dioxide plume. J. Hazard. Mater. 2013, 256–257, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Flesch, T.K.; Wilson, J.D.; Yee, E. Backward-time lagrangian stochastic dispersion models and their application to estimate gaseous emissions. J. Appl. Meteorol. 1995, 34, 1320–1332. [Google Scholar] [CrossRef]
- Wilson, J.D.; Sawford, B.L. Review of Lagrangian stochastic models for trajectories in the turbulent atmosphere. Bound.-Layer Meteorol. 1996, 78, 191–210. [Google Scholar] [CrossRef]
- Briggs, G. Diffusion Estimation for Small Emissions. Preliminary Report; Atmospheric Turbulence and Diffusion Lab., National Oceanic and Atmospheric Administration: Oak Ridge, TN, USA, 1973.
- Hanna, S.R.; Briggs, G.A.; Hosker, R.P., Jr. Handbook on Atmospheric Diffusion; Atmospheric Turbulence and Diffusion Lab., National Oceanic and Atmospheric Administration: Oak Ridge, TN, USA, 1982.
- Krysta, M.; Bocquet, M.; Sportisse, B.; Isnard, O. Data assimilation for short-range dispersion of radionuclides: An application to wind tunnel data. Atmos. Environ. 2006, 40, 7267–7279. [Google Scholar] [CrossRef]
- Reddy, K.V.U.; Cheng, Y.; Singh, T.; Scott, P.D. Data assimilation in variable dimension dispersion models using particle filters. In Proceedings of the 2007 10th International Conference on Information Fusion, Quebec City, QC, Canada, 9–12 July 2007. [Google Scholar]
- Zheng, D.; Leung, J.; Lee, B.; Lam, H. Data assimilation in the atmospheric dispersion model for nuclear accident assessments. Atmos. Environ. 2007, 41, 2438–2446. [Google Scholar] [CrossRef]
- Pelliccioni, A.; Tirabassi, T. Air dispersion model and neural network: A new perspective for integrated models in the simulation of complex situations. Environ. Model. Softw. 2006, 21, 539–546. [Google Scholar] [CrossRef]
- Wang, B.; Chen, B.; Zhao, J. The real-time estimation of hazardous gas dispersion by the integration of gas detectors, neural network and gas dispersion models. J. Hazard. Mater. 2015, 300, 433–442. [Google Scholar] [CrossRef]
- Yeganeh, B.; Motlagh, M.S.P.; Rashidi, Y.; Kamalan, H. Prediction of CO concentrations based on a hybrid Partial Least Square and Support Vector Machine model. Atmos. Environ. 2012, 55, 357–365. [Google Scholar] [CrossRef]
- Ma, D.; Zhang, Z. Contaminant dispersion prediction and source estimation with integrated Gaussian-machine learning network model for point source emission in atmosphere. J. Hazard. Mater. 2016, 311, 237–245. [Google Scholar] [CrossRef]
- Gifford, F.A., Jr. Use of routine meteorological observations for estimating atmospheric dispersion. Nucl. Saf. 1961, 2, 47–51. [Google Scholar]
- Pasquill, F. The estimation of the dispersion of windborne material. Met. Mag. 1961, 90, 33. [Google Scholar]
- Carrascal, M.; Puigcerver, M.; Puig, P. Sensitivity of Gaussian plume model to dispersion specifications. Theor. Appl. Climatol. 1993, 48, 147–157. [Google Scholar] [CrossRef]
- Zhu, Z.; Qiu, S.; Chen, B.; Wang, R.; Qiu, X. Data-driven hazardous gas dispersion modeling using the integration of particle filtering and error propagation detection. Int. J. Environ. Res. Public Health 2018, 15, 1640. [Google Scholar] [CrossRef] [PubMed]
- Bouttier, F.; Courtier, P. Data assimilation concepts and methods March 1999. Meteorol. Train. Course Lect. Ser. ECMWF 2002, 718, 59. [Google Scholar]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. F-Radar Signal Process. 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Senne, K. Stochastic processes and filtering theory. IEEE Trans. Autom. Control 1972, 17, 752–753. [Google Scholar] [CrossRef]
- Boznar, M.; Lesjak, M.; Mlakar, P. A neural network-based method for short-term predictions of ambient SO2 concentrations in highly polluted industrial areas of complex terrain. Atmos. Environ. Part B Urban Atmos. 1993, 27, 221–230. [Google Scholar] [CrossRef]
- Krasnopolsky, V.M.; Schiller, H. Some neural network applications in environmental sciences. Part I: Forward and inverse problems in geophysical remote measurements. Neural Netw. 2003, 16, 321–334. [Google Scholar] [CrossRef]
- Qiu, S.; Chen, B.; Wang, R.; Zhu, Z.; Wang, Y.; Qiu, X. Estimating contaminant source in chemical industry park using UAV-based monitoring platform, artificial neural network and atmospheric dispersion simulation. RSC Adv. 2017, 7, 39726–39738. [Google Scholar] [CrossRef]
- Barad, M.L. Project Prairie Grass, a Field Program in Diffusion; Air Force Cambridge Research Center: Bedford, MA, USA, 1958; Volume 1. [Google Scholar]
- Steven Hanna, J.; Olesen, H.R. Indianapolis Tracer Data and Meteorological Data; National Environmental Research Institute: Roskilde, Denmark, 2005.
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Chen, B.; Qiu, S.; Ma, L.; Zhu, Z.; Wang, Y.; Qiu, X. Hazardous source estimation using an artificial neural network, particle swarm optimization and a simulated annealing algorithm. Atmosphere 2018, 9, 119. [Google Scholar] [CrossRef]
- Cervone, G.; Franzese, P. Non-Darwinian evolution for the source detection of atmospheric releases. Atmos. Environ. 2011, 45, 4497–4506. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Huang, L.; Ristic, B. Evaluation of Bayesian source estimation methods with Prairie Grass observations and Gaussian plume model: A comparison of likelihood functions and distance measures. Atmos. Environ. 2017, 152, 519–530. [Google Scholar] [CrossRef]
- Wang, R.; Chen, B.; Qiu, S.; Zhu, Z.; Ma, L.; Qiu, X.; Duan, W. Real-Time data driven simulation of air contaminant dispersion using particle filter and UAV sensory system. In Proceedings of the 2017 IEEE/ACM 21st International Symposium on Distributed Simulation and Real Time Applications (DS-RT), Rome, Italy, 18–20 October 2017; pp. 1–4. [Google Scholar]
- Cui, J.; Lang, J.; Chen, T.; Cheng, S.; Shen, Z.; Mao, S. Investigating the impacts of atmospheric diffusion conditions on source parameter identification based on an optimized inverse modelling method. Atmos. Environ. 2019, 205, 19–29. [Google Scholar] [CrossRef]
- Ma, D.; Gao, J.; Zhang, Z.; Wang, Q. An Improved Firefly Algorithm for Gas Emission Source Parameter Estimation in Atmosphere. IEEE Access 2019, 7, 111923–111930. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 27. [Google Scholar] [CrossRef]
- Ma, D.; Deng, J.; Zhang, Z. Comparison and improvements of optimization methods for gas emission source identification. Atmos. Environ. 2013, 81, 188–198. [Google Scholar] [CrossRef]


| Mechanism (White-Box) Model | Data (Black-Box) Model | |
|---|---|---|
| Model representation | Cause-effect relationship between variables | Associational relationship between variables |
| Structure of the model | System knowledge required Dynamic map of (input, state) to output | No knowledge about system required Static map of input to output |
 (State Q within model) |  (No state within model) | |
| Modeling means | Physical and/or operational laws | Intelligent techniques |
| Condition for valid prediction | Model validation | System structure remains unchanged before and after training |
| Anomaly/non-existing system | Applicable (as in rare event or new design) | Not applicable |
| Parameters | Symbol | Unit | Whether Choosing as an Input Parameter |
|---|---|---|---|
| Downwind distance | Dx | m | Y |
| Crosswind distance | Dy | m | Y |
| Source height | H | m | N |
| Interest point height | z | m | Y |
| Source release rate | q | g s−1 | Y |
| Atmospheric stability level | STA | / | Y |
| Wind direction | d | deg | Y |
| Wind speed | v | m s-1 | Y |
| Mixed layer height | zm | m | N |
| Cloud height | zc | m | N |
| Cloud cover rate | Pc | % | N |
| Temperature | T | K | N |
| Time (s) | Atmospheric Stability | Influence Coefficient | |||
|---|---|---|---|---|---|
| a | b | c | d | ||
| 0 | Level A | 0.23 | 1.00 | 0.10 | 1.16 |
| 400 | Level B | 0.23 | 0.97 | 0.16 | 1.02 |
| 800 | Level C | 0.22 | 0.94 | 0.25 | 0.89 |
| 1200 | Level D | 0.22 | 0.91 | 0.40 | 0.76 |
| Experiment Number | Atmospheric Dispersion Model | Description |
|---|---|---|
| A | Gaussian multi-puffs model (white-box model) | Control group: comparison with experiment B |
| B | Gaussian multi-puffs model with data assimilation (gray-box model) | Experimental group: test modeling effect of data assimilation |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Wang, Y.; Wang, R.; Zhu, Z.; Ma, L.; Qiu, X.; Dai, W. The Gray-Box Based Modeling Approach Integrating Both Mechanism-Model and Data-Model: The Case of Atmospheric Contaminant Dispersion. Symmetry 2020, 12, 254. https://doi.org/10.3390/sym12020254
Chen B, Wang Y, Wang R, Zhu Z, Ma L, Qiu X, Dai W. The Gray-Box Based Modeling Approach Integrating Both Mechanism-Model and Data-Model: The Case of Atmospheric Contaminant Dispersion. Symmetry. 2020; 12(2):254. https://doi.org/10.3390/sym12020254
Chicago/Turabian StyleChen, Bin, Yiduo Wang, Rongxiao Wang, Zhengqiu Zhu, Liang Ma, Xiaogang Qiu, and Weihui Dai. 2020. "The Gray-Box Based Modeling Approach Integrating Both Mechanism-Model and Data-Model: The Case of Atmospheric Contaminant Dispersion" Symmetry 12, no. 2: 254. https://doi.org/10.3390/sym12020254
APA StyleChen, B., Wang, Y., Wang, R., Zhu, Z., Ma, L., Qiu, X., & Dai, W. (2020). The Gray-Box Based Modeling Approach Integrating Both Mechanism-Model and Data-Model: The Case of Atmospheric Contaminant Dispersion. Symmetry, 12(2), 254. https://doi.org/10.3390/sym12020254





