Asymptotically Flat, Spherical, Self-Interacting Scalar, Dirac and Proca Stars

Abstract

We present a comparative analysis of the self-gravitating solitons that arise in the Einstein–Klein–Gordon, Einstein–Dirac, and Einstein–Proca models, for the particular case of static, spherically symmetric spacetimes. Differently from the previous study by Herdeiro, Pombo and Radu in 2017, the matter fields possess suitable self-interacting terms in the Lagrangians, which allow for the existence of Q-ball-type solutions for these models in the flat spacetime limit. In spite of this important difference, our analysis shows that the high degree of universality that was observed by Herdeiro, Pombo and Radu remains, and various spin-independent common patterns are observed.

1. Introduction and Motivation

1.1. General Remarks

The (modern) idea of solitons, as extended particle-like configurations, can be traced back (at least) to Lord Kelvin, around one and half centuries ago, who proposed that atoms are made of vortex knots [1]. However, the first explicit example of solitons in a relativistic field theory was found by Skyrme [2,3], (almost) one hundred years later. The latter, dubbed Skyrmions, exist in a model with four (real) scalars that are subject to a constraint. They were proposed as field theory realizations of baryons; nonetheless, Skyrmions capture the basic properties of a generic soliton.

In the context of this work, solitons are defined as spatially localized, singularity-free solutions of a field theory model, which possess a finite mass and angular momentum (the fields may possess a non-trivial time-dependence, as for the solitons in this work. However, this dependence is absent at the level of the energy-momentum tensor. Additionally, in our definition, we shall ignore the issue of stability and do not impose the solutions possessing a topological charge). As already suspected in the literature before Skyrme’s seminal work (in a historical setting, a concrete realization of the idea of (relativistic) solitons was put forward in 1939 by Rosen [4], who looked for localized configurations which could be used as representations of extended particles), many non-linear field theories possess such solutions. The study of solitons has attracted a lot of attention in the last 50 years; they have important applications in various contexts, ranging from, e.g., the models of condensed matter physics to high energy physics and cosmology. Moreover, solitons are also significant for a nonperturbative quantum description of states. Famous examples of solitons include the sphalerons in the Standard Model [5] and the magnetic monopoles [6,7] in various extensions thereof.

A review of soliton physics in the non-gravitating case can be found in the textbooks [8,9]; also see the reviews [10,11]. In this work, we shall focus on a special class of solitons in four spacetime dimensions that are time-dependent (at the level of the matter field), but non-dissipative (with a time independent spacetime geometry), and carrying a Noether charge Q that is associated with a global $U\left(1\right)$ symmetry. We shall restrict ourselves to models with a single matter field (except for the fermionic case) and possessing a standard kinetic term. These solitons do not possess topological properties, but the field theory Lagrangian must have suitable self-interactions.

Three different models are considered here: (ungauged) field theories describing particles of spin $s=0,1/2,1$, with the goal of providing a comparative analysis of their spherically symmetric solitonic solutions. As such, this work is an extension of that in Ref. [12], which dealt with the same matter fields, but without self-interactions. The latter introduce a novel feature: self-interactions allow for the existence of solitonic solutions, even on a fixed flat spacetime background, i.e., ignoring gravity. As we shall see, self-interactions lead to a more intricate landscape of (gravitating) solutions, with some new qualitative features when compared to the picture that is revealed in [12].

Historically, in the non-gravitating case, solitons in a complex scalar field model have been known for more than 50 years, being dubbed $Q-balls$ by Coleman [13] (also see the previous work [14]). These are central for our discussion, sharing most of the basic features with the higher spin generalizations. Within a Dirac field model with a positive quartic self-interaction term, Ivanenko [15], Weyl [16], Heisenberg [17], and Finkelstein et al. [18,19] have made early attempts to construct particle-like solutions. However, the first rigorous numerical study of such configurations was been done by Soler in 1976 [20]. The case of a (Abelian) vector field has been ignored until recently; the study of Q-ball-like solutions was initiated by Loginov [21].

In all three cases, a large literature has grown based on these early studies, which includes generalizations in various directions. A particularly interesting case concerns the study of backreaction of these solutions on the spacetime geometry. This is a legitimate question, since the existence of solitons relies on the nonlinearity of the field theory and General Relativity (GR) is intrinsically highly nonlinear. Therefore, gravitational interactions could significantly alter the flat spacetime solitons.

The results in the literature prove that all flat space solitons survive when including gravity effects; however, a more complicated picture emerges when compared to the non-self-interacting case. The study of gravitating generalization of the flat spacetime Q-balls has started with Friedberg et al. [22]. The higher spin fields are less studied; GR generalization of the self-interacting spinors were only considered recently by Dzhunushaliev and Folomeev [23], while the gravitating Q-Proca stars have been studied by Brihaye et al. [24] and Minamitsuji [25].

The main purpose of this work is to review various existing results on this type of solitons, putting them together under a consistent set of notations and conventions. A comparative study is presented, which starts with the generic framework and scaling symmetries (Section 2). There and afterwards, the mathematical description of each of the three models is made in parallel in order to emphasise their similarities. The basic properties of solutions in a flat spacetime background are discussed in Section 3, where we adapt Deser’s argument [26] to find virial identities that yield some insight on the existence of such configurations. Gravity is included in Section 4; a curved spacetime generalization of the Deser-type virial identities is also discussed. Extending the models’ framework to include GR effects allows for the possibility to add a black hole (BH) horizon at the center of soliton, a possibility that is indeed realized for other well-known solutions, such as Skyrmions, magnetic monopoles, and sphalerons (see e.g., the review work [27]). However, as we shall discuss in Section 4 (and Appendix B), the situation is different for the considered (spherically symmetric) solutions and there are no BH generalizations, regardless of the presence of self-interactions. We also discuss the physical interpretation of the fermionic solutions. Section 5 presents concluding remarks and some open questions.

1.2. Conventions

Throughout, we set $c=ħ=1$ and adopt a metric signature $+2$. Greek letters $\alpha ,\beta ,\gamma \dots$ are used for coordinate indices, whereas latin letters $a,b,c,\dots$ are used for tetrad basis indices. Symmetrization and antisymmetrization of indices is denoted with round and square brackets, $\left(\right)$ and $\left[\right]$, respectively. We use ${\partial }_{\mu }$, ${\nabla }_{\mu }$, and ${\widehat{D}}_{\mu }$ to denote partial, covariant, and spinor derivatives, respectively.

The flat spacetime metric in spherical coordinates reads

$$\begin{array}{c}\hfill d{s}^2=-d{t}^2+d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\phi }^2),\end{array}$$

(1)

with $x^0=t$, $x^1=r$, $x^2=\theta$, and $x^3=\phi$.

The conventions for scalars are those presented in Ref. [28]. In the Proca field case, we shall use the notation and conventions in [29,30]. For fermions, we shall follow the framework (including the definitions and conventions) in [31], as reviewed in Appendix A.

For the matter content, we shall consider three different fields $\psi$, with the specific form:

• spin 0:
  $\Phi$ is a complex scalar field, which is equivalent to a model with two real scalar fields, ${\Phi }^R,{\Phi }^I$, via $\Phi ={\Phi }^R+i{\Phi }^I$.
• spin 1/2:
  ${\Psi }^{\left(A\right)}$ are massive spinors, with four complex components, the index $\left(A\right)$ corresponding to the number of copies of the Lagrangian. For a spherically symmetric configuration, one should consider (at least) two spinors ($A=1,2$), with equal mass $\mu$. A model with a single spinor necessarily possesses a nonzero angular momentum density and it cannot be spherically symmetric.
• spin 1:
  $\mathcal{A}$ is a complex 4-potential, with the field strength $\mathcal{F}=d\mathcal{A}$. Again, the model can be described in terms of two real vector fields, $\mathcal{A}={\mathcal{A}}^R+i{\mathcal{A}}^I$.

Some relations get a simpler form by defining

$$\begin{array}{c}\hfill {\psi }^2\equiv \{{\Phi }^{*}\Phi ;{\mathcal{A}}_{\alpha }{\overline{\mathcal{A}}}^{\alpha };i{\overline{\Psi }}^{\left(A\right)}{\Psi }^{\left(A\right)}\},\end{array}$$

(2)

for spin $0,1/2$, and 1, respectively, while we denote ${\psi }^4\equiv {\left({\psi }^2\right)}^2$ and ${\psi }^6\equiv {\left({\psi }^2\right)}^3$.

The numerical construction of the solutions reported in this work is standard. In our approach, we use a Runge–Kutta ordinary differential equation solver. For each model, we evaluate the initial conditions that are close to the origin at $ϵ={10}^{-6}$ for global tolerance ${10}^{-14}$, adjusting for shooting parameters (which are some constants that enter the near origin expansion of the solutions) and integrating towards $r\to \infty$. The accuracy of the solutions was also monitored by computing virial relations that were satisfied by these systems, as discussed below. For a given set of input parameters, the solutions form a discrete set labelled by the number of nodes, n, of (some of) the matter function(s). Only fundamental states, which have the minimal number of radial nodes, are considered in this work.

2. The General Framework

2.1. The Action and Field Equations

We consider Einstein’s gravity that is minimally coupled to spin$-s$ matter fields ${\psi }_{\left(s\right)}=\{\Phi ;\Psi ;\mathcal{A}\}$, with $s=0,1/2,1$. The action reads

$$\begin{array}{c}\hfill S=\frac{1}{4\pi }\int d^{4}x\sqrt{-g}\left[\frac{1}{4G}R-L_{\left(s\right)}\right],\end{array}$$

(3)

where

$$\begin{array}{c}\hfill L_{\left(s\right)}=L_{\left(s\right)}^{\left(0\right)}+U_{\left(s\right)}^{\left(\mathrm{int}\right)};\end{array}$$

(4)

the kinetic part of the matter Lagrangians reads, respectively,

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:L_{\left(0\right)}^{\left(0\right)}=g^{\alpha \beta }{\Phi }_{,\alpha }^{*}{\Phi }_{,\beta },\hfill \\ \hfill & & \mathrm{Dirac}:L_{(1/2)}^{\left(A\right)\left(0\right)}=i\left[\frac{1}{2}\left(\left\{\widehat{D}{\overline{\Psi }}^{\left(A\right)}\right\}{\Psi }^{\left(A\right)}-{\overline{\Psi }}^{\left(A\right)}\widehat{D}{\Psi }^{\left(A\right)}\right)\right],\hfill \\ \hfill & & \mathrm{Proca}:L_{\left(1\right)}^{\left(0\right)}=\frac{1}{4}{\mathcal{F}}_{\alpha \beta }{\overline{\mathcal{F}}}^{\alpha \beta }.\hfill \end{array}$$

(5)

$U_{\left(s\right)}^{\left(\mathrm{int}\right)}$ in (4) is a potential term, which includes self-interactions. In what follows, we shall consider the simplest form of $U_{\left(s\right)}^{\left(\mathrm{int}\right)}$, which allows for solitonic solutions in a flat spacetime background, with polynomial terms. As such, apart from the mass term, $U_{\left(s\right)}^{\left(\mathrm{int}\right)}$ contains quartic and sextic terms only. Afterwards, all three cases can be treated in a unitary way by defining

$$\begin{array}{c}\hfill U_{\left(s\right)}^{\left(\mathrm{int}\right)}=\mathcal{M}{\psi }^2-\lambda {\psi }^4+\nu {\psi }^6\equiv U,\end{array}$$

(6)

where we have denoted

$$\begin{array}{c}\hfill \mathcal{M}\equiv \left\{{\mu }^2;\mu ;\frac{1}{2}{\mu }^2\right\},\end{array}$$

(7)

for spin $0,1/2$ and 1, respectively. In all cases, $\mu$ corresponds to the mass of the elementary quanta of the field(s). Additionally, $\lambda ,\nu$ are the input parameters of the theory, which are not fixed a priori.

We shall also denote

$$\dot{U}\equiv \frac{\partial U}{\partial {\psi }^2}=\mathcal{M}-2\lambda {\psi }^2+3\nu {\psi }^4,\ddot{U}\equiv \frac{\partial \dot{U}}{\partial {\psi }^2}=-2\lambda +6\nu {\psi }^2.$$

(8)

Extremizing the action (3) leads to the Einstein field equations

$$\begin{array}{c}\hfill R_{\alpha \beta }-\frac{1}{2}R{g}_{\alpha \beta }=2G{T}_{\alpha \beta },\end{array}$$

(9)

where the energy–momentum tensor reads, respectively,

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:T_{\alpha \beta }={\Phi }_{,\alpha }^{*}{\Phi }_{,\beta }+{\Phi }_{,\beta }^{*}{\Phi }_{,\alpha }-g_{\alpha \beta }{L}_{\left(0\right)},\hfill \\ & & \mathrm{Dirac}:T_{\alpha \beta }=\sum _A{T}_{\alpha \beta }^{\left(A\right)},\mathrm{with}{T}_{\alpha \beta }^{\left(A\right)}=-\frac{i}{2}\left[{\overline{\Psi }}^{\left(A\right)}{\gamma }_{(\alpha }{\widehat{D}}_{\beta )}{\Psi }^{\left(A\right)}-\left\{{\widehat{D}}_{(\alpha }{\overline{\Psi }}^{\left(A\right)}\right\}{\gamma }_{\beta )}{\Psi }^{\left(A\right)}-g_{\alpha \beta }{L}_{(1/2)}\right],\hfill \\ & & \mathrm{Proca}:T_{\alpha \beta }=\frac{1}{2}({\mathcal{F}}_{\alpha \sigma }{\overline{\mathcal{F}}}_{\beta \gamma }+{\overline{\mathcal{F}}}_{\alpha \sigma }{\mathcal{F}}_{\beta \gamma })g^{\sigma \gamma }+\dot{U}({\mathcal{A}}_{\alpha }{\overline{\mathcal{A}}}_{\beta }+{\overline{\mathcal{A}}}_{\alpha }{\mathcal{A}}_{\beta })-g_{\alpha \beta }{L}_{\left(1\right)},\hfill \end{array}$$

(10)

and to the matter field equations,

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:({\nabla }^2-\dot{U})\Phi =0,\hfill \\ & & \mathrm{Dirac}:(\widehat{D}-\dot{U}){\Psi }^{\left(A\right)}=0,\hfill \\ \hfill & & \mathrm{Proca}:\frac{1}{2}{\nabla }_{\alpha }{\mathcal{F}}^{\alpha \beta }-\dot{U}{\mathcal{A}}^{\beta }=0.\hfill \end{array}$$

(11)

In the Proca case, taking the four-divergence of the field Equation (11) results in a generalization of the Lorenz condition, which is a dynamical requirement, rather than a gauge choice. This condition takes a particularly simple form in the Ricci-flat case, with

$$\left({\nabla }_{\alpha }{\mathcal{A}}^{\alpha }\right)\dot{U}+\ddot{U}{\nabla }_{\alpha }\left({\overline{\mathcal{A}}}_{\beta }{\mathcal{A}}^{\beta }\right)=0.$$

(12)

In all cases, the action of the matter fields $\psi$ possesses a global $U\left(1\right)$ invariance, under the transformation $\psi \to e^{i\alpha }\psi$, with $\alpha$ constant. This implies the existence of a conserved four-current, which reads

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:j^{\alpha }=-i({\Phi }^{*}{\partial }^{\alpha }\Phi -\Phi {\partial }^{\alpha }{\Phi }^{*}),\hfill \\ & & \mathrm{Dirac}:j^{\alpha }=\overline{\Psi }{\gamma }^{\alpha }\Psi ,\hfill \\ \hfill & & \mathrm{Proca}:j^{\alpha }=\frac{i}{2}\left[{\overline{\mathcal{F}}}^{\alpha \beta }{\mathcal{A}}_{\beta }-{\mathcal{F}}^{\alpha \beta }{\overline{\mathcal{A}}}_{\beta }\right].\hfill \end{array}$$

(13)

This current is conserved via the field equations,

$$\begin{array}{c}\hfill j_{;\alpha }^{\alpha }=0.\end{array}$$

(14)

It follows that integrating the timelike component of this four-current in a spacelike slice $\Sigma$ yields a conserved quantity—the Noether charge:

$$\begin{array}{c}\hfill Q={\int }_{\Sigma }{j}^t.\end{array}$$

(15)

2.2. The Ansätze and Explicit Equations

2.2.1. The Metric and Matter Fields

The spherically symmetric configurations are most conveniently studied in Schwarzschild-like coordinates, within the following metric Ansatz:

$$\begin{array}{c}\hfill d{s}^2=-N\left(r\right){\sigma }^2\left(r\right)d{t}^2+\frac{d{r}^2}{N\left(r\right)}+r^2(d{\theta }^2+{sin}^2\theta d{\phi }^2),\mathrm{with}N\left(r\right)\equiv 1-\frac{2m\left(r\right)}{r}.\end{array}$$

(16)

The matter field Ansatz, which is compatible with a spherically symmetric geometry, reads:

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:\Phi =\varphi \left(r\right)e^{-iwt},\hfill \end{array}$$

(17)

introducing a single real function $\varphi \left(r\right)$;

$$\begin{array}{ccc}& & \mathrm{Proca}:\mathcal{A}=\left[F\left(r\right)dt+iH\left(r\right)dr\right]e^{-iwt},\hfill \end{array}$$

(18)

introducing two real potentials $F\left(r\right)$ and $H\left(r\right)$.

The case of a Dirac field is more involved. For a spherically symmetric configurations, we have to consider two Dirac fields, $A=1,2$, with

$$\begin{array}{ccc}\hfill & & \mathrm{Dirac}:{\Psi }^{\left(A\right)}={\mathrm{e}}^{-\mathrm{i}wt}{\mathcal{R}}^{\left(A\right)}\left(r\right)\otimes {\Theta }^{\left(A\right)}(\theta ,\phi ),\hfill \end{array}$$

(19)

where

$$\begin{array}{c}\hfill {\mathcal{R}}^{\left(1\right)}=-i{\mathcal{R}}^{\left(2\right)}=\left[\begin{array}{c}z\left(r\right)\\ -i\overline{z}\left(r\right)\end{array}\right],{\Theta }^{\left(1\right)}=\left[\begin{array}{c}-\kappa sin\frac{\theta }{2}\\ cos\frac{\theta }{2}\end{array}\right]e^{i\frac{\phi }{2}},{\Theta }^{\left(2\right)}=\left[\begin{array}{c}\kappa cos\frac{\theta }{2}\\ sin\frac{\theta }{2}\end{array}\right]e^{-i\frac{\phi }{2}},\end{array}$$

with $\kappa =\pm 1$ and $z\left(r\right)$ a complex function. In what follows, we shall only consider the case $\kappa =1$ (note that qualitatively similar solutions with $\kappa =-1$ also exist). Additionally, in the above Ansatz, it is convenient to define

$$\begin{array}{c}\hfill z\left(r\right)=e^{i\pi /4}f\left(r\right)-e^{-i\pi /4}g\left(r\right),\end{array}$$

(20)

where $f\left(r\right)$ and $g\left(r\right)$ are two real functions, a choice that simplifies the equations.

The reason that choose two independent $s=1/2$ fields, with the Ansatz (19) and (20), is the following. For both spinors, the $individual$ energy-momentum tensors are not spherically symmetric (this feature is present regardless of the self-interaction potential in the Lagrangian), since $T_{\phi }^{t\left(A\right)}\ne 0$ (while the other nonzero components $T_r^{r\left(A\right)}$, $T_{\theta }^{\theta \left(A\right)}$= $T_{\phi }^{\phi \left(A\right)}$ and $T_t^{t\left(A\right)}$ only depend on r). However, $T_{\phi }^{t\left(1\right)}+T_{\phi }^{t\left(2\right)}=0$, such that the full configuration is spherically symmetric, being compatible with the line element (16).

Within this framework, the explicit expressions of ${\psi }^2$, as defined in (2), are

$$\begin{array}{c}\hfill {\psi }^2=\left\{{\varphi }^2,4(g^2-f^2),H^{2}N-\frac{F^2}{N{\sigma }^2}\right\}\end{array}$$

(21)

for spin $0,1/2$ and 1, respectively. In all cases, $w>0$ is the frequency of the matter field.

2.2.2. The Explicit Equations

The equations for the mass function $m\left(r\right)$ read, respectively,

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:m^{\prime }=G{r}^2\left(N{{\varphi }^{\prime }}^2+\frac{w^2{\varphi }^2}{N{\sigma }^2}+U\right),\hfill \\ \hfill & & \mathrm{Dirac}:m^{\prime }=2G{r}^2\left(4\sqrt{N}(g{f}^{\prime }-f{g}^{\prime })+\frac{8fg}{r}+U\right),\hfill \\ \hfill & & \mathrm{Proca}:m^{\prime }=G{r}^2\left[\frac{{(F^{\prime }-wH)}^2}{2{\sigma }^2}+({\mu }^2-6\lambda {\mathcal{A}}^2+10\nu {\mathcal{A}}^4)\frac{F^2}{2N{\sigma }^2}+\frac{U}{{\mathcal{A}}^2}N{G}^2\right].\hfill \end{array}$$

(22)

The equations for the metric function $\sigma \left(r\right)$ read, respectively,

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:\frac{{\sigma }^{\prime }}{\sigma }=2Gr\left({{\varphi }^{\prime }}^2+\frac{w^2{\varphi }^2}{N^2{\sigma }^2}\right),\hfill \\ & & \mathrm{Dirac}:\frac{{\sigma }^{\prime }}{\sigma }=8G\frac{r}{\sqrt{N}}\left(g{f}^{\prime }-f{g}^{\prime }+\frac{w(f^2+g^2)}{N\sigma }\right),\hfill \\ \hfill & & \mathrm{Proca}:\frac{{\sigma }^{\prime }}{\sigma }=\frac{2Gr}{N}\left(H^{2}N+\frac{F^2}{N{\sigma }^2}\right)\dot{U}.\hfill \end{array}$$

(23)

The equations for the matter fields are

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:{\varphi }^{″}+\left(\frac{2}{r}+\frac{N^{\prime }}{N}+\frac{{\sigma }^{\prime }}{\sigma }\right){\varphi }^{\prime }+\frac{w^2}{N^2{\sigma }^2}\varphi -\dot{U}\frac{\varphi }{N}=0,\hfill \\ \hfill & & \mathrm{Dirac}-\mathrm{f}:f^{\prime }+\left(\frac{N^{\prime }}{4N}+\frac{{\sigma }^{\prime }}{2\sigma }+\frac{1}{r\sqrt{N}}+\frac{1}{r}\right)f-\frac{wg}{N\sigma }+\frac{g}{\sqrt{N}}\dot{U}=0,\hfill \\ & & \mathrm{Dirac}-\mathrm{g}:g^{\prime }+\left(\frac{N^{\prime }}{4N}+\frac{{\sigma }^{\prime }}{2\sigma }-\frac{1}{r\sqrt{N}}+\frac{1}{r}\right)f+\frac{wf}{N\sigma }+\frac{f}{\sqrt{N}}\dot{U}=0,\hfill \\ \hfill & & \mathrm{Proca}-\mathrm{F}:F^{\prime }-wH+\frac{2N{\sigma }^{2}H}{w}\dot{U}=0,\hfill \\ \hfill & & \mathrm{Proca}-\mathrm{H}:\frac{d}{dr}\left\{\frac{r^2[wH-F^{\prime }]}{\sigma }\right\}+\frac{2r^{2}F}{N\sigma }\dot{U}=0.\hfill \end{array}$$

(24)

An additional supplementary constraint is also present, which is a second order equation for the metric functions $m\left(r\right)$ and $\sigma \left(r\right)$, with first order derivatives of matter fields. However, this equation is a differential consequence of the above field equations; it is used to check the accuracy of the numerical results.

Let us remark that the above equations can be derived from the following effective action

$$\begin{array}{c}\hfill S_{\mathrm{eff}}=\int dr{\mathcal{L}}_{\mathrm{eff}},\mathrm{with}{\mathcal{L}}_{\mathrm{eff}}=\frac{1}{G}\sigma m^{\prime }-{\mathcal{L}}_{\left(s\right)},\end{array}$$

(25)

where

$$\begin{array}{ccc}\hfill & & {\mathcal{L}}_{\left(0\right)}=r^2\sigma \left(N{\varphi }^{\prime 2}-\frac{w^2{\varphi }^2}{N{\sigma }^2}+U\right),\hfill \\ & & {\mathcal{L}}_{(1/2)}=8r^2\sigma \left(\sqrt{N}(g{f}^{\prime }-f{g}^{\prime })-\frac{w}{\sigma \sqrt{N}}(f^2+g^2)+\frac{2fg}{r}+\frac{1}{4}U\right),\hfill \\ \hfill & & {\mathcal{L}}_{\left(1\right)}=r^2\sigma \left(-\frac{{(F^{\prime }-wH)}^2}{2{\sigma }^2}+U\right).\hfill \end{array}$$

(26)

Given the above framework, the energy density measured by a static observer, $\rho =-T_t^t$, is

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:\rho =N{\varphi }^{\prime 2}+\frac{w^2}{N{\sigma }^2}{\varphi }^2+U,\hfill \\ & & \mathrm{Dirac}:\rho =8\left((g{f}^{\prime }-f{g}^{\prime })\sqrt{N}+\frac{2fg}{r}+\frac{1}{4}U\right),\hfill \\ \hfill & & \mathrm{Proca}:\rho =\frac{{(F^{\prime }-wH)}^2}{2{\sigma }^2}+\frac{U}{{\mathcal{A}}^2}N{H}^2+\frac{F^2}{N{\sigma }^2}\left(\frac{1}{2}{\mu }^2-3\lambda {\mathcal{A}}^2+5\nu {\mathcal{A}}^4\right).\hfill \end{array}$$

(27)

The mass of the flat space solutions is computed as the integral of $\rho$,

$$\begin{array}{c}\hfill M=\int dr{r}^2\rho ,\end{array}$$

(28)

while, in the self-gravitating case, it can be read off from the asymptotic behaviour of the $g_{tt}$ metric potential

$$\begin{array}{c}\hfill g_{tt}=-N{\sigma }^2=-1+\frac{2MG}{r}+\cdots \end{array}$$

(29)

As for the Noether charge, it reads

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:Q=2w{\int }_0^{\infty }dr{r}^2\frac{{\varphi }^2}{N\sigma },\hfill \\ \hfill & & \mathrm{Dirac}:Q=4{\int }_0^{\infty }dr{r}^2\frac{(f^2+g^2)}{\sqrt{N}},\hfill \\ \hfill & & \mathrm{Proca}:Q=2{\int }_0^{\infty }dr{r}^2\frac{(wH-F^{\prime })N}{\sigma }.\hfill \end{array}$$

(30)

2.3. Units and Scaling Symmetries

The matter fields in action (3) have the following dimensions: (with $L=lenght$):

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:[\Phi ]=\frac{1}{L},\hfill \\ & & \mathrm{Dirac}:[\Psi ]=\frac{1}{L^{3/2}},\hfill \\ \hfill & & \mathrm{Proca}:\left[{\mathcal{A}}_a\right]=\frac{1}{L}.\hfill \end{array}$$

(31)

Additionally, the coupling constants that enter the potential are (generically) dimension-full, with:

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:\left[\mu \right]=\frac{1}{L},\left[\lambda \right]=L^0,\left[\nu \right]=L^2,\hfill \\ & & \mathrm{Dirac}:\left[\mu \right]=\frac{1}{L},\left[\lambda \right]=L^2,\left[\nu \right]=L^5,\hfill \\ \hfill & & \mathrm{Proca}:\left[\mu \right]=\frac{1}{L},\left[\lambda \right]=L^0,\left[\nu \right]=L^2.\hfill \end{array}$$

(32)

Turning now to scaling symmetries, we notice the existence of $three$ different transformations, which, in all cases, leave invariant the equations of motion (in the relations below, the functions or constants that are not mentioned explicitly remain invariant).

The first one (s0) is very simple

$$\begin{array}{c}\hfill \left(s0\right):\sigma \to c\sigma ,w\to cw,\end{array}$$

(33)

with c some arbitrary positive constant. However, this invariance is fixed when imposing the asymptotic flatness condition $\sigma \to 1$ as $r\to \infty$.

More importantly, the equations of motion are invariant under a scaling of the radial coordinate, together with other functions and parameters of the model. In the scalar and Proca cases, this transformation reads:

$$\begin{array}{c}\hfill \left(s1\right):\mathrm{scalar}\mathrm{and}\mathrm{Proca}:r=c\overline{r},w=\frac{1}{c}\overline{w},\mu =\frac{1}{c}\overline{\mu },\lambda =\frac{\overline{\lambda }}{c^2},\nu =\frac{\overline{\nu }}{c^4},m=c\overline{m}.\end{array}$$

(34)

In the Dirac case, the corresponding symmetry is more complicated, with

$$\begin{array}{ccc}\hfill & & \left(s1\right):\mathrm{Dirac}:r=c\overline{r},w=\frac{1}{c}\overline{w},\mu =\frac{1}{c}\overline{\mu },\nu =c\overline{\nu };m=c\overline{m},f=\frac{\overline{f}}{\sqrt{c}},g=\frac{\overline{g}}{\sqrt{c}}.\hfill \end{array}$$

(35)

In all cases, the product $m\mu$ and the ratio $w/\mu$ are left invariant by the symmetry $\left(s1\right)$. Under this transformation, the global quantities behave as

$$\begin{array}{c}\hfill M=c\overline{M},Q=c^2\overline{Q}.\end{array}$$

(36)

The symmetry $\left(s1\right)$ is usually employed in order to work in units of length set by the field mass,

$$\begin{array}{c}\hfill \overline{\mu }=1,i.e.c=\frac{1}{\mu }.\end{array}$$

(37)

Finally, the equations are also invariant under a suitable scaling of the matter field(s) functions, together with some coupling constants (while the radial coordinate or the field frequency are not affected):

$$\begin{array}{ccc}\hfill & & \left(s2\right):\lambda =\frac{\overline{\lambda }}{c^2},\nu =\frac{\overline{\nu }}{c^2},G=\frac{\overline{G}}{c^2},\hfill \end{array}$$

(38)

together with

$$\begin{array}{ccc}\hfill & & \left(s2\right):\mathrm{scalar}:\varphi =\overline{\varphi }c,\mathrm{Dirac}:f=\overline{f}c,g=\overline{g}c,\mathrm{Proca}:F=\overline{F}c,H=\overline{H}c,\hfill \end{array}$$

(39)

while the global quantities transform as

$$\begin{array}{c}\hfill M=c^2\overline{M},Q=c^2\overline{Q}.\end{array}$$

(40)

The symmetries $\left(s1\right)$ and $\left(s2\right)$ are used, in practice, in order to simplify the numerical study of the solitons. First, the symmetry $\left(s2\right)$ can be used to set $\overline{G}=1$; i.e., essentially one absorbs Newton’s constant in the expression of the matter field(s). This is the usual approach for the models without self-interaction, see, e.g., the discussion in [12].

However, the probe limit of the solutions becomes less transparent for this choice. An alternative route, employed in this work, is to use (38) and (39) to set the coefficient of the quartic term to unity,

$$\begin{array}{c}\hfill \overline{\lambda }=1,i.e.c=\frac{1}{\sqrt{\lambda }}.\end{array}$$

(41)

It follows that two mass scales naturally emerge, one set by gravity $M_{\mathrm{Pl}}=1/\sqrt{G}$ and the other one, $M_0$, set by the field(s) coupling constants, with

$$\begin{array}{c}\hfill \mathrm{scalar}\mathrm{and}\mathrm{Proca}:M_0=\frac{\mu }{\sqrt{\lambda }};\mathrm{Dirac}:M_0=\frac{1}{\sqrt{\lambda }}.\end{array}$$

(42)

The ratio of these fundamental mass scales defines the dimensionless coupling constant

$$\begin{array}{c}\hfill \alpha =\frac{M_0}{M_{\mathrm{Pl}}},\end{array}$$

(43)

which is relevant in the physics of the solutions.

Another dimensionless input parameter is the scaled constant for the sextic term in the potential U, with

$$\begin{array}{c}\hfill \mathrm{scalar}\mathrm{and}\mathrm{Proca}:\beta =\frac{\nu {\mu }^2}{{\lambda }^2};\mathrm{Dirac}:\beta =\frac{\nu \mu }{{\lambda }^2}.\end{array}$$

(44)

As such, the mass and charge of the non-gravitating solutions is given in units set by $\mu ,\lambda$, while, in the gravitating case, in order to make contact with the previous results without self-interaction, we use units that are set by G and $\mu$.

A priori, the range of $\alpha$ is unbounded, $0⩽\alpha <\infty$. The limit $\alpha \to 0$ corresponds to $G\to 0$, i.e., the probe limit—one solves the matter field(s) equations on a fixed geometry, which should be a solution of the vacuum Einstein equations. The limit $\alpha \to \infty$ corresponds to $\lambda \to 0$, i.e., no quartic, or sextic term (when using $\beta$, if $\nu$ is finite) in the action. Thus, solutions of the Einstein-matter field equations without self-interaction are approached in the second limit.

This choice of units with $\mu =\lambda =1$ (after employing the above scaling symmetries) has the advantage of greatly simplifying the numerical study of the solutions. For example, the Einstein equations read

$$\begin{array}{c}\hfill R_{\alpha \beta }-\frac{1}{2}{g}_{\alpha \beta }=2{\alpha }^2{T}_{\alpha \beta },\end{array}$$

(45)

the only input parameters being

$$\begin{array}{c}\hfill \{\alpha ,\beta \mathrm{and}w\},\end{array}$$

(46)

with w the scaled frequency. Additionally, the scaled scalar potential reads

$$\begin{array}{c}\hfill U={\psi }^2-{\psi }^4+\beta {\psi }^6,\end{array}$$

(47)

For ${\psi }^2>0$, U is strictly positive for $\beta >1/4$. The case $\beta =1/4$ is special, since the potential becomes $U={\psi }^2{(1-{\psi }^2/2)}^2$, and, thus, possesses three degenerate minima, at $\psi =\{0,\pm \sqrt{2}\}$. A discussion of these aspects (for a spin-zero field) can be found in Ref. [32].

3. The Probe Limit: Flat Spacetime Solutions

3.1. Deser’s Argument and Virial-Type Identities

Before performing a numerical study of the solutions, it is useful to derive virial-type identities. For a flat spacetime background, we can adapt a simple argument given long ago by Deser [26] (used therein to rule out the existence of finite energy time-independent solutions in Yang–Mills theory) in order to obtain virial-type identities and a simple relation between the mass of solutions and the trace of the energy-momentum tensor (the same virial identities are found by adapting Derrick’s scaling argument [33].)—see also [34].

Working in Cartesian coordinates $x^a$ ($a=1,2,3$), assume the existence of a stationary soliton in some field theory model. Following [26], consider the following (trivial) identity observe that Deser’s argument cannot be extended to a curved spacetime background)

$$\begin{array}{c}\hfill \frac{\partial }{\partial x^a}\left(x^b{T}_b^a\right)=T_a^a+x^b\frac{\partial T_b^a}{\partial x^a},\end{array}$$

(48)

together with its volume integral. The left hand side vanishes from regularity and finite energy requirements (note that, in the spin-1/2 case, one considers the total energy-momentum tensor). The second term in (48) vanishes from energy-momentum conservation (plus staticity) and, thus, we are left with the virial-type identity

$$\begin{array}{c}\hfill \int d^{3}x{T}_a^a=0.\end{array}$$

(49)

It follows that the total mass-energy of a static soliton in $d=3+1$ dimensions is determined by the trace of the energy-momentum tensor

$$\begin{array}{c}\hfill M=-\int d^{3}x{T}_t^t=-\int d^{3}x{T}_{\mu }^{\mu }.\end{array}$$

(50)

When applied to the specific Ansätze in this work, (49) results in the following expressions:

• scalar field:

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2\left[\frac{1}{3}{{\varphi }^{\prime }}^2+({\mu }^2-w^2){\varphi }^2+\nu {\varphi }^6\right]=\lambda {\int }_0^{\infty }dr{r}^2{\varphi }^4.\end{array}$$

(51)

This relation can be simplified by using the equation for $\varphi$ in a simpler form

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2({\mu }^2-w^2){\varphi }^2=\frac{\lambda }{2}{\int }_0^{\infty }dr{r}^2{\varphi }^4.\end{array}$$

(52)

This clearly shows that the (flat space) Q-ball solutions are supported by the quartic self-interacting term, with $\lambda >0$ (i.e., the sextic term is not relevant at this level).

• Dirac field:

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2\left(g{f}^{\prime }-f{g}^{\prime }+\frac{2fg}{r}+\frac{3}{8}U-\frac{3}{2}w(f^2+g^2)\right)=0\end{array}$$

(53)

which can also be written, via field equations, in the alternative form

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2\left(\mu {\psi }^2+\lambda {\psi }^4\right)={\int }_0^{\infty }dr{r}^2\left(4w(f^2+g^2)+3\nu {\psi }^6\right).\end{array}$$

(54)

One concludes that, for $\nu =0$ and $\lambda >0$, the solutions are supported by the harmonic time dependence. However, the above relation does not clarify the role that is played by the nonlinear quartic term for the existence of solitons.

• Proca field:

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2\left(\frac{1}{2}{(F^{\prime }-wG)}^2-3U+2G^2\frac{dU}{d{\mathcal{A}}^2}\right)=0.\end{array}$$

(55)

After eliminating the kinetic term ${(F^{\prime }-wG)}^2$, via field equations, the above relation takes the suggestive form:

$$\begin{array}{ccc}\hfill & & {\int }_0^{\infty }dr{r}^2\left[{\mu }^2(3F^2+(\frac{{\mu }^2}{w^2}-1)G^2+\frac{16{\lambda }^2{G}^2}{w^2}{\mathcal{A}}^4+\frac{6\nu }{w^2}{\mathcal{A}}^4\left(w^2(F^2+G^2)+2G^2({\mu }^2+3\nu {\mathcal{A}}^2\right)\right]=\hfill \\ \hfill & & 2\lambda {\int }_0^{\infty }dr{r}^2{\mathcal{A}}^2\left(3F^2+G^2+\frac{4G^2}{w^2}({\mu }^2+6\nu {\mathcal{A}}^2)\right).\hfill \end{array}$$

(56)

From the bound state condition ${\mu }^2⩾w^2$, it is clear that the existence of finite mass solutions requires a quartic term, $\lambda \ne 0$ ($\nu$ being irelevant). However, since ${\mathcal{A}}^2$ may take both positive or negative values, one cannot use the above relation in order to predict the sign of $\lambda$.

It is also interesting to note that the mass of the flat space Proca solitons takes the simple form

$$\begin{array}{c}\hfill M={\int }_0^{\infty }dr{r}^2\left({\mu }^2{\mathcal{A}}^2-2\nu {\mathcal{A}}^6\right).\end{array}$$

(57)

3.2. Numerical Results

3.2.1. General Remarks

The corresponding equations are found by taking

$$\begin{array}{c}\hfill N=\sigma =1,\end{array}$$

(58)

in the corresponding general equations presented in Section 2, and we shall not display them here. Moreover, the boundary conditions that are satisfied by the functions $\psi$ at $r=0,\infty$ are similar to those in the gravitating case, as given in the next Section.

The case of a scalar field is special for a flat spacetime metric. The frequency parameter w is not relevant, since $w^2$ acts as an effective $tachyonic$ contribution to the mass term and, thus, it can be absorbed into ${\mu }^2$, by defining ${\mu }^2-w^2\to {\mu }^2$. After this redefinition, the scalar field is static, $\Phi =\varphi \left(r\right)$ and, thus, the Noether charge vanishes. Therefore, all Q-ball solutions in a flat spacetime background can be interpreted as $static$ scalar solitons, in a model with a shifted scalar field mass term [35], for a new potential

$$\begin{array}{c}\hfill U=U_{\left(w\right)}-w^2{\varphi }^2.\end{array}$$

(59)

Note that, although $\varphi$ formally satisfies the same equation as before, the energy-momentum tensor and the total mass of these solutions are different. Additionally, the virial identities imply that the redefined potential U is necessarily negative for some range of $\varphi$, which is realised by the solutions, $U<0$. Moreover, one can prove the following relation [35]

$$\begin{array}{c}\hfill M(w=0)=M\left(w\right)-wQ,\end{array}$$

(60)

which relates the mass of a static solution ($w=0$ and the redefined potential (59)) to the mass and Noether charge of solutions with a given w (the other parameters in the potential are kept fixed).

No similar relation seems to exist for higher spin fields. However, it is interesting to notice the existence in this case of a curious static, purely electric solution, i.e., with $H=0$, $w=0$. The electric potential $F\left(r\right)$ essentially satisfies the same equation as a scalar Q-ball,

$$\begin{array}{c}\hfill F^{″}+\frac{2F^{\prime }}{r}-({\mu }^2+4\lambda F^2+6\nu F^4)F=0.\end{array}$$

(61)

The existence of solutions with proper asymptotics requires $\lambda <0$, being constructed within the same scheme as in the generic case.

To the best of our knowledge, this case has not been discussed in the literature. However, they possess some unphysical features. For example, by using the virial identity (57) together with the above equations, one can prove that the total mass of this configuration is negative (moreover, we have verified that M remains negative when including gravity effects)

$$\begin{array}{c}\hfill M=-\frac{1}{3}{\int }_0^{\infty }dr{r}^2{F\prime }^2<0.\end{array}$$

(62)

In all cases, the sextic self-interaction term is not necessary for the existence of solutions. Because the $\beta =0$ case has some special properties, we shall discuss it separately at the end of this section.

3.2.2. Solutions with a Sextic Self-Interaction Term, $\beta >0$

In what follows, in order to simplify the picture, we shall assume $\beta >1/4$, such that the potential $U\left({\psi }^2\right)$ (as given by (6)) is strictly positive (assuming ${\psi }^2>0$, which, as we shall see, is not necessarily the case).

Because no exact solutions are known, the solitons are constructed numerically. Figure 1, Figure 2 and Figure 3 (left panels) show the profile of typical solutions. One notices that, in the Proca case, ${\psi }^2={\mathcal{A}}^2$ is negative for small enough r, while ${\psi }^2=i{\overline{\Psi }}^{\left(A\right)}{\Psi }^{\left(A\right)}$ is positive in the Dirac case.

The numerical results indicate that the $s=0,1/2,1$ flat spacetime solitons follow the same pattern, which can be summarized, as follows. First, in all cases, the solutions only exist in a certain frequency range, $w_{\min }<w<w_{\max }=\mu$, with $w_{\min }$ determined by $\beta$. Second, the solutions with $w<\mu$ decay exponentially in the far field, with no radiation, as $\psi \sim e^{-\sqrt{{\mu }^2-w^2}r}$. Finally, the most interesting qualitative feature is perhaps the existence in all cases of a mass gap. That is, at a critical value of the frequency, both the mass and charge of the solutions assume their minimal (nonzero) value, from where they monotonically increase towards both limiting values of the frequency (see Figure 1, Figure 2 and Figure 3 (right panels)). When considering the mass of the solutions as a function of the charge, there are thus two branches, merging at the minimal charge/mass. One expects that a subset of solutions with M smaller than the mass of Q free particles (bosons or fermions) may be stable, which is possible along the lower frequency branch.

3.2.3. Solutions without a Sextic Self-Interaction Term, $\beta =0$

This case is likely physically less relevant (since the potential U is not positive definite); however, it possesses some interesting properties, which depend, to some extent, on the spin of the field.

Starting with the scalar case, some numerical results are displayed in Figure 1 (right panel, inset). Note that all of these solutions are unstable, since $M>Q$, and, thus, they have excess energy. We remark that solutions with a negative energy density region, $\rho <0$, found on a small $r-$interval, are found for small enough w (although $M>0$ always).

In fact, the equation for the scalar field has an interesting form, with the frequency parameter being irrelevant. After using the alternative rescaling

$$\begin{array}{c}\hfill r\to r/\sqrt{{\mu }^2-w^2},\varphi \to \varphi \sqrt{\frac{{\mu }^2-w^2}{\lambda }},\end{array}$$

(63)

one can see that no free parameter exists in this case. The scalar field satisfies the kink-like equation

$$\begin{array}{c}\hfill \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{d\varphi }{dr}\right)=\varphi -2{\varphi }^3,\end{array}$$

(64)

which does not seem to possess an exact solution (Equation (64) is discussed by many authors, being relevant for the issue of false vacuum decay [36]—e.g., an existence proof can be found in Ref. [37]). Additionally, one can show that the following relation holds

$$\begin{array}{c}\hfill M(w;\mu ,\lambda )=\frac{M(w=0;\mu ,\lambda )}{\sqrt{{\mu }^2-w^2}},\end{array}$$

(65)

with $M(w=0;1,1)\simeq 1.503$.

The pattern that is exhibited by the Proca solutions without a sextic term is different, as displayed in Figure 3. As found in Ref. [24], the limit $w=0$ is not approached in this case. Instead, a minimal value of w is reached, with a backbending towards a critical solution possessing finite charges. Because $M>Q$, one expects all of these solutions to be unstable. Additionally, the mass is still positive, $M>0$, and we did not notice the existence of negative energy densities (although we could not find an analytical argument to show that $\rho >0$).

Finally, the pattern of Dirac solitons without a sextic self-interaction (which was the original case in the pioneering work by Soler [20] ) seems to be similar to the one that is found in the $\beta >0$ case, see Figure 2 (right panel). In particular, both M and Q still diverge at the limits of the w-interval.

4. Including the Gravity Effects

4.1. The Boundary Conditions

The boundary conditions satisfied by the metric functions at the origin are

$$\begin{array}{c}\hfill m\left(0\right)=0,\sigma \left(0\right)={\sigma }_0,\end{array}$$

(66)

while at infinity, one imposes

$$\begin{array}{c}\hfill m(\infty )=M,\sigma (\infty )=1,\end{array}$$

(67)

with $\sigma \left(0\right)$, M numbers fixed by numerics. The matter functions should vanish as $r\to \infty$

$$\begin{array}{c}\hfill \varphi (\infty )=f(\infty )=g(\infty )=F(\infty )=H(\infty )=0,\end{array}$$

(68)

while the boundary conditions at the origin are

$$\begin{array}{ccc}\hfill & & \mathrm{scalar}:\frac{d\varphi \left(r\right)}{dr}{|}_{r=0}=0,\hfill \\ & & \mathrm{Dirac}:f\left(0\right)=0,\frac{dg\left(r\right)}{dr}{|}_{r=0}=0,\hfill \\ \hfill & & \mathrm{Proca}:\frac{dF\left(r\right)}{dr}{|}_{r=0}=0,H\left(0\right)=0.\hfill \end{array}$$

(69)

Let us mention that, in each case, one can construct an approximate form of the solutions both at $r=0$ and at infinity, which is compatible with the boundary conditions above.

4.2. Virial Identities

The reduced action (25) allows for us to prove that the solutions satisfy the (simple enough) interesting virial identities, which generalize for a curved geometry Deser’s relations (51), (53) and (55).

Following [38,39] (wherein generalizations for a curved geometry of Derrick’s argument for flat spacetime [33] were established), assume the existence of a solution that is described by $m\left(r\right)$, $\sigma \left(r\right)$ and $\psi \left(r\right)$ (with $\psi =\{\varphi ;f,g;F,H\}$ the matter fields) with suitable boundary conditions at $r=0$ and at infinity. Subsequently, each member of the one-parameter family $m_{\Lambda }\left(r\right)\equiv m(\Lambda r),$ ${\sigma }_{\Lambda }\left(r\right)\equiv \sigma (\Lambda r),$ and ${\psi }_{\Lambda }\left(r\right)\equiv \psi (\Lambda r),$ assumes the same boundary values at $r=0$ and at $r=\infty$, and the action $S_{\Lambda }\equiv S_{eff}[m_{\Lambda },{\sigma }_{\Lambda },{\psi }_{\Lambda }]$ must have a critical point at $\Lambda =1$, i.e., ${[dS/d\Lambda ]}_{\Lambda =1}=0$. Thus, the putative solution must satisfy the following virial relations (here, it is useful to work with unscaled variables, i.e., before considering the transformations (s2), (s3)):

• scalar field:

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2\sigma \left[{{\varphi }^{\prime }}^2+\frac{w^2(1-4N){\varphi }^2}{N^2{\sigma }^2}+3U\right]=0;\end{array}$$

(70)

• Dirac field:

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2\sigma \left[\sqrt{H}(g{f}^{\prime }-f{g}^{\prime })\left(2+\frac{m}{rN}\right)+\frac{4fg}{r}-\frac{w(f^2+g^2)}{\sigma \sqrt{N}}\left(3-\frac{m}{rN}\right)-3U\right]=0;\end{array}$$

(71)

• Proca field:

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2\sigma [{\mu }^2\left({\mathcal{A}}^2\left(4-\frac{1}{N}\right)+2H^2(1-N)\right)+2\lambda {\mathcal{A}}^2\left({\mathcal{A}}^2\left(5-\frac{2}{N}\right)+4H^2(1-N)\right)\\ \hfill +6\nu {\mathcal{A}}^4\left({\mathcal{A}}^2\left(2-\frac{1}{N}\right)+2H^2(1-N)+4G^2(1-N)\right)-\frac{(wH-F^{\prime })(3wH-F^{\prime })}{{\sigma }^2}]=0.\end{array}$$

(72)

This relation can be further simplified after using the Proca field equations to yield

$$\begin{array}{c}\hfill {\int }_0^{\infty }dr{r}^2\sigma \left[{\mu }^2\left(4-\frac{1}{N}\right){\mathcal{A}}^2+2\lambda \left(5-\frac{2}{N}\right){\mathcal{A}}^4+6\nu \left(2-\frac{1}{N}\right){\mathcal{A}}^6\right]=\\ \hfill 2{\int }_0^{\infty }dr{r}^2\sigma H^2({\mu }^2+4\lambda {\mathcal{A}}^2+6\nu {\mathcal{A}}^4)\left[2N-1+\frac{N^2{\sigma }^2}{2w^2}({\mu }^2+4\lambda {\mathcal{A}}^2+6\nu {\mathcal{A}}^4)\right]\end{array}$$

(73)

These expressions are not transparent, with the effects of gravity and self-interaction being mixed. As such, their main use is to test the accuracy of the numerical results. However, the situation changes once we set $\lambda =\nu =0$ (i.e., no self-interaction). Subsequently, one can see that the solutions are supported by an harmonic time dependence of the matter fields, $w\ne 0$, except for the Dirac case, where we could not prove a similar result.

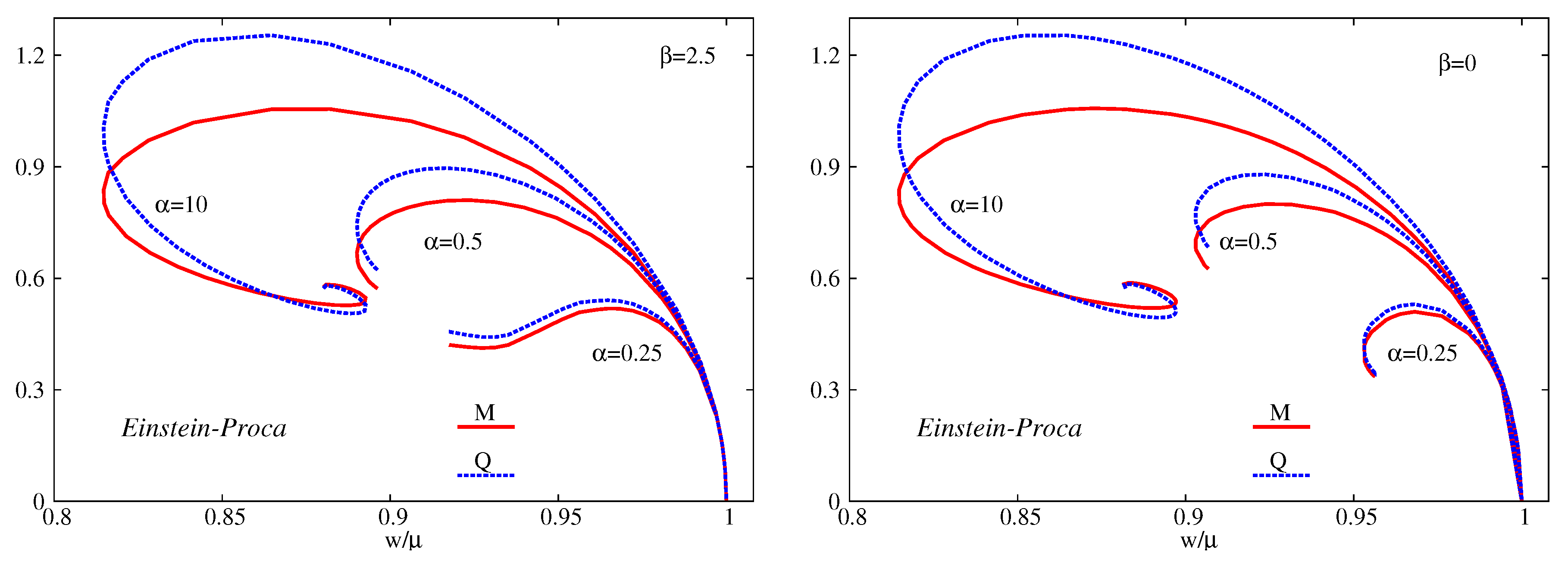
4.3. General Features

The flat space solitons can be generalized to curved spacetime. The presence of higher order self-interacting terms in the potential is not crucial for the existence of gravitating solutions. However, they affect some of their quantitative features.

A common pattern emerges again, with the basic generic properties of the gravitating solutions being summarized, as follows. First, the solutions are topologically trivial, with $0⩽r<\infty$. They possess no horizon; the size of the $S^2$-sector of the metric shrinks to zero as $r\to 0$. At infinity, a Minkowski background is approached. Second, perhaps the most interesting feature is that gravity regularizes the divergencies of the mass and charge that are found in the probe case at the limit(s) of the w-interval. In particular, this regularization implies that no mass gap exists for gravitating configurations: $M,Q\to 0$ as $w\to \mu$. Additionally, assuming the existence of a sextic self-intertion term, with $\beta >1/4$, in all cases, the family of solutions describes a continuous curve in a mass M (or charge Q), $vs.$ frequency, w, diagram. This curve starts from $M=Q=0$ for $w=\mu$, in which limit the fields become very diluted and the solution trivializes. At some intermediate frequency, a maximal mass is attained (that may be a global, or only local, maximum, depending on $\alpha ,\beta )$.

The effects of the quartic and sextic self-interacting terms in the potential (6) become irrelevant for large enough $\alpha$. For example, the $\alpha =10$ curves that are displayed in Figure 4, Figure 5 and Figure 6 are well approximated by the corresponding Einstein-scalar/Dirac/Proca results, with $\beta =\nu =0$, the maximal relative difference being of only a few percent (towards the critical value of frequency).

One can also identify some specific features, as follows. The scalar solutions with $\beta >1/4$ (i.e., a positive potential, $U>0$) and the Proca starts with large $\alpha$ describe a spiral in a $(M,w)$-diagram. As in similar cases, likely, these spirals approach, at their centre, a critical singular solution. The Dirac solutions with $\beta =0$ also describe a spiral. For general Proca solutions with $\beta =0$ and Dirac solutions with $\beta \ne 0$, the $(M,w)$-curves appear to end in a critical configuration before describing a spiral. In the Proca case, this feature is discussed in [24].

The scalar field solutions with $\beta =0$ possess a more complicated pattern. For small $\alpha$, they possess a static limit. Moreover, two disconnected branches of solutions exist for some intermediate range of $\alpha$ e.g., $\alpha =0.5$ in Figure 4 (right panel). In addition to the familiar spiral starting at $w/\mu =1$ and ending for some critical nonzero $w=w_c$, one finds a secondary set, which extends from $w=0$ to some maximal value of $w<w_c$.

Finally, let us mention the existence of another interesting possibility, with quartic interaction only and $\lambda <0$, in which case no flat spacetime solitons are found. The corresponding solutions were discussed in [40] for a scalar field, and in [25] for a Proca field. No similar study exists so far for a fermionic field. In the bosonic case, perhaps the most interesting feature is that their maximal mass is proportional with $\sqrt{\left|\lambda \right|}$, and, thus, can increase dramatically.

5. Other Aspects

5.1. No Hair Results

It is interesting to inquire whether the solutions above may allow the existence of a black hole horizon, inside. Indeed, this is a well known feature that is found for a variety of other solitons, see e.g., the review work [27]. However, this is not the case for the (relatively) simpler solutions in this work.

The situation can be summarized, as follows:

• Scalar case
  Peña and Sudarsky established a no-scalar-hair theorem, ruling out a class of spherically symmetric BHs with scalar hair [41]. Their proof also covers the case of the potential (6) considered in this work, and it still holds if the hair has the harmonic time-dependence that we consider.
• Dirac case
  No hair results for the Einstein–Dirac case with a massive spinor (no self-interaction ) were proposed in [42,43]. The nonexistence of stationary states for the nonlinear Dirac equation with a quartic self-interaction on the Schwarzschild metric has been proven in [44].
• Proca case
  A no hair theorem has been proven in [30] for a massive, non-selfinterating Proca field. In Appendix B, we generalize it for an arbitrary Proca potential $U\left({\mathcal{A}}^2\right)$.

5.2. The Issue of Particle Numbers: Bosons vs. Fermions

In all of the results displayed above, we have equally treated the bosonic and fermionic fields. However, while the classical treatment of the Dirac equation is mathematically justified (a discussion on classical spinors and their possible physical justification can be found, e.g., in Ref. [45]), physically, its fermionic nature should be imposed at the level of the occupation number: at most, a single, particle, in accordance to Pauli’s exclusion principle.

Similarly to the non-self-interacting case that is discussed in [12], the one particle condition is imposed, as follows. Let us suppose that we have a numerical solution with some values for the mass and charge ($M_{\left(\mathrm{num}\right)}$, $Q_{\left(\mathrm{num}\right)}$). Subsequently, we can use the symmetry (34)–(36) in order to map it to a ’new’ solution with

$$\begin{array}{c}\hfill {\overline{Q}}_{\left(\mathrm{num}\right)}=Q_0,\end{array}$$

(74)

where $Q_0>0$ is arbitrary. This assumption fixes the value of the scaling parameter c,

$$\begin{array}{c}\hfill c=\sqrt{\frac{Q_{\left(\mathrm{num}\right)}}{Q_0}},\end{array}$$

(75)

such that the $numerical$ mass of the ’new’ solution will be [12]

$$\begin{array}{c}\hfill {\overline{M}}_{\left(\mathrm{num}\right)}=M_{\left(\mathrm{num}\right)}\sqrt{\frac{Q_0}{Q_{\left(\mathrm{num}\right)}}}.\end{array}$$

(76)

Note that the values of w, $\mu$, $\lambda$, and $\nu$ should also be scaled according to (34) and (35).

This transformation is used to normalize the total charge of a fermion to one, $Q_0=1$. With this condition $Q=1$, the $(M,w)$-curves in Figure 2 (right panels) and Figure 5 are not sequences of solutions with fixed parameters in the potential and varying Q; instead, they get mapped into sequences with fixed Q and varying $\mu ,\nu$. Consequently, one is discussing a sequence of solution of different models (since $\mu$, $\nu$ are input parameters in the action).

Figure 7 shows the corresponding results, for both the probe limit case and including gravity effects. An interesting feature here is that the mass of $Q=1$ non-gravitating configuration can still take arbitrary large values. However, as expected, gravity effects lead to a picture that is qualitatively similar to that found in the $\lambda =\nu =0$ case [12]. Again, both the total mass, M and the mass of the field $\mu$ are bounded and never exceed, roughly, $M_{Pl}$.

6. Further Remarks. Conclusions

The main purpose of this work was to provide a comparative analysis of three different types of solitonic solutions of GR coupled with matter fields of spin $s=0,1/2,1$. A unified framework has been proposed, analysing these cases side-by-side under a consistent set of notations and conventions. Differently from the previous work [12], the matter fields herein are self-interacting, such that all three models possess (Q-ball-like) solutions on the flat spacetime limit. As such, a more complicated landscape of gravitating solutions is found, with some new qualitative features when compared to the picture that is revealed in [12].

However, despite this fact, our study shows that there is, again, a certain universality in the properties of the solitons, being to some extent independent of their (fundamental) spin. As with linear matter fields, the basic ingredients are again: $\left(\mathbf{i}\right)$ a harmonic time dependence of the matter fields; $\left(\mathbf{ii}\right)$ complex field(s)/multiplets such that the energy–momentum is still real; and, $\left(\mathbf{iii}\right)$ the existence of of mass term as a trapping mechanism, creating bound states with $w<\mu$. Additionally, if one requires the presence of a well defined flat space limit, then $\left(\mathbf{iv}\right)$ the fields should possess at least a quartic self-interaction term.

As an avenue for future work, it would be interesting to go beyond the case of spherical symmetry and consider a comparative study of axially symmetric, spinning solutions. In the non-self-interacting case, this was the subject of the recent work [46], where a common pattern was again revealed to exist. The situation in the presence of self-interactions is less studied; only the scalar field case has, so far, been discussed in the literature [47,48]. Indeed, even flat space spinning solitons with spin $s=1/2,1$ are yet unreported in the literature. Moreover, even in the static case, new families of non-spherically symmetric solitons should exist, generalizing, for a self-interacting potential (and possibly for a higher spin), the $s=0$ multipolar boson stars recently reported in [49].

Finally, let us remark that, for a bosonic field, $s=0,1$, the no-hair theorems (as reviewed in the previous Section) can be circumvented for an horizon that rotates synchronously with the field, leading to BHs with scalar or Proca hair [30,50]. However, this does not seem to be the case for fermions, regardless of the presence of a self-interacting potential.