Abstract
Spontaneous Symmetry Breaking (SSB) in theories is usually described as a 2nd-order phase transition. However, most recent lattice calculations indicate instead a weakly 1st-order phase transition as in the one-loop and Gaussian approximations to the effective potential. This modest change has non-trivial implications. In fact, in these schemes, the effective potential at the minima has two distinct mass scales: (i) a first mass associated with its quadratic curvature and (ii) a second mass associated with the zero-point energy which determines its depth. The two masses describe different momentum regions in the scalar propagator and turn out to be related by , where is the ultraviolet cutoff of the scalar sector. Our lattice simulations of the propagator are consistent with this two-mass picture and, in the Standard Model, point to a value GeV. However, despite its rather large mass, this heavier excitation would interact with longitudinal W’s and Z’s with the same typical coupling of the lower-mass state and would therefore represent a rather narrow resonance. Two main novel implications are emphasized in this paper: (1) since vacuum stability depends on the much larger , and not on , SSB could originate within the pure scalar sector regardless of the other parameters of the theory (e.g., the vector-boson and top-quark mass) (2) if the smaller mass were fixed at the value 125 GeV measured at LHC, the hypothetical heavier state would then naturally fit with the peak in the 4-lepton final state observed by the ATLAS Collaboration at 700 GeV.
PACS:
11.30.Qc; 12.15.-y; 13.85.-t
1. Introduction
Spontaneous Symmetry Breaking (SSB) through the vacuum expectation value of a fundamental scalar field, the BEH field [1,2], is an essential element of the Standard Model. This original idea has been recently confirmed by the discovery at LHC [3,4] of a narrow scalar resonance with mass GeV whose characteristics fit well with the theoretical expectations. This has produced the widespread belief that any change of this general picture could only originate from new physics.
However, this conclusion might not be entirely true. In fact, at present, only the gauge and Yukawa interactions of the 125 GeV resonance have been tested. Instead, the possible effects of a genuine scalar self-coupling are still below the precision of the observations. This suggests that some uncertainty on the origin of SSB may still persist.
Originally, the underlying mechanism was identified in a classical double-well, scalar potential. However, later, after Coleman and Weinberg [5], the classical potential was replaced by the quantum effective potential which includes the zero-point energy of all fields in the theory.
Yet, SSB could still originate within the pure sector if the other fields give a negligible contribution to the vacuum energy. To fully appreciate this point, we must start from scratch and consider one aspect which has still to be clarified: the nature of the phase transition in a pure scalar theory in 4D. More precisely, is it a 2nd-order phase transition or a (weakly) 1st-order transition? Surprising as it may be, this apparently minor change can have substantial phenomenological implications.
To this end, in Section 2, Section 3 and Section 4 we will give a general overview of the problem and argue that SSB in pure theory is a weak 1st-order phase transition. Then, in this picture, besides the known resonance with mass 125 GeV, we expect a new excitation of the BEH field with a much larger mass 700 GeV. Since vacuum stability depends on this larger , and not on , SSB could well originate within the pure scalar sector regardless of the remaining parameters of the theory (as the vector boson or top-quark mass).
However, despite such large mass, this heavier state would interact with longitudinal W’s and Z’s with the same typical strength of the lower-mass state. As such, it would represent a rather narrow resonance. On this basis, in Section 5 and Section 6, we will consider these more phenomenological aspects and their implications for the present LHC experiments.
2. SSB: 2nd- or (Weak) 1st-Order Phase Transition?
To introduce the problem, let us start with the classical potential ()
Here, there is no ambiguity. As one varies the parameter, one finds a 2nd-order phase transition occurring for . However, in the full quantum theory is this conclusion still so obvious? To this end, one should look at the effective potential and study vacuum stability depending on the physical mass, say , in the symmetric vacuum at
Clearly, this is locally stable if . However, for , is this symmetric vacuum also globally stable? Or, instead, could the SSB transition be 1st-order and occur for some very small but still positive ? Then, if this were true, the lowest-energy state for the classically scale-invariant case would correspond to the broken-symmetry phase with an expectation .
This dilemma, on the nature of the phase transition, goes back to the pioneering work of Coleman and Weinberg [5]. After subtracting a independent constant and quadratic divergences, in this massless limit of , their original 1-loop result was
where is a large ultraviolet cutoff. As it is well known, this 1-loop form could equivalently be expressed as the sum of classical background + zero-point energy of a field with a dependent mass given by
namely
By using this notation, there are non-trivial minima for those values, say , where
Therefore, since the massless theory exhibits SSB, the 1-loop potential indicates a 1st-order phase transition. Actually, it is a weak 1st-order transition because, in units of the in Equation (6), the mass in the symmetric phase is bounded to be smaller than a critical mass [6]
With such extremely small critical mass, SSB emerges as an infinitesimally weak 1st-order transition which could hardly be distinguished from a 2nd-order transition unless one looks on an extremely fine scale.
As is well known [5], though, the standard Renormalization-Group (RG) improvement of the 1-loop potential contradicts this scenario. Indeed, leading-logarithmic terms entering the effective potential are re-absorbed into an effective coupling giving a re-summed expression
Thus, by restricting to , the 1-loop minimum disappears and we would again predict a 2nd-order transition at . The standard view is that it is this latter point of view to be reliable.
To see why things are not so simple, let us consider another approximation scheme. Specifically, the Gaussian effective potential [7,8]. Diagrammatically, this corresponds to the infinite re-summation of all one-loop bubbles with mass and has a variational nature by exploring the Hamiltonian operator within the Gaussian functional states. For this reason, it is a very natural alternative because a Gaussian set of Green’s functions would fit with the “triviality” of theory in 4D. An early calculation [9] of the Gaussian effective potential for the one-component theory confirmed the 1st-order scenario in agreement with the 1-loop potential. This is because the existing corrections beyond 1-loop reproduce the some functional form and thus support the same 1st-order picture.
Further calculations, by Bryhaye and one of us [10,11], confirmed that by imposing , the Gaussian effective potential for the O(2) and O(N)-symmetric scalar theories exhibits SSB thus again supporting the weak 1st-order picture. In particular, it was noted the non-uniformity of the two limits and ultraviolet cutoff .
To fully appreciate the substantial equivalence with the one-loop potential, we observe that the infinite additional terms in the Gaussian effective potential can be expressed in a form analogous to Equation (5) with a simple redefinition of the classical background and of the dependent mass in the zero-point energy, i.e.,
with
This shows that the 1-loop potential also admits a non-perturbative interpretation. In fact, by displaying the same basic structure of classical background + zero-point energy, it represents the prototype of all gaussian and post-gaussian calculations [12,13]. At the same time, it also explains why 1-loop and Gaussian approximations, although differing in terms of the bare parameters, can become identical in a suitable renormalization scheme [14,15].
This concordance among various approximations may cast some doubts on the re-summation in Equation (8) and its 2nd-order scenario. Nevertheless, at the time of those works, the precise motivation for the discrepancy was not understood. Thus, the whole problem of SSB in pure theories did not attract much attention, also due to the lack of definite phenomenological implications.
However, two subsequent theoretical developments, producing new evidence in favor of the 1st-order scenario, have refreshed anew the interest into the whole problem:
(i) the first development was concerning the physical mechanisms [6] underlying SSB as a 1st-order transition. In fact, once SSB really coexists with a physical mass for the elementary quanta of the symmetric phase, these quanta, the “phions” [6], should be considered to be real particles although, being “frozen” in the broken-symmetry vacuum, they would not be directly observable (like quarks). Now, the conventional picture of corresponds to a repulsive interaction. Only its strength decreases at large distance. However, then, this is somewhat mysterious. In fact, if the interaction remains always repulsive, how could this broken-symmetry vacuum with , a Bose condensate of phions, have a lower energy than the empty state with no phions? Here, a crucial observation [6] was that phions, moreover the + contact repulsion, also feel a attraction arising at 1-loop and which becomes more and more important when (From the scattering amplitude , computed from Feynman graphs, one can define an interparticle potential which is nothing but the 3D Fourier transform of , see Feinberg et al. [16,17].). By including both effects, one can now understand [6] why, for small enough , the attraction can dominate and the lowest-energy state becomes a state with a non-zero density of phions Bose-condensed in the zero-momentum state.
However, then, if SSB is produced by these two competing effects (short-range repulsion and long-range attraction) we now understand the failure of the standard RG-analysis. In fact, the attractive term originates from the ultraviolet-finite part of the 1-loop graphs. Therefore, to correctly include higher-order effects, one should renormalize both the tree-level contact repulsion and the 1-loop, long-range attraction, as if there were two different coupling constants in the theory. This different procedure has been adopted by Stevenson [18], see Figure 1. By avoiding double counting, he has shown that the simple 1-loop result and its RG-improvement, in this new scheme, now agree very well so that the weak 1st-order scenario is confirmed.
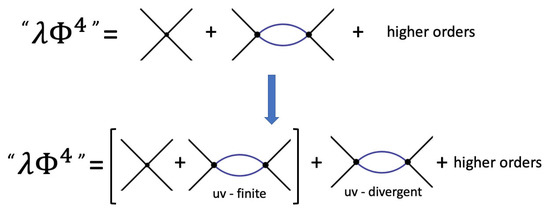
Figure 1.
The re-arrangement of perturbation theory introduced by Stevenson [18] in his alternative analysis of . The quanta of the symmetric phase with mass , besides the contact + repulsion, also feel a attraction from the Fourier transform of the ultraviolet-finite part of the 1-loop term [6]. Its range diverges in the limit and, for below a critical mass , the attraction will dominate and induce SSB. Since higher-order contributions simply renormalize these two basic effects, the resulting RG-improvement, in this new scheme, now confirms the 1st-order phase transition scenario as at 1-loop.
(ii) recent lattice simulations of pure in 4D [19,20,21], obtained with different algorithms in the Ising limit of the theory (and on the present largest available lattices), indicate that the SSB phase transition is weakly 1st-order.
Since the above arguments (i) and (ii) confirm the 1st-order picture of SSB, and the general validity of the 1-loop and Gaussian approximations to the effective potential, we will now consider in Section 3 some important physical implications of this scenario.
3. Two-Mass Scales in the Broken Phase
To explore the physical implications of a 1st-order scenario of SSB, we will restrict to the one-loop approximation Equation (5) of which is equivalent to the Gaussian approximation result Equation (9). Equation (5) is just a different way of re-writing Equation (3) but intuitively supports the traditional view where the broken-symmetry phase is a simple massive theory with mass as in Equation (6). Thus, one expects that up to small perturbative corrections, this is the mass parameter entering the scalar propagator.
To see why, again, things are not so simple, let us compute the quadratic shape of the effective potential, i.e., its second derivative at the minimum. This other quantity, say , has the value
where . Now, the derivatives of the effective potential are just (minus) the n-point functions for zero external momentum. In particular, one finds
Therefore, by expressing the inverse propagator as
we find for . This means that apparently, it is this smaller mass , and not , which enters the (low-momentum) propagator. However, now, in the limit, and are vastly different scales (i.e., do not differ by small perturbative corrections). Thus one may ask: which is the right mass?
To better understand this point, let us sharpen the meaning of by using the general relation which expresses the zero-point-energy (“zpe”) in terms of the trace of the logarithm of , i.e.,
Thus, after subtracting a constant and quadratic divergences, to match the 1-loop Equation (5), we can impose appropriate limits in the logarithmic divergent part (i.e., and )
This relation indicates that reflects the typical, average at non-zero . Therefore, if we trust in the 1-loop relation , we should observe large deviations in the propagator if we try to extrapolate to higher- with the 1-particle form which is valid for . In other words, in a 1st-order picture of SSB, the idea of a simple massive propagator seems to be wrong.
To show that these are not just speculations, let us compare with lattice calculations of the scalar propagator in the broken-symmetry phase. The simulation was performed [22] in the 4D Ising limit which has always been considered a convenient laboratory to exploit the non-perturbative aspects of the theory. It is the in the limit of an infinite bare coupling , as sitting exactly at the Landau pole. As such, for a finite cutoff , it represents the best possible definition of the local limit for a non-zero, low-energy coupling (where ). For the convenience of the reader, we will report here the main results of [22].
In the Ising limit, the broken-symmetry phase corresponds to values of the basic hopping parameter , with the critical [19,20]. We computed the field vacuum expectation value
and the connected propagator
where with we are indicating the average over lattice configurations.
In terms of the Fourier transform of the propagator, the extraction of is straightforward, i.e.,
Instead had to be extracted from the data for the Fourier transformed propagator at higher momentum. To this end, we first fitted the data to the 2-parameter form
in terms of the lattice squared momentum with . The quality of this fit was then studied to understand how reliable the determination is from the higher-momentum region. Finally, the propagator data were re-scaled by the factor . In this way, deviations from a straight line will show up clearly if a fitted mass fails to describe the lattice data when .
The results in the symmetric phase, see Figure 2, show that there, with just a single lattice mass one can describe all data down to .
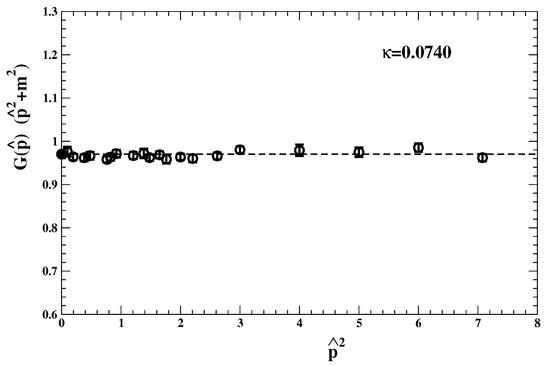
Figure 2.
The data for the re-scaled lattice propagator ref. [22] in the symmetric phase at depending on the square lattice momentum with . In this case, the mass fitted from higher-, , describes well the data down to . The dashed line is the fitted .
In the broken phase, for , the results for the largest lattice are reported in Figure 3 and Figure 4. The larger mass obtained from the higher-momentum fit was . As one can see from Figure 3, this fitted mass describes the data for not too small momentum. But for the deviations from a straight line become highly significant statistically. In this low- limit, in fact, the data would require the other mass , see Figure 4.
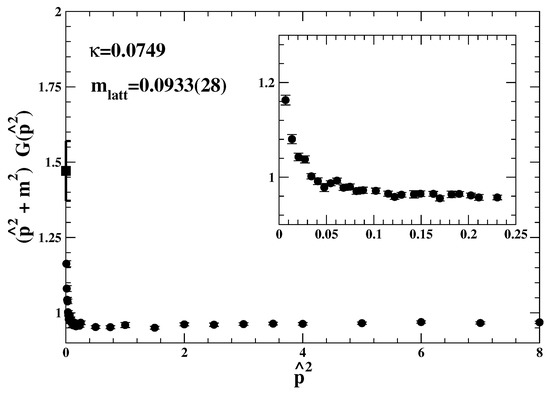
Figure 3.
The data for the re-scaled lattice propagator ref. [22] in the broken phase at . The mass used for the re-scaling, , was obtained from fitting to all data with . The black square at is as computed from the fitted for .
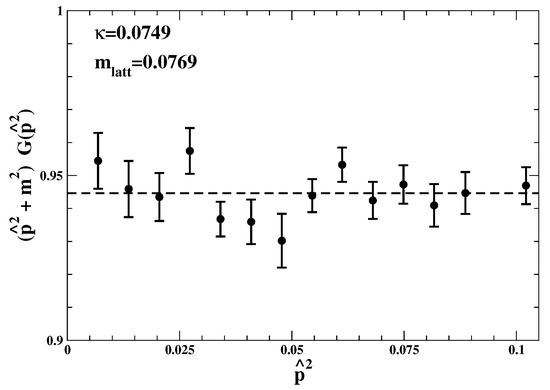
Figure 4.
The lattice data of ref. [22] at for . The mass used here for the re-scaling has been fixed at the value .
The difference between and has the high statistical significance of 6 sigma. More importantly, once is directly computed from the zero-momentum limit of and is extracted from its behavior at higher , the extrapolation of the results toward the critical point [22] is well consistent with the expected increasing logarithmic trend .
4. The Relative Magnitude of mh, Mh and ⟨Φ⟩
As summarized in Section 3, our lattice simulations supports the idea of a scalar propagator which, in the broken phase, interpolates between two different mass scales and (Two-mass scales also require some interpolating form for the scalar propagator in loop corrections. Since some precise measurements, e.g., of the b-quark or from NC experiments [23], still favor a rather large BEH particle mass, this could help to improve the present rather low quality of the overall Standard Model fit). The lattice data are also consistent with the trend predicted by the one-loop and Gaussian approximations to the effective potential. Since the two masses do not scale uniformly in the limit (This non- uniform scaling is crucial not to run in contradiction with the “triviality” of in 4D [22]. In fact, this implies a continuum limit with a Gaussian set of Green’s functions and therefore with a massive free-field propagator. Thus, in an ideal continuum theory, there can only be one mass depending on the unit of mass ( or ) adopted for measuring momenta), the question naturally arises about the extension to the Standard Model and their relationship with the fundamental weak scale 246.2 GeV. In fact, it seems that we should now introduce two different coupling constants, say and . However, then, since , are we faced with a weak- or a strong-coupling theory?
To approach the problem in a systematic way, let us first return to the one-loop relations Equations (5) and (6) in Section 2 and observe that the vacuum energy depends on , not on , namely
This means that the critical temperature to restore the symmetry, , and the whole stability of the broken-symmetry phase will depend on , not on .
This remark will be crucial to understand the cutoff dependence of the various scales and to formulate a description of SSB which in principle can be extended to the limit. In fact, since for any non-zero low-energy coupling there is a Landau pole , we will consider the entire set of pairs (,), (,), (,)...with larger and larger cutoffs, smaller and smaller couplings but all with the same vacuum energy as in Equation (20). This amounts to impose
a condition which can be derived from the more general requirement of RG-invariance for the effective potential in the (, , ) 3-space
It is important that in this RG-analysis, besides a first invariant mass scale , if we introduce an anomalous dimension for the vacuum field
there will be a second invariant [22] associated with the RG-evolution in the (, , ) 3-space, namely
This invariant fixes a particular normalization (The anomalous dimension of reflects the fact that from Equation (6), the cutoff-independent combination is and not itself implying [22]. This somewhat resembles the definition of the physical gluon condensate in QCD which is and not just .) of and is then the natural candidate to represent the weak scale 246.2 GeV. The minimization of the effective potential is then translated into a proportionality of the two invariants through some constant K, say
Such guiding principle indicates that and scale uniformly while at the same time, and . Therefore, by assuming the theoretical predictions for the ratio , and computing the ratio from our lattice data for the propagator, we have extracted the constant K. As shown in [22] such procedure, where the cutoff-dependent L drops out, leads to a final estimate or
which includes various statistical and theoretical uncertainties and updates the previous work of refs. [24,25].
We emphasize that the relation does not introduce a new large coupling which modifies the phenomenology of the broken phase. This is clearly quite distinct from the other coupling but should not be viewed as a coupling producing observable interactions. Since reflects the magnitude of the vacuum energy density, it would be natural to consider as a collective self-interaction of the vacuum condensate which persists when . This original view [14,15] can intuitively be formulated in terms of a scalar condensate whose increasing density [6] compensates for the decreasing strength of the two-body coupling (This view of SSB has some analogy with the occurring of superconductivity in solid-state physics. There, the superconductive phase occurs even for an arbitrary small two-body attraction between the two electrons in a Cooper pair. However, the energy density and the collective quantities of the superconductive phase (as energy gap, critical temperature, etc.) depend on a much larger coupling obtained by re-scaling with the large density of states at the Fermi surface. This means that the same macroscopic description could be obtained with smaller and smaller and Fermi systems with suitably larger and larger N. In this analogy is the counterpart of and of ).
Instead, is the right coupling for the individual interactions of the vacuum excitations, i.e., the BEH field and the Goldstone bosons. Consistently with the “triviality” of theory, these interactions will become weaker and weaker when .
With this description of the scalar sector, and by using the Equivalence Theorem [26,27], the same conclusion applies to the high-energy interactions of the BEH field with the longitudinal vector bosons in the full theory. In fact, the limit of zero-gauge coupling is smooth [28]. Therefore, up to corrections proportional to , a heavy BEH resonance will interact exactly with the same strength as in the theory [29]. For the convenience of the reader, this point will be summarized in Section 5. In Section 6, we will instead consider some phenomenological implications for the present LHC experiments.
5. Observable Interactions for a Large Mh
As anticipated, the quantity should be understood as a collective self-coupling of the scalar condensate whose effects are re-absorbed into the vacuum structure. As such, it is basically different from the coupling defined through the function
For , whatever the bare contact coupling at the asymptotically large , at finite scales this gives with . It is this latter coupling which governs the residual interactions among the fluctuations with very small deviations from a purely quadratic potential for .
By introducing the W-mass and with the notations of [30], a convenient way [29] to express these residual interactions in the scalar potential is ()
The two parameters and , which are usually set to unity, take into account the basic difference , i.e.,
Then, one can consider that corner of the parameter space [29], namely large but , that does not exist in the conventional view where one assumes .
A possible objection to this scenario might concern its validity in the full gauge theory. In fact, the original calculation [31] in the unitary gauge could give the impression of the opposite view. Specifically, that with a heavy Higgs resonance of mass , longitudinal scattering is indeed governed by the large parameter . Since this is an important point, we will repeat here the main argument of [29].
In the unitary-gauge calculation of high-energy scattering, the lowest-order amplitude is formally but one ends up with
In this chain, comes from the vertices. The originates from the external longitudinal polarizations and the factor emerges after expanding the Higgs field propagator
Then the leading contribution cancels against a similar term from the other diagrams (which otherwise would give an amplitude growing with s) and the from the expansion of the propagator is effectively “promoted” to the role of coupling constant. In this way, one gets exactly the same result as in a pure theory with a contact coupling .
However, this is only the tree approximation. To obtain the full result, let us observe that the Equivalence Theorem is a non perturbative statement which holds to all orders in the pure scalar self-interactions [28]. Therefore, we have not to worry to re-sum the infinite series of higher-order vector-boson graphs. However, from the amplitude at a scale for
we can deduce the result for the longitudinal vector bosons in the theory, i.e.,
Then, in the present perspective of a large but finite , where and now coexist and could be experimentally determined, at the putative strong interactions proportional to should actually be viewed as weak interactions controlled by the much smaller coupling
Analogously, the conventional very large width into longitudinal vector bosons computed with the coupling , say , should instead be re-scaled by . This gives
In this way, through the decays of the heavier state, the scalar coupling could finally become visible.
6. Some Predictions for the LHC Experiments
Let us take seriously the idea of a BEH field with two vastly different mass scales, namely 125 GeV and 700 GeV. Is there any experimental signal from the LHC experiments? If so, what kind of phenomenology should we expect?
To address these questions, we will use a small but definite experimental evidence: the peak in the 4-lepton final state which is presently observed by the ATLAS Collaboration [32] for an invariant mass 700 GeV. We emphasize that this should be taken seriously. In fact, an independent analysis of these data and their combination [33] with the corresponding ones of the CMS Collaboration indicates an evident excess, over the background, at the level of about 5 sigma.
Of course, the 4-lepton channel is only one decay channel of a hypothetical heavier BEH resonance and, for a more complete analysis, we should also consider the other final states. For instance the decay into two photons, a channel that in the past has been showing other intriguing evidence for the near energy 750 GeV. However, the 4-lepton channel, has the advantage of being experimentally very clean and, just for this reason, is called the “golden” channel to detect a possible heavy BEH resonance. At the same time, as in ref. [34], the main effect can be analyzed at a very simple level. For this reason, one can meaningfully start from here.
Let us consider the peak in the number of events observed by ATLAS in the 4-lepton channel for an invariant mass 700 GeV (). From Figure 4a of [32] this corresponds to
above the very small background 1 event. By subtracting this background, we get
Since the ATLAS efficiency for reconstructed 4-lepton events at large transverse momentum is about 100%, for the given luminosity of 36.1 , we obtain a peak cross-section
For our estimates, we will assume the invariant mass 700 GeV to be the same pole mass 700 GeV of our heavier excitation of the BEH field. Moreover, if we consider this as a relatively narrow resonance, the corrections due to its virtual propagation should be small [35] and one could approximate the result in terms of on-shell branching ratios as
In this relation, the boson branching fraction into charged leptons is known precisely and one finds .
Concerning the other branching ratio , for 700 GeV, the only unconventional aspect of our picture concerns the coupling of the heavy BEH resonance to longitudinal vector bosons which is proportional to and not to . Therefore, given a decay width , we could use the conventional estimate for 700 GeV [36,37]
and, by replacing instead
obtain as
Equivalently, given a value of we can compute
Here, we will follow this latter strategy and assume GeV which gives
Thus, to obtain , we only need to estimate the total decay width. Here, we will retain exactly the other contributions reported in the literature [36,37] for 700 GeV
and the same dimensionless ratio
These input numbers (which have very small uncertainties) will then produce a total decay width
and a branching ratio
Let us now consider the total cross-section , for production of a heavy BEH resonance with mass 700 GeV. Here, the two main contributions derive from more elementary parton processes where two gluons or two vector bosons fuse to produce the heavy state (here would be emitted by two quarks inside the protons). For this reason, the two process are usually called Gluon-Gluon Fusion (GGF) and Vector-Boson Fusion (VBF) mechanisms, i.e.,
The traditional importance of the latter process for large is understood by noticing that the process is the inverse of the decay and therefore can be expressed [38] as a convolution with the parton densities of the same BEH resonance decay width. Thus, once its coupling to longitudinal W’s and Z’s were proportional to , with a conventional width 172 GeV for 700 GeV, the VBF mechanism would become important. However, this coupling is not present in our model, where instead we expect
For this reason, the whole VBF will also be correspondingly reduced from its conventional value fb, i.e.,
This is much smaller than the uncertainty in the pure GGF contribution and will be ignored in the following.
In the end, the GGF term. Here, we will separately adopt two slightly different estimates. On the one hand, the value fb of ref. [36] and on the other hand, the value fb of ref. [37]. These values refer to TeV and will be re-scaled by about for the present center of mass energy TeV. In the two cases, the errors take into account uncertainties in the normalization scale and in the parametrization of the parton distributions.
Altogether, for 0.054 and , our predictions for the 4-lepton cross-section and the number of events (for luminosity of 36.1 and 139 ) are reported in Table 1.

Table 1.
For 700 GeV and 125 GeV, we report our predictions for the peak cross-section and the number of events at two values of the luminosity. The two total cross sections are our extrapolation to TeV of the values in [36,37] for TeV. As explained in the text, only the GGF mechanism is relevant in our model.
From this comparison we deduce that without introducing any free parameter, our model can easily reproduce the presently observed number of events . This is why, our hypothetical new resonance could naturally fit with the ATLAS peak. At present, this is the only possible conclusion and a real test of our picture is postponed to the analysis of the entire statistics 139 . If the new 700 GeV were really there, the peak should become four times higher but remain well above the background which is very small at that energy. Thus, the profile of the resonance should become visible and direct determinations of the total decay width should be feasible. An experimental result GeV would favor an experimental branching ratio close to our reference value 0.054 and, therefore, improve the agreement of our smaller with the value 125 GeV which is measured directly at LHC. Thus, the description of SSB given here would find a first experimental confirmation.
Author Contributions
Conceptualization, M.C. and L.C.; methodology, M.C. and L.C.; software, M.C. and L.C.; validation, M.C. and L.C.; formal analysis, M.C. and L.C.; investigation, M.C. and L.C.; resources, M.C. and L.C.; data curation, M.C. and L.C.; writing—original draft preparation, M.C. and L.C.; writing—review and editing, M.C. and L.C.; visualization, M.C. and L.C.; supervision, M.C. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This paper is dedicated to Yves Brihaye in the occasion of his 65th birthday.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Englert, F.; Brout, R. Broken Symmetry and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 1964, 13, 321–323. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken symmetries, massless particles and gauge fields. Phys. Lett. 1964, 12, 132–133. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Coleman, S.R.; Weinberg, E.J. Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Phys. Rev. D 1973, 7, 1888–1910. [Google Scholar] [CrossRef]
- Consoli, M.; Stevenson, P.M. Physical mechanisms generating spontaneous symmetry breaking and a hierarchy of scales. Int. J. Mod. Phys. A 2000, 15, 133. [Google Scholar] [CrossRef]
- Barnes, T.; Ghandour, G.I. Variational Treatment of the Effective Potential and Renormalization in Fermi-Bose Interacting Field Theories. Phys. Rev. D 1980, 22, 924. [Google Scholar] [CrossRef]
- Stevenson, P.M. The Gaussian Effective Potential. 2. Lambda phi**4 Field Theory. Phys. Rev. D 1985, 32, 1389–1408. [Google Scholar] [CrossRef]
- Consoli, M.; Ciancitto, A. Indications of the occurrence of spontaneous symmetry breaking in massless λϕ4. Nucl. Phys. B 1985, 254, 653–677. [Google Scholar] [CrossRef][Green Version]
- Brihaye, Y.; Consoli, M. Spontaneous symmetry breaking in an O(2) invariant scalar theory. Phys. Lett. B 1985, 157, 48–52. [Google Scholar] [CrossRef]
- Brihaye, Y.; Consoli, M. Gaussian Quantization, O(N) Theory and the Goldstone Theorem. Nuovo Cim. A 1986, 94, 1–14. [Google Scholar] [CrossRef]
- Stancu, I.; Stevenson, P.M. Second Order Corrections to the Gaussian Effective Potential of λϕ4 Theory. Phys. Rev. D 1990, 42, 2710–2725. [Google Scholar] [CrossRef] [PubMed]
- Cea, P.; Tedesco, L. Perturbation theory with a variational basis: The Generalized Gaussian effective potential. Phys. Rev. D 1997, 55, 4967–4989. [Google Scholar] [CrossRef]
- Consoli, M.; Stevenson, P.M. The Nontrivial effective potential of the ’trivial’ λϕ4 theory: A Lattice test. Z. Phys. C 1994, 63, 427–436. [Google Scholar] [CrossRef]
- Consoli, M.; Stevenson, P.M. Mode-dependent field renormalization and triviality in λϕ4 theory. Phys. Lett. B 1997, 391, 144–149. [Google Scholar] [CrossRef]
- Feinberg, G.; Sucher, J. Long-Range Forces from Neutrino-Pair Exchange. Phys. Rev. 1968, 166, 1638–1644. [Google Scholar] [CrossRef]
- Feinberg, G.; Sucher, J.; Au, C.K. The Dispersion Theory of Dispersion Forces. Phys. Rept. 1989, 180, 83. [Google Scholar] [CrossRef]
- Stevenson, P.M. The Long-range interaction in massless λϕ4 theory. Mod. Phys. Lett. A 2009, 24, 261–271. [Google Scholar] [CrossRef]
- Lundow, P.H.; Markström, K. Critical behavior of the Ising model on the four-dimensional cubic lattice. Phys. Rev. E 2009, 80, 031104. [Google Scholar] [CrossRef]
- Lundow, P.H.; Markstrom, K. Non-vanishing boundary effects and quasi-first order phase transitions in high dimensional Ising models. Nucl. Phys. B 2011, 845, 120–139. [Google Scholar] [CrossRef]
- Akiyama, S.; Kuramashi, Y.; Yamashita, T.; Yoshimura, Y. Phase transition of four-dimensional Ising model with higher-order tensor renormalization group. Phys. Rev. D 2019, 100, 054510. [Google Scholar] [CrossRef]
- Consoli, M.; Cosmai, L. The mass scales of the Higgs field. Int. J. Mod. Phys. A 2020, 35, 2050103. [Google Scholar] [CrossRef]
- Chanowitz, M.S. Z-prime Bosons, the NuTeV Anomaly, and the Higgs Boson Mass. Phys. Atom. Nucl. 2010, 73, 680–688. [Google Scholar] [CrossRef]
- Cea, P.; Consoli, M.; Cosmai, L. Indications on the Higgs boson mass from lattice simulations. Nucl. Phys. Proc. Suppl. 2004, 129, 780–782. [Google Scholar] [CrossRef]
- Cea, P.; Cosmai, L. The Higgs boson: From the lattice to LHC. ISRN High Energy Phys. 2012, 2012, 637950. [Google Scholar] [CrossRef]
- Cornwall, J.M.; Levin, D.N.; Tiktopoulos, G. Derivation of Gauge Invariance from High-Energy Unitarity Bounds on the s Matrix. Phys. Rev. D 1974, 10, 1145. [Google Scholar] [CrossRef]
- Chanowitz, M.S.; Gaillard, M.K. The TeV Physics of Strongly Interacting W’s and Z’s. Nucl. Phys. B 1985, 261, 379–431. [Google Scholar] [CrossRef]
- Bagger, J.; Schmidt, C. Equivalence Theorem Redux. Phys. Rev. D 1990, 41, 264. [Google Scholar] [CrossRef]
- Castorina, P.; Consoli, M.; Zappala, D. An Alternative heavy Higgs mass limit. J. Phys. G 2008, 35, 075010. [Google Scholar] [CrossRef][Green Version]
- Veltman, M.J.G.; Yndurain, F.J. Radiative corrections to W W scattering. Nucl. Phys. B 1989, 325, 1–17. [Google Scholar] [CrossRef][Green Version]
- Lee, B.W.; Quigg, C.; Thacker, H.B. Weak Interactions at Very High-Energies: The Role of the Higgs Boson Mass. Phys. Rev. D 1977, 16, 1519. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abdinov, O.; Abeloos, B.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Search for heavy ZZ resonances in the ℓ+ℓ-ℓ+ℓ- and ℓ+ℓ-νν¯ final states using proton–proton collisions at s=13TeV with the ATLAS detector. Eur. Phys. J. C 2018, 78, 293. [Google Scholar] [CrossRef] [PubMed]
- Cea, P. Evidence of the true Higgs boson HT at the LHC Run 2. Mod. Phys. Lett. A 2019, 34, 1950137. [Google Scholar] [CrossRef]
- Consoli, M.; Cosmai, L. A resonance of the Higgs field at 700 GeV and a new phenomenology. arXiv 2020, arXiv:2007.10837. Available online: https://arxiv.org/abs/2007.10837 (accessed on 20 July 2020).
- Goria, S.; Passarino, G.; Rosco, D. The Higgs Boson Lineshape. Nucl. Phys. B 2012, 864, 530–579. [Google Scholar] [CrossRef]
- Djouadi, A. The Anatomy of electro-weak symmetry breaking. I: The Higgs boson in the standard model. Phys. Rept. 2008, 457, 1–216. [Google Scholar] [CrossRef]
- Dittmaier, S.; Mariotti, C.; Passarino, G.; Tanaka, R.; Baglio, J.; Bolzoni, P.; Boughezal, R.; Brein, O.; Collins-Tooth, C.; Dawson, S.; et al. Handbook of LHC Higgs Cross Sections: 1. Inclusive Observables. arXiv 2011, arXiv:1101.0593. [Google Scholar]
- Kane, G.L.; Repko, W.; Rolnick, W. The Effective W+-, Z0 Approximation for High-Energy Collisions. Phys. Lett. B 1984, 148, 367–372. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).