Locating Movable Parcel Lockers under Stochastic Demands
Abstract
1. Introduction
2. Literature Review
3. Robust Optimization Model under Stochastic Demands
3.1. Problem Description and Assumptions
3.2. Optimization Model under Stochastic Demands
3.2.1. Optimization Model under Deterministic Demands
3.2.2. Robust Optimization
4. Experiments and Results
4.1. Parameter Settings
4.1.1. Purchase Cost
4.1.2. Maintenance Cost
4.1.3. Travel Cost
4.1.4. Rent for Land
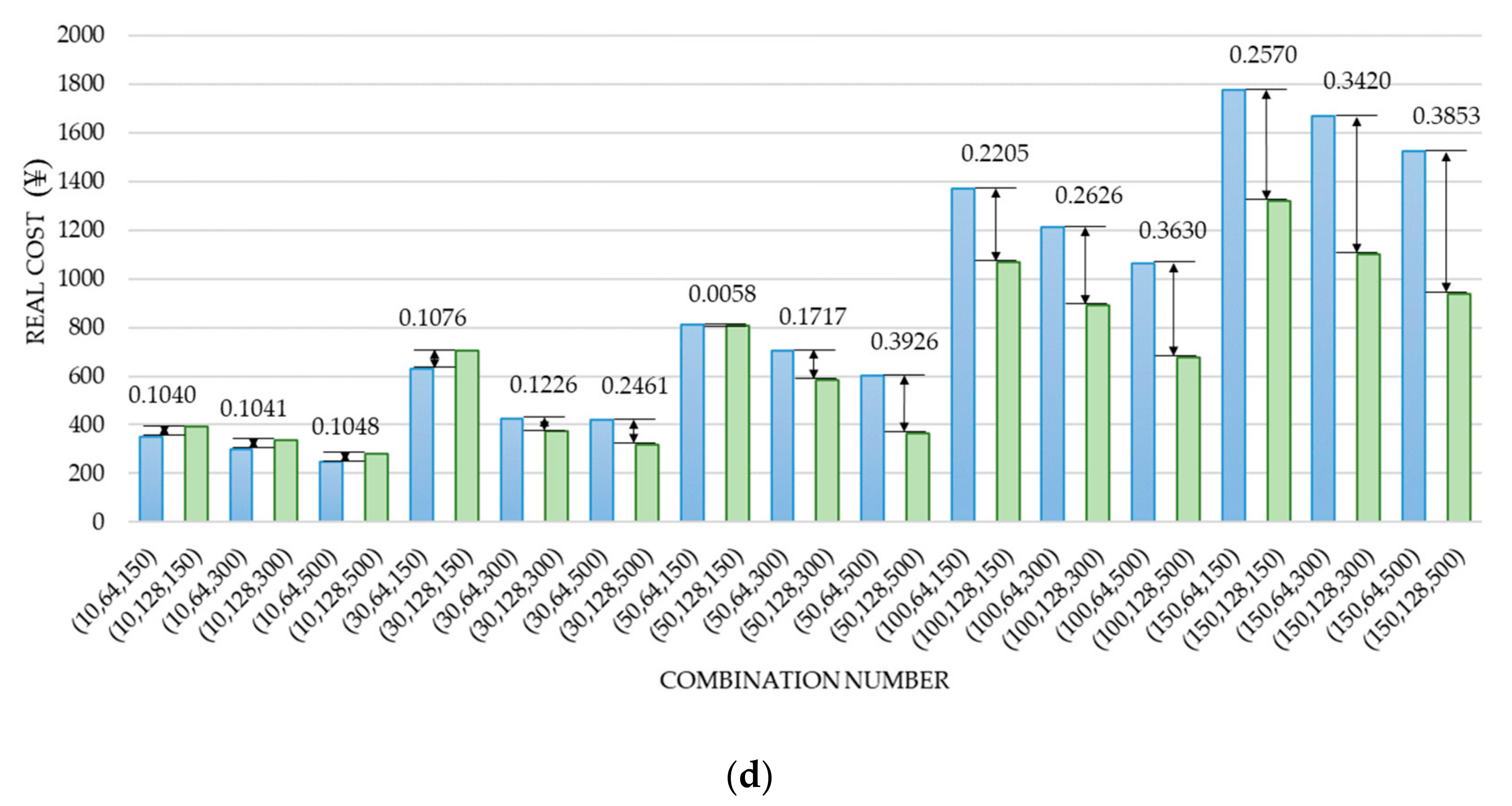
4.2. The Robustness of Solutions
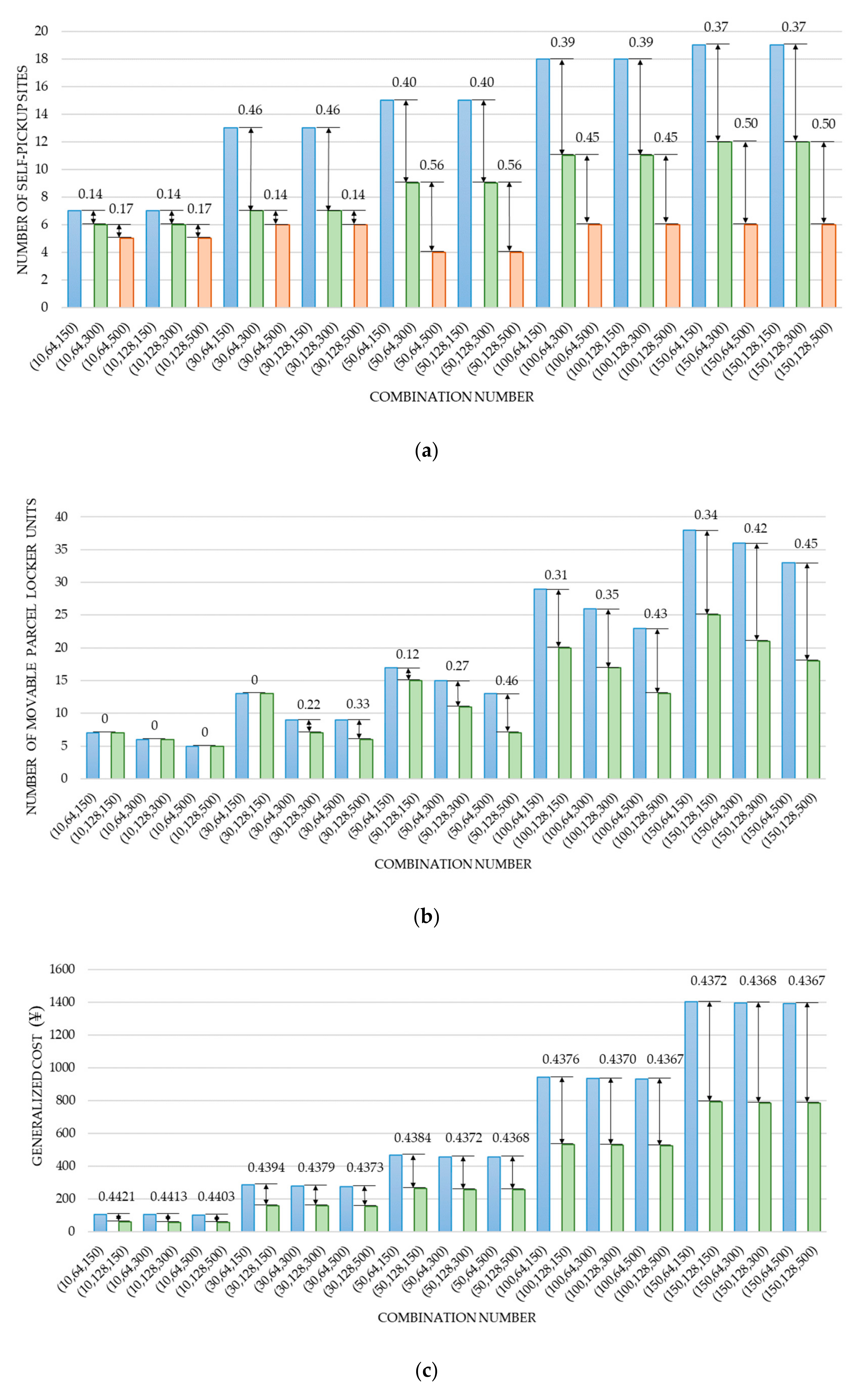
4.3. The Impacts of Key Parameters on the Optimization Results
4.3.1. Impacts on the Number of Self-Pickup Sites
4.3.2. Impacts on the Number of Movable Parcel Locker Units
4.3.3. Impacts on the Costs
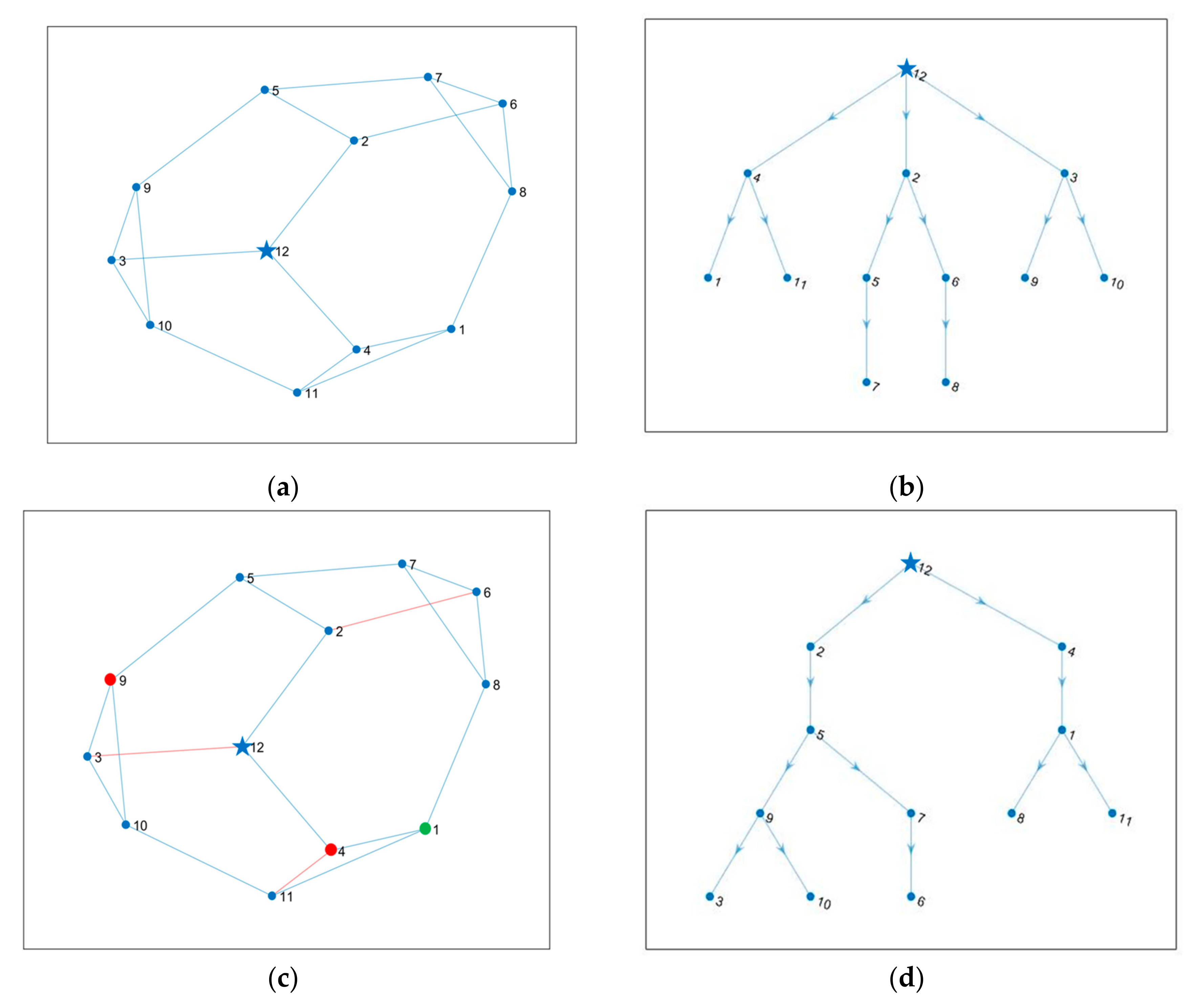
4.4. The Impacts of Mobility Restrictions on the Optimization Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ATKearney. Available online: https://www.atkearney.com (accessed on 18 March 2020).
- Wang, X.T.; Wang, H. A study on sustaining corporate innovation with E-commerce in China. Sustainability 2019, 11, 6604. [Google Scholar] [CrossRef]
- E-commerce Europe. Available online: https://www.ecommerce-europe.eu/news-item/double-digit-growth-global-b2c-e-commerce-sales-2015/ (accessed on 18 March 2020).
- Francke, J.; Visser, J. Internet shopping and its impacts on mobility. Igarss 2014, 1, 1–5. [Google Scholar]
- Syntun. Available online: http://www.syntun.com.cn/2019nian11yue1ri-11ri-qi-jian-kuang-huan-gou-wu-jie-quan-wang-da-bao-gao.html (accessed on 1 April 2020). (In Chinese).
- Xu, M.; Ferrand, B.; Roberts, M. The last mile of e-commerce-unattended delivery from the consumers and eTailers’ perspectives. Int. J. Electron. Market. Retail. 2008, 2, 20–38. [Google Scholar] [CrossRef]
- GOV.UK. Available online: www.foresight.gov.uk (accessed on 9 February 2020).
- Song, L.; Cherrett, T.; McLeod, F.; Guan, W. Addressing the last mile problem: Transport impacts of collection and delivery points. Transp. Res. Rec. 2009, 2097, 9–18. [Google Scholar] [CrossRef]
- Moroz, M.; Polkowski, Z. The last mile issue and urban logistics: Choosing parcel machines in the context of the ecological attitudes of the Y generation consumers purchasing online. Transp. Res. Procedia. 2016, 16, 378–393. [Google Scholar] [CrossRef]
- He, Z.; Zhang, W.; Jia, N. Estimating carbon dioxide emissions of freeway traffic: A spatiotemporal cell-based model. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1976–1986. [Google Scholar] [CrossRef]
- Xiong, J.; He, Z.; Guan, W.; Ran, B. Optimal timetable development for community shuttle network with metro stations. Transp. Res. Part C Emerg. Technol. 2015, 60, 540–565. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, X.; Ni, L.; Lin, Y. Location-routing problem with simultaneous home delivery and customer’s pickup for city distribution of online shopping purchases. Sustainability 2016, 8, 828. [Google Scholar] [CrossRef]
- Iwan, S.; Kijewska, K.; Lemke, J. Analysis of parcel lockers’ efficiency as the last mile delivery solution—The results of the research in Poland. Transp. Res. Procedia. 2016, 12, 644–655. [Google Scholar] [CrossRef]
- Faugere, L.; Montreuil, B. Hyperconnected pickup & delivery locker networks. In Proceedings of the 4th International Physical Internet Conference, Graz, Austria, 4–6 July 2017. [Google Scholar]
- DHL. Available online: https://www.dpdhl.com/en/about-us.html (accessed on 31 March 2020).
- Zenezini, G.; Lagorio, A.; Pinto, R.; Marco, A.D.; Golini, R. The Collection-and-Delivery Points implementation process from the courier, express and parcel operator’s perspective. IFAC-PapersOnLine 2018, 51, 594–599. [Google Scholar] [CrossRef]
- Industry News. “Contactless distribution” brings about a turnaround of logistics industry. Green Packag. 2020, 2, 21–22. (In Chinese) [Google Scholar]
- Ducret, R. Parcel deliveries and urban logistics: Changes and challenges in the courier express and parcel sector in Europe—The French case. Res. Transp. Bus. Manag. 2014, 11, 15–22. [Google Scholar] [CrossRef]
- BEE EXPRESS. Available online: https://a.eqxiu.com/s/B7D37aS7?share_level=1&from_user=20200326f3c10538&from_id=d44a19c6-d&share_time=1585190638775&from=singlemessage (accessed on 2 April 2020). (In Chinese).
- Deutsch, Y.; Golany, B. A parcel locker network as a solution to the logistics last mile problem. Int. J. Prod. Res. 2018, 56, 251–261. [Google Scholar] [CrossRef]
- Lemke, J.; Iwan, S.; Korczak, J. Usability of the parcel lockers from the customer perspective: The research in Polish cities. Transp. Res. Procedia. 2016, 16, 272–287. [Google Scholar] [CrossRef]
- Kedia, A.S.K.; Kusumastuti, D.; Nicholson, A. Acceptability of Collection and Delivery Points from consumers’ perspective: A qualitative case study of Christchurch city. Case Stud. Transp. Policy. 2017, 5, 587–595. [Google Scholar] [CrossRef]
- Lachapelle, U.; Burke, M.; Brotherton, A.; Leung, A. Parcel locker systems in a car dominant city: Location, characterisation and potential impacts on city planning and consumer travel access. J. Transp. Geogr. 2018, 71, 1–14. [Google Scholar] [CrossRef]
- Liu, S.; Lin, B.; Wang, J.; Wu, J. Modeling the multi-period and multi-classification-yard location problem in a railway network. Symmetry 2018, 10, 135. [Google Scholar] [CrossRef]
- Guo, X.; Song, R.; He, S.; Bi, M.; Jin, G. Integrated optimization of stop location and route design for community shuttle service. Symmetry 2018, 10, 678. [Google Scholar] [CrossRef]
- Guo, X.; Song, R.; He, S.; Hao, S.; Zheng, L.; Jin, G. A multi-objective programming approach to design feeder bus route for high-speed rail stations. Symmetry 2019, 11, 514. [Google Scholar] [CrossRef]
- Ji, S.F.; Luo, R.J.; Peng, X.S. A probability guided evolutionary algorithm for multi-objective green express cabinet assignment in urban last-mile logistics. Int. J. Prod. Res. 2019, 57, 3382–3404. [Google Scholar] [CrossRef]
- Lee, H.; Chen, M.W.; Pham, H.T.; Choo, S. Development of a decision making system for installing unmanned parcel lockers: Focusing on residential complexes in Korea. KSCE J. Civ. Eng. 2019, 23, 2713–2722. [Google Scholar] [CrossRef]
- Tan, K.C.; Cheong, C.Y.; Goh, C.K. Solving multiobjective vehicle routing problem with stochastic demand via evolutionary computation. Eur. J. Oper. Res. 2006, 177, 813–839. [Google Scholar] [CrossRef]
- Martí, J.M.C.; Tancrez, J.S.; Seifert, R.W. Carbon footprint and responsiveness trade-offs in supply chain network design. Int. J. Prod. Econ. 2015, 166, 129–142. [Google Scholar] [CrossRef]
- Wen, M.L.; Qin, Z.F.; Kang, R.; Yang, Y. The capacitated facility location-allocation problem under uncertain environment. J. Intell. Fuzzy Syst. 2015, 29, 2217–2226. [Google Scholar] [CrossRef]
- Sun, H.L.; Zhou, Z.J.; Xue, Y.F. Emergency location-routing problem with uncertain demand under path risk. Shanghai Jiaotong Daxue Xuebao 2013, 47, 962–966. (In Chinese) [Google Scholar]
- Bieniek, M. A note on the facility location problem with stochastic demands. Omega 2015, 55, 53–60. [Google Scholar] [CrossRef]
- Albareda-Sambola, M.; Fernández, E.; Saldanha-Da-Gama, F. Heuristic solutions to the facility location problem with general Bernoulli demands. INFORMS J. Comput. 2017, 29, 737–753. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Gabrel, V.; Lacroix, M.; Murat, C.; Remli, N. Robust location transportation problems under uncertain demands. Discrete Appl. Math. 2014, 164, 100–111. [Google Scholar] [CrossRef]
- Huang, M.; Ren, L.; Lee, L.H.; Wang, X.W.; Kuang, H.B.; Shi, H.B. Model and algorithm for 4PLRP with uncertain delivery time. Inf. Sci. 2016, 330, 211–225. [Google Scholar] [CrossRef]
- Lin, D.S.; Zhang, Z.Y.; Wang, J.X.; Liang, X.; Shi, Y.Q. Low-carbon logistics distribution center location with uncertain demand. Kongzhi Yu Juece Control Decis. 2020, 35, 492–500. [Google Scholar]
- Tanonkou, G.A.; Benyoucef, L.; Xie, X.L. A scenario analysis of a location problem with uncertain demand. Int. J. Comput. Appl. Technol. 2008, 32, 290–297. [Google Scholar] [CrossRef]
- Zhang, B.; Ma, Z.J.; Jiang, S. Location-routing-inventory problem with stochastic demand in logistics distribution systems. In Proceedings of the 2008 International Conference on Wireless Communications, Networking and Movable Computing, WiCOM 2008, Dalian, China, 12–14 October 2008. [Google Scholar]
- Li, H.B.; Yan, J.; Ren, M.M. Bender’s algorithm for facility location problem with uncertain demand. In Proceedings of the Innovative Computing and Information, ICCIC 2011, Wuhan, China, 17–18 September 2011; Dai, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Brenna, M.; Lazaroiu, G.C.; Roscia, M.; Saadatmandi, S. Dynamic model for the EV’s charging infrastructure planning through finite element method. IEEE Access. 2020, 8, 102399–102408. [Google Scholar] [CrossRef]
- Balinski, M. Integer Programming: Methods, Uses, Computation. In 50 Years of Integer Programming 1958–2008; Jünger, M., Naddef, D., Pulleyblank, W.R., Rinaldi, G., Liebling, T.M., Nemhauser, G.L., Reinelt, G., Wolsey, L.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 133–197. [Google Scholar]
- Gong, Y.M. Integer programming. In Operations Research Course, 2nd ed.; Hu, Y.Q., Guo, Y.H., Eds.; Tsinghua University Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- MathWorks. Available online: https://www.mathworks.com/help/optim/ug/intlinprog.html?s_tid=srchtitle (accessed on 6 April 2020).
- Longo, M.; Foiadelli, F.; Yaïci, W. Simulation and optimisation study of the integration of distributed generation and electric vehicles in smart residential district. Int. J. Energy Environ. Eng. 2019, 10, 271–285. [Google Scholar] [CrossRef]
- Beijing Municipal Commission of Development and Reform. Available online: http://www.bjmy.gov.cn/art/2019/5/31/art_3334_267683.html (accessed on 2 April 2020). (In Chinese)
- The People’s Government of Beijing Municipality. Available online: http://www.bjdch.gov.cn/n2001806/n2917336/n2917339/c7722611/content.html (accessed on 2 April 2020). (In Chinese)
- Phommixay, S.; Doumbia, M.L.; Lupien St-Pierre, D. Review on the cost optimization of microgrids via particle swarm optimization. Int. J. Energy Environ. Eng. 2020, 11, 73–89. [Google Scholar] [CrossRef]
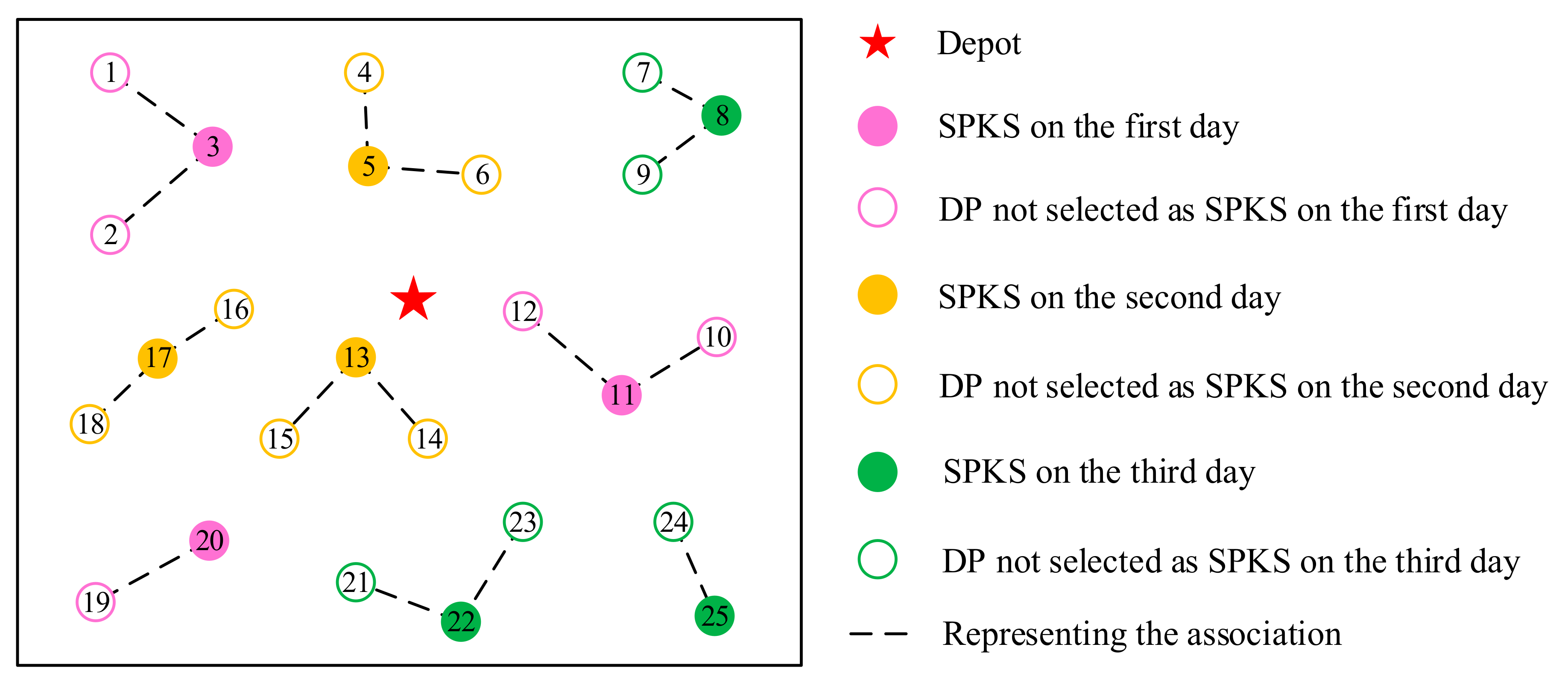
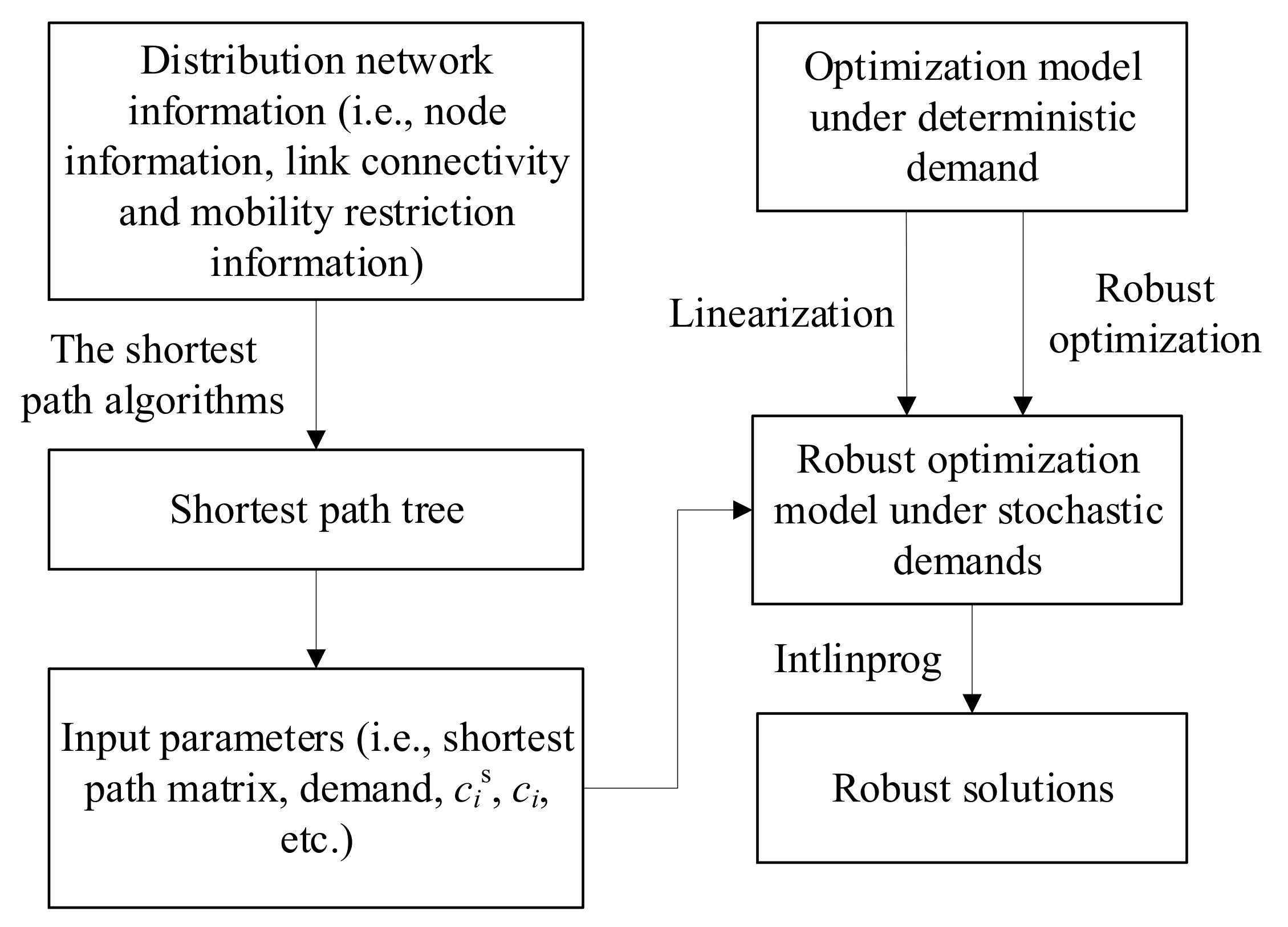
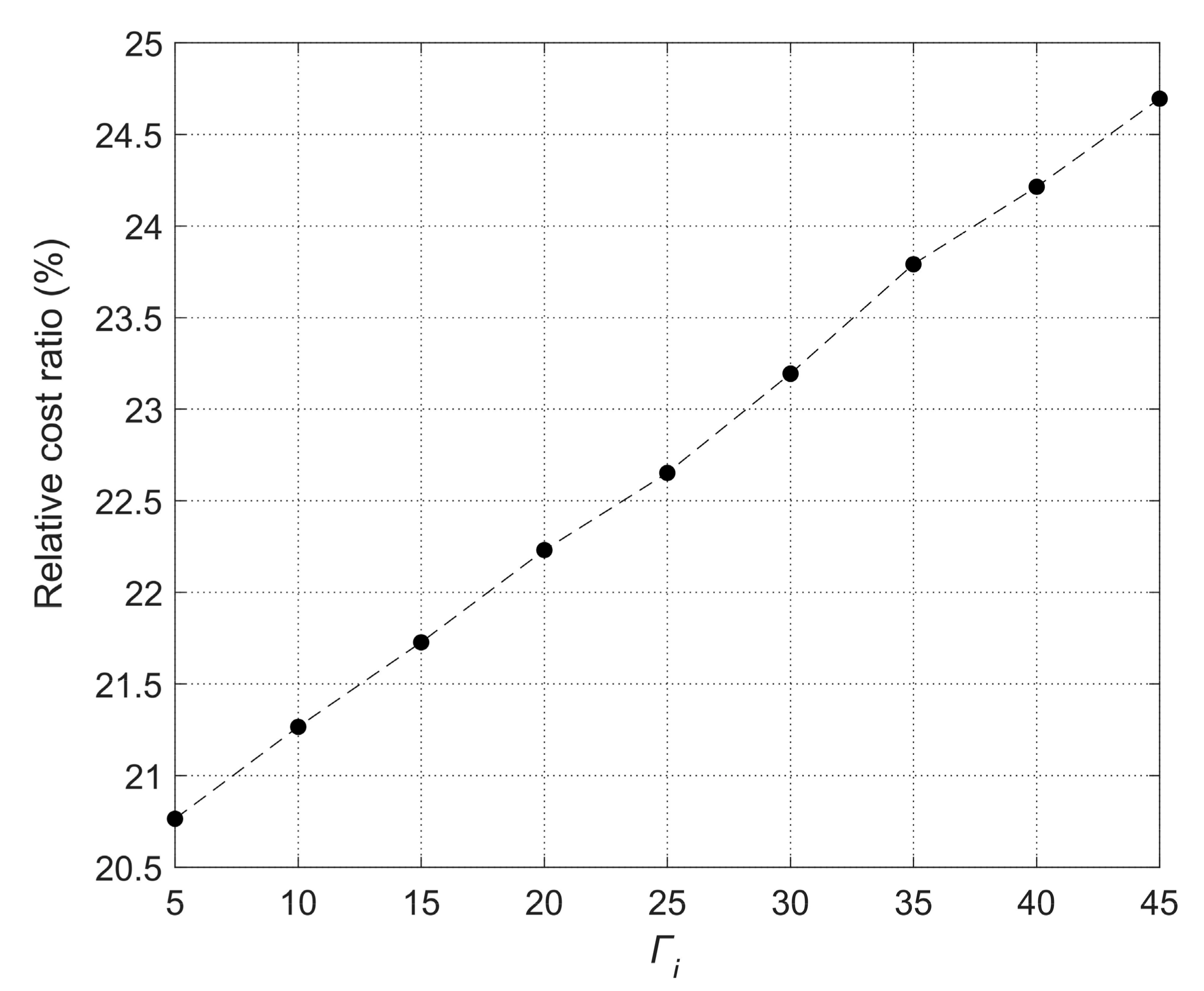
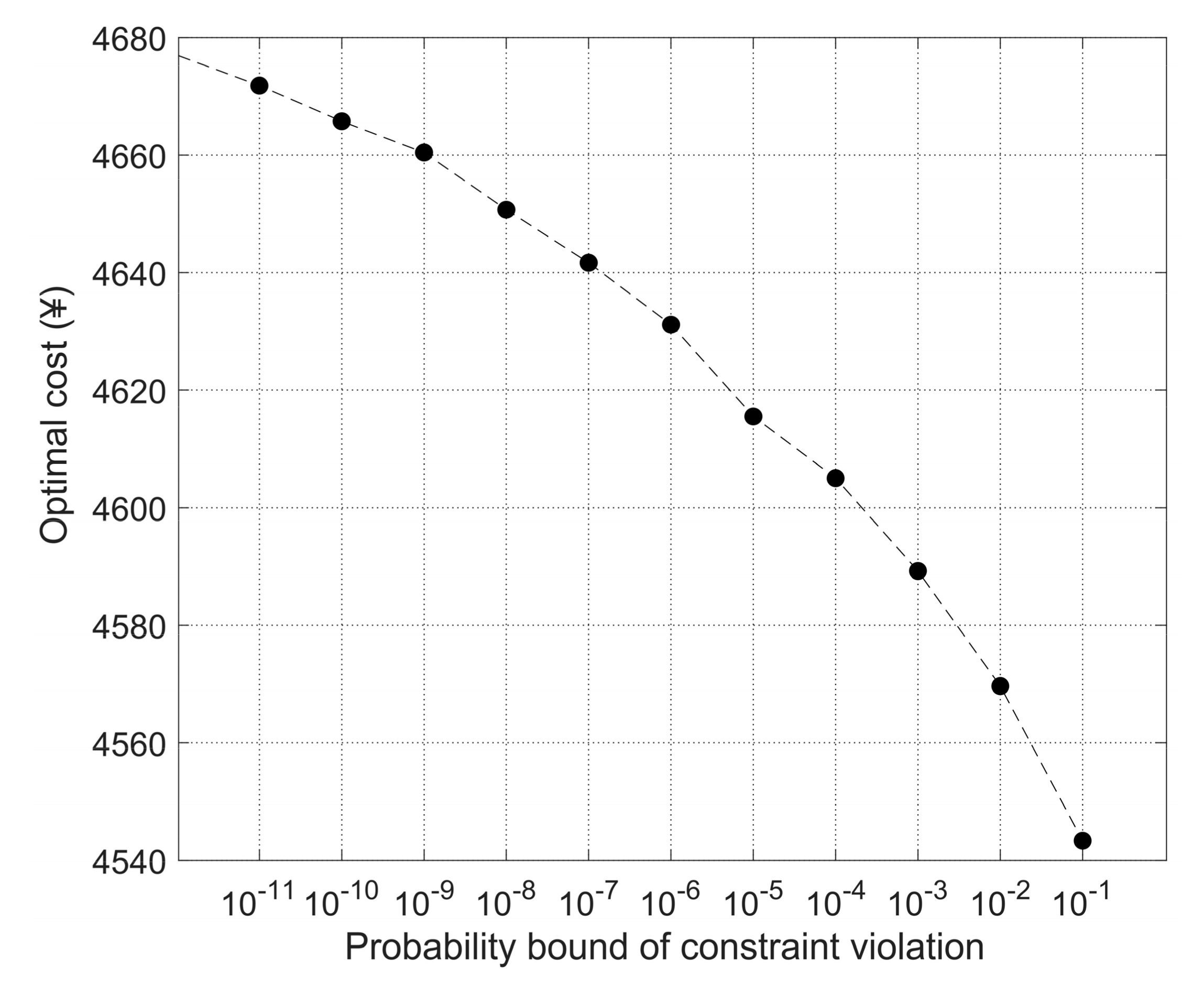
| Sets | Descriptions |
|---|---|
| I | Demand point set |
| Set of demand points that cannot be selected as self-pickup sites | |
| Set of demand points that must be selected as self-pickup sites | |
| E | Set of edges weighted by the shortest distance between demand points |
| Parameters | Descriptions |
| Purchase and maintenance costs of a movable parcel locker unit | |
| Land rental rate for a movable parcel locker unit at site i and the transportation cost of a unit from the depot to site i | |
| The generalized cost for one locker | |
| A | Number of lockers equipped on a movable parcel locker unit |
| W | A very large positive number |
| Distance between demand point j and self-pickup site i | |
| r | Maximum walking distance acceptable to customers |
| Customer’s delivery demand at the demand point j except for the demand met by fixed parcel lockers | |
| M | A very large positive number |
| Average delivery demand at the demand point j | |
| Maximum variation in demand at the demand point j | |
| A parameter adjusting the trade-off between robustness and risk. It is the number of demand points with demand variation at the self-pickup site i | |
| Decision variables | Descriptions |
| Total number of lockers set up at the self-pickup site i | |
| Number of movable parcel locker units placed at the self-pickup site i | |
| Binary variable, which is 1 if the demand point j is allocated to the self-pickup site i and, otherwise, 0. |
| Items | Numerical Values |
|---|---|
| Power consumption during driving | 400 W |
| Power consumption during parking | 40 W |
| Battery capacity | 1.2 kWh |
| Charge for commercial electricity | ¥0.78/kWh |
| Communication cost | ¥0.04/parcel |
| Price of battery | ¥400 |
| Rent for land | About ¥3//day |
| Charging efficiency | 80% |
| Probability Bound | Optimal Cost (¥) | Relative Cost Ratio (%) | Lockers | Relative Locker Ratio (%) | Optgap | Time (s) | |
|---|---|---|---|---|---|---|---|
| 4 | 4520.80 | 20.66 | 6096 | 20.71 | 0.00 | 5.53 | |
| 8 | 4535.08 | 21.05 | 6115 | 21.09 | 0.00 | 4.62 | |
| 13 | 4553.85 | 21.55 | 6140 | 21.58 | 0.00 | 7.59 | |
| 18 | 4571.93 | 22.03 | 6164 | 22.06 | 0.00 | 1.94 | |
| 23 | 4591.43 | 22.55 | 6190 | 22.57 | 0.00 | 4.43 | |
| 27 | 4605.78 | 22.93 | 6209 | 22.95 | 0.00 | 17.8 | |
| 33 | 4631.14 | 23.61 | 6243 | 23.62 | 0.00 | 8.17 | |
| 37 | 4646.19 | 24.01 | 6263 | 24.02 | 0.00 | 3.12 | |
| 40 | 4653.76 | 24.21 | 6273 | 24.22 | 0.00 | 1.33 | |
| 43 | 4665.74 | 24.53 | 6289 | 24.53 | 0.00 | 51.19 | |
| 46 | 4676.99 | 24.83 | 6304 | 24.83 | 0.00 | 16.89 | |
| 49 | 4684.58 | 25.04 | 6314 | 25.03 | 0.00 | 3.75 |
| Scenarios | Self-Pickup Sites | Sub-Demand Points | Lockers | Cost (¥) |
|---|---|---|---|---|
| Normal situation | 2 | 2 6 | 244 | 264.89 |
| 4 | 14 | 301 | ||
| 7 | 7 | 113 | ||
| 8 | 8 | 60 | ||
| 9 | 59 | 333 | ||
| 10 | 310 | 250 | ||
| 11 | 11 | 132 | ||
| Movement restrictions | 1 | 14 | 301 | 283.04 |
| 2 | 2 6 | 244 | ||
| 3 | 39 | 296 | ||
| 7 | 57 | 289 | ||
| 8 | 8 | 60 | ||
| 10 | 10 | 111 | ||
| 11 | 11 | 132 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Bi, M.; Lai, J.; Chen, Y. Locating Movable Parcel Lockers under Stochastic Demands. Symmetry 2020, 12, 2033. https://doi.org/10.3390/sym12122033
Wang Y, Bi M, Lai J, Chen Y. Locating Movable Parcel Lockers under Stochastic Demands. Symmetry. 2020; 12(12):2033. https://doi.org/10.3390/sym12122033
Chicago/Turabian StyleWang, Yang, Mengyu Bi, Jianhui Lai, and Yanyan Chen. 2020. "Locating Movable Parcel Lockers under Stochastic Demands" Symmetry 12, no. 12: 2033. https://doi.org/10.3390/sym12122033
APA StyleWang, Y., Bi, M., Lai, J., & Chen, Y. (2020). Locating Movable Parcel Lockers under Stochastic Demands. Symmetry, 12(12), 2033. https://doi.org/10.3390/sym12122033






