Non-Minimal Lorentz Violation in Macroscopic Matter
Abstract
:1. Introduction
2. Theory
2.1. Hamiltonian
2.2. Equations of Motion
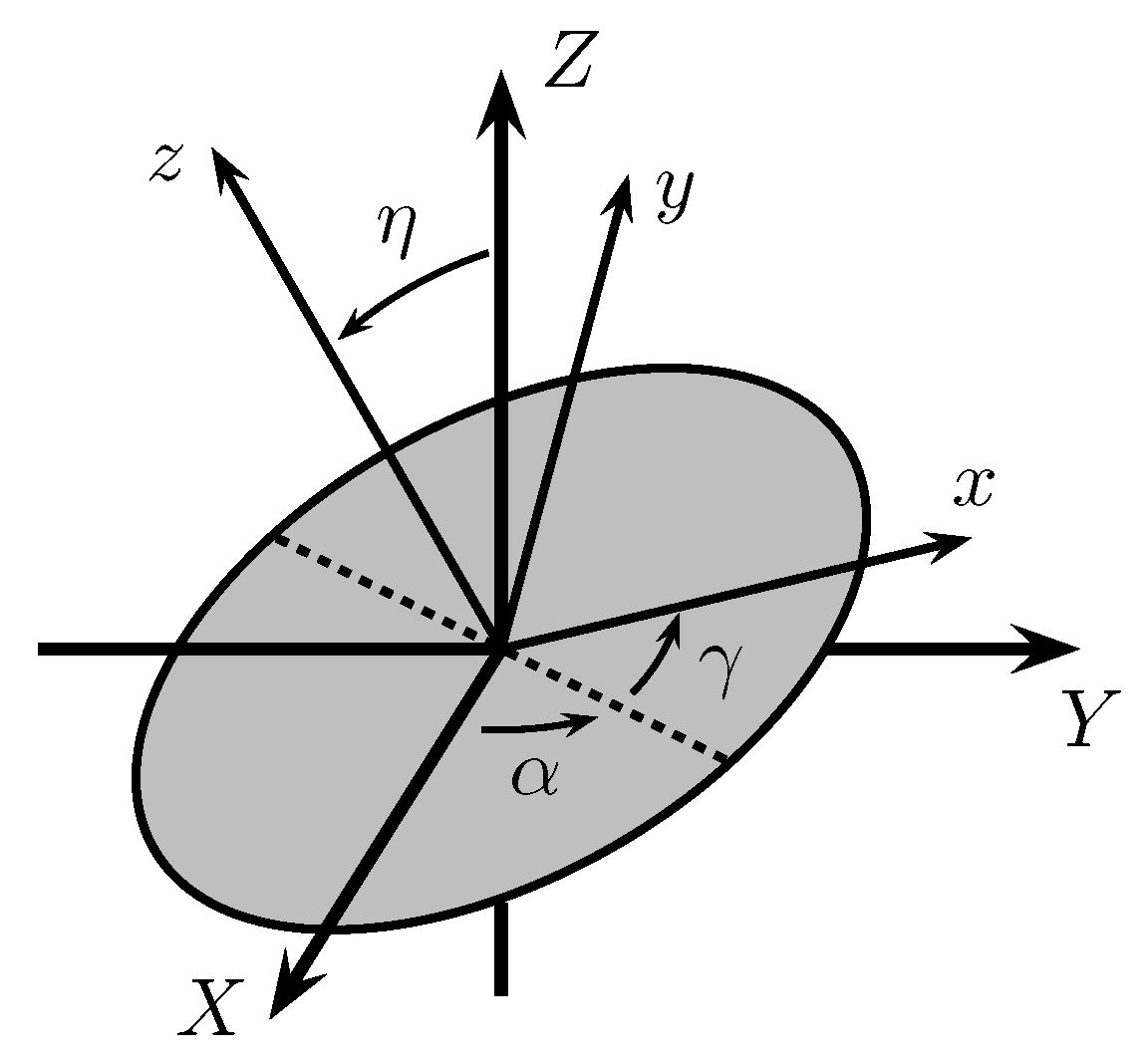
2.3. Lorentz Transformations
3. Applications
3.1. Tests of the Equivalence Principle
3.2. Orbits
3.3. Acoustic Resonators
4. Summary
Funding
Conflicts of Interest
Appendix A
References
- Kostelecký, V.A.; Samuel, S. Spontaneous Breaking of Lorentz Symmetry in String Theory. Phys. Rev. D 1989, 39, 683. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Potting, R. CPT and strings. Nucl. Phys. B 1991, 359, 545–570. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecký, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760. [Google Scholar] [CrossRef] [Green Version]
- Colladay, D.; Kostelecký, V.A. Lorentz violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef] [Green Version]
- Bluhm, R. Overview of the SME: Implications and phenomenology of Lorentz violation. Lect. Notes Phys. 2006, 702, 191. [Google Scholar]
- Tasson, J.D. What Do We Know About Lorentz Invariance? Rep. Prog. Phys. 2014, 77, 062901. [Google Scholar] [CrossRef]
- Hees, A.; Bailey, Q.G.; Bourgoin, A.; Bars, H.P.L.; Guerlin, C.; Le Poncin-Lafitte, C. Tests of Lorentz symmetry in the gravitational sector. Universe 2016, 2, 30. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Russell, N. Data Tables for Lorentz and CPT Violation. Rev. Mod. Phys. 2011, 83, 11. [Google Scholar] [CrossRef] [Green Version]
- Bluhm, R.; Kostelecký, V.A. Spontaneous Lorentz violation, Nambu-Goldstone modes, and gravity. Phys. Rev. D 2005, 71, 065008. [Google Scholar] [CrossRef] [Green Version]
- Bluhm, R.; Fung, W.H.; Kostelecký, V.A. Spontaneous Lorentz and Diffeomorphism Violation, Massive Modes, and Gravity. Phys. Rev. D 2008, 77, 065020. [Google Scholar] [CrossRef] [Green Version]
- Bailey, Q.G.; Kostelecký, V.A. Signals for Lorentz violation in post-Newtonian gravity. Phys. Rev. D 2006, 74, 045001. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Electrodynamics with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2009, 80, 015020. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Neutrinos with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2012, 85, 096005. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Fermions with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2013, 88, 096006. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Testing local Lorentz invariance with gravitational waves. Phys. Lett. B 2016, 757, 510–514. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Tasson, J. Prospects for Large Relativity Violations in Matter-Gravity Couplings. Phys. Rev. Lett. 2009, 102, 010402. [Google Scholar] [CrossRef] [Green Version]
- Colladay, D.; McDonald, P. Redefining spinors in Lorentz violating QED. J. Math. Phys. 2002, 43, 3554–3564. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Signals for Lorentz violation in electrodynamics. Phys. Rev. D 2002, 66, 056005. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Cosmological constraints on Lorentz violation in electrodynamics. Phys. Rev. Lett. 2001, 87, 251304. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Sensitive polarimetric search for relativity violations in gamma-ray bursts. Phys. Rev. Lett. 2006, 97, 140401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kostelecký, V.A.; Mewes, M. Lorentz-violating electrodynamics and the cosmic microwave background. Phys. Rev. Lett. 2007, 99, 011601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, M.L.; Ade, P.; Bock, J.; Bowden, M.; Cahill, G.; Castro, P.G.; Church, S.; Culverhouse, T.; Friedman, R.B.; Ganga, K.; et al. Improved measurements of the temperature and polarization of the CMB from QUaD. Astrophys. J. 2009, 705, 978. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. 2013, 208, 19. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Constraints on relativity violations from gamma-ray bursts. Phys. Rev. Lett. 2013, 110, 201601. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; Benabed, K.; et al. Planck intermediate results. XLIX. Parity-violation constraints from polarization data. Astron. Astrophys. 2016, 596, A110. [Google Scholar]
- Kislat, F. Constraints on Lorentz Invariance Violation from Optical Polarimetry of Astrophysical Objects. Symmetry 2018, 10, 596. [Google Scholar] [CrossRef] [Green Version]
- Friedman, A.S.; Leon, D.; Crowley, K.D.; Johnson, D.; Teply, G.; Tytler, D.; Keating, B.G.; Cole, G.M. Constraints on Lorentz Invariance and CPT Violation using Optical Photometry and Polarimetry of Active Galaxies BL Lacertae and S5 B0716 + 714. Phys. Rev. D 2019, 99, 035045. [Google Scholar] [CrossRef] [Green Version]
- Pogosian, L.; Shimon, M.; Mewes, M.; Keating, B. Future CMB constraints on cosmic birefringence and implications for fundamental physics. Phys. Rev. D 2019, 100, 023507. [Google Scholar] [CrossRef] [Green Version]
- Friedman, A.S.; Gerasimov, R.; Kislat, F.; Leon, D.; Stevens, W.; Tytler, E.; Keating, B.G. Improved Constraints on Anisotropic Birefringent Lorentz Invariance and CPT Violation from Broadband Optical Polarimetry of High Redshift Galaxies. Phys. Rev. D 2020, 102, 043008. [Google Scholar] [CrossRef]
- Ding, Y.; Kostelecký, V.A. Lorentz-violating spinor electrodynamics and Penning traps. Phys. Rev. D 2016, 94, 056008. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Li, Z. Gauge field theories with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2019, 99, 056016. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Li, Z. Backgrounds in gravitational effective field theory. arXiv 2020, arXiv:2008.12206. [Google Scholar]
- Kostelecký, V.A.; Tasson, J. Matter-gravity couplings and Lorentz violation. Phys. Rev. D 2011, 83, 016013. [Google Scholar] [CrossRef] [Green Version]
- Altschul, B. Synchrotron and inverse compton constraints on Lorentz violations for electrons. Phys. Rev. D 2006, 74, 083003. [Google Scholar] [CrossRef] [Green Version]
- Altschul, B. Astrophysical limits on Lorentz violation for all charged species. Astropart. Phys. 2007, 28, 380–384. [Google Scholar] [CrossRef] [Green Version]
- Altschul, B. Limits on Neutron Lorentz Violation from the Stability of Primary Cosmic Ray Protons. Phys. Rev. D 2008, 78, 085018. [Google Scholar] [CrossRef] [Green Version]
- Stecker, F.W. Limiting superluminal electron and neutrino velocities using the 2010 Crab Nebula flare and the IceCube PeV neutrino events. Astropart. Phys. 2014, 56, 16–18. [Google Scholar] [CrossRef] [Green Version]
- Satunin, P. One-loop correction to the photon velocity in Lorentz-violating QED. Phys. Rev. D 2018, 97, 125016. [Google Scholar] [CrossRef] [Green Version]
- Shao, L. Lorentz-Violating Matter-Gravity Couplings in Small-Eccentricity Binary Pulsars. Symmetry 2019, 11, 1098. [Google Scholar] [CrossRef] [Green Version]
- Altschul, B. Limits on Neutron Lorentz Violation from Pulsar Timing. Phys. Rev. D 2007, 75, 023001. [Google Scholar] [CrossRef] [Green Version]
- Hohensee, M.A.; Leefer, N.; Budker, D.; Harabati, C.; Dzuba, V.A.; Flambaum, V.V. Limits on Violations of Lorentz Symmetry and the Einstein Equivalence Principle using Radio-Frequency Spectroscopy of Atomic Dysprosium. Phys. Rev. Lett. 2013, 111, 050401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hohensee, M.A.; Mueller, H.; Wiringa, R.B. Equivalence Principle and Bound Kinetic Energy. Phys. Rev. Lett. 2013, 111, 151102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flowers, N.A.; Goodge, C.; Tasson, J.D. Superconducting-Gravimeter Tests of Local Lorentz Invariance. Phys. Rev. Lett. 2017, 119, 201101. [Google Scholar] [CrossRef] [Green Version]
- Lane, C.D. Probing Lorentz violation with Doppler-shift experiment. Phys. Rev. D 2005, 72, 016005. [Google Scholar] [CrossRef] [Green Version]
- Altschul, B. Laboratory Bounds on Electron Lorentz Violation. Phys. Rev. D 2010, 82, 016002. [Google Scholar] [CrossRef] [Green Version]
- Botermann, B.; Bing, D.; Geppert, C.; Gwinner, G.; Hänsch, T.W.; Huber, G.; Karpuk, S.; Krieger, A.; Kühl, T.; Nörtershäuser, W.; et al. Test of Time Dilation Using Stored Li+ Ions as Clocks at Relativistic Speed. Phys. Rev. Lett. 2014, 113, 120405. [Google Scholar] [CrossRef] [Green Version]
- Muller, H.; Herrmann, S.; Saenz, A.; Peters, A.; Lammerzahl, C. Optical cavity tests of Lorentz invariance for the electron. Phys. Rev. D 2003, 68, 116006. [Google Scholar] [CrossRef] [Green Version]
- Muller, H. Testing Lorentz invariance by use of vacuum and matter filled cavity resonators. Phys. Rev. D 2005, 71, 045004. [Google Scholar] [CrossRef] [Green Version]
- Muller, H.; Stanwix, P.L.; Tobar, M.E.; Ivanov, E.; Wolf, P.; Herrmann, S.; Senger, A.; Kovalchuk, E.; Peters, A. Relativity tests by complementary rotating Michelson-Morley experiments. Phys. Rev. Lett. 2007, 99, 050401. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Lane, C.D. Constraints on Lorentz violation from clock comparison experiments. Phys. Rev. D 1999, 60, 116010. [Google Scholar] [CrossRef] [Green Version]
- Wolf, P.; Chapelet, F.; Bize, S.; Clairon, A. Cold Atom Clock Test of Lorentz Invariance in the Matter Sector. Phys. Rev. Lett. 2006, 96, 060801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altschul, B. Testing Electron Boost Invariance with 2S-1S Hydrogen Spectroscopy. Phys. Rev. D 2010, 81, 041701. [Google Scholar] [CrossRef] [Green Version]
- Hohensee, M.A.; Chu, S.; Peters, A.; Muller, H. Equivalence Principle and Gravitational Redshift. Phys. Rev. Lett. 2011, 106, 151102. [Google Scholar] [CrossRef] [Green Version]
- Matveev, A.; Parthey, C.G.; Predehl, K.; Alnis, J.; Beyer, A.; Holzwarth, R.; Udem, T.; Wilken, T.; Kolachevsky, N.; Abgrall, M.; et al. Precision Measurement of the Hydrogen 1S-2S Frequency via a 920-km Fiber Link. Phys. Rev. Lett. 2013, 110, 230801. [Google Scholar] [CrossRef]
- Dzuba, V.A.; Flambaum, V.V. Limits on gravitational Einstein equivalence principle violation from monitoring atomic clock frequencies during a year. Phys. Rev. D 2017, 95, 015019. [Google Scholar] [CrossRef] [Green Version]
- Pihan-Le Bars, H.; Guerlin, C.; Lasseri, R.D.; Ebran, J.P.; Bailey, Q.G.; Bize, S.; Khan, E.; Wolf, P. Lorentz-symmetry test at Planck-scale suppression with nucleons in a spin-polarized 133Cs cold atom clock. Phys. Rev. D 2017, 95, 075026. [Google Scholar] [CrossRef] [Green Version]
- Sanner, C.; Huntemann, N.; Lange, R.; Tamm, C.; Peik, E.; Safronova, M.S.; Porsev, S.G. Optical clock comparison for Lorentz symmetry testing. Nature 2019, 567, 204–208. [Google Scholar] [CrossRef] [Green Version]
- Pruttivarasin, T.; Ramm, M.; Porsev, S.G.; Tupitsyn, I.I.; Safronova, M.; Hohensee, M.A.; Haeffner, H. A Michelson-Morley Test of Lorentz Symmetry for Electrons. Nature 2015, 517, 592. [Google Scholar] [CrossRef] [Green Version]
- Megidish, E.; Broz, J.; Greene, N.; Häffner, H. Improved Test of Local Lorentz Invariance from a Deterministic Preparation of Entangled States. Phys. Rev. Lett. 2019, 122, 123605. [Google Scholar] [CrossRef] [Green Version]
- Smiciklas, M.; Brown, J.M.; Cheuk, L.W.; Romalis, M.V. A new test of local Lorentz invariance using 21Ne-Rb-K comagnetometer. Phys. Rev. Lett. 2011, 107, 171604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flambaum, V.V.; Romalis, M.V. Effects of the Lorentz invariance violation on Coulomb interaction in nuclei and atoms. Phys. Rev. Lett. 2017, 118, 142501. [Google Scholar] [CrossRef] [PubMed]
- Lo, A.; Haslinger, P.; Mizrachi, E.; Anderegg, L.; Muller, H.; Hohensee, M.; Goryachev, M.; Tobar, M.E. Acoustic tests of Lorentz symmetry using quartz oscillators. Phys. Rev. X 2016, 6, 011018. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Vargas, A.J. Lorentz and CPT tests with hydrogen, antihydrogen, and related systems. Phys. Rev. D 2015, 92, 056002. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Vargas, A.J. Lorentz and CPT Tests with Clock-Comparison Experiments. Phys. Rev. D 2018, 98, 036003. [Google Scholar] [CrossRef] [Green Version]
- Schreck, M. Classical Lagrangians and Finsler structures for the nonminimal fermion sector of the Standard-Model Extension. Phys. Rev. D 2016, 93, 105017. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Rawnak, M.F. Lorentz and CPT tests with charge-to-mass ratio comparisons in Penning traps. Phys. Rev. D 2020, 102, 056009. [Google Scholar] [CrossRef]
- Ledesma, F.G.; Mewes, M. Spherical-harmonic tensors. Phys. Rev. Res. 2020, 2, 043061. [Google Scholar] [CrossRef]
- Bertschinger, T.H.; Flowers, N.A.; Moseley, S.; Pfeifer, C.R.; Tasson, J.D.; Yang, S. Spacetime Symmetries and Classical Mechanics. Symmetry 2018, 11, 22. [Google Scholar] [CrossRef] [Green Version]
- Clyburn, M.; Lane, C.D. Lorentz Violation at the Level of Undergraduate Classical Mechanics. Symmetry 2020, 12, 1734. [Google Scholar] [CrossRef]
- Cavasinni, V.; Iacopini, E.; Polacco, E.; Stefanini, G. Galileo’s experiment on free falling bodies using modern optical techniques. Phys. Lett. A 1986, 116, 157–161. [Google Scholar] [CrossRef] [Green Version]
- Niebauer, T.M.; Mchugh, M.P.; Faller, J.E. Galilean Test for the Fifth Force. Phys. Rev. Lett. 1987, 59, 609. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuroda, K.; Mio, N. Test of a composition-dependent force by a free-fall interferometer. Phys. Rev. Lett. 1989, 62, 1941. [Google Scholar] [CrossRef] [PubMed]
- Kuroda, K.; Mio, N. Limits on a possible composition-dependent force by a Galilean experiment. Phys. Rev. D 1990, 42, 3903. [Google Scholar] [CrossRef] [PubMed]
- Carusotto, S.; Cavasinni, V.; Mordacci, A.; Perrone, F.; Polacco, E.; Iacopini, E.; Stefanini, G. Test of the g universality with a Galileo’s type experiment. Phys. Rev. Lett. 1992, 69, 1722–1725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carusotto, S.; Cavasinni, V.; Perrone, F.; Polacco, E.; Iacopini, E.; Stefanini, G. g-universality test with a Galileo’s type experiment. Nuovo Cim. B 1996, 111, 1259–1275. [Google Scholar] [CrossRef]
- Overduin, J.; Everitt, F.; Worden, P.; Mester, J. STEP and fundamental physics. Class. Quant. Grav. 2012, 29, 184012. [Google Scholar] [CrossRef] [Green Version]
- Nobili, A.M.; Shao, M.; Pegna, R.; Zavattini, G.; Turyshev, S.G.; Lucchesi, D.M.; De Michele, A.; Doravari, S.; Comandi, G.L.; Saravanan, T.R.; et al. ‘Galileo Galilei’ (GG): Space test of the weak equivalence principle to 10(-17) and laboratory demonstrations. Class. Quant. Grav 2012, 29, 184011. [Google Scholar] [CrossRef] [Green Version]
- Touboul, P.; Métris, G.; Rodrigues, M.; André, Y.; Baghi, Q.; Bergé, J.; Boulanger, D.; Bremer, S.; Carle, P.; Chhun, R.; et al. MICROSCOPE Mission: First Results of a Space Test of the Equivalence Principle. Phys. Rev. Lett. 2017, 119, 231101. [Google Scholar] [CrossRef] [Green Version]
- Von Eötvös, R. Über die anziehung der erde auf verschiedene substanzen. Math. Naturwiss. Ber. Ung. 1890, 8, S65–S68. [Google Scholar]
- Roll, P.G.; Krotkov, R.; Dicke, R.H. The equivalence of inertial and passive gravitational mass. Ann. Phys. 1964, 26, 442–517. [Google Scholar] [CrossRef]
- Braginskii, V.B.; Panov, V.I. Verification of the equivalence of inertial and gravitational masses. Sov. Phys. JETP 1972, 34, 463. [Google Scholar]
- Adelberger, E.G.; Stubbs, C.W.; Heckel, B.R.; Su, Y.; Swanson, H.E.; Smith, G.; Gundlach, J.H.; Rogers, W.F. Testing the equivalence principle in the field of the Earth: Particle physics at masses beloved 1 μeV. Phys. Rev. D 1990, 42, 3267. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Heckel, B.R.; Adelberger, E.G.; Gundlach, J.H.; Harris, M.; Smith, G.L.; Swanson, H.E. New tests of the universality of free fall. Phys. Rev. D 1994, 50, 3614. [Google Scholar] [CrossRef] [PubMed]
- Schlamminger, S.; Choi, K.Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the equivalence principle using a rotating torsion balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pihan-Le Bars, G.; Guerlin, C.; Hees, A.; Peaucelle, R.; Tasson, J.D.; Bailey, Q.G.; Mo, G.; Delva, P.; Meynadier, F.; Touboul, P.; et al. New Test of Lorentz Invariance Using the MICROSCOPE Space Mission. Phys. Rev. Lett. 2019, 123, 231102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sondag, A.; Dittus, H. Electrostatic Positioning System for a free fall test at drop tower Bremen and an overview of tests for the Weak Equivalence Principle in past, present and future. Adv. Space Res. 2016, 58, 644–677. [Google Scholar] [CrossRef]
- Iafolla, V.; Nozzoli, S.; Lorenzini, E.C.; Milyukov, V. Methodology and instrumentation for testing the weak equivalence principle in stratospheric free fall. Rev. Sci. Instrum. 1998, 69, 4146–4151. [Google Scholar] [CrossRef]
- Reasenberg, R.D.; Phillips, J.D. A Laboratory Test of the Equivalence Principle as Prolog to a Spaceborne Experiment. Int. J. Mod. Phys. D 2007, 16, 2245–2258. [Google Scholar] [CrossRef]
- Reasenberg, R.D.; Patla, B.R.; Phillips, J.D.; Thapa, R. Design and characteristics of a WEP test in a sounding-rocket payload. Class. Quant. Grav. 2012, 29, 184013. [Google Scholar] [CrossRef] [Green Version]
- The Euler Angles Are Estimated Using the Data. Available online: https://ssd.jpl.nasa.gov/horizons.cgi (accessed on 30 July 2020).
- Iorio, L. Orbital effects of Lorentz-violating Standard Model Extension gravitomagnetism around a static body: A sensitivity analysis. Class. Quant. Grav. 2012, 29, 175007. [Google Scholar] [CrossRef] [Green Version]
- Hees, A.; Bailey, Q.G.; Le Poncin-Lafitte, C.; Bourgoin, A.; Rivoldini, A.; Lamine, B.; Meynadier, F.; Guerlin, C.; Wolf, P. Testing Lorentz symmetry with planetary orbital dynamics. Phys. Rev. D 2015, 92, 064049. [Google Scholar] [CrossRef] [Green Version]
- Battat, J.B.R.; Chandler, J.F.; Stubbs, C.W. Testing for Lorentz Violation: Constraints on Standard-Model Extension Parameters via Lunar Laser Ranging. Phys. Rev. Lett. 2007, 99, 241103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bourgoin, A.; Hees, A.; Bouquillon, S.; Le Poncin-Lafitte, C.; Francou, G.; Angonin, M.C. Testing Lorentz symmetry with Lunar Laser Ranging. Phys. Rev. Lett. 2016, 117, 241301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bourgoin, A.; Le Poncin-Lafitte, C.; Hees, A.; Bouquillon, S.; Francou, G.; Angonin, M.C. Lorentz Symmetry Violations from Matter-Gravity Couplings with Lunar Laser Ranging. Phys. Rev. Lett. 2017, 119, 201102. [Google Scholar] [CrossRef] [Green Version]
- Jennings, R.J.; Tasson, J.D.; Yang, S. Matter-Sector Lorentz Violation in Binary Pulsars. Phys. Rev. D 2015, 92, 125028. [Google Scholar] [CrossRef] [Green Version]
- Shao, L. Tests of local Lorentz invariance violation of gravity in the standard model extension with pulsars. Phys. Rev. Lett. 2014, 112, 111103. [Google Scholar] [CrossRef] [Green Version]
- Shao, L. New pulsar limit on local Lorentz invariance violation of gravity in the standard-model extension. Phys. Rev. D 2014, 90, 122009. [Google Scholar] [CrossRef] [Green Version]
- Shao, L.; Bailey, Q.G. Testing velocity-dependent CPT-violating gravitational forces with radio pulsars. Phys. Rev. D 2018, 98, 084049. [Google Scholar] [CrossRef] [Green Version]
- Shao, L.; Bailey, Q.G. Testing the Gravitational Weak Equivalence Principle in the Standard-Model Extension with Binary Pulsars. Phys. Rev. D 2019, 99, 084017. [Google Scholar] [CrossRef] [Green Version]
- Shao, L.; Caballero, R.N.; Kramer, M.; Wex, N.; Champion, D.J.; Jessner, A. A new limit on local Lorentz invariance violation of gravity from solitary pulsars. Class. Quant. Grav. 2013, 30, 165019. [Google Scholar] [CrossRef] [Green Version]
- Goryachev, M.; Kuang, Z.; Ivanov, E.N.; Haslinger, P.; Muller, H.; Tobar, M.E. Next Generation of Phonon Tests of Lorentz Invariance using Quartz BAW Resonators. IEEE Trans. UFFC 2018, 65, 991–1000. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| Coefficients | Free Fall | MICROSCOPE | Torsion Pendulum |
|---|---|---|---|
| Merc. | Ven. | Earth | Mars | Jup. | Sat. | Ur. | Nept. | |
|---|---|---|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mewes, M. Non-Minimal Lorentz Violation in Macroscopic Matter. Symmetry 2020, 12, 2026. https://doi.org/10.3390/sym12122026
Mewes M. Non-Minimal Lorentz Violation in Macroscopic Matter. Symmetry. 2020; 12(12):2026. https://doi.org/10.3390/sym12122026
Chicago/Turabian StyleMewes, Matthew. 2020. "Non-Minimal Lorentz Violation in Macroscopic Matter" Symmetry 12, no. 12: 2026. https://doi.org/10.3390/sym12122026
APA StyleMewes, M. (2020). Non-Minimal Lorentz Violation in Macroscopic Matter. Symmetry, 12(12), 2026. https://doi.org/10.3390/sym12122026





