Partition and Colored Distances in Graphs Induced to Subsets of Vertices and Some of Its Applications

Abstract

If G is a graph and $\mathcal{P}$ is a partition of $V\left(G\right)$, then the partition distance of G is the sum of the distances between all pairs of vertices that lie in the same part of $\mathcal{P}$. A colored distance is the dual concept of the partition distance. These notions are motivated by a problem in the facility location network and applied to several well-known distance-based graph invariants. In this paper, we apply an extended cut method to induce the partition and color distances to some subsets of vertices which are not necessary a partition of $V\left(G\right)$. Then, we define a two-dimensional weighted graph and an operator to prove that the induced partition and colored distances of a graph can be obtained from the weighted Wiener index of a two-dimensional weighted quotient graph induced by the transitive closure of the Djoković–Winkler relation as well as by any partition that is coarser. Finally, we utilize our main results to find some upper bounds for the modified Wiener index and the number of orbits of partial cube graphs under the action of automorphism group of graphs.

1. Introduction

If G is a graph and $\mathcal{P}$ is a partition of $V\left(G\right)$, then the colored distance of G is the sum of the distances between all pairs of vertices that lie in the different parts of $\mathcal{P}$. This concept was defined by Dankelmann, Goddard, and Slater [1] and is based on a location problem [2]. Klavžar and Nadjafi-Arani further developed this metric and introduced the dual concept of a colored distance called partition distance [3]. Dankelmann et al. tackled a few applications of colored distance toward the facility location problem, median graphs, and the average distance of graphs (see [2,4]). Klavžar et al. [3] demonstrated that the dual concept has more practical value and addressed some applications in mathematical chemistry and network analysis [5,6] to obtain general bounds as well as to classify corresponding extremal graphs. Moreover, they expressed some basic graph invariants such as the diameter and the clique number by utilizing the partition distance. They also showed that some of these applications cannot be achieved when using the colored distance.

The usefulness of the cut method and the extended cut method in metric graph theory has been proved [7]. For instance, the method has been used to define distance-based graph invariants. These methods are based on the Djoković–Winkler relation where we apply the canonical metric representation to find the distance moments between pairs of vertices [8,9,10]. Especially in metric graph theory, the methods have already been used to explain distance-based graph invariants based on quotient graphs and cuts (see the survey [11]). In [12,13], results achieved in [11] were used to analyze the modified Wiener index [14]. Trees with the maximal value of the modified Wiener index are analyzed in [15].

The main contributions of this paper involve applying the extended cut method and introducing new expressions and bounds for distance-based quantities (e.g., modified Wiener index). This paper is organized as follows. We start by presenting some preliminary definitions and theorems that we need for proving our main results. In Section 3, we prove a generalization toward computing the partition and colored distances based on the canonical metric representation. The generalization is twofold. First, we examine partition and colored distances in graphs induced to subsets of vertices of a graph. Second, the calculation of colored distances is being performed by computing a two-dimensional version of the Wiener index of its quotient graph. In Section 4, we apply our main theorems to derive some bounds for the modified Wiener index and the number of orbits of a partial cube graph G under the action of $Aut\left(G\right).$

2. Preliminaries

Let G be a simple graph and define $d_G(u,v)$ (for short $d(u,v)$) as the length of a shortest path between two vertices u and v in G. Let $S\subseteq V\left(G\right)$ and define $W\left(S\right)={\sum }_{\{x,y\}\in V\left(G\right)}{d}_G(x,y).$ If $S=V\left(G\right)$, then $W\left(G\right)$ is called the Wiener index. Similarly, average distance, $\mu \left(G\right)=\frac{W\left(G\right)}{\left(\genfrac{}{}{0pt}{}{V\left(G\right)}{2}\right)},$ is an equivalent number to $W\left(G\right)$ (see [16,17,18,19]). The Djoković–Winkler relation $\mathsf{\Theta }$ [8,10] is a reflexive and symmetric relation between edges of graphs such that two edges $e=xy$ and $f=uv$ of a connected graph G are under the relation $\mathsf{\Theta }$ if $d_G(x,u)+d_G(y,v)\ne d_G(x,v)+d_G(y,u)$. The transitive closure ${\mathsf{\Theta }}^{*}$ of $\mathsf{\Theta }$ is an equivalence relation on $E\left(G\right)$. The equivalence classes of ${\mathsf{\Theta }}^{*}$ are shown by $\mathcal{F}=\{F_1,\dots ,F_r\}$, which is called the ${\mathsf{\Theta }}^{*}$-partition. Define the quotient graph $G/F_i$ as follows: For any $i\in \left[r\right]$, let the connected components of the graph G-$F_i$ exist as vertices, and two vertices P and Q are adjacent iff there is at least an edge $uv\in F_i$ such that $u\in P$ and $v\in Q$. Consider a vertex weighted graph $(G,w)$; then, the Wiener index $W(G,w)$ is defined as follows [20]:

$$W(G,w)=\sum _{\{u,v\}\in \left(\genfrac{}{}{0pt}{}{V\left(G\right)}{2}\right)}w\left(u\right)w\left(v\right)d_G(u,v),$$

If $w\equiv 1$, then $W(G,w)=W\left(G\right)$.

An isometric subgraph H of a graph G is a subgraph of G such that the distance between any pair of vertices in H is the same as that in $G.$ A partial cube [21] is an isometric subgraph of a hypercube. Winkler showed that a connected graph is a partial cube if and only if it is bipartite and the relation $\mathsf{\Theta }$ is transitive—that is, $\mathsf{\Theta }={\mathsf{\Theta }}^{*}$ [10].

If G is a graph and $\{V_1,\dots ,V_t\}$ is the partition of $V\left(G\right)$ into the orbits under the action of $\mathrm{Aut}\left(G\right)$, then the modified Wiener index [14] of G is defined by

$$MW\left(G\right)=\left|V\left(G\right)\right|{\displaystyle \sum _{i=1}^t}\frac{1}{|V_i|}\sum _{\{u,v\}\in \left(\genfrac{}{}{0pt}{}{V_i}{2}\right)}{d}_G(u,v).$$

(1)

The modified Wiener index can also be expressed by

$$MW\left(G\right)=\frac{\left|V\right(G\left)\right|}{2Aut\left(G\right)}\sum _{u\in V\left(G\right)}\sum _{\alpha \in Aut\left(G\right)}{d}_G(u,\alpha \left(u\right)).$$

(2)

Let G be a graph of order n and let $S=(n_1,n_2,\dots ,n_k)$ with $n_1+n_2+\dots +n_k=n.$ An S-coloring $\mathcal{P}=\{S_1,S_2,\dots ,S_k\}$ is a partition of $V\left(G\right)$ with $|S_i|=n_i.$ The colored distance of $W_{\overline{\mathcal{P}}}\left(G\right)$ is the sum of the distances between vertices of different colors. The sum of distances between vertices with same colors, the partition distance of G, is $W_{\mathcal{P}}\left(G\right)=W\left(S_1\right)+\dots +W\left(S_k\right).$ Note that $W_{\overline{\mathcal{P}}}\left(G\right)=W\left(G\right)-W_{\mathcal{P}}\left(G\right).$

Henceforth, we collect those results that we will make use of from [3,22,23].

Lemma 1.

(i) Let P be a shortest path in G. Then, no two edges of P are in the relation Θ.

(ii) Let$e=uv$be an edge of a graph G, and let W be a$u,v$-walk in G that does not contain e. Then, there exists an edge f of W such that$e\mathsf{\Theta }f$.

(iii) Let F be a${\mathsf{\Theta }}^{*}$-class of a connected graph G and let$u,v\in V\left(G\right)$. If P is a shortest$u,v$-path and Q is an arbitrary$u,v$-path, then$|Q\cap F|\ge |P\cap F|$.

There are many research studies in which the authors applied weighted quotient graphs induced by the ${\mathsf{\Theta }}^{*}$-relation method for computing several distance-based graph invariants. For more details, see the survey [11]. The method is called the cut method. The following theorems are recent results that we extend to subsets of vertices.

Theorem 1.

[3] ([Theorem 2.2]) Let G be a connected graph and let $\mathcal{P}=\{V_1,\dots ,V_k\}$ be a partition of $V\left(G\right)$. If $\{F_1,\dots ,F_r\}$ is the ${\mathsf{\Theta }}^{*}$-partition of $E\left(G\right)$, then

$$W_{\mathcal{P}}\left(G\right)={\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^k}W(G/F_i,w_i^{\left(j\right)}),$$

where $w_i^{\left(j\right)}\left(C\right)=|C\cap V_j|$ for any $C\in V(G/F_i)$.

We say that a partition $\mathcal{E}=\{E_1,\dots ,E_t\}$ of $E\left(G\right)$ is coarser than $\mathcal{F}=\{F_1,\dots ,F_r\}$ if each set $E_j$ is the union of one or more ${\mathsf{\Theta }}^{*}$-classes of G. Theorem 1 then generalizes this as follows:

Theorem 2.

[3] ([Theorem 2.3]) Let $(G,w)$ be a connected weighted graph and let $\mathcal{P}=\{V_1,\dots ,V_k\}$ be a partition of $V\left(G\right)$. If $\{E_1,\dots ,E_r\}$ is a partition of $E\left(G\right)$ coarser than the ${\mathsf{\Theta }}^{*}$-partition, then

$$W_{\mathcal{P}}(G,w)={\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^k}W(G/E_i,w_i^{\left(j\right)}),$$

where $w_i^{\left(j\right)}\left(C\right)={\sum }_{x\in C\cap V_j}w\left(x\right)$ for any $C\in V(G/E_i)$.

Cut methods that apply to classes larger than partial cubes or a partition coarser than ${\mathsf{\Theta }}^{*}$-partition are called extended cut methods [11]. Now, we are ready to formulate our results.

3. Extended Cut Methods on Some Subsets of Vertices

In this section, we extend Theorems 1 and 2 regarding some subsets of vertices that are not necessary a partition of $V\left(G\right).$ This modification enables us to induce the partition and colored distances in a graph regarding some arbitrary subsets of vertices. Then, we prove and state the induced partition and colored distances based on the extended cut method. Moreover, we reduce the computation of the distances between unordered pairs of vertices to a corresponding appropriately weighted quotient graph of $G.$ The quotient graphs are weighted by a two-dimensional version with an operator.

The following theorem is an extension of Theorem 2. The idea of the proof is similar with the argument presented in [3] and we omit it. We point out that in the proof of Theorem 2, Klavžar et al. considered $\mathcal{P}=\{V_1,\dots ,V_k\}$ to be a partition of $V\left(G\right)$ and for any vertices $x,y\in V\left(G\right)$, $x\ne y$, that belong to some $V_j$, $j\in \left[k\right]$, selected a shortest $x,y$-path. Then, they utilized a double counting technique to prove the theorem. To prove Theorem 3, it is not necessary to assume that $\mathcal{P}$ is a partition of $V\left(G\right)$. In fact, if $\mathcal{P}=\{V_1,\dots ,V_k\}$ is the set of some distinct subsets of $V\left(G\right)$ (not necessarily the partition of $V\left(G\right)$), then we select a shortest path between each pair vertices of $V_j$, $j\in \left[k\right]$, and continue the proof using the same idea as used in the proof of Theorem 2. Moreover, we extend the definition of $W_{\mathcal{P}}(G,w)$ accordingly.

Theorem 3.

Let$(G,w)$be a connected weighted graph and let$\mathcal{P}=\{V_1,\dots ,V_k\}$be a set containing k distinct subsets of$V\left(G\right)$. If$\{E_1,\dots ,E_r\}$is a partition of$E\left(G\right)$coarser than the${\mathsf{\Theta }}^{*}$-partition, then

$$W_{\mathcal{P}}(G,w)={\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^k}W(G/E_i,w_i^{\left(j\right)}),$$

where$w_i^{\left(j\right)}\left(C\right)={\sum }_{x\in C\cap V_j}w\left(x\right)$for any$C\in V(G/E_i)$.

Several invariants of wide interest in basic graph theory, mathematical chemistry, and computer science can be expressed as instances of Theorem 3. For example, for computing the modified Wiener index, we need to obtain the summation of distances between unordered pair vertices of an orbit under the action Aut(G) [14]. Second, in the k-generalized Wiener index [24], we need to compute the summation of distances between vertices of the same degree k. In basic graph theory, k-diameter $d_k\left(G\right)$ of a graph G was introduced as $\max \left\{W\right(S):|S|=k\}$—that is, as the maximum overall partition distances of size k. Note that $d_2\left(G\right)=\mathrm{diam}\left(G\right)$ and $d_{\left|V\right(G\left)\right|}\left(G\right)=W\left(G\right)$ [25]. One of the main problems in computer science is the network clustering. In a clustering problem, we select some nodes as a cluster node in the network and we need to cluster nodes to transfer their data together [26]. In this case, we need to find the distance between cluster nodes—that is, a partition distance of cluster nodes.

In [3,23] and also the survey [11], Klavžar and Nadjafi-Arani introduced the extended cut method. Generally, they used a partition of vertices and introduced the partition distance of graphs. Klavžar and Nadjafi-Arani obtained a formula based on the extended cut method for the partition distance of graph. However, they expressed colored distance using the Wiener index and partition distances of a graph as follows:

Corollary 1.

[3] ([Corollary 2.6]) Let G be a connected graph and let $\mathcal{P}=\{V_1,\dots ,V_k\}$ be a partition of $V\left(G\right)$. If $\{F_1,\dots ,F_r\}$ is the ${\mathsf{\Theta }}^{*}$-partition of $E\left(G\right)$, then

$$W_{\overline{\mathcal{P}}}\left(G\right)={\displaystyle \sum _{i=1}^r}\left[W(G/F_i,w_i)-{\displaystyle \sum _{j=1}^k}W(G/F_i,w_i^{\left(j\right)})\right],$$

where $w_i\left(C\right)=\left|C\right|$ and $w_i^{\left(j\right)}\left(C\right)=|C\cap V_j|$ for any $C\in V(G/F_i)$.

The weakness of this corollary is twofold. First, using the definition of corresponding quotient graph based on canonical metric representation, it is not possible to state $W_{\overline{\mathcal{P}}}$ by cuts with the same weight function. Second, it is not possible to determine the colored distance when we are working with some subsets of vertices that are not necessarily a partition of $V\left(G\right)$. Hence, we need to obtain $W_{\overline{\mathcal{P}}}$ from ${\mathsf{\Theta }}^{*}$-partition and extend our results when we consider some subsets of vertices. In this case, we need to redefine the weighted function w as a two-dimensional function $w^2$ with an operation “.” where $w^2:V\left(G\right)\to {\mathbb{R}}^2.$ Let $v_i\in V\left(G\right)$ and define $w^2\left(v_i\right)=(x_i,y_i)$ with an operation “.” such that $w^2\left(v_i\right).w^2\left(v_j\right)=x_i{y}_j+x_j{y}_i.$ Similar to the weighted Wiener index $(G,w)$, we introduce the distance between two vertices $v_i$ and $v_j$ of a weighted graph $(G,w^2)$ as $\overline{d}(v_i,v_j)=w^2\left(v_i\right).w^2\left(v_j\right)d(v_i,v_j).$ Then, the colored distance of a weighted graph $(G,w^2)$ can be calculated as follows:

Theorem 4.

Let G be a connected graph and let$\mathcal{P}=\{V_1,\dots ,V_k\}$be a set containing k distinct subsets of$V\left(G\right)$and$\overline{V_i}={\cup }_{t=1}^k{V}_t-V_i.$If$\mathcal{F}=\{F_1,\dots ,F_r\}$is the${\mathsf{\Theta }}^{*}$-partition of$E\left(G\right)$, then

$$W_{\overline{\mathcal{P}}}={\displaystyle \sum _{j=1}^r}{\displaystyle \sum _{i=1}^k}W(G/F_j,w^2{}_i^{\left(j\right)})$$

(3)

where$w^2{}_i^{\left(j\right)}\left(C\right)=\left(|C\cap V_i|,|C\cap \overline{V_i}|\right)$for any$C\in V(G/F_j)$.

Proof. 

Let A be a set of shortest paths such that there exist exactly one shortest path $P(u,v)$ for each pair of vertices $(u,v),$ where $u\in V_i$ and $v\in V_j,$ $1\le i<j\le k.$ Create an incidence matrix $M=\left[m_{ij}\right]$ that is a matrix that shows the relationship between two classes of objects. If the first class is A and the second is $\mathcal{F}$, the matrix has one row for each element of A and one column for each element of $\mathcal{F}$. We assign $|E\left(P_i(u,v)\right)\cap F_j|$ for the corresponding entry in row $P_i(u,v)$ and column $F_j$. In a special case, if G is a partial cube, then M is a 0,1 matrix in which $m_{ij}=1$ if and only if the path $P_i(u,v)$ contains exactly one edge of $F_j.$ We apply a double counting on summation of M arrays. Indeed, the summation of arrays of ith row corresponding to $P_i(u,v)$ is equal to $d(u,v).$ So, due to the elements of the set A, the summation of M arrays shows $W_{\overline{\mathcal{P}}}.$ An array of jth column is greather than or equal than 1 if and only if there is a shortest path in A that goes through an edge of $F_j.$ Hence, initially, we compute the number of shortest paths in A that have an edge in $F_j.$ For calculating this number, let $C_{j,1},\dots ,C_{j,i_j}$ be the connected components of $G\setminus F_j$ and

$$C_{j,t}^i=(x_{j,t}^i,y_{j,t}^i)=\left(\sum _{x\in C_{j,t}\cap V_i}w\left(x\right),\sum _{x\in C_{j,t}\cap \overline{V_i}}w\left(x\right)\right).$$

Thus, the number of shortest paths in A passed through $F_j$ are equal to:

$${\displaystyle \sum _{p=1}^{i_j}}{\displaystyle \sum _{q=p+1}^{i_j}}{\displaystyle \sum _{s=1}^k}(x_{j,p}^s{y}_{j,q}^s+y_{j,p}^s{x}_{j,q}^s).$$

Alternately, using the definition of the quotient graphs $G/F_j$, the shortest path $P_i(u,v)$ induces a path of length t in $G/F_i$ so that $d_{G/F_j}(C_u,C_v)\le t$. Let $d_{G/F_j}(C_u,C_v)<t$ hold and let R be a shortest $C_u,C_v$-path in $G/F_j$. Then, R can be naturally lifted into an $u,v$-path in G which contains less that t edges from $F_j$. Since this contradicts Lemma 1(iii), we conclude that $d_{G/F_j}(C_u,C_v)\ge t$ and, consequently, $d_{G/F_j}(C_u,C_v)=t$—that is,

$$d_{(G/F_j,w_j)}(C_{j,p},C_{j,q})=|E\left(P_i(u,v)\right)\cap F_j|.$$

Hence, the summation of the $j\mathrm{th}$ column of M is equal to:

$$\begin{array}{ccc}& & {\displaystyle \sum _{p=1}^{i_j}}{\displaystyle \sum _{q=p+1}^{i_j}}{\displaystyle \sum _{s=1}^k}(x_{j,p}^s{y}_{j,q}^s+y_{j,p}^s{x}_{j,q}^s)d(C_{j,p},C_{j,q})\hfill \\ & =& {\displaystyle \sum _{p,q}}{w}_j^2\left(C_{j,p}\right).w_j^2\left(C_{j,q}\right)d(C_{j,p},C_{j,q}).\hfill \end{array}$$

Summing over all columns, we get:

$$W_{\overline{\mathcal{P}}}={\displaystyle \sum _{j=1}^r}\sum _{p<q,s}(x_{j,p}^s{y}_{j,q}^s+y_{j,p}^s{x}_{j,q}^s)d_{(G/F_j,w_j)}(C_{j,p},C_{j,q})={\displaystyle \sum _{j=1}^r}W(G/F_j,w_j^2),$$

which completes the proof. □

If $(G,w)$ is a connected weighted graph, then we can utilize

$$w\left(u\right)w\left(v\right)|E\left(P_i(u,v)\right)\cap F_j|$$

instead of $|E\left(P_i(u,v)\right)\cap F_j|$ in the incidence matrix. The main idea of the above argument comes from [23] ([Theorem 3.3]) where the first author with S. Klavžar extended the cut method for a partition of $E\left(G\right)$ coarser than the ${\mathsf{\Theta }}^{*}$-partition. The main difference between these two theorems is how to choose the set of shortest paths. In [23], the set of selected shortest paths is Y in G such that for every pair of vertices $u,v\in V\left(G\right)$, $u\ne v$, there exists a unique shortest $u,v$-path in the list, while in Theorem 4, the set A is a special set that enables us to calculate the summation of distances between all pair of vertices selected in A. In fact, coloring helps us to see the selected vertices more clearly. Since the proof of the extended cut method proceeds similar to how the proof Theorem 4 proceeds, we omit the details and state the generalized version of above theorem as follows:

Theorem 5.

Let$(G,w)$be a connected weighted graph and let$\mathcal{P}=\{V_1,\dots ,V_k\}$be a set containing k distinct subsets of$V\left(G\right)$and$\overline{V_j}={\cup }_{i=1}^k{V}_i-V_j.$ If $\{E_1,\dots ,E_r\}$ is a partition of $E\left(G\right)$ coarser than the ${\mathsf{\Theta }}^{*}$-partition, then

$$W_{\overline{\mathcal{P}}}={\displaystyle \sum _{j=1}^k}{\displaystyle \sum _{i=1}^r}W(G/E_i,w^2{}_i^{\left(j\right)})$$

(4)

where $w^2{}_i^{\left(j\right)}\left(C\right)=\left({\sum }_{x\in C\cap V_j}w\left(x\right),{\sum }_{x\in C\cap \overline{V_j}}w\left(x\right)\right)$ for any $C\in V(G/E_i)$.

Theorems 3 and 5 are quite powerful. Using a sample computer application, we calculate the summation of distances between two subsets of vertices $V_1$ and $V_2$ in a hypercube graph G. Let $V_1$ and $V_2$ be the sets of white and black vertices, respectively. Clearly, we can ascertain that the parallel edges of G are the partition $\mathcal{F}$ of $E\left(G\right)$. 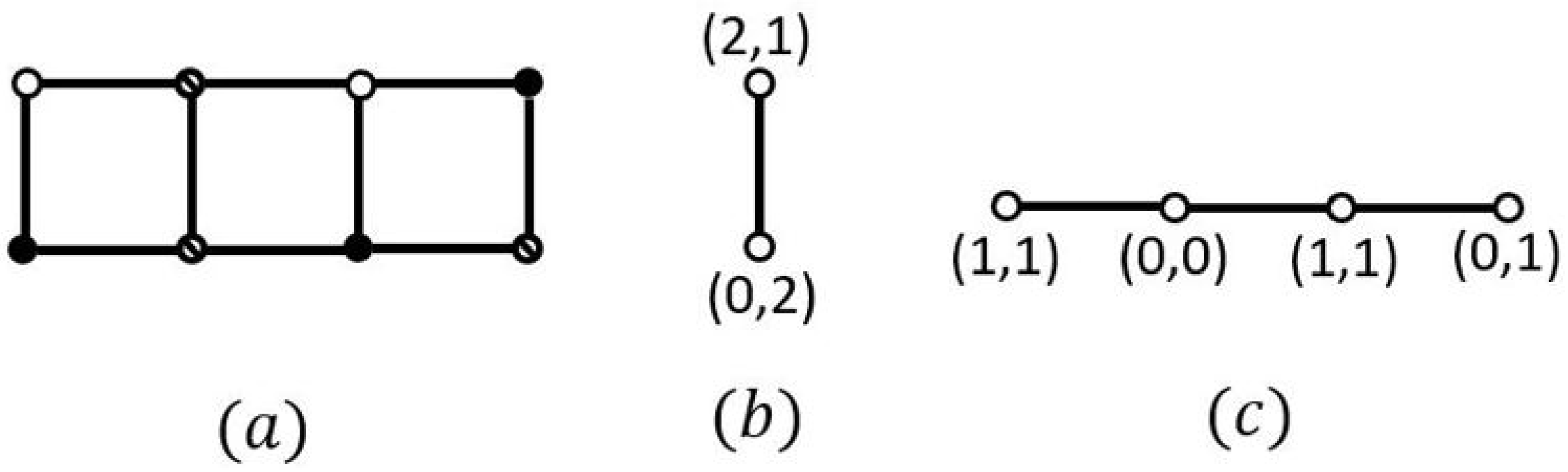Let $\mathcal{F}=\{F_1,F_2,F_3,F_4\}$ in which $E_1=\left\{F_1\right\}$ shows the vertical parallel edges and $E_2=\{F_2,F_3,F_4\}$ are three horizontal paralleled pair edges of G (see Figure 1a). Let $\mathcal{E}=\{E_1,E_2\}$ be a coarser partition of $\mathcal{F}$. The quotient graphs $G/E_1$ and $G/E_2$ with the weight ${\omega }^2\left(v_i\right)$ for each vertex $v_i$ are shown in Figure 1b,c respectively. Now, apply Theorem 5 to obtain the summation of distances between each pair of vertices $V_1$ and $V_2$.

$$\begin{array}{ccc}\hfill W_{\overline{\mathcal{P}}}& =& {\displaystyle \sum _{j=1}^2}{\displaystyle \sum _{i=1}^2}W(G/E_i,w^2{}_i^{\left(j\right)})\hfill \\ & =& 2\times 2\times 1+1\times 1\times 2+1\times 1\times 2+1\times 1\times 3+1\times 1\times 1=12.\hfill \end{array}$$

Let $V_p,V_q\subset V\left(G\right)$ be two distinct subsets of vertices and let $d(V_p,V_q)$ denote the summation of distances for each pair of vertices $(u,v)$ in which $u\in V_p$ and $v\in V_q.$ The following corollary is a special case of Theorem 5 when we have just two subsets of vertices.

Corollary 2.

Let$(G,w)$be a connected weighted graph and let$\mathcal{P}=\{V_1,\dots ,V_k\}$be a set containing k distinct subsets of$V\left(G\right)$. If$\{E_1,\dots ,E_r\}$is a partition of$E\left(G\right)$coarser than the${\mathsf{\Theta }}^{*}$-partition, then

$$d(V_p,V_q)={\displaystyle \sum _{i=1}^r}W(G/E_i,w^2{}_i)$$

(5)

where$w^2{}_i\left(C\right)=\left({\sum }_{x\in C\cap V_p}w\left(x\right),{\sum }_{x\in C\cap V_q}w\left(x\right)\right)$for any$C\in V(G/E_i)$.

Corollary 2 plays the main role in our results in the next section. Alternately, the distance summations between some subsets of $V\left(G\right)$ can be calculated by taking a summation on Equation (5). For instance, from Theorem 5 and Corollary 2, it is easy to see that

$$W_{\overline{\mathcal{P}}}={\displaystyle \sum _{j=1}^k}{\displaystyle \sum _{i=1}^r}W(G/E_i,w^2{}_i^{\left(j\right)})=\sum _{p\ne q}d(V_p,V_q)=\sum _{p\ne q}{\displaystyle \sum _{i=1}^r}W(G/E_i,w^2{}_i).$$

(6)

In the following, it is important to mention some special features of the Theorems 3 and 5. In fact, we can omit the distinct assumption for $V_i$s. In this case, if a node $v_i$ has several colors ($v_i$ belongs to different elements of $\mathcal{P}$), we need to define the color of $v_i$ due to our desires. For example, if we consider that the vertex $v_i$ belongs to two different subsets ($v_i$ has two colors, for instance, red and blue), and we need to find the distance between blue vertices such that the distance between $v_i$ and other blue vertices is a term of our desire, we consider the color of $v_i$ to be blue. Next, set all shortest paths between $v_i$ and blue vertices in $A.$ Alternately, if we need to consider $v_i$ as a red vertex, we have to deposit the corresponding shortest paths in $A.$

4. Some Bounds on the Modified Wiener Index and the Number of Orbits

In this section, we apply Theorem 4 and Corollary 2 to partial cubes and trees to derive some upper bounds for modified Wiener index and the number of orbits of the automorphism group. Before that, the eccentricity of a vertex v is defined to be the greatest distance from v to any other vertex. The radius r of a graph is the minimum eccentricity of any vertex; in other words, $r={\min }_{v\in V}ϵ\left(v\right)={\min }_{v\in V}{\max }_{u\in V}d(v,u).$ A vertex with minimal eccentricity is called the center of a graph. The trees have exactly one center (centered trees) or precisely two adjacent centers (bicentered trees). In bicenterd trees, the edge between two centers is called the edge center.

Lemma 2.

Let G be a graph of order n and$\{V_1,\cdots ,V_t\}$be the set of orbits of$Aut\left(G\right)$. Then,

$$MW\left(G\right)=\frac{n}{2}\sum _{v_i}W\left(v_i\right)$$

in which$v_i$is the orbit representative of$V_i$and$W\left(v_i\right)={\sum }_{u\in V_i}d(u,v_i).$

Proof. 

Assume that u and v belong to an arbitrary orbit $V_i.$ Due to the orbit properties of an automorphism group, it is easy to see that ${\sum }_{w\in V_i}d(u,w)={\sum }_{w\in V_i}d(v,w).$ Therefore,

$$W\left(V_i\right)=\sum _{u,v\in V_i}d(u,v)=|V_i|\sum _{v_i\in V_i}d(u,v_i)=\left|V_i\right|W\left(v_i\right),$$

Then, by substituting to (1), the result follows. □

Lemma 3.

If T is a centered tree, then the center of T is an orbit of T with one element. Moreover, the elements of an arbitrary orbit are an independent set of$T.$When T is a bicentered tree, the same results hold with a difference that the edge center maybe be an orbit.

Proof. 

Initially, let T be a centered tree. Since the elements of each orbit are symmetric, the center of T is a unique vertex with special properties and it is an orbit with one element. Next, we show that the elements of an orbit are an independent set. Let $e=uv$ be an edge of T such that u and v belong to the same orbit. Let c be the center of T and $\alpha \in Aut\left(T\right)$ such that $\alpha \left(u\right)=v.$ Alternately, T is a centered tree, so $\alpha \left(c\right)=c$—that is, $d(c,u)=d(c,v).$ Hence, there is a closed walk $P:c,\dots ,u,v,\dots ,c$ in T of odd length. It means that T has a cycle that is a contradiction. Thus, the elements of an orbit form an independent set. If T is a bicentered tree based on the structure of T, maybe both of the centers form an orbit or separately each one becomes an orbit with one element. Let $c_1,c_2$ be the centers of T and let both of them belong to different orbits. Then, with the same argument, we can prove that there is no edge between vertices of an orbit. When $c_1,c_2$ belong to the same orbit, then there exist two cases. $\alpha \left(c_1\right)=c_1$, and $\alpha \left(c_1\right)=c_2.$ The proof of the first case is the same as before. For the second one, we have $d(c_1,u)=d(c_2,v).$ In this case, the walk $P:c_1,\cdots ,u,v,\cdots ,c_2,c_1$ is a closed walk in T that is a contradiction and the proof is complete. □

Corollary 3.

Let T be a tree of order n and radius r with t orbits; then,$r\le t\le n.$

Proof. 

Since the distance between the center of T and the elements of an orbit is a fixed number, $r\le t.$ Alternately, the number of orbits is maximum when $Aut\left(T\right)=\left\{e\right\}$ that is, each node is an orbit or $t=n$. So, the proof is complete. □

In the next theorem, we apply Corollary 2 to find an upper bound for the modified Wiener index in partial cube graphs based on the number of orbits of the automorphism graph.

Theorem 6.

Let G be a partial cube of order n and$\{F_1,\dots ,F_k\}$is the${\mathsf{\Theta }}^{*}$-partition of$E\left(G\right).$Let$\{V_1,\dots ,V_t\}$be the set of orbits of$Aut\left(G\right)$then

$$MW\left(G\right)\le \frac{nk(n-t)}{2},$$

and the bound is the best possible.

Proof. 

Let $\{F_1,\dots ,F_k\}$ be the ${\mathsf{\Theta }}^{*}$-partition of $E\left(G\right)$ and $\{v_1,\cdots ,v_t\}$ demonstrates the set of orbit representatives of $\{V_1,\cdots ,V_t\}$ respectively. Apply Corollary 2 for an orbit $V_j$ and consider $V_p=v_j$ and $V_q=V_j-\left\{v_j\right\}$. Since for each $1\le i\le r$ the graph $G-F_i$ parted to two connected components C and $C^{\prime },$ so its quotient graph is a weighted edge $e_i={\alpha }_i{\beta }_i.$ Thus, $w_{i_j}^2\left({\alpha }_i\right)=\left(\right|V_q\cap C|,0)$ and $w_{i_j}^2\left({\beta }_i\right)=\left(\right|V_q\cap C^{\prime }|,1)$. Therefore,

$$\begin{array}{ccc}\hfill W\left(v_j\right)& =& d(v_j,V_j-\left\{v_j\right\})={\displaystyle \sum _{u\in V_j}}d(v_j,u)={\displaystyle \sum _{i=1}^k}W(G/F_i,w_{i_j}^2)\hfill \\ & =& {\displaystyle \sum _{i=1}^k}{w}_{i_j}^2\left({\alpha }_i\right).w_{i_j}^2\left({\beta }_i\right)d({\alpha }_i,{\beta }_i)={\displaystyle \sum _{i=1}^k}|V_q\cap C|\le k(|V_j|-1).\hfill \end{array}$$

(7)

It concludes that,

$$\begin{array}{ccc}\hfill MW\left(G\right)& =& \frac{n}{2}{\displaystyle \sum _{v_i}}W\left(v_i\right)\hfill \\ & \le & \frac{n}{2}k{\displaystyle \sum _{i=1}^t}\left(\right|V_i|-1)=\frac{nk(n-t)}{2},\hfill \end{array}$$

(8)

This value is attained by the modified Wiener index of a path with three vertexes or each graph whose automorphism group is identity. Therefore our bound is best possible and the proof is complete. □

We know that trees are a subset of partial cube graphs and each edge of a tree is an element of ${\mathsf{\Theta }}^{*}$-partition. The following corollary is obtained from Theorem 6 directly.

Corollary 4.

Let T be a tree of order n and$Aut\left(T\right)$has t orbits. Then,

$$MW\left(G\right)\le \frac{n(n-1)(n-t)}{2}.$$

Moreover, the equality holds if and only if$Aut\left(T\right)\cong \left\{e\right\},$$T=K_2$or$T=P_3$.

Proof. 

Since, the trees are partial cubes and each edge of a tree is an element of ${\mathsf{\Theta }}^{*}$-partition, we can obtain the upper bound from Theorem 6. For equality, it is enough to show that equality holds in (7) for each arbitrary $i,j$. Consider the same notation used in Theorem 6. Clearly, when $Aut\left(T\right)\cong \left\{e\right\}$ each orbit is formed from a vertex and $|V_j|-1=0.$

Next, let $Aut\left(T\right)\ncong \left\{e\right\}$, and there is $e\ne \alpha \in Aut\left(T\right)$ in which, for two distinct vertices $u,v\in V_j$, we have $\alpha \left(u\right)=v.$ If u and v are not pendant vertices, then it is enough to consider the pendant edge $e_i$ as an element of ${\mathsf{\Theta }}^{*}$-partition. Thus, $w_{i_j}^2\left({\alpha }_i\right).w_{i_j}^2\left({\beta }_i\right)=0<\left|V_j\right|-1$. Let $u,v$ be pendant vertices and $r\ge 2$. In this case, consider the edge $e_i$ as a nonpendant edge. Similar to last argument, we can prove that the Equation (7) does not hold. If $r=1$, then $T\cong S_n$ where $S_n$ shows a star graph with n vertex. One can easily see that if $n\ge 4$, then there is an edge for which the Equation (7) is not satisfied and the result follows. □

Theorem 7.

Let T be an n-vertex tree and$\{V_1,\dots ,V_t\}$be the set of orbits of$Aut\left(T\right)$. r shows the radius of tree. Then,

1. 

If T is a centered tree, then

$$MW\left(G\right)\le nr(n-\frac{3r+1}{2})$$

and the equality holds if and only if T is the star graph$S_n$or the path$P_n$.

2. 

If T is a bicentered tree, then

$$MW\left(G\right)\le n(r-1)(n-\frac{3r}{2})+\frac{n}{2}(n-r)$$

and the equality holds if and only if T is the path$P_n$.

Proof. 

Initially, let T be a centered tree with its center named c. Assume that $s=\{v_0=c,\cdots ,v_t\}$ demonstrates the set of orbit representatives of $S=\{V_0,\cdots ,V_t\}$. $V_0$ denotes a one-element orbit that contains the center of T. Consider the vertices of a graph with level $i\ge 1$ by $L_i=\{V_{i_1}\cdots ,V_{i_k}\}$ where it is the set of all orbits such that $d(v_{i_j},c)=i.$ Since T is a tree and by Lemma 3, there are no edge between vertices of $L_i$. Define

$$E_t^{i,j}=\{e=uv\in E\left(T\right)|u\in V_{{(t-1)}_i}\mathrm{and}v\in V_{t_j}\}.$$

Indeed, the set

$$\mathcal{E}=\left\{E_t^{i,j}\right|1\le t\le r,1\le i\le {(t-1)}_k,1\le j\le t_k\},$$

is a partition of $E\left(G\right)$ coarser than the ${\mathsf{\Theta }}^{*}$-partition. Let $v_{{\ell }_i}\in V_{{\ell }_i}$ be the orbit representative and apply Corollary 2 with considering $V_p=v_{{\ell }_i}$ and $V_q=V_{{\ell }_i}-\left\{v_{{\ell }_i}\right\}$ as two separate subsets of $V\left(T\right)$. Consider the quotient graph $T/E_t^{i,j}$ that is a star graph $(S_{T/E_t^{i,j}},w^2)$. If $t>\ell$, since for all connected components C except one of them $C\cap V_p=C\cap V_q=\varnothing$, then for each pair of vertices C and $C^{\prime }$ from $(S_{T/E_t^{i,j}},w^2)$, we have $\overline{d}(C,C^{\prime })=0$—that is, $W(T/E_t^{i,j},w^2)=0$. With similar argument, we can prove that when $1\le t\le \ell$ and the shortest paths between $V_{{\ell }_i}$ and $V_{t_j}$ $(V_{{\ell }_i}\ne V_{t_j})$ is passing from c, we have $W(T/E_t^{i,j},w^2)=0.$ Next, let $1\le t\le \ell$ and the shortest paths between $V_{{\ell }_i}$ and $V_{t_j}$ $(t\ne \ell ),$ never pass from $c.$ In this case, the quotient graph $T/E_t^{i,j}$—that is, the star graph $(S_{T/E_t^{i,j}},w^2)$—is weighted by $(0,0)$ in the center and for each pendant vertex; for instance C, the weight is equal to $w^2\left(C\right)=({\sum }_{x\in C\cap V_p}w\left(x\right),{\sum }_{x\in C\cap V_q}w\left(x\right))$. Hence,

$$W\left(v_{{\ell }_i}\right)=d(V_p,V_q)={\displaystyle \sum _{E_t^{i,j}}}W(T/E_t^{i,j},w^2)={\displaystyle \sum _{E_t^{i,j}}}{\displaystyle \sum _{C,C^{\prime }}}{w}^2\left(C\right).w^2\left(C^{\prime }\right)d(C,C^{\prime })$$

Since, the center $C,$ of the quotient graph $(S_{T/E_t^{i,j}},w^2)$ has the weight $(0,0)$, for each vertex $C^{\prime }$, we have $\overline{d}(C,C^{\prime })=w^2\left(C\right).w^2\left(C^{\prime }\right)d(C,C^{\prime })=0$. On the other hand, if C and $C^{\prime }$ are two pendant vertices of $(S_{T/E_t^{i,j}},w^2)$, then

$$\begin{array}{ccc}\hfill \overline{d}(C,C^{\prime })& =& w^2\left(C\right).w^2\left(C^{\prime }\right)d(C,C^{\prime })=2w^2\left(C\right).w^2\left(C^{\prime }\right)\hfill \\ & =& 2\left[{\displaystyle \sum _{x\in C\cap V_p}}w\left(x\right)\times {\displaystyle \sum _{x\in C^{\prime }\cap V_q}}w\left(x\right)\right.\hfill \\ & +& \left.{\displaystyle \sum _{x\in C^{\prime }\cap V_p}}w\left(x\right)\times {\displaystyle \sum _{x\in C\cap V_q}}w\left(x\right)\right].\hfill \end{array}$$

(9)

Clearly, $V_p$ has one element, hence the maximum value of (9) or, generally, the maximum value of $W(G/E_t^{i,j},w^2)$ happened when the connected component corresponding to $v_p=v_{{\ell }_i}$ called $C_{v_p}$ has no vertices from $V_q=V_{{\ell }_i}-\left\{v_{{\ell }_i}\right\}$—that is,

$$\begin{array}{ccc}\hfill W(T/E_t^{i,j},w^2)& =& {\displaystyle \sum _{C,C^{\prime }\in (S_{T/E_t^{i,j}},w^2)}}\overline{d}(C,C^{\prime })\hfill \\ & =& {\displaystyle \sum _{C\in (S_{T/E_t^{i,j}},w^2)}}\overline{d}(C,C_{v_p})\le 2\left(\right|V_{{\ell }_i}|-1).\hfill \end{array}$$

(10)

Note in Equation (10) that if $C_i,C_j\ne C_{v_p}$ then $w^2\left(C_i\right)=(0,{\sum }_{x\in C_i\cap V_q}w\left(x\right))$ and $w^2\left(C_j\right)=(0,{\sum }_{x\in C_j\cap V_q}w\left(x\right))$ and $w^2\left(C_i\right).w^2\left(C_j\right)=0$. Therefore,

$$\begin{array}{ccc}\hfill W\left(v_{{\ell }_i}\right)& =& {\displaystyle \sum _{E_t^{i,j}}}W(T/E_t^{i,j},w^2)\hfill \\ & =& {\displaystyle \sum _{E_t^{i,j}}}{\displaystyle \sum _{C\in (S_{T/E_t^{i,j}},w^2)}}\overline{d}(C,C_{v_p})\le 2\ell \left(\right|V_{{\ell }_i}|-1).\hfill \end{array}$$

(11)

It should be noted that, in the last equation, the value ℓ comes from this fact that for each $1\le t\le \ell$, the value $W(T/E_t^{i,j},w^2)\ne 0$.

Finally, we obtain the main result by applying the Equation (11) in the modified Wiener index as follows:

$$\begin{array}{ccc}\hfill MW\left(G\right)& =& \frac{n}{2}{\displaystyle \sum _{v_i}}W\left(v_i\right)=\frac{n}{2}{\displaystyle \sum _{v_i}}{\displaystyle \sum _{\mathcal{E}}}W(G/E_i,w^2)\hfill \\ & =& \frac{n}{2}{\displaystyle \sum _{E_t^{i,j}}}{\displaystyle \sum _{C\in (S_{T/E_t^{i,j}},w^2)}}d(C,C_{v_p})\le \frac{n}{2}{\displaystyle \sum _{V_{{\ell }_i}\in S}}2\ell \left(\right|V_{{\ell }_i}|-1)\hfill \\ & =& n[{\displaystyle \sum _{i=1}^r}i\left(\right|V_{i_1}|+\cdots +|V_{i_{k_i}}\left|\right)-{\displaystyle \sum _{i=1}^r}i{k}_i]\hfill \\ & \le & n[r{\displaystyle \sum _{i=1}^t}|V_i|-[(r-1)\left(\right|V_{1_1}|+\cdots +|V_{1_{k_1}}\left|\right)\hfill \\ & +& (r-2)\left(\right|V_{2_1}|+\cdots +|V_{2_{k_2}}\left|\right)+\cdots \hfill \\ & +& \left(\right|V_{{(r-1)}_1}|+\cdots +|V_{{(r-1)}_{k_{r-1}}}\left|\right)]-\frac{r(r+1)}{2}]\hfill \\ & \le & n[r(n-1)-2[(r-1)+(r-2)+\cdots +1]-\frac{r(r+1)}{2}]\hfill \\ & =& nr(n-\frac{3r+1}{2}).\hfill \end{array}$$

(12)

The proof is complete in this case.

For equality, from Inequality (12), we obtain that $|V_{i_1}|+\cdots +|V_{i_{k_i}}|=2$ for each $1\le i\le r-1$, and $k_i=1$ for each $1\le i\le r$—that is, $r=1$, or if $r\ge 2$, then T is a path of odd order (T is a centered tree). Alternately, the Inequality (11) is equal in the path and star graph. It means that the equality is satisfied when $T\cong S_n$ or $T\cong P_n.$ Vice versa, when $T\cong S_n$, then $r=1$, and if $T\cong P_n$ (n is odd), then $r=\frac{n-1}{2},$ so one can easily see that the equality holds.

When T is a bicentered tree, then we have the edge center $e=uv.$ We treat e as a vertex and define the ${\mathsf{\Theta }}^{*}$-partition $\mathcal{E}$ similar to the previous case. That is somewhat a tree of radius $r-1.$ Now, we can realize the ${\mathsf{\Theta }}^{*}$-partition as $\mathcal{E}\cup \left\{e\right\}$, and Equation (11) changes to

$$W\left(v_{{\ell }_i}\right)\le 2\ell \left(\right|V_{{\ell }_i}|-1)+\left(\right|V_{{\ell }_i}|-1).$$

The additional term comes from the edge center e where the quotient graph $T-e$ is an edge. To complete the proof, we need to continue as before with some changes in the summation indices. □

Indeed, our approach gives a new method for computing distance-based graph invariants such as the modified Wiener index, terminal Wiener index, and so on. There are many research studies in chemistry, biology, or information theory in which the authors obtained some equalities or bounds for distance-based graph invariants on molecule graphs or networks, such as dendrimer nanostars, fullerenes, or mesh networks [27,28,29,30,31]. Almost all of the mentioned researches have been applied to a traditional summation method between vertices, whereas in this paper, we prove a method based on a two-dimensional weight and an equivalence relation.

5. Concluding Remarks

Studying partitions and colored distances has been crucial in metric graph theory, as the usefulness of those problems when defining/analyzing quantitative graph measures has been proved. As we have mentioned repeatedly in the paper, its motivation stems from the facility location network problem [1,2]. Those concepts are usually defined on the whole vertex set of a graph. In this manuscript, we tackled the problem of inducing these definitions locally and consider subsets of vertices. For a special case, we demonstrated that the modified Wiener index is a concept that requires finding the distances between vertices of an orbit. Previous definitions for partitions and colored distances were not able to compute the modified Wiener index. In this way, we considered the canonical metric representation method and defined a two-dimensional weight for vertices of graphs with an operator. Then, we applied quotient graphs and cuts to calculate the induced partition and colored distances for some subsets of vertices. Two-dimensional weights for quotient graphs are extensions of traditional one-dimensional weights introduced for canonical metric representation. The problem of finding a minimum-cost spanning tree is one of the classic algorithmic questions in computer science and graph theory. In many cases, distances can be used to define cost functions. For instance, the problem of finding a minimum average distance (MAD) tree is one of the well-known problems in computer science (see the survey [32]). A MAD tree of a graph is defined as a spanning tree with minimum average distance or, equivalently, with the minimum Wiener index. In addition to the modified Wiener index, e.g., the MAD tree, the relative Wiener index, and the k-diameter of a graph G are a few concepts that would be interesting to consider in terms of certain induced partitions and colored distances. We will consider these problems in future works.