1. Introduction
Stochastic volatility models and jump diffusion models such as classical Heston model [
1] and Merton jump diffusion model [
2] have played an important role in the option pricing theory. The models have aimed at replicating the stochastic volatility effect (along with the mean-reversion) and the jump-effect as displayed in the financial market. For decades, the models have been proven to be useful in pricing options, but they are deemed as inadequate for modeling the short-time behavior of the implied volatility of the options using the real data.
It was discovered by Alos et al. [
3] that the introduction of fractional components with Hurst parameter
is capable of generating the term structure of at-the-money skew of order
for every
and small time to maturity
T. In addition, Fukasawa [
4] managed to show that (through an example of martingale expansion’s application) the stochastic volatility model with volatility term driven by fractional Brownian motion with Hurst parameter
H can generate at-the-money volatility skew of order
for the small time to maturity
T. This motivated the authors of [
5] to further explore through real empirical data to verify that the use of fractional Brownian motion in a stochastic volatility model is useful and adequate in replicating the roughness behavior of volatility in the financial market. Fractional Brownian motion with Hurst parameter
in volatility model is subsequently named as rough volatility. On a side note, Hurst parameter
H is used to control the roughness of the fractional Brownian motion, i.e., when
, the rough volatility displays anti-persistency effect, and, for
, the volatility would display long-memory effect. Prior to the use of rough volatility, fractional Brownian motion with Hurst parameter
was proposed by Comte and Renault [
6] to model the long-memory effect of volatility. A linear sum of classical Brownian motion and fractional Brownian motion called mixed fractional Brownian motion
was also proposed and developed by Cheridito et al. [
7] to price model stock movement and price options.
Rough Bergomi model by Bayer, C., & Friz, P., Gatheral, J. [
8] was among the first models proposed to incorporate the rough volatility component. The initial model proposed is slow in simulation such that the authors ruled out the possibility of optimization in practice. Nevertheless, the authors proposed an efficient expansion method for the implied volatility to the second order in the volatility of volatility component. Furthermore, further advancements in reducing the computational costs were made by the authors of [
9,
10], i.e., they introduced a faster scheme that utilizes hybrid methods for the Brownian semistationary process in the simulation and variance reduction techniques for a significant runtime reduction in the simulation process.
Rough Heston model is our main discussion of this paper. It possesses the rough quality of the classical Heston model and was introduced by El Euch and Rosenbaum [
11] as a stochastic Volterra equation. The model is used to describe the high degree of endogeneity (orders that have no real economic motivation) of the liquid market and the no statistical arbitrage mechanism which should present on a highly liquid electronic markets. In addition, the liquid asymmetry (average impact of a sell order is greater than the impact of a buy order) and presence of metaorders (large orders whose execution is split in time by trading algorithm) are also features of rough Heston model. Accordingly, the authors of [
11] obtained the characteristic function of the rough Heston model to compute the option price using the Fourier inversion method. Coincidentally, the computation for option price under the rough Heston model is also computationally expensive. One of the brilliant achievements of El Euch and Rosenbaum [
11] is that, under the numerical experiments, the authors were able to numerically verify that pricing option price under rough Heston model consists of explosive behavior for term-structure at-the-money implied volatility skew (the same goes to the rough Bergomi model) as
. Explosive behavior for the short-time term structure of at-the-money implied volatility skew is one of the crucial components in pricing options for short maturity time (see [
4,
8,
12]). In addition, Gatheral and Radoicic [
13] used rational approximations on fractional Riccati equation which in return substantially reduces the computational cost (see [
14] for a review and [
15] for an improvement on the method). Recent advancements by the authors of [
16,
17] made effort in reducing the computational cost of the rough Heston model.
We study an approximation formula for option prices under the rough Heston model.
Section 1 serves as prerequisites to our study. In particular, the approximation method is obtained using the decomposition formula proposed in [
18,
19,
20]. Accordingly, the error bounds of the approximation formula are studied in
Section 2 under a simple assumption. Details of the proof in
Section 2 are listed in
Appendix A. Subsequently, in
Section 3, we propose a second-order approximation to the implied volatility similar to the work of Alos, Elisa and De Santiago, Rafael and Vives, Josep [
19]. We then match the coefficients and thus obtain some of the short-time implied volatility behaviors for our approximation formula for implied volatility. Ultimately, one important result that we obtain is that the approximation formula for implied volatility does display explosive behavior for the term structure at-the-money volatility skew. Through the numerical experiments, as shown in
Section 4, we manage to verify that the option prices under rough Heston model computed using the approximation formula and the Fourier inversion method with fractional Adams scheme [
11,
21] are extremely consistent with one another for short maturity time. In addition, we find that, by comparing the implied volatility computed by Fourier inversion method with fractional Adams scheme [
11,
21] under rough Heston model, approximation formula for option prices (transformed back to implied volatility) and short-time term structure of the at-the-money skew equation have roughly the same order of explosive behavior for the term structure of at-the-money implied volatility skew. Lastly, we give a conclusion to our work in
Section 5.
Prerequisites
Consider the price model process with rough Heston dynamics:
where
S is the stock price,
is the correlation between stock return and the volatility movement,
,
is the mean reversion level,
is the rate at which the process
reverts to the mean reversion level
,
is the magnitude of random movement,
and
are independent Brownian motion defined in a filtered probability space (
) with
, and
is the volatility of the return that is positive and square-integrable function adapted to the filtration.
Let
and we describe Equation (
2) in the forward variance form:
where
is the forward variance curve. Following the work of Alos et al. [
20], we denote the future expected variance
as
and the martingale as
The connection between
and
can be easily established as
then it follows that
The Delta–Gamma–Vega relationship can be established as
where
is some function that solves the Black–Scholes equation with
X being the log-spot price with the dynamics specified in Equation (
3) and
w depends on
. Otherwise,
can be formulated as
where
is the cumulative distribution function of standard normal distribution and
with the assumption of risk-free interest rate
throughout the paper.
Theorem 1 (Decomposition formula)
. Assume as some function that solves the Black–Scholes equation where x is the log-spot price with the dynamics specified in Equation (3) and w depends on the from Equation (4). Then, for all Proof. Applying Itô’s formula to
, we have
We use Equations (
3), (
8) and (
9) to simplify
Integrating up to time
T and taking conditional expectation of Equation (
14) on
, the result follows.□
Theorem 1 is the decomposition formula from [
20] with slight changes of the notation as corresponds to the original work in [
18]. Equation (
12) is exact rather than an approximation, i.e., it describes the interaction between the movement of log-stock movement and the future expected variance from time
t to
T. It is known that Equation (
12) under conditional expectation can be difficult to compute, therefore approximation of the equation is needed. In this study, we provide an approximation formula for Equation (
12) using the rough Heston model dynamics under a simple assumption. It is found that the errors are bounded and decreasing as the time to maturity gets smaller. Let
as a simplification.
We consider the following assumption throughout this study:
Assumption 1 (A1).
The relevance of Assumption 1 for the practical application is discussed at the end of
Section 4. We prove some bounds under Assumption 1.
Lemma 1. Assume the model in (2) and (3) and Assumption 1; then, for all ,and for Proof. Since
is
-martingale, it is not hard to see that from Equations (
2) and (
3)
Remembering that
, rearranging we obtain
For
, we compute
as
Furthermore, we can obtain two more bounds by considering the following
Again, for
, we compute
as
For
,
and the result follows.□
Lemma 2. Let . Then, for every , there exists such thatwhere Proof. See Lemma 2.1 in [
18] or similar result in Lemma 4.1 of [
3].□
Proposition 1. Assuming the volatility model (2), the conditional expectation iswherewith as the generalized Mittag–Leffler function. Proof. See pages 7–8 in [
22], Proposition 3.1 in [
23] or Proposition 2.1 in [
24]. □
3. Second-Order Approximation and Small-Time Behavior of Implied Volatility
The outline of this section is roughly the same as that of Alos, Elisa and De Santiago, Rafael and Vives, Josep [
19], but we focus on the rough Heston model rather than classical Heston model. We expand the function
f with respect to the two scales in order to obtain the second-order approximation for the implied volatility. Consider the asymptotic sequence
and the function
f can be expanded as
. Then, consider the scale function
and expand each
as
. Combining the expansions
and
f, we obtain the following
We thus let
and
with
be the implied volatility function expanded to these two scales:
Let
as the second-order approximation to the implied volatility. Then, let
as the future average volatility and
such that
is the approximation formula to the option price obtained in Theorem 2. Ultimately, we have
where
is the Vega of the Black–Scholes formula
. Similarly, we can expand the
around
using the Taylor Expansion and Equation (
37) as such
Let
and
; then, comparing the first-order approximation of Equation (
41) to Equation (
40), we can obtain the following
Similarly, as noted by Alos, Elisa and De Santiago, Rafael and Vives, Josep [
19], the smile effect of the implied volatility can be shown by the quadratic term
which has impact of the
in its term. Suppose we let
, and we let
. The error between the option pricing formula using the approximation of the implied volatility in Equation (
38) and the option price under rough Heston model is as follows:
The first term of Equation (
44) has an error of
or
. Under Assumption 1, and by Theorem 2, we know that the second term of (
44) has a small time (when
) error of
which is a decreasing term proportional to
and
. The total errors of option prices on the approximation to the implied volatility are of the order of
. Noticeably, the errors converges to zero as
and
. We prove some results that would assist in obtaining the short-time behavior on the approximation of implied volatility.
Proposition 2. Assume volatility dynamics of Equation (4); then, Proof. From the definition of
and Proposition 1, we can obtain the following
Let
; we can subsequently notice that it is sufficient to prove that
Then, by the above result and Fubini’s theorem, we can obtain the following
which is the desired result.□
Proposition 3. Assume volatility dynamics of Equation (4); for and ,as . Proof. From Proposition 1, we can obtain the following
From Proposition 2 and by the Fubini’s theorem again, we can obtain the following:
Substitute
and notice that it can be solved using the Beta function, such that
Then, for
and
, we can deduce the following asymptotic expansion
as
.□
Remark 2. Proposition 2 is equivalent to the case of the classical Heston model. Furthermore, by utilizing Proposition 3, we ultimately yield the same result from [19] in the case of for the rest of the result in this paper. 3.1. Limiting Behavior of When
We utilize some of the derivations from [
19]. The limiting behavior of
as
can be computed in term of the asymptotic formula as follows
Lemma 3. Assume model (3) and (4). Then, we can obtain the asymptotic formula of asas . Proof. From Equation (
A7) and Proposition 3, we can obtain the limiting behavior of
when
as
Then, the limiting behavior of
can be obtained as following
The result follows from the limiting behavior of Equation (
57) and Proposition 2.
We focus on the asymptotic formula of in the next lemma.□
Lemma 4. Assume model (3) and (4). Then, we can obtain the asymptotic formula of asas . Proof. From Equation (
A7) and Proposition 3, the limiting behavior of
when
can be obtained as
Then, the limiting behavior of
can be obtained as follows
Similarly, the result follows from the limiting behavior of Equation (
60) and Proposition 2.□
Remark 3. From Lemmas 3 and 4, when the option is close to maturity , the second-order approximation to the implied volatility can be writtenas the asymptotic formula. Furthermore, the expression (62) becomes exact and equivalent to the result found by Alos, Elisa and De Santiago, Rafael and Vives, Josep [19] when . 3.2. Term Structure of At-The-Money Implied Volatility Skew
This subsection is crucial in showing that the approximation formula for the implied volatility under rough Heston model is capable of replicating the explosive behavior of the implied volatility under the rough volatility model as stated in [
4,
5]. When the option is at-the-money, we have
and this leads to
. Consequently, the term structure of the at-the-money implied volatility skew can be computed as
Lemma 5. When the option is at-the-money, the term structure of implied volatility skew has the asymptotic formula ofas . Proof. From the result of Lemmas 3 and 4, we have the following as
:
Let and the result follows.□
Remark 4. From Lemma 5, we can also observe the following: for the uncorrelated case () and correlated case in model (3) and (4), the slope of implied volatility (with respect to and ) is positive when and negative when . The result is slightly different than the implied volatility behavior when , where yields different positive and negative region (slope is negative when and positive when ). The empirical result in Figure 8 (page 11) of [8] shows that Lemma 5 is valid as . On a side note, Lemma 5 confirms that the term structure of at-the-money approximation of implied volatility under rough Heston model has explosive behavior of order , i.e., it possesses an important feature which the classical Heston model does not possess. The presence of explosive behavior in the term structure of at-the-money implied volatility skew fits the empirical observation from [4,5]. 3.3. Limiting Behavior of Rate of Change of with Respect to T When the Option Is At-The-Money
In this section, we discuss the behavior of the rate of change of implied volatility with respect to T when and the option is at-the-money.
Lemma 6. When the option is at-the-money, the skew of the approximation of implied volatility at has the asymptotic formula of Proof. Approximation to implied volatility when the option is at-the-money can be formulated as
From Lemmas 3 and 4 and Remark 3, it is easy to see that, when the option is at-the-money (
),
. To find the rate of change of
with respect to
T, we use the definition of derivative as follows
We solve the above expression separately. The first term of the above expression can be computed using L’Hopital’s rule repetitively as follows
We have
. Then, it follows that
By Proposition 3, we have the following
as
. Hence,
as
. Finally,
as
. From the previous result in Lemma 3, we know that
as
; then, along with Proposition 2, the second term of Equation (
63) can be computed in terms of asymptotic formula
as
. Similarly, by the previous result in Lemma 3 such that
as
and Proposition 2, the third term of Equation (
63) can be computed as
Then, the result follows with the sum of three computed terms (
74)–(
76). □
Remark 5. Lemma 6 satisfies the result of from the work of Alos, Elisa and De Santiago, Rafael and Vives, Josep [19]. Furthermore, when the option is at-the-money, we can obtain a rough approximation of implied volatility in terms of T as contrary to Remark 3 which provides constant term when the option is at-the-money. An integration of the result in Equation (66) with respect to T near gives us the following approximation: 4. Numerical Experiments
Through numerical experiments, we can show that the approximation formula for the rough Heston model possesses the explosive behavior of at-the-money implied volatility skew, which is desirable in a stochastic volatility model to match the empirical implied volatility data in the market. Although Theorem 2 shows that, under Assumption 1, the approximation formula for the rough Heston model is bounded from the rough Heston model using the same set of parameters, we decided to conduct the numerical experiments using calibration approach, i.e., calibrate a new set of parameters used on approximation formula based on the artificial data given by rough Heston model. We wish to note that the components or terms of
and
can be obtained using Proposition 1. The following parameters for the rough Heston model are set:
Then, we calibrate the approximation Formula (
40) to the rough Heston model through minimizing the squared errors of implied volatility and subsequently we obtain the following parameters:
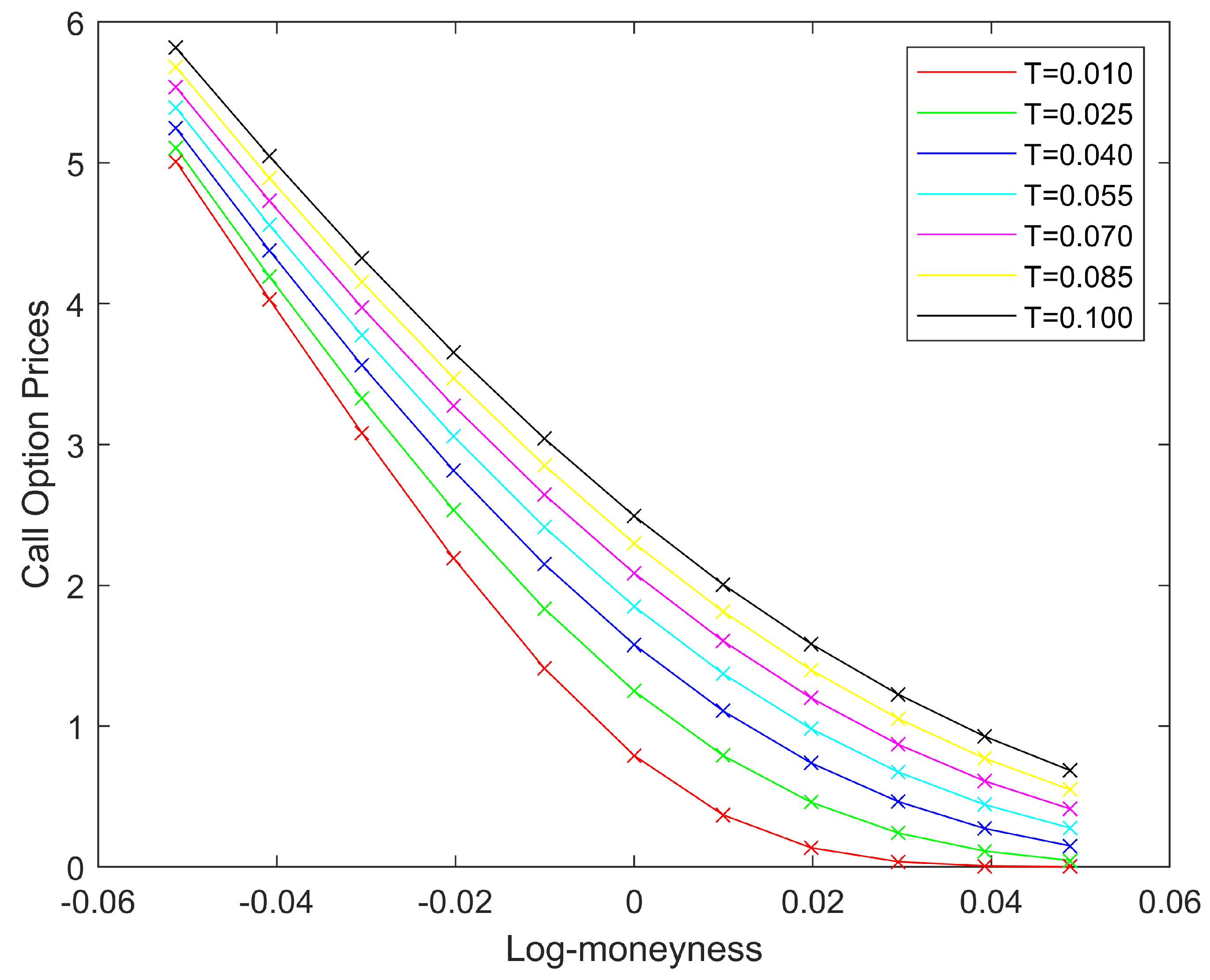
Figure 1 shows a calibrated option prices from
to
. After the calibration of the parameters, the approximation formula for option prices under the rough Heston model are capable of displaying a great fit to the option prices computed using Fourier inversion method with the fractional Adams scheme [
21], as displayed in [
11].
The implied volatility plots are shown in
Figure 2. In the plot, we can observe that the implied volatilities computed using the approximation formula (
40) match the ones produced by the Fourier inversion method with the fractional Adams scheme [
11,
21] under the rough Heston model very well, except for at
where the implied volatility is understated when the option is deep out-of-money and in-the-money.
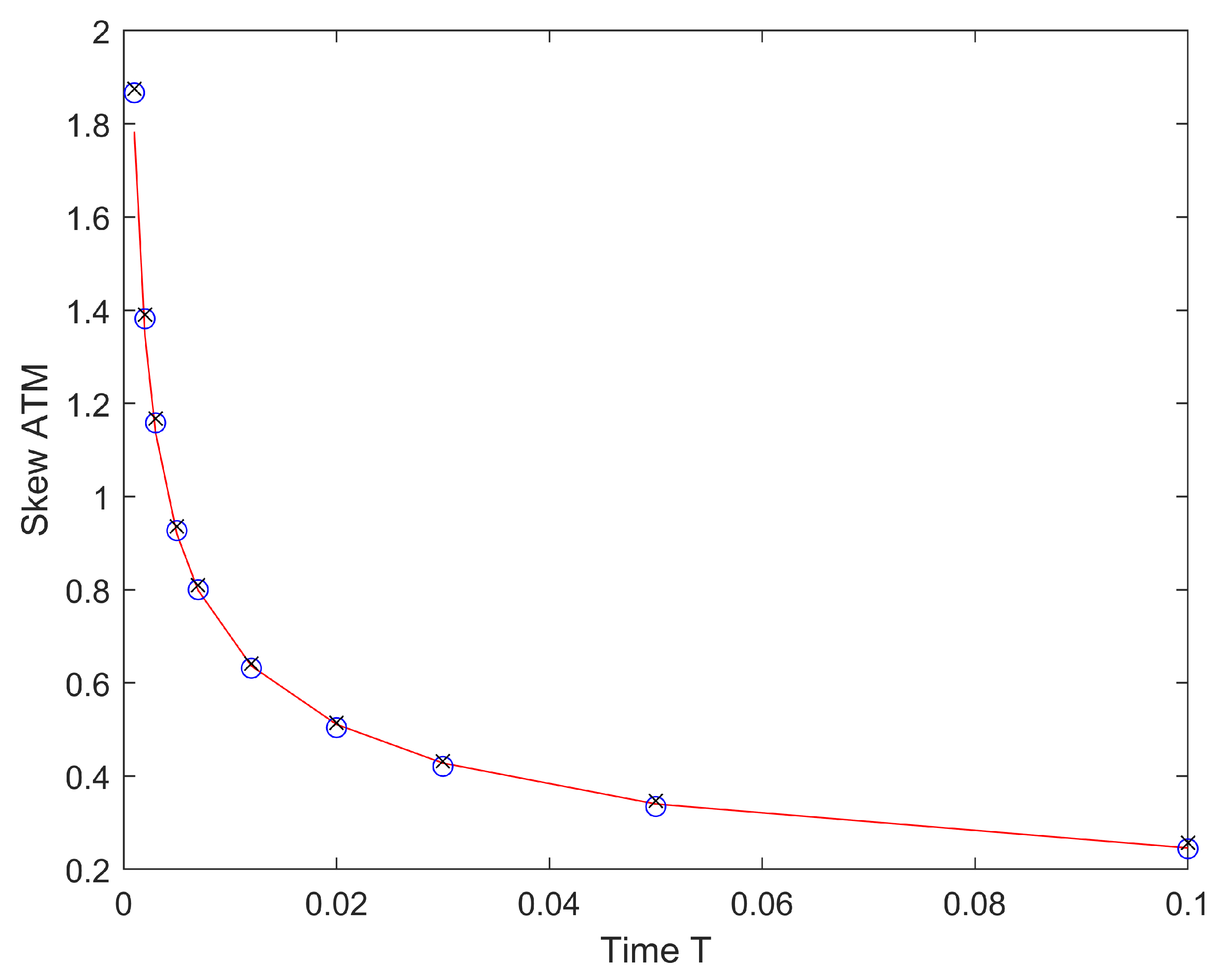
One result that sets apart from many other stochastic volatility and jump diffusion models is the short-time behavior of term-structure at-the-money implied volatility skew, i.e., derivative of implied volatility with respect to log-strike for the at-the-money call option. In
Figure 3, we display the term structure of the at-the-money implied volatility skew using three different methods—Fourier inversion method with fractional Adams scheme [
11,
21], approximation formula for option prices (
40) (transformed back to implied volatility) and Equation (
63). The result is pretty much consistent with the ones demonstrated by the approximation formula for rough Heston model (
40) and Equation (
63). Explosive behavior on the short-time term-structure of at-the-money implied volatility skew is a remarkable feature on a stochastic volatility model and the behavior is commonly observed in the empirical data in the financial market.
It is important to realize that our work is relying on Assumption 1. In terms of practical application, Assumption 1 will be fulfilled whenever the current variance process is equivalent or below the mean reversion level . In other words, the usual flat forward variance curve ( for all t) frequently used by many practitioners will satisfy Assumption 1 too. Other than that, we would say that Assumption 1 will be satisfied roughly of the time under the normal market condition.