A Flux-Limited Model for Glioma Patterning with Hypoxia-Induced Angiogenesis
Abstract
1. Introduction
2. Modeling
- variables: time , position , velocity of glioma cells , velocity of ECs ; we assume the cell speeds to be constant; denotes the unit sphere in ;
- , are unit vectors denoting the directions of vectors and , respectively;
- : (mesoscopic) density function of glioma cells and : macroscopic density of glioma;
- : (mesoscopic) density function of ECs and : macroscopic density of ECs.
- : (known) directional distribution function of tissue fibers with orientation . It holds that ; for , it holds then that ;
- : mean fiber orientation. We also denote and call it mean fiber direction;
- : variance–covariance matrix for orientation distribution of tissue fibers, and, correspondingly, ;
- : concentration of protons (acidity), a macroscopic quantity;
- : concentration of VEGF, also a macroscopic quantity;
- : constant glioma turning rate;
- : EC turning rate.
2.1. Glioma Cells
2.2. Endothelial Cells
2.3. Full Macroscopic System
3. Numerical Simulations
3.1. Nondimensionalization and Choice of Parameters
3.2. Description of Tissue
3.3. Initial Conditions
3.4. Numerical Method
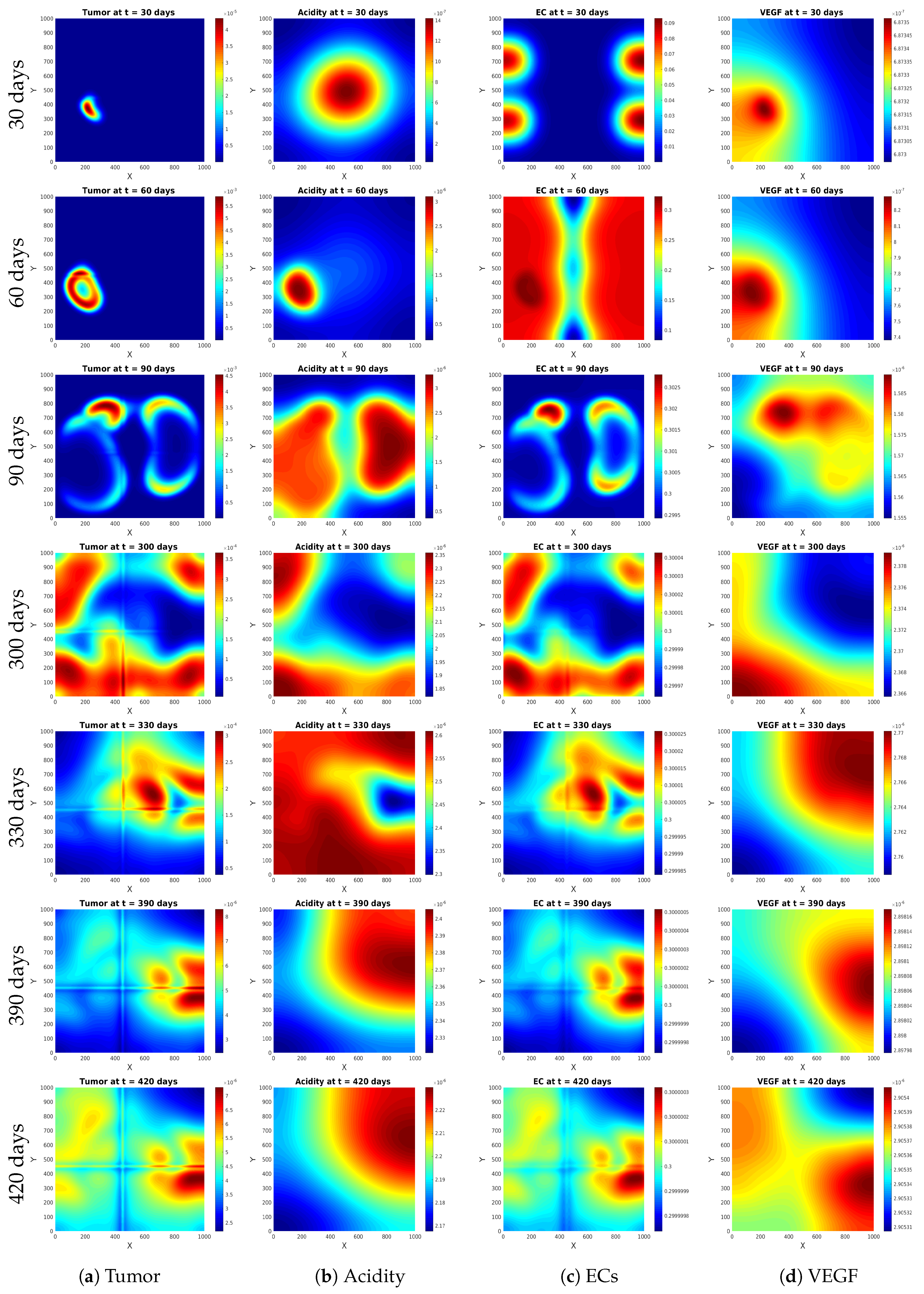
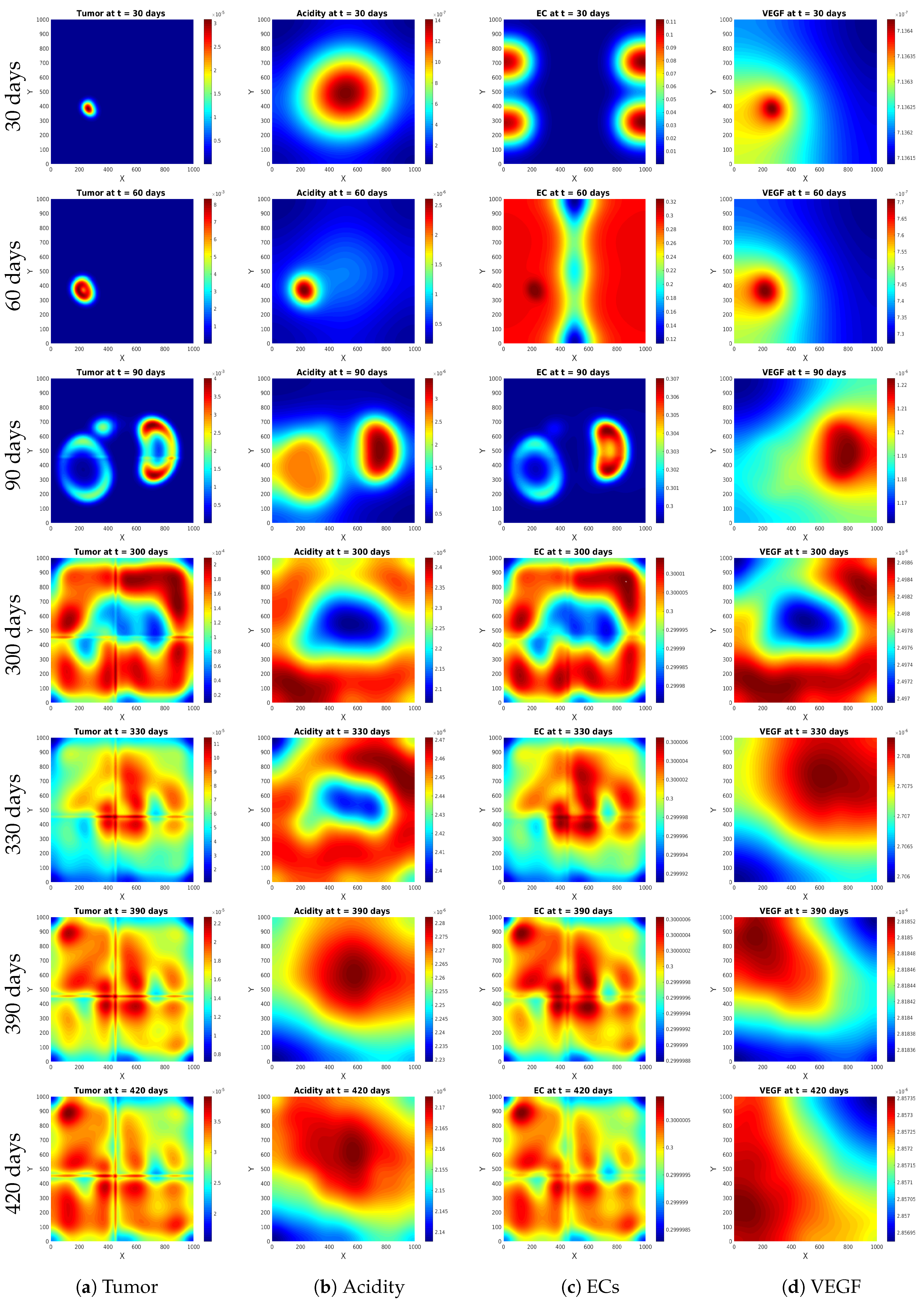
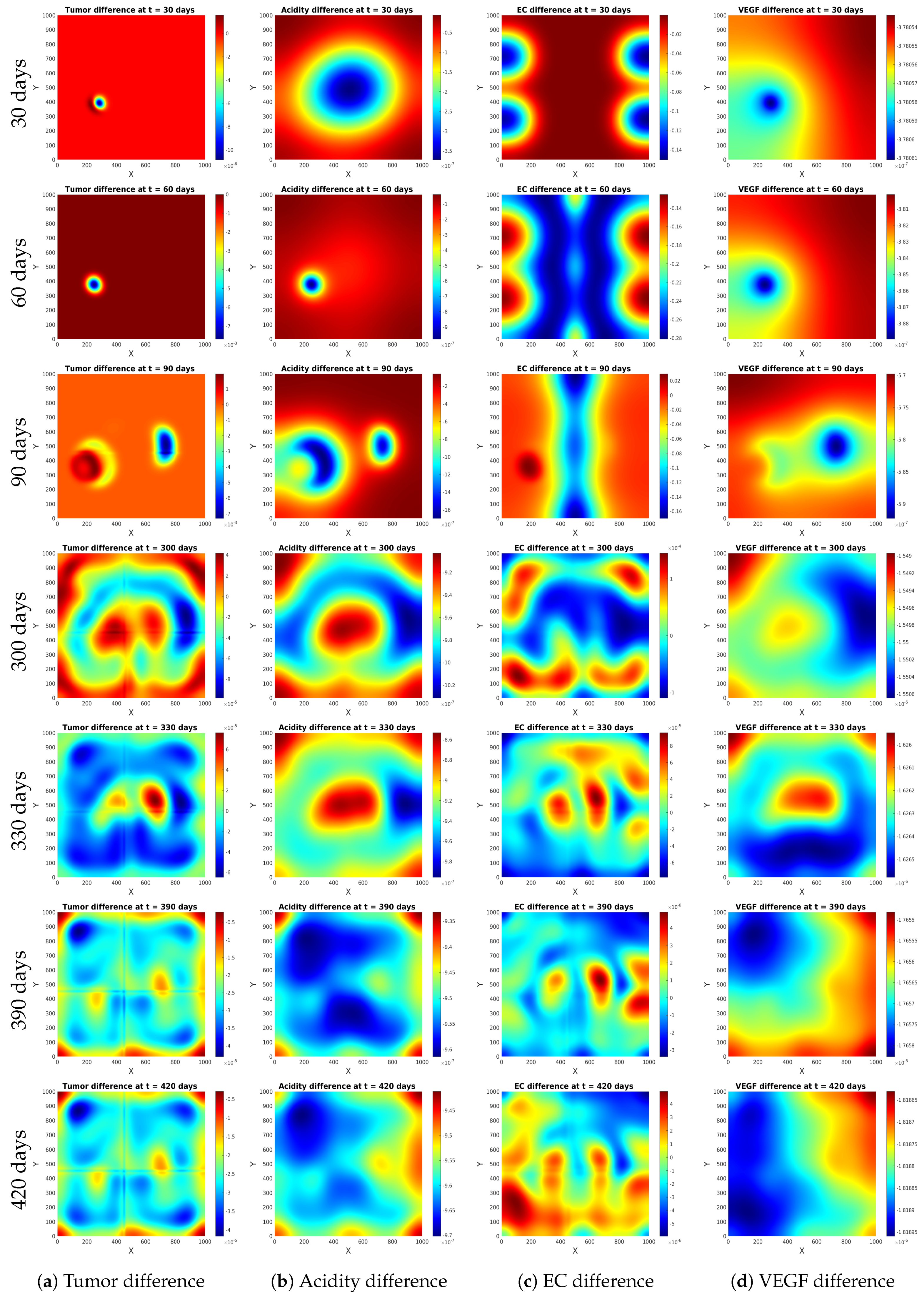
3.5. Numerical Experiments
Experiment 1
Experiment 2
Experiment 3
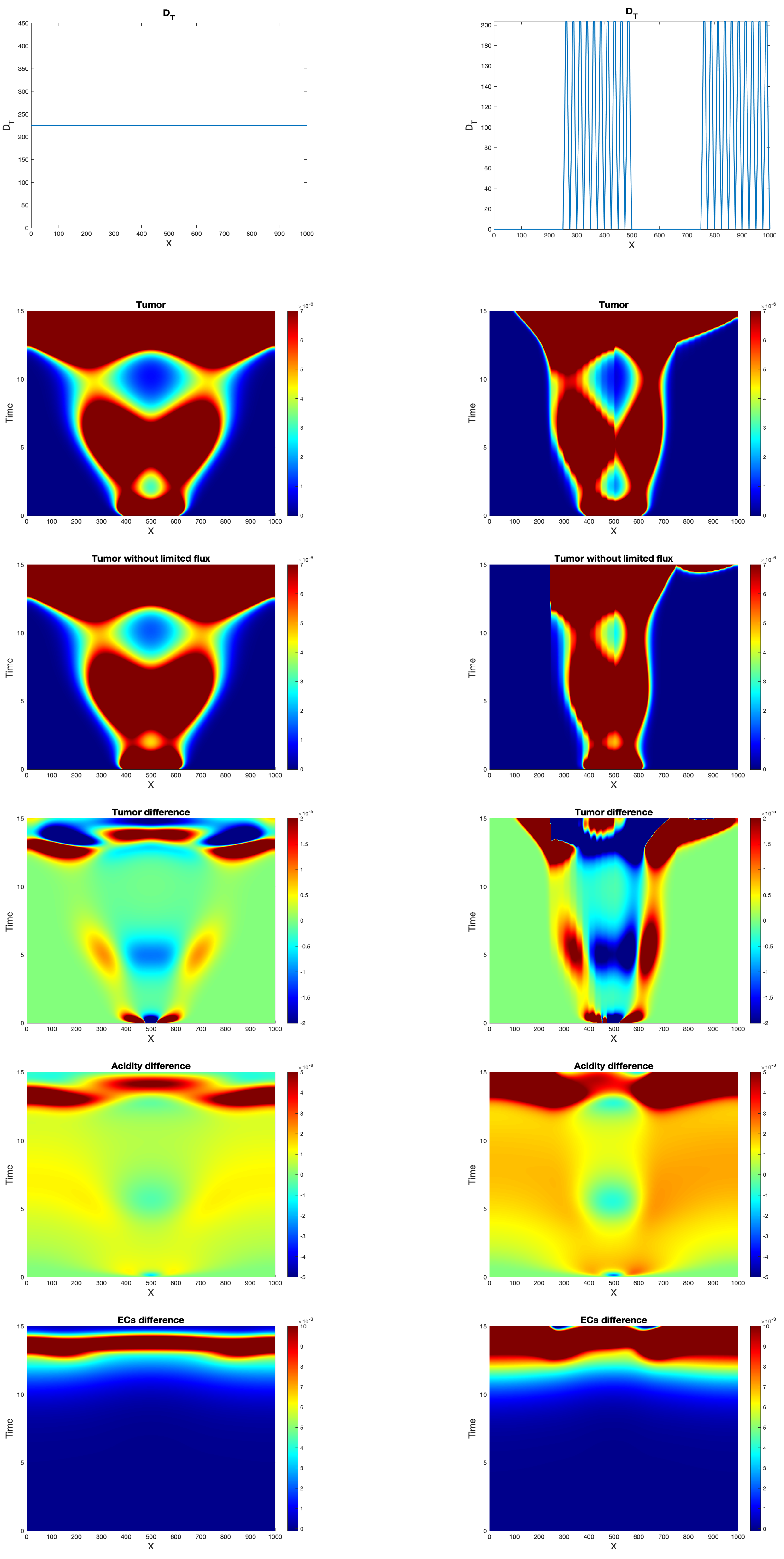
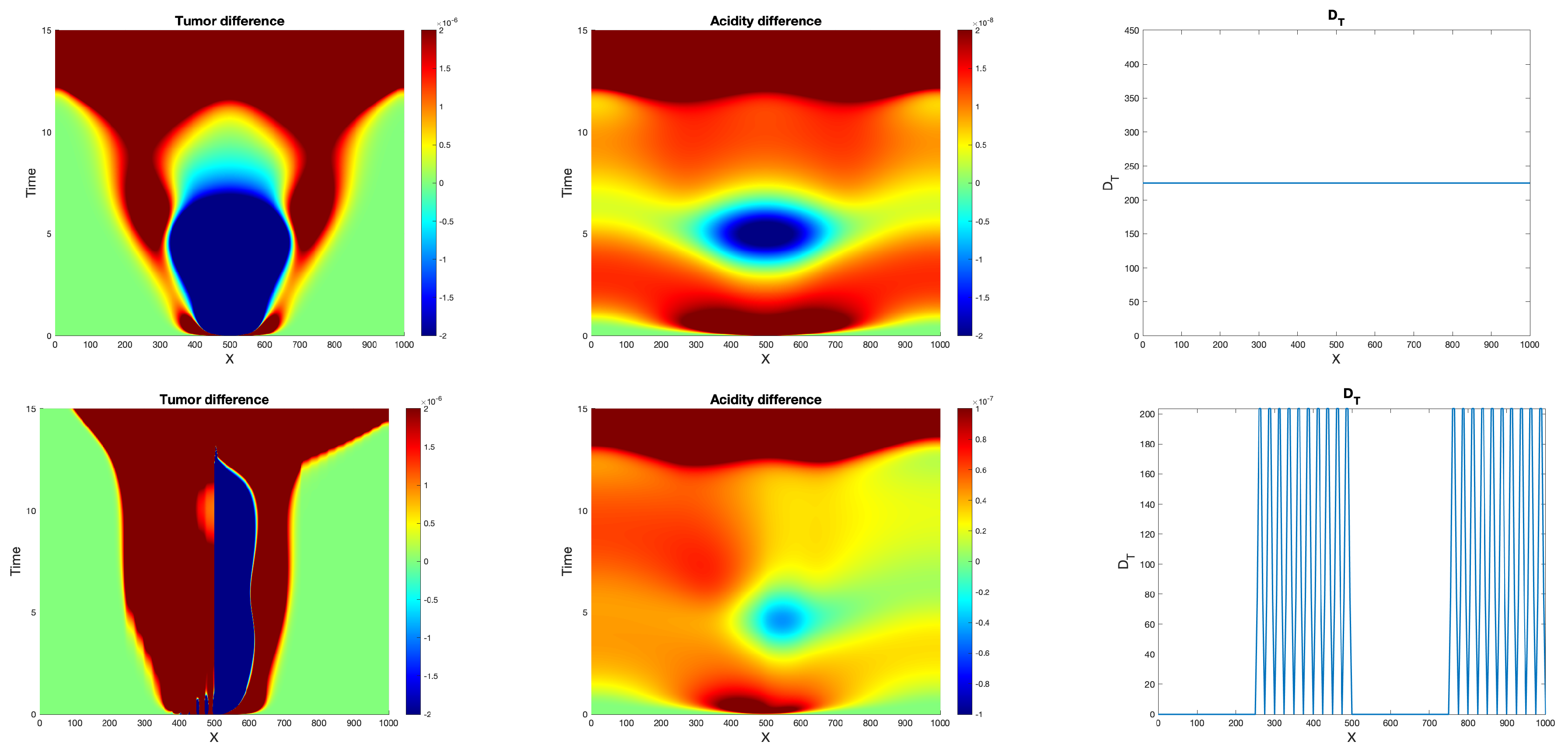
Experiment 4: Effects of flux limitations
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Kleihues, P.; Soylemezoglu, F.; Schäuble, B.; Scheithauer, B.; Burger, P. Histopathology, classification and grading of gliomas. Glia 1995, 5, 211–221. [Google Scholar] [CrossRef] [PubMed]
- Perry, A.; Wesseling, P. Histologic classification of gliomas. In Handbook of Clinical Neurology; Elsevier: Amsterdam, The Netherlands, 2016; pp. 71–95. [Google Scholar] [CrossRef]
- Brat, D.J.; Castellano-Sanchez, A.A.; Hunter, S.B.; Pecot, M.; Cohen, C.; Hammond, E.H.; Devi, S.N.; Kaur, B.; Van Meir, E.G. Pseudopalisades in glioblastoma are hypoxic, express extracellular matrix proteases, and are formed by an actively migrating cell population. Cancer Res. 2004, 64, 920–927. [Google Scholar] [CrossRef] [PubMed]
- Brat, D.J.; Van Meir, E.G. Vaso-occlusive and prothrombotic mechanisms associated with tumor hypoxia, necrosis, and accelerated growth in glioblastoma. Lab. Investig. 2004, 84, 397–405. [Google Scholar] [CrossRef] [PubMed]
- Rong, Y.; Durden, D.L.; Van Meir, E.G.; Brat, D.J. ‘Pseudopalisading’ necrosis in glioblastoma: A familiar morphologic feature that links vascular pathology, hypoxia, and angiogenesis. J. Neuropathol. Exp. Neurol. 2006, 65, 529–539. [Google Scholar] [CrossRef] [PubMed]
- Wippold, F.; Lämmle, M.; Anatelli, F.; Lennerz, J.; Perry, A. Neuropathology for the neuroradiologist: Palisades and pseudopalisades. Am. J. Neuroradiol. 2006, 27, 2037–2041. [Google Scholar] [PubMed]
- Tate, M.C.; Aghi, M.K. Biology of angiogenesis and invasion in glioma. Neurotherapeutics 2009, 6, 447–457. [Google Scholar] [CrossRef]
- Onishi, M.; Ichikawa, T.; Kurozumi, K.; Date, I. Angiogenesis and invasion in glioma. Brain Tumor Pathol. 2011, 28, 13–24. [Google Scholar] [CrossRef]
- Brat, D.J.; Castellano-Sanchez, A.; Kaur, B.; Van Meir, E.G. Genetic and biologic progression in astrocytomas and their relation to angiogenic dysregulation. Adv. Anat. Pathol. 2002, 9, 24–36. [Google Scholar] [CrossRef]
- Batchelor, T.T.; Reardon, D.A.; de Groot, J.F.; Wick, W.; Weller, M. Antiangiogenic Therapy for Glioblastoma: Current Status and Future Prospects. Clin. Cancer Res. 2014, 20, 5612–5619. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, K.; Wang, J.; Li, X.; Zhao, P. Chemoresistance caused by the microenvironment of glioblastoma and the corresponding solutions. Biomed. Pharmacother. 2019, 109, 39–46. [Google Scholar] [CrossRef]
- Martirosyan, N.; Rutter, E.; Ramey, W.; Kostelich, E.; Kuang, Y.; Preul, M. Mathematically modeling the biological properties of gliomas: A review. Math. Biosci. Eng. 2015, 12, 879–905. [Google Scholar] [CrossRef] [PubMed]
- Alfonso, J.C.L.; Talkenberger, K.; Seifert, M.; Klink, B.; Hawkins-Daarud, A.; Swanson, K.R.; Hatzikirou, H.; Deutsch, A. The biology and mathematical modelling of glioma invasion: A review. J. R. Soc. Interface 2017, 14, 20170490. [Google Scholar] [CrossRef] [PubMed]
- Hatzikirou, H.; Deutsch, A.; Schaller, C.; Simon, M.; Swanson, K. Mathematical Modeling of Glioblastoma Tumor Development: A Review. Math. Model. Methods Appl. Sci. 2005, 15, 1779–1794. [Google Scholar] [CrossRef]
- Cai, Y.; Wu, J.; Li, Z.; Long, Q. Mathematical modelling of a brain tumour initiation and early development: A coupled model of glioblastoma growth, pre-existing vessel co-option, angiogenesis and blood perfusion. PLoS ONE 2016, 11, e0150296. [Google Scholar] [CrossRef] [PubMed]
- Caiazzo, A.; Ramis-Conde, I. Multiscale modelling of palisade formation in gliobastoma multiforme. J. Theor. Biol. 2015, 383, 145–156. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Li, J.; Surulescu, C. Multiscale modeling of glioma pseudopalisades: Contributions from the tumor microenvironment. arXiv 2020, arXiv:2007.05297. [Google Scholar]
- Alfonso, J.; Köhn-Luque, A.; Stylianopoulos, T.; Feuerhake, F.; Deutsch, A.; Hatzikirou, H. Why one-size-fits-all vaso-modulatory interventions fail to control glioma invasion: In silico insights. Sci. Rep. 2016, 6, 37283. [Google Scholar] [CrossRef]
- Martínez-González, A.; Calvo, G.; Pérez Romasanta, L.; Pérez-García, V. Hypoxic cell waves around necrotic cores in glioblastoma: A biomathematical model and its therapeutic implications. Bull. Math. Biol. 2012, 74, 2875–2896. [Google Scholar] [CrossRef]
- Bellomo, N.; Bellouquid, A.; Gibelli, L.; Outada, N. A Quest Towards a Mathematical Theory of Living Systems; Birkhäuser: Basel, Switzerland, 2017. [Google Scholar]
- Chauvière, A.; Hillen, T.; Preziosi, L. Modeling cell movement in anisotropic and heterogeneous network tissues. Netw. Heterog. Media 2007, 2, 333. [Google Scholar] [CrossRef]
- Conte, M.; Surulescu, C. Mathematical modeling of glioma invasion: Acid-and vasculature mediated go-or-grow dichotomy and the influence of tissue anisotropy. arXiv 2020, arXiv:2007.12204. [Google Scholar]
- Corbin, G.; Engwer, C.; Klar, A.; Nieto, J.; Soler, J.; Surulescu, C.; Wenske, M. Modeling glioma invasion with anisotropy-and hypoxia-triggered motility enhancement: From subcellular dynamics to macroscopic PDEs with multiple taxis. arXiv 2020, arXiv:2006.12322. [Google Scholar] [CrossRef]
- Corbin, G.; Hunt, A.; Klar, A.; Schneider, F.; Surulescu, C. Higher-order models for glioma invasion: From a two-scale description to effective equations for mass density and momentum. Math. Model. Methods Appl. Sci. 2018, 28, 1771–1800. [Google Scholar] [CrossRef]
- Dietrich, A.; Kolbe, N.; Sfakianakis, N.; Surulescu, C. Multiscale modeling of glioma invasion: From receptor binding to flux-limited macroscopic PDEs. arXiv 2020, arXiv:2010.03277. [Google Scholar]
- Engwer, C.; Hillen, T.; Knappitsch, M.; Surulescu, C. Glioma follow white matter tracts: A multiscale DTI-based model. J. Math. Biol. 2015, 71, 551–582. [Google Scholar] [CrossRef] [PubMed]
- Engwer, C.; Knappitsch, M.; Surulescu, C. A multiscale model for glioma spread including cell-tissue interactions and proliferation. Math. Biosci. Eng. 2016, 13, 443–460. [Google Scholar] [CrossRef]
- Engwer, C.; Hunt, A.; Surulescu, C. Effective equations for anisotropic glioma spread with proliferation: A multiscale approach and comparisons with previous settings. Math. Med. Biol. A J. IMA 2016, 33, 435–459. [Google Scholar] [CrossRef]
- Hillen, T. M 5 mesoscopic and macroscopic models for mesenchymal motion. J. Math. Biol. 2006, 53, 585–616. [Google Scholar] [CrossRef]
- Hillen, T.; Painter, K.J. Transport and anisotropic diffusion models for movement in oriented habitats. In Dispersal, Individual Movement and Spatial Ecology; Springer: Berlin/Heidelberg, Germany, 2013; pp. 177–222. [Google Scholar]
- Hunt, A.; Surulescu, C. A multiscale modeling approach to glioma invasion with therapy. Vietnam. J. Math. 2017, 45, 221–240. [Google Scholar] [CrossRef]
- Zhigun, A.; Surulescu, C. A novel derivation of rigorous macroscopic limits from a micro-meso description of signal-triggered cell migration in fibrous environments. arXiv 2020, arXiv:2010.04148. [Google Scholar]
- Aylaj, B.; Bellomo, N.; Chouhad, N.; Knopoff, D. On the Interaction Between Soft and Hard Sciences: The Role of Mathematical Sciences. Vietnam. J. Math. 2020. [Google Scholar] [CrossRef]
- Painter, K.; Hillen, T. Mathematical modelling of glioma growth: The use of Diffusion Tensor Imaging (DTI) data to predict the anisotropic pathways of cancer invasion. J. Theor. Biol. 2013, 323, 25–39. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://bionumbers.hms.harvard.edu/bionumber.aspx?s=n&v=0&id=108941 (accessed on 17 July 2020).
- Webb, B.; Chimenti, M.; Jacobson, M.; Barber, D. Dysregulated pH: A perfect storm for cancer progression. Nat. Rev. Cancer 2011, 11, 671–677. [Google Scholar] [CrossRef] [PubMed]
- Diao, W.; Tong, X.; Yang, C.; Zhang, F.; Bao, C.; Chen, H.; Liu, L.; Li, M.; Ye, F.; Fan, Q.; et al. Behaviors of glioblastoma cells in in vitro microenvironments. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Prag, S.; Lepekhin, E.; Kolkova, K.; Hartmann-Petersen, R.; Kawa, A.; Walmod, P.; Belman, V.; Gallagher, H.; Berezin, V.; Bock, E.; et al. NCAM regulates cell motility. J. Cell Sci. 2002, 115, 283–292. [Google Scholar]
- Sidani, M.; Wessels, D.; Mouneimne, G.; Ghosh, M.; Goswami, S.; Sarmiento, C.; Wang, W.; Kuhl, S.; El-Sibai, M.; Backer, J.; et al. Cofilin determines the migration behavior and turning frequency of metastatic cancer cells. J. Cell Biol. 2007, 179, 777–791. [Google Scholar] [CrossRef]
- Martin, G.; Jain, R. Noninvasive Measurement of Interstitial pH Profiles in Normal and Neoplastic Tissue Using Fluorescence Ratio Imaging Microscopy. Cancer Res. 1994, 54, 5670–5674. [Google Scholar]
- Stein, A.; Demuth, T.; Mobley, D.; Berens, M.; Sander, L. A mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro experiment. Biophys. J. 2007, 92, 356–365. [Google Scholar] [CrossRef]
- Eikenberry, S.; Sankar, T.; Preul, M.; Kostelich, E.; Thalhauser, C.; Kuang, Y. Virtual glioblastoma: Growth, migration and treatment in a three-dimensional mathematical model. Cell Prolif. 2009, 42, 511–528. [Google Scholar] [CrossRef]
- Czirok, A. Endothelial cell motility, coordination and pattern formation during vasculogenesis. Wiley Interdiscip. Rev. Syst. Biol. Med. 2013, 5, 587–602. [Google Scholar] [CrossRef]
- Available online: https://www.lab.anhb.uwa.edu.au/mb140/MoreAbout/Endothel.htm (accessed on 22 June 2020).
- Plank, M.; Sleeman, B.; Jones, P. A mathematical model of tumour angiogenesis, regulated by vascular endothelial growth factor and the angiopoietins. J. Theor. Biol. 2004, 229, 435–454. [Google Scholar] [CrossRef]
- Shamsi, M.; Saghafian, M.; Dejam, M.; Sanati-Nezhad, A. Mathematical modeling of the function of Warburg effect in tumor microenvironment. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Gevertz, J.L.; Torquato, S. Modeling the effects of vasculature evolution on early brain tumor growth. J. Theor. Biol. 2006, 243, 517–531. [Google Scholar] [CrossRef] [PubMed]
- Weickert, J. Anisotropic Diffusion in Image Processing; Teubner Stuttgart: Stuttgart, Germany, 1998; Volume 1. [Google Scholar]
- Burini, D.; Chouhad, N. A multiscale view of nonlinear diffusion in biology: From cells to tissues. Math. Model. Methods Appl. Sci. 2019, 29, 791–823. [Google Scholar] [CrossRef]
- Bellomo, N.; Bellouquid, A.; Nieto, J.; Soler, J. Multiscale biological tissue models and flux-limited chemotaxis for multicellular growing systems. Math. Models Methods Appl. Sci. 2010, 20, 1179–1207. [Google Scholar] [CrossRef]
- Perthame, B.; Vauchelet, N.; Wang, Z. The Flux Limited Keller-Segel System; Properties and Derivation from Kinetic Equations. arXiv 2018, arXiv:1801.07062. [Google Scholar] [CrossRef]
- Conte, M.; Casas-Tintò, S.; Soler, J. Modeling invasion patterns in the glioblastoma battlefield. bioRxiv 2020. [Google Scholar] [CrossRef]
- Kim, Y.; Lawler, S.; Nowicki, M.; Chiocca, E.; Friedman, A. A mathematical model for pattern formation of glioma cells outside the tumor spheroid core. J. Theor. Biol. 2009, 260, 359–371. [Google Scholar] [CrossRef]
- Hillen, T.; Painter, K.; Winkler, M. Anisotropic diffusion in oriented environments can lead to singularity formation. Eur. J. Appl. Math. 2013, 24, 371–413. [Google Scholar] [CrossRef]
- Winkler, M.; Surulescu, C. Global weak solutions to a strongly degenerate haptotaxis model. Comm. Math. Sci. 2017, 15, 1581–1616. [Google Scholar] [CrossRef]
- Winkler, M. Singular structure formation in a degenerate haptotaxis model involving myopic diffusion. J. Math. Pures Appl. 2018, 112, 118–169. [Google Scholar] [CrossRef]
- Bellomo, N.; Winkler, M. Finite-time blow-up in a degenerate chemotaxis system with flux limitation. Trans. Am. Math. Soc. Ser. B 2017, 4, 31–67. [Google Scholar] [CrossRef]
- Bellomo, N.; Winkler, M. A degenerate chemotaxis system with flux limitation: Maximally extended solutions and absence of gradient blow-up. Comm. Partial. Differ. Equ. 2017, 42, 436–473. [Google Scholar] [CrossRef]
- Kolbe, N.; Sfakianakis, N.; Stinner, C.; Surulescu, C.; Lenz, J. Modeling multiple taxis: Tumor invasion with phenotypic heterogeneity, haptotaxis, and unilateral interspecies repellence. Discret. Contin. Dyn. Syst. B 2020. [Google Scholar] [CrossRef]


| Parameter | Meaning | Value | Reference |
|---|---|---|---|
| glioma carrying capacity | 0.3–0.8 | this work, [35] | |
| acidity threshold for cancer cell death | [36] | ||
| s | speed of glioma cells | 15–20 | [37,38] |
| turning frequency coefficient | 360/h | [26,39] | |
| proton production rate | mol/(L·h) | this work, [40] | |
| proton removal rate | –3.6 /h | this work | |
| acidity diffusion coefficient | –3.6 m/h | this work, [17] | |
| glioma growth/decay rate, influenced by acidity | (4.16–8.3) /h | [41,42] | |
| glioma growth rate, influenced by ECs | (3–3.95) /h | this work | |
| advection constant | [23] | ||
| weight coefficient related to acidic stress | –3 /m | this work | |
| weight coefficient related to cell population pressure | –/m | this work | |
| speed of ECs | 15–20 m/h | [22,43] | |
| turning rate of ECs | 36/h | this work | |
| EC proliferation rate | (1.25–2.08) /h | this work, [22] | |
| coefficient of chemotactic sensitivity of ECs | 0.72–21.6 h | this work | |
| carrying capacity of ECs | 0.1–0.3 cells/m | this work, [44] | |
| diffusion coefficient of VEGF | –m/h | [45,46] | |
| VEGF threshold value | – mol/L | this work, [47] | |
| VEGF production rate | mol/(L·h) | [45] | |
| VEGF uptake rate | –3.6/h | this work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.; Surulescu, C. A Flux-Limited Model for Glioma Patterning with Hypoxia-Induced Angiogenesis. Symmetry 2020, 12, 1870. https://doi.org/10.3390/sym12111870
Kumar P, Surulescu C. A Flux-Limited Model for Glioma Patterning with Hypoxia-Induced Angiogenesis. Symmetry. 2020; 12(11):1870. https://doi.org/10.3390/sym12111870
Chicago/Turabian StyleKumar, Pawan, and Christina Surulescu. 2020. "A Flux-Limited Model for Glioma Patterning with Hypoxia-Induced Angiogenesis" Symmetry 12, no. 11: 1870. https://doi.org/10.3390/sym12111870
APA StyleKumar, P., & Surulescu, C. (2020). A Flux-Limited Model for Glioma Patterning with Hypoxia-Induced Angiogenesis. Symmetry, 12(11), 1870. https://doi.org/10.3390/sym12111870





