Tetra- and Penta-Quark Structures in the Constituent Quark Model

Abstract

With the development of high energy physics experiments, a large amount of exotic states in the hadronic sector have been observed. In order to shed some light on the nature of the tetraquark and pentaquark candidates, a constituent quark model, along with the Gaussian expansion method, has been employed systematically in real- and complex-range investigations. We review herein the double- and fully-heavy tetraquarks, but also the hidden-charm, hidden-bottom and doubly charmed pentaquarks. Several exotic hadrons observed experimentally were well reproduced within our approach; moreover, their possible compositeness and other properties, such as their decay widths and general patterns in the spectrum, are analyzed. Besides, we report also some theoretical predictions of tetra- and penta-quark states which have not seen by experiment yet.

1. Introduction

A large number of conventional hadrons, baryons (three quarks) and mesons (quark-antiquark) are described well within a constituent quark model picture [1,2,3], which was first proposed by M. Gell-Mann in 1964 [4]. However, with decades of experimental efforts in high energy physics, many exotic states have been observed by different collaborations such as BABAR, Belle, BES, CDF, CLEO-c, LHCb, etc. A remarkable example is the $X(3872)$, which was announced by the Belle collaboration in 2003 [5] looking at the $B^{\pm }\to K^{\pm }{\pi }^{+}{\pi }^{-}J/\psi$ decay. Soon after, the CDF [6], D0 [7] and BABAR [8] collaborations confirmed the existence of this charmonium-like state. Less than twenty years have passed since the discovery of the $X(3872)$ state and dozens of so-called XYZ particles have been observed worldwide in B factories, $\tau$-charm facilities and hadron–hadron colliders. Some examples are the $Y(3940)$ discovered by the Belle collaboration when analyzing the $\omega J/\psi$ invariant mass spectrum in 2004 [9]; the charged charmonium-like state $Z^{+}(4430)$ observed in the $B\to K{\pi }^{\pm }\psi (3686)$ decay by the same collaboration in 2008 [10]; and the $Y(4260)$ signal found in the $e^{+}{e}^{-}\to \gamma {\pi }^{+}{\pi }^{-}J/\psi$ channel by the BABAR collaboration in 2005 [11], and confirmed later by the CLEO [12] and Belle [13] collaborations within the same decay process. The interested reader is directed to the Review of Particle Physics (RPP) [14] where other exotic states as $Y(4140)$, $Y(4274)$, $Z^{+}(4051)$, $Z^{+}(4200)$, etc., are collected by the Particle Data Group.

Continuing with the interest of meson-like structures, the discovery of a fully heavy 4-body system $QQ\overline{Q}\overline{Q}$ is quite appealing. In 2017, a benchmark measurement of the $\mathsf{{\rm Y}}(1S)$ pair production at $\sqrt{s}$ = 8 TeV in $pp$ collision was implemented by the CMS collaboration [15], and an excess at 18.4 GeV in the $\mathsf{{\rm Y}}{\mathsf{\ell }}^{+}{\mathsf{\ell }}^{-}$ decay channel was proposed in a subsequent preliminary investigation using the CMS data [16,17,18]. Moreover, a significant peak at ∼$18.2\mathrm{GeV}$ was also seen in Cu+Au collisions at RHIC [19]. However, no evidence has been found in the $\mathsf{{\rm Y}}(1S){\mu }^{+}{\mu }^{-}$ invariant mass spectrum by the LHCb collaboration [20]. Hence, more experiments are needed in order to confirm the fully-bottom tetraquark signal. Nevertheless, a fully-charm narrow structure at 6.9 GeV and a broad one around $6.2$∼$6.8\mathrm{GeV}$ have been recently reported in the di-$J/\psi$ invariant mass spectrum by the LHCb collaboration [21].

The number of achievements within the baryon sector are quite remarkable. In 2015, the LHCb Collaboration reported the observation of two hidden-charm pentaquark states in the $J/\psi p$ invariant mass spectrum through the ${\mathsf{\Lambda }}_b^0\to J/\psi K^{-}p$ decay [22]. One state was labeled as $P_c{(4380)}^{+}$ whose mass and width were, respectively, $(4380\pm 8\pm 29)\mathrm{MeV}$ and $(205\pm 18\pm 86)\mathrm{MeV}$; the other one was called $P_c{(4450)}^{+}$ with mass and width $(4449.8\pm 1.7\pm 2.5)\mathrm{MeV}$ and $(39\pm 5\pm 19)\mathrm{MeV}$. These resonances were confirmed by the same collaboration in a subsequent model-independent study [23]. Only few years later, with much more statistics in the same decay channel, the LHCb collaboration [24] observed that the structure at 4450 MeV was resolved into two narrow peaks at 4440 and 4457 MeV. Accordingly, these two pentaquark states were marked as $P_c^{+}(4440)$ and $P_c^{+}(4457)$ whose total widths are $20.6\pm {4.9}_{-10.1}^{+8.7}\mathrm{MeV}$ and $6.4\pm {2.0}_{-1.9}^{+5.7}\mathrm{MeV}$, respectively. Besides, a new narrow pentaquark $P_c^{+}(4312)$ ($\mathsf{\Gamma }=9.8\pm {2.7}_{-4.5}^{+3.7}\mathrm{MeV}$) was also reported. Meanwhile, according to the $b\to c\overline{c}s$ weak decay process, b-flavored pentaquark states were searched in the final states $J/\psi K^{+}{\pi }^{-}p$, $J/\psi K^{-}{\pi }^{-}p$, $J/\psi K^{-}{\pi }^{+}p$, and $J/\psi \varphi p$ by the LHCb collaboration [25].

These prominent experimental findings triggered extensive theoretical investigations on the multiquark systems. Firstly, in the double-heavy tetraquarks sector, the di-meson with $bb\overline{u}\overline{d}$ constituents had already been proposed [26] in 1988. After then, a narrow $bb\overline{u}\overline{d}$ tetraquark state with mass $10389\pm 12\mathrm{MeV}$ and quantum numbers $J^P=1^{+}$ was obtained in Ref. [27] using a theoretical framework based on heavy quark limit [28]. This exotic state is also supported by dynamical quark model studies [29,30,31]. Additionally, Ref. [32] calculated $bb\overline{u}\overline{d}$ masses, lifetimes and decay modes within a quark model formalism. Furthermore, the double-bottom tetraquark state with $I(J^P)=0(1^{+})$ is also predicted by a relativistic quark model [33]. Reference [34] gives some indications on where to find it in heavy-ion collisions at the LHC. For the antiparticle case, the $\overline{b}\overline{b}ud$ bound state is stable against strong decays, Lattice QCD [35] predicted a mass of $10476\pm 24\pm 10\mathrm{MeV}$ and spin-parity $J^P=1^{+}$. This deeply bound tetraquark state is also supported by investigations using the same formalism in Refs. [36,37]. Other kinds of open-flavor tetraquarks have been investigated too; the $bc\overline{u}\overline{d}$ axial-vector tetraquark is predicted at $7105\pm 155\mathrm{MeV}$ using QCD sum rules [38] and the $I(J^P)=0(1^{+})$$ub\overline{c}\overline{d}$ tetraquark state with binding energy between 15 and $61\mathrm{MeV}$ with respect to the $\overline{D}{B}^{\ast }$ threshold is claimed in Ref. [39]. Additionally, there are also extensive proposals [40,41,42,43,44,45,46,47,48,49,50,51,52] on the explorations of $QQ\overline{q}\overline{q}$ states experimentally. Decay properties of open-bottom and doubly heavy tetraquarks are investigated in [53,54,55,56,57]; the production of double-heavy tetraquarks at a future Tera-Z factory and at the LHC is estimated by Monte Carlo simulations in Refs. [58,59]. Finally, possible $QQ\overline{s}\overline{s}$ tetraquark structures have been recently investigated within the chiral quark model [60,61].

The debates on fully-heavy tetraquarks are even more intense. Numerous theoretical investigations using very different approaches expect the experimental confirmation of $QQ\overline{Q}\overline{Q}$ tetraquark states. In particular, the fully-charm and hidden-bottom tetraquarks are the most studied sectors. For instance, the ground state of $bb\overline{b}\overline{b}$ tetraquarks mass is $18.72\pm 0.02\mathrm{GeV}$ considering a non-relativistic effective field theory investigation [62]. Similarly, masses of fully-bottom tetraquarks with quantum numbers $0^{+}$ and $2^{+}$ are suggested to be ∼$18.8\mathrm{GeV}$ in QCD sum rules [63]. Note, too, that the predicted $J^P=0^{+}$$bb\overline{b}\overline{b}$ state was confirmed by a diffusion Monte Carlo approach [64] and by a symmetry analysis [65]. The existence of $bb\overline{b}\overline{b}$ tetraquark is supported by the relativized quark model [66], the non-relativistic quark model [67] and QCD sum rules [68]. This tetraquark state was estimated to be around $0.1\mathrm{GeV}$ below threshold in diquark–antidiquark configuration [69]. Very recently, we also performed a systematic study of the $QQ\overline{Q}\overline{Q}$ tetraquark states using an effective potential model [70] based on the results of lattice QCD investigations of heavy quark pairs [71], a possible hint of deeply bound $bb\overline{b}\overline{b}$ tetraquark states around $18.0\mathrm{GeV}$ is found.

The fully-charm tetraquark sector has acquire even more attention due to the recent report by the LHCb collaboration of a new structure at $6.9\mathrm{GeV}$ and another broad one around $6.2$∼$6.8\mathrm{GeV}$ in the di-$J/\psi$ invariant mass spectrum [21]; besides, there is also the hint of a structure ∼7.2 GeV. Actually, the possibility of finding $cc\overline{c}\overline{c}$ tetraquarks in the cross section of $pp\to 2J/\psi +X$ at $\sqrt{s}=7\mathrm{TeV}$ was already investigated in Ref. [72]. Additionally, searching for the fully-heavy tetraquark states are valuable theoretically from the view point of Ref. [73]. A narrow $cc\overline{c}\overline{c}$ tetraquark resonance in the mass region 5–6 GeV was predicted by the Bethe-Salpeter formalism [74], fully-charm tetraquarks with quantum numbers $0^{+}$ and $2^{+}$ at a mass of ∼$6.0\mathrm{GeV}$ were predicted in QCD sum rules [63,65], and similar conclusions can be found Refs. [67,75] using a non-relativistic quark model. In recent theoretical investigations, the mass of the S-wave $cc\overline{c}\overline{c}$ tetraquark within an energy region from 5.96 to 6.32 GeV was determined using a non-relativistic diquark–antidiquark model [76]. Besides, the two structures at 6.5 and 6.9 GeV were identified as the S- and P-wave fully-charm tetraquarks in a potential model [77]. However, a quite opposite conclusion was obtained in a dynamical study by means of a diquark model [78]. Furthermore, the assignment of the two structues as radial excitations is favored by QCD sum rules [79], relativized quark model [80] and the string junction picture [81]. In the constituent quark model [70,82], the spin-parity of the structure at 6.9 GeV is suggested to be $2^{+}$. Molecular configurations for these two structures were proposed by perturbation QCD [83]; however, a compact tetraquark structure was obtained in the holography inspired stringy hadron model [84]. Meanwhile, the experimental data and theoretical importance of the $cc\overline{c}\overline{c}$ tetraquarks were reviewed in the articles [85,86]. Apart from the spectrum of fully-charm tetraquarks, their strong decay properties [87], produced via $\overline{p}p$ annihilation reaction [88] and dynamical simulation [89], were also extensively investigated.

Many quark model based investigations related with the existence of a bound state in fully-charm and hidden-bottom tetraquarks deserve to be cited such as [50,90,91,92,93,94]; there is also lattice QCD calculations as, for instance, Ref. [95]. Finally, possible stable or narrow states in the $bb\overline{b}\overline{c}$ and $bc\overline{b}\overline{c}$ sectors were made available by quark models studies [90,91]. The features of color-magnetic and Coulomb interactions, along with different color configurations within the fully-heavy tetraquark states, were studied in reference [96] by various models. In addition, the charmonium-like and bottomonium-like states $Z_c(3900)$, $Z_c(4020)$, $Z_b(10610)$ and $Z_b(10650)$ are well identified as the $D^{(\ast )}{\overline{D}}^{\ast }$ and $B^{(\ast )}{\overline{B}}^{\ast }$ molecular resonances, respectively, in a chiral effective field theory study [97].

As for the single heavy tetraquark states, the LHCb collaboration recently reported two structures, $X_0(2900)$ and $X_1(2900)$, in the $B^{\pm }\to D^{+}{D}^{-}{K}^{\pm }$ decay channel analyzed with model-depend [98] and model-independent [99] assumptions. This fact may indicate the first evidence of an open-charm tetraquark state whose quark content is $cs\overline{u}\overline{d}$. This open charm state was predicted before the experiment within the color-magnetism model [100] and using a coupled channel unitary approach [101]. After the experimental report, extensive theoretical investigations were devoted to this subject, and the spin-parity for the lower state, $X_0(2900)$, is generally favored to be $0^{+}$. In particular, $X_0(2900)$ can be identified as a radial excitation of $ud\overline{s}\overline{c}$ tetraquark state in a two-body potential model [102]. QCD sum rules [103,104], the one-boson-exchange model [105,106], the quark delocalization color screening model [107], effective field theory [108] and a strong decay investigation [109] suggest that $X_0(2900)$ is a S-wave ${\overline{D}}^{\ast }{K}^{\ast }$ ($D^{\ast }{\overline{K}}^{\ast }$) molecular state. On the other hand, references [110,111], which also used a QCD sum rules approach, confirmed the $0^{+}$ quantum numbers but as a compact tetraquark state. The idea of a $cs\overline{u}\overline{d}$ compact tetraquark in ${00}^{+}$ state is also supported by reference [112]. There are still several different views these structures reported by the LHCb collaboration, e.g., $X_0(2900)$ was identified as a ${\overline{D}}^{\ast }{K}^{\ast }$ molecular state with $I(J^P)=0(1^{+})$ [113]; triangle singularity induces the X exotic states [114,115]; and the compact $ud\overline{s}\overline{c}$ tetraquark in $0^{+}$ state disfavors $X_0(2900)$ in an extended relativized quark model [116]. Finally, several theoretical investigations [102,103,106] suggest for the $X_1(2900)$ the $J^P=1^{-}$ quantum numbers.

The observations of the hidden-charm pentaquarks $P_c^{+}(4380)$, $P_c^{+}(4312)$, $P_c^{+}(4440)$ and $P_c^{+}(4457)$ bring great interest to theoretical investigations. In particular, during 2010–2013, which was before the announcement of $P_c^{+}(4380)$ by the LHCb collaboration [22], several narrow hidden-charm resonances ∼4.3 GeV were predicted by means of coupled-channel unitary studies [117,118,119,120,121], and possible loosely bound hidden-charm molecular states were discussed in the one-boson-exchange model [122]. Then, great deals of subsequent theoretical works devoted to the interpretation of the nature this exotic state, particularly, ${\mathsf{\Sigma }}_c^{(\ast )}{\overline{D}}^{(\ast )}$ molecular state with quantum numbers $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$ is preferred by the boson exchange model [123], the constituent quark model [124,125,126], the Bethe-Salpeter equation [127], QCD sum rules [128,129,130], etc. The spin-parity of ${\frac{3}{2}}^{-}$ is also suggested in a diquark-triquark model investigation [131]. Furthermore, some other non-resonance explanations were also proposed such as kinematic effects and triangle singularities [132,133,134]. Strong decay properties of $P_c^{+}(4380)$ are studied in a molecular configuration [135].

Furthermore, in 2019 the three newly announced pentaquarks, $P_c^{+}(4312)$, $P_c^{+}(4440)$ and $P_c^{+}(4457)$—announced by the LHCb collaborattion [24]—triggered many theoretical investigations again. The main interpretations with ${\mathsf{\Sigma }}_c^{(\ast )}{\overline{D}}^{(\ast )}$ molecular configurations are provided by effective field theory [136,137,138], QCD sum rules [139], potential models [140,141,142,143,144,145], heavy quark spin multiplet structures [146,147], heavy hadron chiral perturbation theory [148], etc. Moreover, the production [149,150] and decay properties [151,152] of these pentaquarks were also investigated. Tables III and IV present our systematic study on the hidden-charm pentaquark states from 2017 [124]; one can notice that the new reported states are described well with the following assignments: $P_c^{+}(4312):$${\frac{1}{2}}^{-}{\mathsf{\Sigma }}_c\overline{D}$, $P_c^{+}(4440):$${\frac{1}{2}}^{-}{\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ and $P_c^{+}(4457):$${\frac{3}{2}}^{-}{\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$; their isospins are all of $I=\frac{1}{2}$. These conclusions were supported by the other subsequent theoretical investigations [136,137,146,151]. Meanwhile, there are also many works devoted to the investigations on other kinds of pentaquark states. E.g., the $\overline{Q}qqqq$ bound state is unavailable in a quark model formalism [153]. However, narrow resonances in doubly heavy pentaquarks are possible in potential models [154,155,156,157]. Besides, the triply charmed pentaquarks like ${\mathsf{\Xi }}_{cc}{D}^{(\ast )}$ molecular state have been suggested within a one-boson-exchange model [158] and QCD sum rules [159]. Additionally, some general reviews on the exotic states of tetraquarks and pentaquarks can be found in references [160,161].

In this review, we mainly focus on a summary of the doubly and fully-heavy tetraquarks, but also on the hidden and doubly-heavy pentaquarks; all of them were systematically studied in the framework of a constituent quark model. We hope that, by comparing various calculated bound and resonance states of tetraquarks and pentaquarks within the same theoretical framework, some general patterns and features in multi-quark systems can be detected. This could shed some light on the future experimental investigations of exotic tetraquark and pentaquark states. However, note too that the obtained states are just tentative ones, since they are investigated in a particular effective potential model.

The structure of this article is as follows: Section 2 is devoted to the theoretical framework where our constituent quark model and wave-functions of tetra- and penta-quark states are illustrated. Then, theoretical results along with discussion about each kind of tetraquark and pentaquark are presented in Section 3. The last section is a summary.

2. Theoretical Framework

Among all the methods for dealing with the issues in hadron physics related to the QCD’s non-perturbative energy region, the constituent quark model is still a powerful and major method applied to the baryon and meson spectra [1,3,162,163,164,165], hadron–hadron interaction [166,167,168,169,170], and exotic states [30,124,171,172,173]. We focus herein on the study of S-wave states of doubly-heavy tetraquarks and hidden and doubly-heavy pentaquarks within this formalism. Meanwhile, lattice-regularized QCD, which is based on first-principles, has also made prominent achievements in studying the multi-quark systems [174,175] and the hadronic interactions [176,177,178]. Hence, a potential model which is in accordance with the lattice QCD investigations on the interaction of a $Q\overline{Q}$ pair is also employed herein in the investigation of fully-heavy tetraquark states; particularly, the doubly, fully-heavy tetraqarks with spin-parity $J^P=0^{+}$, $1^{+}$ and $2^{+}$, in $I=0$ or 1 isospin sectors; the hidden-charm, bottom and doubly charmed pentaquarks with quantum numbers $J^P={\frac{1}{2}}^{-}$, ${\frac{3}{2}}^{-}$ and ${\frac{5}{2}}^{-}$; and the $I=\frac{1}{2}$ or $\frac{3}{2}$ isospin sectors were investigated.

The wave-function of a multi-quark system is exactly constructed considering quantum mechanical principles. Being specific, the wave-functions of color, spin, flavor and spatial degrees of freedom are considered in all possible meson-meson color-singlet, hidden-color, diquark-antidiquark and K-types channels for 4-quark systems; whereas baryon-meson color-singlet and hidden-color channels are the ones specified for 5-quark systems. Moreover, the couplings of all different configurations in one system are also considered. When solving the eigenvalue problem of 4- and 5-quark systems, both real- and complex-range calculations are implemented. In particular, the bound, resonance and scattering states can be classified simultaneously in the later framework according to the so-called ABC theorem [179,180]. The crucial manipulation in the complex scaling method (CSM) is to transform the coordinates of relative motions between quarks with a complex rotation, $\overrightarrow{r}\to \overrightarrow{r}{e}^{i\theta }$, and then solving the complex scaled Schrödinger equation $\left[H(\theta )-E(\theta )\right]\mathsf{\Psi }(\theta )=0$. In particular, Figure 1 shows a schematic distribution of the complex eigenenergies of a 2-body system solved by the CSM according to reference [181].

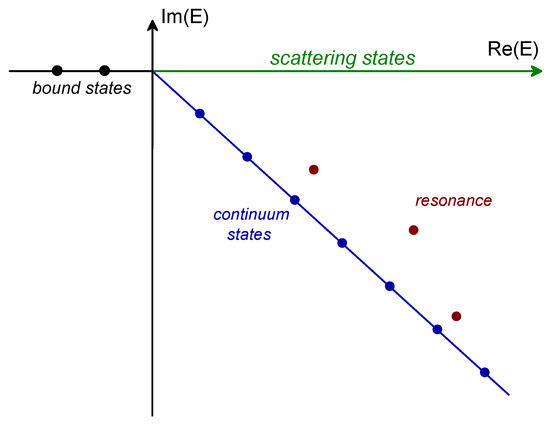
Figure 1. Schematic complex energy distribution in the single-channel two-body system.

2.1. Chiral Quark Model

The general form of a N-body Hamiltonian can be written as

$$H={\displaystyle \sum _{i=1}^N}\left(m_i+\frac{{\overrightarrow{p}}_i^2}{2m_i}\right)-T_{\mathrm{CM}}+{\displaystyle \sum _{j>i=1}^N}V({\overrightarrow{r}}_{ij}),$$

(1)

where the kinetic energy of central mass $T_{\mathrm{CM}}$ is subtracted during calculation and this is due to our treatment of the internal relative motions of the system. The two-body potential in a chiral quark model

$$V({\overrightarrow{r}}_{ij})=V_{\mathrm{CON}}({\overrightarrow{r}}_{ij})+V_{\mathrm{OGE}}({\overrightarrow{r}}_{ij})+V_{\chi }({\overrightarrow{r}}_{ij}),$$

(2)

contains the color confinement, one-gluon exchange and Goldstone-Boson exchange interactions. Furthermore, only the central parts of potential listed in Equation (2) are considered, the spin-orbit and tensor contributions are ignored at present.

The color-confining force should be encoded in the non-Abelian character of QCD. On one hand, multi-gluon exchanges induce an attractive potential which is proportional to the distance between two infinite-heavy quarks, this has been demonstrated by Lattice QCD [182]. On the other hand, light-quark pairs spontaneously created in the QCD vacuum may also lead to a breakup of the created color flux-tube at the same scale [182]. Accordingly, these two phenomenological features are mimicked in the expression:

$$V_{\mathrm{CON}}({\overrightarrow{r}}_{ij})=\left[-a_c(1-e^{-{\mu }_c{r}_{ij}})+\Delta \right]({\overrightarrow{\lambda }}_i^c·{\overrightarrow{\lambda }}_j^c),$$

(3)

where $a_c$, ${\mu }_c$ and $\Delta$ are parameters, ${\lambda }^c$ represents the Gell-Mann matrices in SU(3) color. One can see that we have a linear potential with an effective confinement strength $\sigma =-a_c{\mu }_c({\overrightarrow{\lambda }}_i^c·{\overrightarrow{\lambda }}_j^c)$; however, it will turns to be a constant at large distances.

The one-gluon exchange potential which includes a coulomb interaction and a color-magnetism one is given by

$$\begin{array}{ll}\hfill & V_{\mathrm{OGE}}({\overrightarrow{r}}_{ij})=\frac{1}{4}{\alpha }_s({\overrightarrow{\lambda }}_i^c·{\overrightarrow{\lambda }}_j^c)\left[\frac{1}{r_{ij}}-\frac{1}{6m_i{m}_j}({\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j)\frac{e^{-r_{ij}/r_0(\mu )}}{r_{ij}{r}_0^2(\mu )}\right],\hfill \end{array}$$

(4)

where $m_i$ is the constituent quark mass and the Pauli matrices in spin degree of freedom are denoted by $\overrightarrow{\sigma }$. The contact term of spatial part in color-magnetism interaction has been regularized as

$$\delta ({\overrightarrow{r}}_{ij})\sim \frac{1}{4\pi r_0^2}\frac{e^{-r_{ij}/r_0}}{r_{ij}},$$

(5)

with $r_0({\mu }_{ij})={\widehat{r}}_0/{\mu }_{ij}$ a regulator which depends on the reduced quark mass ${\mu }_{ij}$.

According to reference [183], a parameterized scheme for the QCD strong coupling constant ${\alpha }_s$ is used herein:

$${\alpha }_s({\mu }_{ij})=\frac{{\alpha }_0}{ln\left(\frac{{\mu }_{ij}^2+{\mu }_0^2}{{\mathsf{\Lambda }}_0^2}\right)},$$

(6)

in which ${\alpha }_0$, ${\mu }_0$ and ${\mathsf{\Lambda }}_0$ are all model parameters.

The central terms of the chiral potentials include the pion, kaon, $\eta$ and $\sigma$ exchange interactions and can be written as below

$$\begin{array}{ll}\hfill & V_{\pi }\left({\overrightarrow{r}}_{ij}\right)=\frac{g_{ch}^2}{4\pi }\frac{m_{\pi }^2}{12m_i{m}_j}\frac{{\mathsf{\Lambda }}_{\pi }^2}{{\mathsf{\Lambda }}_{\pi }^2-m_{\pi }^2}{m}_{\pi }\left[Y(m_{\pi }{r}_{ij})-\frac{{\mathsf{\Lambda }}_{\pi }^3}{m_{\pi }^3}Y({\mathsf{\Lambda }}_{\pi }{r}_{ij})\right]({\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j){\displaystyle \sum _{a=1}^3}({\lambda }_i^a·{\lambda }_j^a),\hfill \end{array}$$

(7)

$$\begin{array}{ll}\hfill & V_{\sigma }\left({\overrightarrow{r}}_{ij}\right)=-\frac{g_{ch}^2}{4\pi }\frac{{\mathsf{\Lambda }}_{\sigma }^2}{{\mathsf{\Lambda }}_{\sigma }^2-m_{\sigma }^2}{m}_{\sigma }\left[Y(m_{\sigma }{r}_{ij})-\frac{{\mathsf{\Lambda }}_{\sigma }}{m_{\sigma }}Y({\mathsf{\Lambda }}_{\sigma }{r}_{ij})\right],\hfill \end{array}$$

(8)

$$\begin{array}{ll}\hfill & V_K\left({\overrightarrow{r}}_{ij}\right)=\frac{g_{ch}^2}{4\pi }\frac{m_K^2}{12m_i{m}_j}\frac{{\mathsf{\Lambda }}_K^2}{{\mathsf{\Lambda }}_K^2-m_K^2}{m}_K\left[Y(m_K{r}_{ij})-\frac{{\mathsf{\Lambda }}_K^3}{m_K^3}Y({\mathsf{\Lambda }}_K{r}_{ij})\right]({\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j){\displaystyle \sum _{a=4}^7}({\lambda }_i^a·{\lambda }_j^a),\hfill \end{array}$$

(9)

$$\begin{array}{ll}\hfill & V_{\eta }\left({\overrightarrow{r}}_{ij}\right)=\frac{g_{ch}^2}{4\pi }\frac{m_{\eta }^2}{12m_i{m}_j}\frac{{\mathsf{\Lambda }}_{\eta }^2}{{\mathsf{\Lambda }}_{\eta }^2-m_{\eta }^2}{m}_{\eta }\left[Y(m_{\eta }{r}_{ij})-\frac{{\mathsf{\Lambda }}_{\eta }^3}{m_{\eta }^3}Y({\mathsf{\Lambda }}_{\eta }{r}_{ij})\right]({\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j)\left[cos{\theta }_p\left({\lambda }_i^8·{\lambda }_j^8\right)-sin{\theta }_p\right],\hfill \end{array}$$

(10)

where $Y(x)=e^{-x}/x$ is the Yukawa function and ${\lambda }^a$ is the SU(3) flavor matrices of Gell-Mann. By introducing an angle ${\theta }_p$, the physical $\eta$ meson is considered; meanwhile $m_{\pi }$, $m_K$ and $m_{\eta }$ are the experimental masses of the SU(3) Goldstone-bosons, the mass of the $\sigma$ meson is determined by the PCAC relation $m_{\sigma }^2\simeq m_{\pi }^2+4m_{u,d}^2$ [184]. The chiral coupling constant, $g_{ch}$ is determined from the $\pi NN$ coupling constant as follows

$$\frac{g_{ch}^2}{4\pi }=\frac{9}{25}\frac{g_{\pi NN}^2}{4\pi }\frac{m_{u,d}^2}{m_N^2},$$

(11)

which assumes that SU(3) flavor is an exact symmetry only broken by the different mass of the strange quark.

The chiral quark model parameters are listed in Table 1. They have been fixed in advance reproducing hadron [1,3,162,163,164,165], hadron-hadron [166,167,168,169,170] and multiquark [30,124,171] phenomenology. In particular, the application of this chiral quark model to the study of hidden-charm pentaquark states in reference [124], not only the $P_c^{+}(4380)$ but also the latest three observed $P_c^{+}$ were all successfully interpreted. As for a later purpose, Table 2 shows the predicted ground states for the mesons and baryons needed to determine the meson-meson and meson-baryon thresholds of multiquark systems studied herein.

Table 1. Chiral quark model parameters.

Quark masses	$m_u=m_d$ (MeV)	313
	$m_s$ (MeV)	555
	$m_c$ (MeV)	1752
	$m_b$ (MeV)	5100
Goldstone-bosons	${\mathsf{\Lambda }}_{\pi }={\mathsf{\Lambda }}_{\sigma }$ (fm${}^{-1}$)	4.20
	${\mathsf{\Lambda }}_{\eta }={\mathsf{\Lambda }}_K$ (fm${}^{-1}$)	5.20
	$g_{ch}^2/(4\pi )$	0.54
	${\theta }_P{(}^{\circ })$	−15
Confinement	$a_c$ (MeV)	430
	${\mu }_c$ (fm${}^{-1})$	0.70
	$\Delta$ (MeV)	181.10
OGE	${\alpha }_0$	2.118
	${\mathsf{\Lambda }}_0$(fm${}^{-1}$)	0.113
	${\mu }_0$(MeV)	36.976
	${\widehat{r}}_0$(MeV fm)	28.170

Table 2. Theoretical and experimental (in parentheses) masses of the ground states of selected mesons and baryons, in units of MeV.

$\pi$	$\eta$	$\rho$	$\omega$	D	$D^{\ast }$	$D_s$	$D_s^{\ast }$
149 (135)	689 (548)	772 (770)	696 (783)	1897 (1870)	2017 (2007)	1989 (1968)	2115 (2112)
B	$B^{\ast }$	$B_s$	$B_s^{\ast }$	$B_c$	$B_c^{\ast }$	${\eta }_c$	${\eta }_b$
5278 (5280)	5319 (5325)	5355 (5366)	5400 (5415)	6276 (6276)	6331 (-)	2989 (2984)	9454 (9398)
$J/\psi$	$\mathsf{{\rm Y}}$
3097 (3097)	9505 (9460)
N	${\mathsf{\Lambda }}_c$	${\mathsf{\Sigma }}_c$	${\mathsf{\Sigma }}_c^{\ast }$	${\mathsf{\Xi }}_{cc}$	${\mathsf{\Xi }}_{cc}^{\ast }$	${\mathsf{\Lambda }}_b$	${\mathsf{\Sigma }}_b$
744 (939)	2099 (2286)	2505 (2454)	2549 (2518)	3663 (3519)	3717 (-)	5626 (5619)	5817 (5811)
${\mathsf{\Sigma }}_b^{\ast }$
5834 (5832)

2.2. Cornell Potential

According to lattice QCD investigations [71], in the fully-heavy tetraquark sector $QQ\overline{Q}\overline{Q}$ ($Q=c,b$), the interplay between a pair of heavy quarkonium can be well approximated by the Cornell potential, viz. a linear confinement plus a Coulomb interaction along with a spin-spin dependent term. This can be incorporated into the following Hamiltonian form of four-body systems

$$H={\displaystyle \sum _{i=1}^4}\left(m_i+\frac{{\overrightarrow{p}}_i^2}{2m_i}\right)-T_{\mathrm{CM}}+{\displaystyle \sum _{j>i=1}^4}V({\overrightarrow{r}}_{ij}),$$

(12)

where the center-of-mass kinetic energy $T_{\mathrm{CM}}$ is also subtracted without lost of generality, as in the chiral quark model. In this case, the two-body interactions read as

$$V_{Q\overline{Q}}({\overrightarrow{r}}_{ij})=-\frac{\alpha }{{\overrightarrow{r}}_{ij}}+\sigma {\overrightarrow{r}}_{ij}+\beta e^{-{\overrightarrow{r}}_{ij}}({\overrightarrow{s}}_i·{\overrightarrow{s}}_j).$$

(13)

The three parameters $\alpha$, $\sigma$ and $\beta$ in Equation (13), which are related to the coulomb, confinement and spin-spin interactions, respectively, are determined in Ref. [185] and their values are listed in Table 3. Additionally, Table 4 presents the theoretical and experimental masses of the S-wave $Q\overline{Q}$ mesons; apparently, the deviation between theory and experiment is acceptable. It is also important to note that, based on the investigations by quark models and lattice-QCD computations [186], the quark-quark interaction $V_{QQ}$ is just half of $V_{Q\overline{Q}}$. This conclusion will be employed in our study of the fully-heavy tetraquark states.

Table 3. Potential model parameters.

Quark masses	$m_c$$(MeV)$	1290
	$m_b$$(MeV)$	4700
Coulomb	$\alpha$	0.4105
Confinement	$\sigma$($Ge{V}^2$)	0.2
Spin-Spin	$\gamma$$(GeV)$	1.982
	${\beta }_c$$(GeV)$	2.06
	${\beta }_b$$(GeV)$	0.318

Table 4. Theoretical and experimental masses of the S-wave $Q\overline{Q}$ mesons, unit in MeV.

State	${\mathit{M}}_{\mathit{th}}$	${\mathit{M}}_{\mathit{exp}}$
${\eta }_c(1S)$	2968	2981
${\eta }_c(2S)$	3655	3639
$J/\psi (1S)$	3102	3097
$\psi (2S)$	3720	3686
${\eta }_b(1S)$	9401	9398
${\eta }_b(2S)$	9961	9999
$\mathsf{{\rm Y}}(1S)$	9463	9460
$\mathsf{{\rm Y}}(2S)$	9981	10,023

2.3. Wave-Function of Multi-Quark System

There are four degrees of freedom in the quark level: color, spin, flavor and spatial. A complete antisymmetry N-quarks wave-function which fulfills the Pauli principle is written as

$${\mathsf{\Psi }}_{J{M}_J,I,i,j,k}=\mathcal{A}\left[{\left[{\psi }_L{\chi }_S^{{\sigma }_i}\right]}_{J{M}_J}{\chi }_I^{f_j}{\chi }_k^c\right].$$

(14)

In Equation (14) ${\psi }_L$, ${\chi }_S^{{\sigma }_i}$, ${\chi }_I^{f_j}$ and ${\chi }_k^c$ stand for the spatial, spin, flavor and color wave-functions, respectively. Besides, $\mathcal{A}$ is the antisymmetry operator of the system which considers the fermion nature of two identical particles interchange.

Figure 2 shows six configurations in the double-heavy tetraquark states. In particular, Figure 2a is the dimeson structure, Figure 2b is the diquark-antidiquark configuration and the other cases are the K-types. Furthermore, the light flavor antiquarks $\overline{q}$ can be naturally switched with $\overline{Q}$ in the fully-heavy sectors. Accordingly, there are four exchange terms included in the antisymmetry operator for both the double-heavy and fully-heavy tetraquark states where the two quarks and antiquarks are the same flavor, and it reads as

$$\mathcal{A}=1-(13)-(24)+(13)(24).$$

(15)

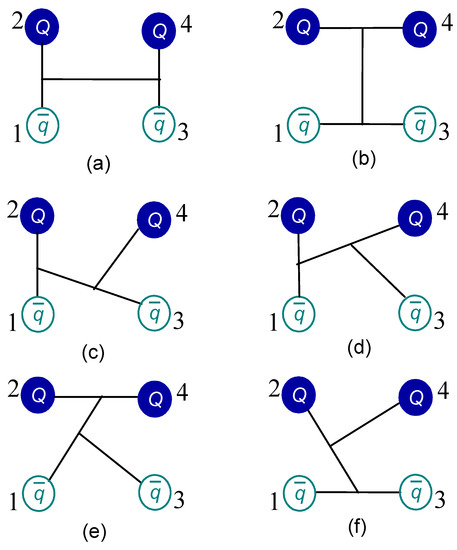
Figure 2. Six types of configurations in $QQ\overline{q}\overline{q}$ tetraquarks. Panel (a) is meson-meson structure, panel (b) is diquark-antidiquark one and the other K-type structures are from panel (c–f). $(Q=c,b;q=u,d,s)$.

However, due to the asymmetry between c- and b-quark, there are only two exchanges for the $\overline{q}c\overline{q}b$ system, namely

$$\mathcal{A}=1-(13).$$

(16)

Figure 3 and Figure 4 present the configurations of hidden-flavor and doubly-heavy flavor pentaquarks, respectively. All of them, along with their couplings, are considered in the calculations presented herein. For the hidden-flavor pentaquarks presented in Figure 3, the quark arrangements are $(qqQ)(\overline{Q}q)$ and $(qqq)(\overline{Q}Q)$, and we have the following antisymmetry operator:

$${\mathcal{A}}_1=1-(15)-(25),$$

(17)

for the $(udQ)(\overline{Q}u)+(uuQ)(\overline{Q}d)$ structure, and

$${\mathcal{A}}_2=1-(13)-(23),$$

(18)

for the $(uud)(\overline{Q}Q)$ configuration. However, for the doubly-heavy case in Figure 4, the antisymmetry operators are

$${\mathcal{A}}_1=1-(35),$$

(19)

$${\mathcal{A}}_2=1-(12)-(35)+(12)(35),$$

(20)

$${\mathcal{A}}_3=1-(12),$$

(21)

$${\mathcal{A}}_4={\mathcal{A}}_2,$$

(22)

and the above equations from (19) to (22) represent the results in configurations of Figure 4a–d, respectively.

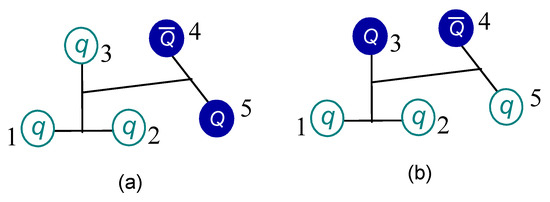
Figure 3. Two types of configurations in $qqq\overline{Q}Q$ hidden-flavor pentaquarks. $(Q=c,b;q=u,d,s)$. The distribution of heavy quark is considered in 3-quark (b) and quark-antiquark (a) cluster, respectively.

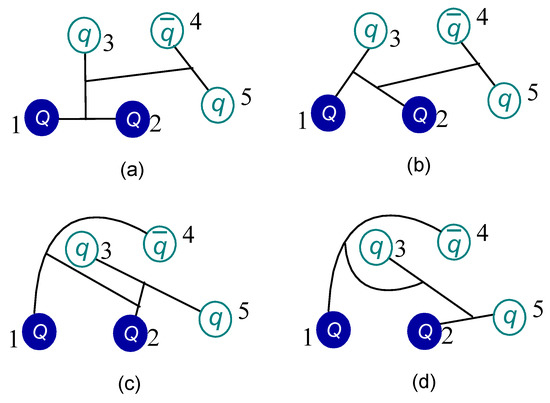
Figure 4. Four types of configurations in $QQq\overline{q}q$ doubly-flavor pentaquarks. $(Q=c,b;q=u,d,s)$. (a,b) are two heavy quarks coupled in one 3-quark cluster, and the other two panels, (c) and (d), stand for these two heavy quarks distributing in each two sub-clusters.

In the following, we shall introduce the tetraquark and pentaquark wave-function in color, flavor, spin and space degrees of freedom.

2.3.1. Color Wave-Function

Much richer color structures in multi-quark systems exist when compared with those in conventional hadrons ($q\overline{q}$ meson and $qqq$ baryon). The wave-functions in color degree of freedom for each configurations are discussed according to the classification of tetraquark and pentaquark states, respectively.

• Tetraquark

The colorless wave-function of a tetraquark in meson-meson configuration, presented in Figure 2a, can be obtained through two channels: color-singlet and hidden-color. Just the former channel is enough if all spatial excitations are considered for the multi-quark system [30,187]. A more economical approach, by employing all possible color configurations along with their couplings, is used herein. Therefore, the wave-functions of color-singlet (two color-singlet clusters coupling, $1\times 1$) and hidden-color (two color-octet clusters coupling, $8\times 8$) channels in meson-meson configuration of Figure 2a are marked with ${\chi }_1^c$ and ${\chi }_2^c$, respectively,

$$\begin{array}{ll}\hfill {\chi }_1^c& =\frac{1}{3}(\overline{r}r+\overline{g}g+\overline{b}b)\times (\overline{r}r+\overline{g}g+\overline{b}b),\hfill \end{array}$$

(23)

$$\begin{array}{ll}\hfill {\chi }_2^c& =\frac{\sqrt{2}}{12}(3\overline{b}r\overline{r}b+3\overline{g}r\overline{r}g+3\overline{b}g\overline{g}b+3\overline{g}b\overline{b}g+3\overline{r}g\overline{g}r\hfill \\ \hfill & +3\overline{r}b\overline{b}r+2\overline{r}r\overline{r}r+2\overline{g}g\overline{g}g+2\overline{b}b\overline{b}b-\overline{r}r\overline{g}g\hfill \\ \hfill & -\overline{g}g\overline{r}r-\overline{b}b\overline{g}g-\overline{b}b\overline{r}r-\overline{g}g\overline{b}b-\overline{r}r\overline{b}b).\hfill \end{array}$$

(24)

Meanwhile, as for the diquark-antidiquark channel shown in Figure 2b, the color wave-functions are ${\chi }_3^c$ (color triplet-antitriplet clusters coupling, $3\times \overline{3}$) and ${\chi }_4^c$ (color sextet-antisextet clusters coupling, $6\times \overline{6}$), respectively. In particular, it is symmetric for the two quarks (antiquarks) interchange in Equation (25) and antisymmetric in Equation (26):

$$\begin{array}{ll}\hfill {\chi }_3^c& =\frac{\sqrt{3}}{6}(\overline{r}r\overline{g}g-\overline{g}r\overline{r}g+\overline{g}g\overline{r}r-\overline{r}g\overline{g}r+\overline{r}r\overline{b}b-\overline{b}r\overline{r}b\hfill \\ \hfill & +\overline{b}b\overline{r}r-\overline{r}b\overline{b}r+\overline{g}g\overline{b}b-\overline{b}g\overline{g}b+\overline{b}b\overline{g}g-\overline{g}b\overline{b}g),\hfill \end{array}$$

(25)

$$\begin{array}{ll}\hfill {\chi }_4^c& =\frac{\sqrt{6}}{12}(2\overline{r}r\overline{r}r+2\overline{g}g\overline{g}g+2\overline{b}b\overline{b}b+\overline{r}r\overline{g}g+\overline{g}r\overline{r}g\hfill \\ \hfill & +\overline{g}g\overline{r}r+\overline{r}g\overline{g}r+\overline{r}r\overline{b}b+\overline{b}r\overline{r}b+\overline{b}b\overline{r}r\hfill \\ \hfill & +\overline{r}b\overline{b}r+\overline{g}g\overline{b}b+\overline{b}g\overline{g}b+\overline{b}b\overline{g}g+\overline{g}b\overline{b}g).\hfill \end{array}$$

(26)

The remaining four structures, Figure 2c–f, are K-types in which the 4-quark wave-function is constructed from the coupling of quarks in turn. In particular, their color bases are obtained by the following coupling coefficients according to the $SU(3)$ color group (The group chain of K-type is obtained in sequence of quark number (1234), each quark and antiquark is represented with [1] and [11], respectively, in the group theory):

• $K_1$-type of Figure 2c: [$C_{\left[11\right],\left[1\right]}^{\left[21\right]}{C}_{\left[21\right],\left[11\right]}^{\left[221\right]}{C}_{\left[221\right],\left[1\right]}^{\left[222\right]}$]${}_5$; [$C_{\left[11\right],\left[1\right]}^{\left[111\right]}{C}_{\left[111\right],\left[11\right]}^{\left[221\right]}{C}_{\left[221\right],\left[1\right]}^{\left[222\right]}$]${}_6$;
• $K_2$-type of Figure 2d: [$C_{\left[11\right],\left[1\right]}^{\left[111\right]}{C}_{\left[111\right],\left[1\right]}^{\left[211\right]}{C}_{\left[211\right],\left[11\right]}^{\left[222\right]}$]${}_7$; [$C_{\left[11\right],\left[1\right]}^{\left[21\right]}{C}_{\left[21\right],\left[1\right]}^{\left[211\right]}{C}_{\left[211\right],\left[11\right]}^{\left[222\right]}$]${}_8$;
• $K_3$-type of Figure 2e: [$C_{\left[1\right],\left[1\right]}^{\left[2\right]}{C}_{\left[2\right],\left[11\right]}^{\left[211\right]}{C}_{\left[211\right],\left[11\right]}^{\left[222\right]}$]${}_9$; [$C_{\left[1\right],\left[1\right]}^{\left[11\right]}{C}_{\left[11\right],\left[11\right]}^{\left[211\right]}{C}_{\left[211\right],\left[11\right]}^{\left[222\right]}$]${}_{10}$;
• $K_4$-type of Figure 2f: [$C_{\left[11\right],\left[11\right]}^{\left[22\right]}{C}_{\left[22\right],\left[1\right]}^{\left[221\right]}{C}_{\left[221\right],\left[1\right]}^{\left[222\right]}$]${}_{11}$; [$C_{\left[11\right],\left[11\right]}^{\left[211\right]}{C}_{\left[211\right],\left[1\right]}^{\left[221\right]}{C}_{\left[221\right],\left[1\right]}^{\left[222\right]}$]${}_{12}$.

These eight group chains generate the following wave-functions for K-types whose subscripts correspond to the numbers labeled in the brackets above,

$$\begin{array}{ll}\hfill {\chi }_5^c& ={\chi }_2^c.\hfill \end{array}$$

(27)

$$\begin{array}{ll}\hfill {\chi }_6^c& ={\chi }_1^c.\hfill \end{array}$$

(28)

$$\begin{array}{ll}\hfill {\chi }_7^c& ={\chi }_1^c.\hfill \end{array}$$

(29)

$$\begin{array}{ll}\hfill {\chi }_8^c& ={\chi }_2^c.\hfill \end{array}$$

(30)

$$\begin{array}{ll}\hfill {\chi }_9^c& =\frac{1}{2\sqrt{6}}(\overline{r}b\overline{b}r+\overline{r}r\overline{b}b+\overline{g}b\overline{b}g+\overline{g}g\overline{b}b+\overline{r}g\overline{g}r+\overline{r}r\overline{g}g+\hfill \\ \hfill & \overline{b}b\overline{g}g+\overline{b}g\overline{g}b+\overline{g}g\overline{r}r+\overline{g}r\overline{r}g+\overline{b}b\overline{r}r+\overline{b}r\overline{r}b)+\hfill \\ \hfill & \frac{1}{\sqrt{6}}(\overline{r}r\overline{r}r+\overline{g}g\overline{g}g+\overline{b}b\overline{b}b).\hfill \end{array}$$

(31)

$$\begin{array}{ll}\hfill {\chi }_{10}^c& =\frac{1}{2\sqrt{3}}(\overline{r}b\overline{b}r-\overline{r}r\overline{b}b+\overline{g}b\overline{b}g-\overline{g}g\overline{b}b+\overline{r}g\overline{g}r-\overline{r}r\overline{g}g-\hfill \\ \hfill & \overline{b}b\overline{g}g+\overline{b}g\overline{g}b-\overline{g}g\overline{r}r+\overline{g}r\overline{r}g-\overline{b}b\overline{r}r+\overline{b}r\overline{r}b).\hfill \end{array}$$

(32)

$$\begin{array}{ll}\hfill {\chi }_{11}^c& ={\chi }_9^c.\hfill \end{array}$$

(33)

$$\begin{array}{ll}\hfill {\chi }_{12}^c& =-{\chi }_{10}^c.\hfill \end{array}$$

(34)

• Pentaquark

Due to the enormous computational demands on exactly solving the 5-body Schrödinger equation, only baryon-meson configuration with color singlet channel ($k=1$), hidden color ones ($k=2,3$) and their couplings are considered in this work. The details of color wave-functions ${\chi }_k^c$ are as below,

$$\begin{array}{lll}\hfill {\chi }_1^c& =& \frac{1}{\sqrt{18}}(rgb-rbg+gbr-grb+brg-bgr)\hfill \\ & & (\overline{r}r+\overline{g}g+\overline{b}b),\hfill \end{array}$$

(35)

$$\begin{array}{lll}\hfill {\chi }_k^c& =& \frac{1}{\sqrt{8}}({\chi }_{3,1}^k{\chi }_{2,8}-{\chi }_{3,2}^k{\chi }_{2,7}-{\chi }_{3,3}^k{\chi }_{2,6}+{\chi }_{3,4}^k{\chi }_{2,5}\hfill \\ & & +{\chi }_{3,5}^k{\chi }_{2,4}-{\chi }_{3,6}^k{\chi }_{2,3}-{\chi }_{3,7}^k{\chi }_{2,2}+{\chi }_{3,8}^k{\chi }_{2,1}),\hfill \end{array}$$

(36)

while $k=2$ and 3 refers to a symmetric and antisymmetric wave-function, respectively. The sub-clusters bases are

$$\begin{array}{l}{\chi }_{3,1}^2=\frac{1}{\sqrt{6}}(2rrg-rgr-grr),{\chi }_{3,1}^3=\frac{1}{\sqrt{2}}(rgr-grr),\hfill \end{array}$$

(37)

$$\begin{array}{l}{\chi }_{3,2}^2=\frac{1}{\sqrt{6}}(rgg+grg-2ggr),{\chi }_{3,2}^3=\frac{1}{\sqrt{2}}(rgg-grg),\hfill \end{array}$$

(38)

$$\begin{array}{l}{\chi }_{3,3}^2=\frac{1}{\sqrt{6}}(2rrb-rbr-brr),{\chi }_{3,3}^3=\frac{1}{\sqrt{2}}(rbr-brr),\hfill \end{array}$$

(39)

$$\begin{array}{l}{\chi }_{3,4}^2=\frac{1}{\sqrt{12}}(2rgb-rbg+2grb-gbr-brg-bgr),\hfill \end{array}$$

(40)

$$\begin{array}{l}{\chi }_{3,4}^3=\frac{1}{\sqrt{4}}(rbg+gbr-brg-bgr),\hfill \end{array}$$

(41)

$$\begin{array}{l}{\chi }_{3,5}^2=\frac{1}{\sqrt{4}}(rbg-gbr+brg-bgr),\hfill \end{array}$$

(42)

$$\begin{array}{l}{\chi }_{3,5}^3=\frac{1}{\sqrt{12}}(2rgb+rbg-2grb-gbr-brg+bgr),\hfill \end{array}$$

(43)

$$\begin{array}{l}{\chi }_{3,6}^2=\frac{1}{\sqrt{6}}(2ggb-gbg-bgg),{\chi }_{3,6}^3=\frac{1}{\sqrt{2}}(gbg-bgg),\hfill \end{array}$$

(44)

$$\begin{array}{l}{\chi }_{3,7}^2=\frac{1}{\sqrt{6}}(rbb+brb-2bbr),{\chi }_{3,7}^3=\frac{1}{\sqrt{2}}(rbb-brb),\hfill \end{array}$$

(45)

$$\begin{array}{l}{\chi }_{3,8}^2=\frac{1}{\sqrt{6}}(gbb+bgb-2bbg),{\chi }_{3,8}^3=\frac{1}{\sqrt{2}}(gbb-bgb),\hfill \end{array}$$

(46)

$$\begin{array}{l}{\chi }_{2,1}=\overline{b}r,{\chi }_{2,2}=\overline{b}g,\hfill \end{array}$$

(47)

$$\begin{array}{l}{\chi }_{2,3}=-\overline{g}r,{\chi }_{2,4}=\frac{1}{\sqrt{2}}(\overline{r}r-\overline{g}g),\hfill \end{array}$$

(48)

$$\begin{array}{l}{\chi }_{2,5}=\frac{1}{\sqrt{6}}(2\overline{b}b-\overline{r}r-\overline{g}g),{\chi }_{2,6}=\overline{r}g,\hfill \end{array}$$

(49)

$$\begin{array}{l}{\chi }_{2,7}=-\overline{g}b,{\chi }_{2,8}=\overline{r}b.\hfill \end{array}$$

(50)

2.3.2. Spin Wave-Function

In the 4-quark and 5-quark systems, the total spin S can take values from 0 to 2, for the former case, and $\frac{1}{2}$ to $\frac{5}{2}$, for the later one. Their spin wave-functions for one certain configuration listed from Figure 2, Figure 3 and Figure 4 are obtained by the couplings of Clebsh-Gordon coefficients in the spin SU(2) group. We now proceed to describe them in the tetraquark and pentaquark states.

• Tetraquark

The spin wave-function ${\chi }_{S,M_S}^{{\sigma }_i}$ of a 4-quark system is organized by two sub-clusters for the dimeson and the diquark-antidiquark structures, and couplings in an increased sequence of quark numbers for K-types. Furthermore, because no spin-orbital dependent potential is included in the model, the third component $(M_S)$ of total spin can be taken the same value as S without losing generality. The details are written as

$$\begin{array}{ll}\hfill {\chi }_{0,0}^{{\sigma }_{l1}}(4)& ={\chi }_{00}^{\sigma }{\chi }_{00}^{\sigma }\hfill \end{array}$$

(51)

$$\begin{array}{ll}\hfill {\chi }_{0,0}^{{\sigma }_{l2}}(4)& =\frac{1}{\sqrt{3}}({\chi }_{11}^{\sigma }{\chi }_{1,-1}^{\sigma }-{\chi }_{10}^{\sigma }{\chi }_{10}^{\sigma }+{\chi }_{1,-1}^{\sigma }{\chi }_{11}^{\sigma })\hfill \end{array}$$

(52)

$$\begin{array}{ll}\hfill {\chi }_{0,0}^{{\sigma }_{l3}}(4)& =\frac{1}{\sqrt{2}}((\sqrt{\frac{2}{3}}{\chi }_{11}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }-\sqrt{\frac{1}{3}}{\chi }_{10}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }){\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }\hfill \\ \hfill & -(\sqrt{\frac{1}{3}}{\chi }_{10}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }-\sqrt{\frac{2}{3}}{\chi }_{1,-1}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }){\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma })\hfill \end{array}$$

(53)

$$\begin{array}{ll}\hfill {\chi }_{0,0}^{{\sigma }_{l4}}(4)& =\frac{1}{\sqrt{2}}({\chi }_{00}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }-{\chi }_{00}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma })\hfill \end{array}$$

(54)

$$\begin{array}{ll}\hfill {\chi }_{1,1}^{{\sigma }_{m1}}(4)& ={\chi }_{00}^{\sigma }{\chi }_{11}^{\sigma }\hfill \end{array}$$

(55)

$$\begin{array}{ll}\hfill {\chi }_{1,1}^{{\sigma }_{m2}}(4)& ={\chi }_{11}^{\sigma }{\chi }_{00}^{\sigma }\hfill \end{array}$$

(56)

$$\begin{array}{ll}\hfill {\chi }_{1,1}^{{\sigma }_{m3}}(4)& =\frac{1}{\sqrt{2}}({\chi }_{11}^{\sigma }{\chi }_{10}^{\sigma }-{\chi }_{10}^{\sigma }{\chi }_{11}^{\sigma })\hfill \end{array}$$

(57)

$$\begin{array}{ll}\hfill {\chi }_{1,1}^{{\sigma }_{m4}}(4)& =\sqrt{\frac{3}{4}}{\chi }_{11}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }-\sqrt{\frac{1}{12}}{\chi }_{11}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }-\sqrt{\frac{1}{6}}{\chi }_{10}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }\hfill \end{array}$$

(58)

$$\begin{array}{ll}\hfill {\chi }_{1,1}^{{\sigma }_{m5}}(4)& =(\sqrt{\frac{2}{3}}{\chi }_{11}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }-\sqrt{\frac{1}{3}}{\chi }_{10}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }){\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }\hfill \end{array}$$

(59)

$$\begin{array}{ll}\hfill {\chi }_{1,1}^{{\sigma }_{m6}}(4)& ={\chi }_{00}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }\hfill \end{array}$$

(60)

$$\begin{array}{ll}\hfill {\chi }_{2,2}^{{\sigma }_1}(4)& ={\chi }_{11}^{\sigma }{\chi }_{11}^{\sigma }\hfill \end{array}$$

(61)

In the above equations, the superscripts $l_1$…$l_4$ and $m_1$…$m_6$ are signs for each structures presented in Figure 2, their specific assignments are summarized in Table 5. Meanwhile, the necessary sub-clusters bases read as

$$\begin{array}{ll}\hfill {\chi }_{11}^{\sigma }& ={\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma },{\chi }_{1,-1}^{\sigma }={\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }\hfill \end{array}$$

(62)

$$\begin{array}{ll}\hfill {\chi }_{10}^{\sigma }& =\frac{1}{\sqrt{2}}({\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }+{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma })\hfill \end{array}$$

(63)

$$\begin{array}{ll}\hfill {\chi }_{00}^{\sigma }& =\frac{1}{\sqrt{2}}({\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }-{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma })\hfill \end{array}$$

(64)

with ${\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma }$ and ${\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma }$ could be defined as $\alpha$ and $\beta$, respectively.

Table 5. Index of spin-wave functions from Equations (51)–(61), their numbers are listed in the column according to each configuration, respectively.

	Dimeson	Diquark-Antidiquark	${\mathit{K}}_1$	${\mathit{K}}_2$	${\mathit{K}}_3$	${\mathit{K}}_4$
$l_1$	1	3
$l_2$	2	4
$l_3$			5	7	9	11
$l_4$			6	8	10	12
$m_1$	1	4
$m_2$	2	5
$m_3$	3	6
$m_4$			7	10	13	16
$m_5$			8	11	14	17
$m_6$			9	12	15	18

• Pentaquark

Based on a baryon and meson sub-clusters couplings formalism, the spin wave-functions of a 5-quark system are

$$\begin{array}{ll}\hfill {\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 1}(5)& =\sqrt{\frac{1}{6}}{\chi }_{\frac{3}{2},-\frac{1}{2}}^{n\sigma }(3){\chi }_{11}^{\sigma }-\sqrt{\frac{1}{3}}{\chi }_{\frac{3}{2},\frac{1}{2}}^{n\sigma }(3){\chi }_{10}^{\sigma }+\sqrt{\frac{1}{2}}{\chi }_{\frac{3}{2},\frac{3}{2}}^{n\sigma }(3){\chi }_{1-1}^{\sigma },\hfill \end{array}$$

(65)

$$\begin{array}{ll}\hfill {\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 2}(5)& =\sqrt{\frac{1}{3}}{\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 1}(3){\chi }_{10}^{\sigma }-\sqrt{\frac{2}{3}}{\chi }_{\frac{1}{2},-\frac{1}{2}}^{n\sigma 1}(3){\chi }_{11}^{\sigma },\hfill \end{array}$$

(66)

$$\begin{array}{ll}\hfill {\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 3}(5)& =\sqrt{\frac{1}{3}}{\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 2}(3){\chi }_{10}^{\sigma }-\sqrt{\frac{2}{3}}{\chi }_{\frac{1}{2},-\frac{1}{2}}^{n\sigma 2}(3){\chi }_{11}^{\sigma },\hfill \end{array}$$

(67)

$$\begin{array}{ll}\hfill {\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 4}(5)& ={\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 1}(3){\chi }_{00}^{\sigma },\hfill \end{array}$$

(68)

$$\begin{array}{ll}\hfill {\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 5}(5)& ={\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 2}(3){\chi }_{00}^{\sigma },\hfill \end{array}$$

(69)

for $S=1/2$, and

$$\begin{array}{ll}\hfill {\chi }_{\frac{3}{2},\frac{3}{2}}^{n\sigma 1}(5)& =\sqrt{\frac{3}{5}}{\chi }_{\frac{3}{2},\frac{3}{2}}^{n\sigma }(3){\chi }_{10}^{\sigma }-\sqrt{\frac{2}{5}}{\chi }_{\frac{3}{2},\frac{1}{2}}^{n\sigma }(3){\chi }_{11}^{\sigma },\hfill \end{array}$$

(70)

$$\begin{array}{ll}\hfill {\chi }_{\frac{3}{2},\frac{3}{2}}^{n\sigma 2}(5)& ={\chi }_{\frac{3}{2},\frac{3}{2}}^{n\sigma }(3){\chi }_{00}^{\sigma },\hfill \end{array}$$

(71)

$$\begin{array}{ll}\hfill {\chi }_{\frac{3}{2},\frac{3}{2}}^{n\sigma 3}(5)& ={\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 1}(3){\chi }_{11}^{\sigma },\hfill \end{array}$$

(72)

$$\begin{array}{ll}\hfill {\chi }_{\frac{3}{2},\frac{3}{2}}^{n\sigma 4}(5)& ={\chi }_{\frac{1}{2},\frac{1}{2}}^{n\sigma 2}(3){\chi }_{11}^{\sigma },\hfill \end{array}$$

(73)

for $S=3/2$, and

$$\begin{array}{ll}\hfill {\chi }_{\frac{5}{2},\frac{5}{2}}^{n\sigma 1}(5)& ={\chi }_{\frac{3}{2},\frac{3}{2}}^{n\sigma }(3){\chi }_{11}^{\sigma },\hfill \end{array}$$

(74)

for $S=5/2$. These expressions can be obtained easily using SU(2) algebra and considering the 3-quark and quark-antiquark sub-clusters individually. The details read as

$$\begin{array}{l}{\chi }_{\frac{3}{2},\frac{3}{2}}^{\sigma }(3)=\alpha \alpha \alpha ,\hfill \end{array}$$

(75)

$$\begin{array}{l}{\chi }_{\frac{3}{2},\frac{1}{2}}^{\sigma }(3)=\frac{1}{\sqrt{3}}(\alpha \alpha \beta +\alpha \beta \alpha +\beta \alpha \alpha ),\hfill \end{array}$$

(76)

$$\begin{array}{l}{\chi }_{\frac{3}{2},-\frac{1}{2}}^{\sigma }(3)=\frac{1}{\sqrt{3}}(\alpha \beta \beta +\beta \alpha \beta +\beta \beta \alpha ),\hfill \end{array}$$

(77)

$$\begin{array}{l}{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma 1}(3)=\frac{1}{\sqrt{6}}(2\alpha \alpha \beta -\alpha \beta \alpha -\beta \alpha \alpha ),\hfill \end{array}$$

(78)

$$\begin{array}{l}{\chi }_{\frac{1}{2},\frac{1}{2}}^{\sigma 2}(3)=\frac{1}{\sqrt{2}}(\alpha \beta \alpha -\beta \alpha \alpha ),\hfill \end{array}$$

(79)

$$\begin{array}{l}{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma 1}(3)=\frac{1}{\sqrt{6}}(\alpha \beta \beta -\alpha \beta \beta -2\beta \beta \alpha ),\hfill \end{array}$$

(80)

$$\begin{array}{l}{\chi }_{\frac{1}{2},-\frac{1}{2}}^{\sigma 2}(3)=\frac{1}{\sqrt{2}}(\alpha \beta \beta -\beta \alpha \beta ),\hfill \end{array}$$

(81)

$$\begin{array}{l}{\chi }_{11}^{\sigma }=\alpha \alpha ,{\chi }_{10}^{\sigma }=\frac{1}{\sqrt{2}}(\alpha \beta +\beta \alpha ),{\chi }_{1-1}^{\sigma }=\beta \beta ,\hfill \end{array}$$

(82)

$$\begin{array}{l}{\chi }_{00}^{\sigma }=\frac{1}{\sqrt{2}}(\alpha \beta -\beta \alpha ).\hfill \end{array}$$

(83)

2.3.3. Flavor Wave-Function

A similar procedure can be implemented in the isospin-space and the total flavor wave-function of multi-quark system is introduced according to each configuration.

• Tetraquark

Generally, there are two kinds of 4-quark systems that we are dealing with, the doubly- and fully-heavy tetraquark states. Hence, the well defined isospin quantum number I can be taken either 0 or 1 for $QQ\overline{q}\overline{q}$ systems ($Q=c,b$ and $q=u,d,s$), but only the isoscalar sector $I=0$ will be considered for $QQ\overline{Q}\overline{Q}$ tetraquarks. Herein, we use ${\chi }_{I,M_I}^{fi}$ to represent the flavor wave-functions and the superscript $i=1,2$ and 3 stand for $cc\overline{q}\overline{q}$, $bb\overline{q}\overline{q}$ and $cb\overline{q}\overline{q}$ systems, respectively. The specific expressions are as following

$$\begin{array}{ll}\hfill & {\chi }_{0,0}^{f1}=\sqrt{\frac{1}{2}}(\overline{u}c\overline{d}c-\overline{d}c\overline{u}c),\hfill \end{array}$$

(84)

$$\begin{array}{ll}\hfill & {\chi }_{1,-1}^{f1}=\overline{u}c\overline{u}c,\hfill \end{array}$$

(85)

$$\begin{array}{ll}\hfill & {\chi }_{0,0}^{f2}=\sqrt{\frac{1}{2}}(\overline{u}b\overline{d}b-\overline{d}b\overline{u}b),\hfill \end{array}$$

(86)

$$\begin{array}{ll}\hfill & {\chi }_{1,-1}^{f2}=\overline{u}b\overline{u}b,\hfill \end{array}$$

(87)

$$\begin{array}{ll}\hfill & {\chi }_{0,0}^{f3}=\sqrt{\frac{1}{2}}(\overline{u}c\overline{d}b-\overline{d}c\overline{u}b),\hfill \end{array}$$

(88)

$$\begin{array}{ll}\hfill & {\chi }_{1,-1}^{f3}=\overline{u}c\overline{u}b,\hfill \end{array}$$

(89)

$$\begin{array}{ll}\hfill & {\chi }_{0,0}^{f1}=\overline{s}c\overline{s}c,{\chi }_{0,0}^{f2}=\overline{s}b\overline{s}b,{\chi }_{0,0}^{f3}=\overline{s}c\overline{s}b.\hfill \end{array}$$

(90)

The third component of the isospin, $M_I$, is set to be equal to the absolute value of total isospin I. This is reasonable because our model does not include an interaction sensible to such dependence.

• Pentaquark

Three different 5-quark systems are studied in this work, namely, hidden-charm, hidden-bottom and doubly charmed pentaquarks. Accordingly, $I=\frac{1}{2}$ and $\frac{3}{2}$ channels are allowed. However, only the hidden-charm pentaquark state in $I=\frac{1}{2}$ sector was discussed in our earliest work. The total 5-quark flavor wave-function is obtained by coupling the bases of the two sub-clusters which are baryons and mesons.

In the $uudQ\overline{Q}$ ($Q=c,b$) systems, we have two kinds of clustering, one is $(udQ)(\overline{Q}u)+(uuQ)(\overline{Q}d)$ and the other is $(uud)(\overline{Q}Q)$, as illustrated in Figure 3. The wave-functions are as below

$$\begin{array}{lll}\hfill {\chi }_1^f& =& \sqrt{\frac{2}{3}}{B}_{11}{M}_{\frac{1}{2},-\frac{1}{2}}-\sqrt{\frac{1}{3}}{B}_{10}{M}_{\frac{1}{2},\frac{1}{2}},\hfill \end{array}$$

(91)

$$\begin{array}{lll}\hfill {\chi }_2^f& =& B_{00}{M}_{\frac{1}{2},\frac{1}{2}},\hfill \end{array}$$

(92)

$$\begin{array}{lll}\hfill {\chi }_3^f& =& B_{\frac{1}{2},\frac{1}{2}}^1{M}_{00},\hfill \end{array}$$

(93)

$$\begin{array}{lll}\hfill {\chi }_4^f& =& B_{\frac{1}{2},\frac{1}{2}}^2{M}_{00},\hfill \end{array}$$

(94)

$$\begin{array}{lll}\hfill {\chi }_5^f& =& B_{\frac{3}{2},\frac{3}{2}}{M}_{00},\hfill \end{array}$$

(95)

$$\begin{array}{lll}\hfill {\chi }_6^f& =& B_{\frac{1}{2},\frac{1}{2}}{M}_{11},\hfill \end{array}$$

(96)

where the necessary bases on sub-clusters are

$$\begin{array}{l}{B}_{11}=uuQ,B_{10}=\frac{1}{\sqrt{2}}(ud+du)Q,B_{1-1}=ddQ,\hfill \end{array}$$

(97)

$$\begin{array}{l}{B}_{00}=\frac{1}{\sqrt{2}}(ud-du)Q,\hfill \end{array}$$

(98)

$$\begin{array}{l}{B}_{\frac{1}{2},\frac{1}{2}}^1=\frac{1}{\sqrt{6}}(2uud-udu-duu),\hfill \end{array}$$

(99)

$$\begin{array}{l}{B}_{\frac{1}{2},\frac{1}{2}}^2=\frac{1}{\sqrt{2}}(ud-du)u,\hfill \end{array}$$

(100)

$$\begin{array}{l}{B}_{\frac{3}{2},\frac{3}{2}}=uuu,\hfill \end{array}$$

(101)

$$\begin{array}{l}{M}_{\frac{1}{2},\frac{1}{2}}=\overline{Q}u,M_{\frac{1}{2},-\frac{1}{2}}=\overline{Q}d,M_{00}=\overline{Q}Q.\hfill \end{array}$$

(102)

As for the $QQqq\overline{q}$ ($Q=c,b$) pentaquarks shown in Figure 4, where the complete configurations in baryon-meson sector are considered, their flavor wave-functions with $I=1/2$ and $3/2$ read as

$$\begin{array}{ll}\hfill & {\chi }_{\frac{1}{2},\frac{1}{2}}^{nf1}(5)=\sqrt{\frac{2}{3}}{B}_{11}^n{M}_{\frac{1}{2},-\frac{1}{2}}-\sqrt{\frac{1}{3}}{B}_{10}^n{M}_{\frac{1}{2},\frac{1}{2}},\hfill \end{array}$$

(103)

$$\begin{array}{ll}\hfill & {\chi }_{\frac{1}{2},\frac{1}{2}}^{nf2}(5)=B_{00}^n{M}_{\frac{1}{2},\frac{1}{2}},\hfill \end{array}$$

(104)

$$\begin{array}{ll}\hfill & {\chi }_{\frac{1}{2},\frac{1}{2}}^{nf3}(5)=B_{\frac{1}{2},\frac{1}{2}}^n{M}_{00},\hfill \end{array}$$

(105)

$$\begin{array}{ll}\hfill & {\chi }_{\frac{1}{2},\frac{1}{2}}^{nf4}(5)=-\sqrt{\frac{2}{3}}{B}_{\frac{1}{2},-\frac{1}{2}}^n{M}_{11}+\sqrt{\frac{1}{3}}{B}_{\frac{1}{2},\frac{1}{2}}^n{M}_{10},\hfill \end{array}$$

(106)

$$\begin{array}{ll}\hfill & {\chi }_{\frac{3}{2},\frac{3}{2}}^{nf1}(5)=B_{\frac{1}{2},\frac{1}{2}}^n{M}_{1,1},\hfill \end{array}$$

(107)

$$\begin{array}{ll}\hfill & {\chi }_{\frac{3}{2},\frac{3}{2}}^{nf2}(5)=B_{1,1}^n{M}_{\frac{1}{2},\frac{1}{2}},\hfill \end{array}$$

(108)

where the third component of isospin is still chosen to be the same as total one, and the superscript $n=1,\dots ,4$ marks each four configurations in Figure 4. The flavor wave functions for the baryon and meson clusters are

$$\begin{array}{ll}\hfill B_{11}^3& =uuc,B_{1-1}^3=ddc,\hfill \end{array}$$

(109)

$$\begin{array}{ll}\hfill B_{11}^4& =ucu,B_{1-1}^4=dcd,\hfill \end{array}$$

(110)

$$\begin{array}{ll}\hfill B_{10}^3& =\frac{1}{\sqrt{2}}(ud+du)c,\hfill \end{array}$$

(111)

$$\begin{array}{ll}\hfill B_{10}^4& =\frac{1}{\sqrt{2}}(ucd+dcu),\hfill \end{array}$$

(112)

$$\begin{array}{ll}\hfill B_{00}^3& =\frac{1}{\sqrt{2}}(ud-du)c,\hfill \end{array}$$

(113)

$$\begin{array}{ll}\hfill B_{00}^4& =\frac{1}{\sqrt{2}}(ucd-dcu),\hfill \end{array}$$

(114)

$$\begin{array}{ll}\hfill B_{\frac{1}{2},\frac{1}{2}}^1& =ccu,B_{\frac{1}{2},-\frac{1}{2}}^1=ccd,\hfill \end{array}$$

(115)

$$\begin{array}{ll}\hfill B_{\frac{1}{2},\frac{1}{2}}^2& =cuc,B_{\frac{1}{2},-\frac{1}{2}}^2=cdc,\hfill \end{array}$$

(116)

$$\begin{array}{ll}\hfill M_{\frac{1}{2},\frac{1}{2}}& =\overline{d}c,M_{\frac{1}{2},-\frac{1}{2}}=-\overline{u}c,\hfill \end{array}$$

(117)

$$\begin{array}{ll}\hfill M_{11}& =\overline{d}u,M_{1-1}=-\overline{u}d,\hfill \end{array}$$

(118)

$$\begin{array}{ll}\hfill M_{10}& =-\frac{1}{\sqrt{2}}(\overline{u}u-\overline{d}d),\hfill \end{array}$$

(119)

$$\begin{array}{ll}\hfill M_{00}& =-\frac{1}{\sqrt{2}}(\overline{u}u+\overline{d}d),\hfill \end{array}$$

(120)

2.3.4. Spatial Wave-Function

The few-body bound state problem is solved by an exact and efficient variational method: the Gaussian expansion method (GEM) [188]. Within this theoretical framework, the intrinsic spatial wave-function is fitted by various widths (${\nu }_n$) of Gaussian bases which are taken in geometric progression form. Equation (121) presents a general expression of the orbital wave-function,

$$\begin{array}{l}\hfill {\varphi }_{nlm}(\overrightarrow{r})=N_{nl}{(r)}^l{e}^{-{\nu }_n{r}^2}{Y}_{lm}(\widehat{r}),\end{array}$$

(121)

where $N_{nl}$ is the normalization constants

$$N_{nl}={\left[\frac{2^{l+2}{(2{\nu }_n)}^{l+\frac{3}{2}}}{\sqrt{\pi }(2l+1)}\right]}^{\frac{1}{2}}.$$

(122)

The angle part of space is trivial in the S-wave multi-quark state, therein the angular matrix element is just a constant due to $Y_{00}=\sqrt{1/4\pi }$. However, as to avoid laborious Racah algebra in solving the angular excitation state, a powerful technique named infinitesimally shifted Gaussian (ISG) [188] is employed. With the spherical harmonic function absorbed into a shifted vector $\overrightarrow{D}$, the new function is

$${\varphi }_{nlm}(\overrightarrow{r})=N_{nl}\underset{\epsilon \to 0}{lim}\frac{1}{{({\nu }_n\epsilon )}^l}{\displaystyle \sum _{k=1}^{k_{max}}}{C}_{lm,k}{e}^{{-{\nu }_n(\overrightarrow{r}-\epsilon {\overrightarrow{D}}_{lm,k})}^2}.$$

(123)

Their applications in the tetraquark and pentaquark states will be discussed individually.

• Tetraquark

The spatial wave function of a 4-body system is

$${\psi }_{L{M}_L}={\left[{\left[{\varphi }_{n_1{l}_1}(\overrightarrow{\rho }){\varphi }_{n_2{l}_2}(\overrightarrow{\lambda })\right]}_l{\varphi }_{n_3{l}_3}(\overrightarrow{R})\right]}_{L{M}_L},$$

(124)

where the three internal Jacobi coordinates for Figure 2a of meson-meson configuration read as

$$\begin{array}{ll}\hfill \overrightarrow{\rho }& ={\overrightarrow{x}}_1-{\overrightarrow{x}}_2,\hfill \end{array}$$

(125)

$$\begin{array}{ll}\hfill \overrightarrow{\lambda }& ={\overrightarrow{x}}_3-{\overrightarrow{x}}_4,\hfill \end{array}$$

(126)

$$\begin{array}{ll}\hfill \overrightarrow{R}& =\frac{m_1{\overrightarrow{x}}_1+m_2{\overrightarrow{x}}_2}{m_1+m_2}-\frac{m_3{\overrightarrow{x}}_3+m_4{\overrightarrow{x}}_4}{m_3+m_4},\hfill \end{array}$$

(127)

and for the diquark-antidiquark structure of Figure 2b are defined as

$$\begin{array}{ll}\hfill \overrightarrow{\rho }& ={\overrightarrow{x}}_1-{\overrightarrow{x}}_3,\hfill \end{array}$$

(128)

$$\begin{array}{ll}\hfill \overrightarrow{\lambda }& ={\overrightarrow{x}}_2-{\overrightarrow{x}}_4,\hfill \end{array}$$

(129)

$$\begin{array}{ll}\hfill \overrightarrow{R}& =\frac{m_1{\overrightarrow{x}}_1+m_3{\overrightarrow{x}}_3}{m_1+m_3}-\frac{m_2{\overrightarrow{x}}_2+m_4{\overrightarrow{x}}_4}{m_2+m_4}.\hfill \end{array}$$

(130)

Moreover, the other K-type configurations from Figure 2c–f present the following Jacobi coordinates

$$\begin{array}{ll}\hfill \overrightarrow{\rho }& ={\overrightarrow{x}}_i-{\overrightarrow{x}}_j,\hfill \end{array}$$

(131)

$$\begin{array}{ll}\hfill \overrightarrow{\lambda }& ={\overrightarrow{x}}_k-\frac{m_i{\overrightarrow{x}}_i+m_j{\overrightarrow{x}}_j}{m_i+m_j},\hfill \end{array}$$

(132)

$$\begin{array}{ll}\hfill \overrightarrow{R}& ={\overrightarrow{x}}_l-\frac{m_i{\overrightarrow{x}}_i+m_j{\overrightarrow{x}}_j+m_k{\overrightarrow{x}}_k}{m_i+m_j+m_k},\hfill \end{array}$$

(133)

where the values of the subscripts $i,j,k,l$ must be in accordance with the definitions of each configuration in Figure 2.

Obviously, the center-of-mass kinetic term $T_{CM}$ can be completely eliminated for a nonrelativistic system in these sets of relative motion coordinates.

• Pentaquark

The spatial wave-function of a 5-body system is also constructed in the relative motion coordinates, Equation (134) presents a general form:

$${\psi }_{L{M}_L}={\left[{\left[{\left[{\varphi }_{n_1{l}_1}(\overrightarrow{\rho }){\varphi }_{n_2{l}_2}(\overrightarrow{\lambda })\right]}_l{\varphi }_{n_3{l}_3}(\overrightarrow{r})\right]}_{l^{\prime }}{\varphi }_{n_4{l}_4}(\overrightarrow{R})\right]}_{L{M}_L},$$

(134)

where in a baryon-meson configuration, the four Jacobi coordinates are defined as

$$\begin{array}{ll}\hfill \overrightarrow{\rho }& ={\overrightarrow{x}}_1-{\overrightarrow{x}}_2,\hfill \end{array}$$

(135)

$$\begin{array}{ll}\hfill \overrightarrow{\lambda }& ={\overrightarrow{x}}_3-\left(\frac{m_1{\overrightarrow{x}}_1+m_2{\overrightarrow{x}}_2}{m_1+m_2}\right),\hfill \end{array}$$

(136)

$$\begin{array}{ll}\hfill \overrightarrow{r}& ={\overrightarrow{x}}_4-{\overrightarrow{x}}_5,\hfill \end{array}$$

(137)

$$\begin{array}{ll}\hfill \overrightarrow{R}& =\left(\frac{m_1{\overrightarrow{x}}_1+m_2{\overrightarrow{x}}_2+m_3{\overrightarrow{x}}_3}{m_1+m_2+m_3}\right)-\left(\frac{m_4{\overrightarrow{x}}_4+m_5{\overrightarrow{x}}_5}{m_4+m_5}\right),\hfill \end{array}$$

(138)

where, again, the $T_{CM}$ part can be entirely subtracted when solving a 5-quark bound state system within a non-relativistic framework and using the above set of Jacobi coordinates.

2.4. Relativity and Mode Independence

Model estimates of the mean momentum, ⟨p⟩, of a light constituent quark, with mass m, inside a meson typically yield ⟨p ∼ m⟩. It might therefore be argued that bound-state calculations involving light quark systems should only be undertaken within models that, at some level, incorporate relativity. This potential weakness of the nonrelativistic quark model has long been considered. For example, reference [189] remarks that a nonrelativistic treatment of quark motion is inaccurate. However, using scales that are internally consistent, it is not ultrarelativistic. Therefore, the nonrelativistic approximation must be useful. The point is also canvassed in reference [190], which opens with the question “Why does the nonrelativistic quark model work?” and proceeds to provide a range of plausible answers. These discussions are complemented by reference [191], which devotes itself to “The significance of the treatment of relativistically moving constituents by an effective nonrelativistic Schrödinger equation [...].” The conclusion of these discourses and many others is simple: the nonrelativistic model has proved very useful, unifying a wide range of observables within a single framework.

This last observation provides our rationale for employing a nonrelativistic model for the analysis herein. Namely, we take a pragmatic view: the nonrelativistic quark model is a useful tool. The practical reason for its success is simple: the model has many parameters; they are fitted to a body of data; and, consequently, on this domain, the model cannot be wrong numerically. If one adds relativistic effects in one way or another, there are similar parameters in the new potential. They, too, are fitted to data; and hence the resulting model cannot produce results that are very different from the original nonrelativistic version. The values of the parameters in the potential are modified, but the potential is not observable, so nothing substantive is altered.

3. Results and Discussions

In the constituent quark model formalism, the possible low-lying bound and resonance states of doubly-, fully-heavy tetraquarks, hidden-charm, hidden-bottom and doubly charmed pentaquarks are systematically investigated by means of the computational approach, Gaussian expansion method. The obtained results along with their corresponding discussions are organized as follows.

3.1. Doubly and Fully Heavy Tetraquarks

In this part, the S-wave $QQ\overline{q}\overline{q}$ and $QQ\overline{Q}\overline{Q}$ ($Q=c,b$, $q=u,d,s$) tetraquark states with $J^P=0^{+}$, $1^{+}$ and $2^{+}$, the isospin $I=0$ or 1 are studied in the chiral quark model and Cornell potential model, respectively. We will discuss them one by one.

3.1.1. $QQ\overline{q}\overline{q}$ Tetraquarks

• Double-charm tetraquarks

According to the Pauli principle, all possible couplings in spin, flavor and color degrees of freedom for the S-wave tetraquark states are considered. Table 6 presents the allowed meson-meson and diqurak-antidiquark channels for doubly charmed tetraquarks in $J^P=0^{+}$, $1^{+}$ and $2^{+}$, $I=0$ and 1 states. However, bound and resonance states are only obtained in the $I(J^P)=0(1^{+})$ state. Their calculated masses are listed in Table 7 where two di-meson channels, $D^{+}{D}^{\ast 0}$ and $D^{\ast +}{D}^{\ast 0}$, two diquark-antidiquark channels, ${(cc)}^{\ast }(\overline{u}\overline{d})$ and $(cc){(\overline{u}\overline{d})}^{\ast }$, along with their couplings, are all considered. Particularly, the first column lists the allowed channels, their related experimental threshold values ($E_{th}^{ex}$) are also marked in parentheses. The color-singlet (S), hidden-color (H) channels and their couplings for di-meson configurations are listed in the second column. The computed mass (M) for each channel along with their binding energy ($E_B$), which is obtained by calculating the difference between the theoretical threshold ($E_{th}$) and the tetraquark mass (M), $E_B=M-E_{th}$, are presented in the 3rd and 4th columns, respectively. Then, the re-scaled masses ($M^{\prime }$), whose theoretical uncertainties coming from the model calculation of meson spectra are avoided, for meson-meson structures are listed in the last column and they are obtained by comparing the experimental threshold values and binding energies, $M^{\prime }=E_{th}^{ex}+E_B$.

Table 6. All possible channels for $cc\overline{q}\overline{q}$$(q=uord)$ tetraquark systems.

${\mathit{J}}^{\mathbf{P}}$	Index	$\mathit{I}=0$		$\mathit{I}=1$
		${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	Channel	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	Channel
		$[\mathit{i};\mathit{j};\mathit{k}]$		$[\mathit{i};\mathit{j};\mathit{k}]$
$0^{+}$	1	$[1;1;1]$	${(D^{+}{D}^0)}^1$	$[1;1;1]$	${(D^0{D}^0)}^1$
	2	$[2;1;1]$	${(D^{\ast +}{D}^{\ast 0})}^1$	$[2;1;1]$	${(D^{\ast 0}{D}^{\ast 0})}^1$
	3	$[1;1;2]$	${(D^{+}{D}^0)}^8$	$[1;1;2]$	${(D^0{D}^0)}^8$
	4	$[2;1;2]$	${(D^{\ast +}{D}^{\ast 0})}^8$	$[2;1;2]$	${(D^{\ast 0}{D}^{\ast 0})}^8$
	5			$[3;1;4]$	$(cc)(\overline{u}\overline{u})$
	6			$[4;1;3]$	${(cc)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$
$1^{+}$	1	$[1;1;1]$	${(D^{+}{D}^{\ast 0})}^1$	$[1;1;1]$	${(D^0{D}^{\ast 0})}^1$
	2	$[3;1;1]$	${(D^{\ast +}{D}^{\ast 0})}^1$	$[3;1;1]$	${(D^{\ast 0}{D}^{\ast 0})}^1$
	3	$[1;1;2]$	${(D^{+}{D}^{\ast 0})}^8$	$[1;1;2]$	${(D^0{D}^{\ast 0})}^8$
	4	$[3;1;2]$	${(D^{\ast +}{D}^{\ast 0})}^8$	$[3;1;2]$	${(D^{\ast 0}{D}^{\ast 0})}^8$
	5	$[4;1;3]$	${(cc)}^{\ast }(\overline{u}\overline{d})$	$[6;1;3]$	${(cc)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$
	6	$[5;1;4]$	$(cc){(\overline{u}\overline{d})}^{\ast }$
$2^{+}$	1	$[1;1;1]$	${(D^{\ast +}{D}^{\ast 0})}^1$	$[1;1;1]$	${(D^{\ast 0}{D}^{\ast 0})}^1$
	2	$[1;1;2]$	${(D^{\ast +}{D}^{\ast 0})}^8$	$[1;1;2]$	${(D^{\ast 0}{D}^{\ast 0})}^8$
	3			$[1;1;3]$	${(cc)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$

Table 7. Lowest-lying states of double-charm tetraquarks with quantum numbers $I(J^P)=0(1^{+})$, unit in MeV.

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	${\mathbf{M}}^{\prime }$
$D^{+}{D}^{\ast 0}$	S	3915	0	3877
$(3877)$	H	4421	$+506$	4383
	S+H	3914	$-1$	3876
	Percentage (S;H): 97.3%; 2.7%
$D^{\ast +}{D}^{\ast 0}$	S	4034	0	4018
$(4018)$	H	4390	$+356$	4374
	S+H	4033	$-1$	4017
	Percentage (S;H): 95.5%; 4.5%
${(cc)}^{\ast }(\overline{u}\overline{d})$		3778
$(cc){(\overline{u}\overline{d})}^{\ast }$		4220
Mixed		3726

Firstly, in the single channel computation for color-singlet (S) and hidden-color cases (H) of the $D^{(\ast )+}{D}^{\ast 0}$ structures, the lowest masses are all above threshold values. However, loosely bound states of $D^{+}{D}^{\ast 0}$ and $D^{\ast +}{D}^{\ast 0}$ are available in a coupled-channels calculation (S+H). Then, after a mass shift correction, according to the difference between the theoretical and experimental thresholds, the re-scaled masses of these two bound states are $3876\mathrm{MeV}$ and $4017\mathrm{MeV}$, respectively. Furthermore, these two bound states can be identified as molecules of $D^{(\ast )+}{D}^{\ast 0}$ because color-singlet channels are dominant with respect the hidden-color ones.

Deeply bound diquark-antidiquark channel ${(cc)}^{\ast }(\overline{u}\overline{d})$ with a binding energy of about $-140\mathrm{MeV}$ is found and the theoretical mass is $3778\mathrm{MeV}$. However, another diquark-antidiquark $(cc){(\overline{u}\overline{d})}^{\ast }$ state is unbound and its mass is above the $D^{+}{D}^{\ast 0}$ and $D^{\ast +}{D}^{\ast 0}$ theoretical thresholds with $E_B=+305\mathrm{MeV}$ and $+186\mathrm{MeV}$, respectively. In a further step, we perform a complete coupled-channels calculation for the channels listed in Table 6, and the lowest-lying bound state mass is $3726\mathrm{MeV}$. By analyzing the distance between any two quarks of the $cc\overline{q}\overline{q}$ system in Table 8, the nature of a compact double-charm tetraquark state is clearly presented. The general size of this tetraquark state is around $0.67\mathrm{fm}$. Meanwhile, tightly bound and compact structure of the obtained tetraquark state is also confirmed in Table 9 where each component in the coupled-channels calculation is presented and the two dominant channels are the color-singlet channel $D^{+}{D}^{\ast 0}$ (25.8%) and diquark-antidiquark ${(cc)}^{\ast }(\overline{q}\overline{q})$ one (36.7%). As to find possible double-charm tetraquark resonance at higher energies, the complex scaling method is employed in the complete coupled channels calculation. Figure 5 shows the distributions of calculated complex energies in the $I(J^P)$ = $0(1^{+})$ channel. Apparently, the bound state is independent of the rotated angle which is varied from 0° to 6° and still locates at 3726 MeV of real-axis. The other energy points are generally aligned along the $D^{(\ast )+}{D}^{\ast 0}$ threshold lines which are scattering states. However, one possible resonance state whose mass and width are ∼4312 MeV and ∼16 MeV, respectively, is obtained in the complex plane and it is marked by an orange circle with three calculated pole almost overlapping. This unchanged pole is far from the $D^{+}{D}^{\ast 0}$ threshold lines, therefore, it can be identified as a $D^{\ast +}{D}^{\ast 0}$ resonance.

Table 8. The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation $(q=u,d)$.

${\mathit{r}}_{\overline{\mathit{u}}\overline{\mathit{d}}}$	${\mathit{r}}_{\overline{\mathit{q}}\mathit{c}}$	${\mathit{r}}_{\mathit{cc}}$
0.658	0.666	0.522

Table 9. Component of each channel in coupled-channels calculation with $I(J^P)=0(1^{+})$, the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively.

${(D^{+}{D}^{\ast 0})}^1$	${(D^{\ast +}{D}^{\ast 0})}^1$	${(D^{+}{D}^{\ast 0})}^8$	${(D^{\ast +}{D}^{\ast 0})}^8$
25.8%	15.4%	10.7%	11.2%
${(cc)}^{\ast }(\overline{u}\overline{d})$	$(cc){(\overline{u}\overline{d})}^{\ast }$
36.7%	0.2%

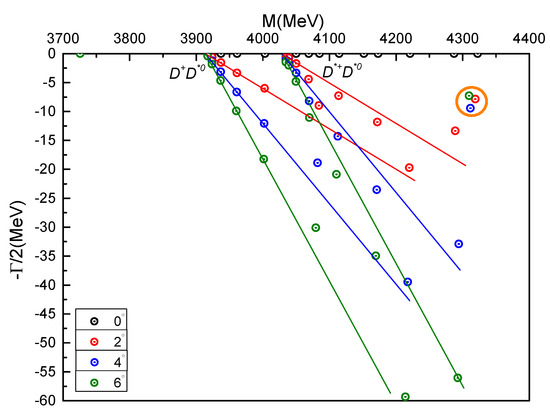
Figure 5. Complex energies of double-charm tetraquarks with $I(J^P)=0(1^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

• Double-bottom tetraquarks

In the $bb\overline{q}\overline{q}$ ($q=u,d$) sector, possible $B^{(\ast )-}{\overline{B}}^{\ast 0}$ meson-meson channels and ${(bb)}^{(\ast )}{(\overline{q}\overline{q})}^{(\ast )}$ diquark-antidiquark structures, in each quantum state, are listed in Table 10. However, it is similar to the doubly charmed case, bound and resonance states are only found in the $I(J^P)=0(1^{+})$ channel. Table 11 shows the calculated results, and the arrangements of each columns are similar to Table 7. Firstly, one can notice that bound states of $B^{-}{\overline{B}}^{\ast 0}$ and $B^{\ast -}{\overline{B}}^{\ast 0}$ in color-singlet channels are obtained, and the ∼$-10$ MeV binding energy is due to the presence of heavier b-flavored quarks. Additionally, in a coupled-channels calculation with hidden-color channels included, deeper binding energies (∼$-35$ MeV) are obtained for these two di-meson channels. The color-singlet and hidden-color channels are around 80% and 20% dominant in the tetraquark states. By considering the systematic uncertainty during calculation, the modified masses for $B^{-}{\overline{B}}^{\ast 0}$ and $B^{\ast -}{\overline{B}}^{\ast 0}$ bound state are $\mathrm{10,596}$ MeV and $\mathrm{10,613}$ MeV respectively.

Table 10. All possible channels for $bb\overline{q}\overline{q}$$(q=uord)$ tetraquark systems.

${\mathit{J}}^{\mathbf{P}}$	Index	$\mathit{I}=0$		$\mathit{I}=1$
		${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	Channel	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	Channel
		$[\mathit{i};\mathit{j};\mathit{k}]$		$[\mathit{i};\mathit{j};\mathit{k}]$
$0^{+}$	1	$[1;2;1]$	${(B^{-}{\overline{B}}^0)}^1$	$[1;2;1]$	${(B^{-}{B}^{-})}^1$
	2	$[2;2;1]$	${(B^{\ast -}{\overline{B}}^{\ast 0})}^1$	$[2;2;1]$	${(B^{\ast -}{B}^{\ast -})}^1$
	3	$[1;2;2]$	${(B^{-}{\overline{B}}^0)}^8$	$[1;2;2]$	${(B^{-}{B}^{-})}^8$
	4	$[2;2;2]$	${(B^{\ast -}{\overline{B}}^{\ast 0})}^8$	$[2;2;2]$	${(B^{\ast -}{B}^{\ast -})}^8$
	5			$[3;2;4]$	$(bb)(\overline{u}\overline{u})$
	6			$[4;2;3]$	${(bb)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$
$1^{+}$	1	$[1;2;1]$	${(B^{-}{\overline{B}}^{\ast 0})}^1$	$[1;2;1]$	${(B^{-}{B}^{\ast -})}^1$
	2	$[3;2;1]$	${(B^{\ast -}{\overline{B}}^{\ast 0})}^1$	$[3;2;1]$	${(B^{\ast -}{B}^{\ast -})}^1$
	3	$[1;2;2]$	${(B^{-}{\overline{B}}^{\ast 0})}^8$	$[1;2;2]$	${(B^{-}{B}^{\ast -})}^8$
	4	$[3;2;2]$	${(B^{\ast -}{\overline{B}}^{\ast 0})}^8$	$[3;2;2]$	${(B^{\ast -}{B}^{\ast -})}^8$
	5	$[4;2;3]$	${(bb)}^{\ast }(\overline{u}\overline{d})$	$[6;2;3]$	${(bb)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$
	6	$[5;2;4]$	$(bb){(\overline{u}\overline{d})}^{\ast }$
$2^{+}$	1	$[1;2;1]$	${(B^{\ast -}{\overline{B}}^{\ast 0})}^1$	$[1;2;1]$	${(B^{\ast -}{B}^{\ast -})}^1$
	2	$[1;2;2]$	${(B^{\ast -}{\overline{B}}^{\ast 0})}^8$	$[1;2;2]$	${(B^{\ast -}{B}^{\ast -})}^8$
	3			$[1;2;3]$	${(bb)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$

Table 11. Lowest-lying states of double-bottom tetraquarks with quantum numbers $I(J^P)=0(1^{+})$, unit in MeV.

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	${\mathbf{M}}^{\prime }$
$B^{-}{\overline{B}}^{\ast 0}$	S	10,585	$-12$	10,592
$(\mathrm{10,604})$	H	10,987	$+390$	10,994
	S + H	10,562	$-35$	10,569
	Percentage (S;H): 83.0%; 17.0%
$B^{\ast -}{\overline{B}}^{\ast 0}$	S	10,627	$-11$	10,639
$(\mathrm{10,650})$	H	10,974	$+336$	10,986
	S + H	10,601	$-37$	10,613
	Percentage (S;H): 79.6%; 20.4%
${(bb)}^{\ast }(\overline{u}\overline{d})$		10,261
$(bb){(\overline{u}\overline{d})}^{\ast }$		10,787
Mixed		10,238 1st
		10,524 2nd

There are two diquark-antidiquark channels under investigated, ${(bb)}^{\ast }(\overline{u}\overline{d})$ and $(bb){(\overline{u}\overline{d})}^{\ast }$, the calculated masses are 10,261 MeV and 10,787 MeV, respectively. Clearly, the former structure is a tightly bound tetraquark state with binding energy $E_B=-336\mathrm{MeV}$. However, the other one is 190 MeV above the $B^{-}{\overline{B}}^{\ast 0}$ theoretical threshold. Our result on this diquark-antidiquark bound state is supported by references [26,27,28,34], and only ∼$130\mathrm{MeV}$ lower than the calculated value in reference [27].

In the third step, a complete coupled-channels calculation is performed. Two bound states whose masses are 10,238 MeV and 10,524 MeV are obtained. The first state is close to the ${(bb)}^{\ast }(\overline{u}\overline{d})$ channel and 23 MeV lower when coupling is included. The second bound state is below the $B^{-}{\overline{B}}^{\ast 0}$ theoretical threshold with $73\mathrm{MeV}$. Furthermore, Table 12 presents the composition of these two bound states in coupled-channels computation. They are both around 42% ${(bb)}^{\ast }(\overline{u}\overline{d})$ and ∼20% $B^{(\ast )-}{\overline{B}}^{\ast 0}$. Accordingly, they can be identified as compact tetraquark bound states when analyzing the internal structure, the distance between any two quarks are calculated in Table 13. Therein, the general size is less than $0.83\mathrm{fm}$ and the values $0.328\mathrm{fm}$ and $0.711\mathrm{fm}$ on two bottom quarks are even smaller for the two obtained bound states.

Table 12. Component of each channel in coupled-channels calculation with $I(J^P)=0(1^{+})$, the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively.

	${(B^{-}{\overline{B}}^{\ast 0})}^1$	${(B^{\ast -}{\overline{B}}^{\ast 0})}^1$	${(B^{-}{\overline{B}}^{\ast 0})}^8$
1st	20.7%	17.9%	9.3%
2nd	25.6%	14.8%	9.5%
	${(B^{\ast -}{\overline{B}}^{\ast 0})}^8$	${(bb)}^{\ast }(\overline{u}\overline{d})$	$(bb){(\overline{u}\overline{d})}^{\ast }$
1st	9.4%	42.6%	0.1%
2nd	9.1%	40.2%	0.8%

Table 13. The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation, $(q=u,d)$.

	${\mathit{r}}_{\overline{\mathit{u}}\overline{\mathit{d}}}$	${\mathit{r}}_{\overline{\mathit{q}}\mathit{b}}$	${\mathit{r}}_{\mathit{bb}}$
1st	0.604	0.608	0.328
2nd	0.830	0.734	0.711

In a complex range investigation of the $I(J^P)=0(1^{+})$$bb\overline{q}\overline{q}$ tetraquarks, apart from the original two bound states, one narrow resonance is also found. Figure 6 shows the distributions of the calculated energy points in the complete coupled case and the rotated angle $\theta$ is also taken from 0° to 6°. In this range, the threshold lines of two meson-meson channels $B^{-}{\overline{B}}^{\ast 0}$ and $B^{\ast -}{\overline{B}}^{\ast 0}$ are well established and the two bound states is stable in the real-axis at 10,238 MeV and 10,524 MeV, respectively. Meanwhile, a fixed resonance pole at ∼10.8 GeV is obtained with the variation of $\theta$. We marked it with a big orange circle in Figure 6, besides the theoretical mass and width of this narrow resonance is 10,814 MeV and $2\mathrm{MeV}$, respectively. Because it is closer to the $B^{\ast -}{\overline{B}}^{\ast 0}$ threshold lines, this meson-meson resonance is expected to be confirmed in future experiments.

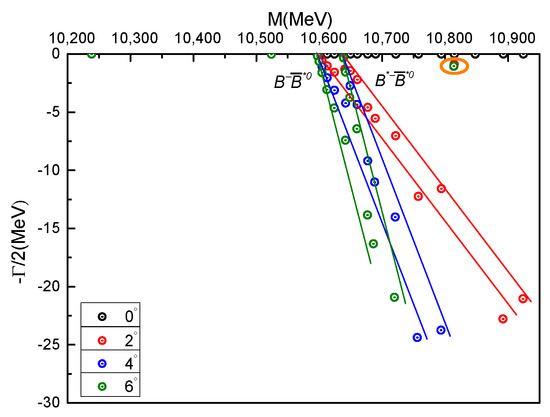
Figure 6. Complex energies of double-bottom tetraquarks with $I(J^P)=0(1^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

• Charm-bottom tetraquarks

Table 14 lists the allowed channels of $cb\overline{q}\overline{q}$ tetraquark with $J^P=0^{+}$, $1^{+}$ and $2^{+}$, $I=0$ and 1, respectively. However, some bound and resonance states are only found in the iso-scalar sector, besides the calculated results on meson-meson configurations are supported by the investigation of reference [192]. We will discuss these tetraquark states according to $I(J^P)$ quantum numbers respectively. Meanwhile, the arrangements of each column in Table 15, Table 16 and Table 17 are still the same as those in Table 7.

Table 14. All possible channels for $cb\overline{q}\overline{q}$$(q=uord)$ tetraquark systems. For a brief purpose, only the $D^{(\ast )0}{B}^{(\ast )0}$ structures are listed and the corresponding $D^{(\ast )+}{\overline{B}}^{(\ast )-}$ ones are absent in $I=0$. However, all these configurations are still employed in constructing the wave functions of 4-quark systems.

${\mathit{J}}^{\mathbf{P}}$	Index	$\mathit{I}=0$		$\mathit{I}=1$
		${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	Channel	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	Channel
		$[\mathit{i};\mathit{j};\mathit{k}]$		$[\mathit{i};\mathit{j};\mathit{k}]$
$0^{+}$	1	$[1;3;1]$	${(D^0{\overline{B}}^0)}^1$	$[1;3;1]$	${(D^0{B}^{-})}^1$
	2	$[2;3;1]$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^1$	$[2;3;1]$	${(D^{\ast 0}{B}^{\ast -})}^1$
	3	$[1;3;2]$	${(D^0{\overline{B}}^0)}^8$	$[1;3;2]$	${(D^0{B}^{-})}^8$
	4	$[2;3;2]$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^8$	$[2;3;2]$	${(D^{\ast 0}{B}^{\ast -})}^8$
	5	$[3;3;3]$	$(cb)(\overline{u}\overline{d})$	$[3;3;4]$	$(cb)(\overline{u}\overline{u})$
	6	$[4;3;4]$	${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$	$[4;3;3]$	${(cb)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$
$1^{+}$	1	$[1;3;1]$	${(D^0{\overline{B}}^{\ast 0})}^1$	$[1;3;1]$	${(D^0{B}^{\ast -})}^1$
	2	$[2;3;1]$	${(D^{\ast 0}{\overline{B}}^0)}^1$	$[2;3;1]$	${(D^{\ast 0}{B}^{-})}^1$
	3	$[3;3;1]$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^1$	$[3;3;1]$	${(D^{\ast 0}{B}^{\ast -})}^1$
	4	$[1;3;2]$	${(D^0{\overline{B}}^{\ast 0})}^8$	$[1;3;2]$	${(D^0{B}^{\ast -})}^8$
	5	$[2;3;2]$	${(D^{\ast 0}{\overline{B}}^0)}^8$	$[2;3;2]$	${(D^{\ast 0}{B}^{-})}^8$
	6	$[3;3;2]$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^8$	$[3;3;2]$	${(D^{\ast 0}{B}^{\ast -})}^8$
	7	$[4;3;3]$	${(cb)}^{\ast }(\overline{u}\overline{d})$	$[4;3;4]$	${(cb)}^{\ast }(\overline{u}\overline{u})$
	8	$[5;3;4]$	$(cb){(\overline{u}\overline{d})}^{\ast }$	$[5;3;3]$	$(cb){(\overline{u}\overline{u})}^{\ast }$
	9	$[6;3;4]$	${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$	$[6;3;3]$	${(cb)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$
$2^{+}$	1	$[1;3;1]$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^1$	$[1;3;1]$	${(D^{\ast 0}{B}^{\ast -})}^1$
	2	$[1;3;2]$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^8$	$[1;3;2]$	${(D^{\ast 0}{B}^{\ast -})}^8$
	3	$[1;3;4]$	${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$	$[1;3;3]$	${(cb)}^{\ast }{(\overline{u}\overline{u})}^{\ast }$

Table 15. Lowest-lying states of charm-bottom tetraquarks with quantum numbers $I(J^P)=0(0^{+})$, unit in MeV.

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	${\mathbf{M}}^{\prime }$
$D^0{\overline{B}}^0$	S	7172	$-4$	7143
$(7147)$	H	7685	$+509$	7656
	S+H	7171	$-5$	7142
	Percentage (S;H): 96.4%; 3.6%
$D^{\ast 0}{\overline{B}}^{\ast 0}$	S	7327	$-9$	7325
$(7334)$	H	7586	$+250$	7584
	S+H	7297	$-39$	7295
	Percentage (S;H): 87.8%; 12.2%
$(cb)(\overline{u}\overline{d})$		7028
${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$		7482
Mixed		6980

Table 16. Lowest-lying states of charm-bottom tetraquarks with quantum numbers $I(J^P)=0(1^{+})$, unit in MeV.

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	${\mathbf{M}}^{\prime }$
$D^0{\overline{B}}^{\ast 0}$	S	7214	$-3$	7190
$(7193)$	H	7694	$+477$	7670
	S+H	7213	$-4$	7189
	Percentage (S;H): 96.8%; 3.2%
$D^{\ast 0}{\overline{B}}^0$	S	7293	$-2$	7286
$(7288)$	H	7707	$+412$	7700
	S+H	7292	$-3$	7285
	Percentage (S;H): 96.8%; 3.2%
$D^{\ast 0}{\overline{B}}^{\ast 0}$	S	7334	$-2$	7332
$(7334)$	H	7691	$+354$	7688
	S+H	7326	$-10$	7324
	Percentage (S;H): 89.3%; 10.7%
${(cb)}^{\ast }(\overline{u}\overline{d})$		7039
$(cb){(\overline{u}\overline{d})}^{\ast }$		7531
${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$		7507
Mixed		6997

Table 17. Lowest-lying states of charm-bottom tetraquarks with quantum numbers $I(J^P)=0(2^{+})$, unit in MeV.

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	${\mathbf{M}}^{\prime }$
$D^{\ast 0}{\overline{B}}^{\ast 0}$	S	7334	$-2$	7332
$(7334)$	H	7720	$+384$	7718
	S+H	7334	$-2$	7332
	Percentage (S;H): 99.8%; 0.2%
${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$		7552
Mixed		7333

• $I(J^P)=0(0^{+})$ state

Table 15 summarizes the calculated results of each meson-meson, diquark-antidiquark channels, along with their couplings. Weakly bound states of $D^0{\overline{B}}^0$ and $D^{\ast 0}{\overline{B}}^{\ast 0}$ in color-singlet channels are obtained first, the binding energies are $-4\mathrm{MeV}$ and $-9\mathrm{MeV}$, respectively. Then, in a coupled-channels computation in which the hidden-color channels are included, a bound state in the $D^{\ast 0}{\overline{B}}^{\ast 0}$ case is pushed down with a binding energy of $E_B=-39\mathrm{MeV}$; note, however, that the coupling effect is quite weak in the $D^0{\overline{B}}^0$ channel. These features on binding energies are confirmed when looking at each component in Table 15, where the proportion of color-singlet channel in the $D^0{\overline{B}}^0$ and $D^{\ast 0}{\overline{B}}^{\ast 0}$ are 96.4% and 87.8%, respectively.

In the diquark-antidiquark sector, by comparing with the $D^0{\overline{B}}^0$ theoretical threshold value, one tightly bound state $(cb)(\overline{u}\overline{d})$ with $E_B=-148\mathrm{MeV}$ and one excited state ${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$ with $E_B=+306\mathrm{MeV}$ are obtained. Furthermore, the lowest bound state is found at 6980 MeV in the fully coupled-channels investigation. Obviously, this should be a compact charm-bottom tetraquark state, since its nature can be confirmed by analyzing the component and inner structure presented in Table 18 and Table 19, respectively. In particular, the size of the tetraquark in $0(0^{+})$ state is less than $0.66\mathrm{fm}$ and the $(cb)(\overline{u}\overline{d})$ channel constitute almost 50%, the sub-dominant components are 26.4% of ${(D^0{\overline{B}}^0)}^1$ and 21.5% of ${(D^{\ast 0}{\overline{B}}^{\ast 0})}^1$.

Table 18. Component of each channel in coupled-channels calculation, the numbers 1 and 8 of superscript are for singlet-color and hidden-color channel respectively, $(q=u,d)$.

$I(J^P)$	${(D^0{\overline{B}}^0)}^1$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^1$	${(D^0{\overline{B}}^0)}^8$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^8$
$0(0^{+})$	26.4%	21.5%	1.6%	1.9%
	$(cb)(\overline{u}\overline{d})$	${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$
	48.5%	0.1%
$0(1^{+})$	${(D^0{\overline{B}}^{\ast 0})}^1$	${(D^{\ast 0}{\overline{B}}^0)}^1$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^1$	${(D^0{\overline{B}}^{\ast 0})}^8$
	20.2%	11.6%	16.8%	1.4%
	${(D^{\ast 0}{\overline{B}}^0)}^8$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^8$	${(cb)}^{\ast }(\overline{u}\overline{d})$	$(cb){(\overline{u}\overline{d})}^{\ast }$
	1.3%	1.8%	46.4%	0.1%
	${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$
	0.4%
$0(2^{+})$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^1$	${(D^{\ast 0}{\overline{B}}^{\ast 0})}^8$	${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$
	98.6%	0.3%	1.1%

Table 19. The distance, in fm, between any two quarks of the found tetraquark bound-states in coupled-channels calculation, $(q=u,d)$.

${\mathbf{IJ}}^{\mathbf{P}}$	${\mathit{r}}_{\overline{\mathit{u}}\overline{\mathit{d}}}$	${\mathit{r}}_{\overline{\mathit{q}}\mathit{c}}$	${\mathit{r}}_{\overline{\mathit{q}}\mathit{b}}$	${\mathit{r}}_{\mathit{cb}}$
${00}^{+}$	0.635	0.653	0.610	0.428
${01}^{+}$	0.632	0.661	0.616	0.434
${02}^{+}$	2.248	1.612	1.597	2.102

The complete coupled-channels calculation is performed in a complex-range where the rotated angle $\theta$ is taken from 0° to 6°. The nature of the tetraquark bound state is clearly shown in Figure 7, where the calculated dots are always fixed in the real-axis and at 6980 MeV. The other energy points which are generally aligned along the corresponding $D^0{\overline{B}}^0$ and $D^{\ast 0}{\overline{B}}^{\ast 0}$ threshold lines are scattering states. We also find a narrow resonance whose mass is around $7.7\mathrm{GeV}$ and its width is ∼$12\mathrm{MeV}$. Although this resonance pole, marked with orange circle, is above $D^0{\overline{B}}^0$ and $D^{\ast 0}{\overline{B}}^{\ast 0}$ thresholds, we can still identify it as a $D^{\ast 0}{\overline{B}}^{\ast 0}$ molecule resonance which is farther away from $D^0{\overline{B}}^0$ lines.

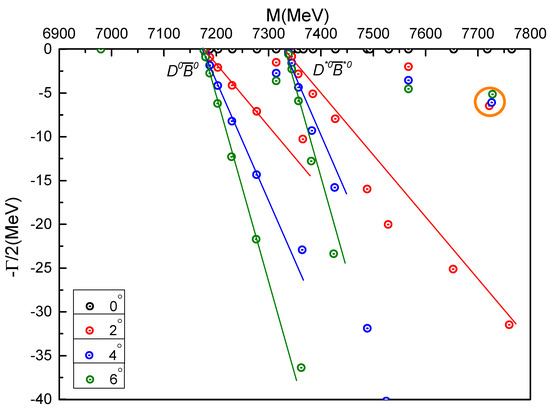
Figure 7. Complex energies of charm-bottom tetraquarks with $I(J^P)=0(0^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

• $I(J^P)=0(1^{+})$ state

There are three channels in the di-meson $D^{(\ast )0}{\overline{B}}^{(\ast )0}$ and diquark-antidiquark ${(cb)}^{(\ast )}{(\overline{u}\overline{d})}^{(\ast )}$ configurations, respectively. Besides, the single channel and the coupled results are all listed in Table 16. Similar to the above discussed doubly heavy tetraquarks, four conclusions can be drawn in a real-range calculation. (i) Loosely bound states are obtained in the color-singlet channels of $D^0{\overline{B}}^{\ast 0}$, $D^{\ast 0}{\overline{B}}^0$ and $D^{\ast 0}{\overline{B}}^{\ast 0}$, their weak binding energies are $E_B=-3\mathrm{MeV}$, $-2\mathrm{MeV}$ and $-2\mathrm{MeV}$, respectively. (ii) The coupling between singlet- and hidden-color channels in meson-meson configuration is weak and more than 90% component is due to the former channel. (iii) One tightly bound diquark-antidiquark state ${(cb)}^{\ast }(\overline{u}\overline{d})$ is found and the theoretical mass is 7039 MeV, the other two diquark-antidiquark masses are above 7.5 GeV. (IV) In a fully coupled-channels calculation, the mass of the bound state reduces to 6997 MeV.

In order to have a better insight into the nature of the obtained bound state in the complete coupled-channels calculation, we may also focus on our results about structure of the tetraquark bound state. As shown in Table 18 and Table 19, the dominant contribution 46.4% is from ${(cb)}^{\ast }(\overline{u}\overline{d})$ channel and other three sub-dominant channels are the color-singlet channels of $D^0{\overline{B}}^{\ast 0}$, $D^{\ast 0}{\overline{B}}^0$ and $D^{\ast 0}{\overline{B}}^{\ast 0}$; their contributions are 20.2%, 11.6% and 16.8%, respectively. This strong coupling effect leads to a compact structure whose size is less than 0.67 fm again.

With the complete coupled-channels computation extended to a complex-range in which $\theta$ is chosen from 0° to 6°, the bound state is confirmed again. Moreover, one more resonance state is found. In Figure 8 one can notice that, apart from the scattering points which are the $D^0{\overline{B}}^{\ast 0}$, $D^{\ast 0}{\overline{B}}^0$ and $D^{\ast 0}{\overline{B}}^{\ast 0}$ channels, one bound state at $6997\mathrm{MeV}$ of real-axis and one narrow resonance state with mass and width $7327\mathrm{MeV}$ and $2.4\mathrm{MeV}$ are obtained. Due to the resonance pole is located in the region between $D^{\ast 0}{\overline{B}}^0$ and $D^{\ast 0}{\overline{B}}^{\ast 0}$ thresholds, it can be identified as the $D^{\ast 0}{\overline{B}}^0$ resonance state according to the definition in CSM.

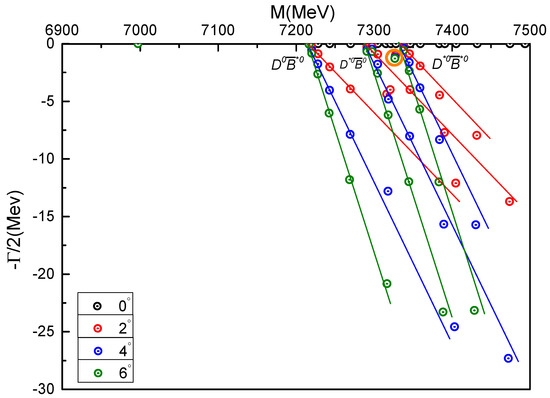
Figure 8. Complex energies of charm-bottom tetraquarks with $I(J^P)=0(1^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

• $I(J^P)=0(2^{+})$ state

Only a meson-meson $D^{\ast 0}{\overline{B}}^{\ast 0}$ channel and a diquark-antidiquark ${(cb)}^{\ast }{(\overline{u}\overline{d})}^{\ast }$ one are available for the highest spin state. Firstly, in single channel calculations, only the $D^{\ast 0}{\overline{B}}^{\ast 0}$ color-singlet channel is loosely bound with $E_B=-2\mathrm{MeV}$. Furthermore, this fact is not changed by the coupling with a hidden-color channel and only 1 MeV decrease is found in the complete coupled-channels case, the lowest mass is 7333 MeV. Hence, a molecular-type structure is possible for the obtained bound state; this is supported by calculating the quark distances where some of them are already beyond $1.6\mathrm{fm}$ when looking at Table 19, moreover, ∼99% contribution comes from color-singlet channel of $D^{\ast 0}{\overline{B}}^{\ast 0}$.

In contrast to the previous tetraquark states, no extra resonance is found in the $I{J}^P={02}^{+}$ channel. It is clearly shown in Figure 9 that all of the calculated poles are aligned along the $D^{\ast 0}{\overline{B}}^{\ast 0}$ threshold lines, except the weakly bound state at 7333 MeV.

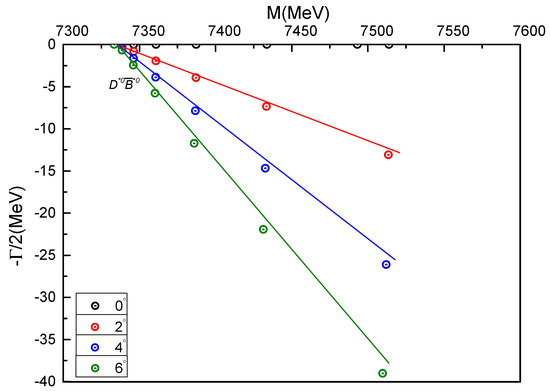
Figure 9. Complex energies of charm-bottom tetraquarks with $I(J^P)=0(2^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

3.1.2. $QQ\overline{s}\overline{s}$ Tetraquarks

As for a natural extension of the work on $QQ\overline{q}\overline{q}$ ($Q=c,b$ and $q=u,d$) systems, the double-heavy tetraquark state in strange quark sector is investigated herein. In addition, for this 4-quark system, a complete set of configurations including meson-meson, diquark-antidiquark and K-type structures (Figure 2) is included. As for a clarify purpose, masses and mean square radii of the $Q\overline{s}$ mesons are listed in Table 20. These results will be useful in identifying possible $QQ\overline{s}\overline{s}$ bound or resonance states. Furthermore, Tables ranging from Table 21, Table 22, Table 23, Table 24, Table 25, Table 26, Table 27, Table 28 and Table 29 summarized our theoretical findings. Particularly, in those tables, the first column shows the allowed channels and, in the parenthesis, the noninteracting meson-meson threshold value of experiment. Color-singlet (S), hidden-color (H) along with other configurations are indexed in the second column, respectively, the third column lists the necessary bases in spin, flavor and color degrees of freedom, the fourth and fifth columns refer to the theoretical mass of each channels and their couplings.

Table 20. Theoretical and experimental masses of $D_s^{(\ast )+}$ and $B_s^{(\ast )}$ mesons, their theoretical sizes are also calculated.

Meson	nL	The.	Exp.
$D_s^{+}$	$1S$	1989 MeV; $0.47$ fm	1969 MeV
	$2S$	2703 MeV; $1.06$ fm	-
$D_s^{\ast +}$	$1S$	2116 MeV; $0.55$ fm	2112 MeV
	$2S$	2767 MeV; $1.14$ fm	-
${\overline{B}}_s^0$	$1S$	5355 MeV; $0.47$ fm	5367 MeV
	$2S$	6017 MeV; $1.01$ fm	-
${\overline{B}}_s^{\ast }$	$1S$	5400 MeV; $0.50$ fm	5415 MeV
	$2S$	6042 MeV; $1.04$ fm	-

Table 21. The lowest-lying eigen-energies of $cc\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(0^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${(D_s^{+}{D}_s^{+})}^1(3938)$	1 (S)	$[1;1;1]$	3978
${(D_s^{\ast +}{D}_s^{\ast +})}^1(4224)$	2 (S)	$[2;1;1]$	4232	3978
${(D_s^{+}{D}_s^{+})}^8$	3 (H)	$[1;1;2]$	4619
${(D_s^{\ast +}{D}_s^{\ast +})}^8$	4 (H)	$[2;1;2]$	4636	4377
$(cc)(\overline{s}\overline{s})$	5	$[3;1;4]$	4433
${(cc)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	6	$[4;1;3]$	4413	4379
$K_1$	7	$[5;1;5]$	4802
$K_1$	8	$[5;1;6]$	4369
$K_1$	9	$[6;1;5]$	4698
$K_1$	10	$[6;1;6]$	4211	4201
$K_2$	11	$[7;1;7]$	4343
$K_2$	12	$[7;1;8]$	4753
$K_2$	13	$[8;1;7]$	4166
$K_2$	14	$[8;1;8]$	4838	4158
$K_3$	15	$[9;1;10]$	4414
$K_3$	16	$[10;1;9]$	4427	4373
$K_4$	17	$[11;1;12]$	4413
$K_4$	18	$[12;1;11]$	4439	4379
All of the above channels:			3978

Table 22. The lowest-lying eigen-energies of $cc\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(1^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${(D_s^{+}{D}_s^{\ast +})}^1(4081)$	1(S)	$[1;1;1]$	4105
${(D_s^{\ast +}{D}_s^{\ast +})}^1(4224)$	2(S)	$[3;1;1]$	4232	4105
${(D_s^{+}{D}_s^{\ast +})}^8$	3(H)	$[1;1;2]$	4401
${(D_s^{\ast +}{D}_s^{\ast +})}^8$	4(H)	$[3;1;2]$	4607	4400
${(cc)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	5	$[6;1;3]$	4424	4424
$K_1$	6	$[7;1;5]$	4537
$K_1$	7	$[8;1;5]$	4536
$K_1$	8	$[9;1;5]$	4528
$K_1$	9	$[7;1;6]$	4440
$K_1$	10	$[8;1;6]$	4445
$K_1$	11	$[9;1;6]$	4371	4305
$K_2$	12	$[10;1;7]$	4417
$K_2$	13	$[11;1;7]$	4419
$K_2$	14	$[12;1;7]$	4326
$K_2$	15	$[10;1;8]$	4699
$K_2$	16	$[11;1;8]$	4787
$K_2$	17	$[12;1;8]$	4802	4266
$K_3$	18	$[13;1;10]$	4442
$K_3$	19	$[14;1;10]$	4443
$K_3$	20	$[15;1;9]$	5013	4424
$K_4$	21	$[16;1;12]$	4427
$K_4$	22	$[17;1;12]$	4426
$K_4$	23	$[18;1;11]$	4953	4423
All of the above channels:			4105

Table 23. The lowest-lying eigen-energies of $cc\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(2^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${(D_s^{\ast +}{D}_s^{\ast +})}^1(4224)$	1 (S)	$[1;1;1]$	4232	4232
${(D_s^{\ast +}{D}_s^{\ast +})}^8$	2 (H)	$[1;1;2]$	4432	4432
${(cc)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	3	$[1;1;3]$	4446	4446
$K_1$	4	$[1;1;5]$	4522
$K_1$	5	$[1;1;6]$	4385	4381
$K_2$	6	$[1;1;7]$	4355
$K_2$	7	$[1;1;8]$	4666	4354
$K_3$	8	$[1;1;10]$	4448	4448
$K_4$	9	$[1;1;12]$	4446	4446
All of the above channels:			4232

Table 24. The lowest-lying eigen-energies of $bb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(0^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${({\overline{B}}_s^0{\overline{B}}_s^0)}^1$ (10,734)	1 (S)	$[1;2;1]$	10,710
${({\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast })}^1$ (10,830)	2(S)	$[2;2;1]$	10,800	10,710
${({\overline{B}}_s^0{\overline{B}}_s^0)}^8$	3 (H)	$[1;2;2]$	11,184
${({\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast })}^8$	4 (H)	$[2;2;2]$	11,205	10,943
$(bb)(\overline{s}\overline{s})$	5	$[3;2;4]$	10,967
${(bb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	6	$[4;2;3]$	10,901	10,896
$K_1$	7	$[5;2;5]$	11,445
$K_1$	8	$[5;2;6]$	10,928
$K_1$	9	$[6;2;5]$	11,259
$K_1$	10	$[6;2;6]$	10,863	10,843
$K_2$	11	$[7;2;7]$	10,877
$K_2$	12	$[7;2;8]$	11,445
$K_2$	13	$[8;2;7]$	10,815
$K_2$	14	$[8;2;8]$	11,441	10,802
$K_3$	15	$[9;2;10]$	10,902
$K_3$	16	$[10;2;9]$	10,960	10,895
$K_4$	17	$[11;2;12]$	10,901
$K_4$	18	$[12;2;11]$	10,980	10,897
All of the above channels:			10,710

Table 25. The lowest-lying eigen-energies of $bb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(1^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${({\overline{B}}_s^0{\overline{B}}_s^{\ast })}^1$ (10,782)	1 (S)	$[1;2;1]$	10,755
${({\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast })}^1$ (10,830)	2 (S)	$[3;2;1]$	10,800	10,755
${({\overline{B}}_s^0{\overline{B}}_s^{\ast })}^8$	3 (H)	$[1;2;2]$	10,949
${({\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast })}^8$	4 (H)	$[3;2;2]$	11,185	10,949
${(bb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	5	$[6;2;3]$	10,906	10,906
$K_1$	6	$[7;2;5]$	11,041
$K_1$	7	$[8;2;5]$	11,048
$K_1$	8	$[9;2;5]$	11,038
$K_1$	9	$[7;2;6]$	10,936
$K_1$	10	$[8;2;6]$	10,949
$K_1$	11	$[9;2;6]$	10,917	10,870
$K_2$	12	$[10;2;7]$	10,911
$K_2$	13	$[11;2;7]$	10,914
$K_2$	14	$[12;2;7]$	10,879
$K_2$	15	$[10;2;8]$	11,216
$K_2$	16	$[11;2;8]$	11,483
$K_2$	17	$[12;2;8]$	11,373	10,840
$K_3$	18	$[13;2;10]$	10,928
$K_3$	19	$[14;2;10]$	10,929
$K_3$	20	$[15;2;9]$	11,557	10,907
$K_4$	21	$[16;2;12]$	10,911
$K_4$	22	$[17;2;12]$	10,908
$K_4$	23	$[18;2;11]$	11,458	10,906
All of the above channels:			10,755

Table 26. The lowest-lying eigen-energies of $bb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(2^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${({\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast })}^1(\mathrm{10,830})$	1(S)	$[1;2;1]$	$\mathrm{10,800}$	$\mathrm{10,800}$
${({\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast })}^8$	2(H)	$[1;2;2]$	$\mathrm{10,959}$	$\mathrm{10,959}$
${(bb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	3	$[1;2;3]$	$\mathrm{10,915}$	$\mathrm{10,915}$
$K_1$	4	$[1;2;5]$	$\mathrm{11,023}$
$K_1$	5	$[1;2;6]$	$\mathrm{10,894}$	$\mathrm{10,879}$
$K_2$	6	$[1;2;7]$	$\mathrm{10,870}$
$K_2$	7	$[1;2;8]$	$\mathrm{11,186}$	$\mathrm{10,869}$
$K_3$	8	$[1;2;10]$	$\mathrm{10,918}$	$\mathrm{10,918}$
$K_4$	9	$[1;2;12]$	$\mathrm{10,916}$	$\mathrm{10,916}$
All of the above channels:			$\mathrm{10,800}$

Table 27. The lowest-lying eigen-energies of $cb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(0^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${(D_s^{+}{\overline{B}}_s^0)}^1(7336)$	1(S)	$[1;3;1]$	7344
${(D_s^{\ast +}{\overline{B}}_s^{\ast })}^1(7527)$	2(S)	$[2;3;1]$	7516	7344
${(D_s^{+}{\overline{B}}_s^0)}^8$	3(H)	$[1;3;2]$	7910
${(D_s^{\ast +}{\overline{B}}_s^{\ast })}^8$	4(H)	$[2;3;2]$	7927	7678
$(cb)(\overline{s}\overline{s})$	5	$[3;3;4]$	7726
${(cb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	6	$[4;3;3]$	7675	7662
$K_1$	7	$[5;3;5]$	8171
$K_1$	8	$[5;3;6]$	8274
$K_1$	9	$[6;3;5]$	8369
$K_1$	10	$[6;3;6]$	8145	7613
$K_2$	11	$[7;3;7]$	7896
$K_2$	12	$[7;3;8]$	8266
$K_2$	13	$[8;3;7]$	7758
$K_2$	14	$[8;3;8]$	8282	7629
$K_3$	15	$[9;3;9]$	8647
$K_3$	16	$[9;3;10]$	8181
$K_3$	17	$[10;3;9]$	8321
$K_3$	18	$[10;3;10]$	8675	8010
$K_4$	19	$[11;3;12]$	8199
$K_4$	20	$[12;3;11]$	8359	8063
All of the above channels:			7344

Table 28. The lowest-lying eigen-energies of $cb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(1^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${(D_s^{+}{\overline{B}}_s^{\ast })}^1(7384)$	1(S)	$[1;3;1]$	7389
${(D_s^{\ast +}{\overline{B}}_s^0)}^1(7479)$	2(S)	$[2;3;1]$	7471
${(D_s^{\ast +}{\overline{B}}_s^{\ast })}^1(7527)$	3(S)	$[3;3;1]$	7516	7389
${(D_s^{+}{\overline{B}}_s^{\ast })}^8$	4(H)	$[1;3;2]$	7900
${(D_s^{\ast +}{\overline{B}}_s^0)}^8$	5(H)	$[2;3;2]$	7891
${(D_s^{\ast +}{\overline{B}}_s^{\ast })}^8$	6(H)	$[3;3;2]$	7920	7684
$(cb){(\overline{s}\overline{s})}^{\ast }$	7	$[6;3;3]$	7683
${(cb)}^{\ast }(\overline{s}\overline{s})$	8	$[5;3;3]$	7680
${(cb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	9	$[4;3;4]$	7725	7671
$K_1$	10	$[7;3;5]$	7796
$K_1$	11	$[8;3;5]$	8172
$K_1$	12	$[9;3;5]$	8009
$K_1$	13	$[7;3;6]$	7695
$K_1$	14	$[8;3;6]$	7760
$K_1$	15	$[9;3;6]$	7634	7620
$K_2$	16	$[10;3;7]$	7607
$K_2$	17	$[11;3;7]$	7621
$K_2$	18	$[12;3;7]$	7510
$K_2$	19	$[10;3;8]$	8137
$K_2$	20	$[11;3;8]$	8211
$K_2$	21	$[12;3;8]$	8209	7505
$K_3$	22	$[13;3;10]$	7705
$K_3$	23	$[14;3;10]$	7706
$K_3$	24	$[15;3;10]$	7682
$K_3$	25	$[13;3;9]$	7734
$K_3$	26	$[14;3;9]$	7733
$K_3$	27	$[15;3;9]$	8298	7666
$K_4$	28	$[16;3;12]$	7687
$K_4$	29	$[17;3;12]$	7677
$K_4$	30	$[18;3;11]$	7771	7670
All of the above channels:			7389

Table 29. The lowest-lying eigen-energies of $cb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(2^{+})$ in the real range calculation. (unit: MeV).

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	Mixed
		$[\mathit{i};\mathit{j};\mathit{k}]$
${(D_s^{\ast +}{\overline{B}}_s^{\ast })}^1(7527)$	1(S)	$[1;3;1]$	7516	7516
${(D_s^{\ast +}{\overline{B}}_s^{\ast })}^8$	2(H)	$[1;3;2]$	7712	7712
${(cb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$	3	$[1;3;3]$	7698	7698
$K_1$	4	$[1;3;5]$	7804
$K_1$	5	$[1;3;6]$	7705	7704
$K_2$	6	$[1;3;7]$	7624
$K_2$	7	$[1;3;8]$	8205	7622
$K_3$	8	$[1;3;9]$	8311
$K_3$	9	$[1;3;10]$	7701	7696
$K_4$	10	$[1;3;12]$	7697	7697
All of the above channels:			7516

• $cc\overline{s}\overline{s}$ tetraquarks

There is no bound state in the doubly charmed $cc\overline{s}\overline{s}$ system, but resonances are found in the $I(J^P)=0(0^{+})$ and $0(2^{+})$ quantum states. Obviously, these results are different from the $cc\overline{q}\overline{q}$ tetraquark states. We will discuss them in the following parts.

• $I(J^P)=0(0^{+})$ state

Table 21 presents all possible channels in $cc\overline{s}\overline{s}$ system with $I(J^P)=0(0^{+})$ quantum numbers. It is clear that the meson-meson channels of $D_s^{+}{D}_s^{+}$ and $D_s^{\ast +}{D}_s^{\ast +}$, both in color-singlet and hidden-color states, are unbound. Moreover, the coupled results in these two color configurations do not change, with the obtained masses 3978 MeV and 4377 MeV, respectively. As for the two diquark-antidiquark channels, masses of $(cc)(\overline{s}\overline{s})$ and ${(cc)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$ are both around 4.4 GeV, i.e., above the $D_s^{(\ast )+}{D}_s^{(\ast )+}$ threshold values. Their coupled-masses, $\sim 4379$ MeV, are quite close to the value of hidden-color channels. However, although there is a strong coupling between them, it is still not enough to have a bound state. Additionally, a bound state is still unavailable in the K-type configurations, masses of the four K-type channels are in the region from 4.2 GeV to 4.8 GeV and there is a degeneration at 4.4 GeV for ${(cc)}^{(\ast )}{(\overline{s}\overline{s})}^{(\ast )}$, $K_3$ and $K_4$ channels. Finally, the lowest mass (3978 MeV) in the complete coupled-channels calculation is the same as that in the color-singlet channels. Therefore, no bound state is found in $cc\overline{s}\overline{s}$ tetraquark with $I(J^P)=0(0^{+})$ state.

Apart from the above real-range study, Figure 10 shows the fully coupled-channels computation in the complex scaling method. Particularly, in the mass region from 3.9 GeV to 5.0 GeV, three meson-meson scattering states, $(1S)D_s^{+}(1S)D_s^{+}$, $(1S)D_s^{\ast +}(1S)D_s^{\ast +}$ and $(1S)D_s^{+}(2S)D_s^{+}$ are well presented. Most of the energy points are basically aligned along the cut lines with rotated angle $\theta$ varied less than 6°. However, there is a stable resonance pole, circled in orange. The calculated mass and width for this state are 4902 MeV and 3.54 MeV, respectively. Since it is about 0.6 GeV above the ground state of two non-interacting $D_s^{\ast +}$ mesons threshold and 0.2 GeV above the first radial excitation $(1S)D_s^{+}(2S)D_s^{+}$ state, this narrow resonance can be identified as the $D_s^{+}{D}_s^{+}$ molecular state.

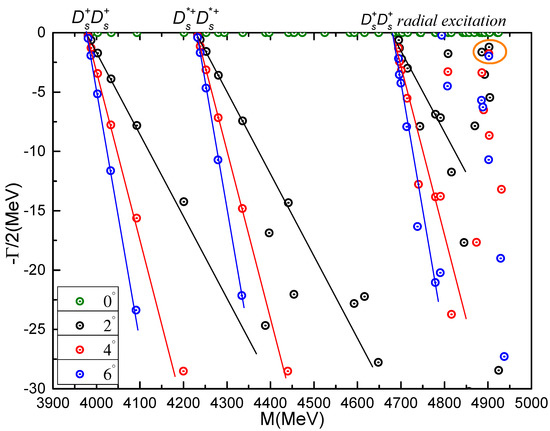
Figure 10. Complex energies of $cc\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(0^{+})$ in the complete coupled channels calculation, $\theta$ varying from 0° to 6°.

2.

$I(J^P)=0(1^{+})$ state

Two di-meson channels, $D_s^{+}{D}_s^{\ast +}$ and $D_s^{\ast +}{D}_s^{\ast +}$, one diquark-antidiquark channel, ${(cc)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$ and four K-types configurations are studied in Table 22. Firstly, each channel along with the couplings in one certain configuration is unbound. Specifically, the couplings are quite weak in both color-singlet and hidden-color channels of meson-meson configurations. However, a reduction of several to hundreds of MeV is obtained in the coupled-channels computations of K-types and their coupled-masses are ∼4.4 GeV. Then, in a complete coupled-channels investigation, the lowest state is still unbound with mass equals to the theoretical threshold of $D_s^{+}{D}_s^{\ast +}$, 4105 MeV. Meanwhile, in comparison with the results of $cc\overline{q}\overline{q}$ tetraquarks in Table 7, one can find that the character of the $D_s^{+}{D}_s^{\ast +}$ state is opposite to the $D^{+}{D}^{\ast 0}$ case which has a binding energy of ∼200 MeV.

Figure 11 shows the distribution of the complex energies for the $D_s^{+}{D}_s^{\ast +}$ and $D_s^{\ast +}{D}_s^{\ast +}$ scattering states, in the complete coupled-channels calculation. From 4.1 GeV to 5.0 GeV, one can find the ground states and first radial excitations. Three poles appear between 4.55 GeV and 4.70 GeV, their masses reduce slowly with the angle and thus they are neither bound states nor resonances.

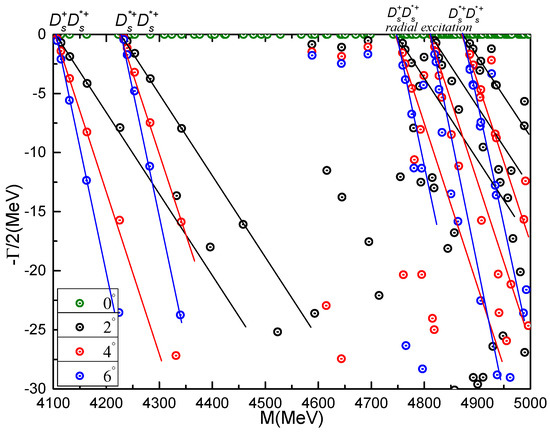
Figure 11. Complex energies of $cc\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(1^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

3.

$I(J^P)=0(2^{+})$ state

Only the $D_s^{\ast +}{D}_s^{\ast +}$ channel in meson-meson configuration need to be considered in this case; besides, there is one diquark-antidiquark channel ${(cc)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$. The calculated masses in color-singlet and hidden-color channels are 4232 MeV and 4432 MeV, respectively. The ${(cc)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$ channel mass is very close to the hidden-color one with $M=4446\mathrm{MeV}$. As for the other K-types configurations, their theoretical masses are also around 4.38 GeV for the $K_1$, $K_2$ structures and 4.45 GeV for the rest two ones. Obviously, all of them are above the $D_s^{\ast +}{D}_s^{\ast +}$ threshold value and this fact do not change in a fully coupled-channels calculation.

Nevertheless, three resonances are found in the complex-range calculation in which all of the channels listed in Table 23 are considered. Figure 12 shows that, apart from the continuum states of $D_s^{\ast +}{D}_s^{\ast +}$, three almost fixed poles are obtained at ∼4.8 GeV. In particular, the three orange circles mark the obtained resonance states of $D_s^{\ast +}{D}_s^{\ast +}$, their masses and widths are (4821 MeV, 5.58 MeV), (4846 MeV, 10.68 MeV) and (4775 MeV, 23.26 MeV), respectively. These poles are also around 0.6 GeV above two non-interacting $D_s^{\ast +}$ mesons threshold, and ∼0.1 GeV below its first radial excitation state.

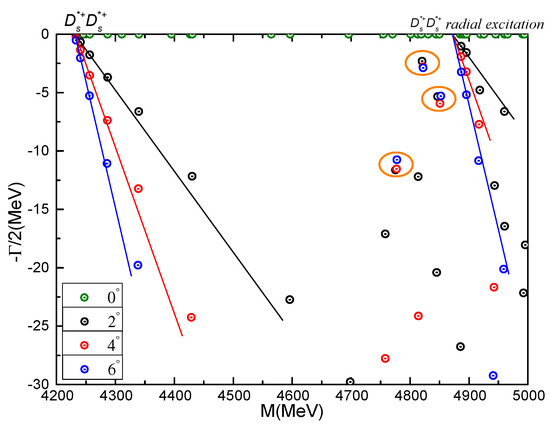
Figure 12. Complex energies of $cc\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(2^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

• $bb\overline{s}\overline{s}$ tetraquarks

In this part, we study the $I(J^P)=0(0^{+})$, $0(1^{+})$ and $0(2^{+})$ states for $bb\overline{s}\overline{s}$ tetraquarks. It is similar to the $cc\overline{s}\overline{s}$ systems that only narrow resonances are found in $0(0^{+})$ and $0(2^{+})$ states. Let us proceed to discuss them in detail.

• $I(J^P)=0(0^{+})$ state

As shown in Table 24, there are two meson-meson, two diquark-antidiquark and 12 K-type channels under investigation. Theoretical masses of each single channel locate in the region from 10.71 GeV to 11.45 GeV; besides, the coupled-mass ∼10.9 GeV in ${\overline{B}}_s^0{\overline{B}}_s^0$ and ${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$ channels is comparable with those of $K_1$, $K_2$, $K_3$ and $K_4$ channels. Although the color-singlet channel mass is the lowest, one bound state is found in the coupled-channels calculation when included all of them.

Additionally, Figure 13 shows the result of complete coupled-channels calculation using the complex scaling method. The states of ground and first radial excitation for ${\overline{B}}_s^0{\overline{B}}_s^0$ and ${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$ channels are generally presented from 10.7 GeV to 11.5 GeV. However, there are three narrow resonance poles obtained near the $2S$ state of ${\overline{B}}_s^0{\overline{B}}_s^0$. Particularly, in the two big orange circles, the calculated dots which the value of rotated angle $\theta$ are 2°, 4° and 6°, respectively are almost overlapped. Their masses and widths are (11.31 GeV, 1.86 MeV), (11.33 GeV, 1.84 MeV) and (11.41 GeV, 1.54 MeV), respectively. Furthermore, with much heavier flavored quark included, more narrow molecular resonance state will be obtained when we compare these results with those of $cc\overline{s}\overline{s}$ tetraquarks in the ${00}^{+}$ state. Herein, we can identify the first two resonances which are about 0.5 GeV above the ${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$ threshold as two ${\overline{B}}_s^{\ast }$ mesons molecule state, and the third one as ${\overline{B}}_s^0{\overline{B}}_s^0$ resonance state due to it is ∼50 MeV above the $(1S){\overline{B}}_s^0(2S){\overline{B}}_s^0$ non-interacting threshold.

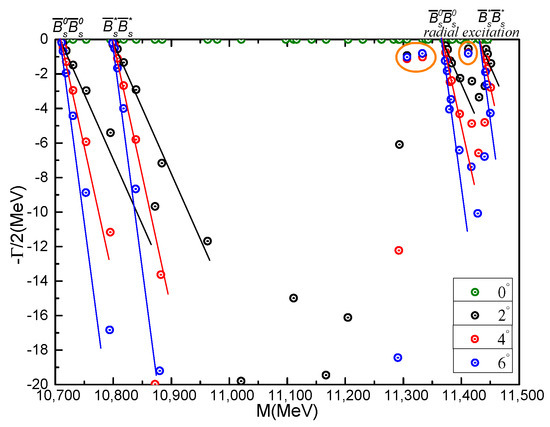
Figure 13. Complex energies of $bb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(0^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

2.

$I(J^P)=0(1^{+})$ state

Table 25 shows the mass calculation of the meson-meson channels of ${\overline{B}}_s^0{\overline{B}}_s^{\ast }$ and ${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$ in color-singlet state; they are 10,755 MeV and 10,800 MeV, respectively. These results are not changed when their hidden-color channels are included. As for the other exotic structures, i.e., diquark-antidiquark $bb\overline{s}\overline{s}$ and K-type channels, the theoretical masses are all ∼10.9 GeV. These excited states do not help in forming a bound state in the complete coupled-channels calculation, with a lowest mass still at 10,755 MeV.

The above conclusion is clearly shown in Figure 14, which is the results in complex-range study. In the mass region from 10.7 GeV to 11.3 GeV, only two scattering states of ${\overline{B}}_s^0{\overline{B}}_s^{\ast }$ and ${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$ channels are obtained; neither bound nor resonance states are present in the theoretical framework. One may notice a gradually varied dots at 11.15 GeV; however, these unstable poles can not be identified as a regular resonance state.

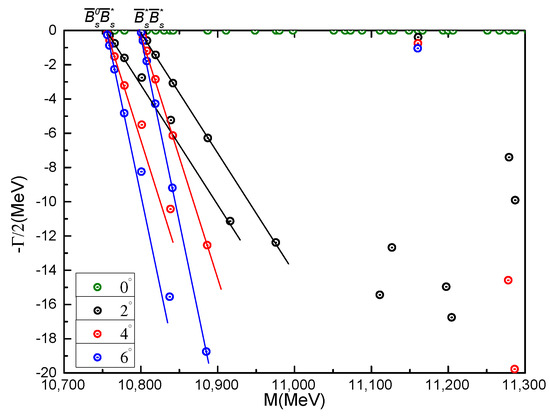
Figure 14. Complex energies of $bb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(1^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

3.

$I(J^P)=0(2^{+})$ state

One ${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$ meson-meson channel is studied in Table 26, but the calculated mass 10.8 GeV in color-singlet channel is just the theoretical threshold value. The other hidden-color, diquark-antidiquark and K-type structures are all above 10.9 GeV in the coupled-channels calculation of each configuration, except the 10.87 MeV for $K_1$ and $K_2$ channels. Again, the lowest energy level is still unbound in the fully coupled-channels computation and the coupled mass is 10.8 GeV.

Nevertheless, when the investigation is extended to the complex-range, new exotic states are obtained. In Figure 15, three narrow resonance states at ∼11.35 GeV are marked with orange circles very near the real-axis. With an angle $\theta$ varied less than 6°, masses and widths of these three fixed poles are (11.33 GeV, 1.48 MeV), (11.36 GeV, 4.18 MeV) and (11.41 GeV, 2.52 MeV), respectively. They are around 0.6 GeV above the ${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$ threshold and thus the nature of two ${\overline{B}}_s^{\ast }$ mesons as molecular states can be drawn herein.

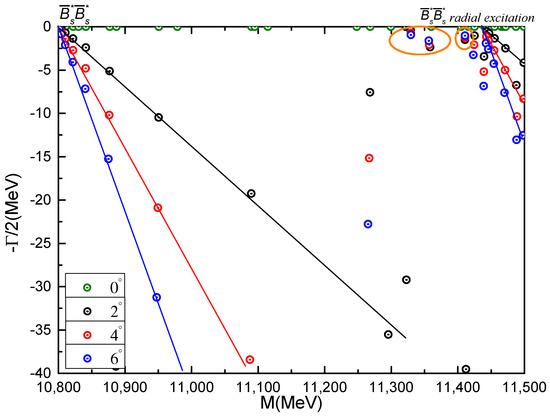
Figure 15. Complex energies of $bb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(2^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

• $cb\overline{s}\overline{s}$ tetraquarks

Bound states are also not found in this sector; however, some narrow resonances in $I(J^P)=0(0^{+})$, $0(1^{+})$ and $0(2^{+})$ channels are obtained. The following parts are devoted to the discussion of them.

1.

$I(J^P)=0(0^{+})$ state

As shown in Table 27, two meson-meson structures, $D_s^{+}{\overline{B}}_s^0$ and $D_s^{\ast +}{\overline{B}}_s^{\ast }$, two diquark-antidiquark channels, $(cb)(\overline{s}\overline{s})$ and ${(cb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$, and 14 K-type configurations are considered in this case. Firstly, the calculated masses of these channels are located in the energy region from 7.34 GeV to 8.67 GeV and no bound state is found. Then, this conclusion remains in the coupled-channels computations for the di-meson, diquark-antidiquark and K-type configurations. In particular, the coupling in $D_s^{+}{\overline{B}}_s^0$ and $D_s^{\ast +}{\overline{B}}_s^{\ast }$ channels is extremely weak; however, from few tens to hundreds of MeV variation is found in the other configuration couplings. Finally, in the real-range fully coupled-channels calculation, the lowest energy level is still at 7344 MeV.

In a further investigation, where the CSM is employed, one can find that two resonance states are marked in Figure 16. At around 0.5 GeV higher than the $D_s^{\ast +}{\overline{B}}_s^{\ast }$ threshold value, two narrow resonance poles with masses and widths equal to (7.92 GeV, 1.02 MeV) and (7.99 GeV, 3.22 MeV) appear and they are stable against the variation of rotated angle $\theta$. Herein, we can identify them as molecular states of $D_s^{\ast +}{\overline{B}}_s^{\ast }$.

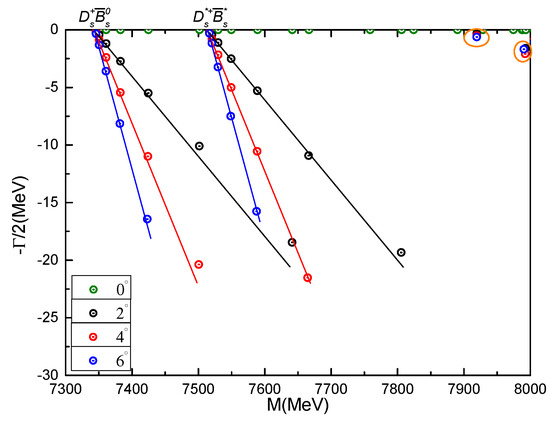
Figure 16. Complex energies of $cb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(0^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

2.

$I(J^P)=0(1^{+})$ state

Table 28 presents 30 channels which include the $D_s^{+}{\overline{B}}_s^{\ast }$, $D_s^{\ast +}{\overline{B}}_s^0$ and $D_s^{\ast +}{\overline{B}}_s^{\ast }$ di-meson channels, $(cb){(\overline{s}\overline{s})}^{\ast }$, ${(cb)}^{\ast }(\overline{s}\overline{s})$ and ${(cb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$ diquark-antidiquark structures and 21 K-type configurations. Masses of each channel are between 7.39 GeV and 8.23 GeV. Particularly, the lowest level is the scattering state of $D_s^{+}{\overline{B}}_s^{\ast }$, with $M=7389$ MeV. Furthermore, the coupled-masses are slightly modified in each configuration: mass of the meson-meson structure in color-singlet channel is still 7389 MeV and the other configurations’ masses are ∼7.67 GeV except for the $K_2$-type channels with $M=7.51$ GeV. Bound state is not found in the fully coupled-channels study, however, two narrow resonances are obtained in the complex-range.

Figure 17 shows the calculated complex energies in the region from 7.3 GeV to 8.0 GeV. Accordingly, one can conclude (i) the majority of the poles belong to the scattering states of $D_s^{+}{\overline{B}}_s^{\ast }$, $D_s^{\ast +}{\overline{B}}_s^0$ and $D_s^{\ast +}{\overline{B}}_s^{\ast }$, (ii) two fixed resonance poles at 7.92 GeV and 7.99 GeV with widths equal to 1.20 MeV and 4.96 MeV, respectively, are obtained. Because they are above the $D_s^{\ast +}{\overline{B}}_s^{\ast }$ threshold lines and far from the other two scattering states, a $D_s^{\ast +}{\overline{B}}_s^{\ast }$ molecular nature for the two resonances is reasonable.

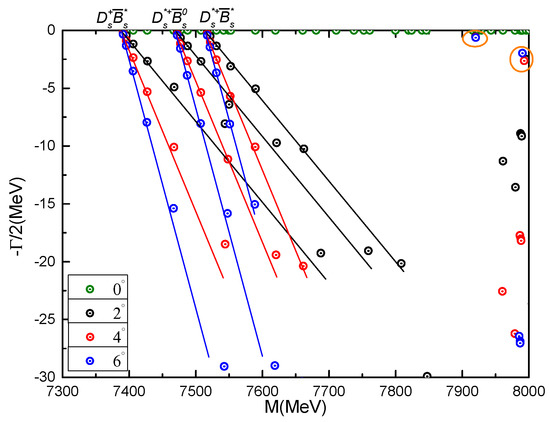
Figure 17. Complex energies of $cb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(1^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

3.

$I(J^P)=0(2^{+})$ state

There is one channel for both di-meson $D_s^{\ast +}{\overline{B}}_s^{\ast }$ and diquark-antidiquark ${(cb)}^{\ast }{(\overline{s}\overline{s})}^{\ast }$ configuration; besides, 7 K-type channels are listed in Table 29. First of all, our results and conclusions are similar to the other $QQ\overline{s}\overline{s}$ sectors, i.e., bound states are not found in neither the single channel calculation nor the coupled-channels case. The theoretical threshold of the lowest state $D_s^{\ast +}{\overline{B}}_s^{\ast }$ is 7516 MeV and the other excited states in coupled-channels are all above 7.72 GeV; in particular, there is a degeneration between $K_3$ and $K_4$ channels whose coupled masses are 7697 MeV.

Unlike the results of $cb\overline{q}\overline{q}$ tetraquarks in $I{J}^P={02}^{+}$ state, two resonance states are obtained in the complex analysis of the complete coupled-channels of $cb\overline{s}\overline{s}$ tetraquarks. One can see in Figure 18 that two stable resonance poles, circled with orange, are ∼0.6 GeV above the $D_s^{\ast +}{\overline{B}}_s^{\ast }$ threshold value and ∼0.1 GeV below its first radial excitation state. Hence, they can be identified as the $D_s^{\ast +}{\overline{B}}_s^{\ast }$ resonances whose masses and widths are (8.05 GeV, 1.42 MeV) and (8.10 GeV, 2.90 MeV), respectively. The other energy points are all scattering states of $D_s^{\ast +}{\overline{B}}_s^{\ast }$.

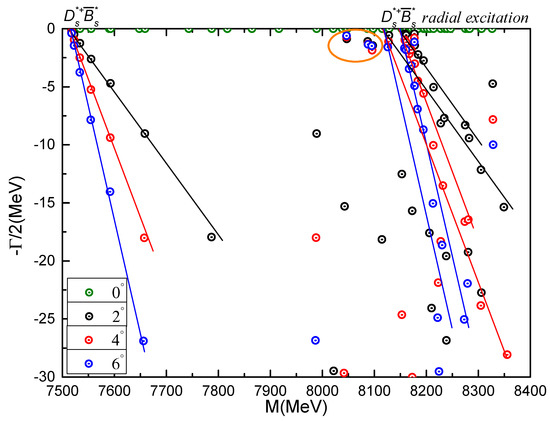
Figure 18. Complex energies of $cb\overline{s}\overline{s}$ tetraquarks with $I(J^P)=0(2^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

Finally, in order to present fair and unambiguous statements for experimentalists, and interested readers, a comparison of our theoretical findings in the isoscalar double-heavy tetraquark sector with other theoretical frameworks are listed in Table 30. In particular, our predictions of the double-charm and hidden-bottom tetraquarks are quite comparable with those in reference [51].

Table 30. Comparison of theoretical masses on the iso-scalar double-heavy tetraquark in bound states by different predictions. (unit: MeV).

	$0^{+}$	$1^{+}$	$2^{+}$	$0^{+}$	$1^{+}$	$2^{+}$	$0^{+}$	$1^{+}$	$2^{+}$
	$\mathit{cc}\overline{\mathit{q}}\overline{\mathit{q}}$			$\mathit{cb}\overline{\mathit{q}}\overline{\mathit{q}}$			$\mathit{bb}\overline{\mathit{q}}\overline{\mathit{q}}$
This work	-	3726	-	6980	6997	7333	-	10,238, 10,524	-
Ref. [33]	-	3935	-	7239	7246	-	-	10,502	-
Ref. [41]	-	3931	-	7206	7244	-	-	10,525	-
Ref. [44]	-	3876	-	-	-	-	-	10,504	-
Ref. [43]	-	-	-	-	-	-	-	10,558	-
Ref. [51]	-	3764	-	-	-	-	-	10,261	-
Ref. [29]	-	3927	-	-	-	-	-	10,426	-
Ref. [45]	-	3905	-	-	-	-	-	-	-

3.1.3. $QQ\overline{Q}\overline{Q}$ Tetraquarks

Recent experimental progress on the $cc\overline{c}\overline{c}$ system by the LHCb collaboration [21] triggers a revived interest in the $QQ\overline{Q}\overline{Q}$ system. Herein, fully charm and fully bottom tetraquarks, will be discussed in the following parts.

1.

$I(J^P)=0(0^{+})$ state

Two meson-meson channels, ${\eta }_c{\eta }_c$, $J/\psi J/\psi$ and two diquark-antidiquark structures, $(cc)(\overline{c}\overline{c})$, ${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$ are investigated herein. Table 31 lists the calculated masses for them along with the coupling. Clearly, the lowest energy level is 6469 MeV of ${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$ channel and the other diquark-antidiquark structure of $(cc)(\overline{c}\overline{c})$ is at 6683 MeV. Besides, the calculated masses of color-singlet and hidden-color channels in the dimeson configurations, ${\eta }_c{\eta }_c$ and $J/\psi J/\psi$, are degenerated since there is no color-dependent interaction in the Cornell-like model. It is 6536 MeV in the ${\eta }_c{\eta }_c$ channel and 6657 MeV in the di-$J/\psi$ one. Herein, the fully coupled-channels calculation is important because different color configurations are not orthogonal. The bottom of Table 31 presents two resonances obtained in such computation. In particular, their masses are 6423 and 6650 MeV, respectively, and the first resonance state is around 50 MeV lower than the mass of ${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$ channel.

Table 31. Possible resonance states of fully-charm tetraquarks with quantum numbers $I(J^P)=0(0^{+})$, unit in MeV.

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$
		$[\mathit{i};\mathit{j};\mathit{k}]$
${\left[{\eta }_c{\eta }_c\right]}^1(5936)$	1	$[1;1;1]$	6536
${\left[{\eta }_c{\eta }_c\right]}^8$	2	$[1;1;2]$	6536
${[J/\psi J/\psi ]}^1(6204)$	3	$[2;1;1]$	6657
${[J/\psi J/\psi ]}^8$	4	$[2;1;2]$	6657
$(cc)(\overline{c}\overline{c})$	5	$[1;1;4]$	6683
${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$	6	$[2;1;3]$	6469
Mixed			64231st
			66502nd

In order to have a better identification of the nature of these two resonance states in the fully coupled-channels calculation. The components and their internal structures are analyzed in Table 32 and Table 33, respectively. Firstly, the couplings are strong for both of these two resonance states. Besides, the meson-meson configuration dominates them. From Table 32, one can find that the components of ${\eta }_c{\eta }_c$ and $J/\psi J/\psi$, which are the sum of their corresponding singlet- and hidden-color channels, are (49%, 45%) for the first resonance state and (31%, 48%) for the another one. Furthermore, they are both of a compact tetraquark configurations with sizes ∼0.34 fm.

Table 32. Component of each channel in the coupled-channels calculation of fully-charm resonance states with $I(J^P)=0(0^{+})$.

	${\left[{\eta }_c{\eta }_c\right]}^1$	${\left[{\eta }_c{\eta }_c\right]}^8$	${[J/\psi J/\psi ]}^1$	${[J/\psi J/\psi ]}^8$
$1st$	31.1%	17.8%	23.7%	21.0%
$2nd$	14.0%	17.0%	21.7%	26.1%
	$(cc)(\overline{c}\overline{c})$	${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$
$1st$	3.0%	3.4%
$2nd$	21.1%	0.1%

Table 33. The distances, between any two quarks of the found fully-charm resonance states with $I(J^P)=0(0^{+})$ in coupled-channels calculation, unit in fm.

	${\mathit{r}}_{\mathit{cc}}$	${\mathit{r}}_{\mathit{c}\overline{\mathit{c}}}$	${\mathit{r}}_{\overline{\mathit{c}}\overline{\mathit{c}}}$
1st	0.325	0.342	0.342
2nd	0.344	0.353	0.353

We also extend the investigation on the complete coupled-channels framework from a real-range to a complex one; the results are shown in Figure 19. In the 6–10 GeV energy region, there are two fixed poles in the real-axis when the rotated angle $\theta$ varied from 0° to 6°. Actually, masses of these two stable poles are just 6423 MeV and 6650 MeV. This fact confirms the two previously obtained resonance states in the fully coupled-channels calculation of real-range. Moreover, the other energy points are unstable and always descend more or less along with the change of $\theta$.

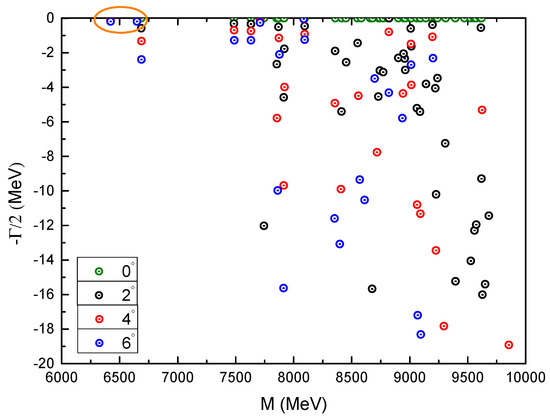
Figure 19. Complex energies of fully-charm tetraquarks with $I(J^P)=0(0^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

2.

$I(J^P)=0(1^{+})$ state

In this sector we still do not find any bound state of $cc\overline{c}\overline{c}$ system; however, resonance states with masses around 6.6 GeV are available. In particular, three almost degenerate states with masses ∼6.67 GeV are presented in Table 34, they are the color-singlet and hidden-color channel of ${\eta }_{c}J/\psi$ and ${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$ diquark-antidiquark channel, respectively. However, no stable resonance state can be found in the di-$J/\psi$ channel. Then, in a fully coupled-channels calculation in which both the meson-meson and diquark-antidiquark structures are considered, lower mass at 6627 MeV is obtained for the $I(J^P)=0(1^{+})$ state. Herein, the coupling between color-singlet and hidden-color channels of ${\eta }_{c}J/\psi$ is also strong with contributions around 56% and 35% for them, respectively. Only less than 10% is from the ${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$ channel. From Table 35 we can conclude that it is a compact tetraquark state, which size is ∼0.35 fm, in the $I(J^P)=0(1^{+})$ state.

Table 34. Possible resonance states of fully-charm tetraquarks with quantum numbers $I(J^P)=0(1^{+})$, unit in MeV.

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$
${[{\eta }_{c}J/\psi ]}^1(6070)$	1	$[1;1;1]$	6671
${[{\eta }_{c}J/\psi ]}^8$	2	$[1;1;2]$	6671
${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$	3	$[3;1;3]$	6674
Mixed			6627
Component (1; 2; 3):    55.5%; 34.7%; 9.8%

Table 35. The distances, between any two quarks of the found fully-charm resonance states with $I(J^P)=0(1^{+})$ in coupled-channels calculation, unit in fm.

${\mathit{r}}_{\mathit{cc}}$	${\mathit{r}}_{\mathit{c}\overline{\mathit{c}}}$	${\mathit{r}}_{\overline{\mathit{c}}\overline{\mathit{c}}}$
0.342	0.357	0.357

Additionally, the complete coupled-channels investigation is also performed in the complex-range framework where a rotated angle is varied from 0° to 6°. The calculated results of complex energies from 6.5 GeV to 10.0 GeV are presented in Figure 20. Obviously, there is a fixed pole in the real-axis, circled with orange. It can be identified as a ${\eta }_{c}J/\psi$ resonance with mass at 6627 MeV. However, the other poles should correspond to the scattering states of ${\eta }_{c}J/\psi$ in higher energy region.

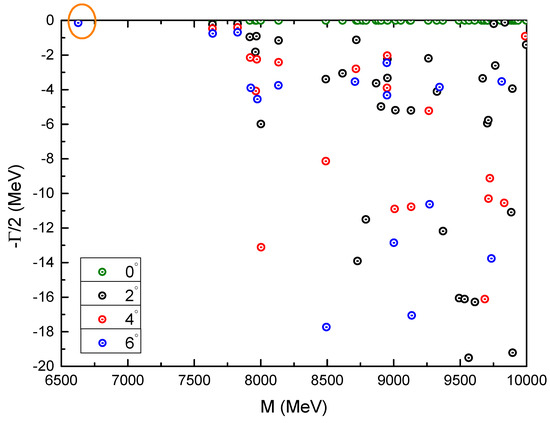
Figure 20. Complex energies of fully-charm tetraquarks with $I(J^P)=0(1^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

3.

$I(J^P)=0(2^{+})$ state

Similar to the $0(1^{+})$ case, two meson-meson $J/\psi J/\psi$ channels and one diquark-antidiquark ${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$ channel are considered in this highest spin state of tetraquark. In particular, masses of them are all around 7.03 GeV and the ${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$ channel is the lowest one with mass at 7026 MeV. Then, in their coupling calculation, the mixed mass is 7014 MeV shown in Table 36. Meanwhile, the percentages of ${[J/\psi J/\psi ]}^1$, ${[J/\psi J/\psi ]}^8$ and ${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$ are around 53%, 33% and 14%, respectively. This strong coupling leads to a compact tetraquark configuration whose size around 0.38 fm is listed in Table 37.

Table 36. Possible resonance states of fully-charm tetraquarks with quantum numbers $I(J^P)=0(2^{+})$, unit in MeV.

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$
${[J/\psi J/\psi ]}^1(6204)$	1	$[1;1;1]$	7030
${[J/\psi J/\psi ]}^8$	2	$[1;1;2]$	7030
${(cc)}^{\ast }{(\overline{c}\overline{c})}^{\ast }$	3	$[1;1;3]$	7026
Mixed			7014
Component (1; 2: 3):  52.8%; 33.0%; 14.2%

Table 37. The distances, between any two quarks of the found fully-charm resonance states with $I(J^P)=0(2^{+})$ in coupled-channels calculation, unit in fm.

${\mathit{r}}_{\mathit{cc}}$	${\mathit{r}}_{\mathit{c}\overline{\mathit{c}}}$	${\mathit{r}}_{\overline{\mathit{c}}\overline{\mathit{c}}}$
0.375	0.389	0.389

By employing the complex scaling method in our model investigation of the complete coupled-channels, the above conclusions are confirmed too. Particularly, one stable resonance pole against the two-body strong decay is obtained at 7014 MeV (see Figure 21). Obviously, this resonance mass is quite close to the reported new structure at 6.9 GeV by the LHCb collaboration [21]. Hence it can be identified as a compact fully charmed tetraquark in $0(2^{+})$ state. However, the other complex energy points always move along with the variation of angle $\theta$.

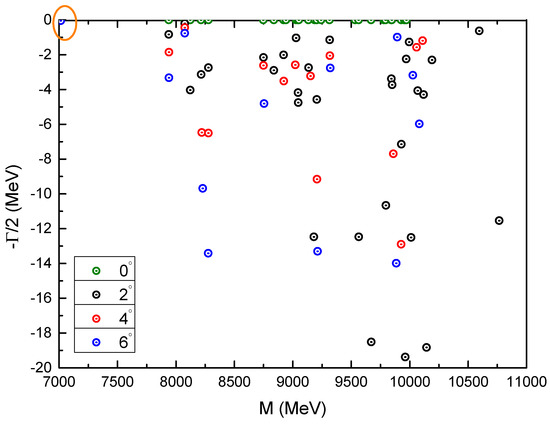
Figure 21. Complex energies of fully-charm tetraquarks with $I(J^P)=0(2^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

• Fully-bottom tetraquarks

Bound states and resonances in $J^P$=$0^{+}$, $1^{+}$ and $2^{+}$, $I=0$ are found in the $bb\overline{b}\overline{b}$ tetraquark systems. Furthermore, they are more compact than the $cc\overline{c}\overline{c}$ resonances. The calculated masses are listed in Table 38, 41 and 43.

Table 38. Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers $I(J^P)=0(0^{+})$, unit in MeV.

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	${\mathbf{E}}_{\mathbf{b}}$
${\left[{\eta }_b{\eta }_b\right]}^1(\mathrm{18,802})$	1	$[1;2;1]$	${\mathrm{17,999}}^{1st}$	$-803$
			${\mathrm{19,036}}^{2nd}$	$+234$
${\left[\mathsf{{\rm Y}}\mathsf{{\rm Y}}\right]}^1(\mathrm{18,926})$	2	$[2;2;1]$	${\mathrm{18,038}}^{1st}$	$-888$
			${\mathrm{19,069}}^{2nd}$	$+143$
${\left[{\eta }_b{\eta }_b\right]}^8$	3	$[1;2;2]$	${\mathrm{17,999}}^{1st}$	$-803$
			${\mathrm{19,036}}^{2nd}$	$+234$
${\left[\mathsf{{\rm Y}}\mathsf{{\rm Y}}\right]}^8$	4	$[2;2;2]$	${\mathrm{18,038}}^{1st}$	$-888$
			${\mathrm{19,069}}^{2nd}$	$+143$
$(bb)(\overline{b}\overline{b})$	5	$[1;2;4]$	${\mathrm{18,068}}^{1st}$
			${\mathrm{19,097}}^{2nd}$
${(bb)}^{\ast }{(\overline{b}\overline{b})}^{\ast }$	6	$[2;2;3]$	${\mathrm{17,975}}^{1st}$
			${\mathrm{19,033}}^{2nd}$
Mixed			${\mathrm{17,917}}^{1st}$
			${\mathrm{18,010}}^{2nd}$
			${\mathrm{19,280}}^{3rd}$

Particularly, the first column shows the allowed channels and, in the parenthesis, the noninteracting meson-meson experimental threshold values. Meson-meson and diquark-antidiquark channels are indexed in the second column, respectively. The necessary bases in spin, flavor and color degrees of freedom are listed in the third column. The fourth column refers to the theoretical mass of each channel and their couplings, binding energies of the di-meson channels are listed in the last column. The details are as follows.

1.

$I(J^P)=0(0^{+})$ state

As shown in Table 38, four meson-meson configurations, which include the singlet- and hidden-color channels of ${\eta }_b{\eta }_b$ and $\mathsf{{\rm Y}}\mathsf{{\rm Y}}$, along with two diquark-antidiquark ones, $(bb)(\overline{b}\overline{b})$ and ${(bb)}^{\ast }{(\overline{b}\overline{b})}^{\ast }$, are calculated in the $0(0^{+})$ state of fully bottom tetraquark. Firstly, two low-lying stable states are found in each single channel computations. Masses of the first energy level of them are ∼18.0 GeV, and the second one is around 19.0 GeV. Obviously, the lowest-lying state of each channel is deeply bound with $E_b$ more than $-800$ MeV and the higher one is a resonance state which is ∼150 MeV above the threshold. Additionally, masses of three stable states in the complete coupled-channels case are also listed in Table 38, in particular, they are 17.92 GeV, 18.01 GeV and 19.28 GeV, respectively. Generally, they are still located at 18.0 GeV and 19.0 GeV.

Natures of these three exotic states can be indicated in Table 39 and Table 40. In particular, the percentages of each meson-meson and diquark-antidiquark channels of $bb\overline{b}\overline{b}$ tetraquark states are listed in Table 39. Therein, the diquark-antidiquark channels are less than 11% for all of these three states. Nevertheless, the couplings between color-singlet and hidden-color channels of ${\eta }_b{\eta }_b$ and $\mathsf{{\rm Y}}\mathsf{{\rm Y}}$ are very strong. Besides, a compact fully-bottom tetraquark configuration is shown in Table 40, where the sizes of two bound states are around 0.16 fm and 0.29 fm for the resonance one. Apparently, the conclusions are consistent with the deeply binding energies obtained before.

Table 39. Component of each channel in the coupled-channels calculation of fully-bottom bound and resonance states with $I(J^P)=0(0^{+})$.

	${\left[{\eta }_b{\eta }_b\right]}^1$	${\left[{\eta }_b{\eta }_b\right]}^8$	${\left[\mathsf{{\rm Y}}\mathsf{{\rm Y}}\right]}^1$	${\left[\mathsf{{\rm Y}}\mathsf{{\rm Y}}\right]}^8$
1st	27.3%	19.4%	21.6%	20.5%
2nd	13.5%	32.8%	14.0%	29.8%
3rd	20.6%	15.8%	30.0%	30.1%
	$(bb)(\overline{b}\overline{b})$	${(bb)}^{\ast }{(\overline{b}\overline{b})}^{\ast }$
1st	0.9%	10.3%
2nd	9.7%	0.2%
3rd	3.5%	0.0%

Table 40. The distances, between any two quarks of the found fully-bottom bound and resonance states with $I(J^P)=0(0^{+})$ in coupled-channels calculation, unit in fm.

	${\mathit{r}}_{\mathit{bb}}$	${\mathit{r}}_{\mathit{b}\overline{\mathit{b}}}$	${\mathit{r}}_{\overline{\mathit{b}}\overline{\mathit{b}}}$
1st	0.160	0.166	0.166
2nd	0.163	0.168	0.168
3rd	0.246	0.292	0.292

Additionally, we also investigate the $bb\overline{b}\overline{b}$ system in a complex-range. With a complex scaling method employed in the fully coupled-channels calculation, the three fully-bottom tetraquark states, which are obtained in the real-range, are all well presented in Figure 22 again. Therein, apart from the scattering points, which always descend with the variation of angle $\theta$, the three poles in the real-axis and circled orange are stable. Hence, the bound and resonance states in $bb\overline{b}\overline{b}$ sector are possible. However, as the statement on the fully-heavy tetraquarks in Section 1, since no color-dependent interaction is considered in our present model, the obtained exotic states, especially the bound states of $bb\overline{b}\overline{b}$ are quite negotiable. Much more efforts both theoretical and experimental are deserved [86].

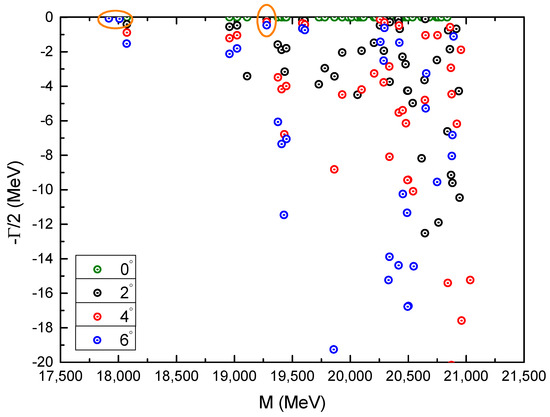
Figure 22. Complex energies of fully-bottom tetraquarks with $I(J^P)=0(0^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

2.

$I(J^P)=0(1^{+})$ state

It is similar to the $cc\overline{c}\overline{c}$ system in $0(1^{+})$ state, di-$\mathsf{{\rm Y}}$ is a scattering state under investigation. Hence Table 41 just lists the bound and resonance states obtained in ${\left[{\eta }_b\mathsf{{\rm Y}}\right]}^1$, ${\left[{\eta }_b\mathsf{{\rm Y}}\right]}^8$ and ${(bb)}^{\ast }{(\overline{b}\overline{b})}^{\ast }$ channels. Particularly, the three bound states with masses both around 18.06 GeV are found in these three configurations, and there is $-802$ MeV binding energy for the ${\eta }_b\mathsf{{\rm Y}}$ dimeson channel. The resonance states’ masses are ∼19.09 GeV. Then in a complete coupled-channels calculation, the lowest bound state is found at 18.01 GeV, the resonances are at 19.34 GeV and 19.63 GeV, respectively. Their components are also listed in the bottom of Table 41 where the ${\eta }_b\mathsf{{\rm Y}}$ meson-meson channel dominates the first two exotic states and strong coupling between di-meson and diquark-antidiquark configurations can be deduced for the third resonance states.

Table 41. Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers $I(J^P)=0(1^{+})$, unit in MeV.

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	${\mathbf{E}}_{\mathbf{b}}$
${\left[{\eta }_b\mathsf{{\rm Y}}\right]}^1(\mathrm{18,864})$	1	$[1;2;1]$	${\mathrm{18,062}}^{1st}$	$-802$
			${\mathrm{19,087}}^{2nd}$	$+223$
${\left[{\eta }_b\mathsf{{\rm Y}}\right]}^8$	2	$[1;2;2]$	${\mathrm{18,062}}^{1st}$	$-802$
			${\mathrm{19,087}}^{2nd}$	$+223$
${(bb)}^{\ast }{(\overline{b}\overline{b})}^{\ast }$	3	$[3;2;3]$	${\mathrm{18,065}}^{1st}$
			${\mathrm{19,093}}^{2nd}$
Mixed			${\mathrm{18,009}}^{1st}$
			${\mathrm{19,338}}^{2nd}$
			${\mathrm{19,627}}^{3rd}$
Component ${(1;2;3)}^{1st}$:  50.9%; 31.9%; 17.2%
Component ${(1;2;3)}^{2nd}$:  48.6%; 51.4%; 0.0%
Component ${(1;2;3)}^{3rd}$:  28.1%; 17.5%; 54.4%

In Table 42 we can notice that sizes of the three $bb\overline{b}\overline{b}$ tetraquark states are quite comparable with those in $0(0^{+})$ case. It is ∼0.16 fm and 0.27 fm for the bound and resonance states, respectively. Meanwhile, Figure 23 shows the distribution of complex energies in the complete coupled-channels calculation of $bb\overline{b}\overline{b}$ system. The bound state, which mass is 18.01 GeV, and the two resonances, which masses at 19.34 GeV and 19.63 GeV, respectively, are stable in the real-axis and independent of the variation of rotated angle $\theta$.

Table 42. The distances, between any two quarks of the found fully-bottom bound and resonance states with $I(J^P)=0(1^{+})$ in coupled-channels calculation, unit in fm.

	${\mathit{r}}_{\mathit{bb}}$	${\mathit{r}}_{\mathit{b}\overline{\mathit{b}}}$	${\mathit{r}}_{\overline{\mathit{b}}\overline{\mathit{b}}}$
1st	0.163	0.169	0.169
2nd	0.248	0.295	0.295
3rd	0.279	0.265	0.265

Figure 23. Complex energies of fully-bottom tetraquarks with $I(J^P)=0(1^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

3.

$I(J^P)=0(2^{+})$ state

In this highest spin state, one meson-meson configuration $\mathsf{{\rm Y}}(1S)\mathsf{{\rm Y}}(1S)$, which include a color-singlet and a hidden-color channel, and one diquark-antidiquark configuration ${(bb)}^{\ast }{(\overline{b}\overline{b})}^{\ast }$ are considered in Table 43. Firstly, bound states at ∼18.24 GeV are obtained in each single channel studies, and the binding energy ∼$-690$ MeV is shallower than the other two quantum states. Furthermore, there are also three resonances found at ∼19.21 GeV. Then, in a complete coupled-channels investigation, masses of the bound and resonance states are 18.19 GeV, 19.45 GeV and 19.71 GeV, respectively. By comparing the components of these exotic states in $1^{+}$ and $2^{+}$, similar features can also be drawn. Furthermore, these compact configurations are also confirmed when analyzing the internal structure of the $bb\overline{b}\overline{b}$ system in Table 44; in particular, the mean square radii are around 0.17, 0.30 and 0.27 fm for the one bound and two resonance states, respectively.

Table 43. Possible bound and resonance states of fully-bottom tetraquarks with quantum numbers $I(J^P)=0(2^{+})$, unit in MeV.

Channel	Index	${\mathit{\chi }}_{\mathit{J}}^{{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{c}}$	$\mathbf{Mass}$	${\mathbf{E}}_{\mathbf{b}}$
${\left[\mathsf{{\rm Y}}\mathsf{{\rm Y}}\right]}^1(\mathrm{18,926})$	1	$[1;2;1]$	${\mathrm{18,238}}^{1st}$	$-688$
			${\mathrm{19,207}}^{2nd}$	$+281$
${\left[\mathsf{{\rm Y}}\mathsf{{\rm Y}}\right]}^8$	2	$[1;2;2]$	${\mathrm{18,238}}^{1st}$	$-688$
			${\mathrm{19,207}}^{2nd}$	$+281$
${(bb)}^{\ast }{(\overline{b}\overline{b})}^{\ast }$	3	$[1;2;3]$	${\mathrm{18,241}}^{1st}$
			${\mathrm{19,211}}^{2nd}$
Mixed			${\mathrm{18,189}}^{1st}$
			${\mathrm{19,451}}^{2nd}$
			${\mathrm{19,708}}^{3rd}$
Component ${(1;2;3)}^{1st}$:  53.2%; 33.2%; 13.6%
Component ${(1;2;3)}^{2nd}$:  48.8%; 51.2%; 0.0%
Component ${(1;2;3)}^{3rd}$:  28.3%; 17.7%; 54.0%

Table 44. The distances, between any two quarks of the found fully-bottom bound and resonance states with $I(J^P)=0(2^{+})$ in coupled-channels calculation, unit in fm.

	${\mathit{r}}_{\mathit{bb}}$	${\mathit{r}}_{\mathit{b}\overline{\mathit{b}}}$	${\mathit{r}}_{\overline{\mathit{b}}\overline{\mathit{b}}}$
$1st$	0.168	0.174	0.174
$2nd$	0.254	0.302	0.302
$3rd$	0.284	0.268	0.268

Additionally, the results obtained in a real-range investigation is supported by a complex-range one, as shown in Figure 24. Therein, three outstanding poles in the real-axis are just the bound and resonance states found in our study. In the varied region from 0° to 6° of angle $\theta$, these three poles are fixed. However, the other energy points are obviously unstable.

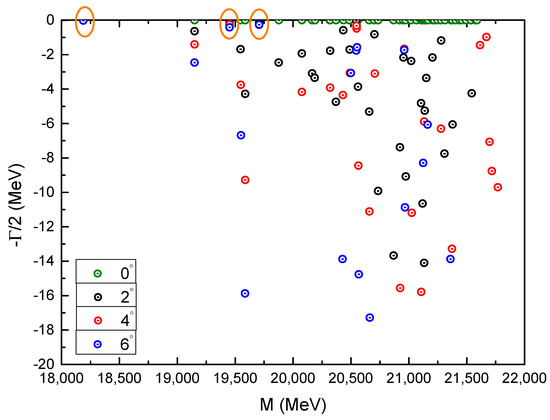
Figure 24. Complex energies of fully-bottom tetraquarks with $I(J^P)=0(2^{+})$ in the coupled channels calculation, $\theta$ varying from 0° to 6°.

At last, Table 45 summarizes our calculated data on the fully-heavy tetraquark resonance states, meanwhile a few results by other literatures are also listed. The obtained bound states in fully-bottom are not discussed herein, and this is partly due to our employed model is color-independent, the obtained resonances should be more reliable. In particular, our results are generally comparable with those in reference [94].

Table 45. Comparison of theoretical masses for the fully-heavy tetraquark resonance states by different predictions. (unit: MeV).

	$0^{+}$	$1^{+}$	$2^{+}$	$0^{+}$	$1^{+}$	$2^{+}$
	$\mathit{cc}\overline{\mathit{c}}\overline{\mathit{c}}$			$\mathit{bb}\overline{\mathit{b}}\overline{\mathit{b}}$
This work	6449, 6659	6657	7022	19,005, 19,049	19,067	19,189
Ref. [76]	5960, 6198	6009, 6246	6100, 6323	18,723, 18,754	18,738, 18,768	18,768, 18,797
Ref. [66]	5883	6120	6246	18,748	18,828	18,900
Ref. [67]	5966	6051	6223	18,754	18,808	18,916
Ref. [91]	7016	6899	6956	20,275	20,212	20,243
Ref. [93]	6487	6500	6524	19,322	19,329	19,341
Ref. [94]	6420, 6436	6425, 6450	6432, 6479	19,246, 19,297	19,247, 19,311	19,249, 19,325

3.2. Hidden and Open Heavy Flavor Pentaquarks

In this part, three types of 5-quarks systems will be introduced according to the investigations by the chiral quark model. Particularly, hidden charm $qqqc\overline{c}$, hidden bottom $qqqb\overline{b}$ and doubly charmed $ccq\overline{q}$ pentaquarks in spin-parity $J^P={\frac{1}{2}}^{-}$, ${\frac{3}{2}}^{-}$ and ${\frac{5}{2}}^{-}$, and $I=\frac{1}{2}$ or $\frac{3}{2}$ are calculated. However, in comparison with the tetraquark sector, a much higher-dimension matrix is needed to deal with each configuration of the pentaquark system. Only color-singlet baryon-meson, hidden-color structures, and their couplings are considered. The details are presented below.

3.2.1. Hidden Charm Pentaquarks

In the $qqqc\overline{c}$ ($q=u,d$) sector, several pentaquark states reported by the LHCb collaboration can be well explained in our work. In particular, the $P_c^{+}(4380)$ can be identified as the ${\mathsf{\Sigma }}_c^{\ast }\overline{D}$ molecule state with $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$, $P_c^{+}(4312)$, $P_c^{+}(4440)$ and $P_c^{+}(4457)$ can be explained as the molecule states of $\frac{1}{2}{\frac{1}{2}}^{-}$${\mathsf{\Sigma }}_c\overline{D}$, $\frac{1}{2}{\frac{1}{2}}^{-}$${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ and $\frac{1}{2}{\frac{3}{2}}^{-}$${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$, respectively. Let us discuss them in the following parts.

• $I(J^P)=\frac{1}{2}({\frac{1}{2}}^{-})$ state

Seven baryon-meson channels, $N{\eta }_c$, $NJ/\psi$, ${\mathsf{\Lambda }}_c\overline{D}$, ${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }$, ${\mathsf{\Sigma }}_c\overline{D}$, ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ and ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$ are studied in the lowest spin state. Table 46 shows the calculated results. Particularly, the first column lists the necessary bases in spin, flavor and color degrees of freedom. Mass of 5-quark system is in the second one. The theoretical and experimental thresholds of each channels are in the third and fifth column, respectively. In the fourth column, the binding energy of state is presented. A modified mass $E^{\prime }$ which is obtained by the summation of binding energy $E_B$ and experimental threshold value $E_{th}^{Exp}$ is in the last column.

Table 46. The lowest eigen-energies of the $udc\overline{c}u$ system with $J^P={\frac{1}{2}}^{-}$ (unit: MeV). The percentages of color-singlet (S) and hidden-color (H) channels are also given.

Channel	E	${\mathit{E}}_{\mathbf{th}}^{\mathbf{Theo}}$	${\mathit{E}}_{\mathbf{B}}$	${\mathit{E}}_{\mathbf{th}}^{\mathbf{Exp}}$	E’
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=4,5,j=3,4,k=1$	3745	3745	0	3919($N{\eta }_c$)	3919
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=4,5,j=3,4,k=2,3$	4714
color-singlet+hidden color	3745
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=2,3,j=3,4,k=1$	3841	3841	0	4036($NJ/\psi$)	4036
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=2,3,j=3,4,k=2,3$	4964
color-singlet+hidden color	3841
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=4,5,j=2,k=1$	3996	3996	0	4151(${\mathsf{\Lambda }}_c\overline{D}$)	4151
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=4,5,j=2,k=2,3$	4663
color-singlet+hidden color	3996
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=2,3,j=2,k=1$	4115	4115	0	4293(${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }$)	4293
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=2,3,j=2,k=2,3$	4599
color-singlet+hidden color	4115
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=4,5,j=1,k=1$	4398	4402	$-4$	4320(${\mathsf{\Sigma }}_c\overline{D}$)	4316
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=4,5,j=1,k=2,3$	4835
color-singlet+hidden color	4394	4402	$-8$	4320	4312
		percentage(S;H): 91.0%; 7.0%
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=2,3,j=1,k=1$	4518	4520	$-2$	4462(${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$)	4460
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=2,3,j=1,k=2,3$	4728
color-singlet+hidden color	4479	4520	$-41$	4462	4421
		percentage(S;H): 67.4%; 32.6%
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=1,j=1,k=1$	4563	4566	$-3$	4527(${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$)	4524
${\chi }_{1/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=1,j=1,k=2,3$	4476
color-singlet+hidden color	4461	4566	$-105$	4527	4422
		percentage(S;H): 23.0%; 77.0%
mixed (only color singlet)	3745
mixed (color singlet+hidden color)	3745

The $N{\eta }_c$, $NJ/\psi$, ${\mathsf{\Lambda }}_c\overline{D}$ and ${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }$ channels present a binding energy $E_B=0$, indicating that they are scattering states. However, resonance states are available in the ${\mathsf{\Sigma }}_c\overline{D}$, ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ and ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$ channels. Particularly, binding energies $E_B=-4$ MeV, $-2$ MeV and $-3$ MeV are found for the color-singlet channels of these three states, respectively. In additional, deeper binding energies are obtained through the couplings with hidden-color channels for the ${\mathsf{\Sigma }}_c\overline{D}$, ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ and ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$, the new $E_B$ are $-8$ MeV, $-41$ MeV and $-105$ MeV, respectively. The main contributions are color-singlet channels for the first two states (91% in ${\mathsf{\Sigma }}_c\overline{D}$ and 67% in ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$), but ∼80% component is the hidden-color channel for ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$ state. After a mass shift by considering the systematical error, the rescaled masses $E^{\prime }$ for the three resonance states are 4312 MeV, 4421 MeV and 4422 MeV, respectively. Accordingly, the first one is nicely consistent with $P_c^{+}(4312)$ and can be identified as the ${\mathsf{\Sigma }}_c\overline{D}$ state. The nature of ${\mathsf{\Sigma }}_c$ baryon and $\overline{D}$ meson molecular state is confirmed in Table 47, in which the distances between any two quarks are shown and the obtained 2.1 fm for the $c\overline{c}$ pair in hidden charm pentaquark state is quite comparable with the size of deuteron. Besides, there is a degeneration between the coupled masses of ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ and ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$ states, however, the $P_c^{+}(4440)$ is preferred to be explained as a ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ state since its threshold value and the mass of color-singlet channel are more reasonable. The molecular nature for this pentaquark state can also be guessed from Table 47. Meanwhile, a complete coupled-channels mass which includes all baryon-meson structures is listed in the bottom of Table 46, clearly, 3745 MeV is just the theoretical threshold value of $N{\eta }_c$. Therefore, no bound state is found in the fully coupled-channels case.

Table 47. Distances between any two quarks (unit: fm).

${\mathbf{J}}^{\mathbf{P}}$	Channel	${\mathbf{r}}_{12}$	${\mathbf{r}}_{13}$	${\mathbf{r}}_{14}$	${\mathbf{r}}_{34}$
${\frac{1}{2}}^{-}$	${\chi }_{1/2}^{\sigma i}{\chi }_j^{f}i=4,5,j=1,k=1$ (${\mathsf{\Sigma }}_c\overline{D}$)	0.8	0.7	2.1	2.1
	${\chi }_{1/2}^{\sigma i}{\chi }_j^{f}i=4,5,j=1,k=2,3$	1.0	0.8	0.8	0.4
	${\chi }_{1/2}^{\sigma i}{\chi }_j^{f}i=2,3,j=1,k=1$ (${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$)	0.8	0.7	2.2	2.1
	${\chi }_{1/2}^{\sigma i}{\chi }_j^{f}i=2,3,j=1,k=2,3$	0.9	0.8	0.8	0.4
	${\chi }_{1/2}^{\sigma i}{\chi }_j^{f}i=1,j=1,k=1$ (${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$)	0.9	0.8	2.1	2.0
	${\chi }_{1/2}^{\sigma i}{\chi }_j^{f}i=1,j=1,k=2,3$	0.9	0.8	0.8	0.4
${\frac{3}{2}}^{-}$	${\chi }_{3/2}^{\sigma i}{\chi }_j^{f}i=3,4,j=1,k=1$ (${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$)	0.8	0.7	2.4	2.3
	${\chi }_{3/2}^{\sigma i}{\chi }_j^{f}i=3,4,j=1,k=2,3$	1.1	0.9	0.9	0.5
	${\chi }_{3/2}^{\sigma i}{\chi }_j^{f}i=2,j=1,k=1$ (${\mathsf{\Sigma }}_c^{\ast }\overline{D}$)	0.9	0.8	2.2	2.2
	${\chi }_{3/2}^{\sigma i}{\chi }_j^{f}i=2,j=1,k=2,3$	1.0	0.9	0.9	0.5
	${\chi }_{3/2}^{\sigma i}{\chi }_j^{f}i=1,j=1,k=1$ (${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$)	0.9	0.8	2.6	2.4
	${\chi }_{3/2}^{\sigma i}{\chi }_j^{f}i=1,j=1,k=2,3$	0.9	0.9	0.8	0.4
${\frac{5}{2}}^{-}$	${\chi }_{5/2}^{\sigma i}{\chi }_j^{f}i=1,j=1,k=1$ (${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$)	0.9	0.8	2.4	2.3
	${\chi }_{5/2}^{\sigma i}{\chi }_j^{f}i=1,j=1,k=2,3$	1.3	1.4	1.3	0.8

• $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$ state

Among the five baryon-meson channels listed in Table 48 for $\frac{1}{2}({\frac{3}{2}}^{-})$ state, $NJ/\psi$ and ${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }$ are still unbound neither in the single channel calculation nor the hidden-color channel included and this is similar to the $\frac{1}{2}({\frac{1}{2}}^{-})$ case. However, several resonance states with shallow binding energies of ${\mathsf{\Sigma }}_c^{(\ast )}{\overline{D}}^{(\ast )}$ configurations are obtained. Specifically, binding energies of the three states of ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$, ${\mathsf{\Sigma }}_c^{\ast }\overline{D}$ and ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$ in color-singlet channels are all ∼2 MeV. Besides, except $E_B=-3$ MeV for the ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ state in a coupled-channels calculation, there are dozens MeV decreased when hidden-color channels of the other two states included. Furthermore, the most contributions are still from their color-singlet channels and the percentages of singlet are 96%, 83% and 61% for ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$, ${\mathsf{\Sigma }}_c^{\ast }\overline{D}$ and ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$, respectively.

Table 48. The lowest eigen-energies of the $udc\overline{c}u$ system with $J^P={\frac{3}{2}}^{-}$ and ${\frac{5}{2}}^{-}$(unit: MeV).

Channel	E	${\mathit{E}}_{\mathbf{th}}^{\mathbf{Theo}}$	${\mathit{E}}_{\mathbf{B}}$	${\mathit{E}}_{\mathbf{th}}^{\mathbf{Exp}}$	E’
$J^P=3/2^{-}$
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=3,4,j=3,4,k=1$	3841	3841	0	4036($NJ/\psi$)	4036
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=3,4,j=3,4,k=2,3$	4722
color-singlet+hidden color	3841
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=3,4,j=2,k=1$	4115	4115	0	4293(${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }$)	4293
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=3,4,j=2,k=2,3$	4680
color-singlet+hidden color	4115
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=3,4,j=1,k=1$	4518	4520	$-2$	4462(${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$)	4460
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=3,4,j=1,k=2,3$	4961
color-singlet+hidden color	4517	4520	$-3$	4462	4459
		percentage(S;H): 96.3%; 3.7%
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=2,j=1,k=1$	4444	4447	$-3$	4385(${\mathsf{\Sigma }}_c^{\ast }\overline{D}$)	4382
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=2,j=1,k=2,3$	4754
color-singlet+hidden color	4432	4447	$-15$	4385	4370
		percentage(S;H): 82.6%; 17.4%
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=1,j=1,k=1$	4564	4566	$-2$	4527(${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$)	4525
${\chi }_{3/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=1,j=1,k=2,3$	4623
color-singlet+hidden color	4549	4566	$-17$	4527	4510
		percentage(S;H): 61.1%; 38.9%
mixed (only color-singlet)	3841
mixed (color-singlet+hidden color)	3841
$J^P=5/2^{-}$
${\chi }_{5/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=1,j=1,k=1$	4563	4566	$-3$	4527(${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$)	4524
${\chi }_{5/2}^{\sigma i}{\chi }_j^f{\chi }_k^{c}i=1,j=1,k=2,3$	5002
color-singlet+hidden color	4477	4566	$-89$	4527	4438
		percentage(S;H): 66.2%; 33.8%

Although the lowest mass remains at 3841 MeV in a fully coupled channels computation, the obtained ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ resonance with mass equals to 4459 MeV is a robust support for the $P_c^{+}(4457)$ which is also a new hidden charm pentaquark state reported by the LHCb collaboration. This exotic state can be identified as a ${\mathsf{\Sigma }}_c$ baryon and ${\overline{D}}^{\ast }$ meson molecular state whose theoretical size is around 2.3 fm according to the results in Table 47.

• $I(J^P)=\frac{1}{2}({\frac{5}{2}}^{-})$ state

There is only one baryon-meson channel ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$ under consideration in the highest spin state. Firstly, there is −3 MeV binding energy in the color-singlet channel calculation and after a mass shift with $E^{\prime }=E_{th}^{Exp}+E_B$, 4524 MeV resonance mass is obtained. However, the hidden-color channel mass is higher and at 5002 MeV. A strong coupling between this two channels leads to a deeper binding energy which is −89 MeV, and the modified mass in coupled-channels is 4438 MeV. The components of this resonance state is comparable with 66% for the color-singlet channel of ${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$ and 34% of its hidden-color one. Hence it is also a good candidate for the hidden charm pentaquark in high spin state.

Finally, Table 49 lists several theoretical masses on the hidden-charm pentaquark states with the purpose of having a better insight into this sector.

Table 49. Comparison of theoretical masses on the hidden-charm pentaquark systems by different predictions, the predicted masses and states are summarized in each column, respectively. (unit: MeV).

	$\frac{1}{2}\frac{1}{2}$${}^{-}$	$\frac{1}{2}\frac{3}{2}$${}^{-}$	$\frac{1}{2}\frac{5}{2}$${}^{-}$
This work	${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }(4291)$	${\mathsf{\Sigma }}_c^{\ast }\overline{D}(4370)$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4438)$
	${\mathsf{\Sigma }}_c\overline{D}(4312)$	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4459)$
	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4421)$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4510)$
	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4422)$
Ref. [125]	${\mathsf{\Sigma }}_c\overline{D}(4306)$	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4309)$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4517)$
	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4444)$	${\mathsf{\Sigma }}_c^{\ast }\overline{D}(4450)$
	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4503)$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4514)$
Ref. [126]	${\mathsf{\Sigma }}_c\overline{D}(4307)$	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4445)$	-
	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4450)$	${\mathsf{\Sigma }}_c^{\ast }\overline{D}(4376)$
	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4525)$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4523)$
Ref. [128]	-	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4370)$	-
		${\mathsf{\Sigma }}_c^{\ast }\overline{D}(4450)$
Ref. [136]	${\mathsf{\Sigma }}_c\overline{D}(4311)$	${\mathsf{\Sigma }}_c^{\ast }\overline{D}(4376)$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4523)$
	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4440)$	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4457)$
	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4500)$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4510)$
Ref. [137]	${\mathsf{\Sigma }}_c\overline{D}(4317)$	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4461)$	-
	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4427)$
Ref. [146]	${\mathsf{\Sigma }}_c\overline{D}(4306)$	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4452)$	-
	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }(4453)$
Ref. [145]	${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }(4327)$	${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }(4367)$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }(4546)$
	${\mathsf{\Lambda }}_c\overline{D}(4372)$	$NJ/\psi (4367)$
	${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }(4480)$	${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }(4476)$

3.2.2. Hidden Bottom Pentaquarks

In this part, we extend the investigation on hidden charm pentaquark state to the hidden bottom sector. Spin-parity $J^P={\frac{1}{2}}^{+}$, ${\frac{3}{2}}^{-}$ and ${\frac{5}{2}}^{-}$, and both in the isospin $I=\frac{1}{2}$ and $\frac{3}{2}$ of $qqqb\overline{b}$ systems are considered. The allowed baryon-meson channels in each $I(J^P)$ quantum state are summarized in Table 50. Several resonance states are found in these quantum states except the $\frac{3}{2}({\frac{1}{2}}^{-})$ case.

Table 50. All allowed channels for hidden-bottom pentaquark systems with negative parity.

		$\mathit{I}=\frac{1}{2}$		$\mathit{I}=\frac{3}{2}$
${\mathit{J}}^{\mathbf{P}}$	Index	${\chi }_J^{{\sigma }_i}$; ${\chi }_I^{f_j}$; ${\chi }_k^c$	Channel	${\chi }_J^{{\sigma }_i}$; ${\chi }_I^{f_j}$; ${\chi }_k^c$	Channel
		$[i;j;k]$		$[i;j;k]$
${\frac{1}{2}}^{-}$	1	$[4,5;3,4;1]$	${(N{\eta }_b)}^1$	$[1;1;1]$	${(\Delta \mathsf{{\rm Y}})}^1$
	2	$[4,5;3,4;2,3]$	${(N{\eta }_b)}^8$	$[1;1;3]$	${(\Delta \mathsf{{\rm Y}})}^8$
	3	$[2,3;3,4;1]$	${(N\mathsf{{\rm Y}})}^1$	$[4;2;1]$	${({\mathsf{\Sigma }}_b\overline{B})}^1$
	4	$[2,3;3,4;2,3]$	${(N\mathsf{{\rm Y}})}^8$	$[4,5;2;2,3]$	${({\mathsf{\Sigma }}_b\overline{B})}^8$
	5	$[5;2;1]$	${({\mathsf{\Lambda }}_b\overline{B})}^1$	$[2;2;1]$	${({\mathsf{\Sigma }}_b{\overline{B}}^{\ast })}^1$
	6	$[4,5;2;2,3]$	${({\mathsf{\Lambda }}_b\overline{B})}^8$	$[2,3;2;2,3]$	${({\mathsf{\Sigma }}_b{\overline{B}}^{\ast })}^8$
	7	$[3;2;1]$	${({\mathsf{\Lambda }}_b{\overline{B}}^{\ast })}^1$	$[1;2;1]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^1$
	8	$[2,3;2;2,3]$	${({\mathsf{\Lambda }}_b{\overline{B}}^{\ast })}^8$	$[1;2;3]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^8$
	9	$[4;1;1]$	${({\mathsf{\Sigma }}_b\overline{B})}^1$
	10	$[4,5;1;2,3]$	${({\mathsf{\Sigma }}_b\overline{B})}^8$
	11	$[2;1;1]$	${({\mathsf{\Sigma }}_b{\overline{B}}^{\ast })}^1$
	12	$[2,3;1;2,3]$	${({\mathsf{\Sigma }}_b{\overline{B}}^{\ast })}^8$
	13	$[1;1;1]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^1$
	14	$[1;1;3]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^8$
${\frac{3}{2}}^{-}$	1	$[3,4;3,4;1]$	${(N\mathsf{{\rm Y}})}^1$	$[2;1;1]$	${(\Delta {\eta }_b)}^1$
	2	$[3,4;3,4;2,3]$	${(N\mathsf{{\rm Y}})}^8$	$[2;1;3]$	${(\Delta {\eta }_b)}^8$
	3	$[4;2;1]$	${({\mathsf{\Lambda }}_b{\overline{B}}^{\ast })}^1$	$[1;1;1]$	${(\Delta \mathsf{{\rm Y}})}^1$
	4	$[3,4;2;2,3]$	${({\mathsf{\Lambda }}_b{\overline{B}}^{\ast })}^8$	$[1;1;3]$	${(\Delta \mathsf{{\rm Y}})}^8$
	5	$[3;1;1]$	${({\mathsf{\Sigma }}_b{\overline{B}}^{\ast })}^1$	$[3;2;1]$	${({\mathsf{\Sigma }}_b{\overline{B}}^{\ast })}^1$
	6	$[3,4;1;2,3]$	${({\mathsf{\Sigma }}_b{\overline{B}}^{\ast })}^8$	$[3,4;2;2,3]$	${({\mathsf{\Sigma }}_b{\overline{B}}^{\ast })}^8$
	7	$[2;1;1]$	${({\mathsf{\Sigma }}_b^{\ast }\overline{B})}^1$	$[2;2;1]$	${({\mathsf{\Sigma }}_b^{\ast }\overline{B})}^1$
	8	$[2;1;3]$	${({\mathsf{\Sigma }}_b^{\ast }\overline{B})}^8$	$[2;2;3]$	${({\mathsf{\Sigma }}_b^{\ast }\overline{B})}^8$
	9	$[1;1;1]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^1$	$[1;2;1]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^1$
	10	$[1;1;3]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^8$	$[1;2;3]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^8$
${\frac{5}{2}}^{-}$	1	$[1;1;1]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^1$	$[1;1;1]$	${(\Delta \mathsf{{\rm Y}})}^1$
	2	$[1;1;3]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^8$	$[1;1;3]$	${(\Delta \mathsf{{\rm Y}})}^8$
	3			$[1;2;1]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^1$
	4			$[1;2;3]$	${({\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast })}^8$

Particularly, from Table 51, Table 52, Table 53, Table 54 and Table 55, the first column lists the channels on our obtained bound states, their experimental values of the noninteracting baryon-meson threshold ($E_{th}^{ex}$) are also shown in parentheses. The second column labels the color-singlet (S), hidden-color (H) and coupled-channels (S+H) computation. Then, the calculated theoretical mass (M) and binding energy ($E_B$) of pentaquark state is presented in the third and fourth columns, respectively. A re-scaled mass ($M^{\prime }$), which is obtained by attending to the experimental baryon-meson threshold, $M^{\prime }=E_{th}^{ex}+E_B$, and with a purpose of removing the theoretical uncertainty, is listed in the last column. The percentages of color-singlet (S) and hidden-color (H) channels are also given when the coupled-channels calculation is performed. Hence, we will discuss them according to the $I(J^P)$ state, respectively.

Table 51. Lowest-lying states of hidden-bottom pentaquarks with quantum numbers $I(J^P)=\frac{1}{2}({\frac{1}{2}}^{-})$, unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.

Channel	Color	M	${\mathit{E}}_{\mathbf{B}}$	M’
${\mathsf{\Sigma }}_b\overline{B}$	S	$\mathrm{11,080}$	$-15$	$\mathrm{11,074}$
$(\mathrm{11,089})$	H	$\mathrm{11,364}$	$+269$	$\mathrm{11,358}$
	S+H	$\mathrm{11,078}$	$-17$	$\mathrm{11,072}$
	Percentage (S;H): 98.5%; 1.5%
${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	S	$\mathrm{11,115}$	$-21$	$\mathrm{11,113}$
$(\mathrm{11,134})$	H	$\mathrm{11,257}$	$+121$	$\mathrm{11,255}$
	S+H	$\mathrm{11,043}$	$-93$	$\mathrm{11,041}$
	Percentage (S;H): 57.9%; 42.1%
${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	$\mathrm{11,127}$	$-26$	$\mathrm{11,128}$
$(\mathrm{11,154})$	H	$\mathrm{10,921}$	$-232$	$\mathrm{10,922}$
	S+H	$\mathrm{10,861}$	$-292$	$\mathrm{10,862}$
	Percentage (S;H): 15.8%; 84.2%

Table 52. Lowest-lying states of hidden-bottom pentaquarks with quantum numbers $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$, unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.

Channel	Color	M	${\mathit{E}}_{\mathbf{B}}$	M’
${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	S	$\mathrm{11,124}$	$-12$	$\mathrm{11,122}$
$(\mathrm{11,134})$	H	$\mathrm{11,476}$	$+340$	$\mathrm{11,475}$
	S+H	$\mathrm{11,122}$	$-14$	$\mathrm{11,120}$
	Percentage (S;H): 99.6%; 0.4%
${\mathsf{\Sigma }}_b^{\ast }\overline{B}$	S	$\mathrm{11,097}$	$-15$	$\mathrm{11,094}$
$(\mathrm{11,109})$	H	$\mathrm{11,175}$	$+63$	$\mathrm{11,172}$
	S+H	$\mathrm{11,045}$	$-67$	$\mathrm{11,042}$
	Percentage (S;H): 55.5%; 44.5%
${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	$\mathrm{11,138}$	$-15$	$\mathrm{11,139}$
$(\mathrm{11,154})$	H	$\mathrm{11,051}$	$-102$	$\mathrm{11,052}$
	S+H	$\mathrm{10,958}$	$-195$	$\mathrm{10,959}$
	Percentage (S;H): 22.2%; 77.8%

Table 53. Lowest-lying states of hidden-bottom pentaquarks with quantum numbers $I(J^P)=\frac{1}{2}({\frac{5}{2}}^{-})$, unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.

Channel	Color	M	${\mathit{E}}_{\mathbf{B}}$	M’
${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	$\mathrm{11,141}$	$-12$	$\mathrm{11,151}$
$(\mathrm{11,154})$	H	$\mathrm{11,547}$	$+394$	$\mathrm{11,548}$
	S+H	$\mathrm{11,140}$	$-13$	$\mathrm{11,141}$
	Percentage (S;H): 99.6%; 0.4%

Table 54. Lowest-lying states of hidden-bottom pentaquarks with quantum numbers $I(J^P)=\frac{3}{2}({\frac{3}{2}}^{-})$, unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.

Channel	Color	M	${\mathit{E}}_{\mathbf{B}}$	M’
${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	S	$\mathrm{11,136}$	0	$\mathrm{11,134}$
$(\mathrm{11,134})$	H	$\mathrm{11,310}$	$+174$	$\mathrm{11,308}$
	S+H	$\mathrm{11,021}$	$-115$	$\mathrm{11,019}$
	Percentage (S;H): 64.7%; 35.3%
${\mathsf{\Sigma }}_b^{\ast }\overline{B}$	S	$\mathrm{11,112}$	0	$\mathrm{11,109}$
$(\mathrm{11,109})$	H	$\mathrm{11,041}$	$-71$	$\mathrm{11,038}$
	S+H	$\mathrm{10,999}$	$-113$	$\mathrm{10,996}$
	Percentage (S;H): 18.4%; 81.6%
${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	$\mathrm{11,153}$	0	$\mathrm{11,154}$
$(\mathrm{11,154})$	H	$\mathrm{11,102}$	$-51$	$\mathrm{11,103}$
	S+H	$\mathrm{11,048}$	$-105$	$\mathrm{11,049}$
	Percentage (S;H): 15.7%; 84.3%

Table 55. Lowest-lying states of hidden-bottom pentaquarks with quantum numbers $I(J^P)=\frac{3}{2}({\frac{5}{2}}^{-})$, unit in MeV. The baryon-meson channels that do not appear here have been also considered in the computation but no bound states were found.

Channel	Color	M	${\mathit{E}}_{\mathbf{B}}$	M’
${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	$\mathrm{11,052}$	$-101$	$\mathrm{11,053}$
$(\mathrm{11,154})$	H	$\mathrm{10,974}$	$-179$	$\mathrm{10,975}$
	S+H	$\mathrm{10,931}$	$-222$	$\mathrm{10,932}$
	Percentage (S;H): 19.9%; 80.1%

-

$I(J^P)=\frac{1}{2}({\frac{1}{2}}^{-})$ state

There are 14 possibilities which include $N{\eta }_b$, $N\mathsf{{\rm Y}}$, ${\mathsf{\Lambda }}_b\overline{B}$, ${\mathsf{\Lambda }}_b{\overline{B}}^{\ast }$, ${\mathsf{\Sigma }}_b\overline{B}$, ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ both in singlet- and hidden-color channel. However, resonance states are only obtained in the ${\mathsf{\Sigma }}_b^{(\ast )}{\overline{B}}^{(\ast )}$ configurations and they are listed in Table 51. Particularly, there are around $-20$ MeV binding energy for the color-singlet channels of ${\mathsf{\Sigma }}_b\overline{B}$, ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$. Their modified masses $M^{\prime }$ are 11.07 GeV, 11.11 GeV and 11.13 GeV, respectively. As for their hidden-color channels, only the ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ channel with $E_B=-232$ MeV is found, the other two are at least 120 MeV above their corresponding theoretical threshold values.

In additional, within a calculation which the coupling on color-singlet and hidden-color channels are considered, the ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ resonances with much deeper binding energies (more than $-90$ MeV) are obtained, their coupled masses are 11.04 GeV and 10.86 GeV, respectively. Therefore, compact configuration of hidden bottom pentaquark state is favored herein. However, the coupling in ${\mathsf{\Sigma }}_b\overline{B}$ resonance is quite weak with only 2 MeV binding energy decreased and the rescaled mass is still ∼11.07 GeV, this can be identified as a molecule state. Moreover, these results are confirmed by two facts: (i) the color-singlet channel is almost 99% in ${\mathsf{\Sigma }}_b\overline{B}$, 58% in ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ and only 16% in ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$, (ii) in Table 56, the calculated size for ${\mathsf{\Sigma }}_b\overline{B}$ resonance state is around 1 fm. However, ∼0.7 fm for the other two resonance states and especially, the distance between a $b\overline{b}$ pair in ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ states is only ∼0.3 fm.

Table 56. The distance, in fm, between any two quarks of the found pentaquark bound-states.

$\mathbf{I}({\mathbf{J}}^{\mathbf{P}})$	Channel	Mixing	${\mathit{r}}_{\mathbf{qq}}$	${\mathit{r}}_{\mathbf{qQ}}$	${\mathit{r}}_{\mathbf{q}\overline{\mathbf{Q}}}$	${\mathit{r}}_{\mathbf{Q}\overline{\mathbf{Q}}}$
$\frac{1}{2}({\frac{1}{2}}^{-})$	${\mathsf{\Sigma }}_b\overline{B}$	S	1.17	0.87	1.02	1.00
		S+H	1.13	0.84	0.98	0.94
	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	S	1.09	0.81	0.92	0.82
		S+H	0.94	0.70	0.71	0.34
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	1.06	0.79	0.88	0.75
		S+H	0.91	0.71	0.70	0.24
$\frac{1}{2}({\frac{3}{2}}^{-})$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	S	1.23	0.90	1.09	1.09
		S+H	1.21	0.90	1.07	1.07
	${\mathsf{\Sigma }}_b^{\ast }\overline{B}$	S	1.18	0.88	1.04	1.01
		S+H	0.98	0.74	0.74	0.34
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	1.17	0.87	1.02	0.97
		S+H	0.95	0.72	0.72	0.25
$\frac{1}{2}({\frac{5}{2}}^{-})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	1.25	0.92	1.11	1.13
		S+H	1.25	0.92	1.11	1.11
$\frac{3}{2}({\frac{3}{2}}^{-})$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	S+H	1.02	0.78	0.77	0.27
	${\mathsf{\Sigma }}_b^{\ast }\overline{B}$	S+H	1.02	0.84	0.82	0.26
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S+H	1.05	0.83	0.81	0.26
$\frac{3}{2}({\frac{5}{2}}^{-})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	S	1.03	0.86	0.86	0.29
		S+H	1.00	0.86	0.84	0.26

• $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$ state

We only find resonances in the ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$, ${\mathsf{\Sigma }}_b^{\ast }\overline{B}$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ states. Table 52 presents the predicted mass, binding energy and components of these hidden bottom pentaquarks. Firstly, in the color-singlet channels calculation, the binding energies are $-12\mathrm{MeV}$, $-15\mathrm{MeV}$ and $-15\mathrm{MeV}$ for the ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$, ${\mathsf{\Sigma }}_b^{\ast }\overline{B}$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ channels, respectively.

However, when the hidden-color channels are incorporated into computation, a strong coupling effect is obtained in the later two states and the binding energies are $-67$ MeV and $-195$ MeV, respectively. In contrast, the coupling is very weak and only 2 MeV decreased when hidden-color channel included in ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ state. The modified masses are 11.12 GeV, 11.04 GeV and 10.96 GeV for the ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$, ${\mathsf{\Sigma }}_b^{\ast }\overline{B}$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ states in the coupled-channels study, respectively. Furthermore, Table 52 also presents the percentages of singlet- and hidden-channels of the three resonance states. In particular, it is almost the complete color-singlet component in the ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ state. But the main part (78%) is the hidden-color channel in ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ state, and also a considerable percentage (45%) in the ${\mathsf{\Sigma }}_b^{\ast }\overline{B}$.

These results are consistent with the analysis on the internal structures of ${\mathsf{\Sigma }}_b^{(\ast )}{\overline{B}}^{(\ast )}$ resonance states. In Table 56 one can notice that a compact configuration within 0.7 fm for both the ${\mathsf{\Sigma }}_b^{\ast }\overline{B}$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ states confirms the previous facts of deep binding energy and strong coupling. However, it is a ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ molecule state which size is around 1.1 fm in the coupled-channels calculation.

• $I(J^P)=\frac{1}{2}({\frac{5}{2}}^{-})$ state

Only one ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ configuration needs to be considered in the highest spin state and Table 53 shows the calculated mass of this resonance state. Clearly, there are $-12$ MeV binding energy in the color-singlet channel. Besides, this result is comparable with the colorless channel of ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ in the other two spin-parity states.

In a further step with hidden-color channel included, only a weak coupling with $E_B=-13$ MeV is obtained and the rescaled mass which is obtained as the previous procedure is 11.14 GeV. Accordingly, this resonance can be identified as the ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ molecule state with 99.6% color-singlet component and ∼1.1 fm size shown in Table 56.

• $I(J^P)=\frac{3}{2}({\frac{3}{2}}^{-})$ state

In this spin-parity channel, neither bound nor resonance state is found in the $\Delta {\eta }_b$ and $\Delta \mathsf{{\rm Y}}$ configurations, however, resonance states are possible in the ${\mathsf{\Sigma }}_b^{(\ast )}{\overline{B}}^{(\ast )}$ configurations. The details are listed in Table 54.

Firstly, only scattering states are found in the ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$, ${\mathsf{\Sigma }}_b^{\ast }\overline{B}$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ channels when only color-singlet configurations are included. However, hidden-color structures help in obtaining resonance states with deep binding energies. Namely, coupled-masses of these three resonance states are all below the corresponding theoretical thresholds about 110 MeV. The modified masses are 11.02 GeV, 10.99 GeV and 11.05 GeV for the ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$, ${\mathsf{\Sigma }}_b^{\ast }\overline{B}$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ states, respectively. Furthermore, their calculated sizes listed in Table 56 are ∼0.8 fm which is a compact 5-quarks configuration. This feature is supported by the fact that the coupling between singlet- and hidden-channels is strong and the percentage of the later configuration is quite considerable, 35% in ${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$ and both more than 81% in ${\mathsf{\Sigma }}_b^{\ast }\overline{B}$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$.

• $I(J^P)=\frac{3}{2}({\frac{5}{2}}^{-})$ state

There are two baryon-meson channels devote to the highest spin and isospin state, $\Delta \mathsf{{\rm Y}}$ and ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$. Table 55 just lists the results of ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$ resonance state, however, it is a scattering state of $\Delta \mathsf{{\rm Y}}$ channel. Firstly, in the single-channel calculation of color-singlet and hidden-color configuration, there are more than $-100$ MeV binding energy obtained and especially $E_B=-179$ MeV for the later structure. Additionally, a binding energy of $-222$ MeV is obtained in their coupled-channels computation and the modified mass is 10.93 GeV. Apparently, this can be identified as a color resonance which about 80% component is the hidden-color channel of ${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$. Moreover, the size ∼0.8 fm in Table 56 confirms a compact structure too.

Furthermore, Table 57 lists a summary of several theoretical predictions on the hidden-bottom pentaquark states.

Table 57. Comparison of theoretical masses on the hidden-bottom pentaquark systems by different predictions, the predicted masses and states are summarized in each column, respectively. (unit: MeV).

	$\frac{1}{2}\frac{1}{2}$${}^{-}$	$\frac{1}{2}\frac{3}{2}$${}^{-}$	$\frac{1}{2}\frac{5}{2}$${}^{-}$	$\frac{3}{2}\frac{1}{2}$${}^{-}$	$\frac{3}{2}\frac{3}{2}$${}^{-}$	$\frac{3}{2}\frac{5}{2}$${}^{-}$
This work	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,041})$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,120})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,141})$	-	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,019})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{10,932})$
	${\mathsf{\Sigma }}_b\overline{B}(\mathrm{11,072})$	${\mathsf{\Sigma }}_b^{\ast }\overline{B}(\mathrm{11,042})$			${\mathsf{\Sigma }}_b^{\ast }\overline{B}(\mathrm{10,996})$
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{10,862})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{10,959})$			${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,049})$
Ref. [125]	${\mathsf{\Sigma }}_b\overline{B}(\mathrm{11,126})$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,138})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,146})$	-	-	-
	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,131})$	${\mathsf{\Sigma }}_b^{\ast }\overline{B}(\mathrm{11,134})$
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,136})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,144})$
Ref. [126]	${\mathsf{\Sigma }}_b\overline{B}(\mathrm{11,079})$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,122})$	-	-	-	-
	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,123})$	${\mathsf{\Sigma }}_b^{\ast }\overline{B}(\mathrm{11,103})$
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,153})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,150})$
Ref. [152]	${\mathsf{\Sigma }}_b\overline{B}(\mathrm{11,080})$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,130})$	-	-	-	-
	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,125})$
Ref. [138]	${\mathsf{\Sigma }}_b\overline{B}(\mathrm{11,076})$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,127})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,149})$	-	-	-
	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,113})$	${\mathsf{\Sigma }}_b^{\ast }\overline{B}(\mathrm{11,096})$
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,131})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,139})$
Ref. [193]	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,145})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,146})$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }(\mathrm{11,146})$	-	-	-
	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,117})$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }(\mathrm{11,118})$
	${\mathsf{\Sigma }}_b\overline{B}(\mathrm{11,072})$	${\mathsf{\Sigma }}_b^{\ast }\overline{B}(\mathrm{11,102})$

3.2.3. Doubly Charmed Pentaquarks

Along with the hidden-charm pentaquark states announced experimentally, an open-flavor 5-quark system is also quite charming. In this part, the $ccqq\overline{q}$ ($q=u,d$) pentaquarks with spin-parity $J^P={\frac{1}{2}}^{-}$, ${\frac{3}{2}}^{-}$ and ${\frac{5}{2}}^{-}$, isospin $I=\frac{1}{2}$ and $\frac{3}{2}$ are all investigated. Table 58 and Table 59 listed the allowed channels in each $I(J^P)$ states. However, since a large amount of computational effort is needed for exactly solving the 5-body Schrödinger equation, we still perform the study in the baryon-meson sector in which both color-singlet and hidden-color channels are considered. Nevertheless, as shown in Figure 4, there are four configurations in the 3+2 clusters.

Table 58. All possible channels for open-charm pentaquark systems with $J^P=1/2^{-}$.

${\mathbf{J}}^{\mathbf{P}}$	Index	$\mathit{I}=\frac{1}{2}$		$\mathit{I}=\frac{3}{2}$
		${\mathit{\chi }}_{\mathit{J}}^{\mathit{n}{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{\mathit{n}{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{n}\mathit{c}}$;	Channel	${\mathit{\chi }}_{\mathit{J}}^{\mathit{n}{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{\mathit{n}{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{n}\mathit{c}}$;	Channel
		$[\mathit{i};\mathit{j};\mathit{k};\mathit{n}]$		$[\mathit{i};\mathit{j};\mathit{k};\mathit{n}]$
${\frac{1}{2}}^{-}$	1	$[4;3;1;1,2]$	${({\mathsf{\Xi }}_{cc}\eta )}^1$	$[4;2;1;1,2]$	${({\mathsf{\Xi }}_{cc}\pi )}^1$
	2	$[4,5;3;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\eta )}^8$	$[4,5;2;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\pi )}^8$
	3	$[2;3;1;1,2]$	${({\mathsf{\Xi }}_{cc}\omega )}^1$	$[2;2;1;1,2]$	${({\mathsf{\Xi }}_{cc}\rho )}^1$
	4	$[2,3;3;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\omega )}^8$	$[2,3;2;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\rho )}^8$
	5	$[4;4;1;1,2]$	${({\mathsf{\Xi }}_{cc}\pi )}^1$	$[1;2;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^1$
	6	$[4,5;4;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\pi )}^8$	$[1;2;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^8$
	7	$[2;4;1;1,2]$	${({\mathsf{\Xi }}_{cc}\rho )}^1$	$[4;3;1;3,4]$	${({\mathsf{\Sigma }}_{c}D)}^1$
	8	$[2,3;4;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\rho )}^8$	$[4,5;3;2,3;3,4]$	${({\mathsf{\Sigma }}_{c}D)}^8$
	9	$[1;3;1,1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\omega )}^1$	$[2;3;1;3,4]$	${({\mathsf{\Sigma }}_c{D}^{\ast })}^1$
	10	$[1;3;3,1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\omega )}^8$	$[2,3;3;2,3;3,4]$	${({\mathsf{\Sigma }}_c{D}^{\ast })}^8$
	11	$[1;4;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^1$	$[1;3;1;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^1$
	12	$[1;4;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^8$	$[1;3;3;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^8$
	13	$[5;2;1;3,4]$	${({\mathsf{\Lambda }}_{c}D)}^1$
	14	$[4,5;2;2,3;3,4]$	${({\mathsf{\Lambda }}_{c}D)}^8$
	15	$[3;2;1;3,4]$	${({\mathsf{\Lambda }}_c{D}^{\ast })}^1$
	16	$[2,3;2;2,3;3,4]$	${({\mathsf{\Lambda }}_c{D}^{\ast })}^8$
	17	$[4;1;1;3,4]$	${({\mathsf{\Sigma }}_{c}D)}^1$
	18	$[4,5;1;2,3;3,4]$	${({\mathsf{\Sigma }}_{c}D)}^8$
	19	$[2;1;1;3,4]$	${({\mathsf{\Sigma }}_c{D}^{\ast })}^1$
	20	$[2,3;1;2,3;3,4]$	${({\mathsf{\Sigma }}_c{D}^{\ast })}^8$
	21	$[1;1;1;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^1$
	22	$[1;1;3;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^8$

Table 59. All possible channels for open-charm pentaquark systems with $J^P=3/2^{-}$ and $5/2^{-}$.

${\mathbf{J}}^{\mathbf{P}}$	Index	$\mathit{I}=\frac{1}{2}$		$\mathit{I}=\frac{3}{2}$
		${\mathit{\chi }}_{\mathit{J}}^{\mathit{n}{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{\mathit{n}{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{n}\mathit{c}}$;	Channel	${\mathit{\chi }}_{\mathit{J}}^{\mathit{n}{\mathit{\sigma }}_{\mathit{i}}}$; ${\mathit{\chi }}_{\mathit{I}}^{\mathit{n}{\mathit{f}}_{\mathit{j}}}$; ${\mathit{\chi }}_{\mathit{k}}^{\mathit{n}\mathit{c}}$;	Channel
		$[\mathit{i};\mathit{j};\mathit{k};\mathit{n}]$		$[\mathit{i};\mathit{j};\mathit{k};\mathit{n}]$
${\frac{3}{2}}^{-}$	1	$[3;3;1;1,2]$	${({\mathsf{\Xi }}_{cc}\omega )}^1$	$[3;2;1;1,2]$	${({\mathsf{\Xi }}_{cc}\rho )}^1$
	2	$[3,4;3;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\omega )}^8$	$[3,4;2;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\rho )}^8$
	3	$[3;4;1;1,2]$	${({\mathsf{\Xi }}_{cc}\rho )}^1$	$[2;2;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\pi )}^1$
	4	$[3,4;4;2,3;1,2]$	${({\mathsf{\Xi }}_{cc}\rho )}^8$	$[2;2;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\pi )}^8$
	5	$[2;4;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\pi )}^1$	$[1;2;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^1$
	6	$[2;4;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\pi )}^8$	$[1;2;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^8$
	7	$[1;3;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\omega )}^1$	$[3;3;1;3,4]$	${({\mathsf{\Sigma }}_c{D}^{\ast })}^1$
	8	$[1;3;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\omega )}^8$	$[3,4;3;2,3;3,4]$	${({\mathsf{\Sigma }}_c{D}^{\ast })}^8$
	9	$[1;4;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^1$	$[2;3;1;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }D)}^1$
	10	$[1;4;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^8$	$[3;3;3;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }D)}^8$
	11	$[4;2;1;3,4]$	${({\mathsf{\Lambda }}_c{D}^{\ast })}^1$	$[1;3;1;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^1$
	12	$[3,4;2;2,3;3,4]$	${({\mathsf{\Lambda }}_c{D}^{\ast })}^8$	$[1;3;3;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^8$
	13	$[3;1;1;3,4]$	${({\mathsf{\Sigma }}_c{D}^{\ast })}^1$
	14	$[3,4;1;1;3,4]$	${({\mathsf{\Sigma }}_c{D}^{\ast })}^8$
	15	$[2;1;1;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }D)}^1$
	16	$[2;1;3;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }D)}^8$
	17	$[1;1;1;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^1$
	18	$[1;1;3;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^8$
${\frac{5}{2}}^{-}$	1	$[1;3;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\omega )}^1$	$[1;2;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^1$
	2	$[1;3;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\omega )}^8$	$[1;2;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^8$
	3	$[1;4;1;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^1$	$[1;3;1;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^1$
	4	$[1;4;3;1,2]$	${({\mathsf{\Xi }}_{cc}^{\ast }\rho )}^8$	$[1;3;3;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^8$
	5	$[1;1;1;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^1$
	6	$[1;1;3;3,4]$	${({\mathsf{\Sigma }}_c^{\ast }{D}^{\ast })}^8$

Moreover, the complex scaling method is also applied in this sector in order to have a better classification of bound and resonance states in the multiquark systems. Table 60 summarized our results on the obtained $ccqq\overline{q}$ pentaquark states in advance, particularly, the second column shows the channels of bound or resonance states with their theoretical masses marked in the bracket, and the last column lists the binding energy or resonance width for these exotic states. The details are going to be discussed according to the $I(J^P)$ quantum states.

Table 60. Possible bound and resonance states of doubly charm pentaquarks. The last column listed the binding energy or resonance width of each states.

	Quantum State	${\mathbf{E}}_{\mathbf{B}}$/$\mathsf{\Gamma }$ (in MeV)
Bound state	$\frac{1}{2}{\frac{1}{2}}^{-}$${\mathsf{\Lambda }}_c{D}^{\ast }(4291)$	−2
	$\frac{1}{2}{\frac{3}{2}}^{-}$${\mathsf{\Sigma }}_c{D}^{\ast }(4461)$	−1
	$\frac{3}{2}{\frac{1}{2}}^{-}$${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }(4523)$	−4
	$\frac{3}{2}{\frac{3}{2}}^{-}$${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }(4524)$	−3
	$\frac{1}{2}{\frac{3}{2}}^{-}$${\mathsf{\Xi }}_{cc}^{\ast }\pi (3757)$	−3
Resonance state	$\frac{1}{2}{\frac{1}{2}}^{-}$${\mathsf{\Sigma }}_{c}D(4356)$	4.8
	$\frac{1}{2}{\frac{3}{2}}^{-}$${\mathsf{\Sigma }}_c^{\ast }D(4449)$	8.0
	$\frac{3}{2}{\frac{1}{2}}^{-}$${\mathsf{\Sigma }}_{c}D(4431)$	2.6
	$\frac{3}{2}{\frac{1}{2}}^{-}$${\mathsf{\Sigma }}_{c}D(4446)$	2.2
	$\frac{3}{2}{\frac{3}{2}}^{-}$${\mathsf{\Sigma }}_c{D}^{\ast }(4514)$	4.0
	$\frac{3}{2}{\frac{5}{2}}^{-}$${\mathsf{\Xi }}_{cc}^{\ast }\rho (4461)$	3.0

• $I(J^P)=\frac{1}{2}({\frac{1}{2}}^{-})$ state

There are eleven baryon-meson channels under investigation, ${\mathsf{\Xi }}_{cc}\eta$, ${\mathsf{\Xi }}_{cc}\omega$, ${\mathsf{\Xi }}_{cc}\pi$, ${\mathsf{\Xi }}_{cc}\rho$, ${\mathsf{\Xi }}_{cc}^{\ast }\omega$, ${\mathsf{\Xi }}_{cc}^{\ast }\rho$, ${\mathsf{\Lambda }}_{c}D$, ${\mathsf{\Lambda }}_c{D}^{\ast }$, ${\mathsf{\Sigma }}_{c}D$, ${\mathsf{\Sigma }}_c{D}^{\ast }$ and ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$. Our calculated results are listed in Table 61. The lowest channel is ${\mathsf{\Xi }}_{cc}\pi$, whose experimental threshold value is 3657 MeV, which is unbound in our study. The scattering nature is also found in the other channels no matter in the color-singlet, hidden-color structures calculation or the coupling of them. However, a possible resonance state is obtained in the ${\mathsf{\Lambda }}_c{D}^{\ast }$ channel which binding energy $E_B=-2\mathrm{MeV}$ in the color-singlet computation. The coupling with hidden-color channel is extremely weak and the coupled-mass shown in Table 62 is 4291 MeV.

Table 61. The lowest eigen-energies of doubly-charm pentaquarks with $I(J^P)=\frac{1}{2}({\frac{1}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	Channel	M
${\mathsf{\Xi }}_{cc}\eta$	S	4351	${\mathsf{\Xi }}_{cc}\omega$	4358
$(4065)$	H	4787	$(4300)$	4608
	S+H	4351		4358
${\mathsf{\Xi }}_{cc}\pi$	S	3812	${\mathsf{\Xi }}_{cc}\rho$	4434
$(3657)$	H	4620	$(4293)$	4613
	S+H	3812		4434
${\mathsf{\Xi }}_{cc}^{\ast }\omega$	S	4412	${\mathsf{\Xi }}_{cc}^{\ast }\rho$	4488
$(4403)$	H	4568	$(4396)$	4576
	S+H	4412		4488
${\mathsf{\Lambda }}_{c}D$	S	3981	${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$	4551
$(4155)$	H	4299	$(4527)$	4779
	S+H	3981		4551
${\mathsf{\Sigma }}_{c}D$	S	4384	${\mathsf{\Sigma }}_c{D}^{\ast }$	4503
$(4324)$	H	4701	$(4462)$	4691
	S+H	4384		4503

Table 62. The lowest eigen-energies of ${\mathsf{\Lambda }}_c{D}^{\ast }$ with $I(J^P)=\frac{1}{2}({\frac{1}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	M’
${\mathsf{\Lambda }}_c{D}^{\ast }$	S	4098	$-2$	4291
$(4293)$	H	4312	$+212$	4505
	S+H	4098	$-2$	4291

In the complete coupled-channels calculation where the CSM is employed and the rotated angle $\theta$ is varied from 0° to 6°, we find that the previous obtained resonance state of ${\mathsf{\Lambda }}_c{D}^{\ast }$ at $4291\mathrm{MeV}$ in the single channel calculation is pushed above its threshold. The scattering nature is clearly shown in Figure 25, the calculated poles are always moving along with the ${\mathsf{\Lambda }}_c{D}^{\ast }$ threshold lines. Besides, this feature is also reflected by the other baryon-meson channels e.g., ${\mathsf{\Xi }}_{cc}\pi$, ${\mathsf{\Lambda }}_{c}D$, ${\mathsf{\Lambda }}_c{D}^{\ast }$, etc.

Figure 25. (Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers $I(J^P)=\frac{1}{2}({\frac{1}{2}}^{-})$ and for $\theta {(}^{\circ })=0$ (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from $4.35\mathrm{GeV}$ to $4.46\mathrm{GeV}$.

Since there is a dense distribution in the mass region from 4.35 to 4.46 GeV, an enlarged part is present in the bottom panel of Figure 25. Therein, the small separations among ${\mathsf{\Xi }}_{cc}\eta$, ${\mathsf{\Xi }}_{cc}\omega$, ${\mathsf{\Sigma }}_{c}D$, ${\mathsf{\Xi }}_{cc}^{\ast }\omega$ and ${\mathsf{\Xi }}_{cc}\rho$ channels can be distinguished clearly. Apart from the most continuum states, one resonance, whose mass and width are ∼$4416\mathrm{MeV}$ and ∼$4.8\mathrm{MeV}$, is obtained and has been circled with green in the bottom panel. We can identify it as the ${\mathsf{\Sigma }}_{c}D$ molecular resonance state for this pole is above the threshold lines, a re-scaled mass, which is according to the systematic error between theoretical and experimental threshold values, equals to 4356 MeV. Meanwhile, several properties of the ${\mathsf{\Sigma }}_{c}D(4356)$ remind the nature of $P_c^{+}(4312)$, i.e., the $I(J^P)$ quantum numbers are $\frac{1}{2}{\frac{1}{2}}^{-}$ for both the $P_c^{+}(4312)$ and the ${\mathsf{\Sigma }}_{c}D(4356)$ resonances in our calculations, their mass and width are also quite comparable.

• $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$ state

Table 63 and Table 64 present the calculated mass of each baryon-meson channels in the color-singlet, hidden-color and their coupling cases. In particular, they are all scattering states listed in Table 63 and one resonance state of ${\mathsf{\Sigma }}_c{D}^{\ast }$ in Table 64. Obviously, all the color-singlet channels of these ${\mathsf{\Xi }}_{cc}^{(\ast )}\omega$, ${\mathsf{\Xi }}_{cc}^{(\ast )}\rho$, ${\mathsf{\Xi }}_{cc}^{\ast }\pi$, ${\mathsf{\Lambda }}_c{D}^{\ast }$ and ${\mathsf{\Sigma }}_c^{(\ast )}{D}^{(\ast )}$ states are unbound, their hidden-color channels are all above the corresponding threshold values. Only when the hidden-color channel of ${\mathsf{\Sigma }}_c{D}^{\ast }$ included, there is a weak binding energy $E_B=-1$ MeV. The modified mass is 4461 MeV.

Table 63. The lowest eigen-energies of doubly-charm pentaquarks with $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	Channel	M
${\mathsf{\Xi }}_{cc}\omega$	S	4358	${\mathsf{\Xi }}_{cc}\rho$	4434
$(4300)$	H	4619	$(4293)$	4648
	S+H	4358		4434
${\mathsf{\Xi }}_{cc}^{\ast }\pi$	S	3866	${\mathsf{\Xi }}_{cc}^{\ast }\omega$	4412
$(3760)$	H	4671	$(4403)$	4614
	S+H	3866		4412
${\mathsf{\Xi }}_{cc}^{\ast }\rho$	S	4488	${\mathsf{\Lambda }}_c{D}^{\ast }$	4100
$(4396)$	H	4641	$(4293)$	4284
	S+H	4488		4100
${\mathsf{\Sigma }}_c{D}^{\ast }$	S	4503	${\mathsf{\Sigma }}_c^{\ast }D$	4432
$(4462)$	H	4689	$(4389)$	4702
	S+H	4503		4432
${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$	S	4551
$(4527)$	H	4729
	S+H	4551

Table 64. The lowest eigen-energies of ${\mathsf{\Sigma }}_c{D}^{\ast }$ with $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	M’
${\mathsf{\Sigma }}_c{D}^{\ast }$	S	4503	0	4462
$(4462)$	H	4689	$+186$	4648
	S+H	4502	$-1$	4461

As for the ${\mathsf{\Lambda }}_c{D}^{\ast }(4291)$ in $I(J^P)=\frac{1}{2}({\frac{1}{2}}^{-})$ state, ${\mathsf{\Sigma }}_c{D}^{\ast }(4461)$ turns to be a scattering state in the complete coupled-channels calculation. The evidence can be found in Figure 26 where the distribution of complex energies of each channel are well presented and no fixed resonance pole is near the ${\mathsf{\Sigma }}_c{D}^{\ast }$ threshold lines. Nevertheless, one bound state with $E_B=-3$ MeV is obtained in the top panel of Figure 26. Within a 0°–6° variation region of the angle $\theta$, a stable pole circled with purple is at 3863 MeV of the real-axis. The main component should be ${\mathsf{\Xi }}_{cc}^{\ast }\pi$ and the rescaled mass is 3757 MeV.

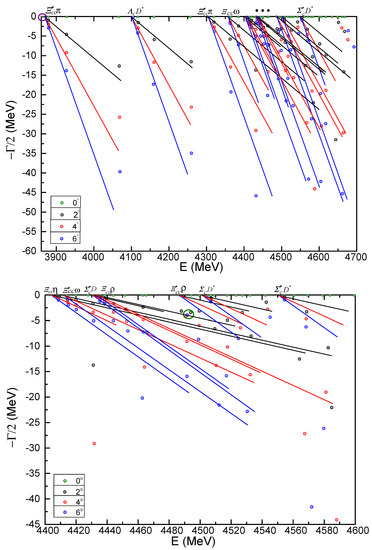
Figure 26. (Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$ and for $\theta {(}^{\circ })=0$ (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from $4.40\mathrm{GeV}$ to $4.60\mathrm{GeV}$.

Additionally, a clear assignment of the channels in a dense energy region 4.4–4.6 GeV is presented in the bottom panel. Therein, one resonance pole is obtained and circled with green. In that small region, the calculated three dots with a rotated angle $\theta$ is 2°, 4° and 6°, respectively, almost overlap. Hence the estimated mass and width of the resonance is $4492\mathrm{MeV}$ and $8.0\mathrm{MeV}$, respectively. It is more reasonable to identify this exotic state as a ${\mathsf{\Sigma }}_c^{\ast }D$ molecule because (i) it is above the ${\mathsf{\Sigma }}_c^{\ast }D$ threshold lines, (ii) larger mass shift for an explanation in ${\mathsf{\Xi }}_{cc}\rho$ channel, (iii) the $P_c^{+}(4457)$ which can be explained as the ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ molecular state also has the quantum numbers $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$ and the width is $6.4\pm 2.0_{-1.9}^{+5.7}$ MeV. Accordingly, a rescaled mass which is respect to the ${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ experimental threshold value is 4449 MeV.

• $I(J^P)=\frac{1}{2}({\frac{5}{2}}^{-})$ state

Three baryon-meson channels ${\mathsf{\Xi }}_{cc}^{\ast }\omega$, ${\mathsf{\Xi }}_{cc}^{\ast }\rho$ and ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ contribute to the highest spin state and the calculated results on their masses in the color-singlet channel, hidden-color one and their couplings in real-range are listed in Table 65. Meanwhile, Figure 27 shows the distributions of the complex energies in the fully coupled-channels calculation of complex-range. Obviously, no bound state is obtained neither in the single-channel nor in the coupled cases, and resonances are also not found. Hence, it is the scattering nature of ${\mathsf{\Xi }}_{cc}^{\ast }\omega$, ${\mathsf{\Xi }}_{cc}^{\ast }\rho$ and ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ in the $\frac{1}{2}({\frac{5}{2}}^{-})$ state.

Table 65. The lowest eigen-energies of doubly-charm pentaquarks with $I(J^P)=\frac{1}{2}({\frac{5}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	Channel	M
${\mathsf{\Xi }}_{cc}^{\ast }\omega$	S	4412	${\mathsf{\Xi }}_{cc}^{\ast }\rho$	4488
$(4403)$	H	4683	$(4396)$	4741
	S+H	4412		4488
${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$	S	4551
$(4527)$	H	4655
	S+H	4551

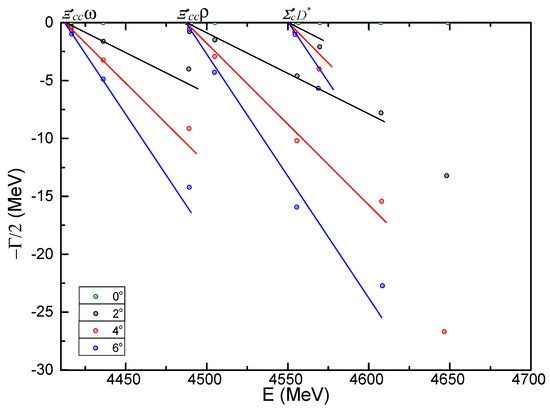
Figure 27. Pentaquark’s complex energies of coupled-channels calculation with quantum numbers $I(J^P)=\frac{1}{2}({\frac{5}{2}}^{-})$ and for $\theta {(}^{\circ })=0$ (green), 2 (black), 4 (red) and 6 (blue).

• $I(J^P)=\frac{3}{2}({\frac{1}{2}}^{-})$ state

In this quantum state, the six allowed baryon-meson channels ${\mathsf{\Xi }}_{cc}\pi$, ${\mathsf{\Xi }}_{cc}^{(\ast )}\rho$ and ${\mathsf{\Sigma }}_c^{(\ast )}{D}^{(\ast )}$ are investigated in the singlet- and hidden-color configurations, first. From Table 66 and Table 67 one can find that resonance only obtained in the ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ channel with color-singlet state and the binding energy is $-3$ MeV. In a subsequent calculation which its hidden-color channel included, only 1 MeV increased for the $E_B$. The modified mass $M^{\prime }$ of ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ resonance is 4523 MeV.

Table 66. The lowest eigen-energies of doubly-charm pentaquarks with $I(J^P)=\frac{3}{2}({\frac{1}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	Channel	M
${\mathsf{\Xi }}_{cc}\pi$	S	3812	${\mathsf{\Xi }}_{cc}\rho$	4434
$(3657)$	H	4682	$(4293)$	4685
	S+H	3812		4434
${\mathsf{\Xi }}_{cc}^{\ast }\rho$	S	4488	${\mathsf{\Sigma }}_{c}D$	4384
$(4396)$	H	4647	$(4324)$	4714
	S+H	4488		4384
${\mathsf{\Sigma }}_c{D}^{\ast }$	S	4503
$(4462)$	H	4627
	S+H	4503

Table 67. The lowest eigen-energies of ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ with $I(J^P)=\frac{3}{2}({\frac{1}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	M’
${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$	S	4548	$-3$	4524
$(4527)$	H	4693	$+142$	4669
	S+H	4547	$-4$	4523

Apart from the real scaling calculation, Figure 28 presents the results of a fully coupled-channels calculation in the complex-range. Particularly, the calculated energy points of the six channels ${\mathsf{\Xi }}_{cc}\pi$, ${\mathsf{\Xi }}_{cc}^{(\ast )}\rho$ and ${\mathsf{\Sigma }}_c^{(\ast )}{D}^{(\ast )}$ distribute in the mass region 3.8–4.8 GeV of the top panel. When the $\theta$ varies from 0° to 6°, they generally present the scattering nature in which the poles always moving along their threshold lines. However, many poles are located in the 4.45–4.62 GeV region, so the middle panel of Figure 28 shows an enlarged result on this part. Clearly, one resonance pole circled green is obtained herein and the theoretical mass and width are 4491 MeV and 2.6 MeV, respectively. It is both above the ${\mathsf{\Sigma }}_{c}D$ and ${\mathsf{\Xi }}_{cc}\rho$ threshold lines, however, there is much more systematic error of the later channel than ${\mathsf{\Sigma }}_{c}D$. Hence this resonance is preferred to be identified as the ${\mathsf{\Sigma }}_c$ baryon and D meson molecular state. After a mass shift according to the experimental threshold value, the resonance mass is 4431 MeV.

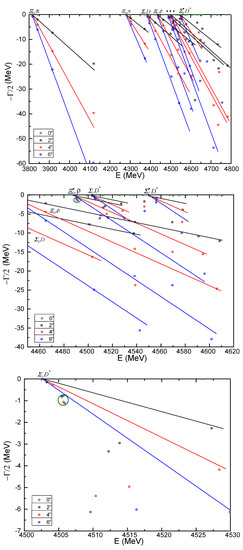
Figure 28. (Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers $I(J^P)=\frac{3}{2}({\frac{1}{2}}^{-})$ and for $\theta {(}^{\circ })=0$ (green), 2 (black), 4 (red) and 6 (blue). (Middle panel): Enlarged top panel, with real values of energy ranging from $4.45\mathrm{GeV}$ to $4.62\mathrm{GeV}$. (Bottom panel): Enlarged top panel, with real values of energy ranging from $4.50\mathrm{GeV}$ to $4.53\mathrm{GeV}$.

Furthermore, there seem to be more structures between the threshold of ${\mathsf{\Xi }}_{cc}\rho$ and ${\mathsf{\Sigma }}_c{D}^{\ast }$, so a further enlarged part from 4.50 GeV to 4.53 GeV is shown in the bottom panel. Apparently, another ${\mathsf{\Sigma }}_{c}D$ resonance state is obtained, the mass and width is $4506\mathrm{MeV}$ and $2.2\mathrm{MeV}$, respectively. Then through a mass shift with respect to its threshold value, the rescaled mass is 4446 MeV.

• $I(J^P)=\frac{3}{2}({\frac{3}{2}}^{-})$ state

There are six channels listed in Table 68 and Table 69 under consideration, namely, ${\mathsf{\Xi }}_{cc}^{(\ast )}\rho$, ${\mathsf{\Xi }}_{cc}^{\ast }\pi$ and ${\mathsf{\Sigma }}_c^{(\ast )}{D}^{(\ast )}$. Firstly, all of the channels in the color-singlet structure are unbound. Besides, it is the same conclusion in the hidden-color channel calculations. However, ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ resonance state is obtained in the coupled-channels study in which both the singlet- and hidden-color channels are employed. The binding energy is $-3$ MeV and a modified mass is 4524 MeV. Clearly, there is a degeneration between this state and the ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ resonance in the $\frac{3}{2}({\frac{1}{2}}^{-})$ state.

Table 68. The lowest eigen-energies of doubly-charm pentaquarks with $I(J^P)=\frac{3}{2}({\frac{3}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	Channel	M
${\mathsf{\Xi }}_{cc}\rho$	S	4434	${\mathsf{\Xi }}_{cc}^{\ast }\pi$	3866
$(4293)$	H	4708	$(3760)$	4692
	S+H	4434		3866
${\mathsf{\Xi }}_{cc}^{\ast }\rho$	S	4488	${\mathsf{\Sigma }}_c{D}^{\ast }$	4503
$(4396)$	H	4678	$(4462)$	4719
	S+H	4488		4503
${\mathsf{\Sigma }}_c^{\ast }D$	S	4432
$(4389)$	H	4695
	S+H	4432

Table 69. The lowest eigen-energies of ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ with $I(J^P)=\frac{3}{2}({\frac{3}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	${\mathbf{E}}_{\mathbf{B}}$	M’
${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$	S	4551	0	4527
$(4527)$	H	4667	$+116$	4643
	S+H	4548	$-3$	4524

Within a complex-range computation in the complete coupled-channels, the scattering states of ${\mathsf{\Xi }}_{cc}^{(\ast )}\rho$, ${\mathsf{\Xi }}_{cc}^{\ast }\pi$ and ${\mathsf{\Sigma }}_c^{(\ast )}{D}^{(\ast )}$ are generally presented in Figure 29. Particularly, the obtained ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$ resonance at 4524 MeV in the real-range calculation turns to a scattering state. Nevertheless, a possible ${\mathsf{\Sigma }}_c{D}^{\ast }$ resonance state is found in the bottom panel of Figure 29. In the big green circle, three calculated poles are almost overlapped and the predicted mass and width is $4555\mathrm{MeV}$ and $4.0\mathrm{MeV}$, respectively. After a mass shift, the resonance can be identified as ${\mathsf{\Sigma }}_c{D}^{\ast }(4514)$ molecular state.

Figure 29. (Top panel): Pentaquark’s complex energies of coupled-channels calculation with quantum numbers $I(J^P)=\frac{3}{2}({\frac{3}{2}}^{-})$ and for $\theta {(}^{\circ })=0$ (green), 2 (black), 4 (red) and 6 (blue). (Bottom panel): Enlarged top panel, with real values of energy ranging from $4.48\mathrm{GeV}$ to $4.65\mathrm{GeV}$.

• $I(J^P)=\frac{3}{2}({\frac{5}{2}}^{-})$ state

There are only two channels under investigation in the highest spin and isospin pentaquark state, ${\mathsf{\Xi }}_{cc}^{\ast }\rho$ and ${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$. In Table 70 one can see that their lowest theoretical mass in the real-range are 4488 MeV and 4551 MeV, respectively. Hence, no bound state is obtained in this case.

Table 70. The lowest eigen-energies of doubly-charm pentaquarks with $I(J^P)=\frac{3}{2}({\frac{5}{2}}^{-})$, and the rotated angle $\theta =0^{\circ }$. (unit: MeV).

Channel	Color	M	Channel	M
${\mathsf{\Xi }}_{cc}^{\ast }\rho$	S	4488	${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$	4551
$(4396)$	H	4727	$(4527)$	4706
	S+H	4488		4551

Figure 30 shows the distributions of complex energies for these two channels. Apart from the scattering states, one stable resonance pole is found and surrounded by a green circle. It can be identified as the ${\mathsf{\Xi }}_{cc}^{\ast }\rho$ resonance with the modified mass and width $4461\mathrm{MeV}$ and $3.0\mathrm{MeV}$.

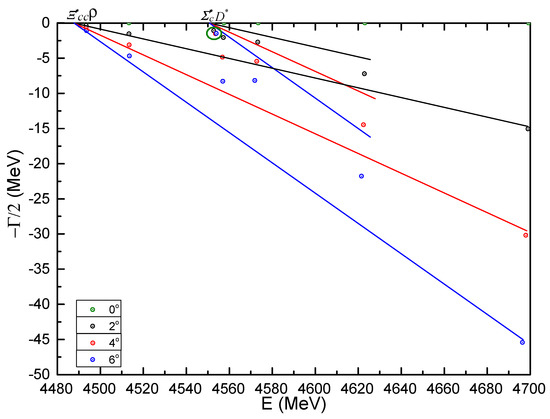
Figure 30. Pentaquark’s complex energies of coupled-channels calculation with quantum numbers $I(J^P)=\frac{3}{2}({\frac{5}{2}}^{-})$ and for $\theta {(}^{\circ })=0$ (green), 2 (black), 4 (red) and 6 (blue).

Finally, as in other multi-quark sectors, Table 71 lists the most highlighted results on double-charm pentaquark states; we hope this kind of summary tables will help experimentalists in their task of hunting them.

Table 71. Comparison of theoretical masses on the double-charm pentaquark systems by different predictions, the predicted masses and states ($P_{cc}$ stands for $ccqq\overline{q}$ petraquark) are summarized in each column, respectively. (unit: MeV).

	$\frac{1}{2}\frac{1}{2}$${}^{-}$	$\frac{1}{2}\frac{3}{2}$${}^{-}$	$\frac{1}{2}\frac{5}{2}$${}^{-}$	$\frac{3}{2}\frac{1}{2}$${}^{-}$	$\frac{3}{2}\frac{3}{2}$${}^{-}$	$\frac{3}{2}\frac{5}{2}$${}^{-}$
This work	${\mathsf{\Sigma }}_{c}D(4356)$	${\mathsf{\Sigma }}_c^{\ast }D(4449)$	-	${\mathsf{\Sigma }}_{c}D(4431)$	${\mathsf{\Sigma }}_c{D}^{\ast }(4514)$	${\mathsf{\Xi }}_{cc}^{\ast }\rho (4461)$
		${\mathsf{\Sigma }}_c{D}^{\ast }(4461)$		${\mathsf{\Sigma }}_{c}D(4446)$	${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }(4524)$
		${\mathsf{\Xi }}_{cc}^{\ast }\pi (3757)$
Ref. [155]	$P_{cc}(3754)$	$P_{cc}(3854)$	$P_{cc}(4591)$	$P_{cc}(4083)$	$P_{cc}(4105)$	$P_{cc}(4591)$
	$P_{cc}(4083)$	$P_{cc}(4105)$	$P_{cc}(4626)$	$P_{cc}(4459)$	$P_{cc}(4455)$
	$P_{cc}(4285)$	$P_{cc}(4460)$		$P_{cc}(4617)$	$P_{cc}(4547)$
	$P_{cc}(4460)$	$P_{cc}(4547)$		$P_{cc}(4770)$	$P_{cc}(4708)$
	$P_{cc}(4589)$	$P_{cc}(4611)$
	$P_{cc}(4617)$	$P_{cc}(4708)$
	$P_{cc}(4770)$
Ref. [156]	$P_{cc}(4590)$	$P_{cc}(4690)$	$P_{cc}(4800)$	-	-	-
	$P_{cc}(4620)$	$P_{cc}(4700)$
	$P_{cc}(4680)$	$P_{cc}(4720)$
	$P_{cc}(4710)$	$P_{cc}(4780)$
	$P_{cc}(4770)$

4. Summary

Motivated by the dozens of exotic hadron states recently reported by experiments worldwide, e.g., the charmonium-like $X(3872)$ observed by the Belle collaboration in 2003 and the pentaquark $P_c^{+}(4380)$ announced by the LHCb collaboration in 2015, we have employed a constituent quark model formalism combined with an exact and high efficiency variational method called Gaussian expansion method, in order to study systematically the double- and all-heavy tetraquarks, and the hidden-charm, hidden-bottom and doubly charmed pentaquarks. In particular, we focus our attention to the spin-parity $J^P=0^{+}$, $1^{+}$ and $2^{+}$ tetraquarks of $QQ\overline{q}\overline{q}$ and $QQ\overline{Q}\overline{Q}$ ($q=u,d,s$ and $Q=c,b$) sectors with isiospin either $I=0$ or 1; besides, $J^P={\frac{1}{2}}^{-}$, ${\frac{3}{2}}^{-}$ and ${\frac{5}{2}}^{-}$$qqq\overline{Q}\overline{Q}$ and $ccqq\overline{q}$ pentaquarks in isospin $I=\frac{1}{2}$ or $\frac{3}{2}$ are systematically investigated in both the real- and complex-range formalisms.

In the double-heavy tetraquark sector, we only obtain tightly bound states and narrow resonances with quantum numbers $I{J}^P={01}^{+}$ for $cc\overline{q}\overline{q}$ and $bb\overline{q}\overline{q}$$(q=u,d)$. For $cb\overline{q}\overline{q}$ tetraquarks, bound and resonance states are found in spin-parity $0^{+}$, $1^{+}$ and $2^{+}$, and isospin $I=0$. All of these exotic states are loosely bound in meson-meson configurations, whereas compact ones are available in diquark-antidiquark structures, except for charm-bottom tetraquark in ${02}^{+}$ state. As shown in Table 72, which summarizes our theoretical findings for possible tetra- and pent-aquark states, the lowest-lying state mass of $cc\overline{q}\overline{q}$ is 3726 MeV, with a binding energy around -190 MeV. Besides, a resonance at 4312 MeV is presented, the dominant $D^{\ast +}{D}^{\ast 0}$ channel has a width of 16 MeV. Similarly, two compact double-bottom tetraquark bound states, whose masses are 10.24 and 10.52 GeV, along with one narrow resonance, $B^{\ast -}{\overline{B}}^{\ast 0}(10814)$, are listed in Table 72. Furthermore, for the charm-bottom tetraquarks, the binding energies of the obtained bound-states are generally around −200 MeV, except for −3 MeV of ${02}^{+}$ state. Two $D^{\ast }{\overline{B}}^{(\ast )}$ resonances in coupled-channels computation appear with masses and widths (7726 MeV, 12 MeV) and (7327 MeV, 2.4 MeV), respectively.

Table 72. Bound and resonance states obtained in tetraquark and pentaquark systems. Mass M, resonance width $\mathsf{\Gamma }$ and binding energy $E_B$ are listed in the third, fourth and fifth column, respectively, unit in MeV.

$\mathit{I}{\mathit{J}}^{\mathit{P}}$	Channel	M	$\mathbf{\Gamma }$	${\mathit{E}}_{\mathit{B}}$	Channel	M	$\mathbf{\Gamma }$	${\mathit{E}}_{\mathit{B}}$
${00}^{+}$	$cb\overline{q}\overline{q}$	6980	−	−196	$D^{\ast 0}{\overline{B}}^{\ast 0}$	7726	12.00	550
	$bb\overline{b}\overline{b}$	17,955	−	−847	$D_s^{+}{D}_s^{+}$	4902	3.54	924
	$bb\overline{b}\overline{b}$	18,030	−	−772	$D_s^{\ast +}{\overline{B}}_s^{\ast }$	7919	1.02	575
					$D_s^{\ast +}{\overline{B}}_s^{\ast }$	7993	3.22	649
					${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$	11,306	1.86	596
					${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$	11,333	1.84	623
					${\overline{B}}_s^0{\overline{B}}_s^0$	11,412	1.54	702
					$cc\overline{c}\overline{c}$	6449	−	513
					$cc\overline{c}\overline{c}$	6659	−	723
					$bb\overline{b}\overline{b}$	19,005	−	203
					$bb\overline{b}\overline{b}$	19,049	−	247
${01}^{+}$	$cc\overline{q}\overline{q}$	3726	−	-189	$D^{\ast +}{D}^{\ast 0}$	4312	16.00	397
	$cb\overline{q}\overline{q}$	6997	−	−220	$D^{\ast 0}{\overline{B}}^0$	7327	2.40	110
	$bb\overline{q}\overline{q}$	10,238	−	−359	$B^{\ast -}{\overline{B}}^{\ast 0}$	10,814	2.00	217
	$bb\overline{q}\overline{q}$	10,524	−	−73	$D_s^{\ast +}{\overline{B}}_s^{\ast }$	7920	1.20	531
	$bb\overline{b}\overline{b}$	18,046	−	−818	$D_s^{\ast +}{\overline{B}}_s^{\ast }$	7995	4.96	606
					$cc\overline{c}\overline{c}$	6657	−	587
					$bb\overline{b}\overline{b}$	19,067	−	203
${02}^{+}$	$cb\overline{q}\overline{q}$	7333	−	−3	$D_s^{\ast +}{D}_s^{\ast +}$	4821	5.58	589
	$bb\overline{b}\overline{b}$	18,223	−	−703	$D_s^{\ast +}{D}_s^{\ast +}$	4846	10.68	614
					$D_s^{\ast +}{D}_s^{\ast +}$	4775	23.26	543
					$D_s^{\ast +}{\overline{B}}_s^{\ast }$	8046	1.42	530
					$D_s^{\ast +}{\overline{B}}_s^{\ast }$	8096	2.90	580
					${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$	11,329	1.48	529
					${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$	11,356	4.18	556
					${\overline{B}}_s^{\ast }{\overline{B}}_s^{\ast }$	11,410	2.52	610
					$cc\overline{c}\overline{c}$	7022	−	818
					$bb\overline{b}\overline{b}$	19,189	−	263
$\frac{1}{2}{\frac{1}{2}}^{-}$	${\mathsf{\Sigma }}_c\overline{D}$	4312	−	−8	${\mathsf{\Sigma }}_{c}D$	4356	4.8	699
	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$	4421	−	−41	${\mathsf{\Lambda }}_c{\overline{D}}^{\ast }$	4291	−	−2
	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$	4422	−	−105	${\mathsf{\Sigma }}_b\overline{B}$	11,072	−	−17
	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	11,041	−	-93	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	10,862	−	−292
$\frac{1}{2}{\frac{3}{2}}^{-}$	${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$	4459	−	-3	${\mathsf{\Sigma }}_c^{\ast }D$	4449	8.0	689
	${\mathsf{\Sigma }}_c^{\ast }\overline{D}$	4370	−	−15	${\mathsf{\Sigma }}_c{D}^{\ast }$	4461	−	−1
	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$	4510	−	−17	${\mathsf{\Xi }}_{cc}^{\ast }\pi$	3757	−	−3
	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	11,120	−	−14	${\mathsf{\Sigma }}_b^{\ast }\overline{B}$	11,042	−	−67
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	10,959	−	−195
$\frac{1}{2}{\frac{5}{2}}^{-}$	${\mathsf{\Sigma }}_c^{\ast }{\overline{D}}^{\ast }$	4438	−	−89	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	11,141	−	−13
$\frac{3}{2}{\frac{1}{2}}^{-}$	${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$	4523	−	−4	${\mathsf{\Sigma }}_{c}D$	4431	2.6	774
					${\mathsf{\Sigma }}_{c}D$	4446	2.2	789
$\frac{3}{2}{\frac{3}{2}}^{-}$	${\mathsf{\Sigma }}_b{\overline{B}}^{\ast }$	11,019	−	−115	${\mathsf{\Sigma }}_c{D}^{\ast }$	4514	4.0	754
	${\mathsf{\Sigma }}_b^{\ast }\overline{B}$	10,996	−	−113	${\mathsf{\Sigma }}_c^{\ast }{D}^{\ast }$	4524	−	−3
	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	11,049	−	−105
$\frac{3}{2}{\frac{5}{2}}^{-}$	${\mathsf{\Sigma }}_b^{\ast }{\overline{B}}^{\ast }$	10,932	−	−222	${\mathsf{\Xi }}_{cc}^{\ast }\rho$	4461	3.0	65

No bound state is found in the three types of tetraquarks: $cc\overline{s}\overline{s}$, $bb\overline{s}\overline{s}$ and $cb\overline{s}\overline{s}$. However, several resonances are still available and listed in Table 72. In particular, for $cc\overline{s}\overline{s}$ tetraquark, narrow di-$D_s^{+}$ resonance is found with $I{J}^P={00}^{+}$ quantum numbers, the predicted mass and width is 4.9 GeV and 3.54 MeV, respectively. Additionally, three $D_s^{\ast +}{D}_s^{\ast +}$ resonances are obtained in $I{J}^P={02}^{+}$ channel, their masses are around 4.8 GeV. Similar results are obtained for the $bb\overline{s}\overline{s}$ tetraquark sector, whose resonances are only obtained in ${00}^{+}$ and ${02}^{+}$. In particular, there are two di-${\overline{B}}_s^{\ast }$ and one di-${\overline{B}}_s^0$ resonances in ${00}^{+}$ state, and three di-${\overline{B}}_s^{\ast }$ ones in ${02}^{+}$ state. Their masses are located in the region 11.3–11.4 GeV. There are also two $D_s^{\ast +}{\overline{B}}_s^{\ast }$ resonances in each ${00}^{+}$, ${01}^{+}$ and ${02}^{+}$ channels. As shown in Table 72, their masses are about 7.99 GeV. The interested reader may visit ‘Section 3.1.1 $QQ\overline{q}\overline{q}$ Tetraquarks’ and ‘Section 3.1.2 $QQ\overline{s}\overline{s}$ Tetraquarks’ for further details and discussion.

For fully-heavy tetraquarks, the recently reported new structure at 6.9 GeV in the di-$J/\psi$ invariant mass spectrum by the LHCb collaboration can be regarded as a compact fully charmed tetraquark in ${02}^{+}$ state. The another broad structure around 6.2∼6.8 GeV is also supported by us with several compact $cc\overline{c}\overline{c}$ resonances in ${00}^{+}$ and ${01}^{+}$ channels. The details are in ‘Section 3.1.3 $QQ\overline{Q}\overline{Q}$ Tetraquarks’.

In the hidden-charm pentaquark sector, the $P_c^{+}(4380)$ can be well explained as a ${\mathsf{\Sigma }}_c^{\ast }\overline{D}$ molecule with $I(J^P)=\frac{1}{2}({\frac{3}{2}}^{-})$. Moreover, the $P_c^{+}(4312)$, $P_c^{+}(4440)$ and $P_c^{+}(4457)$ states can also be identified as the $\frac{1}{2}{\frac{1}{2}}^{-}$${\mathsf{\Sigma }}_c\overline{D}$, $\frac{1}{2}{\frac{1}{2}}^{-}$${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ and $\frac{1}{2}{\frac{3}{2}}^{-}$${\mathsf{\Sigma }}_c{\overline{D}}^{\ast }$ molecules, respectively. The details can be found in ‘Section 3.2.1 Hidden Charm Pentaquarks’.

Deeper bound states are obtained when $qqqb\overline{b}$$(q=u,d)$ pentaquark systems are considered; the discussion of our results can be found in ‘Section 3.2.2. Hidden Bottom Pentaquarks’. Within the scanned spin-parity $J^P={\frac{1}{2}}^{-}$, ${\frac{3}{2}}^{-}$ and ${\frac{5}{2}}^{-}$, and isospin $I=\frac{1}{2}$ or $\frac{3}{2}$, the dominant baryon-meson configurations are ${\mathsf{\Sigma }}_b^{(\ast )}{\overline{B}}^{(\ast )}$. Their mass regions are generally located in 10.8–11.1 GeV, as listed in Table 72.

Additionally, for the doubly charmed pentaquarks, narrow resonances and loosely bound states are available in our study, several ${\mathsf{\Sigma }}_c^{(\ast )}{D}^{(\ast )}$ molecular states are obtained within 4.36–4.51 GeV, as shown in Table 72. Moreover, one shallow bound state ${\mathsf{\Xi }}_{cc}^{\ast }\pi (3757)$ is found in $\frac{1}{2}{\frac{3}{2}}^{-}$ by the coupled-channels calculation, the details are presented in ‘Section 3.2.3 Doubly Charmed Pentaquarks’.

Last but not least, Table 72 summarizes our findings described in this manuscript. Be aware that all reported states are obtained in a particular model investigation and then they are still tentative states; however, further confirmations by experiments such as the LHCb, ATLAS, CMS, BESIII, Belle II, JLAB, PANDA, EIC, etc., are expected. In any case, the experimental findings will also check the validity of the model.