Abstract
The asymptotic approach is suggested for the description of interacting surface and internal oceanic solitary waves. This approach allows one to describe stationary moving symmetric wave patterns consisting of two plane solitary waves of equal amplitudes moving at an angle to each other. The results obtained within the approximate asymptotic theory are validated by comparison with the exact two-soliton solution of the Kadomtsev–Petviashvili equation (KP2-equation). The suggested approach is equally applicable to a wide class of non-integrable equations too. As an example, the asymptotic theory is applied to the description of wave patterns in the 2D Benjamin–Ono equation describing internal waves in the infinitely deep ocean containing a relatively thin one of the layers.
1. Introduction
The investigation of solitary waves in oceans has a long story. Nowadays, there are several books and reviews justifying that they represent a rather ubiquitous phenomenon on the surface and in the bulk of oceans [1,2]. The theoretical models for the description of surface and internal solitary waves are well-developed, among them the Kadomtsev–Petviashvili (KP) equation; two-dimensional versions of the Gardner, Benjamin–Ono (BO), Joseph–Kubota–Ko–Dobbs (JKKD) equations; and others (see, for example, [1,2] and references therein). Only the former one, the KP equation, is completely integrable in the two-dimensional case, whereas in one-dimensional case, a few others are also completely integrable. The KP equation allows one, in particular, to study the interaction of two solitary waves moving at an angle to each other through the exact two-soliton solution. It is amazing that practically all wave patterns predicted within the exact two-soliton solutions are observable on the surface of shallow water (see, for example, a series of photos in paper [3] taken on the shallow beaches of the eastern coast of the Pacific Ocean). One of the examples of an almost symmetric wave pattern of the X-type formed by two interacting solitary waves is shown in Figure 1a); another example representing the Y-type triad of interacting solitary waves is shown in Figure 1b). Similar wave patterns were observed for internal oceanic waves (see, e.g., [4]).

Figure 1.
(colour online). Photographs of the observed wave patterns on shallow water demonstrating an almost symmetric X-type soliton interaction (frame (a)) and a Y-type triad pattern (frame (b)) [3].
Exact solutions for two-soliton interactions at an angle to each other can be obtained only in the exceptional case of the KP model, despite the existence of exact single soliton solutions within many other models such those mentioned above. Meanwhile, the approximate asymptotic method earlier developed for the description of mainly one-dimensional soliton interactions (see, for example, [5,6,7]) can be extended to the two-dimensional case too [8]. In particular, such an approach has been used for the description of two-dimensional lumps [9,10].
In this paper, it will be shown that at least for the description of symmetric configurations consisting of two interacting solitary waves, the asymptotic approach can be applied, and the results obtained are in a good agreement with the exact analytical solution for two interacting plane solitons within the KP equation. Then, the approach is applied to the symmetric configuration of two solitary waves interacting at an angle within the 2D version of the BO (2dBO) equation.
2. Exact Two-Soliton Solution of the Kadomtsev–Petviashvili Equation
As the reference case, consider first the Kadomtsev–Petviashvili equation (dubbed the KP2 equation in the case of the “normal oceanic dispersion” when β > 0):
This equation is written in the coordinate frame moving along the x-axis with the speed of long linear waves c. It is applicable to wave processes in the various physical fields (see [1,11,12,13] and references therein) and, in particular, to the description of quasi-pane surface and internal water waves. In the case of surface water waves, η(x, y, t) describes the perturbation of a free surface, and the coefficients c, α, and β depend on the water depth h:
where g is the acceleration due to gravity. For internal waves in a two-layer fluid, η(x, t) stands for a displacement of a pycnocline from the equilibrium state, and the coefficients in the Boussinesq approximation [2] are:
where h1,2 are thicknesses of the upper and lower layers. In the general case of internal waves in a continuously stratified fluid with a shear flow, the coefficients were derived in [13] and then, in many other papers.
Using well-known Hirota’s ansatz (see, e.g., [1,14,15,16,17,18])
Equation (1) can be presented in the bilinear form:
One-soliton solution to this equation is:
where k and l formally are arbitrary parameters and
However, the KP Equation (1) was derived under the assumption that l/k << 1 [19]. In the original variables, this solution reads:
The soliton amplitude is determined solely by the parameter k: A = 3β k2/α, whereas its speed V depends both on k and l:
where φ = tan−1(l/k) is the angle between the direction of soliton propagation normal to its front and the x-axis. Note that in the Korteweg–de Vries (KdV) equation, which is the particular case of the KP2 equation when φ = 0, the relationship between the soliton speed and amplitude is V = αA/3, so that the angle correction to the soliton speed is relatively small and proportional to φ2 within the KP approximation. The components of soliton velocity V = (Vx, Vy) are:
The two-soliton solution has the form:
and depends on four parameters k1,2 and l1,2,
In general, solution (11) describes the interaction of two plane solitons, experiencing the phase shifts in space after the interaction; the typical configurations are similar to what is shown in Figure 1. It can be shown that such a solution is stationary in some synchronously moving coordinate frames; to the best of the author’s knowledge, this fact was established only in the recent publication [20]. In that paper, a kinematic approach was suggested for the description of interacting soliton patterns withing the KP-type models.
Solution (11) is non-singular if B ≥ 0, and the phase shift between the soliton fronts is determined by the parameter Φ. Solution (11) will not be analyzed here in detail; its analysis can be found in the numerous publications (see, for example, [1,14,15,16,17,18]). This study focuses on the particular case when the wave pattern formed by two interacting solitons is symmetric in the space. To this end, we set k1 = k2 = k > 0, l1 = −l2 = −l > 0 and obtain:
As follows from Equation (13), the two-soliton solution is non-singular if
Taking into account the condition of physical applicability of the KP equation, we obtain:
From this formula, it follows the restriction on the soliton amplitudes: A ≤ cφ2/2α (the same restriction was obtained by Miles [16]). If this restriction is not met, then the stationary two-soliton pattern cannot exist; the solitons, apparently, experience a more complicated nonstationary interaction. This interesting issue has not been studied yet.
In the original variables, solution (11) in the symmetric case has the form:
where θ = ω(k, l) t − k x. Equation (16) represents a wave pattern, which is stationary in the frame moving along the x-axis with the speed:
Far from the point of soliton intersection, their amplitudes are constant and determined by the parameter k: A = 3β k2/α, whereas at the point of front intersection, the pattern amplitude increases and attains the value:
When k varies from zero to , the parameter B varies from 1 to infinity. If k → 0, and l remains finite, we obtain a configuration that is inconsistent with the physical condition of applicability of the KP equation, which requires that |l/k| << 1 [19]. In another limiting case, k → kc, and l remains finite, we obtain a triad solution (see Figure 1b) with the amplitude of the third soliton , whereas the amplitudes of both original solitons equal to , so that we obtain the well-known result A3 = 4A. This case can be physically acceptable, if |l| << kc. Figure 2 illustrates the examples of two symmetric soliton solutions for the cases when: (a) k = 0.05; l2 = −l1 = 0.005, l2/k = 0.1, B = 4; then the phase shift along the x-axis is Φx = ln B/k = 27.73 and along the y-axis is Φy = ln B/l2 = 277.3; (b) k = 0.05; l2 = −l1 = 0.00433012702, l2/k = 0.0866, B = 2 × 109, Φx = ln B/k = 27.73, Φy = ln B/l2 = 428.4.
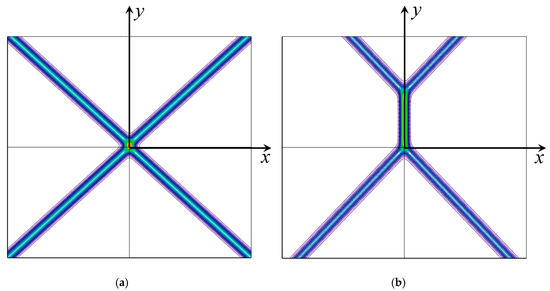
Figure 2.
(Colour online). Contour-plots of soliton fronts as per solution (15): (a) k = 0.05; l2 = −l1 = 0.005, l2/k = 0.1, B = 4; (b) k = 0.05; l2 = −l1 = 0.00433012702, l2/k = 0.0866, B = 2 × 109. Each plot was generated for α = β = 1 and c = 2 in the domain (−103, 103) × (–104, 104).
When k approaches kc, the parameter B increases, the bridge between the soliton fronts also increases, and in the limit when k = kc, the bridge reduces to the third soliton; then the upper pair of soliton fronts disappear at the infinity. As follows from the formula for kc and A, in the triad solution of this type, we have:
3. The Approximate Asymptotic Approach to the Description of Two-Soliton Interaction
For the description of soliton interactions, various asymptotic approaches have been developed basically for the one-dimensional cases (see, for example, [5,6,7] and references therein). There are a few developments of asymptotic methods for the two-dimensional space for the description of plane soliton interactions [8] and for the description of fully localized two-dimensional lumps [9,10]. Here we suggest the asymptotic method for the description of symmetric soliton patterns applicable for a wide class of quasi-one-dimensional equations of the KP-type. To validate the method, we apply it to the KP2 equation first and then to the 2dBO equation.
3.1. Symmetric Configuration of Two Plane Solitons in the KP2 Equation
Let us consider the simplest pattern consisting of two interacting solitons shown in Figure 2. In this case, the pattern is stationary in the coordinate frame moving with the speed Vpat as per Equation (17). Then, the KP2 Equation (1) can be presented in the form:
This equation resembles the Boussinesq equation alias “the equation of a nonlinear string” [1], where y plays a role of time t, and C02 = 2Vpat/c plays a role of the squared speed of long linear waves. Thus, Equation (20) can be considered as the one-dimensional equation in space and “time y” with the following soliton solution:
where ∆2 = 12β/αA, and W2 = (2/c)(Vpat − αA/3); the solution exists if Vpat > α A/3. Soliton fronts shown, for example, in Figure 2 can be treated as the space-time diagrams for the soliton solutions of the Boussinesq Equation (20).
According to the asymptotic theory developed in [5,6,7], a solitary wave having big distances from other solitary waves can be considered as a classical particle in the external fields produced by the asymptotes of all other solitary waves. Considering only two solitons, we can seek a solution to Equation (20) in the form η = η1 + η2 where η1,2 represent two separate soliton solutions described by Equation (21). Then the soliton of amplitude A1 being at a big distance from another soliton of amplitude A2 (see Figure 3) experiences its influence only through the exponentially small asymptotic (a “tail”) of the second soliton field. The tail part of the soliton field follows from the asymptotic solution of Equation (21), η = 4 A2 exp(–2 d/∆), where d is the distance between the soliton maxima along the x-axis. The external field produced by the second soliton and represented by its “tail” can be considered as slowly varying in the space pedestal; at the place of the first soliton, the tail field is almost constant because it is assumed that the characteristic scale of pedestal variation in space is much greater than the characteristic width of the first soliton; this is shown schematically in Figure 3. A soliton solution of Equation (20) on the constant pedestal p is the same as in Equation (21), but with the modified speed, ; the solution exists if Vpat > α A/3 + α p.
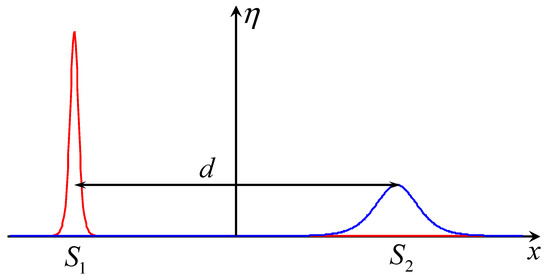
Figure 3.
(Colour online). The sketch of two solitons of different amplitudes being at a distance d = |S1 − S2| from each other and interacting through their tails.
If we denote by S1,2 the positions of soliton centres, then the kinematic condition of soliton motion requires that Ṡ1,2 = ±W1,2, where Ṡ stands for the derivative of S with respect to the “effective time” y, and the signs ± pertain to solitons moving to the right or left. Considering solitons moving towards each other, we can set Ṡ1 = −W1, and Ṡ2 = W2. In the expressions for W1,2, we can substitute instead of the constant pedestals d1,2 the expressions of the tails of reciprocally external solitons or simply the external soliton fields, because we assume that the distance between the solitons is much greater than their characteristic width, |S1 − S2| >> ∆1,2. Thus, we obtain the set of two equations for S1,2:
where the upper sign pertains to the soliton at S2, and the lower sign—to the soliton at S1. Here the slowly varying pedestal p1.2(y) is determined by Equation (21).
This set of equations looks incomplete and seemingly needs to be augmented by the dynamical equations for the soliton amplitudes A1,2(y). However, soliton amplitudes experience variations only within a relatively short time when the “effective particles” experience a head-on collision. Therefore, in the first approximation, we can assume that soliton amplitudes remain unchanged and equal to their values at the infinity, i.e., far from the collision zone where the soliton fronts intersect (see Figure 2a). Substituting in Equation (22) A1,2 = 3β k2/α and Vpat from Equation (17), we obtain:
Note, that for the symmetric solution considered here (see Figure 2) A1 = A2 = A, and a real solution to Equation (23) exists provided that (cf. Equations (14) and (15)). Equation (23) can be readily solved. To this end, we note that S1 + S2 = 0 in the symmetric case; subtracting then one equation from another and denoting X = S2 − S1, we obtain:
where ∆ = (12β/αA)1/2. After the separation of variables in Equation (24), we find:
Bearing in mind that X = S2 – S1 and S1 + S2 = 0, we find solutions for S1 and S2 in the form:
This solution is shown in Figure 4 for the same set of parameters as in Figure 2(a): A1 = A2 = 7.5 × 10−3, k = 0.05; l2 = −l1 = 0.005, l2/k = 0.1, B = 4. The dependences S1,2(y), which represent the soliton fronts in the KP2 equation, are shown in the figure in terms of inverse functions y1,2(S1,2). The directions of the effective (imaginary) particle motion within the approximate approach are shown by small arrows.
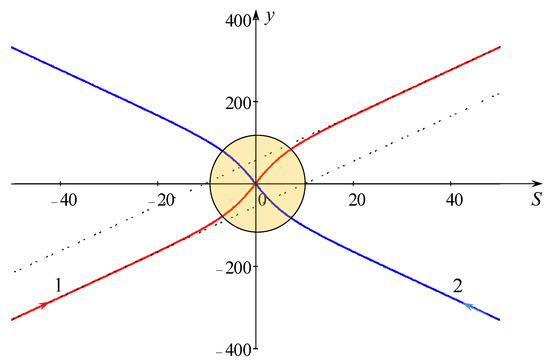
Figure 4.
(colour online). Solutions y1,2(S1,2) as per Equation (26) of the derived set of equations for A1 = A2 = 0.0285 (k1 = k2 = 0.097468), l1 = −0.01771, l2 = −l1. The yellow circle shows the domain where the asymptotic theory is formally inapplicable because the distance between the solitons is not big here.
The asymptotic theory is applicable outside of the circle shown in the figure where the distance between the soliton maxima is much greater than the soliton widths d = |S2 − S1| >> ∆1,2. The lower dashed line in Figure 3 shows the initial trajectory of an imaginary particle 1 before the collision with the imaginary particle 2, and the upper dashed line shows the trajectory of particle 1 after the collision with particle 2. The phase shift between the soliton fronts due to interaction with another soliton can be determined as the difference in the “particle trajectory” experiencing a collision with another particle, S2(y), and the trajectory of freely moving particle. The former trajectory is given by the inversion of Equation (26), and the latter follows from Equation (23) with A1 = 0: S20(y) = (3β l2/αA)1/2y. The “particle trajectory” experiencing collision with another particle can be easily calculated in the asymptotic when y → ∞; then from Equation (26) we obtain:
The phase shifts of the “effective particle” moving from S(0) = 0 to infinity are:
The similar phase shifts appear for the particle moving from S(0) = 0 to minus infinity, therefore, the total phase shifts are Φx and Φy. These expressions for the phase shifts are exactly the same as those which follow from the analytical solution (11), (13) and (16). The phase shift between the fronts of one of the interacting solitons is shown in Figure 4. The phase shift becomes infinite when the condition (19) is fulfilled, and the triad configuration is formed. Figure 5 shows the example of soliton interaction at the near-critical condition when the bridge between them becomes long. This case corresponds to the exact solution shown in Figure 2b with the same parameters: k = 0.05; l2 = −l1 = 0.00433012702, l2/k = 0.0866, B = 2 × 109, Φx = 428.3, and Φy = 4947. One can see again that there is a very good agreement between the asymptotic theory and exact solution even in the case of the big phase shift.
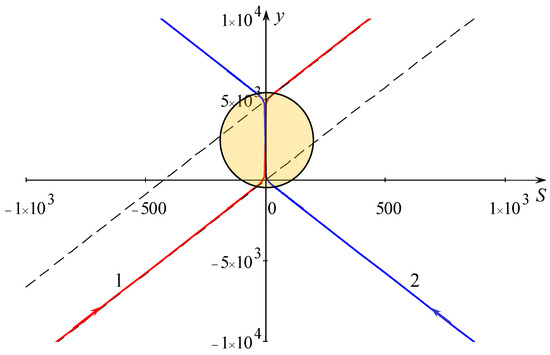
Figure 5.
(Colour online). Solutions y1,2(S1,2) as per Equation (26) of the derived set of equations for A1 = A2 = 0.0285 (k1 = k2 = 0.05), l1 = −0.00433012702, l2 = −l1. The yellow circle shows the domain where the asymptotic theory is formally inapplicable.
3.2. A symmetric Pattern in the 2dBO Equation Formed by Two Plane Solitons
Let us apply now the validated method to the non-integrable 2dBO equation. Such equation was derived for the first time by Ablowitz and Segur [21], and then, by many other authors [8,22,23,24] for the description of quasi-plane internal waves on a pycnocline in a deep ocean with a relatively thin one of the layers. In the coordinate frame moving with the speed of long linear waves, the equation has the form (cf. the KP equations Equation (1)):
where c is the speed of long linear waves, α and β are the nonlinear and dispersive coefficients, respectively, and the symbol stands for the principal value of the integral.
This equation has a single soliton solution representing a plane wave obliquely propagating at an angle to the x-axis.
where
The soliton amplitude is also determined solely by the parameter k: A = 4β k/α, whereas its speed V depends both on k and l:
For the components of a soliton velocity V = (Vx, Vy), the formulae are the same as in Equation (10).
An exact two-soliton solution representing two plane waves propagating at an angle to each other is unknown. Matsuno [8], using the alternative asymptotic method, studied the interaction of plane solitons within the generalized two-dimensional BO-type model which, in contrast to the KP or 2dBO models, does not have a restriction on the smallness of the angle φ of wave propagation with respect to the x-axis. He derived the expression for the phase shift of each soliton front and discovered that the phase shift turns to zero when the angle between the direction of soliton propagation is θ = 120°. For the symmetrical pattern moving along the x-axis, like that shown in Figure 2a), the angle φ = θ/2 = 60° is too big and, obviously, beyond the limits of applicability of the standard 2dBO equation. We use below another approach for the calculation of the phase shift between the soliton fronts, which is based on the asymptotic method described above and validated by comparison with the exact solutions of the KP2 equation.
If two plane solitary waves have the same parameter k > 0 and the parameters l of opposite sign, l2 = −l1, then they form a symmetric pattern which moves stationary along the x-axis with the speed (cf. Equation (16)):
The soliton amplitudes, in this case, are the same and determined by the formula A = 4β k/α. The 2dBO equation for such solutions reduces to the Boussinesq-type equation similar to Equation (20):
where y again plays a role of time, and C02 = 2 Vpat/c plays a role of a squared speed of long linear waves. Therefore, Equation (34) can be treated as the one-dimensional equation in space and “time” with the following soliton solution:
where ∆ = 4β/αA, and W2 = (2/c)(Vpat − αA/4); the solution exists if Vpat > α A/4.
Exploiting the asymptotic approach to soliton interaction described in the previous Section 3.1, we obtain the set of two equations for the soliton centres S1,2:
Substituting in Equation (36) A1,2 = 4β k/α and Vpat from Equation (33) and assuming that each soliton plays a role of external slowly varying pedestal p1.2(y) to another soliton, we obtain:
For the symmetrical solution considered here A1 = A2 = A, a real solution to Equation (37) exists provided that . Equation (37) can be readily solved using the fact that S1 + S2 = 0 in the symmetrical case. Then, we have:
The solution of this differential equation can be presented in terms of incomplete elliptic integrals F(φ, γ) and F(φ, γ) of the first and second kinds, respectively:
where γ2 = (αA)3/8cβ 2l2 = 8β k3/cl2. Graphically, this solution is similar to what is shown in Figure 4 and Figure 5.
The shift of a soliton front due to the intersection with another soliton can be easily found by a comparison of solution (39) in the asymptotics when S1,2 → ±∞. Then, for the phase shift we obtain:
where K(γ) and E(γ) are the complete elliptic integrals of the first and second kinds respectively. As follows from this formula, the phase shift becomes infinite when γ → 1 (in this case K(γ) ≈ → ∞, whereas E(γ) → 1); then a triad of solitary waves is formed.
Two-soliton solutions were studied numerically by Tsuji and Oikawa [24]. They actually investigated the nonstationary dynamics of the initial condition consisting of a linear superposition of two solitary waves (30) of the same amplitudes moving along the x-axis under the angle to each other. In their runs, the following set of parameters was chosen: α = β = 1, c = 2, A = 2, k = 0.5, l1,2 = ± kΩ, where Ω = tan φ = 2, 1, 0.5 in three different runs. In all these runs, the angle φ is not small as it is required in the 2dBO model. Nevertheless, it is of interest to compare the results of the asymptotic theory developed here with the numerical data presented in [24]. In the first run with Ω = 2, the authors observed a stationary moving pattern formed by two solitons; “it seems that there exist very small phase shifts” in the soliton fronts. With the chosen set of parameters, we can estimate the phase shift using Equation (40); this gives Φy = 0.8485. Such a small phase shift is indeed difficult to detect in Figure 3(a) of paper [24]. In two other runs with Ω = 1 and 0.5, the initial conditions used by the authors formally lead to too big values of the parameter γ (see above), which becomes greater than 1. In such cases, according to the developed here asymptotic theory, stationary patterns do not exist. The authors of [24] indeed observed rather complicated nonstationary dynamics of initial perturbations, especially in the latter case of Ω = 0.5 (see Figure 3(b,c) in [24]).
It is interesting to note that according to Equation (40), the phase shift vanishes only when γ → 0, in all other cases the phase shift is nonzero. This is in contrast with the one-dimensional theory of the BO equation, which predicts that the interacting solitons do not experience a phase shift [25,26]. However, as was shown by Matsuno [8], in the exceptional case when the angle between the directions of soliton propagation is θ = 120°, the phase shift vanishes. This result was derived within the generalized two-dimensional BO-type model where there is no restriction on the value of the angle φ = θ/2. The analysis presented here is inapplicable to such a case and is restricted by the condition |φ | << 1. However, if we nevertheless use the asymptotic theory beyond its formal range of applicability and set the same parameters as above with Ω = √3, we obtain the nonzero phase shift, Φy = 0.978.
As one can see from Equation (38), the parameter γ cannot be greater than one (otherwise solution becomes imaginary), which means that the parameter l should not be too small, i.e., solution obtained pertains to solitons moving at certain nonzero angles to the x-axis. Taking into account that the physical applicability of the 2dBO equation requires that the angle φ between the direction of soliton propagation normal to its front and the x-axis must be small, we obtain l/k = tanφ << 1 (cf. Equation (15)):
This ultimately gives the same restriction for the soliton amplitudes as in the case of the KP2 equation: A ≤ cφ 2/2α. The same restriction was obtained for the soliton amplitudes by Matsuno [8] in the case of the generalized two-dimensional BO-type equation. The solitons, apparently, experience a more complicated nonstationary interaction if this restriction is not met. This interesting issue deserves further study.
4. Discussion and Conclusions
In this paper, the asymptotic approach has been developed for the description of stationary patterns formed by two plane solitons interacting at an angle to each other within the KP-type equations. The asymptotic approach has been validated by comparison of the results obtained with the exact two-soliton solution of the completely integrable KP2 equation. It has been demonstrated that the phase shifts of soliton fronts due to soliton interaction derived by the asymptotic method are exactly the same as provided by the exact analytical solution. The asymptotic approach has a wide range of applicability and applies even to the non-integrable quasi-one-dimensional models of the KP-type such as the two-dimensional versions of the Gardner, Benjamin–Ono, and Joseph–Kubota–Ko–Dobbs equations. Apparently, it applies to the two-dimensional set of Boussinesq equations for shallow-water waves too. After successful testing, the asymptotic approach has been used for the description of plane soliton interaction within the 2dBO equation. It is a challenge to compare the theoretical results obtained here with the numerical solutions or experimental observation. Unfortunately, the relevant data are currently unavailable.
In this paper, only a particular case of symmetric soliton interactions with equal amplitudes was considered. The corresponding wave pattern uniformly moves along the x-axis. However, the method can be developed further for the non-symmetric wave pattern stationary moving at an angle to the x- and y-axis [21]; this will be done elsewhere.
Funding
This research was funded by the State task program in the sphere of scientific activity of the Ministry of Science and Higher Education of the Russian Federation (project No. FSWE-2020-0007) and the grant of the President of the Russian Federation for state support of Leading Scientific Schools of the Russian Federation (grant No. NSH-2485.2020.5).
Conflicts of Interest
The author declares no conflict of interest.
References
- Ablowitz, M.J.; Segur, H. Solitons and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Apel, J.R.; Ostrovsky, L.A.; Stepanyants, Y.A.; Lynch, J.F. Internal solitons in the ocean and their effect on underwater sound. J. Acoust. Soc. Am. 2007, 121, 695–722. [Google Scholar] [CrossRef] [PubMed]
- Ablowitz, M.J.; Baldwin, D.E. Nonlinear shallow ocean-wave soliton interactions on flat beaches. Phys. Rev. E 2012, 86, 036305. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Pawlowicz, R. Oblique wave-wave interactions of nonlinear near-surface internal waves in the Strait of Georgia. J. Geophys. Res. 2012, 117, C0631. [Google Scholar] [CrossRef]
- Gorshkov, K.A.; Ostrovsky, L.A. Interaction of solitons in nonintegrable systems: Direct perturbation method and applications. Physica D 1981, 3, 428–438. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Gorshkov, K.A. Perturbation theories for nonlinear waves. In Nonlinear Science at the Down at the XXI Century; Christiansen, P., Soerensen, M., Eds.; Elsevier: Amsterdam, The Netherland, 2000; pp. 47–65. [Google Scholar]
- Ostrovsky, L.A. Asymptotic Perturbation Theory of Waves; Imperial College Press: Singapore, 2015. [Google Scholar]
- Matsuno, Y. Oblique interaction of interfacial solitary waves in a two-layer deep fluid. Proc. R. Soc. Lond. A 1998, 454, 835–856. [Google Scholar] [CrossRef]
- Gorshkov, K.A.; Pelinovsky, D.E.; Stepanyants, Y.A. Normal and anomalous scattering, formation and decay of bound-states of two-dimensional solitons described by the Kadomtsev–Petviashvili equation. JETP 1993, 77, 237–245. [Google Scholar]
- Clarke, S.; Gorshkov, K.; Grimshaw, R.; Stepamyats, Y. Decay of Kadomtsev–Petviashvili lumps in dissipative media. Physica D 2018, 366, 43–50. [Google Scholar] [CrossRef]
- Potapov, A.I.; Soldatov, I.N. Quasi-plane beam of nonlinear longitudinal waves in a plate. Sov. Phys. Acoust. 1984, 30, 486–488. [Google Scholar]
- Pelinovsky, D.E.; Stepanyants, Y.A.; Kivshar, Y.S. Self-focusing of plane dark solitons in nonlinear defocusing media. Phys. Rev. E 1995, 51, 5016–5026. [Google Scholar] [CrossRef]
- Porubov, A.; Maugin, G.; Mareev, V. Localization of two-dimensional non-linear strain waves in a plate. Int. J. Non-Linear Mech. 2004, 39, 1359–1370. [Google Scholar] [CrossRef]
- Satsuma, J. Soliton solution of the two-dimensional Korteweg–de Vries equation. J. Phys. Soc. Jpn. 1976, 40, 286–290. [Google Scholar] [CrossRef]
- Miles, J.W. Obliquely interacting solitary waves. J. Fluid Mech. 1977, 79, 157–169. [Google Scholar] [CrossRef]
- Miles, J.W. Resonantly interacting solitary waves. J. Fluid Mech. 1977, 79, 171–179. [Google Scholar] [CrossRef]
- Anker, D.; Freeman, N.C. Interpretation of three-soliton interactions in terms of resonant triads. J. Fluid Mech. 1978, 87, 17–31. [Google Scholar] [CrossRef]
- Freeman, N.C. A two dimensional distributed soliton solution of the Korteweg–de Vries equation. Proc. R. Soc. Lond. A. 1979, 366, 185–204. [Google Scholar]
- Kadomtsev, B.B.; Petviashvili, V.I. On the stability of solitary waves in weakly dispersive media. Sov. Phys. Dokl. 1970, 15, 539–541. [Google Scholar]
- Ostrovsky, L.A.; Stepanyants, Y.A. Kinematics of interacting solitons in two-dimensional space. Russ. J. Earth Sci. 2020, 20, ES4007. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Segur, H. Long internal waves in fluids of great depth. Stud. Appl. Math. 1980, 62, 249–262. [Google Scholar] [CrossRef]
- Grimshaw, R. Evolution equations for long nonlinear internal waves in stratified shear flows. Stud. Appl. Math. 1981, 65, 159–188. [Google Scholar] [CrossRef]
- Grimshaw, R.; Zhu, Y. Oblique interaction between internal solitary waves. Stud. Appl. Math. 1994, 92, 249–270. [Google Scholar] [CrossRef]
- Tsuji, H.; Oikawa, M. Oblique interaction of internal solitary waves in a two-layer fluid of infinite depth. Fluid Dyn. Res. 2001, 29, 251–267. [Google Scholar] [CrossRef]
- Matsuno, Y. Interaction of the Benjamin–Ono solitons. J. Phys. A 1980, 13, 1519–1536. [Google Scholar] [CrossRef]
- Matsuno, Y. Exact multi-soliton solution of the Benjamin–Ono equation. J. Phys. A 1979, 12, 619–621. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).