Detecting Optimal Leak Locations Using Homotopy Analysis Method for Isothermal Hydrogen-Natural Gas Mixture in an Inclined Pipeline

Abstract

The aim of this article is to use the Homotopy Analysis Method (HAM) to pinpoint the optimal location of leakage in an inclined pipeline containing hydrogen-natural gas mixture by obtaining quick and accurate analytical solutions for nonlinear transportation equations. The homotopy analysis method utilizes a simple and powerful technique to adjust and control the convergence region of the infinite series solution using auxiliary parameters. The auxiliary parameters provide a convenient way of controlling the convergent region of series solutions. Numerical solutions obtained by HAM indicate that the approach is highly accurate, computationally very attractive and easy to implement. The solutions obtained with HAM have been shown to be in good agreement with those obtained using the method of characteristics (MOC) and the reduced order modelling (ROM) technique.

1. Introduction

One of the strategies to reduce gas transportation costs is the use of natural gas pipeline networks by petroleum companies [1]. These networks are capable of supplying gas in long distances under high pressure and through compression stations [2]. Changes in pipeline pressure are a function of gas velocity, valve closure time, and arrangement of the closing valve [3].

When the valve is closed at the end of the pipeline, there is the possibility of the occurrence of maximum pressure, which can be decreased in short times during its closure. It is of utmost importance to control factors affecting transient pressure, such as initial pressure and mass ratio. This is because the damage caused by this pressure is not evident shortly after the event [4,5,6].

Several studies have been conducted on transient flow in the mixtures of hydrogen and natural gas with the use of isothermal flow and horizontal pipelines, which is not the case in reality [2,7,8,9]. Furthermore, another study has made an attempt to study the flow of these mixtures under high pressure through inclined pipelines [10]. In most pipelines working under high pressure, there are slow and fast fluid transients. As gas properties are not constant, a one-dimensional and non-isothermal gas flow model should be presented to simulate these transients [2].

The reason for proposing hydrogen and natural gas mixtures is their transportation through the same pipelines for the purpose of cost reduction. This is while the existing lines are just designed for natural gas, whose properties are significantly different from that of hydrogen [11,12]. The solution to this problem has been the mixture of the both with a great deal of care and attention, as hydrogen is a reactive gas with high pressure that can cause leakage [13,14]. This problem is of great importance since leakage can cause many economic, environmental, and safety problems and threaten industries and citizens by wasting natural gas [14].

According to the reports, two thirds of the 375 pipeline events between 1994 and 1999 were caused by leakage [4]. In addition, high-pressure wave celerity causes pipe splitting, and even, exploding, sometimes making intense holes that lead to inward collapse of pipes, necessitating the careful study of pressure wave celerity.

Studies have been done on leakage and its location for natural gas [15,16], leading to the introduction of methods [17,18], such as the acoustic method (AM) [18,19] and the negative pressure wave method (NPW) [20,21]. Means of transients and using unsteady-state tests, which give rise to small overpressure, can be considered as an appropriate method for detecting leaks locations in pressurised pipes [22]. Autocorrelation analysis of vibro-acoustic signals measured in a test field and amplitude distortion of measured leak noise signals caused by instrumentation have been used for water leak detection in [23,24]. In water-filled small-diameter polyethylene pipes by means of acoustic Emission Measurements, [25] has been used for detecting leak locations. However, there is paucity of research on this issue for hydrogen or its mixture with natural gas [15,16]. In this regard, isothermal and non-isothermal flow models have been proposed for hydrogen and natural gas mixtures [7,8,14].

There have been several studies on the detection of leakage location through novel approaches. For example, new leakage detection using AM [26] and new algorithm based on the attenuation of NPW in isothermal cases have been introduced in recent years [27].

Accordingly, the present study made an attempt to determine leakage location in an inclined pipe for isothermal flow containing hydrogen-natural gas mixture with the use of homotpy analysis method. This method is used for solving the governing equations, leading to quick and accurate analytical solutions for nonlinear transportation equations. Factors affecting pressure and celerity waves in inclined pipes, such as inclination angles and mass ratio of mixtures, have also been discussed. The obtained results are in good agreement for isothermal flow in a horizontal pipeline. Results showed that pressure drop and leak discharge are increased with an increase in the inclination angle, while the celerity wave and the leak location do not seem to be affected.

2. Mathematical Formulation

Figure 1 shows an inclined pipeline, which has a reservoir at the top and a valve at its bottom. The governing equations consist of three partial differential equations that are all coupled, non-linear and hyperbolic. The non-isothermal flow in the pipeline, a homogenous mixture of hydrogen and natural gas, was considered to be one-dimensional that is compressible and covers transient condition [7].

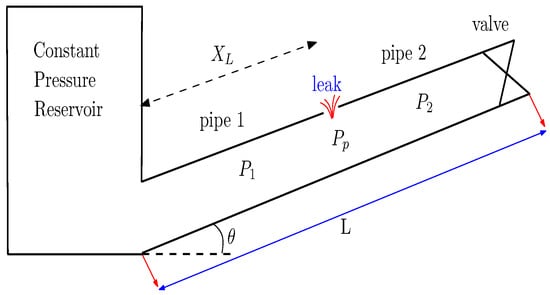
Figure 1. An inclined pipeline with a reservoir at the top and a valve at its bottom.

2.1. Governing Equation

The governing equations for the transport of hydrogen/natural gas mixture in an inclined pipeline from the principle of conserving mass and momentum are given by the following,

$$\begin{array}{ccc}\hfill & & \frac{\partial \rho }{\partial t}+\frac{\partial \rho u}{\partial x}=0,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}& & \frac{\partial \rho u}{\partial t}+\frac{\partial (\rho u^2+P)}{\partial x}+\frac{f\rho u\left|u\right|}{2D}+\rho gsin\left(\theta \right)=0,\hfill \end{array}$$

(2)

with $u=Q/A$, $A=\pi D^2/4$, $\rho$ is density, u is the gas velocity, P is the pressure, e is the gas internal energy per unit mass, D is the diameter of the pipeline, f is the coefficient of friction, g is the gravitational force and $\theta$ is an angle between the friction force and the direction.

Boundary conditions of this equations depend on the types of closure and the valve operational time. The boundary conditions at the initial point $x=0$ and at the end point $x=L$, respectively are given by,

$$\begin{array}{c}\hfill \rho (0,t)={\rho }_0\left(t\right),u(0,t)=u_0\left(t\right),\end{array}$$

(3)

$$\begin{array}{c}\hfill \rho (L,t)={\rho }_L\left(t\right),u(L,t)=u_L\left(t\right),\end{array}$$

(4)

where ${\rho }_0$ and $u_0$ are defined as density and gas velocity at the inlet pipeline, respectively and ${\rho }_L$ and $u_L$ are defined as density and gas velocity at the outlet pipeline, respectively. The initial conditions that are assumed to be in a steady state condition at $t=0$ are [7],

$$\begin{array}{ccc}\hfill & & \frac{\partial \rho u}{\partial x}(x,0)=0,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& & \frac{\partial (\rho u^2+P)}{\partial x}(x,0)+\frac{f\rho u\left|u\right|}{2D}+\rho gsin\left(\theta \right)=0,\hfill \end{array}$$

(6)

The commonly used equation of state for perfect gas is as follows:

$$\begin{array}{c}\hfill P=\rho RT,\end{array}$$

(7)

where,

• R: is the specific gas constant.
• T: is temperature.

The equation of state for the compressible flow, where there is a celerity pressure wave, is:

$$\begin{array}{c}\hfill P=c^2\rho ,\end{array}$$

(8)

The following equations are also achieved from ideal gas relation,

$$C_p-C_v=R,\gamma =\frac{C_p}{C_v},C_v=\frac{R}{\gamma -1}.$$

(9)

where,

• $C_v$: is the specific heat at constant volume.
• $C_p$: is the specific heat at constant pressure.
• R: is the specific gas constant.
• P: is pressure.
• $\gamma$: is the flow process index.

2.2. Hydrogen-Natural Gas Mixture Equation

The mass ratio and the density of hydrogen-natural gas mixture are defined as,

$$\varphi =\frac{m_h}{m_h+m_g},\frac{1}{\rho }=\frac{v_h+v_g}{m_h+m_g},$$

(10)

with ${\rho }_h=\frac{m_h}{v_h}$, ${\rho }_g=\frac{m_g}{v_g}$, ${\rho }_h={\rho }_{h_0}{\left(\frac{P_0}{P}\right)}^{\frac{1}{n_1}}$ and ${\rho }_g={\rho }_{g_0}{\left(\frac{P_0}{P}\right)}^{\frac{1}{n_2}}$. Where $m_g$, $m_h$, $V_g$ and $V_h$ are defined as the mass of natural gas and hydrogen and volume of natural gas and hydrogen, respectively.

Therefore, the expression of the average density of the gas mixture is given by,

$$\rho ={\left[\frac{\varphi }{{\rho }_{h_0}}{\left(\frac{P_0}{P}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{{\rho }_{g_0}}{\left(\frac{P_0}{P}\right)}^{\frac{1}{n_2}}\right]}^{-1}.$$

(11)

The celerity pressure wave for compressible flow is defined as,

$$\begin{array}{c}\hfill c={\left(\frac{\partial \rho }{\partial P}\right)}_s^{-\frac{1}{2}},\end{array}$$

(12)

where the subscript s is defined the constant entropy condition. The derivative of Equation (11) with respect to P, and substituting into Equation (12), then the celerity pressure wave yields [7],

$$c=\left[\frac{\varphi }{{\rho }_{h_0}}{\left(\frac{P_0}{P}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{{\rho }_{g_0}}{\left(\frac{P_0}{P}\right)}^{\frac{1}{n_2}}\right]\times {\left[\frac{1}{P}\left[\frac{\varphi }{n_1{\rho }_{h_0}}{\left(\frac{P_0}{P}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{n_2{\rho }_{g_0}}{\left(\frac{P_0}{P}\right)}^{\frac{1}{n_2}}\right]\right]}^{-\frac{1}{2}}.$$

(13)

The properties of hydrogen and natural gas used in the calculations are shown in the Table 1. For the simulation, the parameters are assumed as Table 2.

Table 1. Hydrogen properties in working conditions, $P=35$ bar and $T=15{}^{\circ }$C = 288 K (See [7]).

Symbol	Fluid Properties	Values (J/kgK)
		Hydrogen	Natural Gas
$C_p$	Specific heat at constant pressure	14,600	1497.5
$C_v$	Specific heat at constant volume	10,440	1056.8
R	Gas constant	4160	440.7

Table 2. Parameters used for the simulation (See [7]).

Symbols	Values	Symbols	Values
Pipe length	L = 600 m	Mass ratio	$\varphi =0,0.5,1$
Time	t = 20	Angle	$\theta =0,\pi /6,\pi /4,\pi /3$
Pipe diameter	D = $0.4$ m	Mass flow	$Q_0$ = 55 kg/s
Friction coefficient	$f=0.03$	Absolute pressure	$P_0$ = 35 bar
Temperature	$T=15{}^{\circ }$C = 288 K

3. Homotopy Analysis Method

A brief description of the standard homotopy analysis method (HAM) presented by [28,29,30,31,32]. This will be followed by a description of the algorithm of the homotopy analysis method (HAM). First, we consider the following differential equation,

$$\mathcal{N}\left[u(x,t)\right]=\mathcal{G}(x,t),$$

(14)

where $\mathcal{N}$ are nonlinear operators, x and t denotes the independent variable, $u(x,t)$ are unknown functions, and $\mathcal{G}(x,t)$ are known analytic functions. For $\mathcal{G}(x,t)=0$, Equation (14) reduces to the homogeneous equation. By means of generalizing the traditional homotopy method, Liao [28] constructed the so-called zero-order deformation equation,

$$\left(1-q\right)\mathcal{L}\left[\mathsf{\Psi }(x,t;q)-u_0(x,t)\right]=q\hslash \mathcal{H}(x,t)\left\{\mathcal{N}\left[\mathsf{\Psi }(x,t;q)\right]-\mathcal{G}(x,t)\right\}$$

(15)

where $p\in [0,1]$ is an embedding parameter, ℏ are nonzero auxiliary functions, $\mathcal{L}$ is an auxiliary linear operator, $u_0(x,t)$ are initial guesses of $u(x,t)$, $\mathcal{H}(x,t)$ denotes a nonzero auxiliary function and $\mathsf{\Psi }(x,t;q)$ are unknown functions. It is important to note that one has great freedom to choose auxiliary objects such as ℏ and $\mathcal{L}$ in HAM. Obviously, when $q=0$ and $q=1$, Equation (15) becomes,

$$\mathsf{\Psi }(x,t;0)=u_0(x,t),\mathsf{\Psi }(x,t;1)=u(x,t),$$

(16)

Thus, as q increases from 0 to 1, the solution $\mathsf{\Psi }(x,t;q)$ varies from the initial guesses $u_0(x,t)$ to the solutions $u(x,t)$. Expanding $\mathsf{\Psi }(x,t;q)$ in Taylor series with respect to q, one has

$$\mathsf{\Psi }(x,t;q)=u_0(x,t)+\sum _{m=1}^{\infty }{u}_m(x,t)q^m,$$

(17)

where,

$$u_m(x,t)=\frac{1}{m!}\frac{{\partial }^m\mathsf{\Psi }(x,t;q)}{\partial q^m}{|}_{q=0},$$

(18)

If the auxiliary linear operator, the initial guesses, the auxiliary parameters ℏ, and the auxiliary functions are so properly chosen, then series Equation (17) converges at $q=1$, and one has,

$$u(x,t)=u_0(x,t)+\sum _{m=1}^{\infty }{u}_m(x,t),$$

(19)

which must be one of the solutions of the original nonlinear equations, as proved by Liao [28]. As $\hslash =-1$ and $\mathcal{H}(x,t)=1$, Equation (15) becomes,

$$\left(1-q\right)\mathcal{L}\left[\mathsf{\Psi }(x,t;q)-u_0(x,t)\right]=q\left\{\mathcal{N}\left[\mathsf{\Psi }(x,t;q)\right]-\mathcal{G}(x,t)\right\},$$

(20)

which is used mostly in the homotopy perturbation method. Define the vectors,

$${\overrightarrow{u}}_m=\left\{u_0(x,t),u_1(x,t),\dots ,u_m(x,t)\right\},$$

(21)

Differentiate the zeroth-order deformation Equation (14) m-times with respect to q and then dividing them by $m!$ and finally setting $q=0$, we get the following mth-order deformation equation,

$$\mathcal{L}\left[u_m(x,t)-{\chi }_m{u}_{m-1}(x,t)\right]=\hslash {\mathcal{R}}_m\left({\overrightarrow{u}}_{m-1}(x,t)\right),$$

(22)

where,

$${\mathcal{R}}_m\left({\overrightarrow{u}}_{m-1}(x,t)\right)=\frac{1}{(1-m)!}\frac{{\partial }^{m-1}\left\{\mathcal{N}\left[\mathsf{\Psi }(x,t;q)\right]-\mathcal{G}(x,t)\right\}}{\partial q^{m-1}},$$

(23)

with,

$$\begin{array}{c}\hfill {\chi }_m=\left\{\begin{array}{c}0,m\le 1\hfill \\ 1,m>1\hfill \end{array}\right.\end{array}$$

(24)

It should be noted that the linear Equation (22), which has linear boundary conditions, governs $u_m(x,t)$ for $m\le 1$ [33]. Boundary conditions stem from the main problem, the solution for which can be provided by Matlab, Maple, or Mathematica. The requirement for the limit of Equation (17) is that it should meet the conditions of the main equation $\mathcal{N}\left[u(x,t)\right]=0$ when it is convergent at $q=1$. It is noteworthy that drawing “ℏ-curves” or “curves for convergence-control parameter” aim to find a proper convergence-control parameter ℏ, a convergent series solution, or and accelerate its convergence rate. It is such that these curves with unknown quantities are drawn against ℏ to approximately find the convergence region, though they are just graphical. This is because it is not possible to find which ${\hslash }_0\in R_h$ provides the fastest convergent series (see Liao [28,34] for further reading). Another note to be made is that a unique solution is achieved when Equation (14) accepts a unique solution; otherwise, many possible solutions will be obtained from HAM.

3.1. Solving the Steady State Equations by High-Order Deformation HAM

We define the vectors,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\overrightarrow{P}\left(x\right)=\left\{P_0\left(x\right),P_1\left(x\right),\dots ,P_m\left(x\right)\right\}\hfill \\ \overrightarrow{u}\left(x\right)=\left\{u_0\left(x\right),u_1\left(x\right),\dots ,u_m\left(x\right)\right\}\hfill \end{array}\right.\end{array}$$

(25)

Differentiating Equations (5) and (6) m times with respect to the embedding parameter q and then setting $q=0$ and finally dividing them by $m!$, we have the so-called mth-order deformation equations,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{L}}_1\left[P_m\left(x\right)-{\chi }_m{P}_{m-1}\left(x\right)\right]=\hslash {\mathcal{R}}_m^1\left({\overrightarrow{P}}_{m-1}\left(x\right),{\overrightarrow{u}}_{m-1}\left(x\right)\right),\hfill \\ {\mathcal{L}}_2\left[u_m\left(x\right)-{\chi }_m{u}_{m-1}\left(x\right)\right]=\hslash {\mathcal{R}}_m^2\left({\overrightarrow{P}}_{m-1}\left(x\right),{\overrightarrow{u}}_{m-1}\left(x\right)\right),\hfill \end{array}\right.\end{array}$$

(26)

with the initial conditions,

$$\begin{array}{c}\hfill P\left(0\right)=P_0,u\left(0\right)=u_0,\end{array}$$

(27)

where,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{R}}_m^1\left({\overrightarrow{P}}_{m-1}\left(x\right),{\overrightarrow{u}}_{m-1}\left(x\right)\right)=\frac{d{P}_{m-1}\left(x\right)}{dx}+\sum _{i=0}^{m-1}{P}_{m-1-i}\left(x\right)\sum _{j=0}^i\frac{1}{u_j\left(x\right)}\frac{d{u}_{i-j}\left(x\right)}{dx},\hfill \\ {\mathcal{R}}_m^2\left({\overrightarrow{P}}_{m-1}\left(x\right),{\overrightarrow{u}}_{m-1}\left(x\right)\right)=\frac{d{u}_{m-1}\left(x\right)}{dx}+\sum _{i=0}^{m-1}{u}_{m-1-i}\left(x\right)\sum _{j=0}^i\frac{1}{P_j\left(x\right)}\frac{d{P}_{i-j}\left(x\right)}{dx}\hfill \\ +\sum _{i=0}^{m-1}{c}_{m-1-i}\sum _{j=0}^i{c}_{i-j}\sum _{k=0}^j{P}_{j-k}\left(x\right)\sum _{l=0}^k\frac{1}{u_l\left(x\right)}\frac{d{P}_{k-l}\left(x\right)}{dx}\hfill \\ +\frac{f}{2D}\left|u_{m-1}\left(x\right)\right|+u_{m-1}\left(x\right)gsin\left(\theta \right),\hfill \end{array}\right.\end{array}$$

(28)

with the celerity pressure wave $c_i$ defined as follows,

$$\begin{array}{ccc}\hfill & & c_i=\left[\frac{\varphi }{{\rho }_{h_0}}{\left(\frac{P_0}{P_i\left(x\right)}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{{\rho }_{g_0}}{\left(\frac{P_0}{P_i\left(x\right)}\right)}^{\frac{1}{n_2}}\right]\hfill \\ & & \times {\left[\frac{1}{P_i\left(x\right)}\left[\frac{\varphi }{n_1{\rho }_{h_0}}{\left(\frac{P_0}{P_i\left(x\right)}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{n_2{\rho }_{g_0}}{\left(\frac{P_0}{P_i\left(x\right)}\right)}^{\frac{1}{n_2}}\right]\right]}^{-\frac{1}{2}}.\hfill \end{array}$$

with the following linear operators,

$$\begin{array}{c}\hfill {\mathcal{L}}_1\left[{\mathsf{\Psi }}_1(x;q)\right]=\frac{d{\mathsf{\Psi }}_1(x;q)}{dx},{\mathcal{L}}_2\left[{\mathsf{\Psi }}_2(x;q)\right]=\frac{d{\mathsf{\Psi }}_2(x;q)}{dx},\end{array}$$

(29)

with the property that,

$$\begin{array}{c}\hfill {\mathcal{L}}_1\left[C_1\right]=0,{\mathcal{L}}_2\left[C_2\right]=0,\end{array}$$

(30)

which implies that,

$$\begin{array}{c}\hfill {\mathcal{L}}_1^{-1}\left(.\right)={\int }_0^x\left(.\right)dx,{\mathcal{L}}_2\left(.\right)={\int }_0^x\left(.\right)d,\end{array}$$

(31)

Now, the solution of the mth-order deformation Equations (5) and (6) becomes,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_m\left(x\right)={\chi }_m{P}_{m-1}\left(x\right)+\hslash {\mathcal{L}}_1^{-1}\left[\mathcal{H}(x,t){\mathcal{R}}_m^1\left({\overrightarrow{P}}_{m-1}\left(x\right),{\overrightarrow{u}}_{m-1}\left(x\right)\right)\right],\hfill \\ u_m\left(x\right)={\chi }_m{u}_{m-1}\left(x\right)+\hslash {\mathcal{L}}_2^{-1}\left[\mathcal{H}(x,t){\mathcal{R}}_m^2\left({\overrightarrow{P}}_{m-1}\left(x\right),{\overrightarrow{u}}_{m-1}\left(x\right)\right)\right],\hfill \end{array}\right.\end{array}$$

(32)

which can be easily solved by a symbolic computation software such as Matlab, Maple, and Mathematica. Therefore, we will have $P\left(x\right)$ and $u\left(x\right)$ as follows,

$$\begin{array}{ccc}\hfill & & {\displaystyle P\left(x\right)\simeq P_M\left(x\right)=P_0\left(x\right)+\sum _{m=1}^M{P}_m\left(x\right),}\hfill \end{array}$$

(33)

$$\begin{array}{ccc}& & {\displaystyle u\left(x\right)\simeq u_M\left(x\right)=u_0\left(x\right)+\sum _{m=1}^M{u}_m\left(x\right).}\hfill \end{array}$$

(34)

Furthermore, to construct the zeroth-order deformation equations we can define the nonlinear operators ${\mathcal{N}}_1\left[{\mathsf{\Psi }}_1(x;q)\right]$ and ${\mathcal{N}}_2\left[{\mathsf{\Psi }}_2(x;q)\right]$ as follows,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{N}}_1\left[{\mathsf{\Psi }}_1(x;q)\right]={\mathsf{\Psi }}_1(x;q)\frac{d{\mathsf{\Psi }}_2(x;q)}{dx}+{\mathsf{\Psi }}_2(x;q)\frac{d{\mathsf{\Psi }}_1(x;q)}{dx}\hfill \\ {\mathcal{N}}_2\left[{\mathsf{\Psi }}_2(x;q)\right]=\frac{d\left[{\mathsf{\Psi }}_1(x;q){\mathsf{\Psi }}_2{(x;q)}^2+c^2{\mathsf{\Psi }}_1(x;q)\right]}{dx}+\frac{f}{2D}{\mathsf{\Psi }}_1(x;q){\mathsf{\Psi }}_2(x;q)\left|{\mathsf{\Psi }}_2(x;q)\right|+{\mathsf{\Psi }}_1(x;q)gsin\left(\theta \right)\hfill \end{array}\right.\end{array}$$

(35)

with the celerity pressure wave c defined as follows,

$$\begin{array}{ccc}\hfill & & c=\left[\frac{\varphi }{{\rho }_{h_0}}{\left(\frac{P_0}{{\mathsf{\Psi }}_1(x;q)}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{{\rho }_{g_0}}{\left(\frac{P_0}{{\mathsf{\Psi }}_1(x;q)}\right)}^{\frac{1}{n_2}}\right]\hfill \\ & & \times {\left[\frac{1}{{\mathsf{\Psi }}_1(x;q)}\left[\frac{\varphi }{n_1{\rho }_{h_0}}{\left(\frac{P_0}{{\mathsf{\Psi }}_1(x;q)}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{n_2{\rho }_{g_0}}{\left(\frac{P_0}{{\mathsf{\Psi }}_1(x;q)}\right)}^{\frac{1}{n_2}}\right]\right]}^{-\frac{1}{2}}.\hfill \end{array}$$

(36)

3.2. Solving Isothermal Flow of Hydrogen-Natural Gas Mixture by HAM

We define the vectors,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\overrightarrow{P}(x,t)=\left\{P_0(x,t),P_1(x,t),\dots ,P_m(x,t)\right\}\hfill \\ \overrightarrow{u}(x,t)=\left\{u_0(x,t),u_1(x,t),\dots ,u_m(x,t)\right\}\hfill \end{array}\right.\end{array}$$

(37)

Differentiating Equations (1) and (2) m times with respect to the embedding parameter q and then setting $q=0$ and finally dividing them by $m!$, we have the so-called mth-order deformation equations,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{L}}_1\left[P_m(x,t)-{\chi }_m{P}_{m-1}(x,t)\right]=\hslash {\mathcal{R}}_m^1\left({\overrightarrow{P}}_{m-1}(x,t),{\overrightarrow{u}}_{m-1}(x,t)\right),\hfill \\ {\mathcal{L}}_2\left[u_m(x,t)-{\chi }_m{u}_{m-1}(x,t)\right]=\hslash {\mathcal{R}}_m^2\left({\overrightarrow{P}}_{m-1}(x,t),{\overrightarrow{u}}_{m-1}(x,t)\right),\hfill \end{array}\right.\end{array}$$

(38)

with the initial and boundary conditions as follows,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}P(x,0)=P_0\left(x\right),u(x,0)=u_0\left(x\right);\hfill \\ P(0,t)=P_0\left(t\right),u(0,t)=u_0\left(t\right)\mathtt{or}P(L,t)=P_L\left(t\right),u(L,t)=u_L\left(t\right),\hfill \end{array}\right.\end{array}$$

where,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{R}}_m^1\left({\overrightarrow{P}}_{m-1}(x,t),{\overrightarrow{u}}_{m-1}(x,t)\right)=\frac{\partial P_{m-1}(x,t)}{\partial t}+\sum _{i=0}^{m-1}{u}_i(x,t)\frac{\partial P_{m-1-i}(x,t)}{\partial x}\hfill \\ +\sum _{i=0}^{m-1}{P}_i(x,t)\frac{\partial u_{m-1-i}(x,t)}{\partial x},\hfill \\ {\mathcal{R}}_m^2\left({\overrightarrow{P}}_{m-1}\left(x\right),{\overrightarrow{u}}_{m-1}\left(x\right)\right)=\frac{\partial u_{m-1}(x,t)}{\partial t}+\sum _{i=0}^{m-1}{u}_{m-1-i}\left(x\right)\sum _{j=0}^i\frac{1}{P_j(x,t)}\frac{\partial P_{i-j}(x,t)}{\partial t}\hfill \\ +\sum _{i=0}^{m-1}{u}_i(x,t)\frac{\partial u_{m-1-i}(x,t)}{\partial x}\hfill \\ +\sum _{i=0}^{m-1}{u}_{m-1-i}(x,t)\sum _{j=0}^i{u}_{i-j}(x,t)\sum _{k=0}^j\frac{1}{P_k(x,t)}\frac{\partial P_{j-k}(x,t)}{\partial x}\hfill \\ +\sum _{i=0}^{m-1}{c}_{m-1-i}(x,t)\sum _{j=0}^i{c}_{i-j}(x,t)\sum _{k=0}^j\frac{1}{P_k(x,t)}\frac{\partial P_{j-k}(x,t)}{\partial x}\hfill \\ +\frac{f}{2D}\sum _{i=0}^{m-1}{u}_i(x,t)\left|u_{m-1-i}(x,t)\right|+gsin\left(\theta \right)\hfill \end{array}\right.\end{array}$$

(39)

with the celerity pressure wave $c_i$ defined as follows,

$$\begin{array}{ccc}\hfill & & c_i=\left[\frac{\varphi }{{\rho }_{h_0}}{\left(\frac{P_0}{P_i(x,t)}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{{\rho }_{g_0}}{\left(\frac{P_0}{P_i(x,t)}\right)}^{\frac{1}{n_2}}\right]\hfill \\ & & \times {\left[\frac{1}{P_i(x,t)}\left[\frac{\varphi }{n_1{\rho }_{h_0}}{\left(\frac{P_0}{P_i(x,t)}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{n_2{\rho }_{g_0}}{\left(\frac{P_0}{P_i(x,t)}\right)}^{\frac{1}{n_2}}\right]\right]}^{-\frac{1}{2}}.\hfill \end{array}$$

with the following linear operators,

$$\begin{array}{c}\hfill {\mathcal{L}}_1\left[{\mathsf{\Psi }}_1(x,t;q)\right]=\frac{\partial {\mathsf{\Psi }}_1(x,t;q)}{\partial t},{\mathcal{L}}_2\left[{\mathsf{\Psi }}_2(x,t;q)\right]=\frac{\partial {\mathsf{\Psi }}_2(x,t;q)}{\partial t},\end{array}$$

(40)

with the property that,

$$\begin{array}{c}\hfill {\mathcal{L}}_1\left[C_1\right]=0,{\mathcal{L}}_2\left[C_2\right]=0,\end{array}$$

(41)

which implies that,

$$\begin{array}{c}\hfill {\mathcal{L}}_1^{-1}\left(.\right)={\int }_0^t\left(.\right)dt,{\mathcal{L}}_2\left(.\right)={\int }_0^t\left(.\right)dt,\end{array}$$

(42)

Now, the solution of the mth-order deformation Equations (1) and (2) becomes,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_m(x,t)={\chi }_m{P}_{m-1}(x,t)+\hslash {\mathcal{L}}_1^{-1}\left[\mathcal{H}(x,t){\mathcal{R}}_m^1\left({\overrightarrow{P}}_{m-1}(x,t),{\overrightarrow{u}}_{m-1}(x,t)\right)\right],\hfill \\ u_m(x,t)={\chi }_m{u}_{m-1}(x,t)+\hslash {\mathcal{L}}_2^{-1}\left[\mathcal{H}(x,t){\mathcal{R}}_m^2\left({\overrightarrow{P}}_{m-1}(x,t),{\overrightarrow{u}}_{m-1}(x,t)\right)\right],\hfill \end{array}\right.\end{array}$$

(43)

which can be easily solved by a symbolic computation software such as Matlab, Maple, and Mathematica. Therefore, we will have $P(x,t)$ and $u(x,t)$ as follows,

$$\begin{array}{ccc}\hfill & & {\displaystyle P(x,t)\simeq P_M(x,t)=P_0(x,t)+\sum _{m=1}^M{P}_m(x,t),}\hfill \end{array}$$

(44)

$$\begin{array}{ccc}& & {\displaystyle u(x,t)\simeq u_M(x,t)=u_0(x,t)+\sum _{m=1}^M{u}_m(x,t).}\hfill \end{array}$$

(45)

Furthermore, to construct the zeroth-order deformation equations we can define the nonlinear operators ${\mathcal{N}}_1\left[{\mathsf{\Psi }}_1(x,t;q)\right]$ and ${\mathcal{N}}_2\left[{\mathsf{\Psi }}_2(x,t;q)\right]$ as follows,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{N}}_1\left[{\mathsf{\Psi }}_1(x,t;q)\right]=\frac{\partial {\mathsf{\Psi }}_1(x,t;q)}{\partial t}+\frac{\partial \left[{\mathsf{\Psi }}_1(x,t;q){\mathsf{\Psi }}_2(x,t;q)\right]}{\partial x}\hfill \\ {\mathcal{N}}_2\left[{\mathsf{\Psi }}_2(x,t;q)\right]=\frac{\partial \left[{\mathsf{\Psi }}_1(x,t;q){\mathsf{\Psi }}_2(x,t;q)\right]}{\partial t}+\frac{\partial \left[{\mathsf{\Psi }}_1(x,t;q){\mathsf{\Psi }}_2{(x,t;q)}^2+c^2{\mathsf{\Psi }}_1(x,t;q)\right]}{\partial x}\hfill \\ +\frac{f}{2D}{\mathsf{\Psi }}_1(x,t;q){\mathsf{\Psi }}_2(x,t;q)\left|{\mathsf{\Psi }}_2(x,t;q)\right|+{\mathsf{\Psi }}_1(x,t;q)gsin\left(\theta \right)\hfill \end{array}\right.\end{array}$$

with the celerity pressure wave c defined as follows,

$$\begin{array}{ccc}\hfill & \hfill & c=\left[\frac{\varphi }{{\rho }_{h_0}}{\left(\frac{P_0}{{\mathsf{\Psi }}_1(x,t;q)}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{{\rho }_{g_0}}{\left(\frac{P_0}{{\mathsf{\Psi }}_1(x,t;q)}\right)}^{\frac{1}{n_2}}\right]\hfill \\ \hfill & \hfill & \times {\left[\frac{1}{{\mathsf{\Psi }}_1(x,t;q)}\left[\frac{\varphi }{n_1{\rho }_{h_0}}{\left(\frac{P_0}{{\mathsf{\Psi }}_1(x,t;q)}\right)}^{\frac{1}{n_1}}+\frac{1-\varphi }{n_2{\rho }_{g_0}}{\left(\frac{P_0}{{\mathsf{\Psi }}_1(x,t;q)}\right)}^{\frac{1}{n_2}}\right]\right]}^{-\frac{1}{2}}.\hfill \end{array}$$

(46)

3.3. Results and Discussion

For solving the Equations (5) and (6) by suing the homotopy analysis method according the Equations (25)–(36) we can have,

$$\begin{array}{ccc}\hfill & \hfill & {\mathcal{R}}_1^1=0,\hfill \\ \hfill & \hfill & {\mathcal{R}}_m^2=\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0},\hfill \\ \hfill & \hfill & P_1\left(x\right)=P_0,\hfill \\ \hfill & \hfill & u_1\left(x\right)=u_0+\hslash \left(\frac{f{u}_{0}x}{2d}+\frac{gsin\left(\theta \right)x}{u_0}\right),\hfill \\ \hfill & \hfill & {\mathcal{R}}_2^1=\frac{P_0\hslash }{u_0}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right),\hfill \\ \hfill & \hfill & {\mathcal{R}}_2^2=\hslash \left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)+1102500\frac{\hslash }{P_0{u}_0}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)\hfill \\ & \hfill & +\frac{f}{2d}\left(u_0+\hslash \left(\frac{f{u}_{0}x}{2d}+\frac{gsin\left(\theta \right)x}{u_0}\right)\right)+\left(\frac{1}{u_0}-\frac{\hslash x}{{u_0}^2}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)\right)gsin\left(\theta \right)\hfill \\ & \hfill & +\left(\frac{{\hslash }^2\left(2gsin\left(\theta \right)d+f{u_0}^2\right)x^2}{{2u_0}^{4}d}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)\right)gsin\left(\theta \right),\hfill \\ \hfill & \hfill & P_2\left(x\right)=P_0+\frac{{\hslash }^2{P}_{0}x}{u_0}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right),\hfill \\ & \hfill & u_2\left(x\right)=u_0+\hslash \left(\frac{f{u}_{0}x}{2d}+\frac{gsin\left(\theta \right)x}{u_0}\right)\hfill \\ & \hfill & +\hslash \left(\frac{{\hslash }^2\left(2gsin\left(\theta \right)d+f{u_0}^2\right)gsin\left(\theta \right)x^3}{6{u_0}^{4}d}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)\right)\hfill \\ & \hfill & +\frac{\hslash }{2}\left(\frac{f\hslash }{2d}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)-\frac{\hslash gsin\left(\theta \right)}{{u_0}^2}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)\right)x^2\hfill \\ & \hfill & +\hslash \left(\hslash \left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)x+1102500\frac{\hslash x}{P_0{u}_0}\left(\frac{f{u}_0}{2d}+\frac{gsin\left(\theta \right)}{u_0}\right)\right)\hfill \\ & \hfill & +\hslash \left(\frac{f{u}_{0}x}{2d}+\frac{gsin\left(\theta \right)x}{u_0}\right),\hfill \\ & \hfill & ⋮\hfill \end{array}$$

therefore, pressure $P\left(x\right)$ is as follows,

$$\begin{array}{ccc}\hfill & \hfill & P\left(x\right)\simeq P_0+\frac{{3\hslash }^2{P}_{0}xf}{4d}+\frac{{3\hslash }^2{P}_{0}xgsin\left(\theta \right)}{{2u_0}^2}+\frac{5P_0{x}^3{\hslash }^4{g}^2{\left(sin\left(\theta \right)\right)}^{2}f}{24{u_0}^{4}d}\hfill \\ & \hfill & +\frac{P_0{x}^3{\hslash }^4{g}^3{\left(sin\left(\theta \right)\right)}^3}{6{u_0}^6}+\frac{P_0{x}^3{\hslash }^{4}gsin\left(\theta \right)f^2}{12{u_0}^2{d}^2}+\frac{P_0{x}^3{\hslash }^4{f}^3}{96d^3}\hfill \\ & \hfill & -\frac{P_0{x}^2{\hslash }^3{g}^2{\left(sin\left(\theta \right)\right)}^2}{4{u_0}^4}-\frac{P_0{x}^2{\hslash }^{3}fgsin\left(\theta \right)}{8{u_0}^{2}d}+\frac{{\hslash }^3{P}_{0}xf}{4d}\hfill \\ & \hfill & +\frac{{\hslash }^3{P}_{0}xgsin\left(\theta \right)}{2{u_0}^2}+\frac{275625x{\hslash }^{3}f}{2d{u}_0}+275625\frac{x{\hslash }^{3}gsin\left(\theta \right)}{{u_0}^3}+\dots ,\hfill \end{array}$$

(47)

Equation (47) is a approximation solution for pressure P to the problem Equations (25)–(36) in terms of the convergence parameters ℏ and order $m=12$ with $\mathcal{H}\left(x\right)=1$. To find the valid region of ℏ, the ℏ-curves given by the 12th-order HAM approximation at different values of x are drawn in Figure 2; this figure shows the interval of ℏ in which the value of $P_{12}$ is constant at certain x, and M; we chose the horizontal line parallel to x-axis (ℏ) as a valid region which provides us with a simple way to adjust and control the convergence region.

Figure 2. ℏ-curve for HAM approximation solution $P_{12}\left(x\right)$ of the problem Equations (5) and (6) at different values of x.

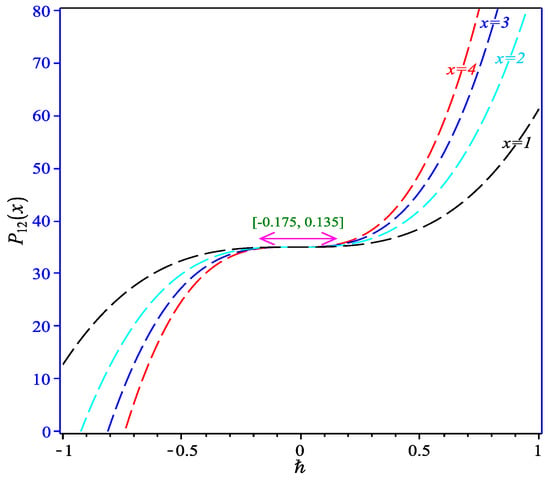
Figure 3 is showing the comparison between the homotopy analysis method with Subani et al., 2017 and Elaoud et al., 2010 methods. In this comparison the order of homotopy analysis method have been used as $M=5$ and $M=12$. The auxiliary parameter ℏ is chosen as $\hslash =-0.15$ from the convergence interval as showed in the Figure 2. As seen from this figure, with order $M=12$ the homotopy analysis method is comparable with Subani et al., 2017 and Elaoud et al., 2010 methods. In this problem the auxiliary parameter $\mathcal{H}(x,t)$ is chosen equal 1.

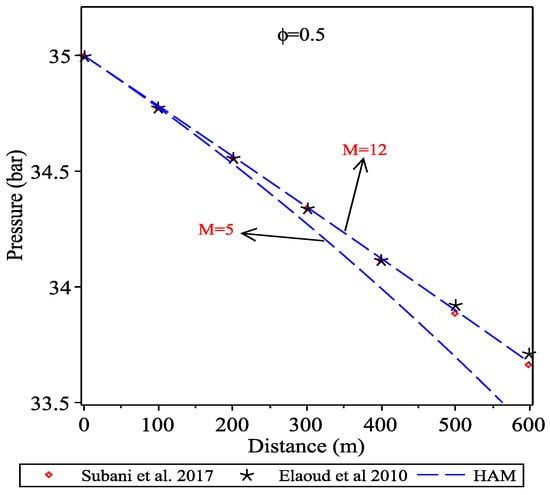
Figure 3. Comparison between homotopy analysis method of orders $M=5,12$ for $\hslash =-0.1$; with Subani et al., 2017 and Elaoud et al., 2010 methods.

Now we want to solve the Equations (1) and (2) with the homotopy analysis method (Equations (37)–(46)) using the following initial approximations,

$$\begin{array}{cc}\hfill & P_0(x,t)=\frac{x(x-L)(1+t)}{(x+t)(x-L+t)}{P}_0\left(x\right)+\frac{t(x-L)(1+x)}{(x+t)(x-L+x)}{P}_0\left(t\right)+\frac{xt(1+x-L)}{xt+x-L}{P}_L\left(t\right),\end{array}$$

(48)

$$\begin{array}{cc}& u_0(x,t)=\frac{x(x-L)(1+t)}{(x+t)(x-L+t)}{u}_0\left(x\right)+\frac{t(x-L)(1+x)}{(x+t)(x-L+x)}{u}_0\left(t\right)+\frac{xt(1+x-L)}{xt+x-L}{u}_L\left(t\right),\end{array}$$

(49)

we guessed the initial approximations Equations (48) and (49) using the initial and boundary conditions (for $x=0,L$ results will be as Equations (3) and (4)). Therefore, using the homotopy analysis method for solving the Equations (1) and (2) with the initial approximation Equations (48) and (49) can obtain the following results,

$$\begin{array}{ccc}\hfill P_0(x,t)& =& -\frac{x{a}_0}{{P_0}^{2}t}+\frac{x}{P_{0}t}+\frac{1}{P_0}-\frac{x{a}_0}{{P_0}^2}-\frac{x{a}_0}{{P_0}^{2}L}-\frac{x}{P_{0}L}-\frac{x}{P_0}-\frac{xt{a}_0}{{P_0}^{2}L}-\frac{xt{a}_0}{{P_0}^2{L}^2}\hfill \\ & & +\frac{xt{P}_L}{{P_0}^{2}L}-\frac{xt{P}_L}{{P_0}^2},\hfill \\ \hfill u_0(x,t)& =& -\frac{x{b}_0}{{u_0}^{2}t}+\frac{x}{u_{0}t}+\frac{1}{u_0}-\frac{x{b}_0}{{u_0}^2}-\frac{x{b}_0}{{u_0}^{2}L}-\frac{x}{u_{0}L}-\frac{x}{u_0}-\frac{xt{b}_0}{{u_0}^{2}L}-\frac{xt{b}_0}{{u_0}^2{L}^2}\hfill \\ & & +\frac{xt{u}_L}{{u_0}^{2}L}-\frac{xt{u}_L}{{u_0}^2},\hfill \\ \hfill {\mathcal{R}}_1^1& =& x{P}_L+u_0{a}_0+2u_0{P}_0+P_0{b}_0+2x{u}_L{a}_0-2x{u}_L{P}_0+2x{b}_0{P}_L-2x{u}_0{P}_L\hfill \\ & & -\frac{x{P}_L}{L}+\frac{x{a}_0}{L}+\frac{x{a}_0}{L^2}+\frac{P_0{b}_0}{L}+2x{P}_0{b}_1+2x{b}_0{a}_0+2x{u}_0{a}_1+2x{u}_0{a}_0\hfill \\ & & +2x{u}_0{P}_0+2x{P}_0{b}_0-2\frac{u_0{P}_0}{t}+\frac{u_0{a}_0}{t}+\frac{P_0{b}_0}{t}+\frac{x{P}_0}{t^2}-\frac{x{a}_0}{t^2}+\frac{u_0{a}_0}{L}\hfill \\ & & +2\frac{u_0{P}_0}{L}+4\frac{x{b}_0{a}_0}{tL}-2\frac{x{P}_0{b}_0}{tL}-2\frac{x{u}_0{a}_0}{tL}-8\frac{x{u}_0{P}_0}{tL}-4\frac{x{P}_0{b}_0}{t^2}\hfill \\ & & +6\frac{x{u}_0{P}_0}{t^2}+2\frac{x{b}_0{a}_0}{t^2}-4\frac{x{u}_0{a}_0}{t^2}+8\frac{x{b}_0{a}_0}{L}+8\frac{x{u}_0{P}_0}{L}+2\frac{x{P}_0{b}_1}{t}\hfill \\ & & +4\frac{x{b}_0{a}_0}{t}+2\frac{x{u}_0{a}_1}{t}-2\frac{x{u}_0{a}_0}{t}-8\frac{x{u}_0{P}_0}{t}-2\frac{x{P}_0{b}_0}{t}+2\frac{x{u}_L{P}_0}{L}\hfill \\ & & +2\frac{x{P}_0{b}_1}{L}+2\frac{x{u}_0{a}_1}{L}+10\frac{x{u}_0{P}_0}{L^2}+6\frac{x{b}_0{a}_0}{L^2}-2\frac{x{b}_0{P}_L}{L}+2\frac{x{u}_0{P}_L}{L}\hfill \\ & & -2\frac{x{u}_L{a}_0}{L},\hfill \\ \\ \hfill {\mathcal{R}}_2^1& =& 1102501-1102500x+u_0+\frac{u_0}{L}+2\frac{x{u}_0{b}_0{a}_0}{t^2{P}_0}+8\frac{x{u}_0{b}_0{a}_0}{P_{0}L}-2\frac{x{u}_0{a}_0}{P_{0}tL}\hfill \\ & & -2\frac{x{u}_0{a_0}^2}{{P_0}^{2}tL}+2\frac{x{b}_0{a}_0}{P_{0}tL}-2\frac{x{u_0}^2{a}_0}{P_{0}tL}-2\frac{x{u_0}^2{a_0}^2}{{P_0}^{2}tL}+\frac{xf{u}_0{b}_0}{tD}+4\frac{x{u}_0{b}_0{a}_0}{P_{0}t}\hfill \\ & & +2\frac{x{u}_0{a}_0{P}_L}{{P_0}^{2}L}+2\frac{x{u_0}^2{a}_0{P}_L}{{P_0}^{2}L}+6\frac{x{u}_0{b}_0{a}_0}{P_0{L}^2}-2\frac{x{u}_0{b}_0{P}_L}{P_{0}L}-2\frac{x{u}_0{u}_L{a}_0}{P_{0}L}\hfill \\ & & +\frac{xf{u}_0{b}_0}{DL}+{u_0}^2+1102500L^{-1}-1102500t^{-1}+gsin\left(\theta \right)-2\frac{x{u_0}^2{a}_0{P}_L}{{P_0}^2}\hfill \\ & & +2\frac{x{u}_0{b}_0{P}_L}{P_0}-3\frac{x{u}_0{a}_0}{P_{0}L}-4\frac{x{u}_0{a_0}^2}{{P_0}^{2}L}+4\frac{x{b}_0{a}_0}{P_{0}L}-2\frac{x{u_0}^2{a}_0}{P_{0}L}-4\frac{x{u_0}^2{a_0}^2}{{P_0}^{2}L}\hfill \\ & & +\frac{xf{u}_0{b}_0}{D}-2\frac{x{u}_0{a}_0}{P_{0}t}-2\frac{x{u}_0{a_0}^2}{{P_0}^{2}t}+2\frac{x{u_0}^2{a}_1}{P_{0}t}-2205000\frac{x{a}_0}{P_{0}tL}\hfill \\ & & -2205000\frac{x{a_0}^2}{{P_0}^{2}tL}-2\frac{x{u_0}^2{a_0}^2}{{P_0}^{2}t}+2\frac{x{b}_0{a}_0}{P_{0}t}-2\frac{x{u_0}^2{a}_0}{P_{0}t}+2\frac{x{u}_0{a}_1}{P_{0}t}\hfill \\ & & -\frac{f{u_0}^{2}x}{tD}+2\frac{x{u}_0{u}_L{a}_0}{P_0}+2205000\frac{x{a}_0{P}_L}{{P_0}^{2}L}+\frac{f{u_0}^{2}x}{DL}+2\frac{x{u}_0{a}_1}{P_{0}L}-3\frac{x{u}_0{a_0}^2}{{P_0}^2{L}^2}\hfill \\ & & -2\frac{x{u}_0{a}_0{P}_L}{{P_0}^2}+3\frac{x{b}_0{a}_0}{P_0{L}^2}-\frac{x{b}_0{P}_L}{P_{0}L}-\frac{x{u}_0{P}_L}{P_{0}L}-\frac{x{u}_L{a}_0}{P_{0}L}+2\frac{x{u_0}^2{a}_1}{P_{0}L}\hfill \\ & & -3\frac{x{u_0}^2{a_0}^2}{{P_0}^2{L}^2}+x{b}_0+3307500\frac{x}{L^2}+x{u_0}^2-\frac{{u_0}^2}{t}+1102500\frac{a_0}{P_0}+4\frac{x{u}_0{b}_0{a}_0}{P_{0}tL}\hfill \\ & & +4\frac{x{u}_0}{L^2}+5\frac{x{u_0}^2}{L^2}-2x{u}_0{u}_L+2x{u}_0{b}_0+2\frac{x{b}_0}{L}+\frac{x{b}_0}{L^2}+2205000\frac{x{P}_L}{P_0}\hfill \\ & & +\frac{u_0{a}_0}{P_0}+3\frac{x{u_0}^2}{t^2}+3\frac{x{u}_0}{t^2}+\frac{{u_0}^2}{L}+1102500\frac{a_0}{P_{0}L}+2\frac{x{u}_0}{L}+2205000\frac{x{a}_1}{P_0}\hfill \\ & & -2205000\frac{x{a}_0}{P_0}-1102500\frac{x{a_0}^2}{{P_0}^2}+4\frac{x{u_0}^2}{L}-2\frac{x{u}_0}{t}-4\frac{x{u_0}^2}{t}+1102500\frac{a_0}{P_{0}t}\hfill \\ & & +\frac{{u_0}^2{a}_0}{P_0}-2\frac{x{b}_0}{t^2}+1102500\frac{x}{t^2}+\frac{1}{2}\frac{f{u_0}^2}{D}-\frac{u_0}{t}-\frac{x{u}_0{a}_0}{t^2{P}_0}-\frac{x{u}_0{a_0}^2}{t^2{P_0}^2}+\frac{x{b}_0{a}_0}{t^2{P}_0}\hfill \\ & & -2\frac{x{u_0}^2{a}_0}{t^2{P}_0}-\frac{x{u_0}^2{a_0}^2}{t^2{P_0}^2}+2\frac{x{u}_0{b}_0{a}_0}{P_0}+\frac{x{b}_0{P}_L}{P_0}+\frac{x{u}_0{P}_L}{P_0}+\frac{x{u}_L{a}_0}{P_0}\hfill \\ & & +2205000\frac{x{a}_1}{P_{0}L}-3307500\frac{x{a_0}^2}{{P_0}^2{L}^2}-2205000\frac{x{a}_0{P}_L}{{P_0}^2}-2205000\frac{x{P}_L}{P_{0}L}\hfill \\ & & +2\frac{x{u}_0{u}_L}{L}+2\frac{x{u}_0{b}_0}{L}-2\frac{x{u}_0}{tL}+2205000\frac{x{a}_1}{P_{0}t}-2205000\frac{x{a}_0}{P_{0}t}\hfill \\ & & -2205000\frac{x{a_0}^2}{{P_0}^{2}t}-4\frac{x{u_0}^2}{tL}+\frac{{u_0}^2{a}_0}{P_{0}t}-2\frac{x{u}_0{b}_0}{t^2}-1102500\frac{x{a_0}^2}{t^2{P_0}^2}+\frac{u_0{a}_0}{P_{0}L}\hfill \\ & & +\frac{{u_0}^2{a}_0}{P_{0}L}-\frac{x{u}_0{a}_0}{P_0}-\frac{x{u}_0{a_0}^2}{{P_0}^2}+2\frac{x{u_0}^2{a}_1}{P_0}-4410000\frac{x{a}_0}{P_{0}L}-4410000\frac{x{a_0}^2}{{P_0}^{2}L}\hfill \\ & & -\frac{x{u_0}^2{a_0}^2}{{P_0}^2}+\frac{x{b}_0{a}_0}{P_0}+2\frac{x{u}_0{a}_1}{P_0}+\frac{u_0{a}_0}{P_{0}t}+\frac{f{u_0}^{2}x}{D},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill P_1(x,t)& =& \frac{xt{P}_L}{xt-L+x}-\frac{x^{2}Lt{a}_1}{\left(x+t\right)\left(x-L+t\right)}-\frac{xLt{a}_0}{\left(x+t\right)\left(x-L+t\right)}\hfill \\ & & -\frac{P_{0}tLx}{\left(x+t\right)\left(2x-L\right)}+2\frac{\hslash x^2{b}_0{a}_0}{tL}-\frac{\hslash x^2{P}_0{b}_0}{tL}-\frac{\hslash x^2{u}_0{a}_0}{tL}\hfill \\ & & -4\frac{\hslash x^2{u}_0{P}_0}{tL}+\frac{1}{2}\hslash x^2{P}_L+\frac{1}{2}\frac{\hslash x^2{P}_0}{t^2}-\frac{1}{2}\frac{\hslash x^2{a}_0}{t^2}+\hslash x^2{u}_L{a}_0\hfill \\ & & -\hslash x^2{u}_L{P}_0+\hslash x^2{P}_0{b}_1+\hslash x^2{b}_0{P}_L-\hslash x^2{u}_0{P}_L+\hslash x^2{b}_0{a}_0\hfill \\ & & +\hslash x^2{u}_0{a}_1+\hslash x^2{u}_0{a}_0+\hslash x^2{u}_0{P}_0+\hslash x^2{P}_0{b}_0-\frac{1}{2}\frac{\hslash x^2{P}_L}{L}\hfill \\ & & +\frac{1}{2}\frac{\hslash x^2{a}_0}{L}+\frac{1}{2}\frac{\hslash x^2{a}_0}{L^2}+\hslash x{u}_0{a}_0+2\hslash x{u}_0{P}_0+\hslash x{P}_0{b}_0\hfill \\ & & +\frac{x^3{a}_1}{\left(x+t\right)\left(x-L+t\right)}+\frac{x^2{a}_0}{\left(x+t\right)\left(x-L+t\right)}+\frac{x^{2}t{P}_L}{xt-L+x}\hfill \\ & & +\frac{\hslash x^2{u}_0{a}_1}{L}+5\frac{\hslash x^2{u}_0{P}_0}{L^2}+3\frac{\hslash x^2{b}_0{a}_0}{L^2}-\frac{\hslash x^2{b}_0{P}_L}{L}+\frac{\hslash x^2{u}_0{P}_L}{L}\hfill \\ & & -\frac{\hslash x^2{u}_L{a}_0}{L}+4\frac{\hslash x^2{u}_0{P}_0}{L}+2\frac{\hslash x^2{b}_0{a}_0}{t}+\frac{\hslash x^2{u}_0{a}_1}{t}+\frac{\hslash x^2{P}_0{b}_1}{t}\hfill \\ & & -2\frac{\hslash x^2{P}_0{b}_0}{t^2}+\frac{\hslash x^2{b}_0{a}_0}{t^2}+3\frac{\hslash x^2{u}_0{P}_0}{t^2}-2\frac{\hslash x^2{u}_0{a}_0}{t^2}+\frac{\hslash x^2{u}_L{P}_0}{L}\hfill \\ & & +\frac{\hslash x^2{P}_0{b}_1}{L}+4\frac{\hslash x^2{b}_0{a}_0}{L}-4\frac{\hslash x^2{u}_0{P}_0}{t}+\frac{\hslash x{P}_0{b}_0}{L}+\frac{\hslash x{u}_0{a}_0}{L}\hfill \\ & & +2\frac{\hslash x{u}_0{P}_0}{L}+\frac{\hslash x{u}_0{a}_0}{t}-2\frac{\hslash x{u}_0{P}_0}{t}+\frac{\hslash x{P}_0{b}_0}{t}+\frac{x^{3}t{a}_1}{\left(x+t\right)\left(x-L+t\right)}\hfill \\ & & -\frac{x^{2}L{a}_1}{\left(x+t\right)\left(x-L+t\right)}+\frac{x^{2}t{a}_0}{\left(x+t\right)\left(x-L+t\right)}-\frac{x{a}_{0}L}{\left(x+t\right)\left(x-L+t\right)}\hfill \\ & & +\frac{P_{0}t{x}^2}{\left(x+t\right)\left(2x-L\right)}-\frac{P_{0}tL}{\left(x+t\right)\left(2x-L\right)}+\frac{P_{0}tx}{\left(x+t\right)\left(2x-L\right)}\hfill \\ & & -\frac{xt{P}_{L}L}{xt-L+x}-\frac{\hslash x^2{u}_0{a}_0}{t}-\frac{\hslash x^2{P}_0{b}_0}{t},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill u_1(x,t)& =& \frac{x^{3}t{b}_1}{\left(x+t\right)\left(x-L+t\right)}-\frac{x^{2}L{b}_1}{\left(x+t\right)\left(x-L+t\right)}+\frac{x^{2}t{b}_0}{\left(x+t\right)\left(x-L+t\right)}\hfill \\ & & -\frac{xL{b}_0}{\left(x+t\right)\left(x-L+t\right)}+\frac{u_{0}t{x}^2}{\left(x+t\right)\left(2x-L\right)}-\frac{u_{0}tL}{\left(x+t\right)\left(2x-L\right)}\hfill \\ & & +\frac{u_{0}tx}{\left(x+t\right)\left(2x-L\right)}+\frac{xt{u}_L}{xt-L+x}-\frac{xt{u}_{L}L}{xt-L+x}+1102500\frac{\hslash x^2{a}_1}{P_{0}L}\hfill \\ & & -1653750\frac{\hslash x^2{a_0}^2}{{P_0}^2{L}^2}-1102500\frac{\hslash x^2{a}_0{P}_L}{{P_0}^2}-1102500\frac{\hslash x^2{P}_L}{P_{0}L}\hfill \\ & & -551250\frac{\hslash x^2{a_0}^2}{t^2{P_0}^2}-\frac{1}{2}\frac{\hslash x^2{u}_0{a_0}^2}{{P_0}^2}+\frac{\hslash x^2{u_0}^2{a}_1}{P_0}-2205000\frac{\hslash x^2{a_0}^2}{{P_0}^{2}L}\hfill \\ & & -\frac{\hslash x^2{u}_0}{tL}-2\frac{\hslash x^2{u_0}^2}{tL}+1102500\frac{\hslash x^2{a}_1}{P_{0}t}-1102500\frac{\hslash x^2{a_0}^2}{{P_0}^{2}t}\hfill \\ & & +\frac{1}{2}\frac{\hslash x^2{b}_0{P}_L}{P_0}+\frac{1}{2}\frac{\hslash x^2{u}_0{P}_L}{P_0}-\frac{1}{2}\frac{\hslash x^2{u_0}^2{a_0}^2}{{P_0}^2}-\frac{\hslash x^2{u}_0{b}_0}{t^2}\hfill \\ & & +\frac{\hslash x^2{u}_0{a}_1}{P_0}+\frac{1}{2}\frac{\hslash x^2{b}_0{a}_0}{P_0}+\frac{\hslash x^2{u}_0{u}_L}{L}+\frac{\hslash x^2{u}_0{b}_0}{L}-\frac{1}{2}\frac{\hslash x^2{u}_0{a}_0}{P_0}\hfill \\ & & -2205000\frac{\hslash x^2{a}_0}{P_{0}L}-1102500\frac{\hslash x^2{a}_0}{P_{0}t}+\frac{1}{2}\frac{\hslash x^{2}f{u_0}^2}{D}+\frac{\hslash x{u_0}^2{a}_0}{P_0}\hfill \\ & & +\frac{1}{2}\frac{\hslash x^2{u}_L{a}_0}{P_0}+1102500\frac{\hslash x{a}_0}{P_{0}t}+\frac{\hslash x{u}_0{a}_0}{P_0}+1102500\frac{\hslash x{a}_0}{P_{0}L}\hfill \\ & & +\frac{1}{2}\frac{\hslash f{u_0}^{2}x}{D}-\frac{\hslash x^2{u_0}^2{a}_0{P}_L}{{P_0}^2}+\frac{\hslash x^2{u}_0{b}_0{P}_L}{P_0}+\frac{\hslash x^2{u}_0{u}_L{a}_0}{P_0}\hfill \\ & & +1102500\frac{\hslash x^2{a}_0{P}_L}{{P_0}^{2}L}+\frac{1}{2}\frac{\hslash x^{2}f{u_0}^2}{DL}-2\frac{\hslash x^2{u_0}^2{a_0}^2}{{P_0}^{2}L}+\frac{1}{2}\frac{\hslash x^{2}f{u}_0{b}_0}{D}\hfill \\ & & -\frac{\hslash x^2{u}_0{a_0}^2}{{P_0}^{2}t}+\frac{\hslash x^2{u_0}^2{a}_1}{P_{0}t}-1102500\frac{\hslash x^2{a_0}^2}{{P_0}^{2}tL}-\frac{\hslash x^2{u_0}^2{a_0}^2}{{P_0}^{2}t}\hfill \\ & & +\frac{\hslash x^2{u}_0{a}_1}{P_{0}t}+\frac{\hslash x^2{b}_0{a}_0}{P_{0}t}-1102500\frac{\hslash x^2{a}_0}{P_{0}tL}-\frac{1}{2}\frac{\hslash x^{2}f{u_0}^2}{tD}\hfill \\ & & +\frac{\hslash x^2{u}_0{a}_1}{P_{0}L}-\frac{3}{2}\frac{\hslash }{}{x}^2{u}_0{a_0}^2{P_0}^2{L}^2-\frac{\hslash x^2{u}_0{a}_0{P}_L}{{P_0}^2}+\frac{3}{2}\frac{\hslash x^2{b}_0{a}_0}{P_0{L}^2}\hfill \\ & & -\frac{1}{2}\frac{\hslash x^2{b}_0{P}_L}{P_{0}L}+\frac{\hslash x^2{u}_0{b}_0{a}_0}{P_0}-\frac{1}{2}\frac{\hslash x^2{u}_0{a}_0}{t^2{P}_0}-\frac{1}{2}\frac{\hslash x^2{u}_0{a_0}^2}{t^2{P_0}^2}\hfill \\ & & +\frac{1}{2}\frac{\hslash x^2{b}_0{a}_0}{t^2{P}_0}-\frac{\hslash x^2{u_0}^2{a}_0}{t^2{P}_0}-\frac{1}{2}\frac{\hslash x^2{u_0}^2{a_0}^2}{t^2{P_0}^2}-2\frac{\hslash x^2{u}_0{a_0}^2}{{P_0}^{2}L}\hfill \\ & & +2\frac{\hslash x^2{b}_0{a}_0}{P_{0}L}-\frac{\hslash x^2{u_0}^2{a}_0}{P_{0}t}-\frac{3}{2}\frac{\hslash x^2{u}_0{a}_0}{P_{0}L}-\frac{\hslash x^2{u_0}^2{a}_0}{P_{0}L}-\frac{\hslash x^2{u}_0{a}_0}{P_{0}t}\hfill \\ & & +\frac{\hslash x{u}_0{a}_0}{P_{0}L}+\frac{\hslash x{u_0}^2{a}_0}{P_{0}L}+\frac{\hslash x{u}_0{a}_0}{P_{0}t}+\frac{\hslash x{u_0}^2{a}_0}{P_{0}t}-\frac{x^{2}Lt{b}_1}{\left(x+t\right)\left(x-L+t\right)}\hfill \\ & & -\frac{xLt{b}_0}{\left(x+t\right)\left(x-L+t\right)}-\frac{u_{0}tLx}{\left(x+t\right)\left(2x-L\right)}-\frac{1}{2}\frac{\hslash x^2{u}_0{P}_L}{P_{0}L}-\frac{1}{2}\frac{\hslash x^2{u}_L{a}_0}{P_{0}L}\hfill \\ & & +\frac{\hslash x^2{u_0}^2{a}_1}{P_{0}L}-\frac{3}{2}\frac{\hslash x^2{u_0}^2{a_0}^2}{{P_0}^2{L}^2}+3\frac{\hslash x^2{u}_0{b}_0{a}_0}{P_0{L}^2}-\frac{\hslash x^2{u}_0{b}_0{P}_L}{P_{0}L}-\frac{\hslash x^2{u}_0{u}_L{a}_0}{P_{0}L}\hfill \\ \\ & & +\frac{1}{2}\frac{\hslash x^{2}f{u}_0{b}_0}{DL}+1102500\frac{\hslash x}{L}+\hslash u_{0}x-1102500\frac{\hslash x}{t}+\hslash x{u_0}^2+\frac{1}{2}\hslash x^2{b}_0\hfill \\ & & +\frac{1}{2}\hslash x^2{u_0}^2+1653750\frac{\hslash x^2}{L^2}+551250\frac{\hslash x^2}{t^2}-\frac{\hslash x{u_0}^2}{t}+\hslash gsin\left(\theta \right)x\hfill \\ & & +\frac{\hslash x^2{b}_0}{L}+\frac{\hslash x^2{u}_0}{L}+\frac{5}{2}\frac{\hslash x^2{u_0}^2}{L^2}-\hslash x^2{u}_0{u}_L+\frac{1}{2}\frac{\hslash x^2{b}_0}{L^2}+2\frac{\hslash x^2{u}_0}{L^2}\hfill \\ & & +\hslash x^2{u}_0{b}_0-2\frac{\hslash x^2{u_0}^2}{t}-1102500\frac{\hslash x^2{a}_0}{P_0}+2\frac{\hslash x^2{u_0}^2}{L}-\frac{\hslash x^2{u}_0}{t}\hfill \\ & & +1102500\frac{\hslash x^2{P}_L}{P_0}+1102500\frac{\hslash x^2{a}_1}{P_0}-551250\frac{\hslash x^2{a_0}^2}{{P_0}^2}-\frac{\hslash x^2{b}_0}{t^2}\hfill \\ & & +\frac{3}{2}\frac{\hslash x^2{u}_0}{t^2}+\frac{3}{2}\frac{\hslash x^2{u_0}^2}{t^2}+\frac{\hslash u_{0}x}{L}+1102500\frac{\hslash x{a}_0}{P_0}+\frac{\hslash x{u_0}^2}{L}-\frac{\hslash u_{0}x}{t}\hfill \\ & & +\frac{x^3{b}_1}{\left(x+t\right)\left(x-L+t\right)}+\frac{x^2{b}_0}{\left(x+t\right)\left(x-L+t\right)}+\frac{x^{2}t{u}_L}{xt-L+x}+\frac{\hslash x^2{u}_0{b}_0{a}_0}{t^2{P}_0}\hfill \\ & & +4\frac{\hslash x^2{u}_0{b}_0{a}_0}{P_{0}L}-\frac{\hslash x^2{u_0}^2{a_0}^2}{{P_0}^{2}tL}+\frac{1}{2}\frac{\hslash x^{2}f{u}_0{b}_0}{tD}+2\frac{\hslash x^2{u}_0{b}_0{a}_0}{P_{0}t}-\frac{\hslash x^2{u}_0{a_0}^2}{{P_0}^{2}tL}\hfill \\ & & +\frac{\hslash x^2{b}_0{a}_0}{P_{0}tL}-\frac{\hslash x^2{u}_0{a}_0}{P_{0}tL}-\frac{\hslash x^2{u_0}^2{a}_0}{P_{0}tL}+\frac{\hslash x^2{u}_0{a}_0{P}_L}{{P_0}^{2}L}+\frac{\hslash x^2{u_0}^2{a}_0{P}_L}{{P_0}^{2}L}\hfill \\ & & +2\frac{\hslash x^2{u}_0{b}_0{a}_0}{P_{0}tL}-551250\hslash x^2+1102501\hslash x,\hfill \end{array}$$

therefore, pressure $P(x,t)$ is as follows,

$$\begin{array}{ccc}\hfill & \hfill & P(x,t)\simeq \frac{2tx{P}_L}{tx-L+x}-\frac{2x^{2}Lt{a}_1}{\left(x+t\right)\left(x-L+t\right)}-\frac{2xLt{a}_0}{\left(x+t\right)\left(x-L+t\right)}\hfill \\ & \hfill & -\frac{2t{P}_{0}Lx}{\left(x+t\right)\left(2x-L\right)}+\frac{2\hslash x^2{b}_0{a}_0}{tL}-\frac{\hslash x^2{P}_0{b}_0}{tL}-\frac{\hslash x^2{u}_0{a}_0}{tL}-\frac{4\hslash x^2{u}_0{P}_0}{tL}\hfill \\ & \hfill & +\frac{1}{2}\hslash x^2{P}_L+\frac{1}{2}\frac{\hslash x^2{P}_0}{t^2}-\frac{1}{2}\frac{\hslash x^2{a}_0}{t^2}+\hslash x^2{u}_L{a}_0-\hslash x^2{u}_L{P}_0+\hslash x^2{P}_0{b}_1\hfill \\ & \hfill & +\hslash x^2{b}_0{P}_L-\hslash x^2{u}_0{P}_L+\hslash x^2{b}_0{a}_0+\hslash x^2{u}_0{a}_1+\hslash x^2{u}_0{a}_0+\hslash x^2{u}_0{P}_0\hfill \\ & \hfill & +\hslash x^2{P}_0{b}_0-\frac{1}{2}\frac{\hslash x^2{P}_L}{L}+\frac{1}{2}\frac{\hslash x^2{a}_0}{L}+\frac{1}{2}\frac{\hslash x^2{a}_0}{L^2}+\hslash x{u}_0{a}_0+2\hslash x{u}_0{P}_0\hfill \\ & \hfill & +\hslash x{P}_0{b}_0+\frac{2x^3{a}_1}{\left(x+t\right)\left(x-L+t\right)}+\frac{2x^2{a}_0}{\left(x+t\right)\left(x-L+t\right)}+\frac{2x^{2}t{P}_L}{tx-L+x}\hfill \\ & \hfill & +\frac{\hslash x^2{u}_0{a}_1}{L}+\frac{5\hslash x^2{u}_0{P}_0}{L^2}+\frac{3\hslash x^2{b}_0{a}_0}{L^2}-\frac{\hslash x^2{b}_0{P}_L}{L}+\frac{\hslash x^2{u}_0{P}_L}{L}-\frac{\hslash x^2{u}_L{a}_0}{L}\hfill \\ & \hfill & +\frac{4\hslash x^2{u}_0{P}_0}{L}+\frac{2\hslash x^2{b}_0{a}_0}{t}+\frac{\hslash x^2{u}_0{a}_1}{t}+\frac{\hslash x^2{P}_0{b}_1}{t}-\frac{2\hslash x^2{P}_0{b}_0}{t^2}+\frac{\hslash x^2{b}_0{a}_0}{t^2}\hfill \\ \\ & \hfill & +\frac{3\hslash x^2{u}_0{P}_0}{t^2}-\frac{2\hslash x^2{u}_0{a}_0}{t^2}+\frac{\hslash x^2{u}_L{P}_0}{L}+\frac{\hslash x^2{P}_0{b}_1}{L}+\frac{4\hslash x^2{b}_0{a}_0}{L}-\frac{4\hslash x^2{u}_0{P}_0}{t}\hfill \\ & \hfill & +\frac{\hslash x{P}_0{b}_0}{L}+\frac{\hslash x{u}_0{a}_0}{L}+\frac{2\hslash x{u}_0{P}_0}{L}+\frac{\hslash x{u}_0{a}_0}{t}-\frac{2\hslash x{u}_0{P}_0}{t}+\frac{\hslash x{P}_0{b}_0}{t}\hfill \\ & \hfill & +\frac{2x^{3}t{a}_1}{\left(x+t\right)\left(x-L+t\right)}-\frac{2x^{2}L{a}_1}{\left(x+t\right)\left(x-L+t\right)}+\frac{2x^{2}t{a}_0}{\left(x+t\right)\left(x-L+t\right)}\hfill \\ & \hfill & -\frac{2x{a}_{0}L}{\left(x+t\right)\left(x-L+t\right)}+\frac{2t{P}_0{x}^2}{\left(x+t\right)\left(2x-L\right)}-\frac{2t{P}_{0}L}{\left(x+t\right)\left(2x-L\right)}\hfill \\ & \hfill & +\frac{2t{P}_{0}x}{\left(x+t\right)\left(2x-L\right)}-\frac{2tx{P}_{L}L}{tx-L+x}-\frac{\hslash x^2{u}_0{a}_0}{t}-\frac{\hslash x^2{P}_0{b}_0}{t}+\dots ,\hfill \end{array}$$

(50)

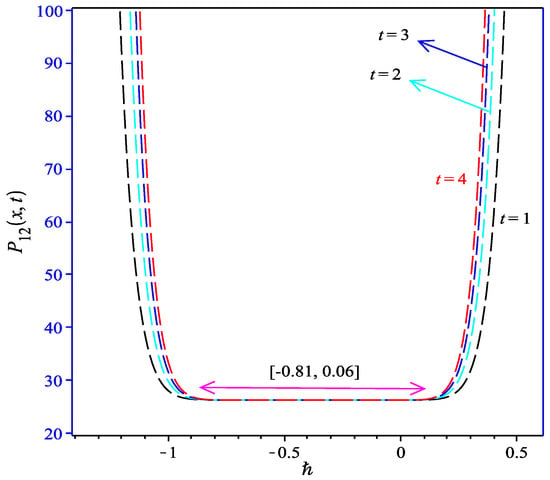
Equation (50) is a approximation solution for pressure $P(x,t)$ to the problem Equations (1) and (2) in terms of the convergence parameters ℏ with $\mathcal{H}\left(x\right)=1$. To find the valid region of ℏ, the ℏ-curves given by the 12th-order HAM approximation at different values of t and $x=0$ are drawn in Figure 4; this figure shows the interval of ℏ in which the value of $P_{12}(0,t)$ is constant at certain t, and M; we chose the horizontal line parallel to t-axis (ℏ) as a valid region which provides us with a simple way to adjust and control the convergence region.

Figure 4. ℏ-curve for HAM approximation solution $P_{12}(x,t)$ of the problem Equations (1) and (2) at different values of t and $x=0$.

3.4. Leak Detection Using Homotopy Analysis Method

Because of a small orifice between the high-pressure pipeline and the environment, the orifice of leak can be simulated leaning on the flow rate. The discharged flow from the orifice can be computed by the following Equation [7],

$$\begin{array}{c}\hfill Q_l=\frac{{\rho }_l{C}_d{A}_l\sqrt{2P_l/{\rho }_l}}{X_L},\end{array}$$

(51)

where $A_l$ is the leak orifice area with radius $r_l$, $P_l$ is the pressure of gas mixture at the leak position and ${\rho }_l$ is the density of gas mixture at the leak position respectively, $C_d$ is a discharge coefficient and $X_L$ is the distance of leak from the reservoir.

Analyzing transient pressure wave for hydrogen/natural gas mixtures is based on transmission and reflection properties of pressure wave effected by a downstream valves sudden closure. When the initial pressure wave reaches the leak, it will produce a reflection as it arrives back at the downstream end section. Then, the difference in time between the initial transient wave and the reflected wave is measured and the leakage position in the pipeline is computed by,

$$\begin{array}{c}\hfill X_L=L-\frac{\Delta t_l{c}_{\Delta t_l}}{2},\end{array}$$

(52)

where $X_L$ is defined as the distance between the leak and upstream end section, $\Delta t_l$ is the difference of time between the initial transient wave and reflected wave and $c_{\Delta t_l}$ is defined as the transient celerity wave at time.

3.5. Results and Discussion

Figure 5 presents the transient pressure of hydrogen natural gas mixture for isothermal flow when leakage occurs at $X_L=L/3$ in horizontal pipeline. The homotopy analysis method of order $M=12$ with $\hslash =-0.5$ has been used. This figure shows the comparison between homotopy analysis method from order 12 and Subani et al. method [7] when $\varphi =0.25$ and $\varphi =0.5$.

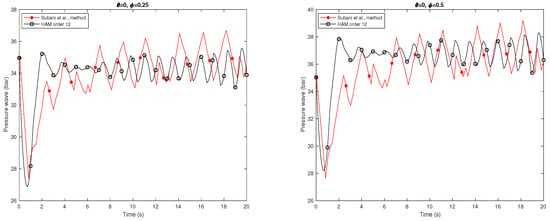
Figure 5. Transient pressure of hydrogen natural gas mixture for isothermal flow when leakage occurs at $X_L=L/3$ in horizontal pipeline when $\varphi =0.25$ and $\varphi =0.5$.

Figure 6 shows the transient pressure of hydrogen natural gas mixture ($\varphi =0.5$) for isothermal flow when leakage occurs at $X_L=L/3$ in an inclined pipeline with $\theta =15$. Black line is homotopy analysis method from order 12 with $\hslash =-0.5$ and red line is Subani et al. method. As indicated in Figure 5 and Figure 6, the leak point are estimated at $t_s=0.81$ and at $t_s=0.808$ for Subani et al. method and HAM respectively.

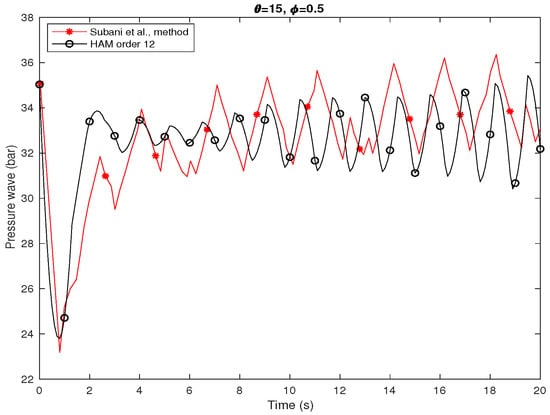
Figure 6. Transient pressure of hydrogen natural gas mixture for isothermal flow when leakage occurs at $X_L=L/3$ in an inclined pipeline when $\theta ={15}^{\circ }$ and $\varphi =0.5$.

The transient pressure of mixture of natural gas and hydrogen with a mass ratio of $\varphi =0.5$ is shown in Figure 7 in case of isothermal flow and leak location at $X_L=L/3$ with diverse angles. The homotopy analysis method from order 12 and $\hslash =-0.5$ has been used. Red line is for $\theta =0$ and black line is for $\theta =15$.

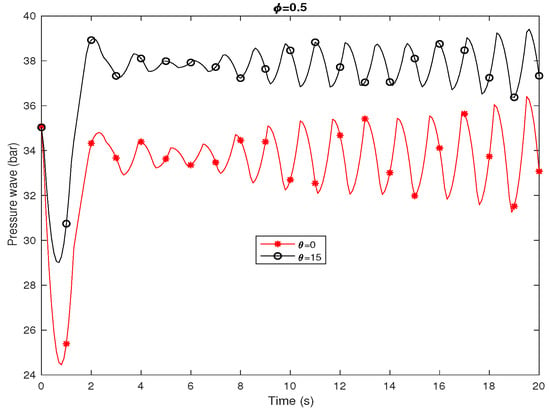
Figure 7. Transient pressure of hydrogen natural gas mixture with $\varphi =0.5$ for isothermal flow when leakage occurs at $X_L=L/3$ with different angles $\theta$. HAM with order 12 and $\hslash =-0.5$.

The celerity wave distribution is presented in Figure 8 as a function of time. In this case, the valve of the horizontal pipeline containing different mass ratios of a mixture of gas and hydrogen is abruptly closed when the leakage is at $X_L=L/3$. The values of celerity wave of the leak point for various mass rations are 819.20 ms${}^{-1}$, 964.60 ms${}^{-1}$ and 1086.60 ms${}^{-1}$ for $\varphi =0.25,0.5$ and $0.75$, respectively.

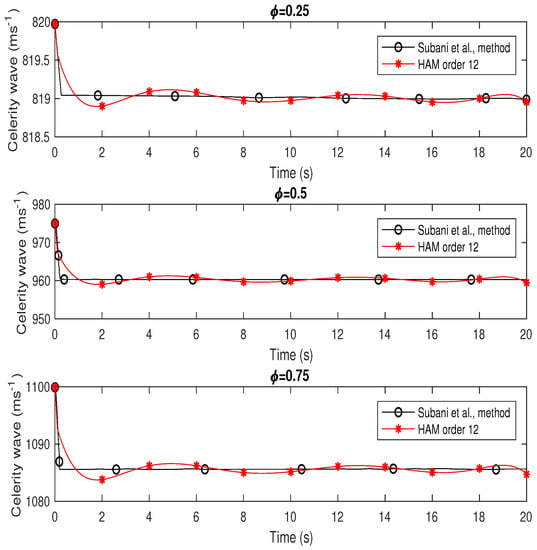
Figure 8. Celerity wave of hydrogen natural gas mixture for isothermal flow when leakage occurs at $X_L=L/3$ in horizontal pipeline with different mass ratio $\varphi$.

As shown in Figure 6 and Figure 7, the occurrence of the leakage is possible when $\Delta t_l$ is equal to $0.808$ s. Equation (53) can be used to calculate the leak location of the mixture of natural gas and hydrogen in case of an isothermal flow in a horizontal pipeline as follows:

$$\begin{array}{c}\hfill X_L=600-\frac{0.808\times 964.6}{2}\simeq 210.3.\end{array}$$

(53)

As seen earlier, there are various mass ratios of the mixture and various angles of the pipeline each with a specific leak location at $X_L=L/3$, the values of which are presented in Table 3. It can be inferred that the leak location is not a function of pipe angle, it is rather a function of the mass ratio of the natural gas and hydrogen mixture. Therefore, mass ratio is of utmost importance here.

Table 3. Leak location for the hydrogen-natural gas mixture for isothermal flow at leakage $X_L=L/3$.

Gas Mixture $\left(\mathit{\varphi }\right)$	Pipeline’s Angle $\left(\mathit{\theta }\right)$	Leak Location (m)
		Subani et al., Method	HAM
0	$0^{\circ }$	439.4	439.8
	${15}^{\circ }$	439.4	439.8
0.25	$0^{\circ }$	268.3	269.04
	${15}^{\circ }$	268.3	269.04
0.5	$0^{\circ }$	211.1	210.3
	${15}^{\circ }$	211.1	210.3
0.75	$0^{\circ }$	160.6	161.01
	${15}^{\circ }$	160.6	161.01
1	$0^{\circ }$	95.8	96.2
	${15}^{\circ }$	95.8	96.2

The real location of leak is 200 m, when the leak location is at $X_L=L/3$. The leak location calculations by Subani et al. and HAM turned out to be $211.10$ m and $210.30$ m, respectively. It is a mixture of natural gas and hydrogen with a mass ratio of $0.5$. When the mass ration is increased to $0.75$, the leakage location is less than 200 m. Therefore, when the mass ratio is decreased, the location is greater than 200 m. This is contrary to the calculations since the calculated value is less than 200 m when the mass ratio is $0.5$. This is an indication of the dependence of leak location of mass ratio of the mixture considered. As Elaoud et al., (2010) state, the most important part in early determination of a leak close to the reservoir or compressor is the bottom of the pipeline.

Figure 9 shows the leak location with respect to the gas mixture ($\varphi$). As can be seen from this figure, there is a steep slope for the values $\varphi \in [0,0.25]$ and $\varphi \in [0.75,1]$, but for values $\varphi \in [0.25,0.75]$ there is a mild slope.

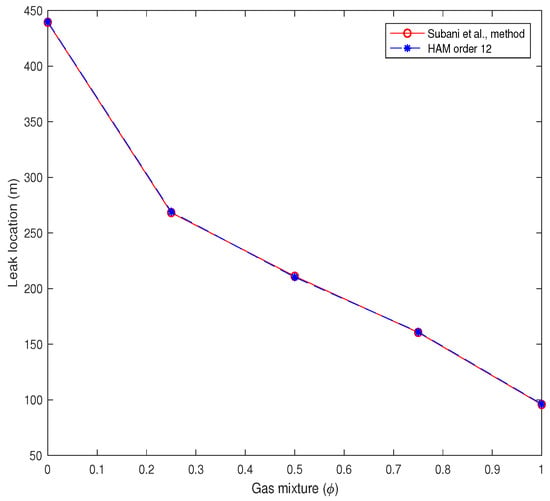
Figure 9. Leak location with respect to the gas mixture ($\varphi$).

In real (physical) pipelines, noise is expected to affect measurements [35,36]. The possible effects of noisy signals on the performance of the proposed method are Brownian motion or Wiener process or White noise, as the physical model of the stochastic procedure, as an indexed collection random variables. A Wiener process (notation $W={\left(W_t\right)}_{t\ge 0}$) is named in the honor of Prof. Norbert Wiener; other name is the Brownian motion (notation $B={\left(B_t\right)}_{t\ge 0}$). Wiener process is Gaussian process. As any Gaussian process, Wiener process is completely described by its expectation and correlation functions. A Brownian motion, also called a Wiener process, is obtained as the integral of a white noise signal as follows,

$$\begin{array}{c}\hfill W\left(t\right)={\int }_0^t\frac{dW\left(\tau \right)}{d\tau }d\tau .\end{array}$$

(54)

The effects of noisy signals on the effectiveness of the proposed method and possible effects of noisy signals on the performance of leak locations will be proposed in the future works, by introducing white noise in the simulations.

For accurate pinpointing, we can use the zero-gradient control (ZGC) method which we have discussed in our recently published paper [6] about optimal mixture and controlling the pressure. In our next manuscript with title “Detecting Optimal Leak Locations using Delta Method and Zero Gradient Control for Non-isothermal Hydrogen/Natural Gas Mixture in an Inclined Pipeline” we used the delta method (DM) and zero gradient control (ZGC) method for detecting optimal leak locations. In our future works we will mixed the proposed methods with Artificial intelligence, Neural Network and Deep Learning [37] to predict and estimate the optimal mixture parameter for achieving more accurate pinpointing.

4. Conclusions

The homotopy analysis method used to solve the flow equations of hydrogen natural gas mixture in an inclined pipeline. To validate the approximation series for pressure compared with the Subani et al. method. The results in Figure 3, Figure 5 and Figure 6 show that the obtained results using proposed method are in good agreement with the reduced order modelling (ROM) proposed by Subani et al, in 2017. Then, homotopy analysis method is working as well as other methods and give the semi-analytical solutions.

The leak locations were detected using the homotopy analysis method for horizontal pipeline ($\theta =0^{\circ }$) and inclined pipeline ($\theta ={15}^{\circ }$) for gas mixture $\varphi =0,0.25,0.5,0.27,1$. Using the homotopy analysis method the celerity wave at leak point of the pipeline are 819.20 ms${}^{-1}$, 964.60 ms${}^{-1}$ and 1086.60 ms${}^{-1}$ for $\varphi =0.25,0.5$ and $0.75$, respectively.

In an inclined pipeline $\theta ={15}^{\circ }$ the leak location for gas mixture $\varphi =0.5$ using the Subani et al. method (ROM) and homotopy analysis method respectively are 211.1 m and 210.3 m. Because of the real leak location is supposed at $200m$ when the leak is located at $X_L=L/3$, the result of HAM method is more accurate than ROM method. As can be seen from Figure 9, with increases the gas mixture $\varphi$ from 0 to 1 the leak location decreases and there is a steep slope for $\varphi \in [0,0.25]\cup [0.75,1]$, and a mild slope for $\varphi \in [0.25,0.75]$.

The proposed HAM method is employed without using linearization, discretization, or transformation. It may be concluded that the HAM is very powerful and efficient in finding the analytical solutions for a wide class of gas transportation equations in a pipeline.