Error Estimation of the Homotopy Perturbation Method to Solve Second Kind Volterra Integral Equations with Piecewise Smooth Kernels: Application of the CADNA Library

Abstract

This paper studies the second kind linear Volterra integral equations (IEs) with a discontinuous kernel obtained from the load leveling and energy system problems. For solving this problem, we propose the homotopy perturbation method (HPM). We then discuss the convergence theorem and the error analysis of the formulation to validate the accuracy of the obtained solutions. In this study, the Controle et Estimation Stochastique des Arrondis de Calculs method (CESTAC) and the Control of Accuracy and Debugging for Numerical Applications (CADNA) library are used to control the rounding error estimation. We also take advantage of the discrete stochastic arithmetic (DSA) to find the optimal iteration, optimal error and optimal approximation of the HPM. The comparative graphs between exact and approximate solutions show the accuracy and efficiency of the method.

1. Introduction

The problem of finding approximate solution for linear Volterra IEs is one of the oldest problems in the applied mathematics researches. Specially, this problem with discontinuous kernel has many applications in the load leveling problems, energy storage with renewable and diesel generation, charge/discharge storages control and others [1,2,3].

There are various methods for solving linear and nonlinear problems [4,5,6,7,8,9,10] specially the Volterra IEs with discontinuous kernel. Muftahov et al. in [11] applied the Lavrentiev regularization and direct quadrature method, Sidorov in [12] used the successive approximations and Noeiaghdam et al. studied the Taylor-collocation method for solving Volterra IEs with discontinuous kernel [1,13]. Also, the nonlinear system of Volterra IE with applications was studied in [14,15]. Furthermore, the existence of a continuous solution depending on free parameters and sufficient conditions for the existence of a unique continuous solution of the system of Volterra IE with discontinuous kernels were derived in [16]. The class of integral operator equations of Volterra type with applications to p-Laplacian equations was illustrated in [17]. The problem of generalized solution (in the Sobolev-Schwartz sense) to the Volterra equations with piecewise continuous kernel was illustrated in [18]. Belbas and Bulka in [19] considered the multiple Volterra IEs. The problem of global solution’s existence and blow-up of nonlinear Volterra IEs were discussed in [20]. For systematic study of the qualitative theory of Volterra IE with discontinuous kernels readers may refer to monograph [21] and part 1 in monograph [22].

The parametric continuation method for the first time was justified by Bernstein [23] for partial differential equations. Here readers may also refer to excellent review by Lusternik [24]. In community of numerical analysts the parametric continuation method is known as the HPM. This method is among of semi-analytical methods that was popularized by J.H. He [25,26,27]. Then, this method has been extended by many other researchers for solving different problems. The HPM was applied to find the approximate analytical solution of the Allen-Cahn equation in [28], to study the maximum power extraction from fractional order doubly fed induction generator based wind turbines in [29], dissipative nonplanar solitons in an electronegative complex plasma in [30] and others [31,32,33]. Convergence of the parameter continuation method in the homotopy method based on the theorem of V.A. Trenogin (see [34], Section 14, p. 146) will be global with respect to a parameter if there is an a priori estimate of the solution for all values of the parameter (this condition can be replaced with a more stringent requirement for the existence of a unique solution bounded for all values of the parameter). If there is no a priori estimate of the solution, then on the basis of the inverse operator theorem (see [34] p. 135), at least local convergence in the homotopy method can be guaranteed. Due to the models complexity, we addressed only some classes of the results in this field. Many other interesting results concerning nonlinear equations with discontinuous symmetric kernels with application of group symmetry have remained beyond this paper. Results of present paper in combination with methods of representation theory and group analysis in the bifurcation theory [35,36] make it possible to construct solutions of nonlinear models with discontinuous kernels using the HPM.

In the mentioned studies and many other researches, the numerical results have been obtained from the floating point arithmetic (FPA) and the accuracy of the method has been discussed using the traditional absolute error as follows

$$|w\left(t\right)-w_n\left(t\right)|<\epsilon ,$$

(1)

where $w\left(t\right)$ and $w_n\left(t\right)$ are the exact and approximate solutions. This condition depends on the existence of the exact solution and optimal value of $\epsilon$. Also, based on condition (1) we will not be able to find the more accurate approximation because we do not have information about optimal $\epsilon$ and in some cases we do not know the exact solution. For small values of $\epsilon$, the numerical algorithm can not be stopped and extra iterations will be produced without improving the accuracy. For large values of $\epsilon$, the numerical algorithm will be stopped in initial steps without producing enough iterations. Moreover, in condition (1), researchers do not have any idea about optimal approximations, optimal errors or numerical instabilities. The aim of this study is to apply the HPM to solve the second kind linear Volterra IEs with jumping kernel and validate the numerical results using the CESTAC method [37,38,39,40]. In this method, instead of applying the condition (1), we need to produce other and better condition without having the disadvantages of (1) as follows:

$$|w_n\left(t\right)-w_{n+1}\left(t\right)|=@.0,$$

(2)

where $@.0$ is the informatical zero sign [41] and $w_n\left(t\right)$ and $w_{n+1}\left(t\right)$ are two successive approximations. Condition (2) is based on the DSA and Theorem 2 can support us to apply this condition theoretically. In this condition, not only we do not need to have the exact solution but also we would be able to identify the optimal approximation, optimal iteration and optimal error of numerical procedure.

Also, the CADNA library is applied as an important software for this validation. The CESTAC method and the CADNA library have been introduced and developed during decades by researchers from LIP6, the computer science laboratory in Sorbonne University in Paris, France (https://www-pequan.lip6.fr/). This principle was introduced in [38] and it was extended to various quadrature rules in [42,43,44] and others [45,46]. The CADNA library should be done on the LINUX operating system and its codes should be written using C, C++ or ADA codes [40,47,48,49]. The CESTAC method is based on the DSA and instead of applying the absolute error to show the precision of method, a termination criterion is applied based on two successive approximations [50,51,52,53]. Thus in this technique we do not need to have the exact solution to compare the results. Also, we will prove that number of common significant digits (NCSD) of two successive approximations are almost equal to the NCSD of exact and approximate solutions. So the new theorem gives the license to apply the new stopping condition instead of previous one. This technique has some advantages than other methods based on the FPA [37,39,50,52,53]. Due to the advantages of the CESTAC method we can find the optimal iteration of iterative and numerical methods, optimal approximation and optimal error. Furthermore, the extra iterations can be neglected and some of numerical instabilities can be detected too [13,54,55,56].

In recent years, this scheme was applied to estimate the round-off errors in different problems such as the numerical integration rules by Newton-Cotes and Gaussian rules [54,57,58,59,60], interpolation [61], solving IEs by Sinc-collocation method [55,62], homotopy analysis method for solving IEs [63] and Taylor-collocation method for discontinuous Volterra IEs [13]. Furthermore, this technique is applied for finding the optimal regularized parameter of the regularization method [56], solving ill-posed problems [56] and many other topics [64,65,66].

This paper is arranged as follows: In the next section, the preliminaries are described regarding to the HPM. In third section, the DSA and the CESTAC method are discussed. Also, algorithm of the CESTAC method and sample code of the CADNA library are presented. In forth section the main idea is described. Then using the HPM we solve the second kind linear Volterra IEs with jumping kernel. Furthermore, the convergence theorem is proved. Also, a theorem is presented which proves that instead of traditional absolute error which depends on the exact and approximate solutions, a termination criterion can be applied which depends on two successive approximations. Section five includes some examples. Also, several tables are presented to show the efficiency of method. The last section is conclusion.

2. Preliminaries

For operator F, given function g and prepared function x we get the following operator equation as

$$F\left(x\right)=g\left(z\right),z\in \mathsf{\Gamma }.$$

(3)

We can write the operator F in the following form

$$F\left(x\right)=\mathcal{L}\left(x\right)+\mathcal{N}\left(x\right),$$

(4)

where the remain part of F showed by $\mathcal{N}$ and $\mathcal{L}$ is the linear operator. Now, Equation (3) can be presented as

$$\mathcal{L}\left(x\right)+\mathcal{N}\left(x\right)=g\left(z\right),z\in \mathsf{\Gamma }.$$

(5)

According to the traditional homotopy [25,26,27], for parameter $\widehat{a}\in [0,1]$, the homotopy operator H can be presented as

$$H(v,\widehat{a})=(1-\widehat{a})(\mathcal{L}\left(v\right)-\mathcal{L}\left(x_0\right))+\widehat{a}(F\left(v\right)-g\left(z\right)),$$

(6)

where $v(z,\widehat{a})$ is defined on $\mathsf{\Gamma }\times [0,1]\to R$ and $x_0$ is the initial guess of Equation (3). Now, by applying Equation (4) we get

$$H(v,\widehat{a})=\mathcal{L}\left(v\right)-\mathcal{L}\left(x_0\right)+\widehat{a}\mathcal{L}\left(x_0\right)+\widehat{a}(\mathcal{N}\left(v\right)-g\left(z\right)).$$

(7)

Putting $\widehat{a}=0$ in Equation (7) leads to $H(v,0)=\mathcal{L}\left(v\right)-\mathcal{L}\left(x_0\right)$ and we get $\mathcal{L}\left(v\right)-\mathcal{L}\left(x_0\right)=0$. Now, for $\widehat{a}=1$ we have $H(v,1)=0$ which it can produce the solution of Equation (3). Thus, when $\widehat{a}:0\to 1$ we can change the solution v from $x_0$ to x. Now, the power series

$$v=\sum _{j=0}^{\infty }{\widehat{a}}^j{v}_j,$$

(8)

can be applied to find the solution of $H(v,\widehat{a})=0$. Then comparing the same powers of parameter $\widehat{a}$ we can find the successive functions $v_j,j=0,\cdots ,n$.

Finally, applying

$$w=\underset{\widehat{a}\to 1}{lim}v=\sum _{j=0}^{\infty }{v}_j,$$

(9)

the solution of Equation (3) can be found and the n-th order approximation is in the following form

$$w_n=\sum _{j=0}^n{v}_j.$$

(10)

3. Stochastic Arithmetic and the CESTAC Method

In this section, the CESTAC method is described and the algorithm of this method is presented. Also, a sample program of the CADNA library is demonstrated and finally advantages of presented method based on the DSA are investigated in comparison with the traditional FPA [37,38,39,40,50].

Assume that some representable values are produced by computer and they are collected in set A. Then $W\in A$ can be produced for $w\in \mathbb{R}$ with $\mathcal{R}$ mantissa bits of the binary FPA in the following form

$$W=w-\chi 2^{E-\mathcal{R}}\xi ,$$

(11)

where sign of w showed by $\chi$, missing segment of the mantissa presented by $2^{-\mathcal{R}}\xi$ and the binary exponent of the result characterized by E. Moreover, there are single and double precisions by choosing $\mathcal{R}=24,53$ [40,50,51,52,53].

Assume $\xi$ is the casual variable that uniformly distributed on $[-1,1]$. After making perturbation on final mantissa bit of w we will have $\left(\mu \right)$ and $\left(\sigma \right)$ as mean and standard deviation for results of W which they have important rule in precision of W. Repeating this process J times for $W_i,i=1,\cdots ,J$ we will have quasi Gaussian distribution for results. It means that $\mu$ for these data equals to the exact w. It is clear that we should find $\mu$ and $\sigma$ based on $W_i,i=1,\cdots ,J$. For more consideration, the following Algorithm 1 is presented where ${\tau }_{\delta }$ is the value of T distribution as the confidence interval is $1-\delta$ with $J-1$ freedom degree [52].

Usually, in order to find the numerical results we need to apply the usual packages like Mathematica and Matlab. Here, instead of them we introduce the CADNA library and the CESTAC method to validate the numerical results [1,55,56,62].

This library should run on LINUX operating system and all commands should be written by C, C++, FORTRAN or ADA codes [13,54,59,60,63].

We have many advantages to apply the CESTAC method and the CADNA library instead of traditional schemes using the FPA. In this method, a novel criterion independence of absolute error and tolerance value like $\epsilon$ is presented. Applying the CADNA library, we can find the optimal iteration, approximation and error of numerical methods. Moreover, the numerical instabilities can be identified [13,54,55,56]. A sample program of the CADNA library is presented as

Algorithm 1:

Step 1- Make the perturbation of the last bit of mantissa to produce J samples of W as $\mathsf{\Phi }=\left\{W_1,W_2,\dots ,W_J\right\}$. Step 2- Find ${\displaystyle W_{ave}=\frac{{\sum }_{i=1}^J{W}_i}{J}}$. Step 3- Compute ${\displaystyle {\sigma }^2=\frac{{\sum }_{i=1}^J{(W_i-W_{ave})}^2}{J-1}}$. Step 4- Find the NCSDs of w and $W_{ave}$ applying ${\displaystyle C_{W_{ave},w}={log}_{10}\frac{\sqrt{J}\left|W_{ave}\right|}{{\tau }_{\delta }\sigma }}$. Step 5- Print $W=@.0$ if $W_{ave}=0,$ or $C_{W_{ave},W}\le 0$.

♯include <cadna.h>

cadna$\_$init(-1);

main()

{

double$\_$st Parameter;

do

{

Write the main codes here;

printf(" %s ",strp(Parameter));

}

while(u[n]-u[n-1]!=0);

cadna$\_$end();

}

4. Main Idea

Consider the following second kind linear IE

$$w\left(t\right)=g\left(t\right)+{\int }_0^{t}k(t,s)w\left(s\right)ds,a=0\le t\le T\le b,$$

(12)

where $k(t,s)$ is discontinuous along continuous curves ${\gamma }_i,i=0,1,\cdots ,m-1$ and it can be written in the following form

$$w\left(t\right)=g\left(t\right)+{\int }_{{\gamma }_0\left(t\right)}^{{\gamma }_1\left(t\right)}{k}_1(t,s)w\left(s\right)ds+{\int }_{{\gamma }_1\left(t\right)}^{{\gamma }_2\left(t\right)}{k}_2(t,s)w\left(s\right)ds+\cdots +{\int }_{{\gamma }_{m-1}\left(t\right)}^{{\gamma }_m\left(t\right)}{k}_m(t,s)w\left(s\right)ds,$$

(13)

and finally for brief form we get

$$w\left(t\right)=g\left(t\right)+\sum _{i=1}^m{\int }_{{\gamma }_{i-1}\left(t\right)}^{{\gamma }_i\left(t\right)}{k}_i(t,s)w\left(s\right)ds.$$

(14)

Indeed, the kernel is the principal part of the IE (14). One may think about considered Volterra IE as generalization of classic Duhamel integral. So, the kernel can be understood as instrumental response function (IF, or spectral sensitivity, transmission function, point spread function, frequency response), see e.g., [67]. In this study, we do not focus on specific physical problems, but more on numerical aspects of solutions only.

Based on the HPM and applying Equations (4) and (5) for solving Equation (14), operators $\mathcal{L}\left(v\right)$ and $\mathcal{N}\left(v\right)$ should be defined as follows

$$\mathcal{L}\left(v\right)=v,$$

and

$$\mathcal{N}\left(v\right)=\sum _{i=1}^m{\int }_{{\gamma }_{i-1}\left(t\right)}^{{\gamma }_i\left(t\right)}{k}_i(t,s)w\left(s\right)ds.$$

(15)

For next step, using Equation (7) the homotopy map can be constructed as follows

$$H(v,\widehat{a})=v\left(t\right)-w_0\left(t\right)+\widehat{a}\left[w_0\left(t\right)-\sum _{i=1}^m{\int }_{{\gamma }_{i-1}\left(t\right)}^{{\gamma }_i\left(t\right)}{k}_i(t,s)w\left(s\right)ds-g\left(t\right)\right],$$

(16)

and we have

$${\displaystyle \sum _{j=0}^{\infty }{\widehat{a}}^j{v}_j\left(t\right)=w_0\left(t\right)+\widehat{a}[g\left(t\right)-w_0\left(t\right)]+\sum _{j=1}^{\infty }{\widehat{a}}^j\sum _{i=1}^m{\int }_{{\gamma }_{i-1}\left(t\right)}^{{\gamma }_i\left(t\right)}{k}_i(t,s)v_{j-1}\left(s\right)ds.}$$

(17)

Now, Equation (17) can be written in the following form

$$\sum _{j=0}^{\infty }{\widehat{a}}^j{v}_j\left(t\right)=w_0\left(t\right)+\widehat{a}[g\left(t\right)-w_0\left(t\right)]+\sum _{j=1}^{\infty }{\widehat{a}}^j{A}_{j-1}\left(t\right),$$

(18)

where

$$A_{j-1}\left(t\right)=\sum _{i=1}^m{\int }_{{\gamma }_{i-1}\left(t\right)}^{{\gamma }_i\left(t\right)}{k}_i(t,s)v_{j-1}\left(s\right)ds.$$

By disjointing the different powers of $\widehat{a}$ in both sides of Equation (18) the following successive iterations can be obtained as

$$\begin{array}{c}{\displaystyle {\widehat{a}}^0:v_0\left(t\right)=w_0\left(t\right),}\hfill \\ \\ {\displaystyle {\widehat{a}}^1:v_1\left(t\right)=g\left(t\right)-w_0\left(t\right)+A_0\left(t\right)}\hfill \\ \\ {\displaystyle =g\left(t\right)-w_0\left(t\right)+\sum _{i=1}^m{\int }_{{\gamma }_{i-1}\left(t\right)}^{{\gamma }_i\left(t\right)}{k}_i(t,s)v_0\left(s\right)ds,}\hfill \\ \\ {\displaystyle {\widehat{a}}^2:v_2\left(t\right)=A_1\left(t\right)=\sum _{i=1}^m{\int }_{{\gamma }_{i-1}\left(t\right)}^{{\gamma }_i\left(t\right)}{k}_i(t,s)v_1\left(s\right)ds,}\hfill \\ ⋮⋮⋮\hfill \\ {\displaystyle {\widehat{a}}^n:v_n\left(t\right)=A_{n-1}\left(t\right)=\sum _{i=1}^m{\int }_{{\gamma }_{i-1}\left(t\right)}^{{\gamma }_i\left(t\right)}{k}_i(t,s)v_{n-1}\left(s\right)ds.}\hfill \end{array}$$

(19)

Applying Equation (10) and successive iterations (19), the approximate solution of Equation (14) can be obtained.

Theorem 1.

Assume that functions $k_i(t,s)$ and $g\left(t\right)$ of Equation (14) are continuous in ${\eta }_1=[a,b]\times [a,b]$ and $\eta =[a,b]$ respectively where these functions are bounded. If

$$\exists {\alpha }_i,N_1;|k_i(t,s)|\le {\alpha }_i,\left|g\left(t\right)\right|\le N_1,\forall s,t\in \eta ,i=1,2,\cdots ,m,$$

then for initial approximation $w_0$ which is continuous in $[a,b]$, the series solution (9) will be uniformly convergent to the exact solution for each $\widehat{a}\in [0,1]$.

Proof. 

Assume $w_0\left(t\right)\in C[a,b]$, then we have a positive number $N_0$ such that $|w_0\left(t\right)|\le N_0$. Therefore, we can write

$$\begin{array}{cc}{\displaystyle |v_0\left(t\right)|}\hfill & {\displaystyle =|w_0\left(t\right)|\le N_0,}\hfill \\ \\ {\displaystyle |v_1\left(t\right)|}\hfill & {\displaystyle =\left|g\left(t\right)-w_0\left(t\right)+{\int }_{{\gamma }_0\left(t\right)}^{{\gamma }_1\left(t\right)}{k}_1(t,s)v_0\left(s\right)ds+{\int }_{{\gamma }_1\left(t\right)}^{{\gamma }_2\left(t\right)}{k}_2(t,s)v_0\left(s\right)ds\right.}\hfill \\ \\ & {\displaystyle \left.+\cdots +{\int }_{{\gamma }_{m-1}\left(t\right)}^{{\gamma }_m\left(t\right)}{k}_m(t,s)v_0\left(s\right)ds\right|}\hfill \\ \\ {\displaystyle }\hfill & {\displaystyle \le \left|g\left(t\right)\right|+|w_0\left(t\right)|+{\int }_{{\gamma }_0\left(t\right)}^{{\gamma }_1\left(t\right)}|k_1(t,s)\left|\right|v_0\left(s\right)|ds+{\int }_{{\gamma }_1\left(t\right)}^{{\gamma }_2\left(t\right)}|k_2(t,s)\left|\right|v_0\left(s\right)|ds}\hfill \\ \\ & {\displaystyle +\cdots +{\int }_{{\gamma }_{m-1}\left(t\right)}^{{\gamma }_m\left(t\right)}|k_m(t,s)\left|\right|v_0\left(s\right)\left|ds\right|}\hfill \\ \\ & {\displaystyle \le N_1+N_0+{\alpha }_1{N}_0({\gamma }_1-{\gamma }_0)+{\alpha }_2{N}_0({\gamma }_2-{\gamma }_1)+\cdots +{\alpha }_m{N}_0({\gamma }_m-{\gamma }_{m-1})=\beta ,}\hfill \\ \\ {\displaystyle |v_2\left(t\right)|}\hfill & {\displaystyle =\left|{\int }_{{\gamma }_0\left(t\right)}^{{\gamma }_1\left(t\right)}{k}_1(t,s)v_1\left(s\right)ds+{\int }_{{\gamma }_1\left(t\right)}^{{\gamma }_2\left(t\right)}{k}_2(t,s)v_1\left(s\right)ds\right.}\hfill \\ \\ & {\displaystyle \left.+\cdots +{\int }_{{\gamma }_{m-1}\left(t\right)}^{{\gamma }_m\left(t\right)}{k}_m(t,s)v_1\left(s\right)ds\right|,}\hfill \end{array}$$

$$\begin{array}{cc}{\displaystyle |v_2\left(t\right)|}\hfill & {\displaystyle \le {\int }_{{\gamma }_0\left(t\right)}^{{\gamma }_1\left(t\right)}|k_1(t,s)\left|\right|v_1\left(s\right)|ds+{\int }_{{\gamma }_1\left(t\right)}^{{\gamma }_2\left(t\right)}|k_2(t,s)\left|\right|v_1\left(s\right)|ds}\hfill \\ \\ & {\displaystyle +\cdots +{\int }_{{\gamma }_{m-1}\left(t\right)}^{{\gamma }_m\left(t\right)}|k_m(t,s)\left|\right|v_1\left(s\right)|ds}\hfill \\ \\ & {\displaystyle \le {\alpha }_1({\gamma }_1-{\gamma }_0)\beta +{\alpha }_2({\gamma }_2-{\gamma }_1)\beta +\cdots +{\alpha }_m({\gamma }_m-{\gamma }_{m-1})\beta }\hfill \\ \\ & {\displaystyle =\beta \sum _{i=1}^m{\alpha }_i({\gamma }_i-{\gamma }_{i-1}).}\hfill \end{array}$$

Accordingly, we obtain the following general form

$$|v_j\left(t\right)|\le \beta \left(\sum _{i=1}^m{\alpha }_i^{j-1}\frac{{({\gamma }_i-{\gamma }_{i-1})}^{j-1}}{(j-1)!}\right),s,t\in [a,b],j\ge 2.$$

(20)

Finally, for series solution (8) and for any $\widehat{a}\in [0,1]$ we can write

$$\sum _{j=0}^{\infty }{\widehat{a}}^j{v}_j\left(t\right)\le \sum _{j=0}^{\infty }\left|v_j\left(t\right)\right|\le \sum _{j=0}^{\infty }{a}_j=N_0+\beta +\beta exp\left(\sum _{i=1}^m{\alpha }_i({\gamma }_i-{\gamma }_{i-1})\right),$$

where $a_0=N_0,a_1=\beta ,a_j=\beta \left({\sum }_{i=1}^m{\alpha }_i^{j-1}\frac{{({\gamma }_i-{\gamma }_{i-1})}^{j-1}}{(j-1)!}\right),j\ge 2$. It means that series solution (8) for any $\widehat{a}\in [0,1]$ is uniformly convergent in interval $[a,b]$. □

From Equation (20), the following remark can be deduced:

Remark 1.

Based on the n-th order approximate solution (10), the error function $E_n={sup}_{t\in [a,b]}|w\left(t\right)-w_n\left(t\right)|$ can be approximated as follows:

$$\begin{array}{cc}{\displaystyle |w\left(t\right)-w_n\left(t\right)|}\hfill & {\displaystyle =\left|\sum _{j=0}^{\infty }{v}_j\left(t\right)-\sum _{j=0}^n{v}_j\left(t\right)\right|=\left|\sum _{j=n+1}^{\infty }{v}_j\left(t\right)\right|\le \sum _{j=n+1}^{\infty }\left|v_j\left(t\right)\right|}\hfill \\ \\ & {\displaystyle \le \beta \sum _{j=n+1}^{\infty }\left(\sum _{i=1}^m{\alpha }_i^{j-1}\frac{{({\gamma }_i-{\gamma }_{i-1})}^{j-1}}{(j-1)!}\right).}\hfill \end{array}$$

Order of error $E_n$ can be obtained in the following form:

$$E_n=\mathcal{O}\left[\sum _{j=n+1}^{\infty }\frac{1}{(j-1)!}\left(\sum _{i=1}^m{\alpha }_i^j{({\gamma }_i-{\gamma }_{i-1})}^j\right)\right]=\mathcal{O}\left(\frac{L^n}{n!}\right),$$

where L is a positive real number.

Definition 1

([38]). For numbers $z_1,z_2\in \mathbb{R}$, the NCSDs can be computed as follows:

(1)

for $z_1\ne z_2$,

$$C_{z_1,z_2}={log}_{10}\left|\frac{z_1+z_2}{2(z_1-z_2)}\right|={log}_{10}\left|\frac{z_1}{z_1-z_2}-\frac{1}{2}\right|,$$

(21)

(2)

for all real numbers $z_1$, $C_{z_1,z_1}=+\infty$.

Theorem 2.

Let $w\left(t\right)$ and $w_n\left(t\right)$ be the exact and numerical solutions of problem (12) which $w_n\left(t\right)$ is obtained by using the HPM and Equation (10). Based on assumptions of Theorem 1 and Remark 1 for n enough large we have

$${\displaystyle C_{w_n\left(t\right),w_{n+1}\left(t\right)}\simeq C_{w_n\left(t\right),w\left(t\right)},}$$

(22)

where $C_{w_n\left(t\right),w\left(t\right)}$ shows the NCSDs of $w_n\left(t\right),w\left(t\right)$ and $C_{w_n\left(t\right),w_{n+1}\left(t\right)}$ is the NCSDs of two successive iterations $w_n\left(t\right),w_{n+1}\left(t\right)$.

Proof. 

Using Definition 1 and Remark 1 we get

$$\begin{array}{cc}{\displaystyle C_{w_n\left(t\right),w_{n+1}\left(t\right)}}\hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{w_n\left(t\right)-w_{n+1}\left(t\right)}-\frac{1}{2}\right|}\hfill \\ \\ \hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{w_n\left(t\right)-w_{n+1}\left(t\right)}\right|+{log}_{10}\left|1-\frac{1}{2w_n\left(t\right)}(w_n\left(t\right)-w_{n+1}\left(t\right))\right|}\hfill \\ \\ \hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{w_n\left(t\right)-w_{n+1}\left(t\right)}\right|+\mathcal{O}\left(w_n\left(t\right)-w_{n+1}\left(t\right)\right)}\hfill \\ \\ \hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{(w_n\left(t\right)-w\left(t\right))-(w_{n+1}\left(t\right)-w\left(t\right))}\right|+\mathcal{O}\left[(w_n\left(t\right)-w\left(t\right))-(w_{n+1}\left(t\right)-w\left(t\right))\right]}\hfill \\ \\ \hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{(w_n\left(t\right)-w\left(t\right))\left[1-\frac{w_{n+1}\left(t\right)-w\left(t\right)}{w_n\left(t\right)-w\left(t\right)}\right]}\right|+\mathcal{O}\left(E_n\right)+\mathcal{O}\left(E_{n+1}\right)}\hfill \\ \\ \hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{w_n\left(t\right)-w\left(t\right)}\right|-{log}_{10}\left|1-\frac{w_{n+1}\left(t\right)-w\left(t\right)}{w_n\left(t\right)-w\left(t\right)}\right|+\mathcal{O}\left(\frac{L^n}{n!}\right)}\hfill \\ \\ \hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{w_n\left(t\right)-w\left(t\right)}\right|-{log}_{10}\left|1-\frac{w_{n+1}\left(t\right)-w\left(t\right)}{w_n\left(t\right)-w\left(t\right)}\right|+\mathcal{O}\left(\frac{L^n}{n!}\right).}\hfill \end{array}$$

(23)

Also,

$$\begin{array}{cc}{\displaystyle C_{w_n\left(t\right),w\left(t\right)}}\hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{w_n\left(t\right)-w\left(t\right)}-\frac{1}{2}\right|}\hfill \\ \\ \hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{w_n\left(t\right)-w\left(t\right)}\right|+\mathcal{O}(w_n\left(t\right)-w\left(t\right))}\hfill \\ \\ \hfill & {\displaystyle ={log}_{10}\left|\frac{w_n\left(t\right)}{w_n\left(t\right)-w\left(t\right)}\right|+\mathcal{O}\left(\frac{L^n}{n!}\right).}\hfill \end{array}$$

(24)

Applying Equations (23) and (24) we have

$$C_{w_n\left(t\right),w_{n+1}\left(t\right)}=C_{w_n\left(t\right),w\left(t\right)}-{log}_{10}\left|1-\frac{w_{n+1}\left(t\right)-w\left(t\right)}{w_n\left(t\right)-w\left(t\right)}\right|+\mathcal{O}\left(\frac{L^n}{n!}\right).$$

From Remark 1, we can write $\frac{w_{n+1}\left(t\right)-w\left(t\right)}{w_n\left(t\right)-w\left(t\right)}=\frac{\mathcal{O}\left(\frac{L^{n+1}}{(n+1)!}\right)}{\mathcal{O}\left(\frac{L^n}{n!}\right)}=\mathcal{O}\left(\frac{1}{n}\right)$. Thus for n enough large we get $\mathcal{O}\left(\frac{1}{n}\right)<<1$ and consequently

$$C_{w_n\left(t\right),w_{n+1}\left(t\right)}\simeq C_{w_n\left(t\right),w\left(t\right)}.$$

□

Theorem 2 shows that when n increases, the NCSDs between two sequential results obtained from the algorithm is almost equal to the common significant digits of the n-th iteration and the exact solution at the given point t which means that for an optimal index like $n=n_{o}pt$, when $w_n\left(t\right)-w_{n+1}\left(t\right)=@.0$ then $w_n\left(t\right)-w\left(t\right)=@.0$.

5. Numerical Results

In this section, several examples of second kind linear Volterra IEs with discontinuous kernel are presented. The numerical process is based on the HPM that we discussed in previous sections. Also, using the CESTAC method and the CADNA library for all examples we will arrange some numerical procedures based on the following algorithm to find the optimal approximation, optimal error and optimal step of the HPM for solving linear Volterra IEs with jumping kernels. Having the exact solution in the examples is only to compare the numerical results based on both conditions (1) and (2). Some comparative graphs between exact and approximate solutions are plotted to show the accuracy and efficiency of the method.

Algorithm 2:

Step 1- Let $n=1$. Step 2- Do the following steps while $\left|w_n\left(t\right)-w_{n+1}\left(t\right)\right|\ne @.0$

{

Step 2-1- Produce $w_n\left(t\right)$ using Equations (10) and (19). Step 2-2- Print $n,w_n\left(x\right),\left|w\left(t\right)-w_n\left(t\right)\right|,\left|w_n\left(t\right)-w_{n+1}\left(t\right)\right|$. Step 2-3- $n=n+1$.

}

Example 1.

Consider the following second kind Volterra IE with discontinuous kernel

$$w\left(t\right)=-t+\frac{13t^2}{9}-\frac{41t^3}{162}-\frac{5t^4}{324}+{\int }_0^{\frac{t}{3}}(s+t)w\left(s\right)ds+{\int }_{\frac{t}{3}}^{t}w\left(s\right)ds,$$

(25)

with exact solution $w\left(t\right)=t^2-t$. Applying the homotopy map (16) and relations (17), (18) and successive iterations (19) we get

$$\begin{array}{cc}{\displaystyle {\widehat{a}}^0:v_0\left(t\right)}\hfill & {\displaystyle =w_0\left(t\right)=g\left(t\right)=-t+\frac{13t^2}{9}-\frac{41t^3}{162}-\frac{5t^4}{324},}\hfill \\ \\ {\displaystyle {\widehat{a}}^1:v_1\left(t\right)}\hfill & {\displaystyle =g\left(t\right)-w_0\left(t\right)+{\int }_0^{\frac{t}{3}}(s+t)v_0\left(s\right)ds+{\int }_{\frac{t}{3}}^t{v}_0\left(s\right)ds}\hfill \\ \\ & {\displaystyle =-\frac{4t^2}{9}+\frac{577t^3}{1458}-\frac{1055t^4}{26244}-\frac{3199t^5}{787320}-\frac{23t^6}{1417176},}\hfill \\ \\ {\displaystyle {\widehat{a}}^2:v_2\left(t\right)}\hfill & {\displaystyle ={\int }_0^{\frac{t}{3}}(s+t)v_1\left(s\right)ds+{\int }_{\frac{t}{3}}^t{v}_1\left(s\right)ds}\hfill \\ \\ & {\displaystyle =\frac{104t^3}{729}+\frac{5365t^4}{59049}-\frac{411953t^5}{63772920}-\frac{1237231t^6}{1721868840}-\frac{761899t^7}{216955473840}-\frac{713t^8}{520693137216},}\hfill \\ \\ {\displaystyle {\widehat{a}}^n:v_n\left(t\right)}\hfill & {\displaystyle ={\int }_0^{\frac{t}{3}}(s+t)v_{n-1}\left(s\right)ds+{\int }_{\frac{t}{3}}^t{v}_{n-1}\left(s\right)ds,n\ge 2,}\hfill \end{array}$$

and finally using series solution (10), the approximate solution for $n=5$ can be obtained as follows

$$\begin{array}{cc}{\displaystyle w_5\left(t\right)}& {\displaystyle =-t+t^2+0.000166742t^7-0.0000302385t^8-1.52193\times {10}^{-6}{t}^9-5.93206\times {10}^{-9}{t}^{10}}\\ \\ & {\displaystyle -2.63436\times {10}^{-12}{t}^{11}-1.3852\times {10}^{-16}{t}^{12}-8.13306\times {10}^{-22}{t}^{13}-4.25383\times {10}^{-28}{t}^{14}.}\end{array}$$

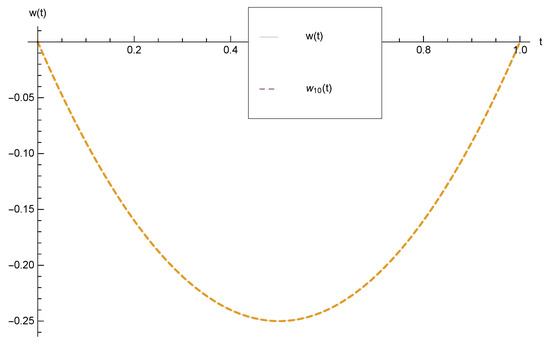
In this example, in order to show the accuracy of method, the CESTAC method and the CADNA library are applied according to Algorithm 2. Also, instead of applying the termination criterion (1) and using the traditional absolute error, the stopping condition (2) is applied. This condition is based on two successive approximations $w_n\left(t\right)$ and $w_{n+1}\left(t\right)$. When the difference of these terms is $@.0$ the CESTAC algorithm will be stopped. It shows that the NCSDs of the difference between two successive iterates is zero. The numerical results using the DSA are presented in

Table 1. Applying Algorithm 2 for Example 1 with $t=0.2$.

n	${\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)$	$|{\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)-{\mathit{w}}_{\mathit{n}+1}\left(\mathit{t}\right)|$	$|\mathit{w}\left(\mathit{t}\right)-{\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)|$
1	−0.158949024126688	0.158949024126688	$0.1050975873312\times {10}^{-2}$
2	−0.159947054328260	$0.9980302015726\times {10}^{-3}$	$0.529456717393\times {10}^{-4}$
3	−0.159997865982876	$0.508116546153\times {10}^{-4}$	$0.21340171239\times {10}^{-5}$
4	−0.159999928407226	$0.2062424350\times {10}^{-5}$	$0.715927734\times {10}^{-7}$
5	−0.159999997943235	$0.695360085\times {10}^{-7}$	$0.2056764\times {10}^{-8}$
6	−0.159999999946935	$0.20037004\times {10}^{-8}$	$0.530644\times {10}^{-10}$
7	−0.159999999999848	$0.52913\times {10}^{-10}$	$0.151\times {10}^{-12}$
8	−0.159999999999976	$0.128\times {10}^{-12}$	$0.231\times {10}^{-13}$
9	−0.159999999999999	$0.23\times {10}^{-13}$	$@.0$
10	−0.160000000000000	$@.0$	$@.0$

for $t=0.2$ in double precision. According to this table the optimal step of iterations for the HPM is $n_{opt}=10$, the optimal approximation is $-0.16$ and the optimal absolute error is $0.231\times {10}^{-13}$. Figure 1, shows the comparison between the exact and approximate solutions for optimal value $n_{opt}=10$ obtained from the CESTAC method.

Example 2.

Consider the following Volterra IE [11]

$$w\left(t\right)=\frac{1}{8}{t}^3-\frac{271}{8192}{t}^4-\frac{1099}{20480}{t}^5-\frac{31}{40960}{t}^6+{\int }_0^{\frac{t}{4}}(1+t+s)w\left(s\right)ds+{\int }_{\frac{t}{4}}^{\frac{t}{2}}(2+ts)w\left(s\right)ds+{\int }_{\frac{t}{2}}^t(1+t+s)w\left(s\right)ds,$$

(26)

where the exact solution is $w\left(t\right)=\frac{t^3}{8}$. Applying the homotopy map (16) and relations (17), (18) and successive iterations (19) we can find the approximate solution in the following form

$$\begin{array}{cc}{\displaystyle w_5\left(t\right)}\hfill & {\displaystyle =0.125t^3-2.60209\times {10}^{-18}{t}^8-2.32004\times {10}^{-6}{t}^9-0.0000188571t^{10}-0.0000644212t^{11}}\hfill \\ \\ & {\displaystyle -0.000118496t^{12}-0.000123946t^{13}-0.0000701359t^{14}-0.0000170219t^{15}-2.00669\times {10}^{-7}{t}^{16}}\hfill \\ \\ & {\displaystyle -2.8387\times {10}^{-10}{t}^{17}-5.39533\times {10}^{-14}{t}^{18}-1.37516\times {10}^{-18}{t}^{19}-4.46435\times {10}^{-24}{t}^{20}}\hfill \\ \\ & {\displaystyle -1.5236\times {10}^{-30}{t}^{21}}\hfill \end{array}$$

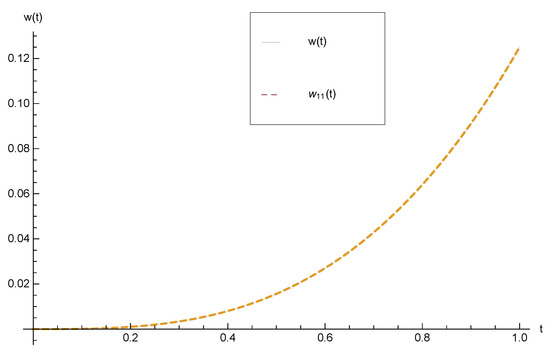
In this example, the DSA and the CADNA library are applied to validate the numerical approximations. Also, using the stopping condition (2) we do not need to have the exact solution to show that accuracy of presented method. The numerical results are presented in

Table 2. Applying Algorithm 2 for Example 2 with $t=0.3$.

n	${\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)$	$|{\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)-{\mathit{w}}_{\mathit{n}+1}\left(\mathit{t}\right)|$	$|\mathit{w}\left(\mathit{t}\right)-{\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)|$
1	$0.333953193046557\times {10}^{-2}$	$0.333953193046557\times {10}^{-2}$	$0.35468069534420\times {10}^{-4}$
2	$0.337246339699770\times {10}^{-2}$	$0.3293146653212\times {10}^{-4}$	$0.253660300229\times {10}^{-5}$
3	$0.337484790802514\times {10}^{-2}$	$0.238451102744\times {10}^{-5}$	$0.15209197485\times {10}^{-6}$
4	$0.337499213815335\times {10}^{-2}$	$0.14423012820\times {10}^{-6}$	$0.7861846644\times {10}^{-8}$
5	$0.337499968103952\times {10}^{-2}$	$0.7542886169\times {10}^{-8}$	$0.31896047\times {10}^{-9}$
6	$0.337499999258881\times {10}^{-2}$	$0.31154929\times {10}^{-9}$	$0.741118\times {10}^{-11}$
7	$0.337499999979560\times {10}^{-2}$	$0.720678\times {10}^{-11}$	$0.20439\times {10}^{-12}$
8	$0.337499999998390\times {10}^{-2}$	$0.18830\times {10}^{-12}$	$0.1609\times {10}^{-13}$
9	$0.337499999999973\times {10}^{-2}$	$0.1582\times {10}^{-13}$	$0.26\times {10}^{-15}$
10	$0.337499999999998\times {10}^{-2}$	$0.25\times {10}^{-15}$	$@.0$
11	$0.337499999999999\times {10}^{-2}$	$@.0$	$@.0$

for $t=0.3$ by applying Algorithm 2. Using these results, the optimal approximation is $0.337499999999999\times {10}^{-2}$ and the optimal absolute error is $0.26\times {10}^{-15}$ and $n_{opt}=11$ is the optimal step of iteration for HPM method for solving Example 2. Comparison between the exact and approximate solutions for $n_{opt}=11$ is demonstrated in Figure 2.

Example 3.

Consider the following linear Volterra IE of the second kind

$$\begin{array}{cc}{\displaystyle w\left(t\right)}\hfill & {\displaystyle =t^5-\frac{811201}{1572864}{t}^6+\frac{38249}{14680064}{t}^7-\frac{3938545}{939524096}{t}^8}\hfill \\ \\ \hfill & {\displaystyle +{\int }_0^{\frac{t}{8}}(1-3t-s)w\left(s\right)ds+{\int }_{\frac{t}{8}}^{\frac{t}{2}}(2+s^3-t)w\left(s\right)ds+{\int }_{\frac{t}{2}}^{\frac{3t}{4}}(2t^{2}s+1)w\left(s\right)ds-4{\int }_{\frac{3t}{4}}^{t}w\left(s\right)ds,}\hfill \end{array}$$

(27)

where the exact solution is $w\left(t\right)=t^5$.

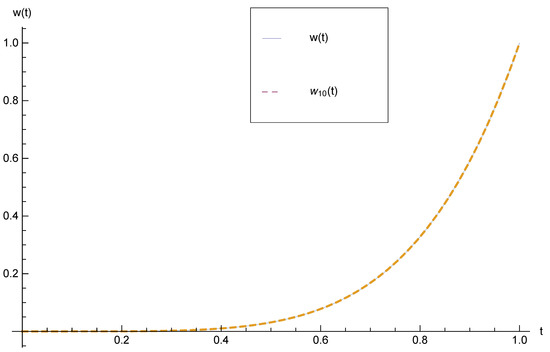
The numerical results are presented in

Table 3. Numerical approximations for Example 3 with $t=0.2$.

n	${\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)$	$|{\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)-{\mathit{w}}_{\mathit{n}+1}\left(\mathit{t}\right)|$	$|\mathit{w}\left(\mathit{t}\right)-{\mathit{w}}_{\mathit{n}}\left(\mathit{t}\right)|$
1	$0.997548914719302\times {10}^{-5}$	$0.997548914719302\times {10}^{-5}$	$0.245108528069\times {10}^{-7}$
2	$0.100010710205707\times {10}^{-4}$	$0.255818733777\times {10}^{-7}$	$0.10710205707\times {10}^{-8}$
3	$0.999995689009746\times {10}^{-5}$	$0.111413047328\times {10}^{-8}$	$0.4310990253\times {10}^{-10}$
4	$0.100000016025571\times {10}^{-4}$	$0.4471245970\times {10}^{-10}$	$0.16025571\times {10}^{-11}$
5	$0.999999994481069\times {10}^{-5}$	$0.16577464\times {10}^{-11}$	$0.5518930\times {10}^{-13}$
6	$0.100000000017666\times {10}^{-4}$	$0.5695594\times {10}^{-13}$	$0.17666\times {10}^{-14}$
7	$0.999999999994729\times {10}^{-5}$	$0.18193\times {10}^{-14}$	$0.527\times {10}^{-16}$
8	$0.100000000000014\times {10}^{-4}$	$0.5418\times {10}^{-16}$	$0.14\times {10}^{-17}$
9	$0.999999999999996\times {10}^{-5}$	$0.15\times {10}^{-17}$	$0.3\times {10}^{-19}$
10	$0.100000000000000\times {10}^{-4}$	$@.0$	$@.0$

. The optimal iteration of the HPM for solving this example is $n_{opt}=10$, the optimal approximation is $0.1\times {10}^{-4}$ and the optimal error is $0.3\times {10}^{-19}$. To validate the results, the CADNA library is applied based on the termination criterion (2). Theorem 2 is able to permit us to apply the stopping condition instead of the traditional condition (1). In Figure 3, the graph of exact and approximate solutions for optimal value $n_{opt}=10$ is studied.

6. Conclusions

Volterra IEs with discontinuous kernel are among applicable problems in power engineering and especially in load leveling problems. In this study, we applied the HPM while the CESTAC method and the CADNA library used to examine the numerical results. Applying this method not only the optimal iteration of the HPM, the optimal approximation and the optimal error can be found but also some of numerical instabilities can be detected. Furthermore, the substantial theorem is provided which approves the appropriateness of the termination criterion (2) instead of traditional absolute error. We will focus on validating the nonlinear Volterra IEs with discontinuous kernel in fuzzy and crisp forms using the CESTAC method for our future works.