Neutrino Oscillations in the Presence of Matter and Continuous Non-Selective Measurement

Abstract

We investigate three-flavor neutrino oscillation affected by an environment mimicking a continuous non-selective measurement. We show that such a coupling that is given by a measured observable affects probability of inter-flavor neutrino transition and a steady-state correlation function of the neutrino’s flavor. We juxtapose and compare our predictions influenced by matter’s scattering and $CP$-violation.

1. Introduction

Time-evolving neutrinos [1] attract attention and stimulate research from very different perspectives [2,3]. Because of very peculiar and intriguing dynamic properties of neutrino oscillations [4,5,6], the most natural particle physics context becomes supplemented by various studies carried in seemingly far research communities such as decoherence [4,7,8,9,10,11,12] or quantum information [5,13,14,15,16]. In this paper, after short review of neutrino oscillation phenomenon, we discuss dynamic properties of inter-flavor transitions and steady-state autocorrelation of neutrino oscillation in a presence of matter and decoherence induced by a measurement-like mechanism effectively identical to a continuous non-selective measurement [17] of two ’observables’ analogous to one of the angular momentum observables: the first corresponds to a potential flavor measurement and the second, very hypothetical, to the measurement of neutrino mass. We study dynamical properties of this model of neutrino oscillation and show that it becomes equipped with a features significantly altering inter-flavor transitions probabilities and steady-state autocorrelation of the ’flavor observable’. We investigate, in detail, the role of scattering-like interaction between neutrinos and normal matter CP-symmetry and its violation.

1.1. Neutrino Oscillation of Three Flavors

Neutrino oscillation occurs when the neutrino of a given flavor $\alpha =\{e,\mu ,\tau \}$ can be after some distance and some time measured in a different flavor state. It is well known [1,3] that it is a consequence of the (non)correspondence between flavor $\{{\nu }_e,{\nu }_{\mu },{\nu }_{\tau }\}$ and massive neutrino states $\{{\nu }_1,{\nu }_2,{\nu }_3\}$, which are connected via Pontecorvo-Maki-Nakagawa-Sakata unitary lepton mixing matrix $U_{PMNS}$:

$$\left(\begin{array}{c}{\nu }_e\\ {\nu }_{\mu }\\ {\nu }_{\tau }\end{array}\right)=U_{PMNS}\left(\begin{array}{c}{\nu }_1\\ {\nu }_2\\ {\nu }_3\end{array}\right),$$

(1)

where the matrix $U_{PMNS}$ in the case of Dirac neutrino (considered in this paper) is parameterized with three mixing angles ${\theta }_{12},{\theta }_{23},{\theta }_{13}$ and one CP (charge conjugation parity)-violating phase $\delta$ [1]:

$$U_{PMNS}=\left(\begin{array}{ccc}{c}_{12}{c}_{13}& s_{12}{c}_{13}& s_{13}{e}^{-i\delta }\\ -s_{12}{c}_{23}-c_{12}{s}_{23}{s}_{13}{e}^{i\delta }& c_{12}{c}_{23}-s_{12}{s}_{23}{s}_{13}{e}^{i\delta }& s_{23}{c}_{13}\\ s_{12}{s}_{23}-c_{12}{c}_{23}{s}_{13}{e}^{i\delta }& -c_{12}{s}_{23}-s_{12}{c}_{23}{s}_{13}{e}^{i\delta }& c_{23}{c}_{13}\end{array}\right)$$

(2)

with $c_{ij}=cos\left({\theta }_{ij}\right)$ and $s_{ij}=sin\left({\theta }_{ij}\right)$ (following Ref. [18] we set $s_{12}^2=0.307$, $s_{13}^2=0.021$ and $s_{23}^2=0.5$) and $\delta$ being the CP-violating phase. The results obtained at the current level of experimental sensitivity are compatible with $\delta =0$; however, as shown below, the hypothetical CP-violation and the (non-vanishing) phase $\delta$ is a highly non-trivial parameter affecting neutrino oscillation.

The time evolution of the neutrino is governed by the Schrödinger equation in the flavor basis:

$$i\frac{d}{dt}{\mathsf{\Psi }}_F={\mathcal{H}}_{\mathcal{F}}{\mathsf{\Psi }}_F,$$

(3)

where ${\mathsf{\Psi }}_F$ describes the flavor neutrino state for a given time t and ${\mathcal{H}}_{\mathcal{F}}$ is the Hamiltonian [1,19,20,21]:

$${\mathcal{H}}_{\mathcal{F}}=H_{kin}+H_{pot},$$

(4)

consisting of the kinetic $H_{kin}$ and $H_{pot}$ potential parts to be described below.

Taking into account an ultrarelativistic limit for the neutrinos (with neutrino’s eigenenergies $E_k=E+\frac{m_k^2}{2E}$ and momentum $p\sim E$)—the kinetic part of the Hamiltonian in the flavor basis reads:

$$H_{kin}=\frac{1}{2E}{U}_{PMNS}\left(\begin{array}{ccc}0& 0& 0\\ 0& \mathsf{\Delta }{m}_{21}^2& 0\\ 0& 0& \mathsf{\Delta }{m}_{31}^2\end{array}\right)U_{PMNS}^{†},$$

(5)

where $\mathsf{\Delta }{m}_{ij}^2=m_i^2-m_j^2$ is the difference between the masses of two oscillating neutrinos. In the following numerical calculations, we set $\mathsf{\Delta }{m}_{12}^2=7.37·{10}^{-5}e{V}^2$ and $\mathsf{\Delta }{m}_{31}^2=2.52·{10}^{-3}e{V}^2$ [18].

For the potential part $H_{pot}$, the main contribution originates from neutrino’s interaction (via the coherent forward elastic scattering and for negligible non-coherent effects) with the matter’s electrons and the weak charge of the nuclei generating charged-current potential $V_{CC}$. The potential part of the Hamiltonian takes then the following form:

$$H_{pot}=\left(\begin{array}{ccc}{V}_C& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right).$$

(6)

The charged-current potential $V_C$ is related to the electron’s density in the matter $V_C=\sqrt{2}{G}_F{n}_e$ with the Fermi coupling constant $G_F$ and the electron number density $n_e$.

1.2. Continuous Non-Selective Measurement

Projective ideal measurement originating form famous von Neumann ideas plays significant role for understanding fundamental differences between classical and quantum models of Nature. However, it is well known that real experiments that are associated with measuring physical quantities almost never can be sufficiently described in terms of von-Neumann scheme [17,22,23]. The reason is easy to express: one can hardly perform a measurement on a quantum system per se. One rather attempts to allow the system under consideration to interact with some other system—a probe—which properties are accessible for classical apparatus. The indirect measurement can be summarized in a following two-step procedure: First, (i) an observable A of a quantum system to be measured couples to a probe ‘position’ Q resulting in a term $H_{int}=A\otimes Q$ in a system-probe total Hamiltonian

$$\begin{array}{ccc}\hfill H_{sys+probe}& =& H_{sys}+H_{probe}+g\left(t\right)H_{int}\hfill \end{array}$$

(7)

Subsequently, (ii) the probe ‘momentum’ P canonically conjugated to Q is (projectively) measured.

If one assumes non-selective measurement—a measurement with the result ignored—carried on a time interval subdivided into intervals of length q, the reduced (with respect to the probe) dynamics of the quantum system is no longer unitary, but rather becomes a quantum completely positive map [24].

Let us recall that a map of a Hilbert space $\Lambda :\mathcal{H}\to \mathcal{H}$ is completely positive if its (trivial) extension $\Lambda \otimes {\mathcal{I}}_{n\times n}:\mathcal{H}\otimes \mathcal{K}\to \mathcal{H}\otimes \mathcal{K}$ with an identity ${\mathcal{I}}_{n\times n}$ of an arbitrary dimension n maps quantum states (positive operators) into quantum states. The concept of complete positivity is one of the possible guidelines for constructing reduced non-unitary dynamics ${\Lambda }_t:{\mathcal{H}}_{sys}\to {\mathcal{H}}_{sys}$ of composite ${\mathcal{H}}_{sys}\otimes {\mathcal{H}}_{probe}$ quantum systems. In particular, for a set of measurement operators $E_x$ (such that ${\sum }_x{E}_x^{†}{E}_x=I$), the non-selective measurement of a system in state $\rho$ results in a transformation $\rho \to {\sum }_x{E}_x\rho E_x^{†}$ and is an example of complete positive map [22]. In the case considered here, the measurement on each time (sub)interval q results in

$$\begin{array}{c}\hfill \rho (t+q)=\int dp{E}_p\rho \left(t\right)E_p^{†}\end{array}$$

(8)

with $E_p=e^{iq{H}_{sys}}⟨p|exp(-iq{H}_{int})|{\varphi }_q⟩$, where $|p⟩\in {\mathcal{H}}_{probe}$ is an eigenstate of P and $|{\varphi }_q⟩\in {\mathcal{H}}_{probe}$ is a state of the probe before measurement. For a finite-time duration of a measurement, expanding Equation (8) to the second order in q, one arrives to the corresponding dynamics of a system density matrix generated by a quantum master equation [25]

$$\begin{array}{c}\hfill \frac{d}{dt}\rho \left(t\right)=-i[H_{sys},\rho \left(t\right)]-\frac{\sigma }{2}\left[A,[A,\rho (t\left)\right]\right]\end{array}$$

(9)

with a parameter $\sigma$ describing back-action of a measurement. For an integrated coupling strength $q\sim {\int }_0^{t}g\left(s\right)ds$ proportional to the length of time (sub)interval q the parameter $\sigma$ reads as

$$\begin{array}{ccc}\hfill {\sigma }^2& :=& \underset{q\to 0}{lim}q⟨{\varphi }_q|Q^2|{\varphi }_q⟩\hfill \end{array}$$

(10)

where the limit describes passage from a step-like to a truly continuous measurement. As the measurement involves conjugate variables $p,Q$ of the probe, the more accurately the observable A is measured, i.e., the more information is gained, the larger $\sigma$ enters Equation (9), as discussed in Ref. [25]. Let us notice that if one identifies $t_z=1/{\sigma }^2$ with a Zeno time, in the limit $t_z\to 0$ one arrives to the celebrated quantum Zeno effect [25,26]. In other words, the case of finite $\sigma$ applied here can be viewed as a ‘non-ideal Zeno effect’.

Further, we consider continuous non-selective measurement of a neutrino described by the master equation Equation (9), with

$$\begin{array}{c}\hfill H_{sys}={\mathcal{H}}_{\mathcal{F}}\end{array}$$

(11)

and we limit our attention to two observables. The first

$$\begin{array}{ccc}\hfill F& =& \sum _{x=e,\mu ,\tau }{a}_x{\mathsf{\Pi }}_x,where{\mathsf{\Pi }}_x=|{\nu }_x⟩⟨{\nu }_x|,x=e,\mu ,\tau \hfill \end{array}$$

(12)

corresponds to a ’favour measurement’. The second, diagonal in a mass-state basis

$$\begin{array}{ccc}\hfill M& =& \sum _{x=1,2,3}{a}_x{\mathsf{\Pi }}_x,where{\mathsf{\Pi }}_x=|{\nu }_x⟩⟨{\nu }_x|,x=1,2,3\hfill \end{array}$$

(13)

will be called a ‘mass-state measurement’. For both observables $F,M$, we assume $a_e=-a_{\tau }=1$ and $a_{\mu }=0$ in analogy to standard representation of one of the angular momentum operators $J_z\sim diag(-1,0,1)$. In other words, we consider two unitary coupled observables $F\sim U_{PMNS}M{U}_{PMNS}^{†}$ formally representing a $J_z$-component of angular momentum in two unitary equivalent bases: the flavor $\{|{\nu }_x⟩{\}}_{x=e,\mu ,\tau }$ and the mass-state $\{|{\nu }_x⟩{\}}_{x=1,2,3}$ basis, respectively.

Let us emphasise that Equation (9), if compared e.g., to a so called singular coupling limit [27], formally describes an open system with a particular, measurement-originated coupling $H_{int}$. To be precise, we are far from a claim that any measurement schemes for the above ‘observables’ are currently experimentally accessible: in particular, it is clearly and obviously the case of the mass-state measurement, which is known to be unavailable for neutrinos. Our aim is to describe a back-effect of a potential non-selective measurement-like quantum-classical environment affecting neutrino oscillation (i.e., a very particular type of decoherence) rather than to analyse any nowadays realistic measurement scenario we simply adopt terminology typical for quantum measurement [17,22].

2. Results

We analyse an effect of non-selective measurement on neutrino oscillation quantified by a probability $P_{e\to x}$ (with $x=e,\mu ,\tau$) of a neutrino’s change of flavor, i.e., of a transition of an electron neutrino into one of three flavors ${\nu }_e\to {\nu }_x$. We compare three cases: (i) free oscillation in an absence of a measurement, (ii) the ‘flavor measurement’ of the observable F Equation (12), and (iii) the ‘mass-state measurement’ given by M in Equation (13).

Effective dynamics in the presence of continuous non-selective measurement leads to a Markovian master equation formally identical to class o dissipative open quantum systems resulting in continuous information leakage from the system to its ‘environment’ which in our case is a ’probe’ in a measurement model. It is expected that neutrinos, evolving according to Equation (9), approach finally their equilibrium [24] which, although non-thermal, is characterized by equal transition probabilities $P_{e\to x}=1/3$ for each $x=e,\mu ,\tau$. However, if one considers short-time transient behaviour, one observes significantly different behaviour of different probabilities as presented in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. Continuous non-selective measurement of both F and M leads to a significant enhancement of $P_{e\to \mu }$ probability in comparison with remaining inter-flavor transitions which become less likely in a short-time evolution as presented in Figure 1. Moreover, continuous measurements, either of F or M, result in the suppression of probability oscillations which becomes particularly visible in a presence of non-vanishing charge-current potential, as presented in Figure 2. In other words, continuous non-selective measurement of neutrino’s flavor (or mass) can be responsible for a potential suppression of neutrino oscillations.

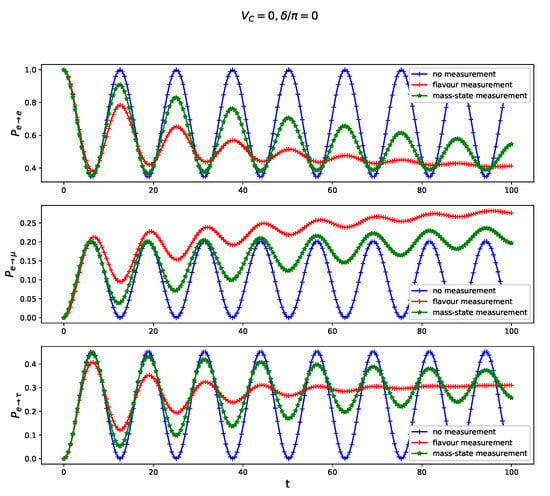
Figure 1. Transition probability for free three-flavor neutrino oscillation juxtaposed with the oscillations modified by a continuous non-selective measurement of the flavor cf. Equation (12) and ‘mass-state’ cf. Equation (13) calculated for vanishing CP-violating phase $\delta =0$ in the absence of normal matter $V_C=0$.The amplitude of a back-action in Equation (9) $\sigma =0.1$ and time t is scaled in units of E.

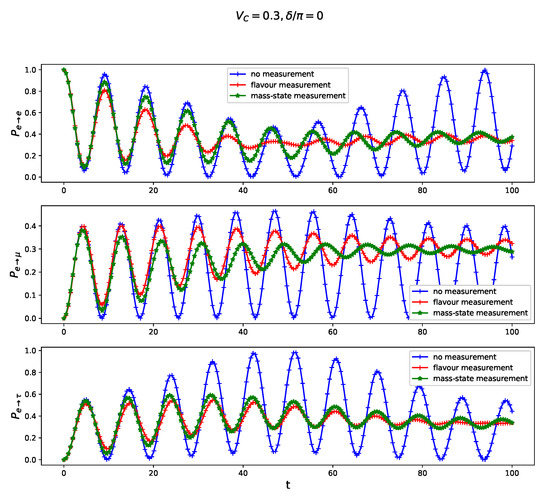
Figure 2. Transition probability for free three-flavor neutrino oscillation juxtaposed with the oscillations modified by a continuous non-selective measurement of the flavor cf. Equation (12) and ’mass-state’ cf. Equation (13) calculated for vanishing CP-violating phase $\delta =0$ in the presence of normal matter indicated by non-vanishing charge current $V_{C}0.3$. The amplitude of a back-action in Equation (9) $\sigma =0.1$ and time t is scaled in units of E.

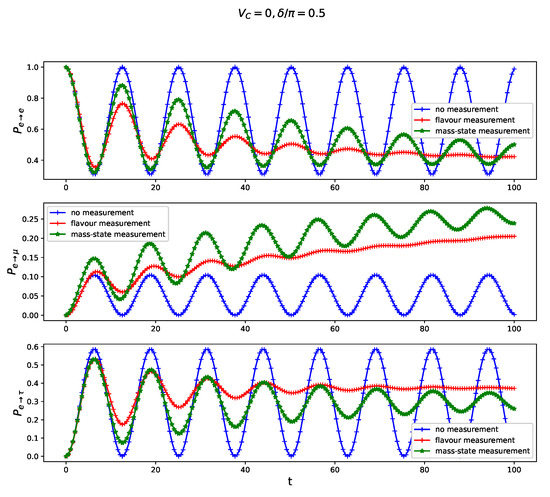
Figure 3. Transition probability for free three-flavor neutrino oscillation juxtaposed with the oscillations modified by a continuous non-selective measurement of the flavor cf. Equation (12) and ‘mass-state’ cf. Equation (13) calculated for non-vanishing CP-violating phase $\delta =\pi /2$ and vanishing charge current $V_C=0$. The amplitude of a back-action in Equation (9) $\sigma =0.1$ and the time is scaled in units of E.

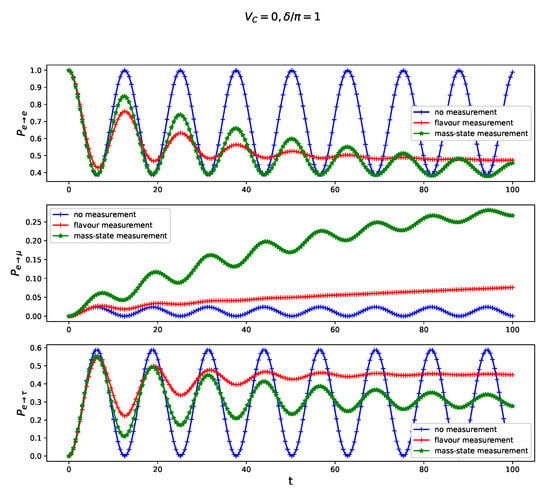
Figure 4. Transition probability for free three-flavor neutrino oscillation juxtaposed with the oscillations modified by a continuous non-selective measurement of the flavor cf. Equation (12) and ’mass-state’ cf. Equation (13) calculated for non-vanishing CP-violating phase $\delta =\pi$ and vanishing charge current $V_C=0$. The amplitude of a back-action in Equation (9) $\sigma =0.1$ and the time is scaled in units of E.

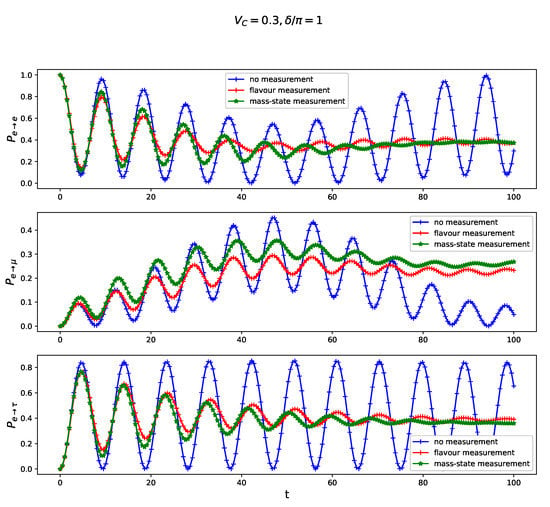
Figure 5. Transition probability for free three-flavor neutrino oscillation juxtaposed with the oscillations modified by a continuous non-selective measurement of the flavor cf. Equation (12) and ’mass-state’ cf. Equation (13) calculated for non-vanishing CP-violating phase $\delta =\pi$ and the charge current $V_C=0.3$. The amplitude of a back-action in Equation (9) $\sigma =0.1$ and the time is scaled in units of E.

For sake of generality, we have assumed, in the model formulation, a not vanishing $\delta \ne 0$ in Equation (2), even though the resulting CP-violation is so far entirely hypothetical. We present in Figure 3 that the most significant impact of the CP-violation indicated by $\delta \ne 0$ occurs for the ${\nu }_e\to {\nu }_{\mu }$ transition quantified by $P_{e\to \mu }$. In particular, let us notice that $P_{e\to \mu }$ in the presence of ‘mass-state measurement’ becomes larger in comparison to ’flavor measurement’ case for CP-violating systems what is indicated by reversed ordering of plots in central sub-panels in Figure 1, Figure 3 and Figure 4. This observation holds true also in the presence of charge-current potential $V_C$, as can be inferred from comparison central panels of Figure 2 and Figure 5.

The two-time steady state correlation function ${⟨F(t+K)F\left(t\right)⟩}_{ss}$ is one of the simplest quantifiers of a multi-time structure of quantum Markov evolution [28]. Here, we study an effect of continuous measurement—either of the ‘mass-state observable’ M or the flavor observable F—on the properties of the steady-state auto-correlation of F. In Figure 6 we juxtapose effects of this measurements in an absence of CP-violation for vanishing (upper panel of Figure 6 and a non-vanishing (lower panel of Figure 6 charge-current potential $V_C$. Let us notice that in a presence of normal matter the steady-state correlation functions become less sensitive for a choice of the observable (either F or M) that is measured. This effect becomes even more apparent, cf. Figure 7, in a system with both non-vanishing CP-violating phase $\delta \ne 0$ and charge-current potential $V_C\ne 0$, which makes the autocorrelation $⟨F\left(t\right)F\left(0\right)⟩$ for both measurement observables harder to distinguish.

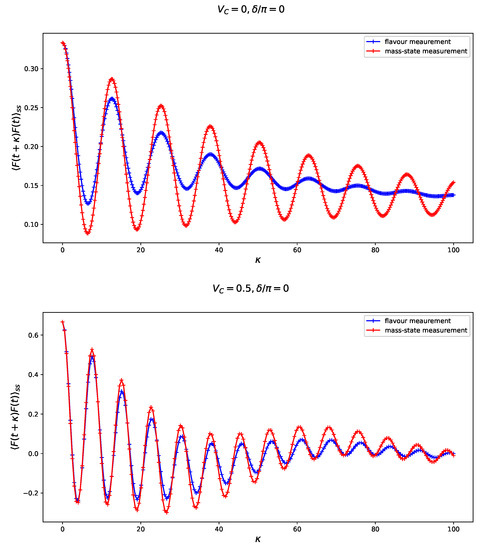
Figure 6. Steady-state autocorrelation function for observable F in Equation (12) affected by a continuous non-selective measurement of the flavor and ‘mass-state’ in an absence of normal matter $V_C=0$ and with vanishing CP-violating phase $\delta =0$ (upper panel) juxtaposed with results for non-vanishing $V_C=0.5$ (lower panel). The amplitude of a back-action in Equation (9) $\sigma =0.1$ and the time is scaled in units of E.

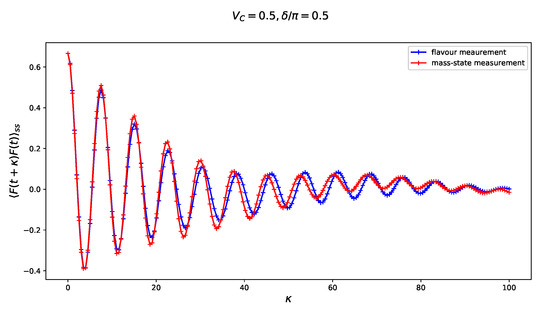
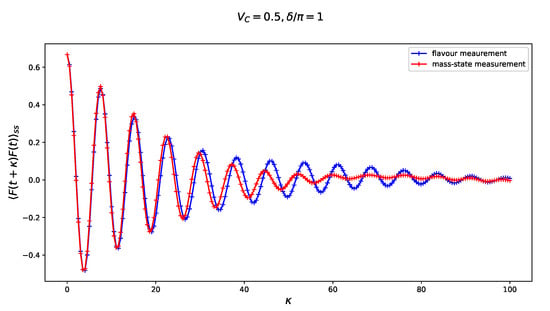
Figure 7. Steady-state autocorrelation function for observable F in Equation (12) affected by a continuous non-selective measurement of the flavor and ‘mass-state’ in the presence of normal matter $V_C=0.5$ and with non-vanishing CP-violating phase $\delta =\pi /2$ (upper panel) juxtaposed with results for $\delta =\pi$ (lower panel). The amplitude of a back-action in Equation (9) $\sigma =0.1$ and the time is scaled in units of E.

3. Discussion

There are various sources of dissipation affecting quantum dynamics in various time scales: one can study thermal or non-thermal decoherence, asymptotic equilibrium or short time transient dynamics of a system far from equilibrium. Our results concern very special source of dissipation in neutrino oscillation that originates from the coupling of one of the observables to a classical surrounding. This model is formally equivalent to a continuous non-selective measurement. For three-flavor oscillation studied in this paper, one can distinguish two bases that are of a great physical importance: the mass state basis and the flavor basis related by the Pontecorvo-Maki-Nakagawa-Sakata unitary lepton mixing matrix Equation (1) and the related (diagonal) observables Equations (12) and (13) of formally related to the symmetry to the angular momentum operators in three dimensional representation of the $su\left(2\right)$ algebra. We investigated short time (with respect to equlibration time) inter-flavor transitions probabilities of an initially electron neutrino. We showed significant impact of both a presence of normal matter indicated by non-vanishing charge current and the potential CP-violation. In particular, one expects an enhancement of the ${\nu }_e\to {\nu }_{\mu }$ transition probability, as presented in Figure 1 and Figure 2, an effect that becomes even stronger for CP-violating systems, as presented in Figure 3, Figure 4 and Figure 5. For remaining transitions ${\nu }_e\to {\nu }_{e,\tau }$, the main effect is the suppression of oscillations which is particularly strong for the systems coupled (’measured’) via M to an environment (probe). Autocorrelation of the ‘flavor observable’ F is the second quantifier studied in this paper, although less obvious in a context of neutrinos, is a very basic for identifying non-trivial multi-time structure of quantum dynamics. In Figure 6, we present the steady-state autocorrelation for two previously studied types of ‘measurement’. Suppression of oscillations in a presence of both normal matter and CP-violation Figure 7 is here the most striking property.

4. Conclusions

There are many aspects of neutrino oscillation that make this phenomenon a natural object of interdisciplinary research. In particular, a three-level simplification of this otherwise highly complex physical system allows for extracting its dynamical properties in various phenomenologically modelled circumstances. Last but not least, it provides an example of a quantum dynamical system of the properties seemingly far from particle physics, closer related to quantum information and measurement theory. Our work, although speculative in character, describes the dynamics of neutrino oscillation in the presence of an environment that mimics continuous non-selective measurement and relates a potential suppression of neutrino oscillation to the (imperfect) Zeno-like mechanism. Selective measurements of neutrinos are extremely difficult and rare, we hope that our model incorporating the ‘almost successful’ non-selective case sheds light on dynamical properties of neutrinos and the role played by fundamental symmetries, such as the celebrated CP-violation.

5. Materials and Methods

For numeric calculations we use the Master equation solver from the Python-based toolbox QuTip [29,30]. In particular, we use qutip.mesolve module to obtain numerical solution (quantum state) of Equation (9) to calculate probabilities $P_{e\to x}$, $x=e,\mu ,\tau$. We use correlation_2op_1t with a parameter state0=None for a steady-state autocorrelation function.