Asymmetries in the Disturbance Compensation Methods for the Stable and Unstable First Order Plants
Abstract
1. Introduction
2. Problem Formulation
2.1. Feedforward Control
2.2. Stabilizing P Control
2.3. P Control as a Closed Loop Feedforward Implementation
2.4. Constrained Setpoint Feedforward Design
2.5. External and Internal Disturbances and Their Compensation
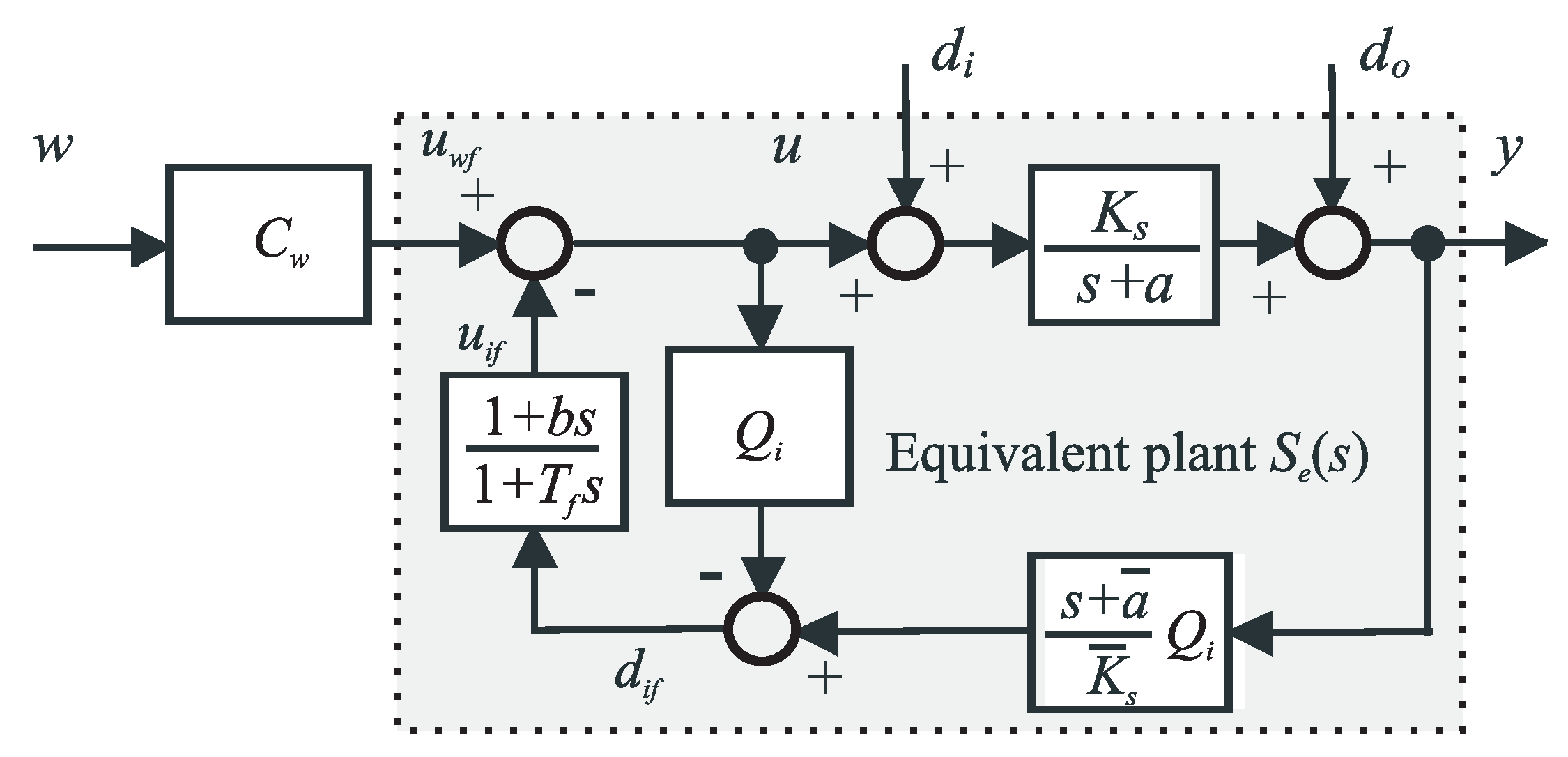
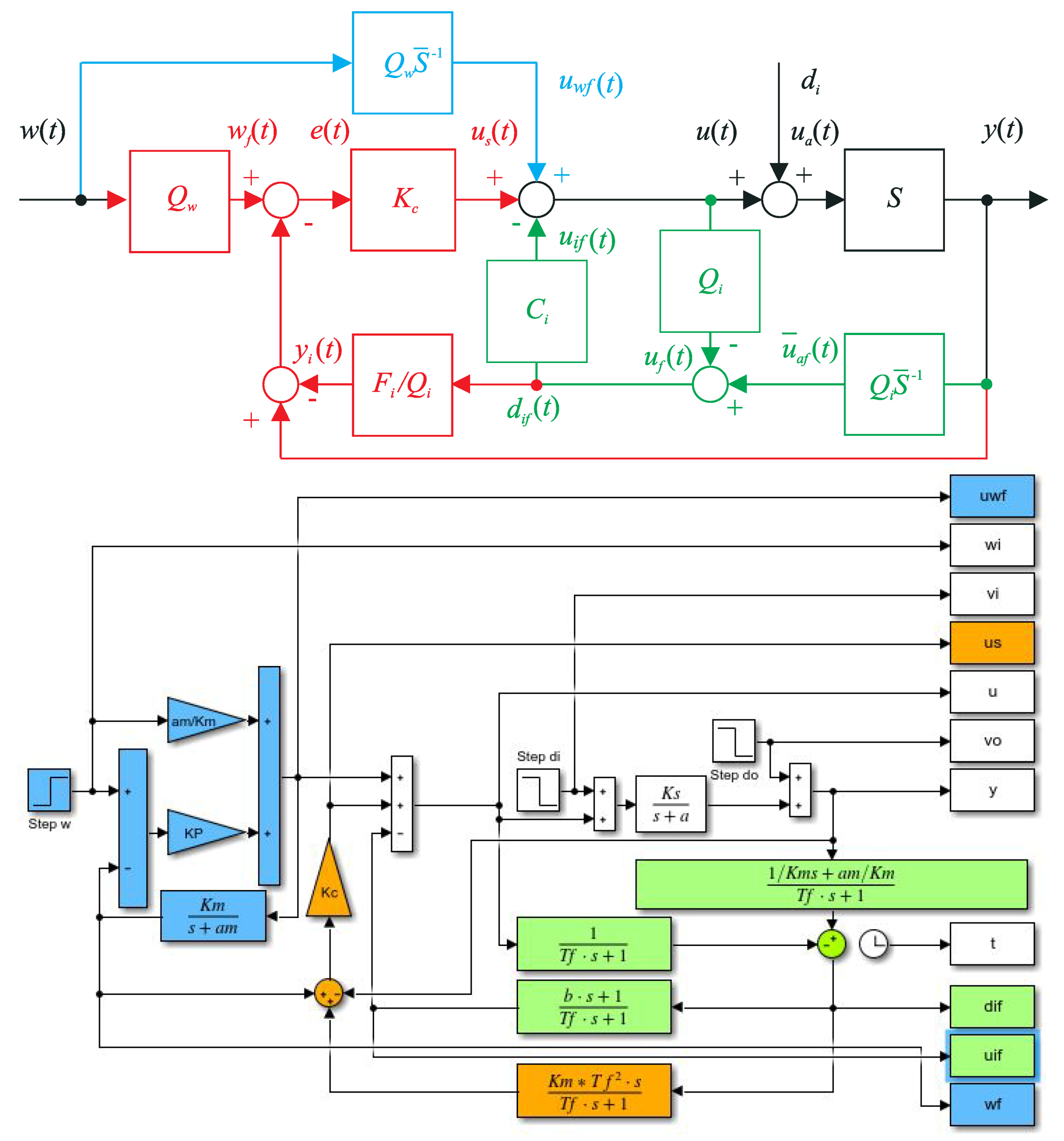
3. Disturbance Observer (DOB)-Based Control with Compensation of Input Disturbances
3.1. Decoupled Setpoint and Disturbance Feedforwards
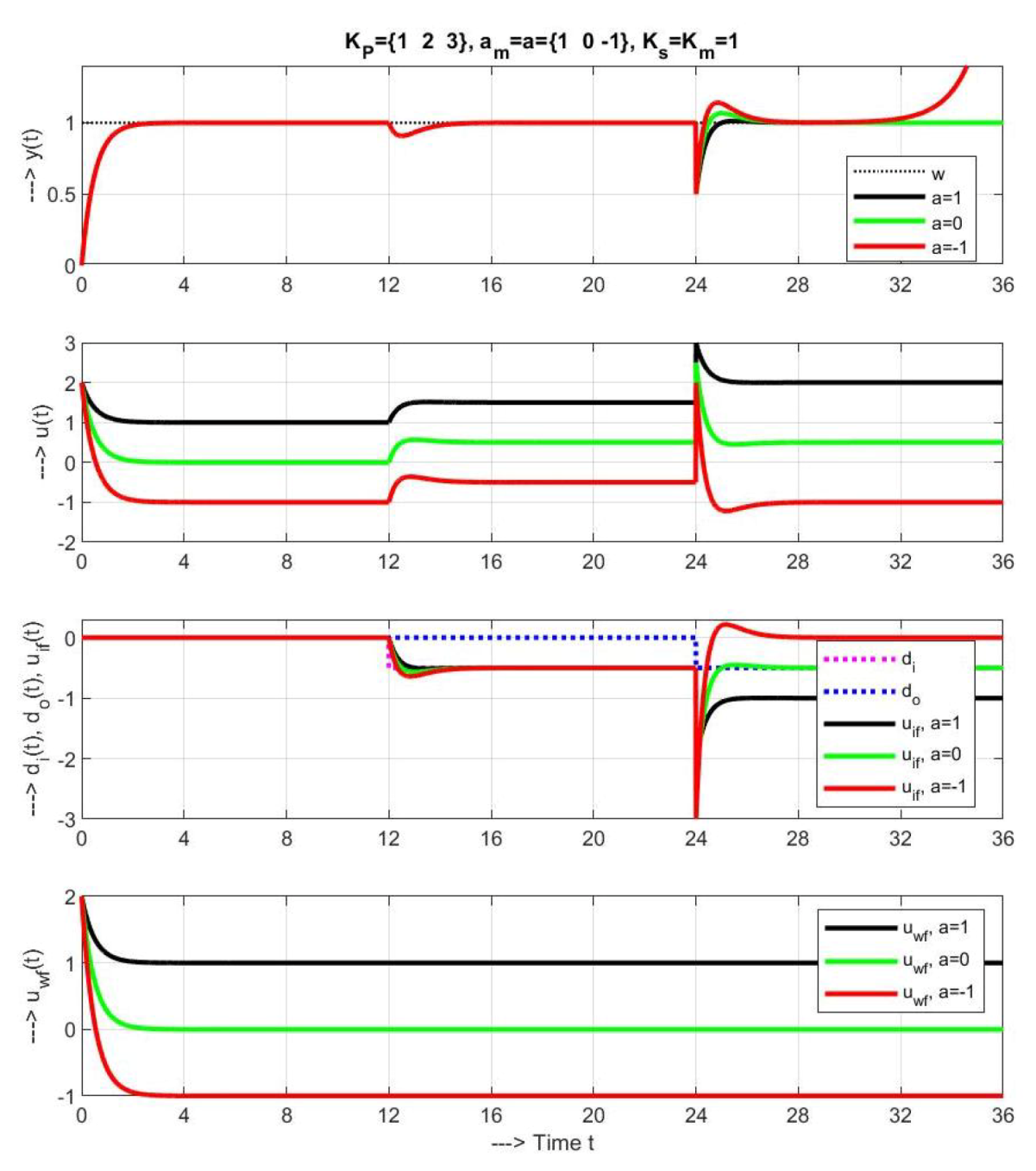
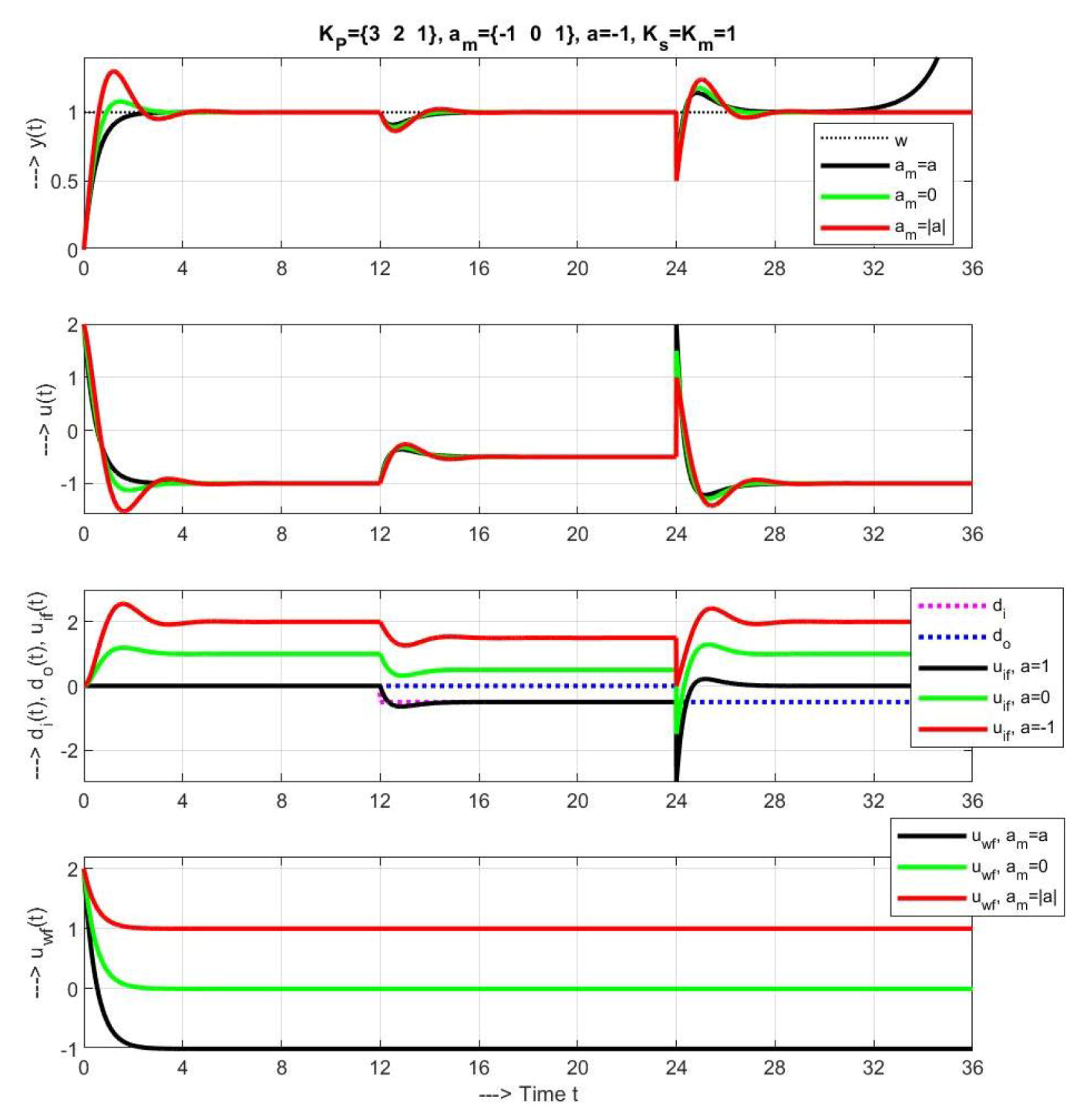
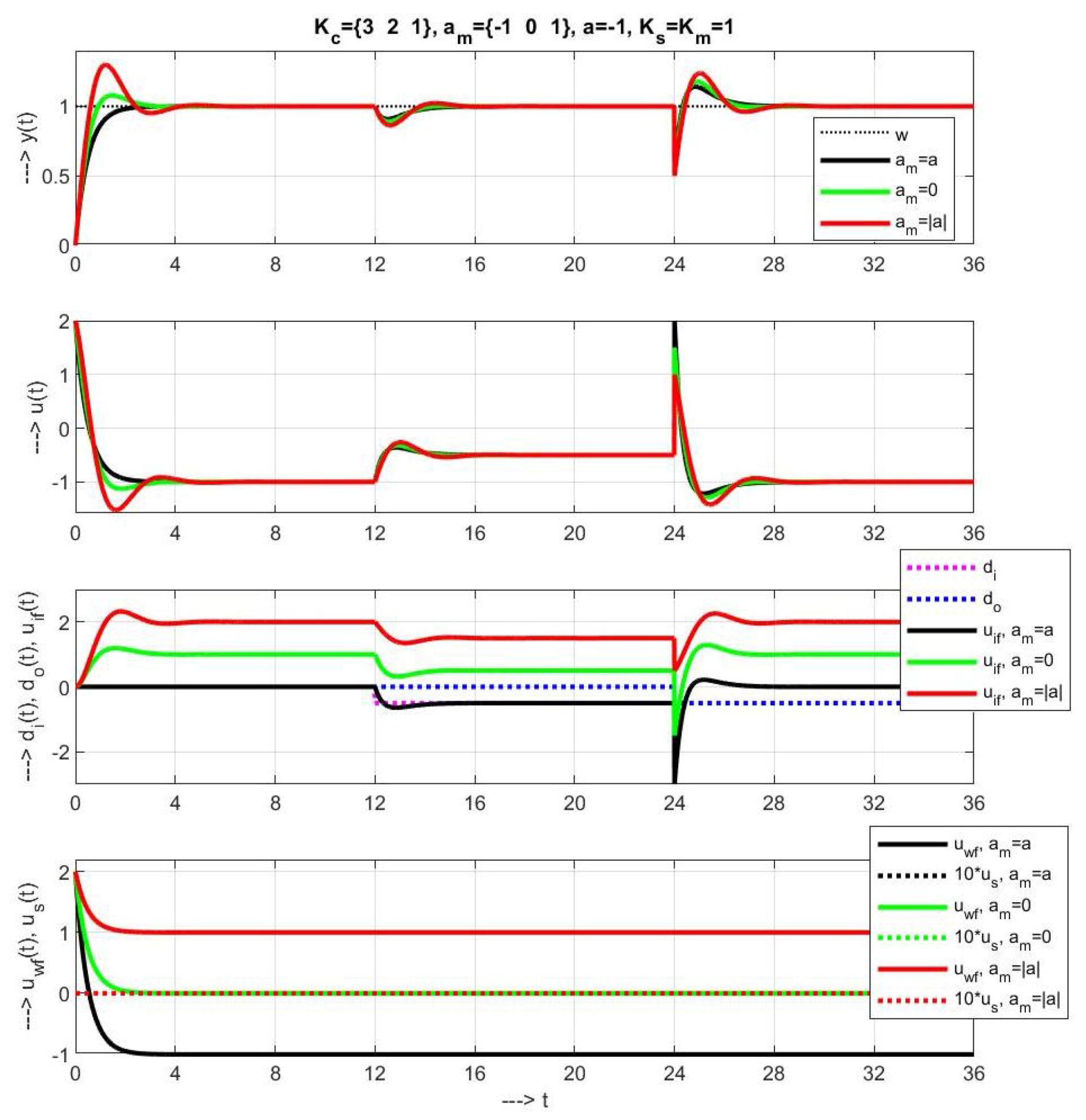
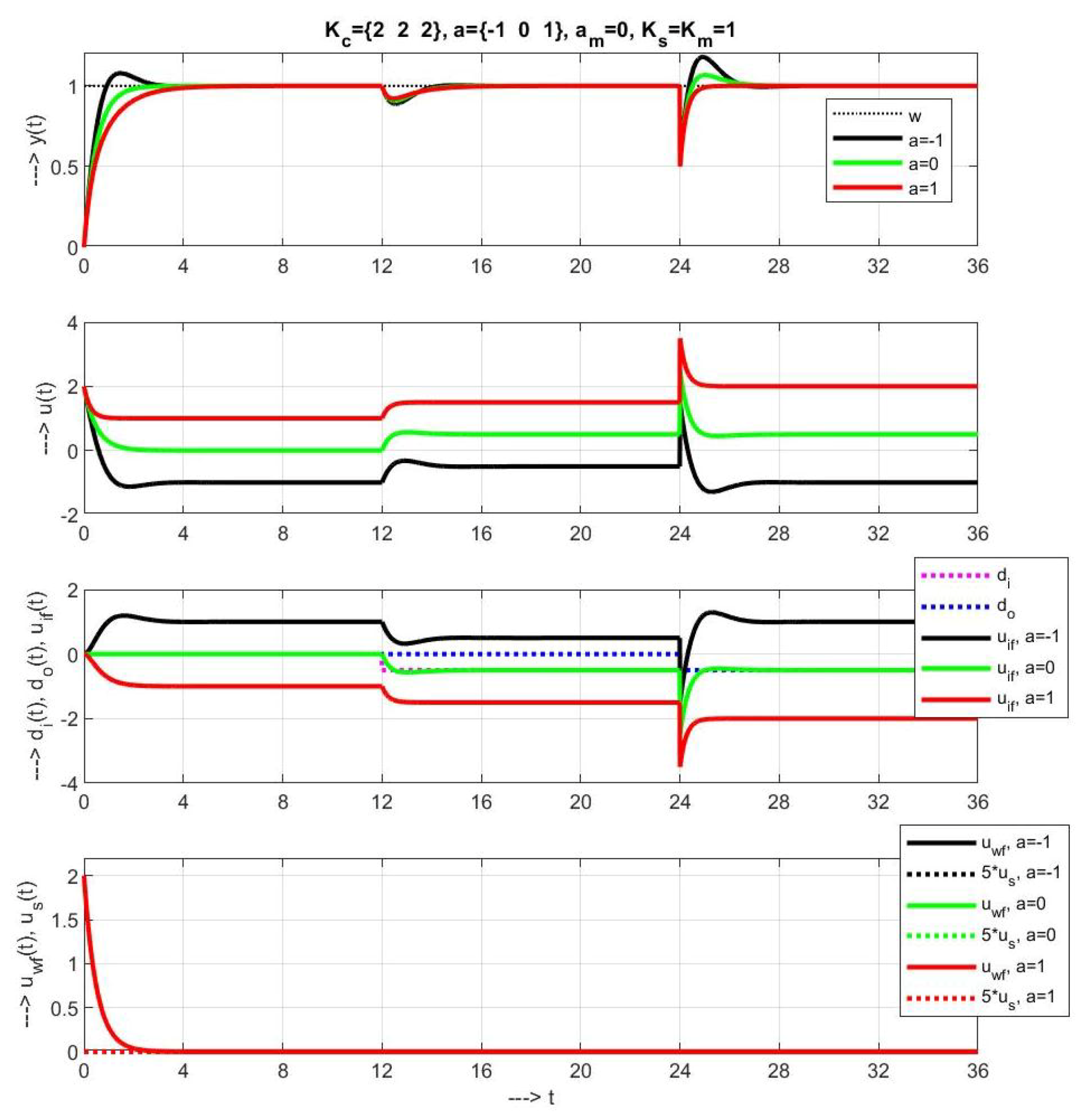
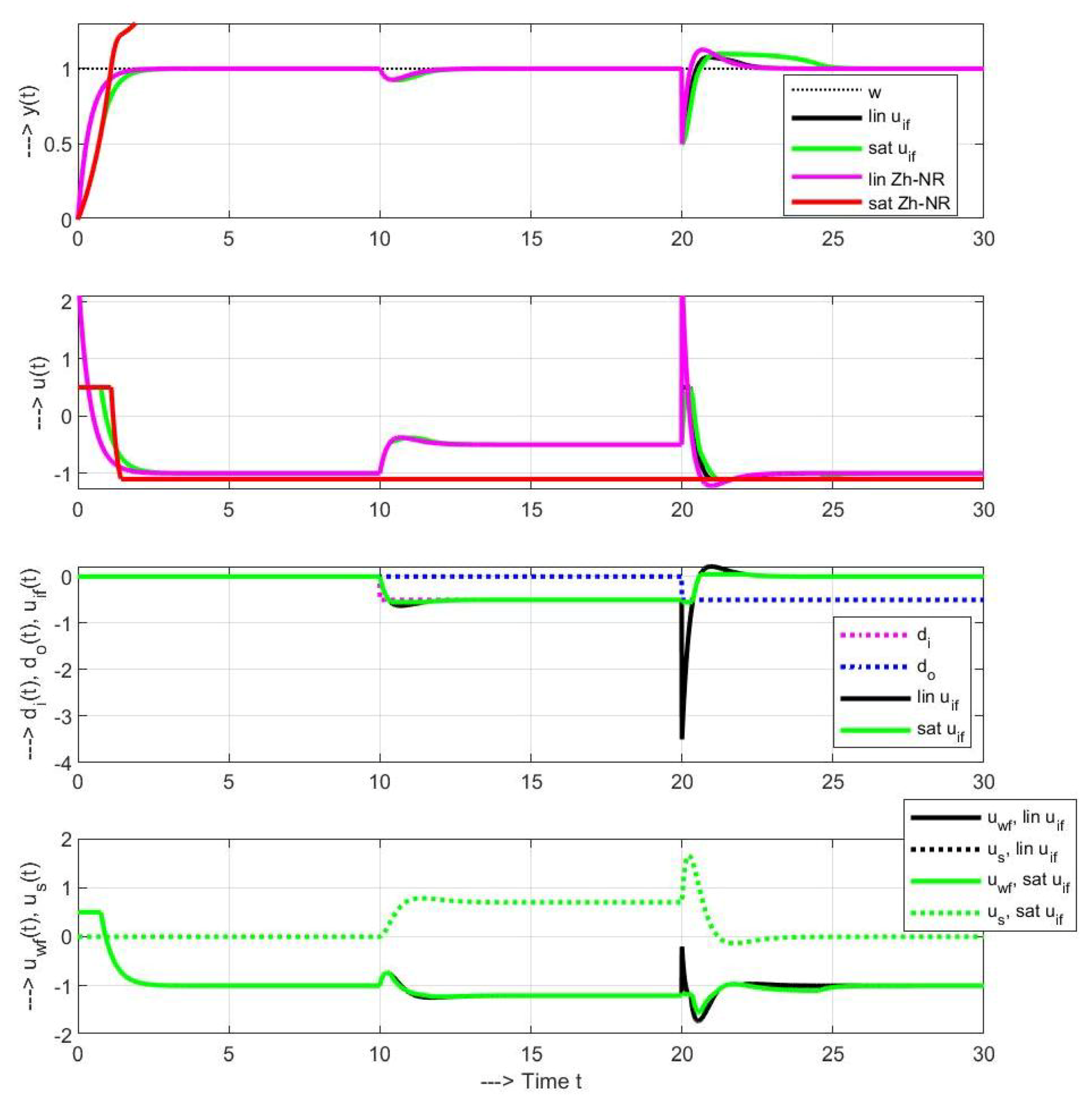
3.2. Sample of Transient Responses
3.3. Explanation of Stability Problems
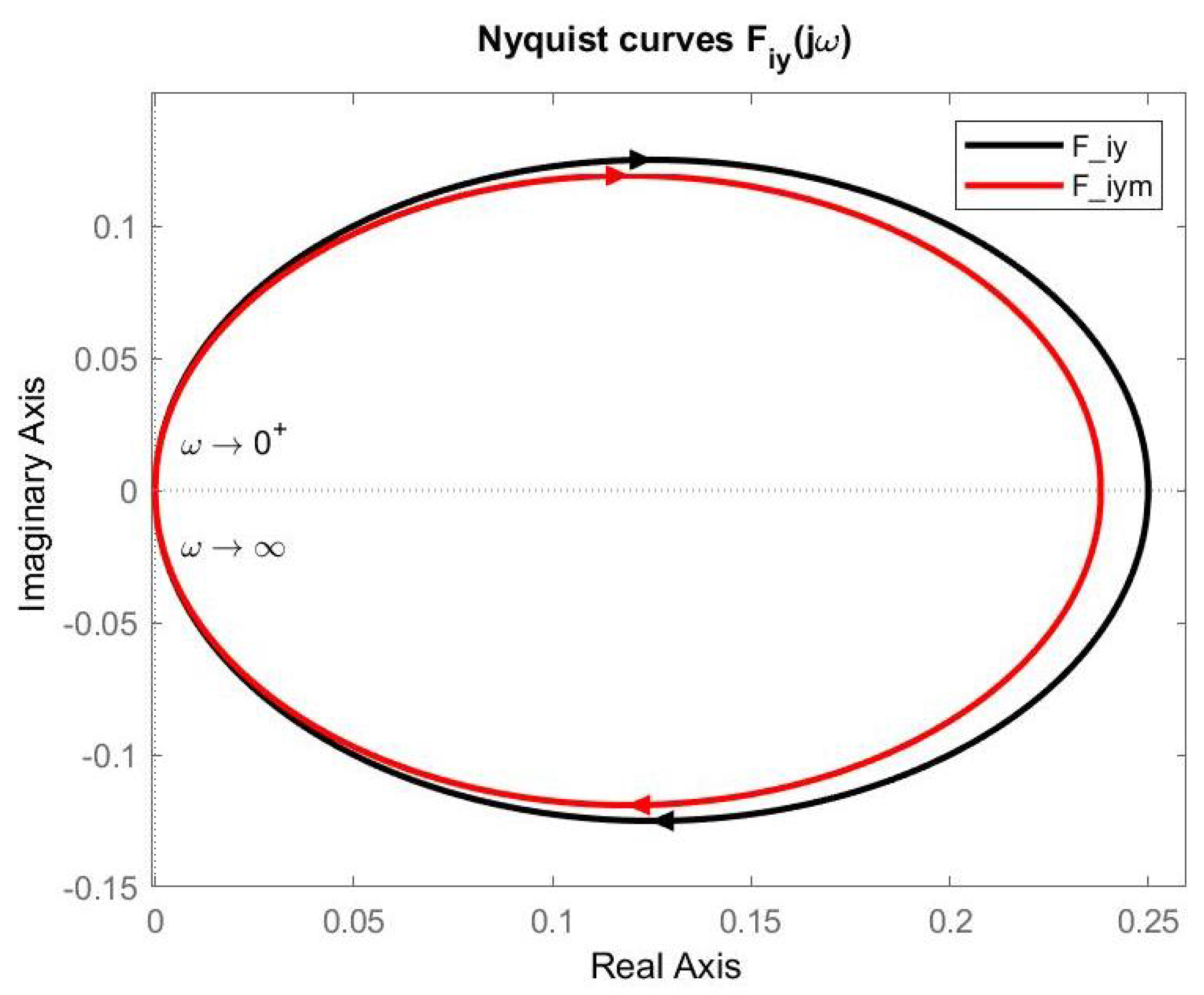
4. Setpoint and Disturbance Reference Model Control
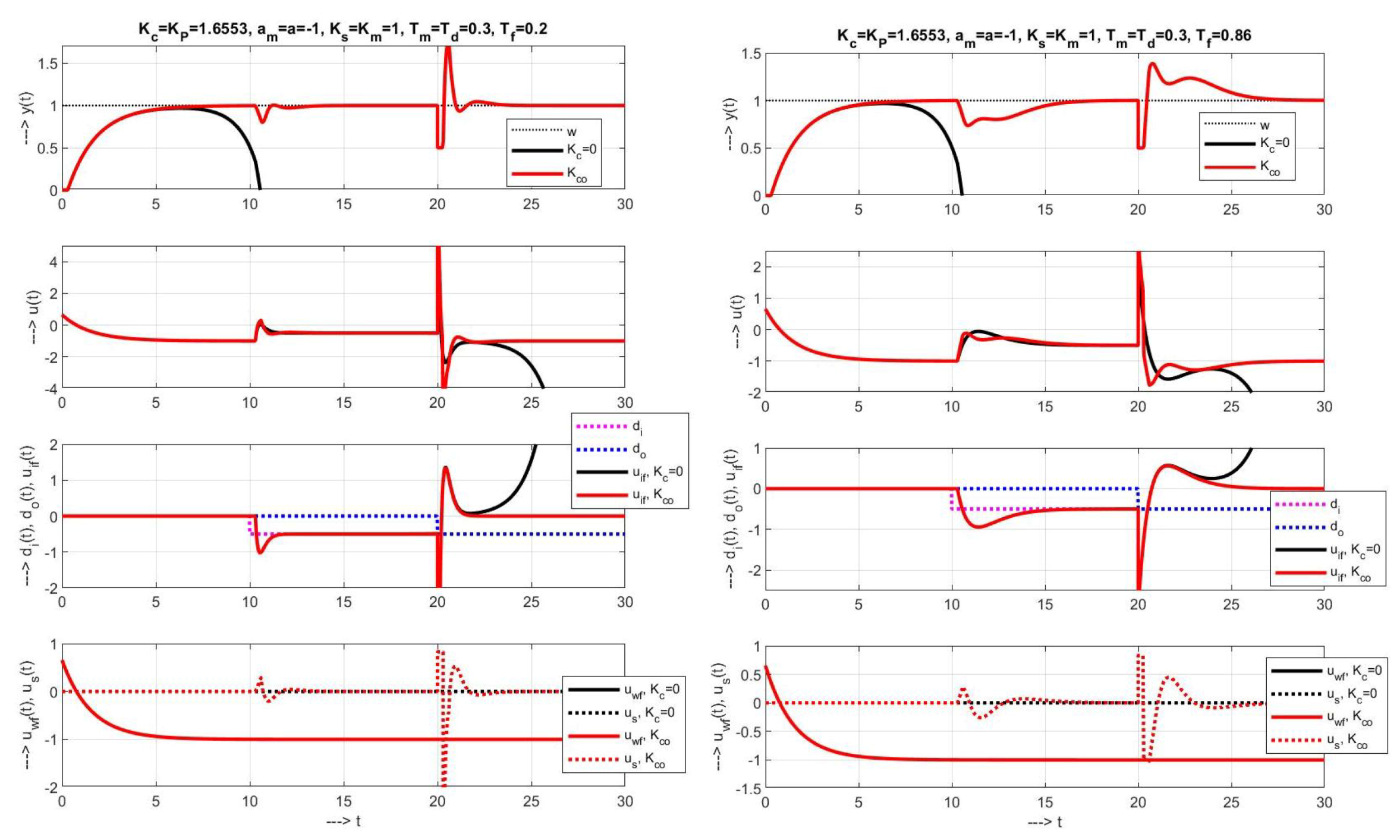
4.1. Reference Model Control with Supervising Stabilizing Controller (Sdob-Rm)
4.2. Constrained Control with Discussion of Some Modifications Proposed
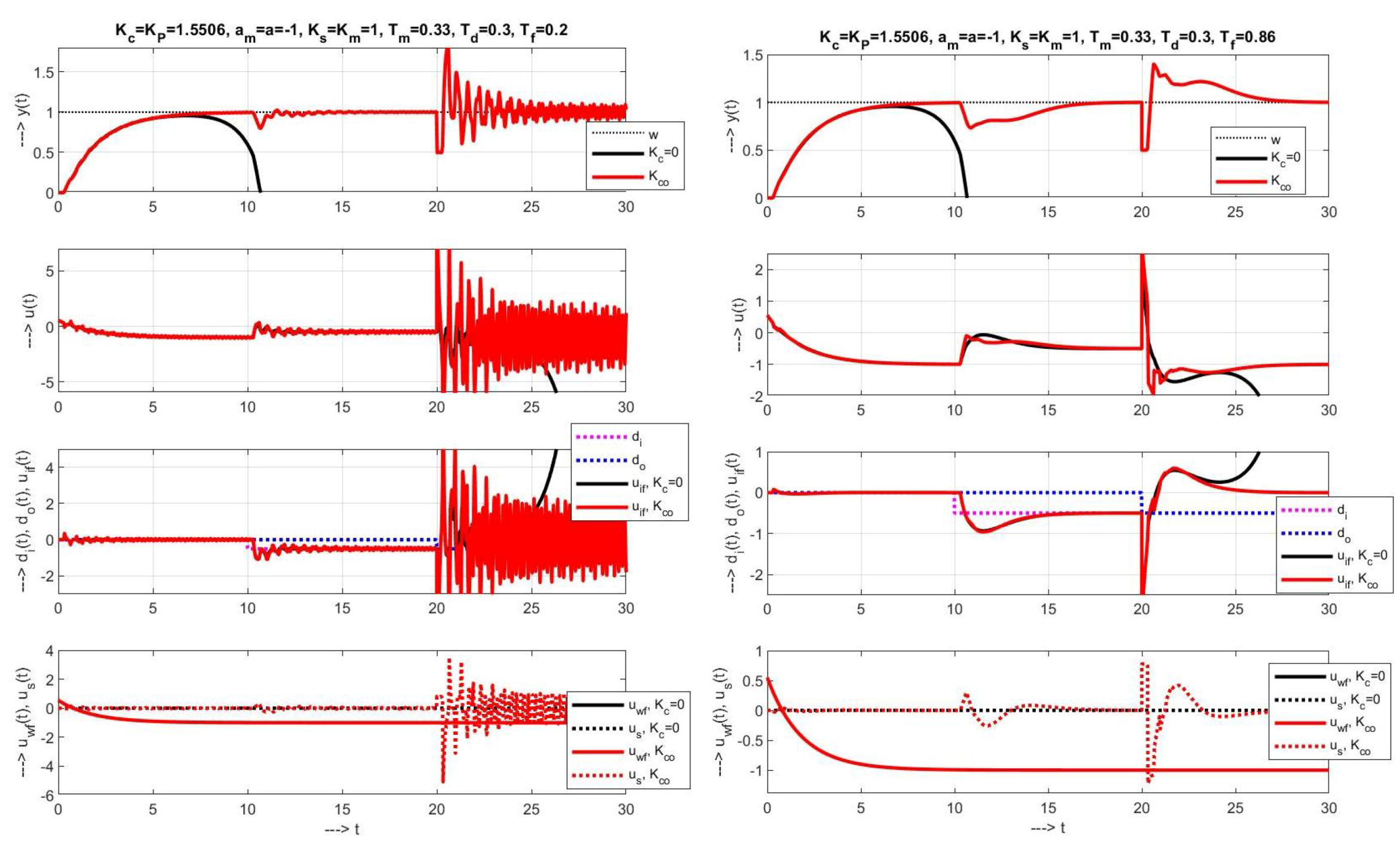
5. Generalization to Time Delayed Systems
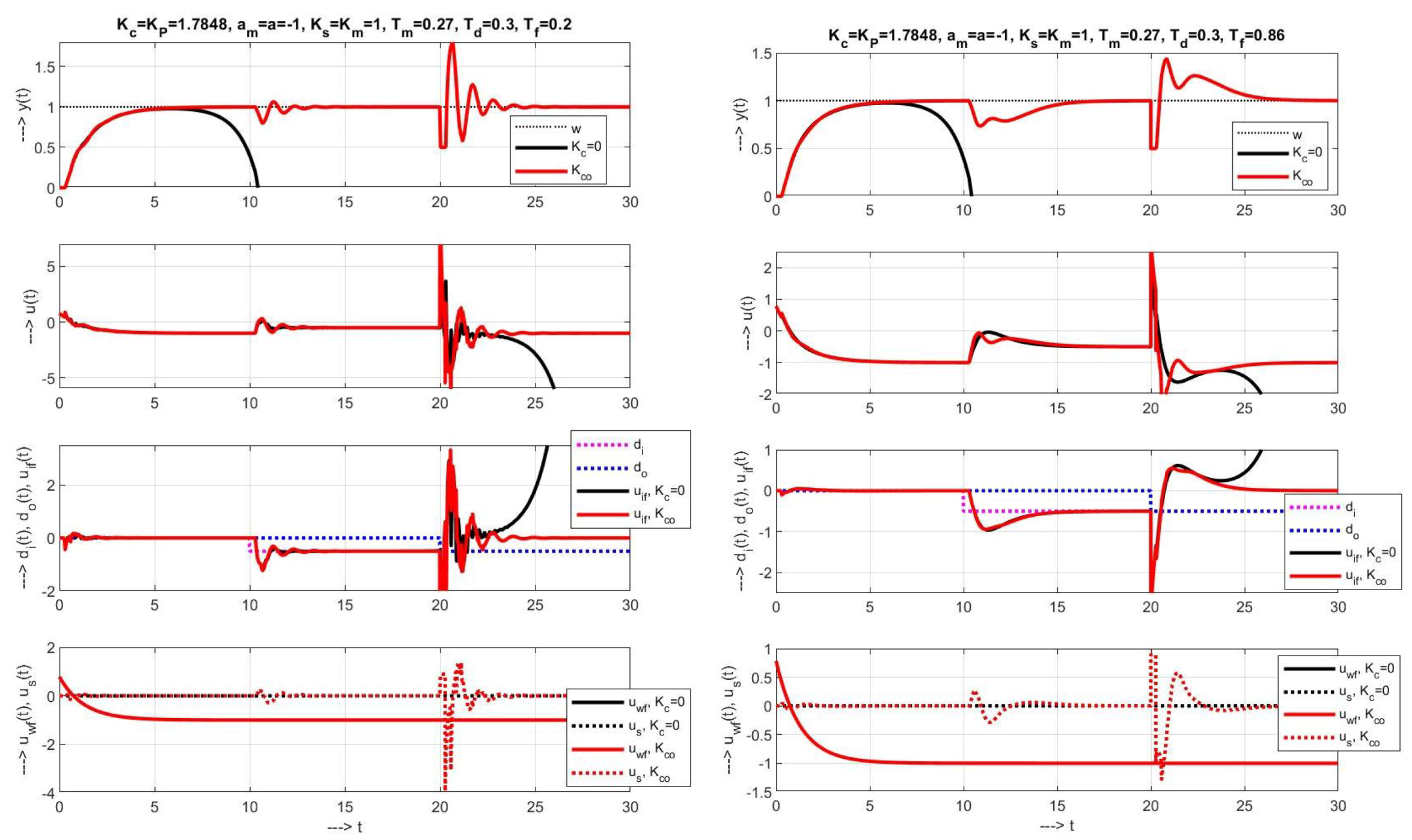
5.1. Setpoint and Disturbance Reference Models
5.2. Proportional Gains for FOTD Systems
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 2DOF | 2 Degree of Freedom |
| DOB | Disturbance observer |
| FOTD | First Order Time Delayed |
| FSP | Filtered Smith Predictor |
| IMC | Internal model control |
| P | Proportional |
| PI | Proportional-Integrative |
| PD | Proportional-Derivative |
| PID | Proportional-Integrative-Derivative |
| RM | Reference model |
| RMC | Reference model control |
| SDOB | Stabilizing disturbance observer |
| SP | Smith Predictor |
| UFOTD | Unstable First Order Time Delayed |
References
- O’Dwyer, A. Handbook of PI and PID Controller Tuning Rules, 3rd ed.; Imperial College Press: London, UK, 2009. [Google Scholar]
- Smith, O. Closser control of loops with dead time. Chem. Eng. Prog. 1957, 53, 217–219. [Google Scholar]
- Huba, M.; Kul’ha, P.; Žákova, K. Observer-Based Control of Unstable Process with Dead Time. In Proceedings of the 10th Conference Process Control’95, Tatranské Matliare, Slovakia, 4–7 June 1995; Volume 1, pp. 35–38. [Google Scholar]
- Garcia, P.; Albertos, P. A new dead-time compensator to control stable and integrating processes with long dead-time. Automatica 2008, 44, 1062–1071. [Google Scholar] [CrossRef]
- Sanz, R.; García, P.; Albertos, P. A generalized smith predictor for unstable time-delay SISO systems. ISA Trans. 2018, 72, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Huba, M.; Bélai, I. Limits of a Simplified Controller Design Based on IPDT models. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 728–741. [Google Scholar]
- Huba, M. Improving noise attenuation in modified filtered Smith predictor. In Proceedings of the 2020 Cybernetics and Informatics (KandI), Velke Karlovice, Czech Republic, 29 January–2 February 2020. [Google Scholar]
- Zhong, Q.; Normey-Rico, J. Control of integral processes with dead-time. Part 1: Disturbance observer-based 2DOF control scheme. IEE Proc. Control Theory Appl. 2002, 149, 285–290. [Google Scholar] [CrossRef]
- Normey-Rico, J.; Camacho, E. Dead-time compensators: A survey. Control. Eng. Pract. 2008, 16, 407–428. [Google Scholar] [CrossRef]
- Normey-Rico, J.; Camacho, E. Unified approach for robust dead-time compensator design. J. Process Control 2009, 19, 38–47. [Google Scholar]
- Vrečko, D.; Vrančič, D.; Jurčič, D.; Strmčnik, S. A new modified Smith predictor: The concept, design and tuning. ISA Trans. 2001, 40, 111–121. [Google Scholar] [CrossRef]
- Torrico, B.C.; Cavalcante, M.U.; Braga, A.P.S.; Normey-Rico, J.E.; Albuquerque, A.A.M. Simple Tuning Rules for Dead-Time Compensation of Stable, Integrative, and Unstable First-Order Dead-Time Processes. Ind. Eng. Chem. Res. 2013, 52, 11646–11654. [Google Scholar] [CrossRef]
- Rossiter, A.; Serbezov, A.; Visioli, A.; Žáková, K.; Huba, M. A survey of international views on a first course in systems and control for engineering undergraduates. IFAC J. Syst. Control 2020, 13, 100092. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar]
- Schrijver, E.; van Dijk, J. Disturbance Observers for Rigid Mechanical Systems: Equivalence, Stability, and Design. ASME J. Dyn. Syst. Meas. Control 2002, 124, 539–548. [Google Scholar] [CrossRef]
- Morari, M.; Zafiriou, E. Robust Process Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Grimholt, C.; Skogestad, S. Optimal PI and PID control of first-order plus delay processes and evaluation of the original and improved SIMC rules. J. Process Control 2018, 70, 36–46. [Google Scholar] [CrossRef]
- Abe, N.; Yamanaka, K. Smith predictor control and internal model control—A tutorial. In Proceedings of the SICE 2003 Annual Conference (IEEE Cat. No.03TH8734), Fukui, Japan, 4–6 August 2003; Volume 2, pp. 1383–1387. [Google Scholar]
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar]
- Ohishi, K. A new servo method in mechantronics. Trans. Jpn. Soc. Elect. Eng. 1987, 107-D, 83–86. [Google Scholar]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Peng, Y.; Vrančič, D.; Hanus, R. Anti-Windup, Bumpless and Conditioned Trnasfer Techniques for PID Controllers. IEEE Control Syst. 1996, 16, 48–57. [Google Scholar]
- Hong, K.; Nam, K. A load torque compensation scheme under the speed measurement delay. IEEE Trans. Ind. Electron. 1998, 45, 283–290. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Stability margins and model-free control: A first look. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 454–459. [Google Scholar]
- Gao, Z. On the centrality of disturbance rejection in automatic control. ISA Trans. 2014, 53, 850–857. [Google Scholar] [CrossRef] [PubMed]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huba, M.; Bistak, P.; Vrancic, D.; Zakova, K. Asymmetries in the Disturbance Compensation Methods for the Stable and Unstable First Order Plants. Symmetry 2020, 12, 1595. https://doi.org/10.3390/sym12101595
Huba M, Bistak P, Vrancic D, Zakova K. Asymmetries in the Disturbance Compensation Methods for the Stable and Unstable First Order Plants. Symmetry. 2020; 12(10):1595. https://doi.org/10.3390/sym12101595
Chicago/Turabian StyleHuba, Mikulas, Pavol Bistak, Damir Vrancic, and Katarina Zakova. 2020. "Asymmetries in the Disturbance Compensation Methods for the Stable and Unstable First Order Plants" Symmetry 12, no. 10: 1595. https://doi.org/10.3390/sym12101595
APA StyleHuba, M., Bistak, P., Vrancic, D., & Zakova, K. (2020). Asymmetries in the Disturbance Compensation Methods for the Stable and Unstable First Order Plants. Symmetry, 12(10), 1595. https://doi.org/10.3390/sym12101595