Abstract
Fuzzy graph models enjoy the ubiquity of being in natural and human-made structures, namely dynamic process in physical, biological and social systems. As a result of inconsistent and indeterminate information inherent in real-life problems which are often uncertain, it is highly difficult for an expert to model those problems based on a fuzzy graph (FG). Vague graph structure (VGS) can deal with the uncertainty associated with the inconsistent and indeterminate information of any real-world problem, where fuzzy graphs may fail to reveal satisfactory results. Likewise, VGSs are very useful tools for the study of different domains of computer science such as networking, capturing the image, clustering, and also other issues like bioscience, medical science, and traffic plan. The limitations of past definitions in fuzzy graphs have led us to present new definitions in VGSs. Operations are conveniently used in many combinatorial applications. In various situations, they present a suitable construction means; therefore, in this research, three new operations on VGSs, namely, maximal product, rejection, residue product were presented, and some results concerning their degrees and total degrees were introduced. Irregularity definitions have been of high significance in the network heterogeneity study, which have implications in networks found across biology, ecology and economy; so special concepts of irregular VGSs with several key properties were explained. Today one of the most important applications of decision making is in medical science for diagnosing the patient’s disease. Hence, we recommend an application of VGS in medical diagnosis.
1. Introduction
Graph theory serves as an exceptionally useful tool in solving combinatorial problems in different areas including geometry, algebra, number theory, topology, and social systems. A graph is basically a model of relations, and it is used to embody the real-life problems entailing the relationships between objects. The vertices and edges of the graph are employed to represent the objects and the relations between objects, respectively. In several optimization problems, the available information is inexact or imprecise for various reasons such as the loss of information, a lack of evidence, imperfect statistical data and insufficient information. Generally, the uncertainty in real-life problems may be present in the information that defines the problem. Fuzzy graph (FG) models are advantageous mathematical tools for treating the combinatorial problems in various domains encompassing research, optimization, algebra, computing, environmental science and topology. Fuzzy graphical models are obviously better than graphical models because of the natural existence of vagueness and ambiguity. Originally, fuzzy set theory is required to deal with many complex issues having incomplete information. In 1965, Zadeh [1] at first suggested the fuzzy set theory. Fuzzy set theory is a very powerful mathematical tool for solving approximate reasoning related problems. These notions effectively illustrate complex phenomena, which are not accurately described using classical mathematics. In a fuzzy set, each object is assigned a single value in the interval [0,1] reflecting its grade of membership. This single value does not allow a separation of evidence for membership and evidence against membership. Hence, Gau and Buehrer [2] organized the fuzzy set theory by presenting the VS notion through changing the value of an element in a set with a sub-interval of . Specifically, a true membership function of and false membership function of are used to define the boundaries of the membership degree. This kind of reasoning is also called interval membership, as opposed to point membership in the context of fuzzy sets. The VSs describe more possibilities than fuzzy sets. A VS is more initiative and helpful due to the existence of false membership degree. VSs are higher order fuzzy sets. The application of higher order fuzzy sets complicates the solution procedure, but if the complexity on computation time, computation volume, or memory space is not a matter of concern, then better results can be achieved. There are some interesting features for handling vague data that are unique to vague sets. For example, VSs allow for a more intuitive graphical representation of vague data, which significantly facilitates better analysis in data relationships, incompleteness, and similarity measures.
Many real-word phenomena provided motivation to describe the FGs. Kauffman [3] define fuzzy graphs using Zadeh’s fuzzy relation [4,5]. Akram et al. [6,7,8,9,10,11] introduced several concepts in FGs. Rashmanlou et al. [12,13,14,15,16] introduced some properties in FGs. Product operations on graphs play a very important role in graph theory. They have applications in different branches, such as coding theory, network designs, chemical graph theory and others. Many scholars discussed product operations on various generalized FGs. Mordeson and Peng [17] defined some of these product operations on FGs. Subsequently, utilizing these operations, the degree of the vertices is obtained from two FGs in [18]. Sahoo and Pal [19] presented some operations on intuitionistic fuzzy graphs. FG theory is growing rapidly, with numerous applications in many domains, including networking, communication, data mining, planning, and scheduling. However, Rosenfeld [20] described another detailed definition including fuzzy vertex and fuzzy edges and various fuzzy analogs of graph theoretic concepts such as paths, cycles, connectedness etc. A vague graph (VG) is a generalized structure of a fuzzy graph that gives more precision, flexibility and compatibility to a system when compared with systems that are designed using fuzzy graphs. In addition, a VG can focus on resolving the uncertainty associated with the inconsistent and indeterminate information of any real-world problem, where fuzzy graphs may not bring about satisfactory results. Ramakrishna [21] recommended the VG notion and evaluated some of their features. Borzooei and Rashmanlou [22,23,24,25] investigated different concepts of VG. Irregularity definitions have been of high significance in the study of network heterogeneity, which has implications in networks found across biology, ecology, technology, and economy. Several graph statistics have existed that have been proposed, many of which are based on the number of vertices in a graph and their degrees. The concepts of the irregularity play a significant role in both graph theory and application in the vague environment. The characterization of highly irregular graphs has also been applied to the question of heterogeneity, yet all of these fail to shed enough light on real-world situations. Efforts continue to be made to find appropriate ways to quantify network heterogeneity; so, Gani and Radha [26,27,28,29] introduced irregular FGs, some properties of conjunction of FGs, and new concepts in regular FGs. Samanta and Pal [30] described irregular bipolar fuzzy graphs. A graph structure (GS) is a generalization of simple graphs. GSs are very useful in the study of different domains of computer science and computational intelligence. GS was introduced first by Sampathkumar [31]. Fuzzy graph structures (FGSs) are more useful than GSs because they deal with the uncertainty and ambiguity of many real-world phenomena, and they are widely useful in the study of some structures, like graphs, signed graphs, semi graphs, edge-colored graphs and edge-labeled graphs. FGSs have many applications in solving various problems of several domains, including communication, data mining, image capturing, and image segmentation. Dinesh [32] defined the concept of FGSs and investigated some related concepts. Ramakrishna and Dinesh [33,34] studied generalized FGSs. Shao et al. [35] introduced new concepts in intuitionistic fuzzy graphs.
VGSs are the generalization of FGSs and extremely useful in the study of some structures, like graphs, colored graphs, signed graphs, and edge-labeled graphs. VGSs are more useful than GSs because they deal with the uncertainty and ambiguity of many real-word phenomena. Hence, in this paper we introduced three operations on VGSs, namely, maximal product, rejection, residue product, and represented some results concerning their degrees and total degrees. As the concept of regularity led to many developments in the structural theory of graphs, meanwhile, the irregular graphs have also been significant while dealing with network heterogeneity, which as many applications across biology, economy, and technology. So, in this research, we explained special concepts of irregular-VGSs with several key properties. Decision making in medical diagnosis is a vast research field in medical science. Hence, we described an application of VGS by applying the new distance measure for medical diagnosis.
2. Preliminaries
A graph is a pair which satisfies The elements of and are the nodes and edges of the graph G, respectively.
An FG is of the form which is a pair of mappings and as is defined as , , and is a symmetric fuzzy relation on and ∧ denotes the minimum.
A (VS) A is a pair on set V where and are taken as real valued functions which can be defined on , so that , for all m belongs V. The interval is known as the vague value of m in A. , in this definition, is taken for degree of membership as the lower bound when m in A and is the lower bound for negative of membership of m in A.
Definition 1
([21]). A pair is said to be a VG on a crisp graph , where is a VS on V and is a VS on such that and , for each edge .
Definition 2
([31]). A graph structure (GS) contains of a non-empty set V with relations on set V that are separated such that each relation , , is symmetric and irreflexive. Graph structure can be described as similar as a graph where each edge is labeled as , .
Definition 3
([32]). Let ψ be the fuzzy set on V and be fuzzy sets on , respectively. If , for all , , then is called FGS of graph structure .
Example 1
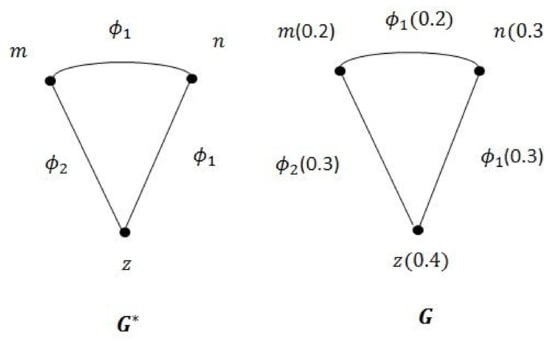
([32]). Consider a GS as shown in Figure 1. Now we define fuzzy set by
We define fuzzy sets , on relations , , respectively, as follows:
By simple computation, it is easy to show that is a FGS.

Figure 1.
Graph structure (GS)- and fuzzy graph structure (FGS)-G.
3. Vague Graph Structures
Product operations on graphs play a very important role in graph theory. In various situations they present a suitable construction means. The first definition of product in fuzzy graphs was introduced in [17]. However, for the first time in this section, two types of products called maximal product, and residue product between the two VGSs were being introduced, which are widely employed in computer networks, and accordingly their properties were evaluated. In addition, another new operation called rejection is introduced, too. Note that the degree and the total degree of vertices that were calculated in the maximal product, rejection and residue product; are presented in (Appendix A).
Definition 4.
is called a VGS of a GS , if is a vague set on V and for each ; is a vague set on such that:
. Note that , for all and , , , where V and are called underlying vertex set and underlying i-edge set of G, respectively.
Example 2.

Let be a graph structure such that , and . Let A, , and be vague subsets of V, , and respectively such that:
Then is a VGS of as shown in Figure 2.

Figure 2.
Vague graph structure G.
Definition 5.
Let and be two vague graph structures with underlying crisp graph structures and , respectively. is called maximal vague graph structure with underlying crisp graph structure , where and . Vague vertex set A and vague relation in maximal product are defined as: ,
.
Example 3.
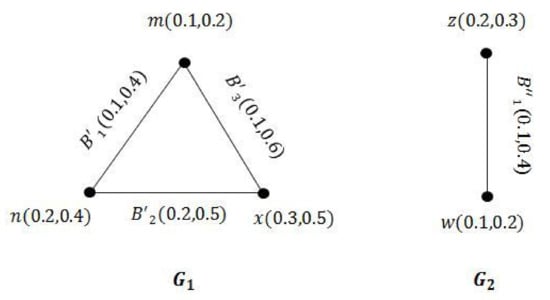
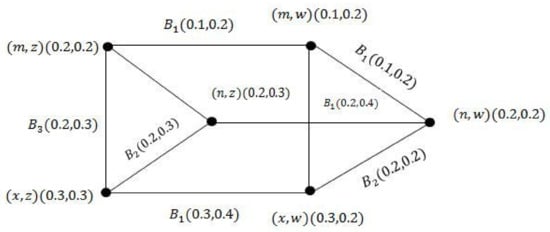

Figure 3.
VGSs and .

Figure 4.
Maximal product of and .
For vertex , we find both true membership and false membership value as follows:
for and .
For edge , we find both true membership value and false membership value.
for and .
Similarly, we can find both true membership and false membership value for all remaining vertices and edges.
Theorem 1.
The maximal product of two VGSs and , is a VGS, too.
Proof.
Let and be two VGSs and , . Then by Definition 4, we have two cases:
(i) if
(ii) if
Hence, is a VGS. □
Definition 6.
The rejection of two VGSs and is defined as:
Example 4.

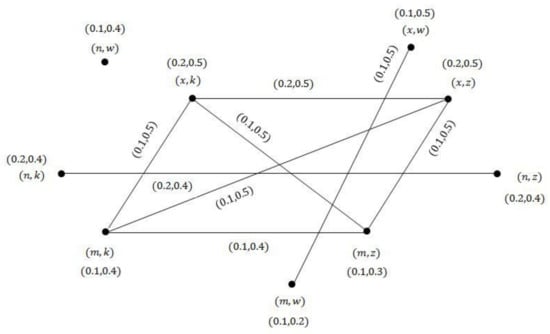
Consider the VGSs and as in Figure 5. We can see that the rejection of two VGSs and , that is in Figure 6.

Figure 5.
Vague graph structures (VGSs) and .

Figure 6.
Rejection of two VGSs.
For vertex , we find both membership value and non-membership value as follows:
for and .
For edge , we find both membership value and non-membership value.
for and .
Now, for edge we have:
for and .
Similarly, we can find both membership value and non-membership value for all remaining vertices and edges.
Proposition 1.
The rejection of two VGSs and , is a VGS.
Proof.
Let and be two VGSs and , . Then by Definition 6 we have:
(i) If and ,
(ii) If and
(iii) If and
Therefore, is a VGS. □
Definition 7.
The residue product of two VGSs and is defined as:
for all .
for all , .
Example 5.

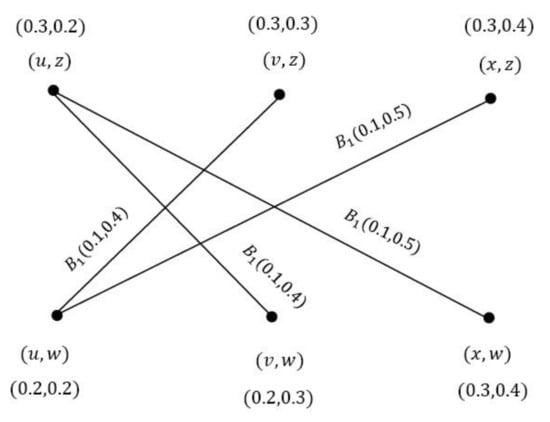

Figure 7.
VGSs and .

Figure 8.
Residue product of two VGSs.
For vertex , we find both membership value and non-membership value as follows:
for and .
Now, for edge we have:
for and .
In the same way, we can find both membership value and non-membership value for all remaining vertices and edges.
Proposition 2.
The residue product of two VGSs and is a VGS.
Proof.
Let and be two VGSs and , . If and , then we have:
□
4. Irregularity in VGSs
The irregularity concepts play an important role in both the graph theory application and theory in the vague environment. The characterizations of highly irregular and neighborly irregular graphs have also been applied to the question of heterogeneity. One of the most broadly studied classes of FGs is IFGs. They are being applied in many contexts, for example, the r-irregular (FGs) with connectivity and edge-connectivity equal to r play a key role in designing reliable communication networks. This idea inspires us to present different types of IVGSs such as totally irregular-VGS (TI-VGS), highly irregular-VGS (HI-VGS), strongly irregular-VGS (SI-VGS), strongly totally irregular-VGS (STI-VGS), highly totally irregular-VGS (HTI-VGS), neighborly edge irregular-VGS (NEI-VGS), neighborly edge totally irregular-VGS (NETI-VGS), and strongly edge totally irregular-VGS (SETI-VGS) and their related theorems.
Definition 8.
An VGS G is said to be an irregular-VGS if there is a vertex which is adjacent to vertices with distinct degrees.
Example 6.
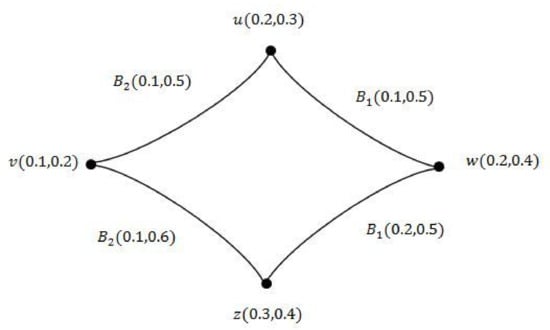
Consider a VGS as shown in Figure 9.

Figure 9.
Irregular VGS (I-VGS) G.
By direct calculation, we have , , , . From this, we see that v is adjacent to vertices of different degrees. Hence, G is an I-VGS.
Definition 9.
A VGS G is said to be a totally irregular-VGS if ∃ a vertex which is adjacent to vertices with different total degrees.
Example 7.
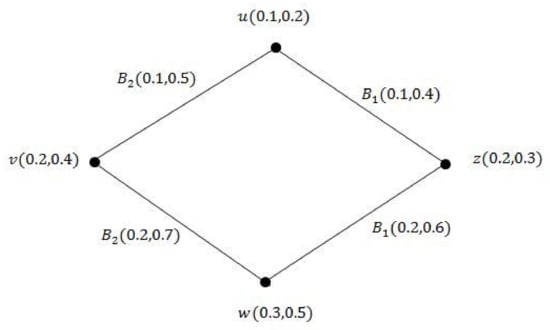
Consider a VGS as shown in Figure 10.

Figure 10.
Totally irregular VGS (TI-VGS) G.
By direct calculation, we have , , , and . From this, we see that u is adjacent to vertices of different degrees. Hence, G is a TI-VGS.
Definition 10.
A VGS G is said to be a strongly I-VGS if every vertex has a different degree.
Example 8.
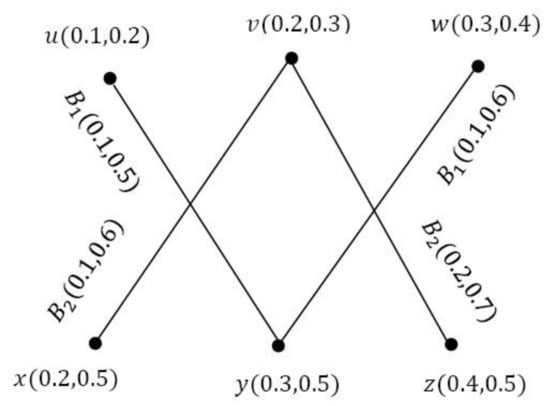
Consider a VGS as shown in Figure 11.

Figure 11.
Strongly I-VGS G.
It is easy to see that , , , , , . We can see that every vertex has a different degree. Hence, G is strongly I-VGS.
The first definition of neighborly irregular in fuzzy graph was introduced in [29]. Neighborly irregular has not been much discussed although the totally irregular and edge irregular concepts are very important and they can be useful in computer science and the problem of finding the shortest path in a computer network. Therefore, the following definitions are provided to highlight the issue.
Definition 11.
A VGS G is said to be a strongly TI-VGS if every vertex has a different total degree.
Example 9.
Consider a VGS G as shown in Figure 11.
By direct calculation we have , , , , , . From this, we see that every vertex has a different total degree. Hence, G is strongly TI-VGS.
Definition 12.
A VGS G is said to be highly I-VGS if every vertex in G is adjacent to vertices of different degrees.
Example 10.
Consider the VGS G as shown in Figure 9. It is easy to see that every vertex is adjacent to vertices of different degrees. Hence, G is highly I-VGS.
Definition 13.
A VGS G is said to be highly TI-VGS if every vertex in G is adjacent to vertices of different total degrees.
Example 11.
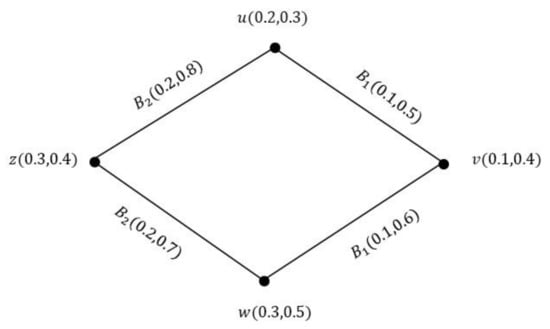
Consider VGS as shown in Figure 12.

Figure 12.
Highly TI-VGS G.
By simple calculation, we have , , , and . So, every vertex is adjacent to vertices of different degrees. Hence, G is a highly TI-VGS.
Definition 14.
The degree and the total degree of an edge of a VGS G are defined by , and , respectively, and we have:
Example 12.
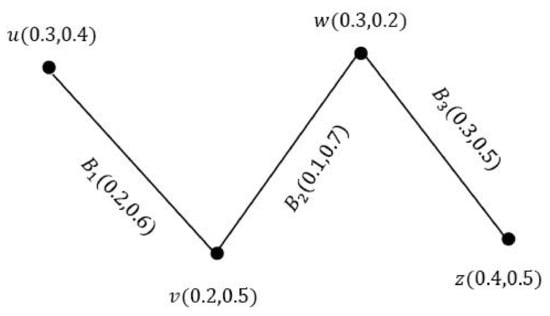
Consider the VGS as shown in Figure 13.

Figure 13.
VGS G.
By direct calculation, we have , , , . The degree of every edge is given as:
Hence, , , . The total degree of every edge is given as:
So, , , and .
Definition 15.
A connected VGS G is said to be a neighborly edge irregular-VGS (NEI-VGS), if every pair of adjacent edges in G has different degrees.
Example 13.
Consider the VGS G as shown in Figure 13. From this, it is easy to see that every pair of adjacent edges has different degrees. Hence, G is an NEI-VGS.
Definition 16.
A connected VGS G is said to be a neighborly edge totally irregular-VGS (NETI-VGS), if every pair of adjacent edges has different total degrees.
Example 14.
Consider the VGS G as shown in Figure 13. From it, we see that every pair of adjacent edges has different total degrees. Therefore, G is an NETI-VGS.
Definition 17.
A VGS G is said to be a strongly edge irregular-VGS (SEI-VGS), if every edge in G has a different degree.
Example 15.
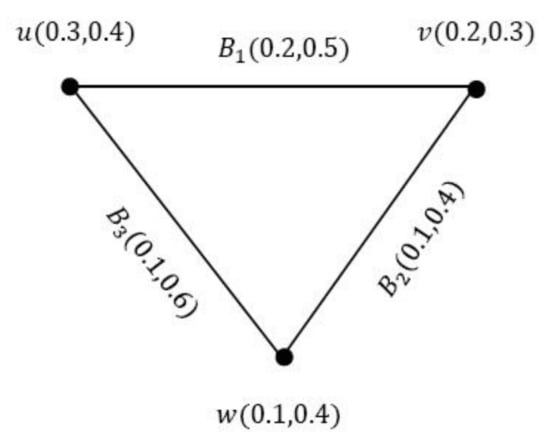
Consider the VGS as shown in Figure 14.

Figure 14.
SEI-VGS G.
By a simple calculation, we have , , and . The degree of each edge is given as:
Since that each edge has different degree, so G is an SEI-VGS.
Definition 18.
A VGS G is said to be a strongly edge totally irregular-VGS (SETI-VGS), if every edge in G has a different total degree.
Example 16.

Consider the VGS as shown in Figure 15.

Figure 15.
SETI-VGS G.
By a simple calculation, we have , , , .
The degree of every edge is given as:
The total degree of each edges is given as:
It shows that every edge in G has a different total degree. Hence, G is an SETI-VGS.
Remark 1.
The SEI-VGS G may not be SETI-VGS.
Example 17.
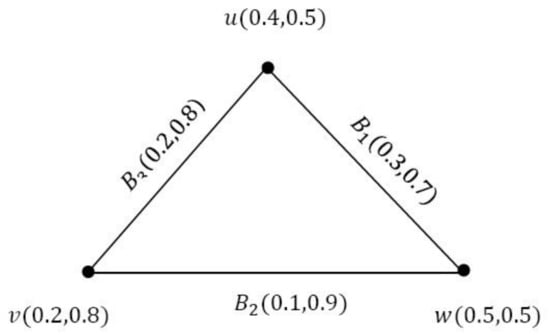
Consider a VGS as shown in Figure 16.

Figure 16.
(SEI-VGS) G.
By direct calculation, we have:
Since every edge in G has a different degree, so G is an SEI-VGS. Now, we calculate the total degree of every edge as follows:
Hence, G is not an SETI-VGS.
Theorem 2.
If is a strongly edge irregular connected VGS (SEIC-VGS), where , is a constant function. Then G is an SETI-VGS.
Proof.
Let G be an SEIC-VGS. Consider as a constant function. Then and , for all , where , and are constants. Consider two edges and in . Since G is an SEI-VGS so , where and are two edges in . This shows that . This implies that . Hence, , where, and are two edges in . Since the edges and were taken to be arbitrary, this shows every two edge in G have different total degrees. Therefore, G is an SETI-VGS. □
Theorem 3.
If is a SETIC-VGS, where is a constant function. Then, G is an SEI-VGS.
Proof.
Let G be an SETIC-VGS. Consider , is a constant function. Then, , , for all , where and are constants. Consider the edges and in . Since G is an SETI-VGS, so , where and are edges in . This results that . This shows that . So, , where and are two edges in . Since that and were arbitrary edges, so every two edges in G have different degrees. Therefore, G is an SEI-VGS. □
Theorem 4.
Let be an SEI-VGS. Then G is an NEI-VGS.
Proof.
Let G be an SEI-VGS. Then, every edge in G has a different degree. This shows that every two neighbor edges have different degrees. Hence, G is an NEI-VGS. □
Theorem 5.
Let be an SETI-VGS. Then, G is an NETI-VGS.
Proof.
Let G be an SETI-VGS. Then, each edge in G has a different total degree. This shows that every two neighbor edges in G have different total degrees. Hence, G is an NETI-VGS. □
Remark 2.
If G is an NEI-VGS, then, it is not compulsory that G is an SEI-VGS.
Example 18.
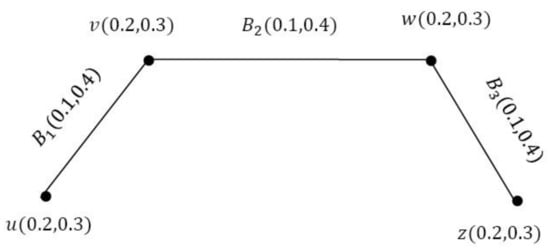
Consider the VGS as shown in Figure 17.

Figure 17.
VGS G.
By simple calculation we have:
The degree of each edge is , , and . Since each two neighbor edges have different degrees, i.e., and . Hence, G is an NEI-VGS. Here, we can see that . Hence, G is not an SEI-VGS.
Theorem 6.
Let be an SEIC-VGS, with as constant function. Then, G is an I-VGS.
Proof.
Let G be an SEIC-VGS, with as constant function. Then, and , for every edge , where and are constants. Likewise, every edge in G has a different degree, so G is an SEI-VGS. Suppose that and be any two neighbor edges in G such that . This shows that . This results that . This implies that . Hence, there is a vertex v in G which is neighbor to the vertices with different degrees. This shows that G is an I-VGS. □
Theorem 7.
Let be an SETIC-VGS, with , as constant function. Then, G is an I-VGS.
Proof.
Let be an SETIC-VGS, with as constant function. Then, and , for every edge , where and are constants and every edge in G has a different total degree. Hence G is an SETI-VGS. Suppose that and be any two neighbor edges in G such that . This shows that . This results that . This represents that . This shows that . Hence, there is a vertex v in G which is neighbor to the vertices with different degrees. This indicates that G is an I-VGS. □
5. Application of VGS in Medical Diagnosis
In this section, an attempt was made to run through a fuzzy decision-making approach using (VS). In addition, an interesting distance measure on VSs has been introduced.
Definition 19.
Let be the universe of discourse. Let and be two VSs. The the new distance measure can be defined as:
To be a distance measure, it is easy to show that all four conditions are satisfied (See Appendix A, Remark A5).
Suppose that be a set of number of possible diseases and be a set of n number of patients. Let, be the symptoms the disease and be the symptoms of patient expressed in VSs. Hence, the distance between the symptoms disease and symptoms of patient can be evaluated as follows using the proposed distance measure:
where and .
We can describe the distances between every pair of disease and patients using the following matrix:
Applying the fact that, less distance between two VSs shows more similarity between them, therefore, it can be described that for the patient the disease most possibly suffered by him or her is the disease corresponding to .
Here, we consider a set of symptoms S, a set of diagnosis D, and a set of patients P. Consider , , and . Our aim is to make the right diagnosis decision for each patient, from the set of symptoms, for each disease.
Now, in Figure 18, we assume is the VGS of the set of patients, and is the VGS of the set of diagnosis where and .
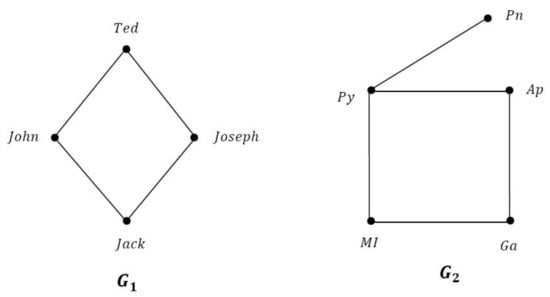
Figure 18.
VGSs and .
The relation between symptom and disease, and the relation between pain and symptom is given in Table 1 and Table 2, respectively.

Table 1.
Symptoms–diseases vague relation.

Table 2.
Patients–symptoms vague relation.
The five diagnoses are now described as vague sets.
Likewise, the patients as vague sets can be described as follows:
Now the vague distance is calculated between the disease and the patients based on their symptoms.
Similarly, the vague distance measure between the patients and the diseases can be found as:
Vague graph structure is shown in Figure 19.
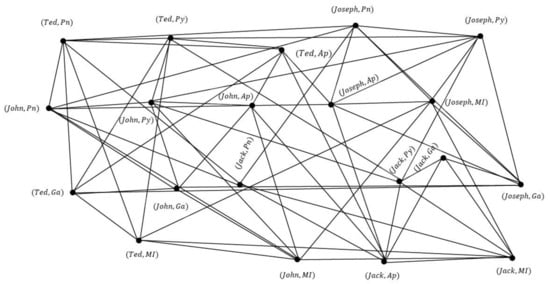
Figure 19.
Maximal product of and .
In this figure, we clearly see that people who have at least one similar symptom, are closer to each other in terms of diagnosis, and this is also acceptable in medical science. Therefore, with the help of maximized multiplication graph, we can find the right diagnosis for different people, with the same symptoms.
Now by applying the following distance matrix, it can be shown to what extent the symptoms of disease differ by the symptoms of patients.
Less distance between patient and disease implies more possibility of having the disease; we can predict which disease is suffered by the four people. Considering the distance matrix, one can see that, if the doctor agrees, Ted suffers from pyelonephritis, John suffers from appendicitis, Joseph suffers from pneumonia, and Jack suffers from gastroenteritis.
6. Conclusions
Graph theory has many applications in solving various problems of several domains, including networking, communication, data mining, clustering, image capturing, image segmentation, planning, and scheduling. However, in some situations, certain aspects of a graph-theoretical system may be uncertain. Applying the fuzzy-graphical methods in meeting the ambiguity and vague notions is very natural. Fuzzy-graph theory has an extensive number of applications in modeling various real-time systems where the inherent information level in the system varies with different levels of precision. Vague graph structures (VGSs) are very useful tools for the study of different domains of computational intelligence and computer science. VGSs have many applications in different sciences such as optimization, topology, neural networks, and operations research. Operations are conveniently used in many combinatorial applications. In various situations they present a suitable construction means. The concepts of the irregularity play a significant role in both graph theory and application in the vague environment. So, in this paper, we described three new operations on VGSs, namely, maximal product, rejection, residue product, and introduced special concepts of irregularity in VGSs. Finally, an application of VGS in medical diagnosis is presented. In our future work we will investigate the concepts of energy, Laplacian matrix, adjacency matrix, spectrum, and density in VGSs and give some applications of energy in VGSs and other sciences.
Author Contributions
All authors have contributed equally to this work. All authors have read and agreed for the possible publication of the manuscript.
Funding
This work was supported by the National Key R & D Program of China (Grant No. 2018YFB1005104), the Guanzhou Academician and Expert Workstation (No. 20200115-9).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Definition A1.
A VGS is -strong if:
for all , .
If G is -strong, , then G is called strong-VGS.
Theorem A1.
The maximal product of two strong VGSs and , is a strong VGS.
Proof.
Let and be two strong VGSs. Then , , for any and , , for any , . Then, proceeding according to the definition of maximal product,
(i) if and . Then
(ii) if and . Then
Therefore, is a strong VGS. □

Figure A1.
VGSs , , and .
Example A1.
Consider the strong VGSs and as in Figure A1. It is easy to see that is a strong VGS, too.
Remark A1.
If the maximal product of two VGSs () is a strong, then and need not to be strong, in general.
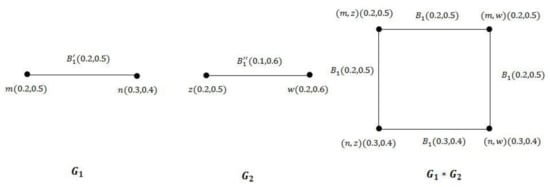
Figure A2.
VGSs , , and .
Example A2.
Consider the VGSs , , and as in Figure A2.
Hence, and are strong, but is not strong. Since but . Hence, .
Theorem A2.
The maximal product of two connected VGSs is a connected VGS.
Proof.
Let and be two connected VGSs with underlying crisp graph structures and , respectively. Let and . Then , for all and , for all (or , for all and , for all ). The maximal product and is written as . Now consider the subgraphs of G with the vertex set , for . Each of these subgraphs of G is connected, since the are the same and since is connected, each is adjacent to at least one of the vertices in . In addition, since is connected, each is adjacent to at least one of the vertices in . Hence, there exists at least one edge between any pair of the above subgraphs. Thus, we have (or ), for all . So, G is a connected VGS. □
Remark A2.
The maximal product of two complete VGSs is not a complete VGS, in general. Because we do not include the case and in the definition of the maximal product of two VGSs.
Remark A3.
The maximal product of two complete VGSs is a strong VGS.
Example A3.
Consider the complete VGSs and as in Figure A1. A simple calculation concludes that is a strong VGS.
Definition A2.
Let and be two VGSs. For any vertex we have:
Theorem A3.
Let and be two VGSs. If , , and , , , then
Proof.
From the definition of a vertex in Cartesian product, we have:
□

Figure A3.
VGSs , , and .
Example A4.
By direct calculations:
It is clear from the above calculations that the degrees of vertices calculated by using the formula of the above theorem and by directed method are the same.
Consider the VGSs , and as in Figure A3. Since , , and by Theorem A3 we have:
Definition A3.
Let and be two VGSs. For any vertex we have:
Example A5.
In this example we find the degree and the total degree of vertices and in Example 3.
Therefore, .
In addition, by definition of total vertex degree in maximal product,
Hence, .
Therefore, and .
Similarly, we can find the degree and the total degree of all vertices in .
Theorem A4.
Let and be two VGSs. If , , and , , then , .
Proof.
From the Definition A3 we have:
□
Example A6.
Consider the VGSs , and as in Figure A3. The total degree of vertex in maximal product is calculated by using the following formula:
By direct calculations:
It is clear from the above calculations that the total degree of vertices calculated by using the formula of the above theorem and by directed method are the same.
Remark A4.
The rejection of two complete VGSs and is a complete VGS.
Definition A4.
Let and be two VGSs. For any vertex we have:
Definition A5.
Let and be two VGSs. For any vertex we have:
Definition A6.
Let and be two VGSs. For any vertex we have:
Definition A7.
Let and be two VGSs. For any vertex we have:
Example A7.
In this example we find the degree and the total degree of vertex in Example 5.
Therefore, . In addition, total degree of vertex is given by:
Hence, .
Similarly, we can find the degree and the total degree of all vertices in .
Remark A5.
is a distance measure.
Proof.
(i) .
As we know, for true membership and false membership . This shows for and , and . Hence, and . So,
Therefore, from Equations (A1) and (A2) we have:
Hence, .
(ii) if and only if . □
Proof.
For, this reason
So, if and only if .
(iii) □
Proof.
(iv) If A, B, and C are three vague sets, then the distance measure satisfies the triangular inequality. I.e., . □
Consider , , and as three vague sets. Now from the basic inequality of real numbers we know that:
So, .
Thus, it is clear that the proposed distance measure satisfies all the metric properties. References
References
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Gau, W.L.; Buehrer, D.J. Vague sets. IEEE Trans. Syst. Man Cybern. 1993, 23, 610–614. [Google Scholar] [CrossRef]
- Kauffman, A. Introduction a la theories des sous-emsembles 503 ous. Masson Cie 1973, 1, 607–618. [Google Scholar]
- Zadeh, L.A. Similarity relations and fuzzy ordering. Inf. Sci. 1971, 3, 177–200. [Google Scholar] [CrossRef]
- Zadeh, L.A. Is there a need for fuzzy logical. Inf. Sci. 2008, 178, 2751–2779. [Google Scholar] [CrossRef]
- Akram, M.; Sitara, M.; Saeid, A.B. Residue product of fuzzy graph structures. J. Multiple-Valued Log. Soft Comput. 2020, 34, 365–399. [Google Scholar]
- Akram, M.; Sitara, M. Certain fuzzy graph structures. J. Appl. Math. Comput. 2019, 61, 25–56. [Google Scholar] [CrossRef]
- Akram, M.; Muzzamal, S. Certain concepts in Intuitionistic Neutrosophic Graph Structures. Information 2017, 8, 154. [Google Scholar] [CrossRef]
- Akram, M.; Naz, S.; Smarandache, F. Generalization of Maximizing Deviation and TOPSIS Method for MADM in Simplified Neutrosophic Hesitant Fuzzy Environment. Symmetry 2019, 11, 1058. [Google Scholar] [CrossRef]
- Asif, M.; Akram, M.; Ali, G. Pythagorean Fuzzy Matroids with Application. Symmetry 2020, 12, 423. [Google Scholar] [CrossRef]
- Sitara, M.; Akram, M.; Yousaf Bhatti, M. Fuzzy graph structures with application. Mathematics 2019, 7, 63. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Borzooei, R.A. Vague graphs with application. J. Intell. Fuzzy Syst. 2016, 30, 3291–3299. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Samanta, S.; Pal, M.; Borzooei, R.A. A study on bipolar fuzzy graphs. J. Intell. Fuzzy Syst. 2015, 28, 571–580. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Borzooei, R.A. Product vague graphs and its applications. J. Intell. Fuzzy Syst. 2016, 30, 371–382. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Samanta, S.; Pal, M.; Borzooei, R.A. Product of bipolar fuzzy graphs and their degree. Int. J. Gen. Syst. 2016, 45, 1–14. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Samanta, S.; Pal, M.; Borzooei, R.A. Bipolar fuzzy graphs with Categorical properties. Int. J. Comput. Intell. Syst. 2015, 8, 808–818. [Google Scholar] [CrossRef]
- Mordeson, J.N.; Chang-Shyh, P. Operations on fuzzy graphs. Inf. Sci. 1994, 79, 159–170. [Google Scholar] [CrossRef]
- Nagoor Gani, A.; Radha, K. The degree of a vertex in some fuzzy graphs. Int. J. Algorithms Comput. Math. 2009, 2, 107–116. [Google Scholar]
- Sahoo, S.; Pal, M. Product of intuitionistic fuzzy graphs and degree. J. Intell. Fuzzy Syst. 2017, 32, 1059–1067. [Google Scholar] [CrossRef]
- Rosenfeld, A. Fuzzy Graphs; Zadeh, L.A., Fu, K.S., Shimura, M., Eds.; Fuzzy Sets and Their Applications; Academic Press: New York, NY, USA, 1975; pp. 77–95. [Google Scholar]
- Ramakrishna, N. Vague graphs. Int. J. Comput. Cogn. 2009, 7, 51–58. [Google Scholar]
- Borzooei, R.A.; Rashmanlou, H. Ring sum in product intuitionistic fuzzy graphs. J. Adv. Res. Pure Math. 2015, 7, 16–31. [Google Scholar] [CrossRef]
- Borzooei, R.A.; Rashmanlou, H. Domination in vague graphs and its applications. J. Intell. Fuzzy Syst. 2015, 29, 1933–1940. [Google Scholar] [CrossRef]
- Borzooei, R.A.; Rashmanlou, H. Degree of vertices in vague graphs. J. Appl. Math. Inform. 2015, 33, 545–557. [Google Scholar] [CrossRef]
- Borzooei, R.A.; Rashmanlou, H.; Samanta, S.; Pal, M. Regularity of vague graphs. J. Intell. Fuzzy Syst. 2016, 30, 3681–3689. [Google Scholar] [CrossRef]
- Nagoor Gani, A.; Radha, K. On regular fuzzy graphs. J. Phys. Sci. 2008, 12, 33–44. [Google Scholar]
- Nagoor Gani, A.; Radha, K. Conjunction of two fuzzy graphs. Int. Rev. Fuzzy Math. 2008, 3, 61–71. [Google Scholar]
- Nagoor Gani, A.; Radha, K. Some sequences in fuzzy graphs. Far East J. Appl. Math. 2008, 31, 321–335. [Google Scholar]
- Nagoor Gani, A.; Radha, K. On irregular fuzzy graphs. Appl. Math. Sci. 2012, 6, 517–523. [Google Scholar]
- Samanta, S.; Pal, M. Irregular bipolar fuzzy graphs. Int. J. Appl. Fuzzy Sets 2012, 2, 91–102. [Google Scholar]
- Sampathkumar, E. Generalized graph structures. Bull. Kerala Math. Assoc. 2006, 3, 65–123. [Google Scholar]
- Dinesh, T. A Study on Graph Structures. Incidence Algebras and Their Fuzzy Analogues. Ph.D. Thesis, Kannur University, Kannur, India, 2011. [Google Scholar]
- Ramakrishnan, R.V.; Dinesh, T. On generalised fuzzy graph structures. Appl. Math. Sci. 2011, 5, 173–180. [Google Scholar]
- Ramakrishnan, R.V.; Dinesh, T. On generalised fuzzy graph structures II. Adv. Fuzzy Math. 2011, 6, 5–12. [Google Scholar]
- Shao, Z.; Kosari, S.; Rashmanlou, H.; Shoaib, M. New concepts in intuitionistic fuzzy graph with application in water supplier systems. Mathematics 2020, 8, 1241. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).