Abstract
In this study, the voltage stability margin for direct current (DC) networks in the presence of constant power loads is analyzed using a proposed convex mathematical reformulation. This convex model is developed by employing a second-order cone programming (SOCP) optimization that transforms the non-linear non-convex original formulation by reformulating the power balance constraint. The main advantage of the SOCP model is that the optimal global solution of a problem can be obtained by transforming hyperbolic constraints into norm constraints. Two test systems are considered to validate the proposed SOCP model. Both systems have been reported in specialized literature with 6 and 69 nodes. Three comparative methods are considered: (a) the Newton-Raphson approximation based on the determinants of the Jacobian matrices, (b) semidefinite programming models, and (c) the exact non-linear formulation. All the numerical simulations are conducted using the MATLAB and GAMS software. The effectiveness of the proposed SOCP model in addressing the voltage stability problem in DC grids is verified by comparing the objective function values and processing time.
1. Introduction
Direct current (DC) electrical networks are promising grids capable of supplying multiple users at different voltage levels from high-voltage DC (HVDC) to low-voltage DC (LVDC) in monopole or bipole configurations [1,2]. The implementation of DC technologies avoids the need for managing reactive power or frequency, in contrast to their alternating current (AC) counterparts. This is an important advantage that makes DC grids easily controllable and operable. Additionally, power losses are lower, and voltage profiles are better in DC grids than in AC systems. Hence, DC networks are more efficient than AC networks [3,4].
Two types of strategies are used to analyze DC electrical networks: dynamical and static approaches. The first strategy is executed in the time domain and is used for developing primary and secondary controllers in power electronic DC-DC converters [5,6]. The second type of analysis, i.e., static studies, is used to determine all the state variables under stationary conditions. The most typical types of analysis are power flow analysis [3], optimal power flow studies [2], economic dispatch approaches [7], and voltage stability analysis [8,9]. In addition, these approaches are combined with the optimal sizing and location of distributed generators for DC grids [10].
In this study, we focus on the voltage stability calculation for DC grids. This is a non-linear non-convex optimization problem recently analyzed in specialized literature, and few approaches for this task have been reported. In [9], a semidefinite programming (SDP) model was proposed by guaranteeing a global and unique solution. Nevertheless, the complexity of this model is mainly due to the quadratic increase in the number of variables and the semidefinite requirements of the matrix that contains all the voltage variables; this causes longer computational times when the number of nodes in the DC system increases. The authors of [8] presented a linear matrix inequalities formulation to determine the maximum load increments in a small DC grid composed of two constant-power loads. However, this approach cannot be extended for multiple loads, because the resulting equations are unsolvable using analytical methods. The authors of [11] employed the classical Newton–Raphson method in conjunction with a linear search to determine the maximum load increment. This is performed by observing the sign variation in the Jacobian matrix in the power flow equations. This method is easily implementable; however, the selection of the step size has an undesirable influence on the final solution. In [12], the voltage stability margin problem in DC grids was solved by incorporating the non-linear formulation into an optimization package known as the general algebraic modeling system (GAMS). Even though this software is efficient for solving non-linear problems, it is not possible to guarantee a global solution to the problem, because the calculations are usually stuck in local solutions.
Unlike in previous works, in this study, a second-order cone programming (SOCP) model is proposed to address the voltage stability margin calculation in DC grids. The main advantage of this approach is that it guarantees a global optimum and unique solution by transforming the exact non-linear non-convex optimization problem into a convex problem [13,14]. In addition, this approach has not been previously proposed for the analysis of voltage stability in DC networks. Therefore, there is a gap in the literature that this study tries to fulfill. The convex approach has lower computational requirements than SDP approaches because it avoids semidefinite matrices in its formulation.
Even if recently reported approaches typically use the exact non-linear formulation (GAMS solvers) and heuristic searches (Newton-Raphson) [11,12] because of the non-convexities introduced by the power balance constraints, it is not possible to ensure a global optimum, even if for both test feeders these solutions coincide with convex approaches, i.e., the semidefinite programming model [9] and the newly proposed SOCP model.
The remainder of this paper is organized as follows: Section 2 presents the classical non-linear non-convex formulation of the voltage stability calculation in DC grids. Section 3 shows the proposed second-order cone programming reformulation and its main assumptions for developing a convex mathematical model. Section 4 presents a small numerical example with three nodes to demonstrate the effect of the load increment and the voltage collapse problem. Section 5 shows the numerical implementation of the proposed SOCP model in two test systems, namely an HVDC network and a medium-voltage DC (MVDC) grid. Section 6 presents the main conclusions drawn from this research.
2. Non-Linear Programming Formulation
The determination of the point of the voltage collapse in electrical DC networks with constant-power loads is formulated as a non-linear non-convex optimization problem [9]. The non-convexities of this problem are related to the power balance equations in the presence of constant-power loads, as these expressions emerge as a hyperbolic relation between voltage and power that generates non-affine equality constraints [8]. The complete optimization model for analyzing the point of voltage collapse in DC grids is formulated as follows:
Objective function:
Set of constraints:
Remark 1.
Please note that the decision variables in the problem of determining the stability margin in DC networks shown in (1)–(5) correspond to the loadability parameter as well as the voltage profiles in all the nodes, i.e., and the power generation in the constant-voltage sources. This suggests that the solution of this problem involves the simultaneous determination of all these variables, which maximizes the chargeability of the grid [12].
The optimization model defined in (1)–(5) receives the following interpretation: Equation (1) is the objective function that corresponds to the maximization of the total power consumption admissible in all the nodes immediately before reaching the point of the voltage collapse. Equation (2) is the power balance constraint. Equation (3) defines the power capabilities in all generation nodes. Equation (4) determines the voltage bounds admissible for secure operation of the DC grid under normal operative scenarios, and Equation (5) determines the positiveness nature of the loadability variable.
Remark 2.
If the variable is zero for all the nodes, then the mathematical model (1)–(5) corresponds to the classical power flow problem for DC grids, which can be solved using classical methods, such as the Gauss–Seidel [2], Newton–Raphson [3] or successive approximation methods [15], among others. All these approaches can guarantee the existence and uniqueness of the solution under well-defined voltage conditions through fixed-point theorems.
Please note that the objective of voltage stability analysis is to determine the maximum power increments in all the constant power loads that carry the DC system to the voltage collapse. Hence, the constraints related to generation capabilities in slack nodes, and voltage bounds in all the nodes are relaxed [12]. Therefore, these constraints are neglected when the objective of the problem is to determine the point at which all the nodes have a voltage collapse [11].
Remark 3.
The mathematical problem (1)–(5) is transformed into a convex one using semidefinite programming or SOCP to guarantee the uniqueness of the mathematical solution of the voltage stability margin determination in DC grids [9,16]. We used the SOCP to solve the voltage stability determination problem, which represents the main contribution of this study. The SOCP model is described in the next section.
Convexity Test
To demonstrate that the power balance equations in DC networks represent a set of non-linear non-convex constraints, we present a small numerical example as follows: consider a DC power system composed of 3 nodes (see the test feeder presented in Section 4), i.e., one voltage-controlled node and two constant-power loads. For this example, let us rewrite the power balance equation at node 2 using the per-unit (p.u.) representation.
for simplicity, let us consider that p.u, p.u, p.u, p.u, p.u, , and , which produces:
If we plot the non-linear function (7), the curve illustrated in Figure 1 is obtained. Please note that the solution space is given by the red curve, which implies that it is convex only if a linear combination is contained in the curve, where t is a real number between 0 and 1. In Figure 1, it can be observed that the line points generated (blue line) by the linear combination are outside the red curve (except the extreme points). This means that the constraint (7) is non-convex. Hence, the power balance constraints in power flow analysis generate a non-convex solution space. This implies that it is impossible to ensure a global optimum in power flow analysis.
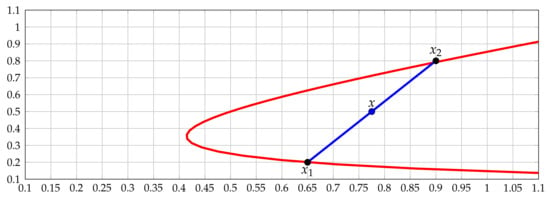
Figure 1.
Numerical test to show the non-convexity of the power balance equations.
3. Second-Order Cone Programming Formulation
The SOCP formulation is a component of optimization convex models. This is an approach that has gained considerable importance in engineering because it can solve a family of convex problems reliably and efficiently by guaranteeing a unique solution (global optimum) [17]. The SOCP formulation minimizes a linear function over a convex region, which consists of the intersection of second-order cones with an affine linear space [18].
To transform the problem of the voltage stability margin (formulated from (1)–(5)) into an SOCP model, it is important to mention that the only one non-convex constraint represents the power balance Equation (2). To perform this transformation, we focus on the product between voltage variables, i.e., , by redefining a new variable y as follows:
Now, if we multiply (8) by , then, the following result yields
where the pre-multiplication by is required to transform the hyperbolic relation between voltages into a conic constraint [19].
Please note that this relaxation is possible because all the voltage variables must be positive for satisfactory operation of DC grid, including in extreme cases, such as the voltage stability margin analyzed in this study.
In (9), it is possible to substitute expression (8), which yields the following result
Please note that (10) is still non-linear non-convex, which implies the need for a relaxation. The first step is to relax the equality constraint using an inequity as follows:
Remark 4.
Please note that the relaxation of the equality imposition by a lower-equality imposition is required at any conic approximation because equality implies that the solution is only in the contour of the cone. The lower-equal symbol implies that all the points inside the cone are possible solutions, including the contour of the cone, which implies that this relaxation passes the convexity test presented in Section 2 [20].
Theorem 1.
Hyperbolic constraint (11) can be transformed into a conic constraint as follows:
Proof.
Because the power flow constraint can be rewritten as a set of convex restrictions, the equivalent SOCP model representing the problem of maximum loadability in DC networks with constant-power loads can be rewritten as follows:
Objective function:
Set of constraints:
Remark 5.
4. Graphical Example
Here, we considered a small DC test feeder composed of three nodes (one of them is the slack node) and two constant-power loads connected to nodes 1 and 2, respectively. This system is used to show the voltage stability margin, i.e., the region of secure operation, graphically. The topology of this test feeder is presented in Figure 2. For this test system, 1000 W and 24 V are considered the power and voltage bases, respectively.
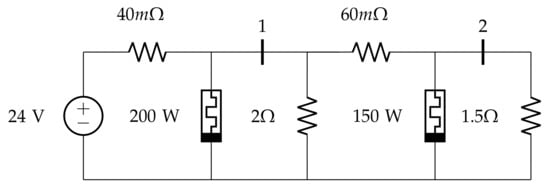
Figure 2.
Small test feeder with two constant power loads.
Figure 3 shows the numerical behavior of the voltage collapse point when different increments have been used at the point of connection of the constant-power loads. Please note that point O is the solution of the classical power flow problem when all are fixed as zero; this point is . From this initial point, we evaluate the evolution of the voltage collapse in the DC grid when its constant-power loads increase. Trajectory O–A shows the evolution of the voltage at load nodes when it is increased only at the load connected at node 1, with the load at node 2 being fixed as p.u. Please note that point A presents the maximum reduction in both load voltages at the same time, i.e., ; both voltages are observed to be lower than p.u. In addition, these points represent the maximum objective function possible in this numerical example, which is p.u, when . Trajectory O–B shows the evolution of the voltage in the DC system when both loads are increased by the same magnitude, i.e., . These increments in the loads produce a maximum objective function of p.u, where one voltage is higher than p.u (see node 2), and the other node is lower than p.u (see node 3). This behavior implies that node 3 conditioned the stability margin behavior of this test system since it is more sensitive to load changes than node 2 is. On the other hand, trajectory O–C presents the voltage evolution of the numerical example when the load connected to node 2 is increased, with the load at node 1 fixed as p.u. This trajectory shows that the voltage at node 2 decreases until , while the voltage at node 1 remains upper that p.u. This behavior confirms that node 2 has a lower possibility of increasing its load consumption since the voltage collapse point is reached when the total load of the DC system is p.u, which is the minimum objective functions across the three cases analyzed. Please note that in Table 1 the numerical behavior of the voltage stability problem in DC networks resumes when constant-power loads start to increase.
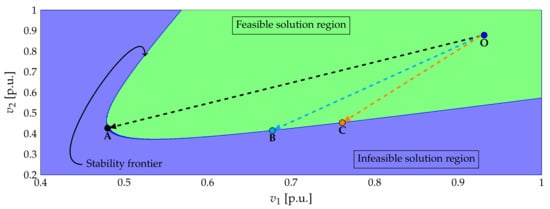
Figure 3.
Voltage collapse trajectories followed by different increments in the constant power consumptions per node.

Table 1.
CPL increments for the different simulation cases.
It is important to mention that the results presented in this numerical example have differences lower than when compared with that in the heuristic approach based on Newton–Raphson sensitivities [11].
Remark 7.
The point of voltage collapse in DC radial networks depends on the location of the load node. Hence, it is possible to conclude from the numerical example that loads connected to the final nodes have lower possibilities of incrementing their consumption when compared with loads near the slack source.
5. Test Systems and Simulation Results
In this section, we present the test system configuration and the numerical results obtained by solving the stability margin calculation problem with different methodologies reported in the specialized literature.
5.1. Test System Configurations
To validate the proposed SOCP model for voltage stability calculations in DC networks, we consider the testing feeders reported in [11]. The first DC network corresponds to the high-voltage DC (HVDC) network, and the second network is an MVDC radial network. The topologies of the test feeders are illustrated in Figure 4. All the numerical information related to load consumption and branch parameters can be obtained from [11].
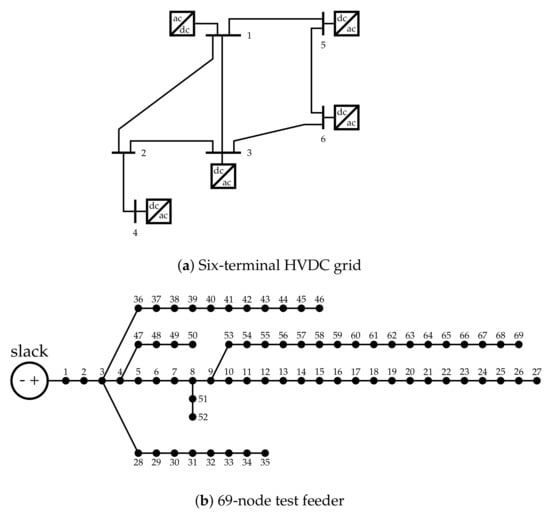
Figure 4.
Electrical configuration of the test systems.
5.2. Numerical Validation
The proposed SOCP formulation was validated by being compared with approaches reported in the specialized literature. The interior point was used for solving the exact non-linear programming formulation (IP-NLP), the Newton–Raphson formulation based on determinants of Jacobian matrices (NR-DJM), and SDP formulations [9,11]. These methodologies were implemented in MATLAB and GAMS.
Table 2 presents the maximum loadability factor, i.e., , for the HVDC and MVDC systems. Please note that the proposed SOCP model allows for reaching the optimal global solution of this problem for both test systems since it is a convex transformation of the exact non-linear non-convex problem.

Table 2.
Voltage stability index for the HVDC and MVDC test feeders.
In the case of the HVDC system, the proposed solution technique, i.e., the SOCP model, as well as the comparative methods, reach the same loadability factor () for all the nodes. In contrast, for the MVDC system, the SDP model presents an underestimation of the loadability factor when compared with the global optimum, i.e., . This error is approximately when the SDP is compared with NR-DJM, IP-NLP, and the proposed approach.
In terms of the computational performance with respect to the processing times required to solve the voltage stability margin problem, all the methodologies listed in Table 2 require between s and 30 s in the case of SOCP. In the case of the proposed approach, for the HVDC system, the processing time is s, while for the MVDC, the time is s. These results confirm that the proposed SOCP model is more efficient when compared with the NR-DJM ( s and s), SDP ( s and s), and the IP-NLP ( s and s) models reported in [11].
In the case of the NR-DJM, it is difficult to select the heuristic parameter reported in [11] to determine the convergence of the algorithm. In case of the 69-node test feeder, before the voltage collapse (), the DJM is approximately , and at the point of the voltage-collapse, it is approximately . This implies that the tuning of this heuristic search requires multiple power flow evaluations. An additional complication of the NR-DJM approach is the selection of the step , because large values of this parameter make the algorithm faster but sacrifice precision, while small values increase the precision of the method. Large values also increase the computational time required for the solution of the problem. In other words, even if the NR-DJM method is intuitive and easy to implement, it requires adequate parametrization of the algorithm, which makes it highly dependent on the programmer. However, this is not the case with the proposed SOCP approach; this approach does not require any adjustment parameter.
Figure 5 depicts the voltage profile for the power flow problem considering all the chargeability factors as zero and the voltage collapse point when all the constant-power loads increase in the same magnitude.
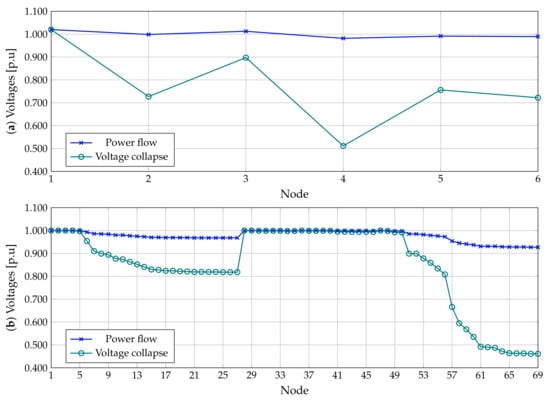
Figure 5.
Voltage behavior in the test system for the initial state of load and voltage collapse: (a) HVDC test system, and (b) MVDC test feeder.
From Figure 5, it is possible to extract the following behaviors:
- 🗸
- The HVDC test feeder with its meshed structure maintains voltages higher than p.u. until the voltage collapse scenario. Please note that node 4 presents the lower voltage profile with p.u., which is a radial extension of this HVDC system.
- 🗸
- The voltage collapse in the MVDC test feeder is evident long after node 57 and onward. This situation occurs in this part (node 57 and onward) of the test feeder since the total load is more significant than regarding routes. Voltage collapse occurs when the maximum voltage drop is p.u. at node 69.
- 🗸
- In both test systems, the voltage collapse occurs when voltages are lower than p.u; while the total load consumptions increase at least three times. This behavior implies that the power system protection disconnects this system before the voltage collapse occurs because of the high currents flowing through the branches.
6. Conclusions and Future Work
A convex reformulation of the voltage stability margin determination in DC networks with constant-power loads was proposed in this paper based on a second-order cone formulation. This model guarantees a global optimum for the problem by approximating the hyperbolic constraints related to the power flow problem. Numerical results, in comparison with those of the Newton–Raphson, SDP, and interior-point approaches, show the efficiency of the proposed SOCP formulation in terms of the objective function calculation and processing times required.
An analysis of voltage stability margin in DC grids enabled the determination of the maximum range of load increments before the collapse of the network. This is important because utilities can use these results for planning and grid reposition procedures (changes in the size of conductors, substations, grid topology) to avoid blackouts when new users are interconnected.
In future work, it will be possible to extend the convex SOCP formulation presented in this paper for optimal power flow analysis, i.e., economic dispatch, in DC networks considering daily operation with a high penetration of renewable energy resources and batteries.
Author Contributions
Conceptualization, O.D.M., W.G.-G., and A.M.-C.; methodology, O.D.M., W.G.-G., and A.M.-C.; formal analysis, O.D.M., W.G.-G., and A.M.-C.; investigation, O.D.M., W.G.-G., and A.M.-C.; resources, O.D.M., W.G.-G., and A.M.-C.; writing—Original draft preparation, O.D.M., W.G.-G., and A.M.-C. All authors have read and agreed to the published version of the manuscript. These authors contributed equally to this work.
Funding
This work was partially supported by the National Scholarship Program Doctorates of the Administrative Department of Science, Technology, and Innovation of Colombia (COLCIENCIAS), by calling contest 727-2015.
Acknowledgments
The authors want to thank Vicerrectoria de Investigación, Innovación y Extensión from Universidad Tecnológica de Pereira for the support provided in this investigation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC microgrids–Part I: A review of control strategies and stabilization techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar]
- Garces, A. Uniqueness of the power flow solutions in low voltage direct current grids. Electr. Power Syst. Res. 2017, 151, 149–153. [Google Scholar] [CrossRef]
- Garcés, A. On the Convergence of Newton’s Method in Power Flow Studies for DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5770–5777. [Google Scholar]
- Gan, L.; Low, S.H. Optimal power flow in direct current networks. IEEE Trans. Power Syst. 2014, 29, 2892–2904. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Candela, J.I.; Luna, A.; Rodriguez, P. A Generalized Voltage Droop Strategy for Control of Multiterminal DC Grids. IEEE Trans. Ind. Appl. 2015, 51, 607–618. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Luna, A.; Rodriguez, P. DC Voltage Control and Power Sharing in Multiterminal DC Grids Based on Optimal DC Power Flow and Voltage-Droop Strategy. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 1171–1180. [Google Scholar] [CrossRef]
- Hamad, A.A.; El-Saadany, E.F. Multi-agent supervisory control for optimal economic dispatch in DC microgrids. Sustain. Cities Soc. 2016, 27, 129–136. [Google Scholar] [CrossRef]
- Barabanov, N.; Ortega, R.; Griñó, R.; Polyak, B. On Existence and Stability of Equilibria of Linear Time-Invariant Systems With Constant Power Loads. IEEE Trans. Circuits Syst. I 2016, 63, 114–121. [Google Scholar] [CrossRef]
- Montoya, O.D. Numerical Approximation of the Maximum Power Consumption in DC-MGs With CPLs via an SDP Model. IEEE Trans. Circuits Syst. II 2019, 66, 642–646. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Gonzalez Montoya, D.; Ramos-Paja, C.A. Optimal sizing and location of distributed generators based on PBIL and PSO techniques. Energies 2018, 11, 1018. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garrido, V.M. Voltage Stability Margin in DC Grids with CPLs: A Recursive Newton–Raphson Approximation. IEEE Trans. Circuits Syst. II 2019, 67, 300–304. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Garzon-Rivera, O.D.; Montoya, O.D.; Ramos-Paja, C.A. Hybrid Metaheuristic Optimization Methods for Optimal Location and Sizing DGs in DC Networks. In Workshop on Engineering Applications; Chapter Applied Computer Sciences in Engineering; Figueroa-García, J., Duarte-González, M., Jaramillo-Isaza, S., Orjuela-Cañon, A., Díaz-Gutierrez, Y., Eds.; Springer: Berlin, Germany, 2019; Volume 1052, pp. 552–564. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Wang, Z.; Low, S.H.; Mei, S. Optimal Power Flow in Stand-Alone DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5496–5506. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, X.; Wu, Q.; Zhou, Q. Second-order conic programming model for load restoration considering uncertainty of load increment based on information gap decision theory. Int. J. Electr. Power Energy Syst. 2019, 105, 151–158. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garrido, V.M.; Gil-González, W.; Grisales-Noreña, L.F. Power Flow Analysis in DC Grids: Two Alternative Numerical Methods. IEEE Trans. Circuits Syst. II 2019, 66, 1865–1869. [Google Scholar] [CrossRef]
- Lavaei, J.; Low, S.H. Zero Duality Gap in Optimal Power Flow Problem. IEEE Trans. Power Syst. 2012, 27, 92–107. [Google Scholar] [CrossRef]
- Hindi, H. A tutorial on convex optimization. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 4, pp. 3252–3265. [Google Scholar]
- Alizadeh, F.; Goldfarb, D. Second-order cone programming. Math Program 2003, 95, 3–51. [Google Scholar] [CrossRef]
- Yuan, Z.; Hesamzadeh, M.R. Second-order cone AC optimal power flow: Convex relaxations and feasible solutions. J. Mod. Power Syst. Clean Energy 2018, 7, 268–280. [Google Scholar] [CrossRef]
- Luo, Z.Q.; Yu, W. An introduction to convex optimization for communications and signal processing. IEEE J. Sel. Areas Commun. 2006, 24, 1426–1438. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).