Stability Analysis and Dual Solutions of Micropolar Nanofluid over the Inclined Stretching/Shrinking Surface with Convective Boundary Condition
Abstract
1. Introduction
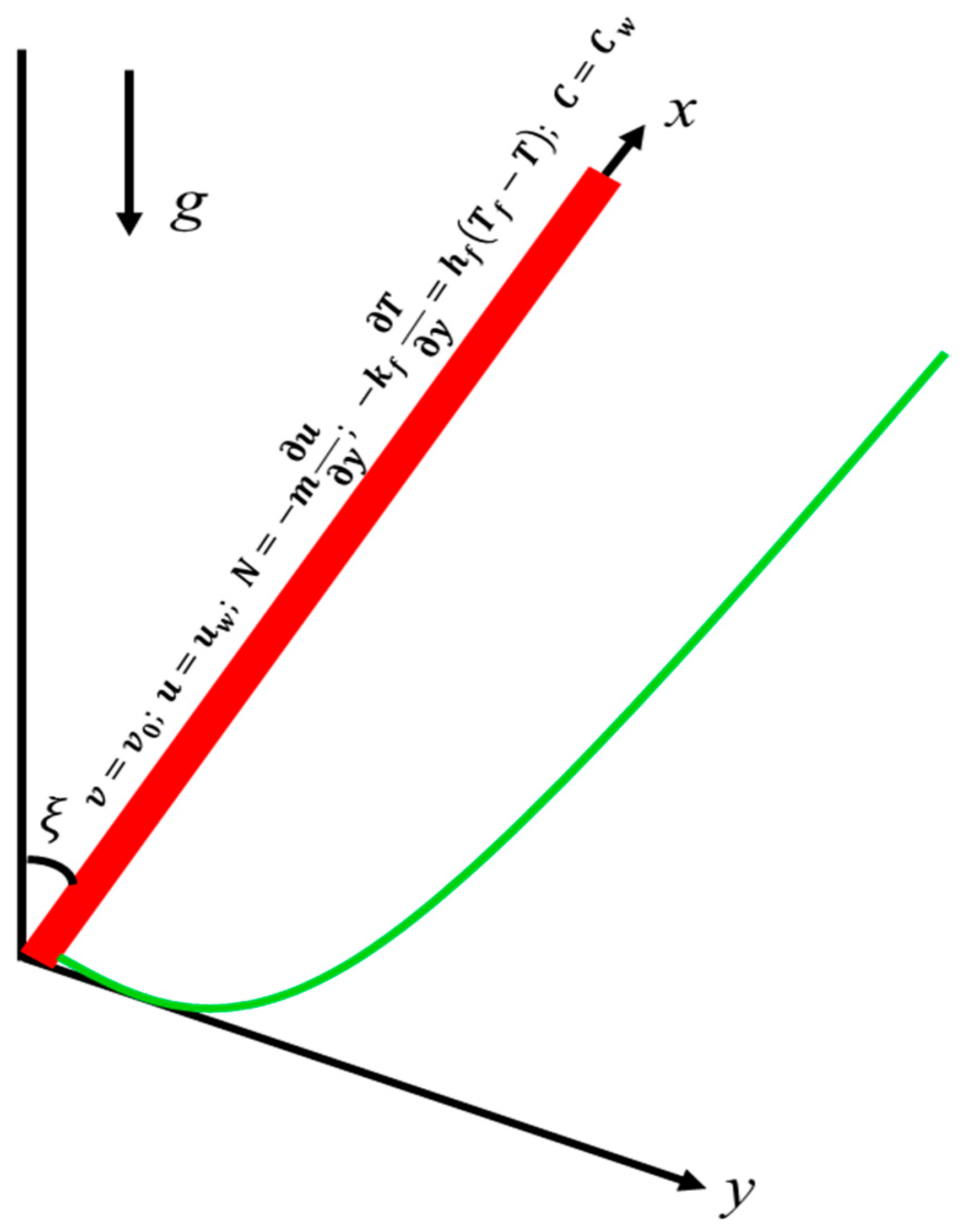
2. Problem Formulation
3. Stability Analysis
4. Numerical Method
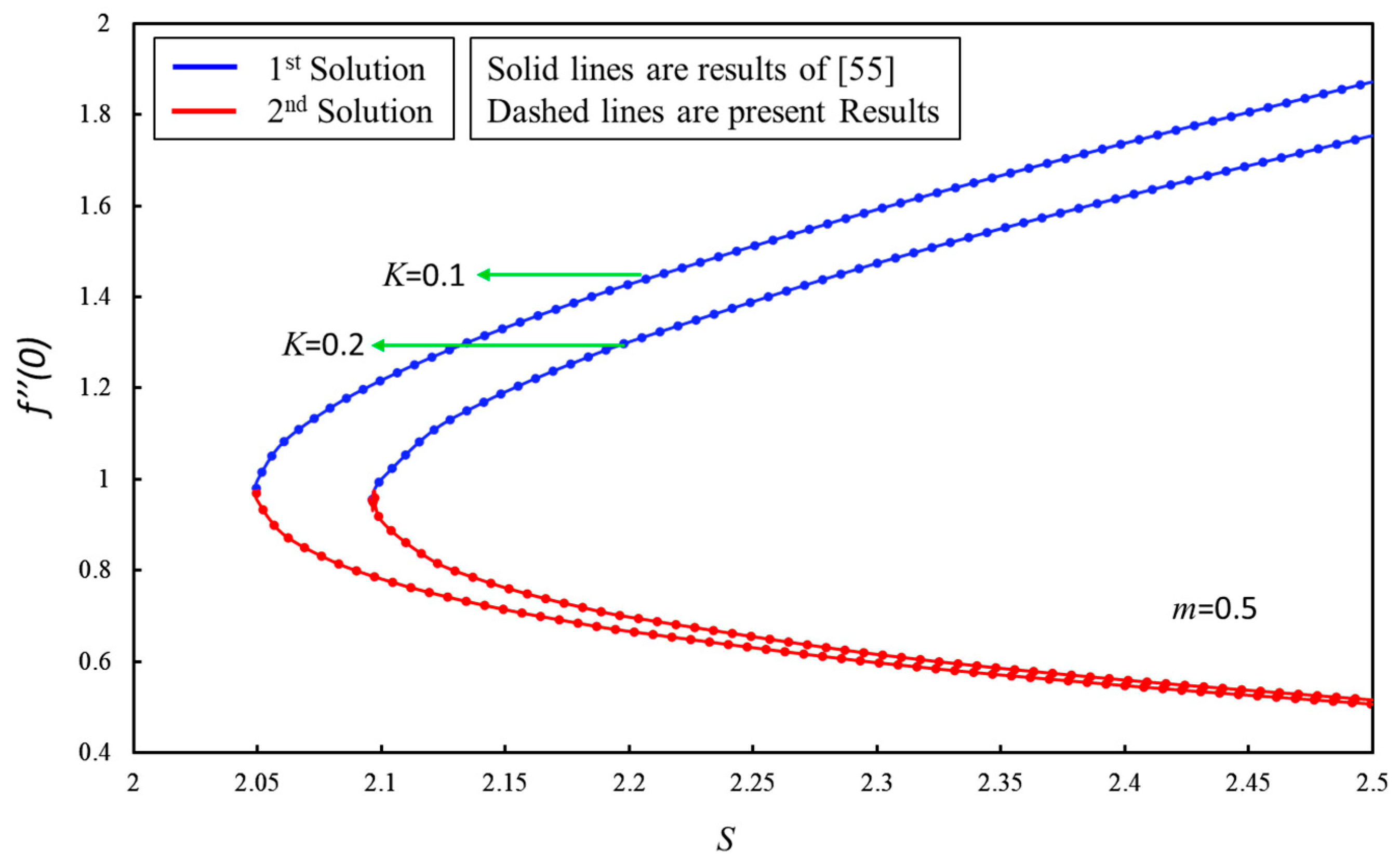
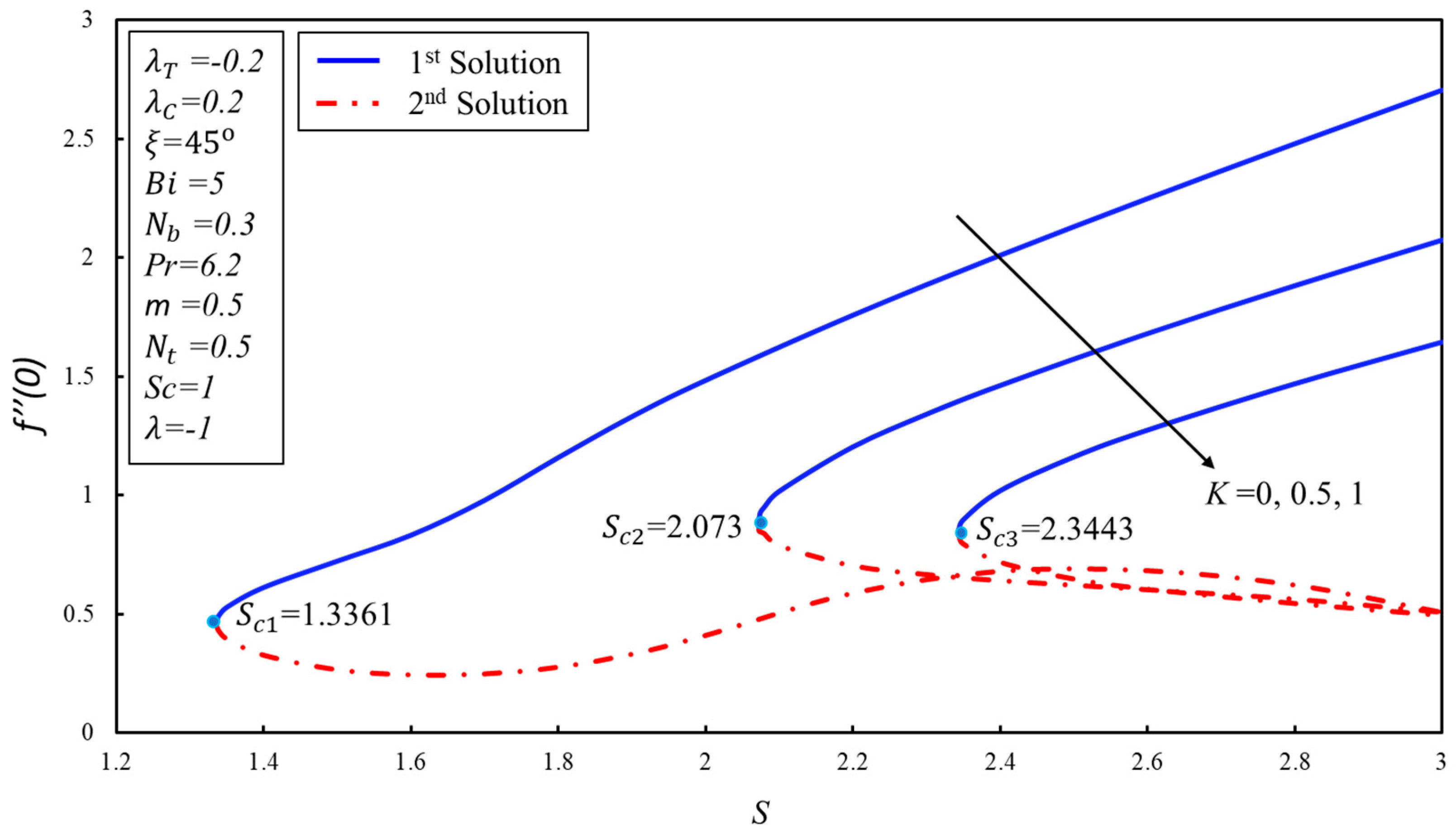
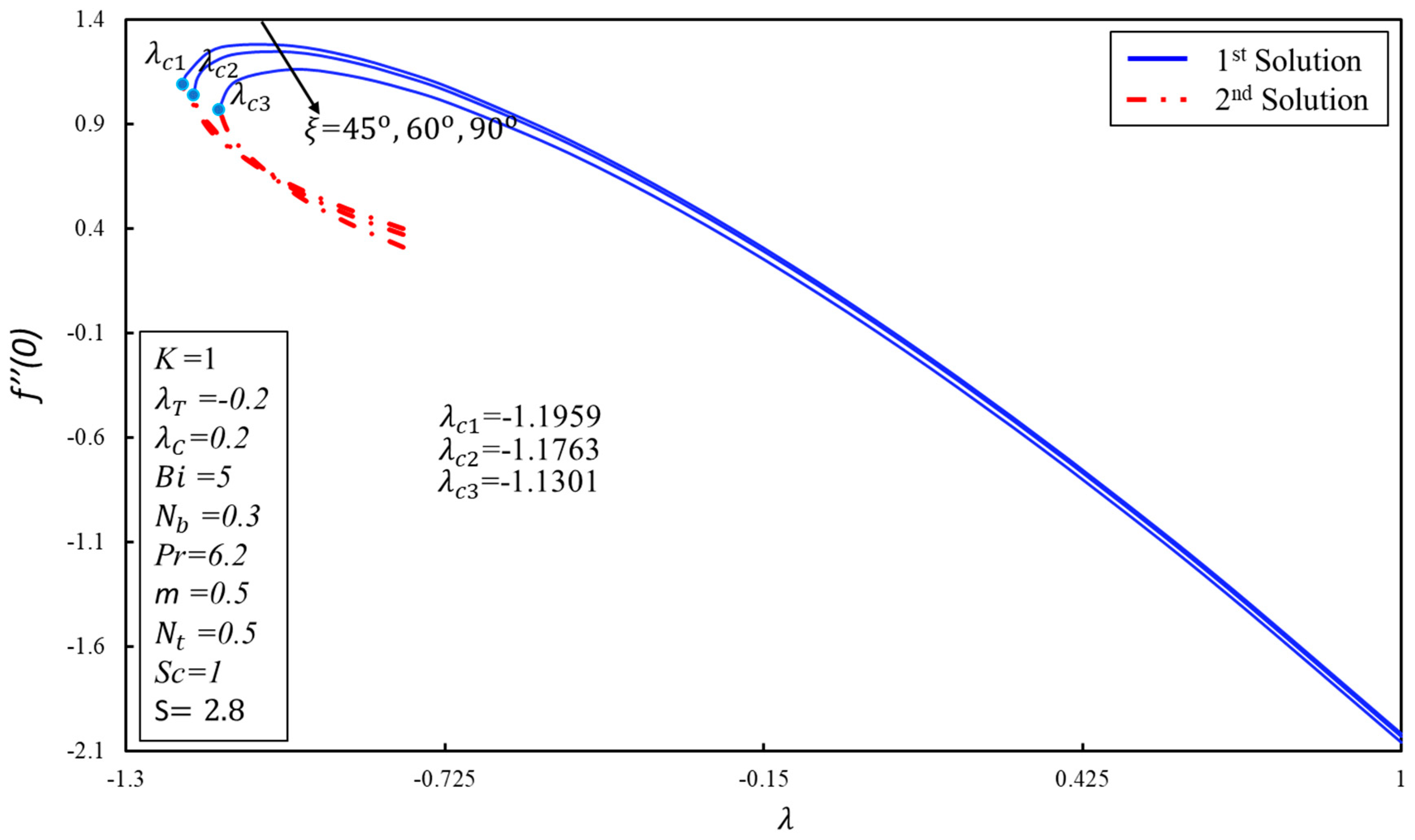
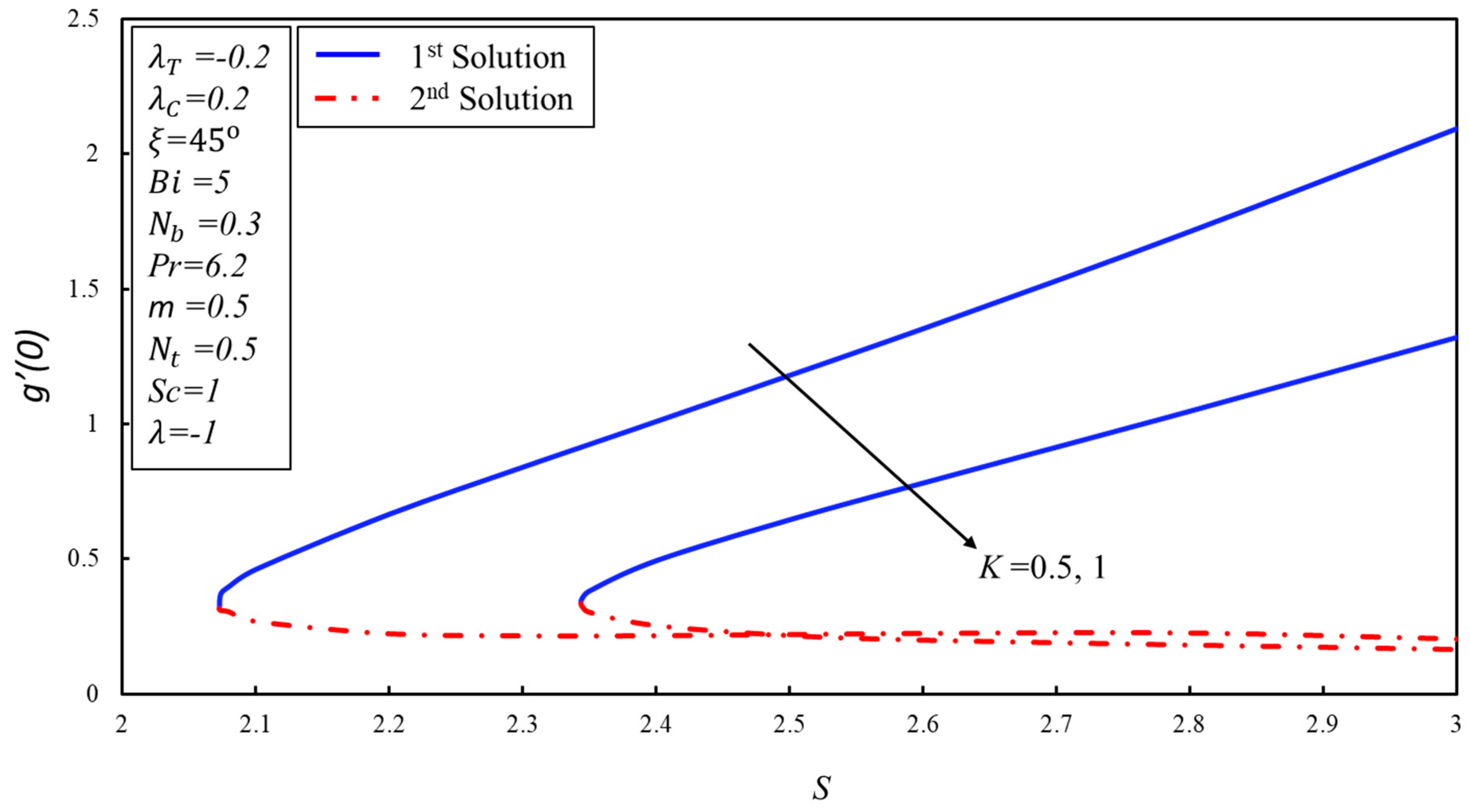
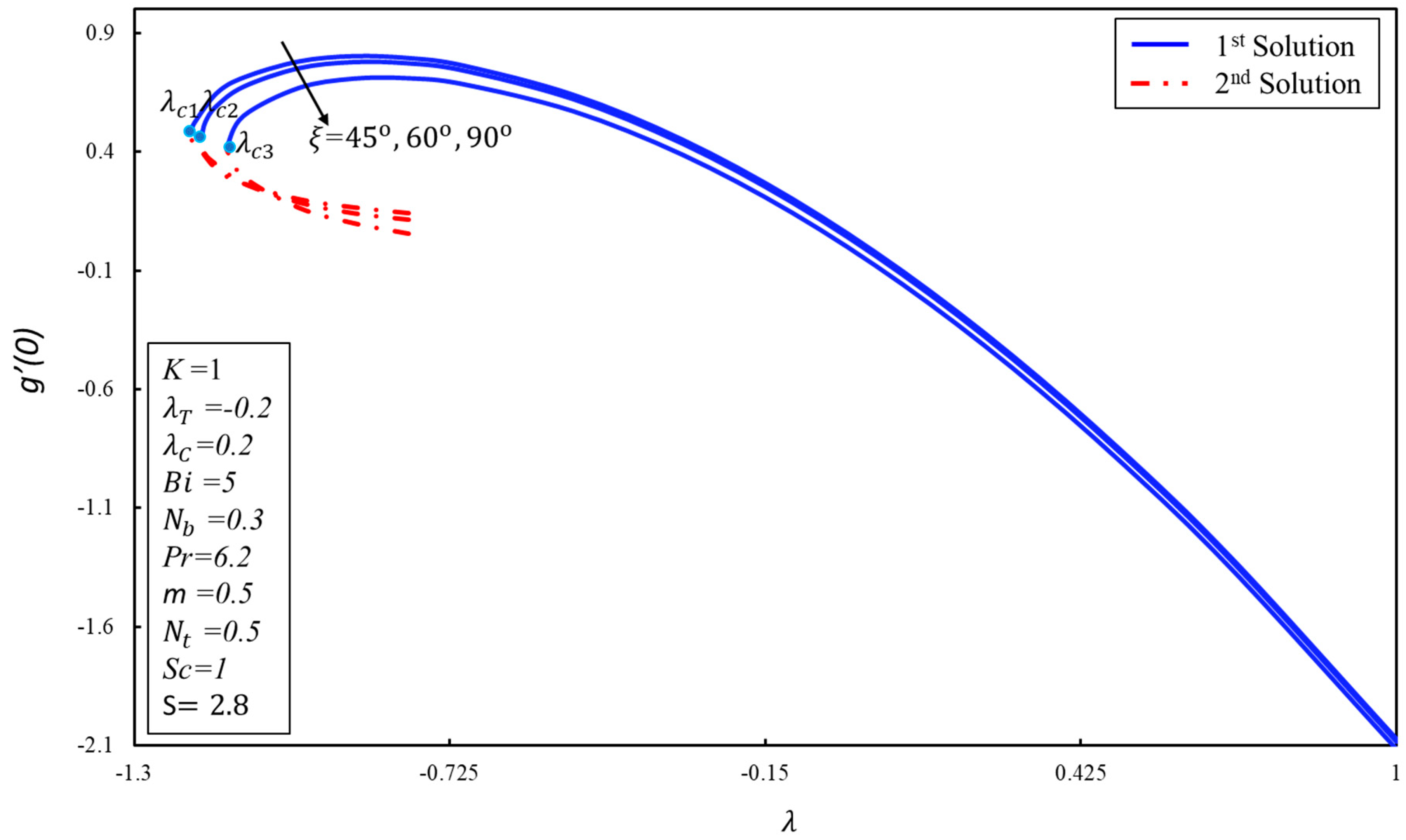
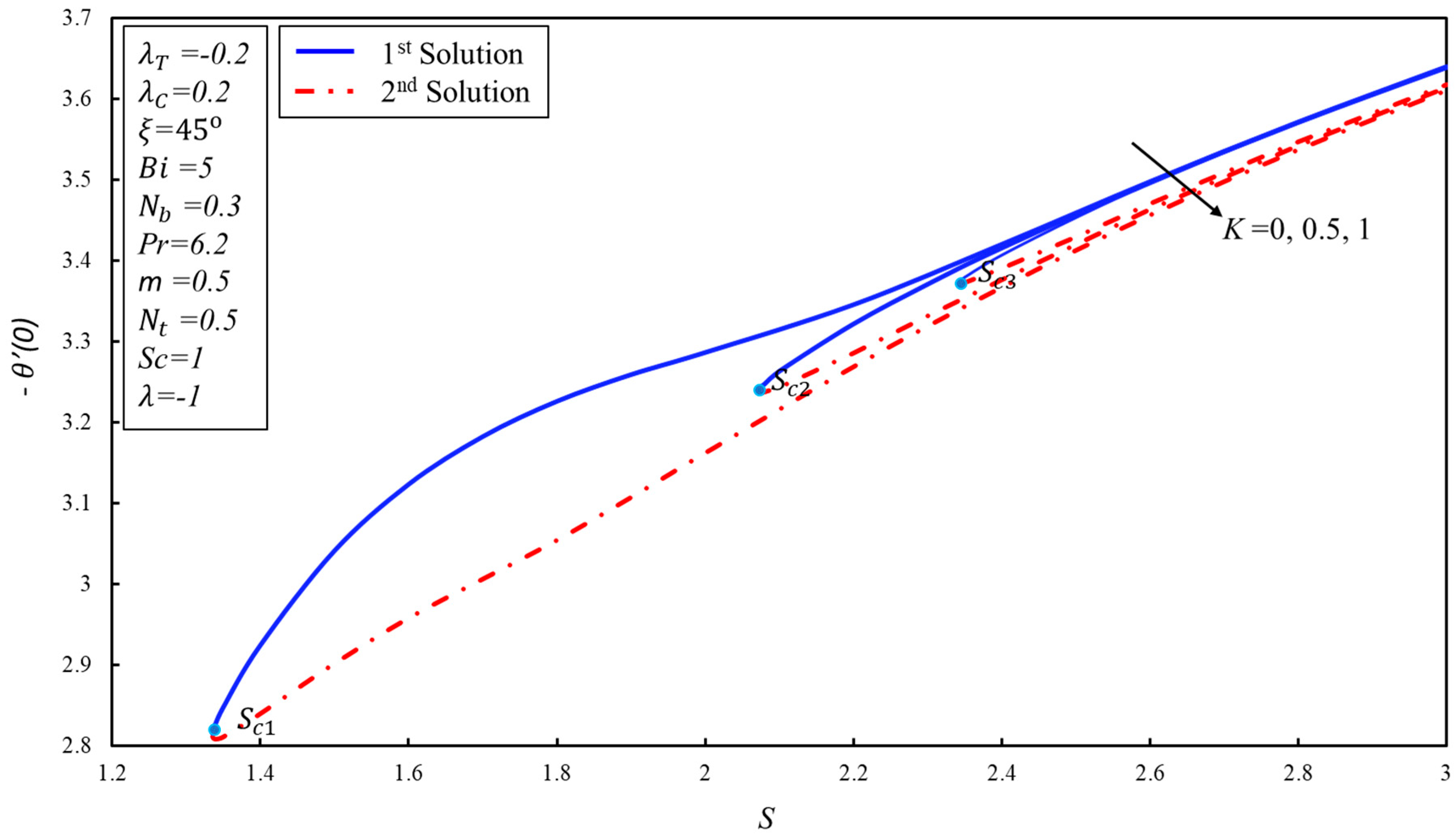
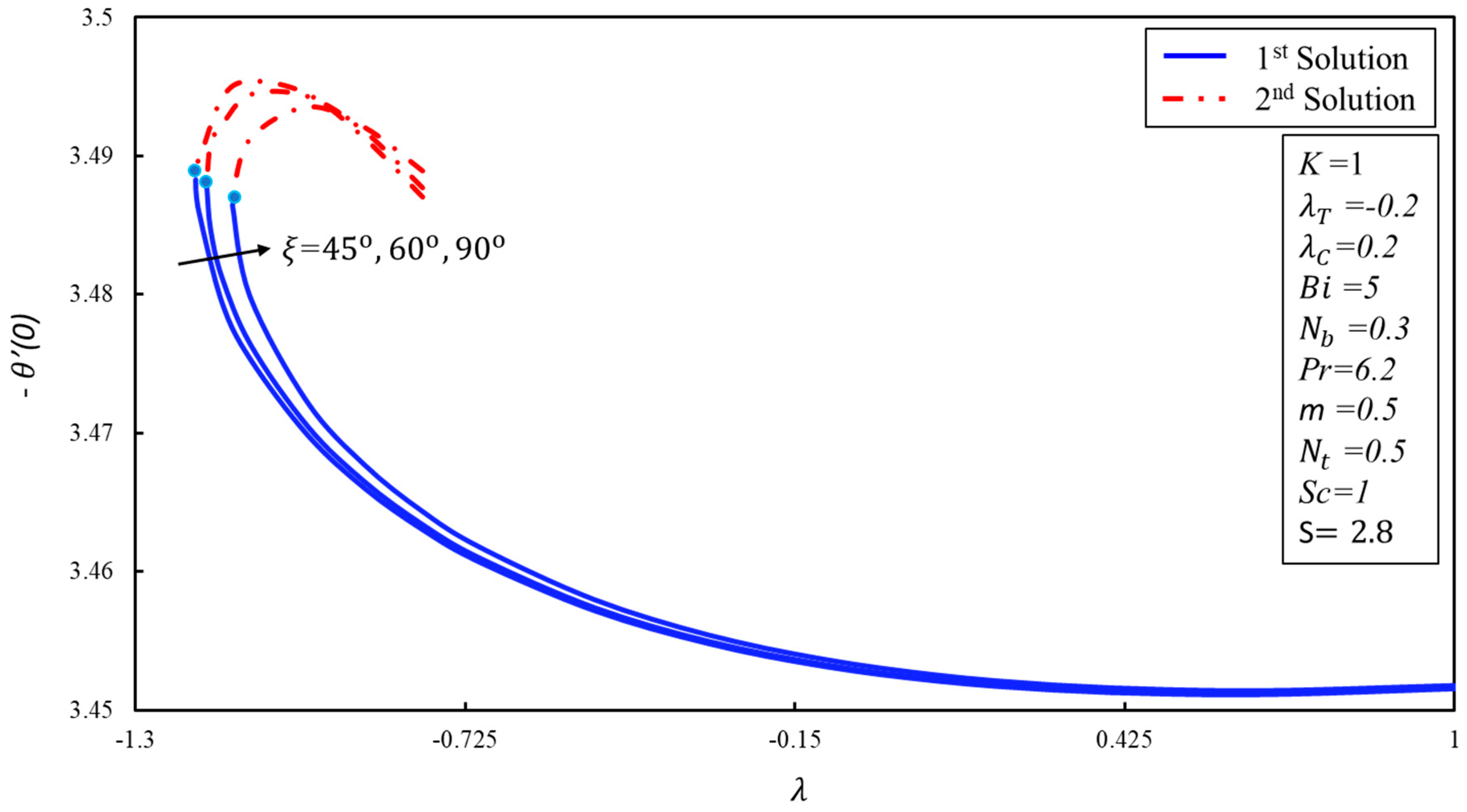
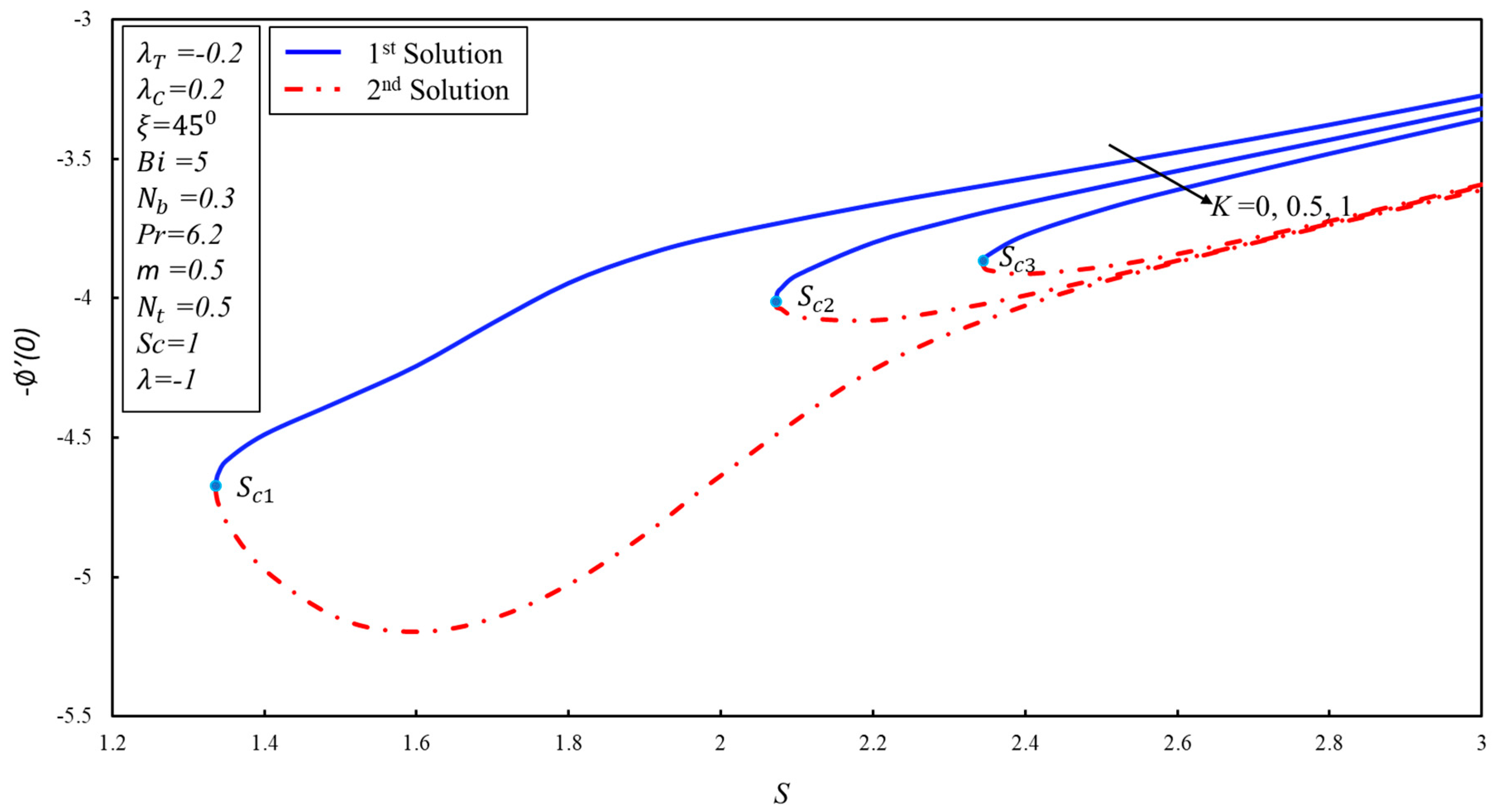
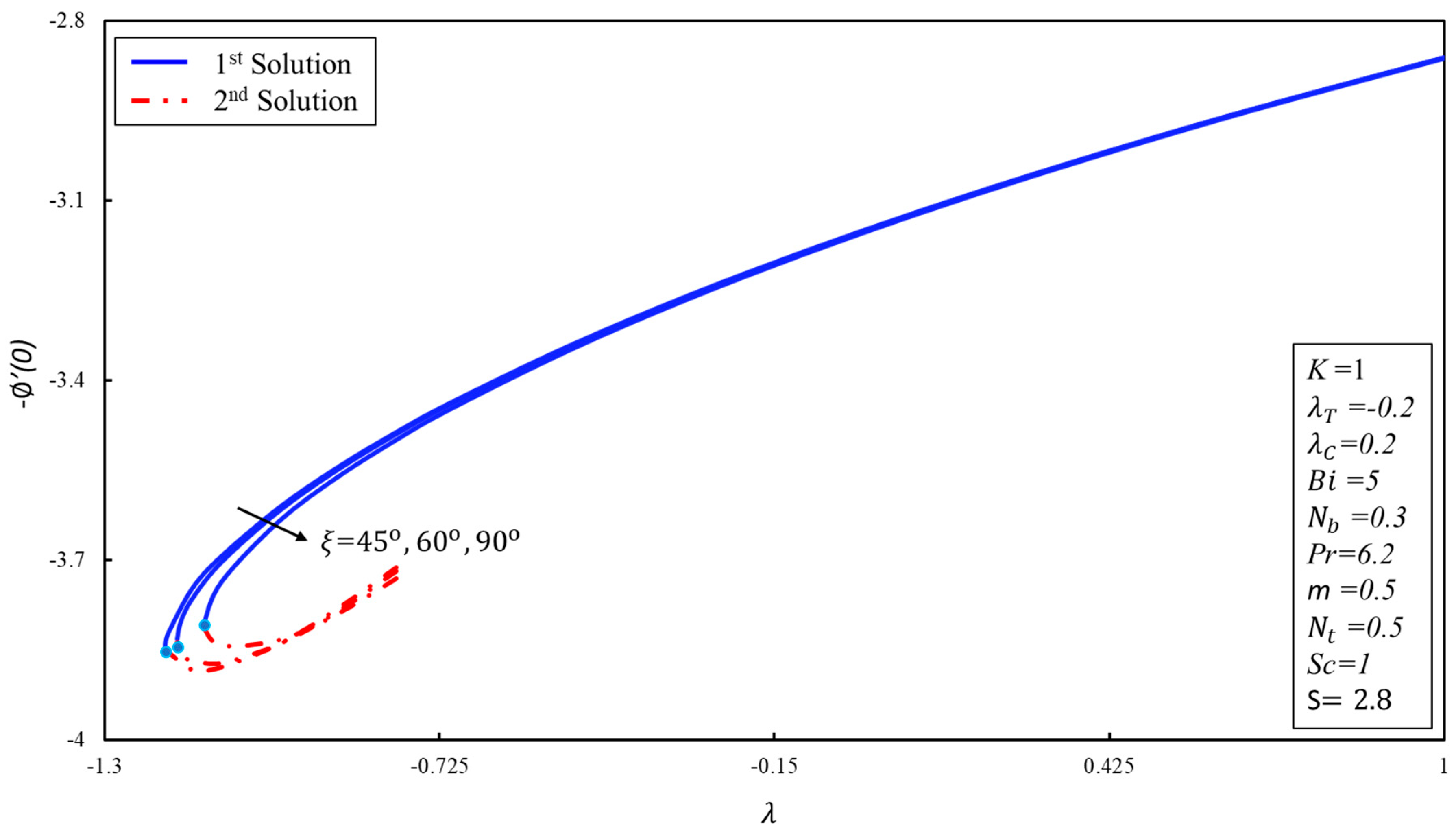
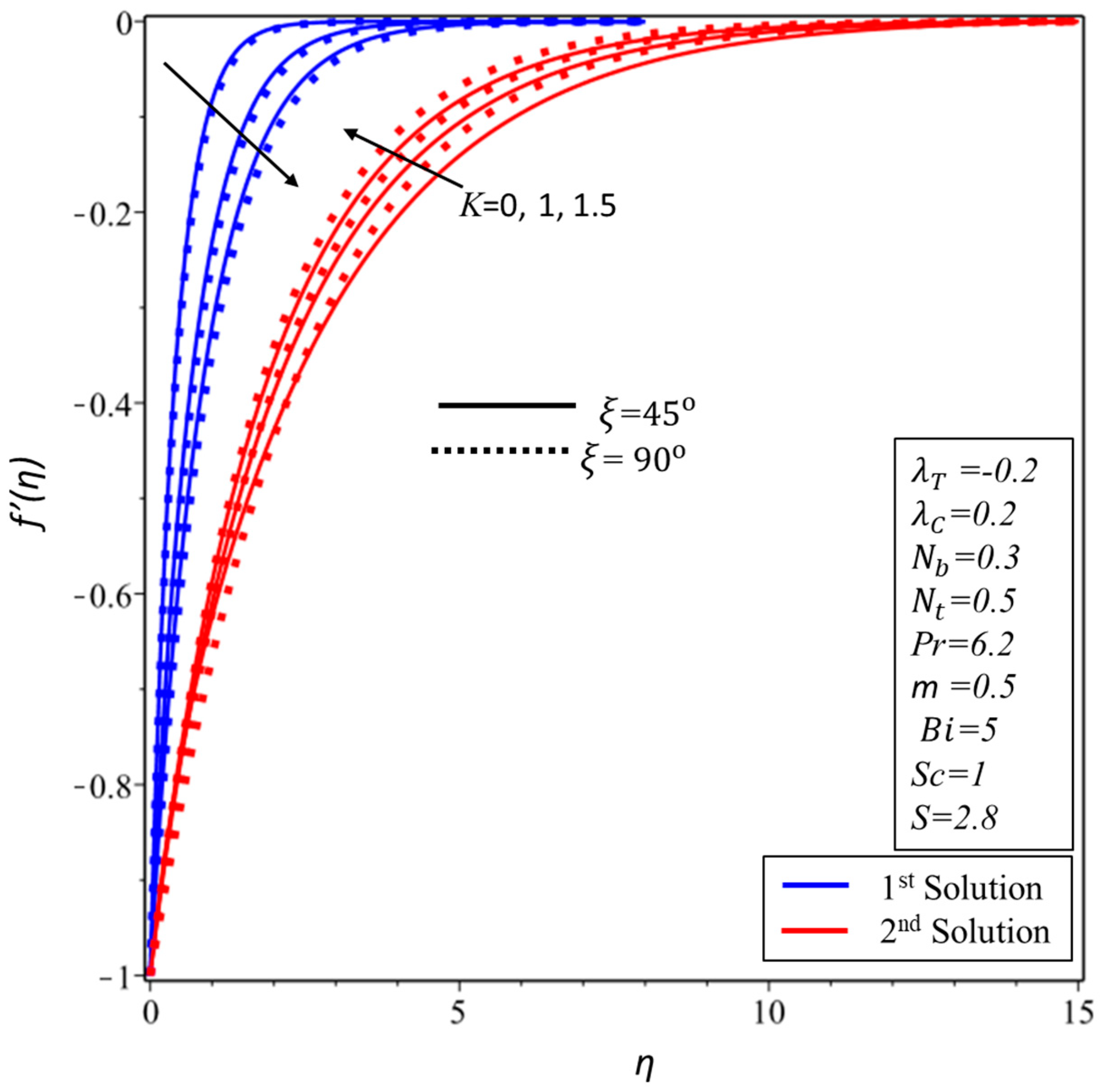
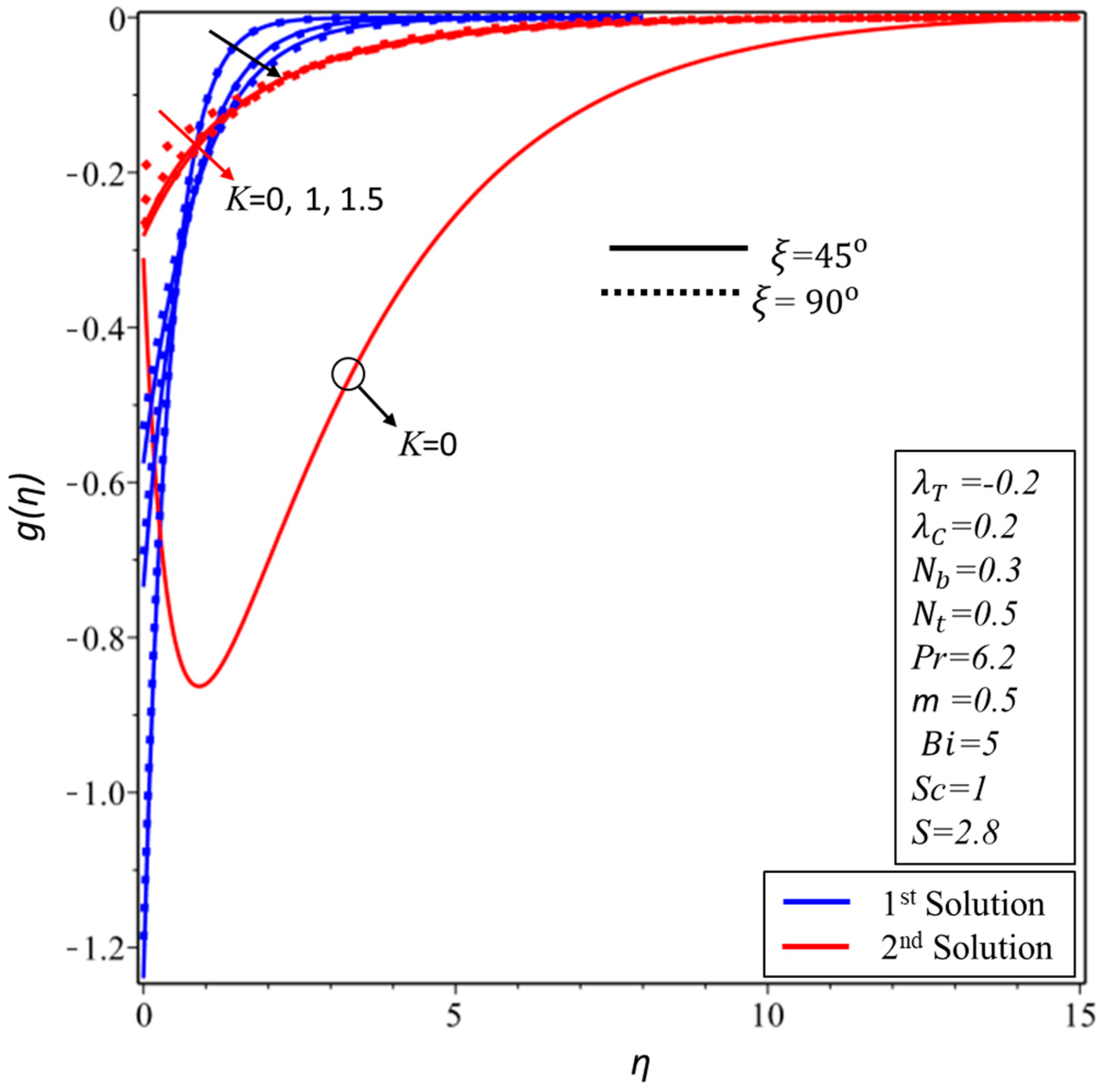
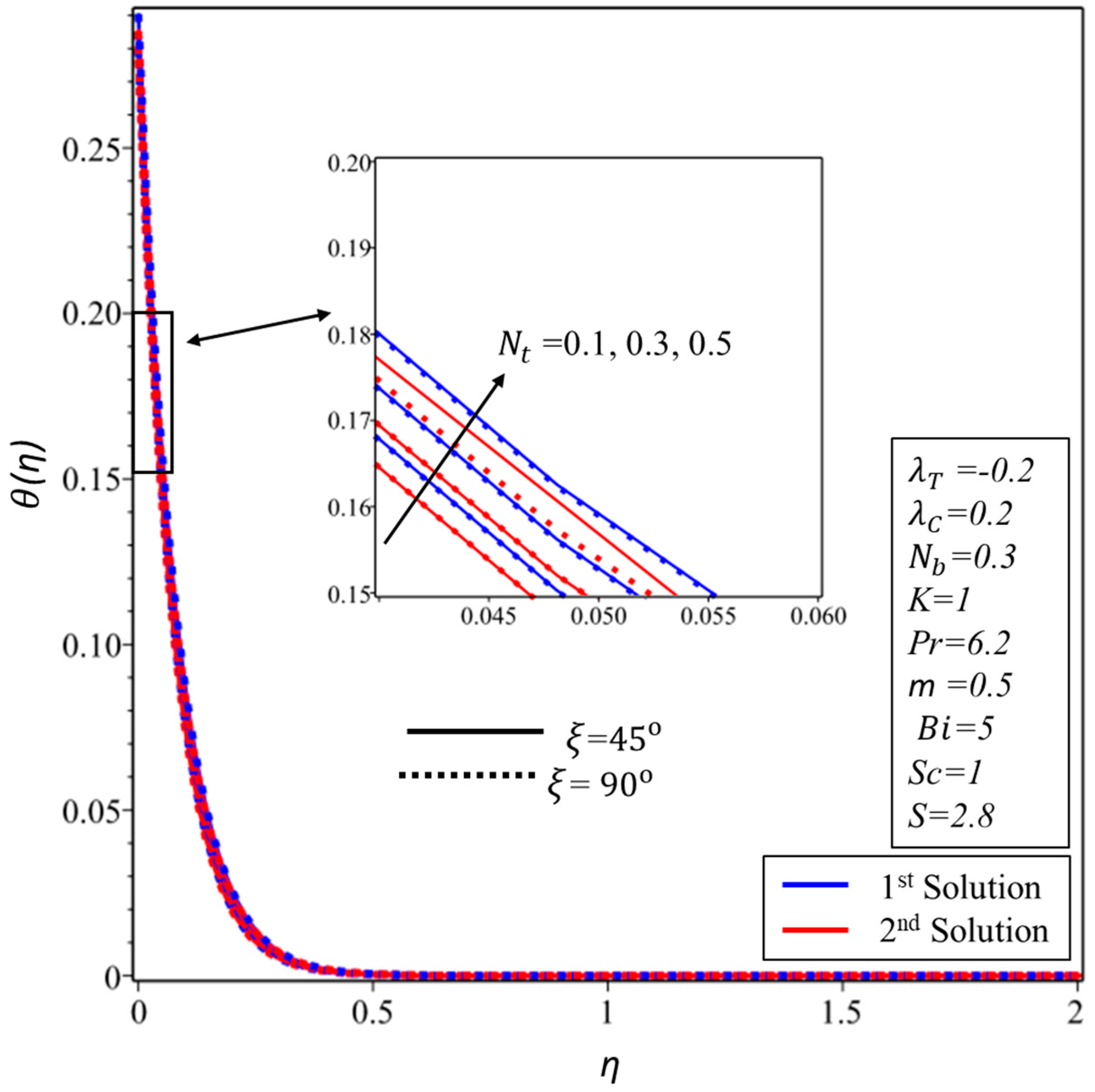
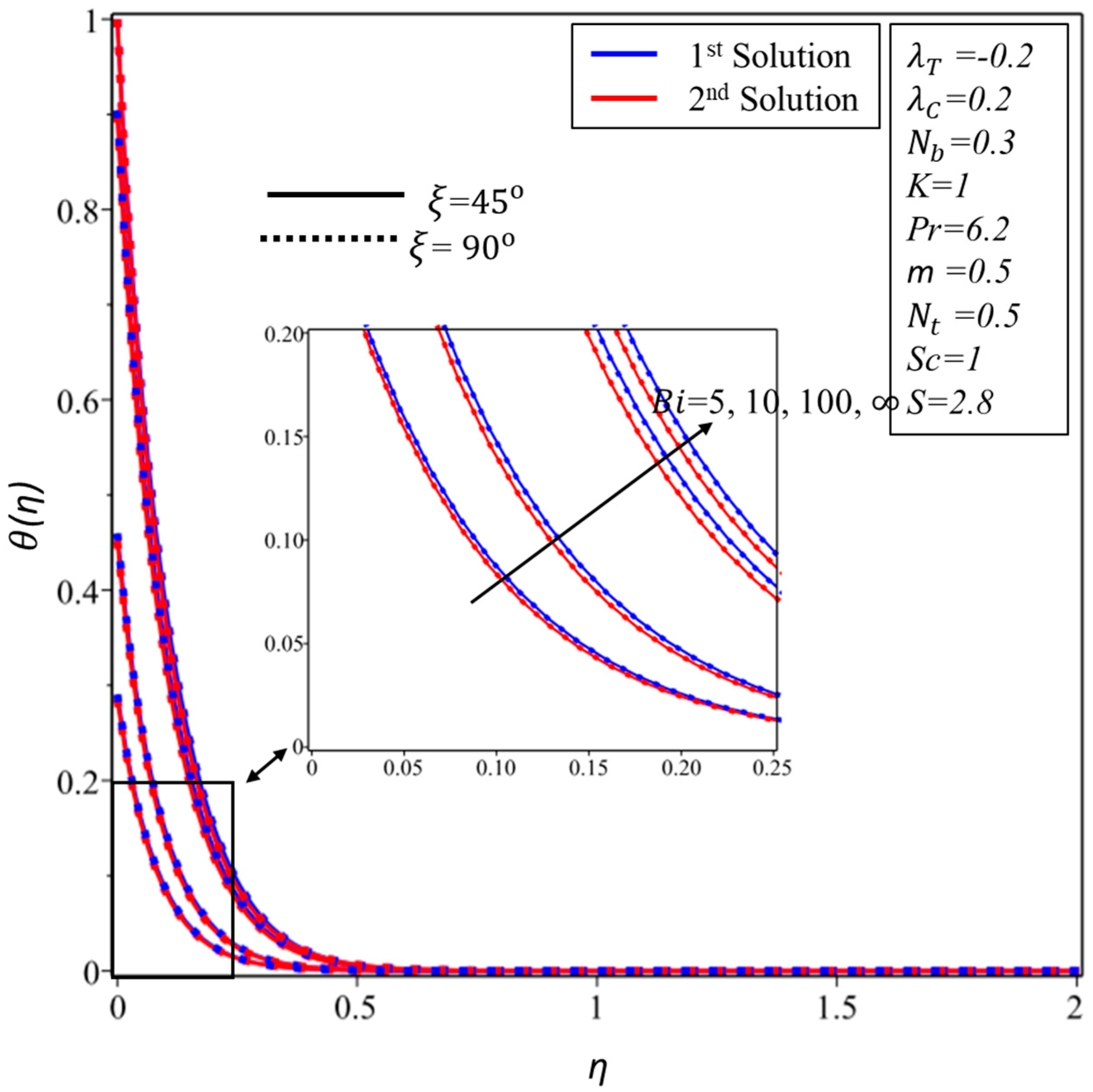
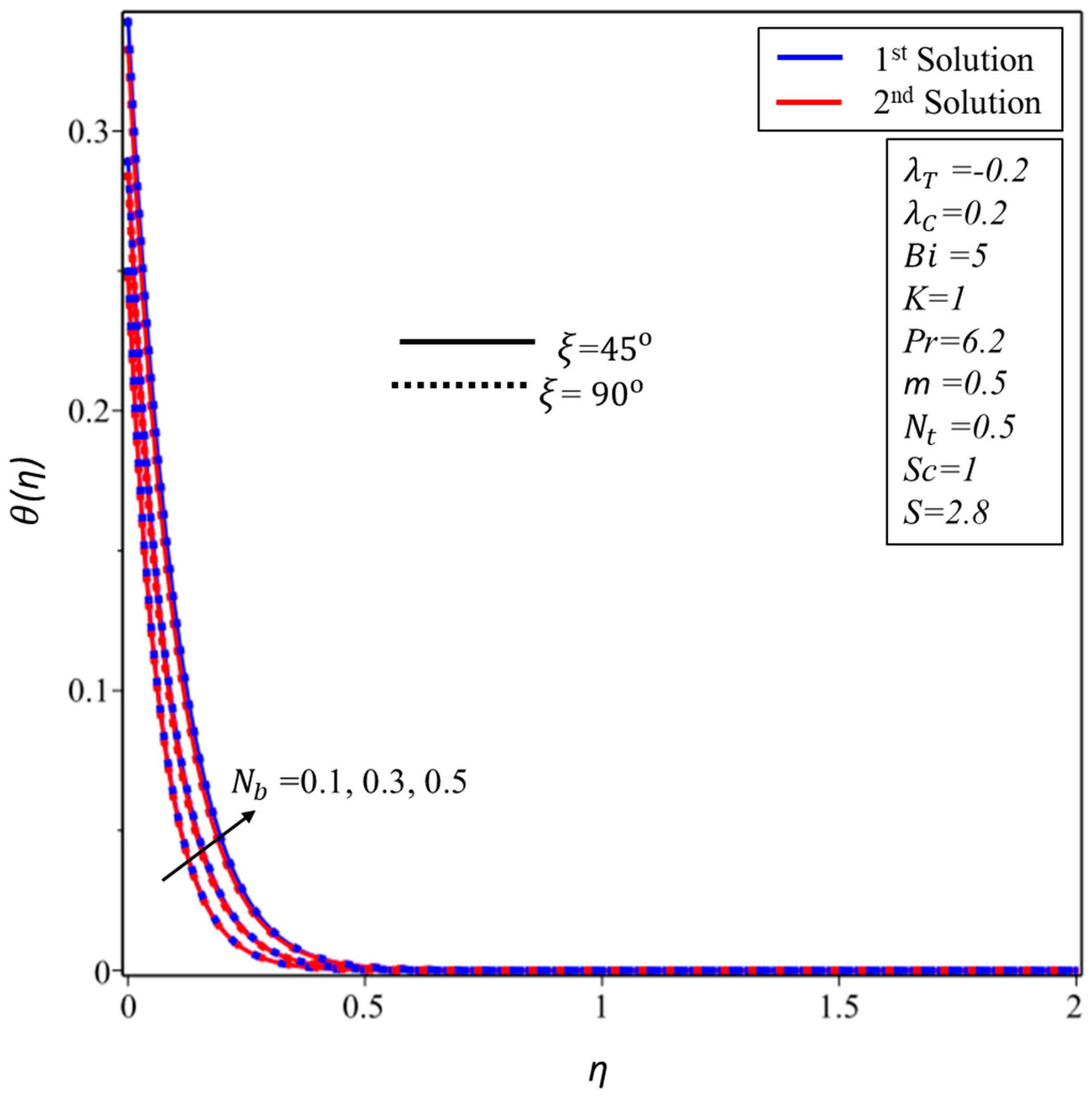
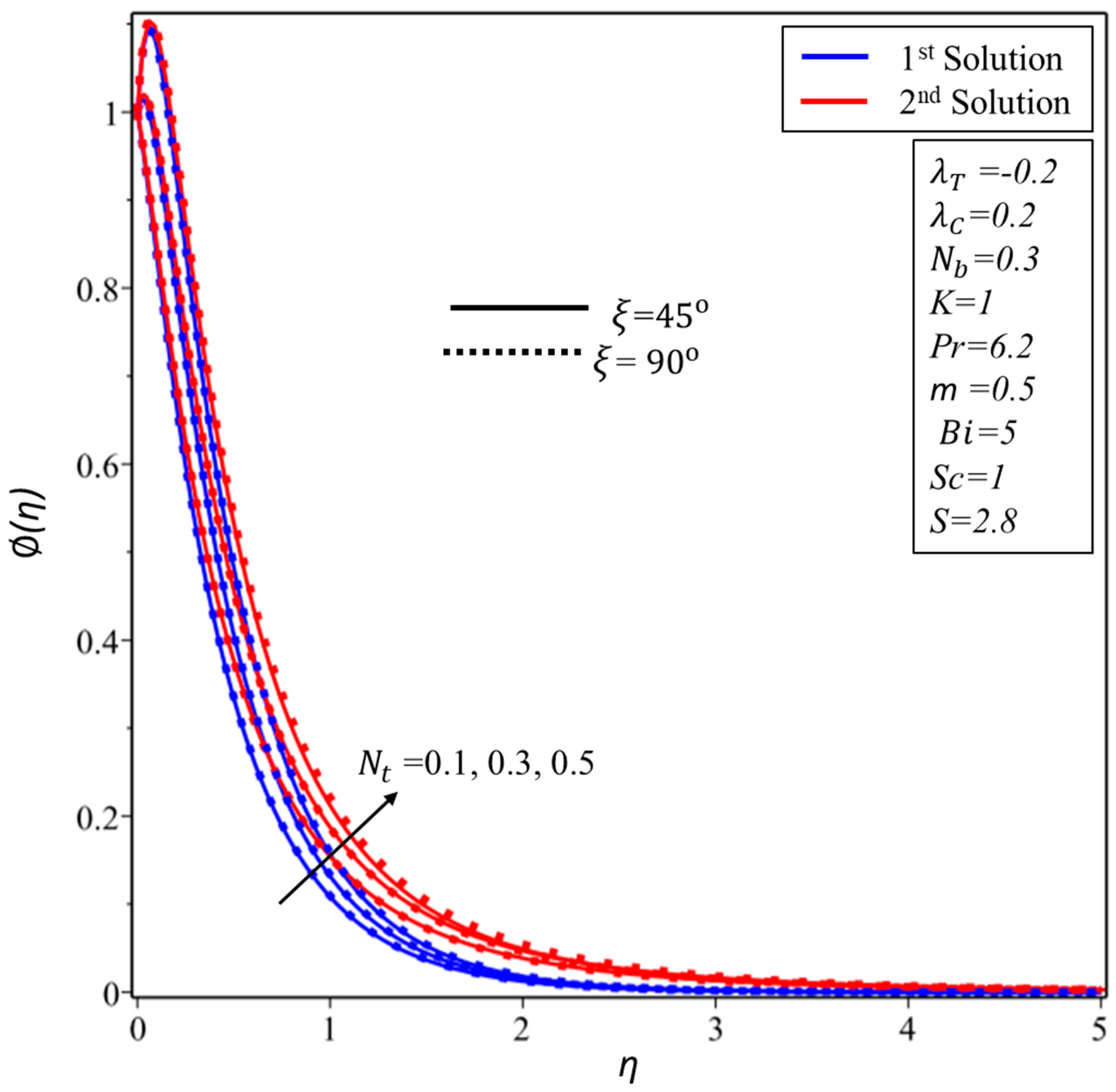
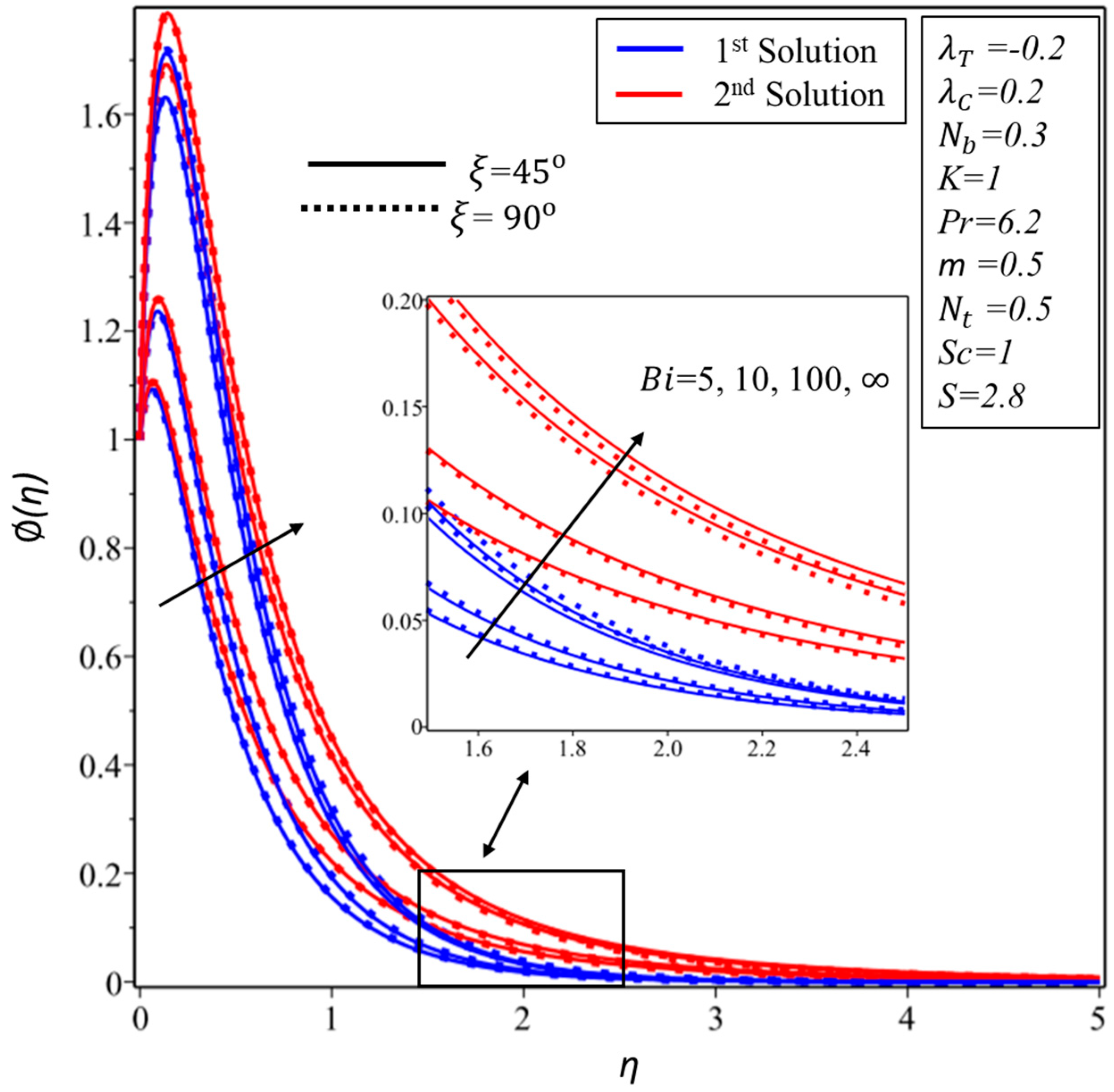
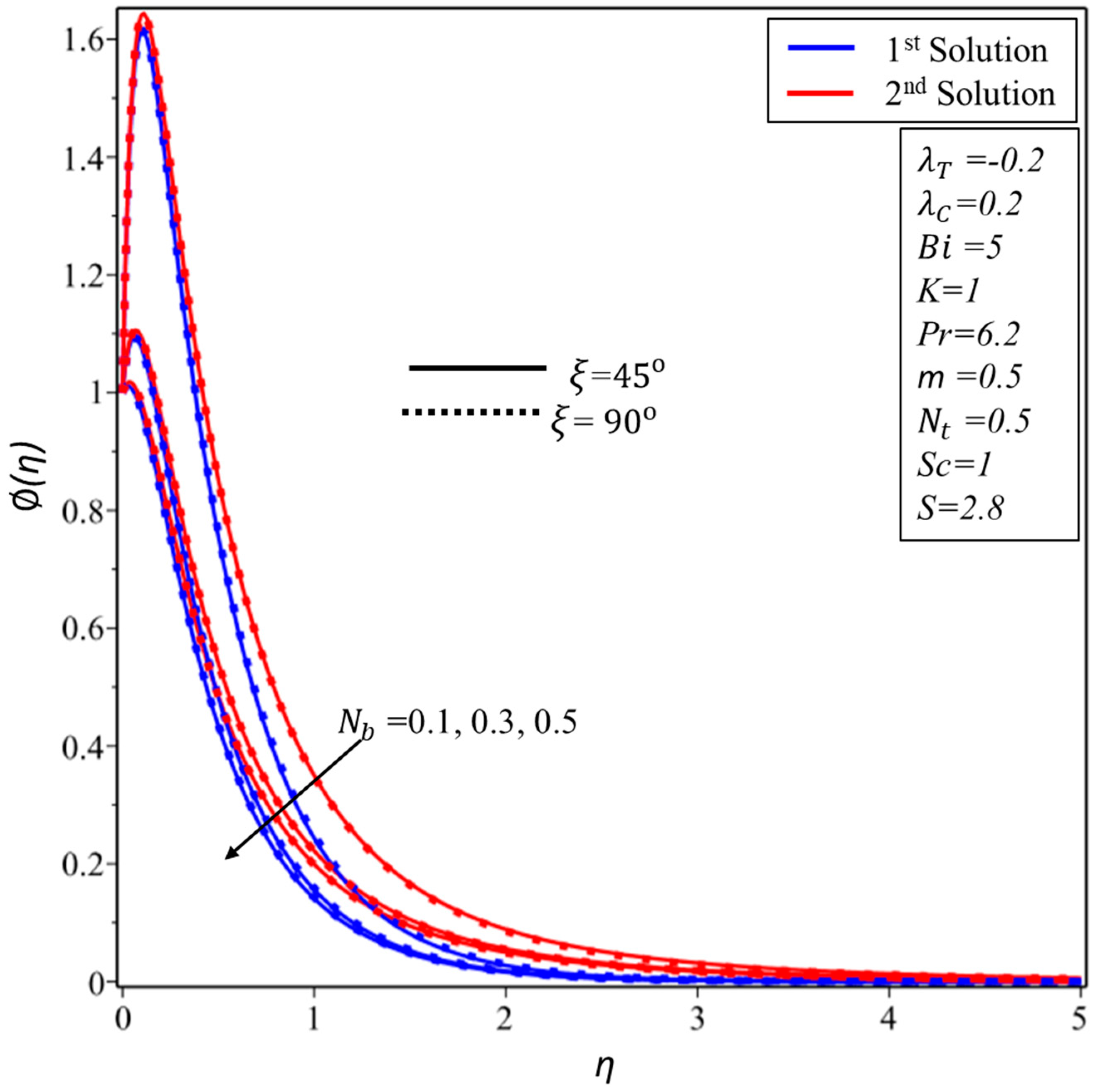
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eringen, A.C. Simple micropolar fluids. Int. J. Eng. Sci. 1964, 2, 205–207. [Google Scholar] [CrossRef]
- Koriko, O.K.; Animasaun, I.L.; Omowaye, A.J.; Oreyeni, T. The combined influence of nonlinear thermal radiation and thermal stratification on the dynamics of micropolar fluid along a vertical surface. Multidiscip. Model. Mater. Struct. 2019, 15, 133–155. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Dawar, A.; Alzahrani, E.O.; Thounthong, P. Study of the Couple Stress Convective Micropolar Fluid Flow in a Hall MHD Generator System. Front. Phys. 2019, 7, 171. [Google Scholar] [CrossRef]
- Lukaszewicz, G. Micropolar Fluids: Theory and Applications; Brikhauser: Basel, Switzerland, 1999. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A.; Khan, M.I. Radiative flow of micropolar nanofluid accounting thermophoresis and Brownian moment. Int. J. Hydrogen Energy 2017, 42, 16821–16833. [Google Scholar] [CrossRef]
- Noor, N.F.M.; Haq, R.U.; Nadeem, S.; Hashim, I. Mixed convection stagnation flow of a micropolar nanofluid along a vertically stretching surface with slip effects. Meccanica 2015, 50, 2007–2022. [Google Scholar] [CrossRef]
- Haq, R.U.; Nadeem, S.; Akbar, N.S.; Khan, Z.H. Buoyancy and radiation effect on stagnation point flow of micropolar nanofluid along a vertically convective stretching surface. IEEE Trans. Nanotechnol. 2014, 14, 42–50. [Google Scholar]
- Patel, H.R.; Mittal, A.S.; Darji, R.R. MHD flow of micropolar nanofluid over a stretching/shrinking sheet considering radiation. Int. Commun. Heat Mass Transf. 2019, 108, 104322. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Numerical Study on Micropolar Nanofluid Flow over an Inclined Surface by Means of Keller-Box. Asian J. Probab. Stat. 2019, 1–21. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.S.M.; Nisar, K.S. Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface. Symmetry 2019, 11, 1379. [Google Scholar] [CrossRef]
- Sithole, H.; Mondal, H.; Magagula, V.M.; Sibanda, P.; Motsa, S. Bivariate Spectral Local Linearisation Method (BSLLM) for unsteady MHD Micropolar-nanofluids with Homogeneous–Heterogeneous chemical reactions over a stretching surface. Int. J. Appl. Comput. Math. 2019, 5, 12. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Elmasry, Y.; Malik, M.Y. Numerical analysis of water based CNTs flow of micropolar fluid through rotating frame. Comput. Methods Progr. Biomed. 2020, 186, 105194. [Google Scholar] [CrossRef]
- Ibrahim, W.; Gadisa, G. Finite element analysis of couple stress micropolar nanofluid flow by non-Fourier’s law heat flux model past stretching surface. Heat Transf. Asian Res. 2019. [Google Scholar] [CrossRef]
- Abbas, Z.; Mushtaq, T.; Shehzad, S.A.; Rauf, A.; Kumar, R. Slip flow of hydromagnetic micropolar nanofluid between two disks with characterization of porous medium. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 465. [Google Scholar] [CrossRef]
- Alzahrani, E.O.; Shah, Z.; Alghamdi, W.; Ullah, M.Z. Darcy–Forchheimer Radiative Flow of Micropoler CNT Nanofluid in Rotating Frame with Convective Heat Generation/Consumption. Processes 2019, 7, 666. [Google Scholar] [CrossRef]
- Abidi, A.; Raizah, Z.; Madiouli, J. Magnetic Field Effect on the Double Diffusive Natural Convection in Three-Dimensional Cavity Filled with Micropolar Nanofluid. Appl. Sci. 2018, 8, 2342. [Google Scholar] [CrossRef]
- Raslan, K.; Mohamadain, S.; Abdel-wahed, M.; Abedel-aal, E. MHD Steady/Unsteady Porous Boundary Layer of Cu–Water Nanofluid with Micropolar Effect over a Permeable Surface. Appl. Sci. 2018, 8, 736. [Google Scholar] [CrossRef]
- Anwar, M.I.; Shafie, S.; Hayat, T.; Shehzad, S.A.; Salleh, M.Z. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 89–100. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I. Mathematical analysis of magnetohydrodynamic (MHD) flow of micropolar nanofluid under buoyancy effects past a vertical shrinking surface: Dual solutions. Heliyon 2019, 5, e02432. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A. MHD micropolar nanofluid flow over an exponentially stretching/shrinking surface: Triple solutions. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 56, 165–174. [Google Scholar]
- Magodora, M.; Mondal, H.; Sibanda, P. Dual solutions of a micropolar nanofluid flow with radiative heat mass transfer over stretching/shrinking sheet using spectral quasilinearization method. Multidiscip. Model. Mater. Struct. 2019. [Google Scholar] [CrossRef]
- Ali Lund, L.; Ching, D.L.C.; Omar, Z.; Khan, I.; Nisar, K.S. Triple local similarity solutions of Darcy-Forchheimer Magnetohydrodynamic (MHD) flow of micropolar nanofluid over an exponential shrinking surface: Stability analysis. Coatings 2019, 9, 527. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Flow of a micropolar fluid due to a porous stretching sheet and heat transfer. Int. J. Non-Linear Mech. 2016, 83, 59–64. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Mixed convection flow of magnetohydrodynamic micropolar fluid due to a porous heated/cooled deformable plate: Exact solutions. Int. J. Heat Mass Transf. 2017, 106, 127–134. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Ishak, A.; Pop, I. Oblique stagnation slip flow of a micropolar fluid towards a stretching/shrinking surface: A stability analysis. Chin. J. Phys. 2018, 56, 3062–3072. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Dero, S.; Khan, I. Linear stability analysis of MHD flow of micropolar fluid with thermal radiation and convective boundary condition: Exact solution. Heat Transf. Asian Res. 2019, 49. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. Rheology of micropolar fluid in a channel with changing walls: Investigation of multiple solutions. J. Mol. Liq. 2016, 223, 890–902. [Google Scholar] [CrossRef]
- Mahmood, A.; Chen, B.; Ghaffari, A. Hydromagnetic Hiemenz flow of micropolar fluid over a nonlinearly stretching/shrinking sheet: Dual solutions by using Chebyshev Spectral Newton Iterative Scheme. J. Magn. Magn. Mater. 2016, 416, 329–334. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar]
- Raju, C.S.K.; Sandeep, N.; Babu, M.J.; Sugunamma, V. Dual solutions for three-dimensional MHD flow of a nanofluid over a nonlinearly permeable stretching sheet. Alex. Eng. J. 2016, 55, 151–162. [Google Scholar] [CrossRef]
- Li, X.; Khan, A.U.; Khan, M.R.; Nadeem, S.; Khan, S.U. Oblique Stagnation Point Flow of Nanofluids over Stretching/Shrinking Sheet with Cattaneo–Christov Heat Flux Model: Existence of Dual Solution. Symmetry 2019, 11, 1070. [Google Scholar] [CrossRef]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Dual solutions for nanofluid flow past a curved surface with nonlinear radiation, Soret and Dufour effects. J. Phys. Conf. Ser. 2018, 1000, 012152. [Google Scholar] [CrossRef]
- Dero, S.; Uddin, M.J.; Rohni, A.M. Stefan blowing and slip effects on unsteady nanofluid transport past a shrinking sheet: Multiple solutions. Heat Transf. Asian Res. 2019, 48, 2047–2066. [Google Scholar] [CrossRef]
- Zaib, A.; Haq, R.U.; Sheikholeslami, M.; Khan, U. Numerical analysis of effective Prandtl model on mixed convection flow of γAl 2 O 3-H 2 O nanoliquids with micropolar liquid driven through wedge. Phys. Scr. 2019. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Khan, I.; Nisar, K.S. Activation energy on MHD flow of titanium alloy (Ti6Al4V) nanoparticle along with a cross flow and streamwise direction with binary chemical reaction and non-linear radiation: Dual Solutions. J. Mater. Res. Technol. 2019. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Dero, S. Multiple solutions of Cu-C 6 H 9 NaO 7 and Ag-C 6 H 9 NaO 7 nanofluids flow over nonlinear shrinking surface. J. Cent. South Univ. 2019, 26, 1283–1293. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Mixed convection stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies 2019, 12, 788. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J. Dual solutions for unsteady stagnation-point flow of Prandtl nanofluid past a stretching/shrinking plate. Defect Diffus. Forum 2018, 388, 124–134, Trans Tech Publications. [Google Scholar] [CrossRef]
- Ali Lund, L.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Kadry, S.; Rho, S.; Mari, I.A.; Nisar, K.S. Effect of Viscous Dissipation in Heat Transfer of MHD Flow of Micropolar Fluid Partial Slip Conditions: Dual Solutions and Stability Analysis. Energies 2019, 12, 4617. [Google Scholar] [CrossRef]
- Junoh, M.M.; Md Ali, F.; Pop, I. Magnetohydrodynamics Stagnation-Point Flow of a Nanofluid Past a Stretching/Shrinking Sheet with Induced Magnetic Field: A Revised Model. Symmetry 2019, 11, 1078. [Google Scholar] [CrossRef]
- Revnic, C.; Ghalambaz, M.; Groşan, T.; Sheremet, M.; Pop, I. Impacts of Non-Uniform Border Temperature Variations on Time-Dependent Nanofluid Free Convection within a Trapezium: Buongiorno’s Nanofluid Model. Energies 2019, 12, 1461. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Md Arifin, N.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. A Stability Analysis for Magnetohydrodynamics Stagnation Point Flow with Zero Nanoparticles Flux Condition and Anisotropic Slip. Energies 2019, 12, 1268. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K.; Vajravelu, K.; Van Gorder, R.A. Stability analysis of the dual solutions for stagnation-point flow over a non-linearly stretching surface. Meccanica 2012, 47, 1623–1632. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K. Stability of dual solutions in stagnation-point flow and heat transfer over a porous shrinking sheet with thermal radiation. Meccanica 2013, 48, 23–32. [Google Scholar] [CrossRef]
- Barletta, A.; Rees, D.A.S. Stability analysis of dual adiabatic flows in a horizontal porous layer. Int. J. Heat Mass Transf. 2009, 52, 2300–2310. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I. Quadruple solutions of mixed convection flow of magnetohydrodynamic nanofluid over exponentially vertical shrinking and stretching surfaces: Stability analysis. Comput. Method. Program. Biomed. 2019, 182, 105044. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M.; Nisar, K.S. Dual Solutions and Stability Analysis of Micropolar Nanofluid Flow with Slip Effect on Stretching/Shrinking Surfaces. Energies 2019, 12, 4529. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Med. 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C.; Pop, I. Effects of thermal radiation on micropolar fluid flow and heat transfer over a porous shrinking sheet. Int. J. Heat Mass Transf. 2012, 55, 2945–2952. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
| Khan and | Pop [56] | Present | Results | ||
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.9524 | 2.1294 | 0.9524 | 2.1294 |
| 0.3 | 0.5201 | 2.5286 | 0.52005 | 2.5285 | |
| 0.5 | 0.3211 | 3.0351 | 0.3212 | 3.0351 | |
| 0.2 | 0.2 | 0.3654 | 2.5152 | 0.3654 | 2.5152 |
| 0.3 | 0.2731 | 2.6555 | 0.2731 | 2.6555 | |
| 0.5 | 0.1681 | 2.8883 | 0.1681 | 2.8883 |
| K | |||
|---|---|---|---|
| 1st Solution | 2nd Solution | ||
| 0 | 3 | 1.53376 | −1.51742 |
| 2.5 | 1.08913 | −1.20287 | |
| 2 | 0.97563 | −0.8101 | |
| 0.5 | 3 | 0.86261 | −0.96571 |
| 2.5 | 0.54185 | −0.67231 | |
| 2 | 0.05935 | −0.03765 | |
| 1 | 3 | 0.45512 | −0.52843 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lund, L.A.; Omar, Z.; Khan, U.; Khan, I.; Baleanu, D.; Nisar, K.S. Stability Analysis and Dual Solutions of Micropolar Nanofluid over the Inclined Stretching/Shrinking Surface with Convective Boundary Condition. Symmetry 2020, 12, 74. https://doi.org/10.3390/sym12010074
Lund LA, Omar Z, Khan U, Khan I, Baleanu D, Nisar KS. Stability Analysis and Dual Solutions of Micropolar Nanofluid over the Inclined Stretching/Shrinking Surface with Convective Boundary Condition. Symmetry. 2020; 12(1):74. https://doi.org/10.3390/sym12010074
Chicago/Turabian StyleLund, Liaquat Ali, Zurni Omar, Umair Khan, Ilyas Khan, Dumitru Baleanu, and Kottakkaran Sooppy Nisar. 2020. "Stability Analysis and Dual Solutions of Micropolar Nanofluid over the Inclined Stretching/Shrinking Surface with Convective Boundary Condition" Symmetry 12, no. 1: 74. https://doi.org/10.3390/sym12010074
APA StyleLund, L. A., Omar, Z., Khan, U., Khan, I., Baleanu, D., & Nisar, K. S. (2020). Stability Analysis and Dual Solutions of Micropolar Nanofluid over the Inclined Stretching/Shrinking Surface with Convective Boundary Condition. Symmetry, 12(1), 74. https://doi.org/10.3390/sym12010074








