Magnetohydrodynamic (MHD) Flow of Micropolar Fluid with Effects of Viscous Dissipation and Joule Heating Over an Exponential Shrinking Sheet: Triple Solutions and Stability Analysis
Abstract
1. Introduction
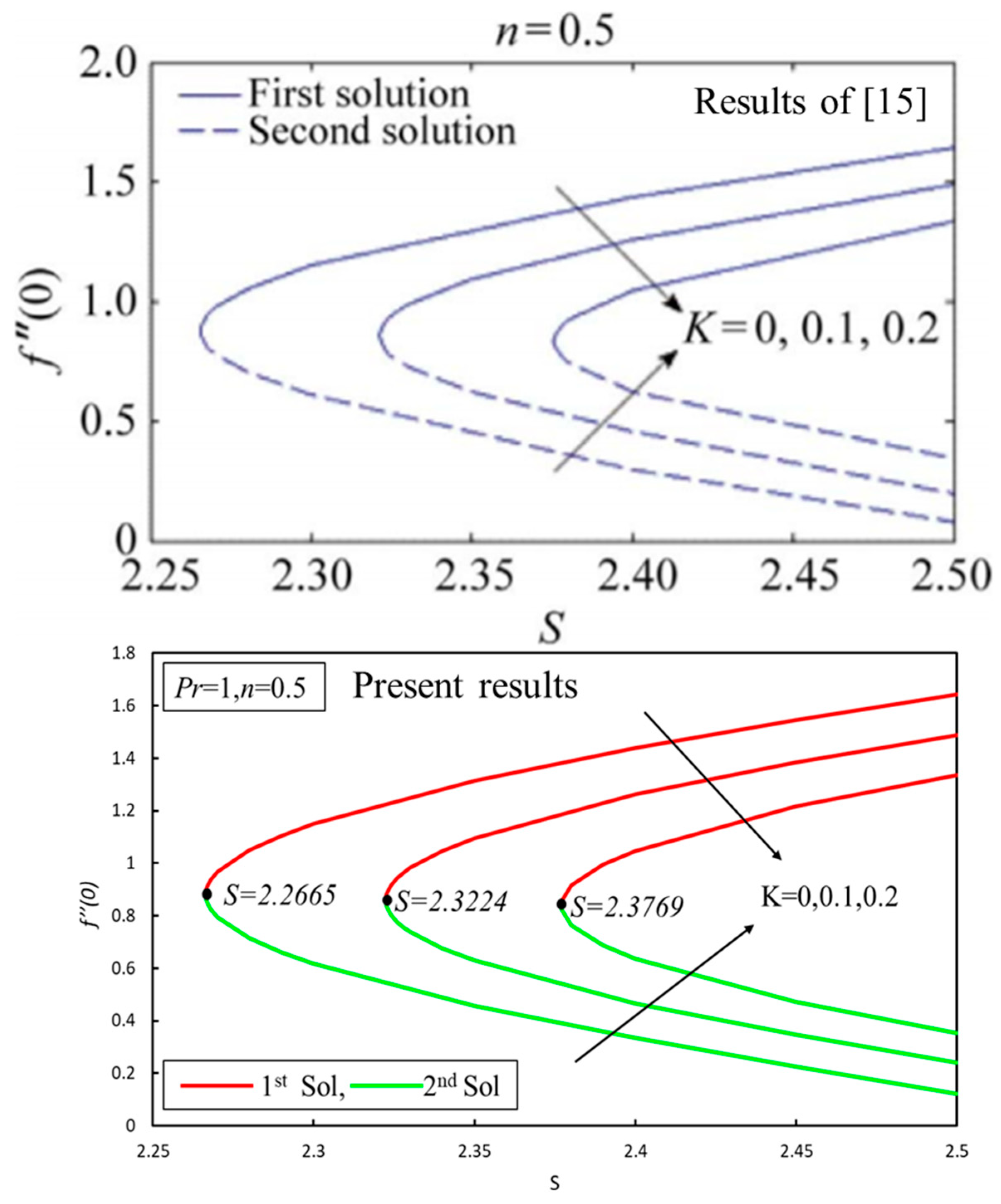
- To extend the problem of Aurangzaib et al. [15] by considering the effect of magnetic, viscous, and Joule heating functions.
- To find the maximum number of the multiple solutions.
- To perform stability analysis of multiple solutions in order to determine a stable solution.
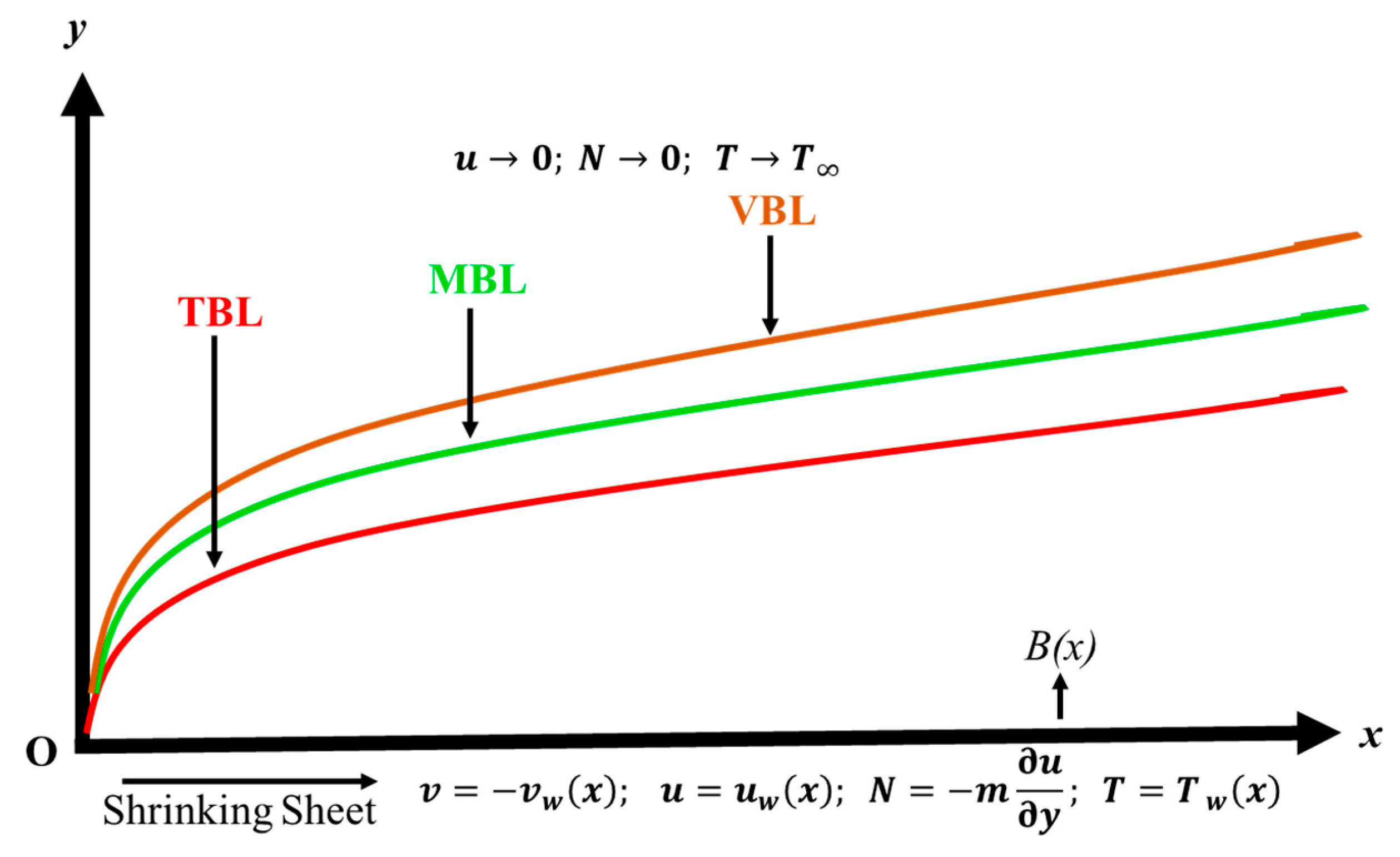
2. Mathematical Formulation
3. Stability Analysis
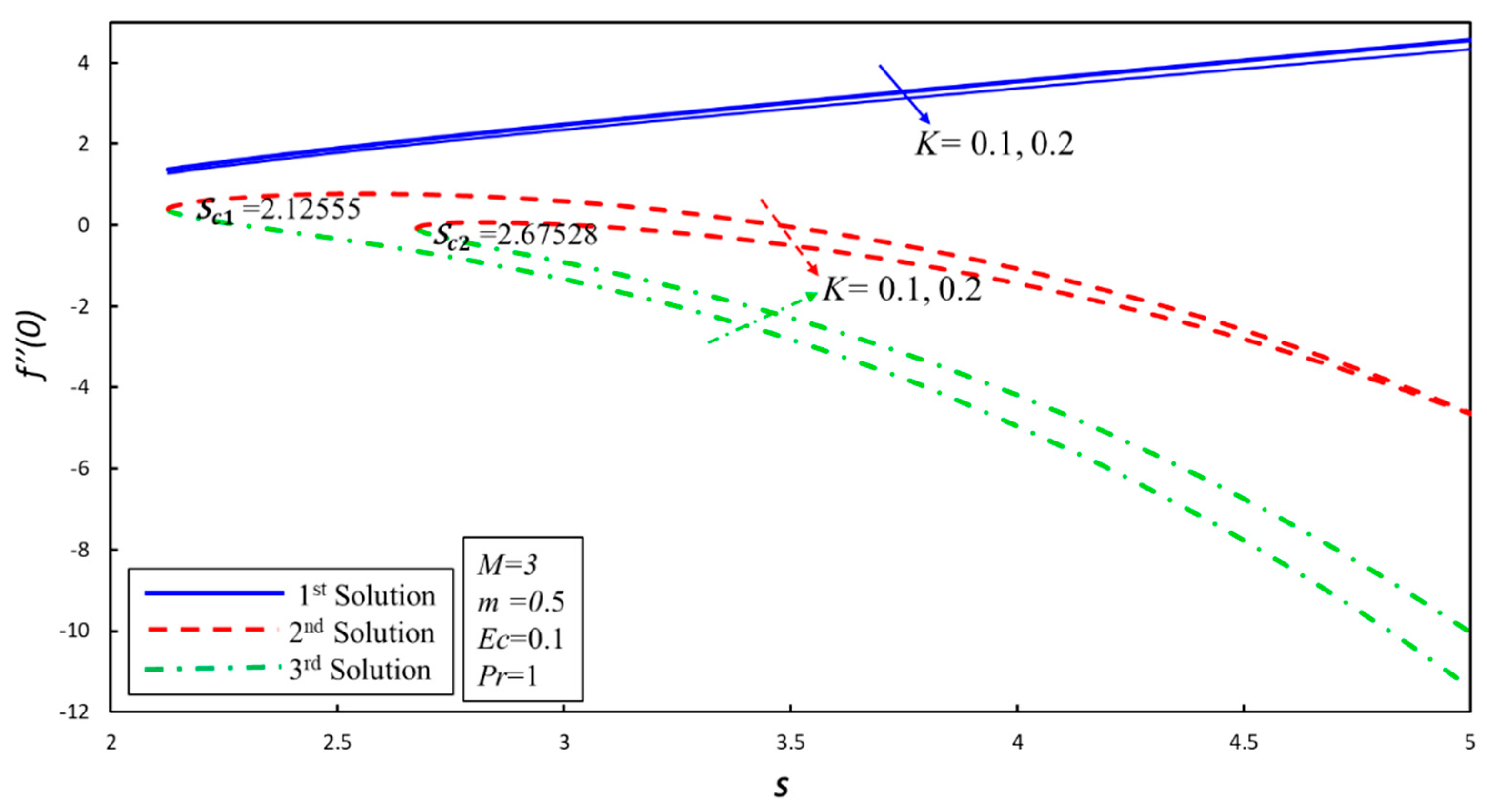
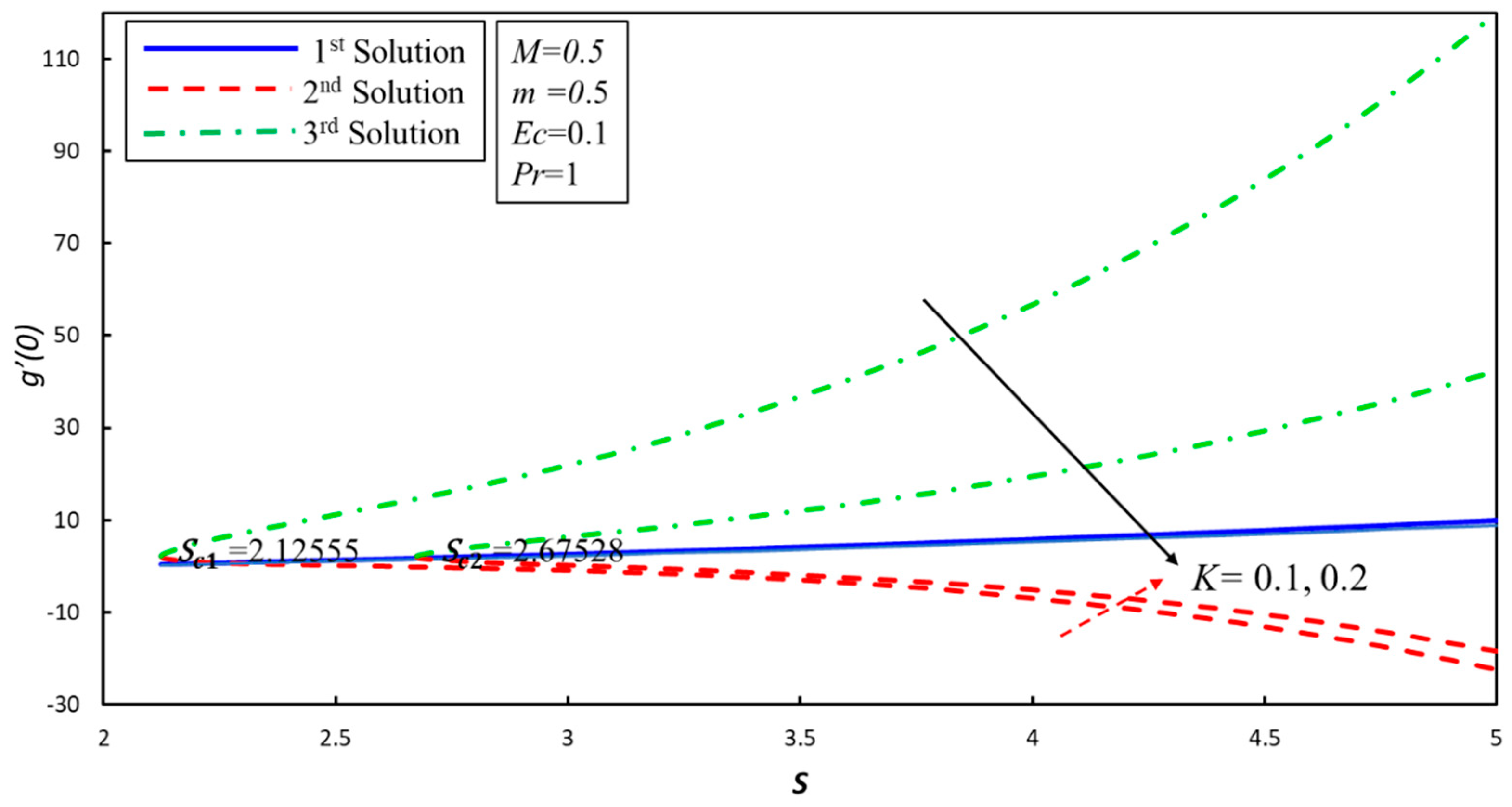
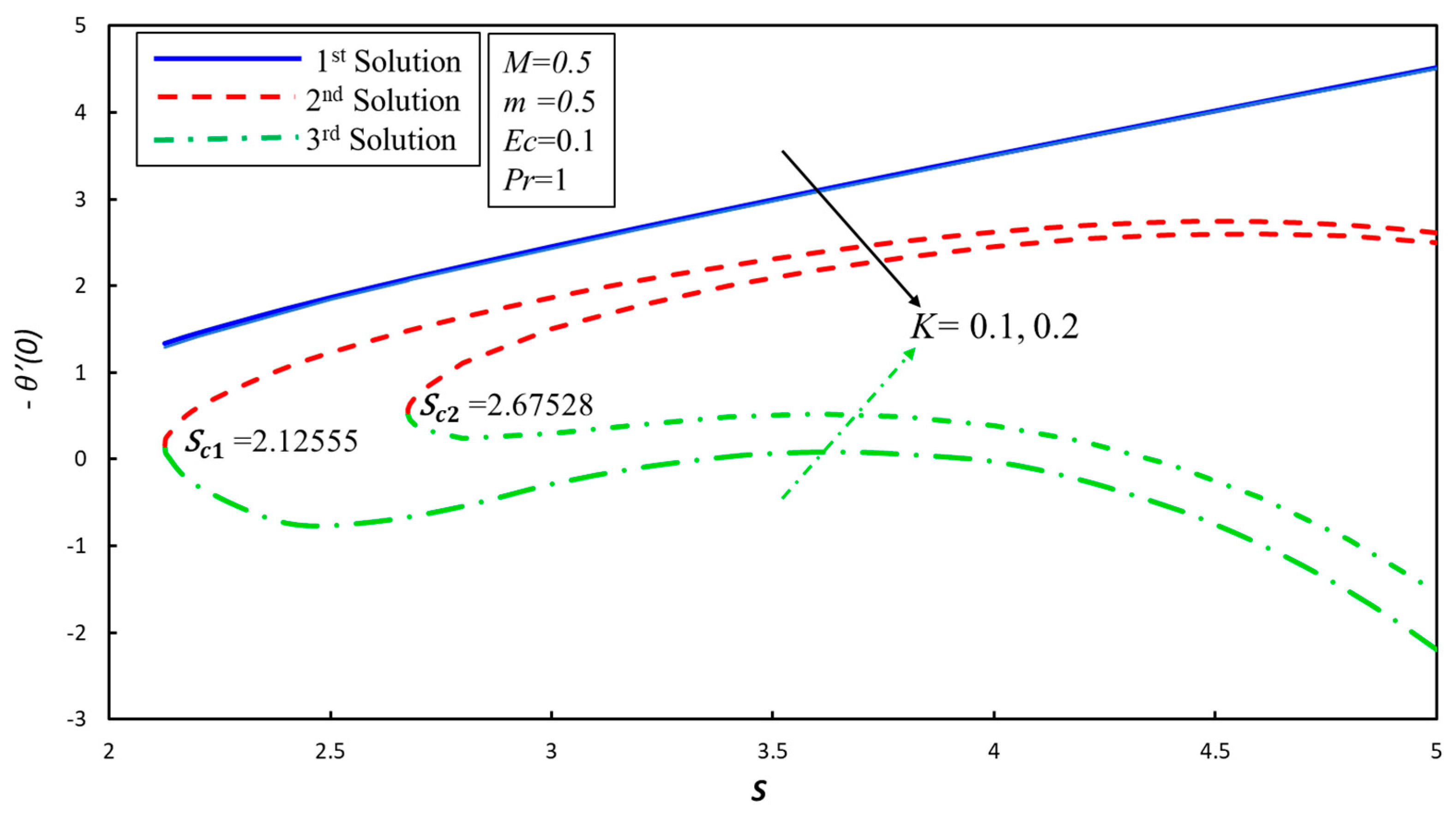
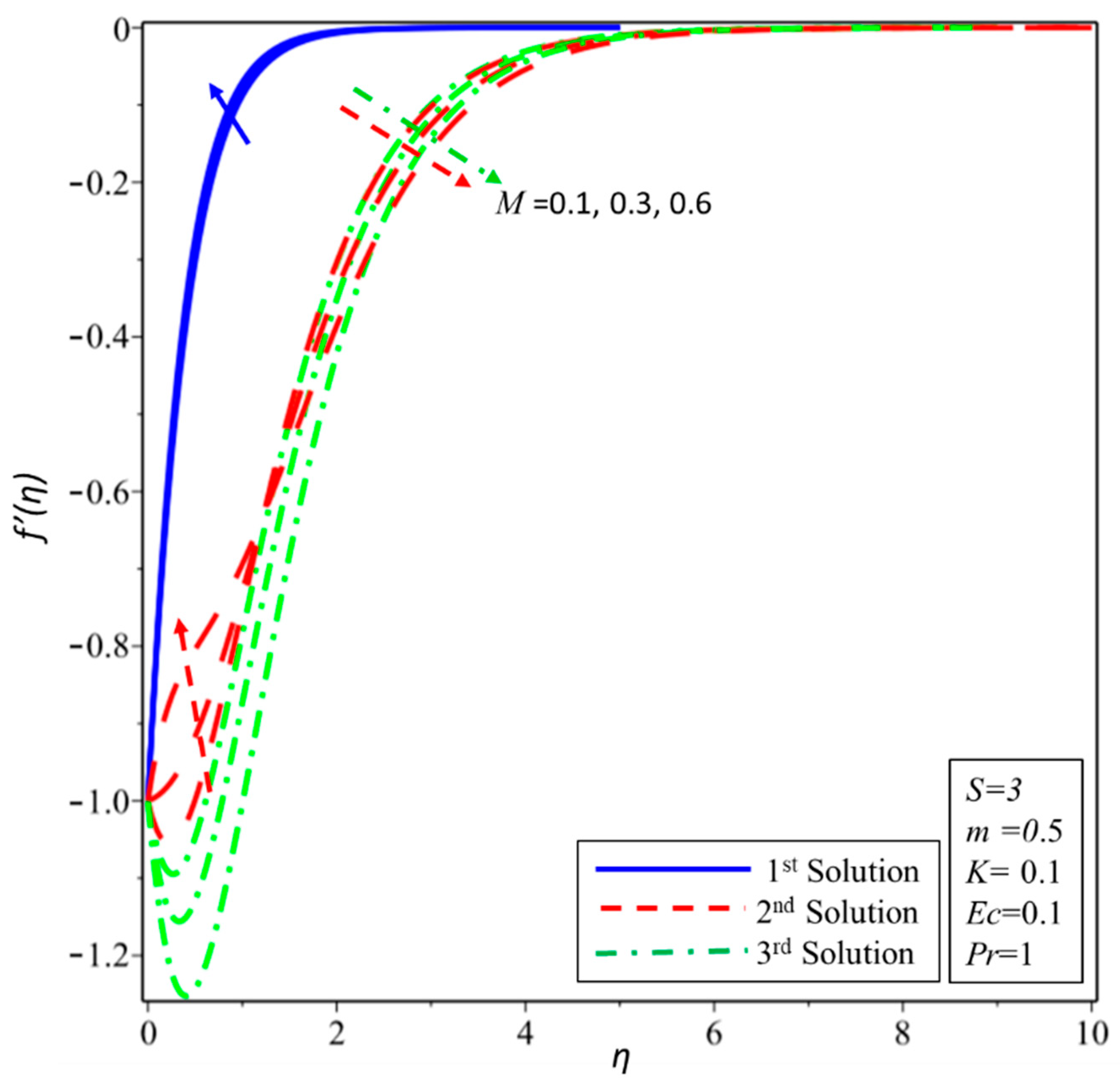
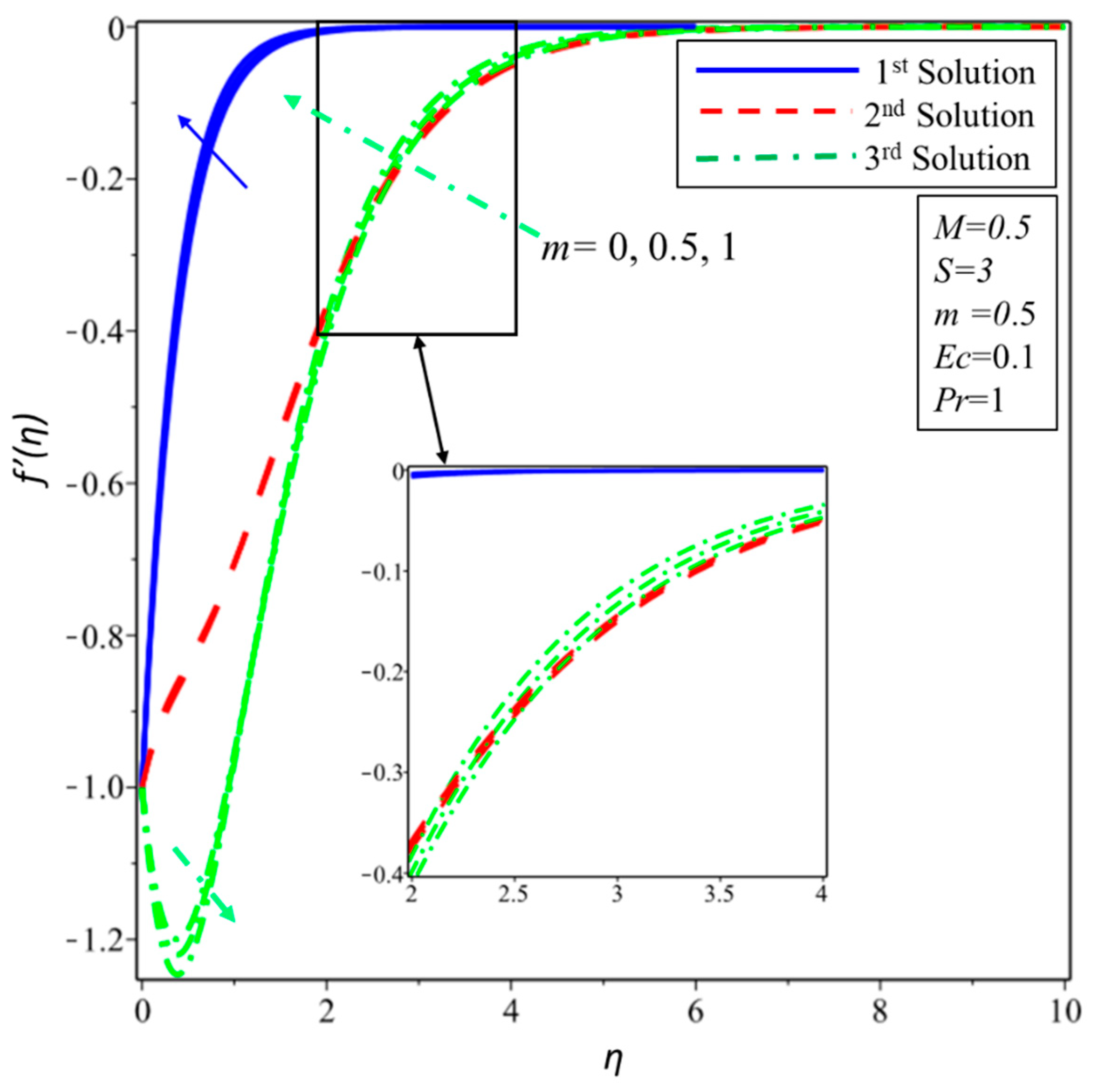
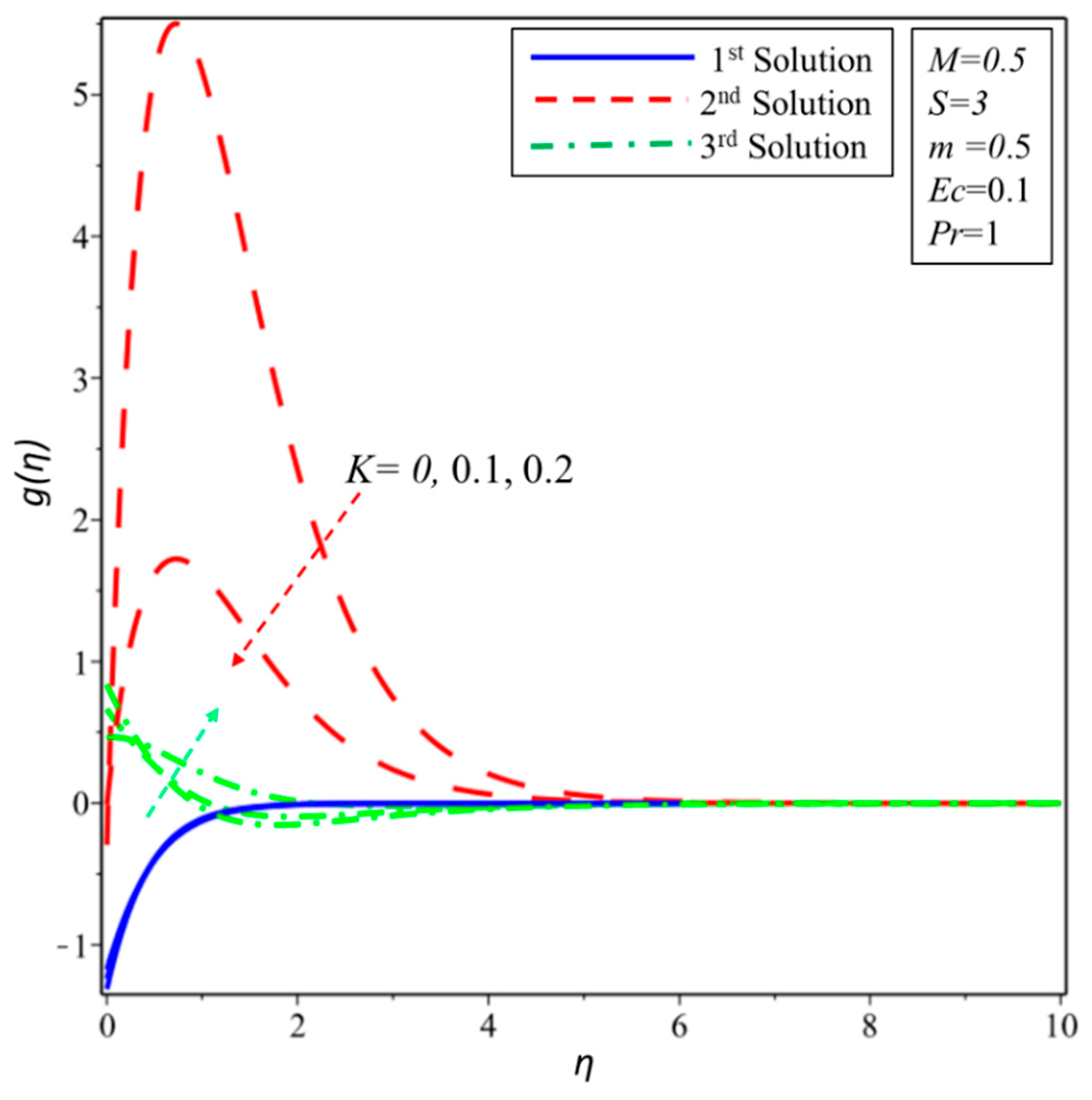
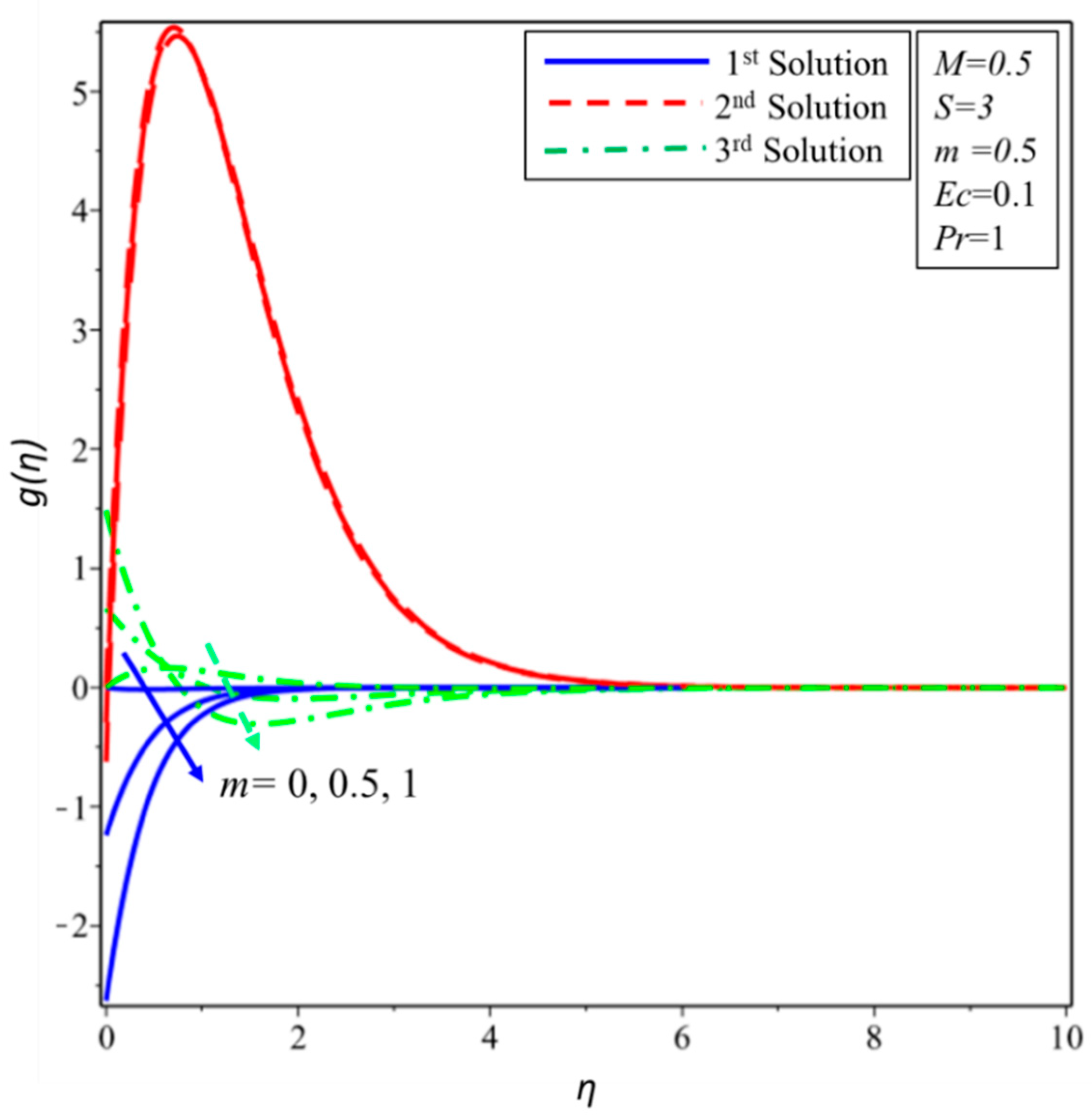
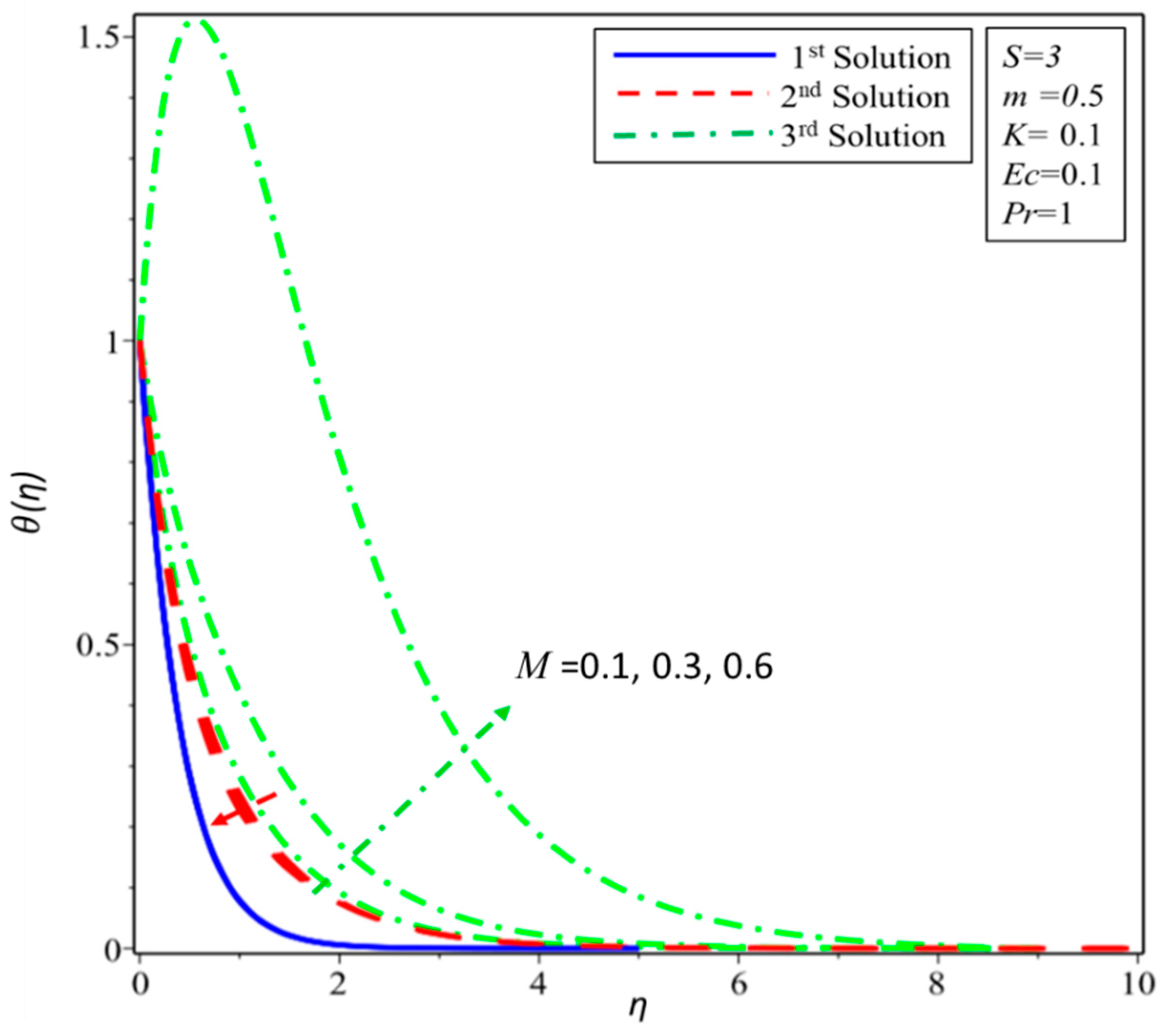
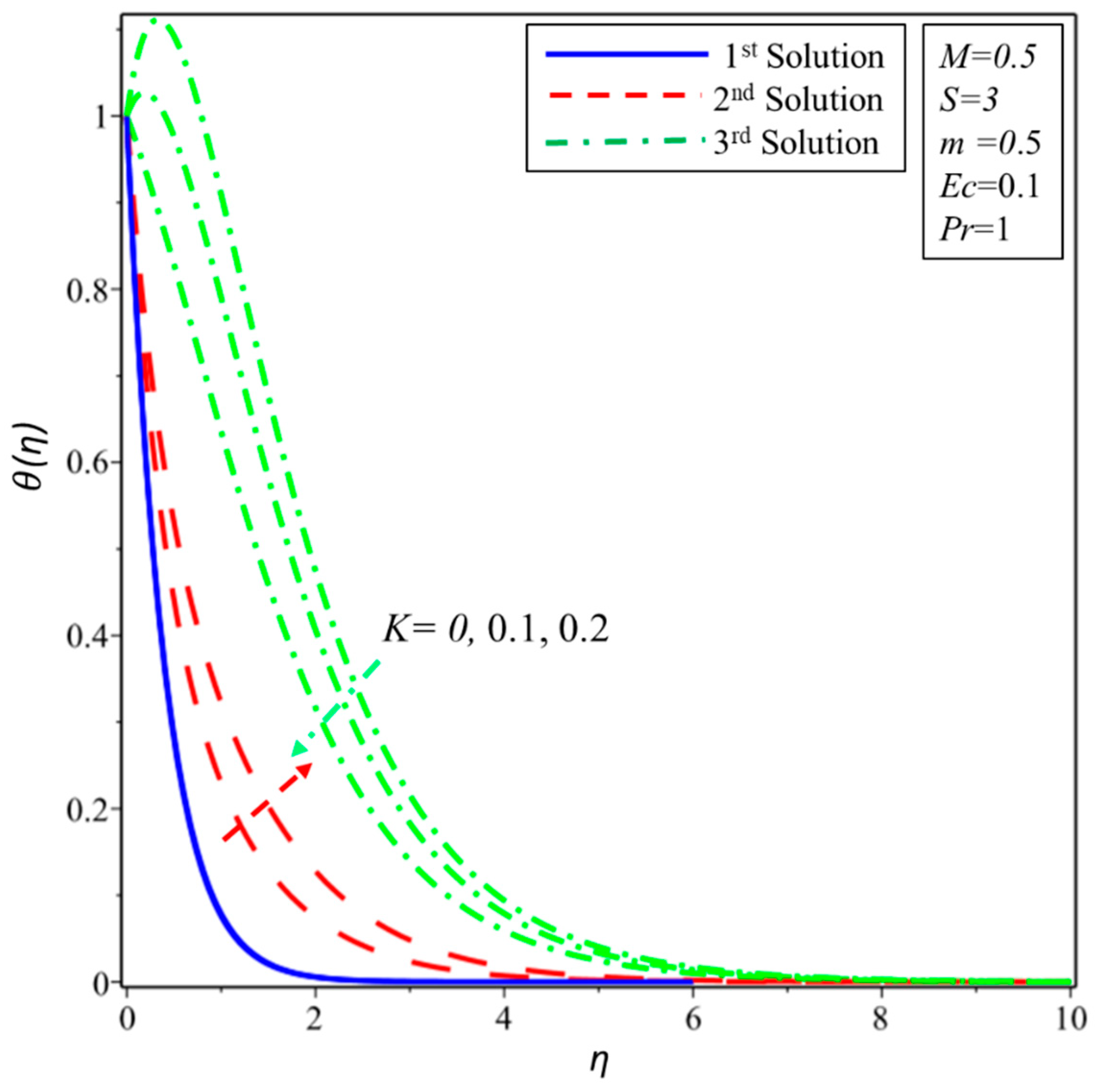
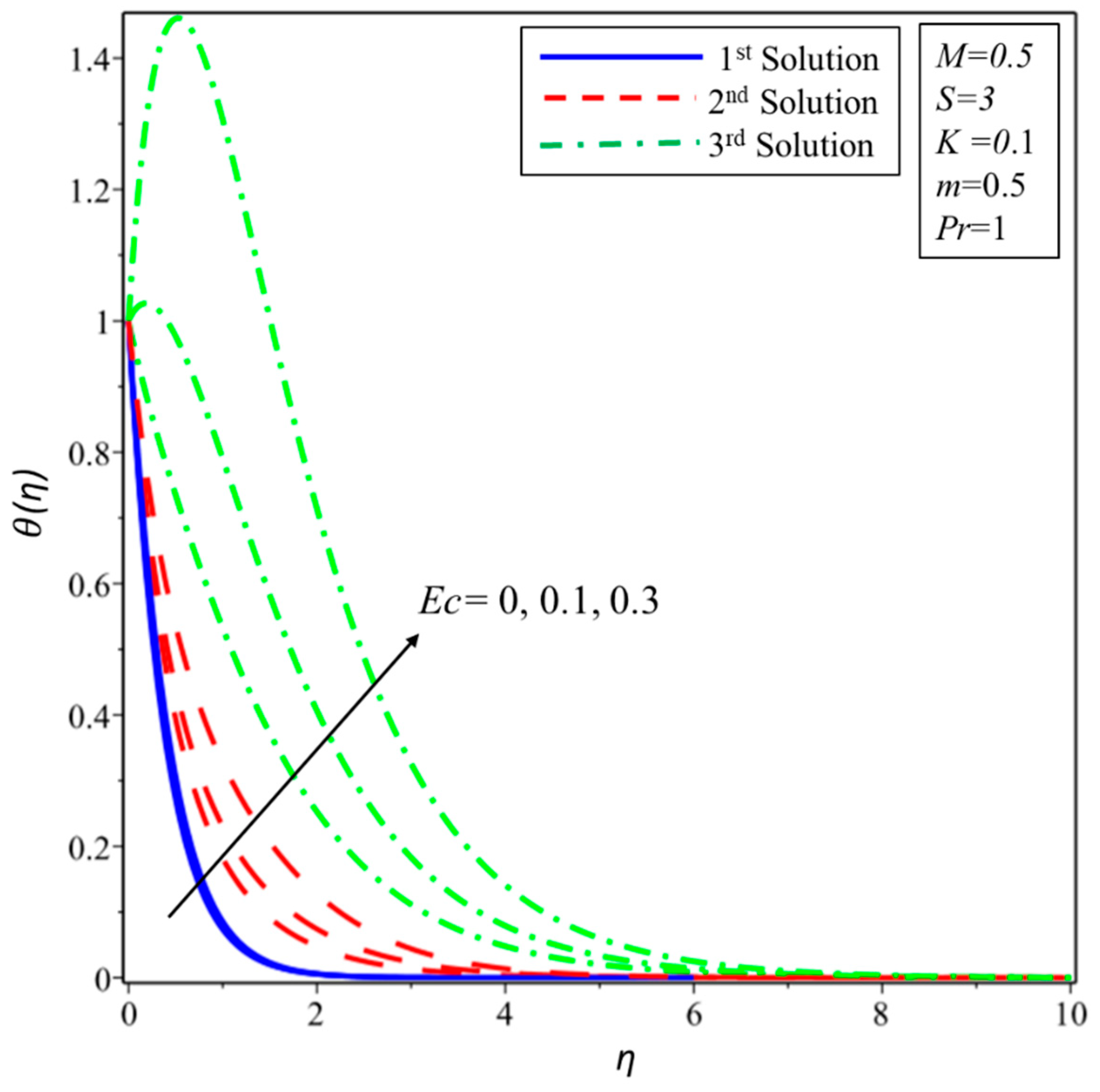
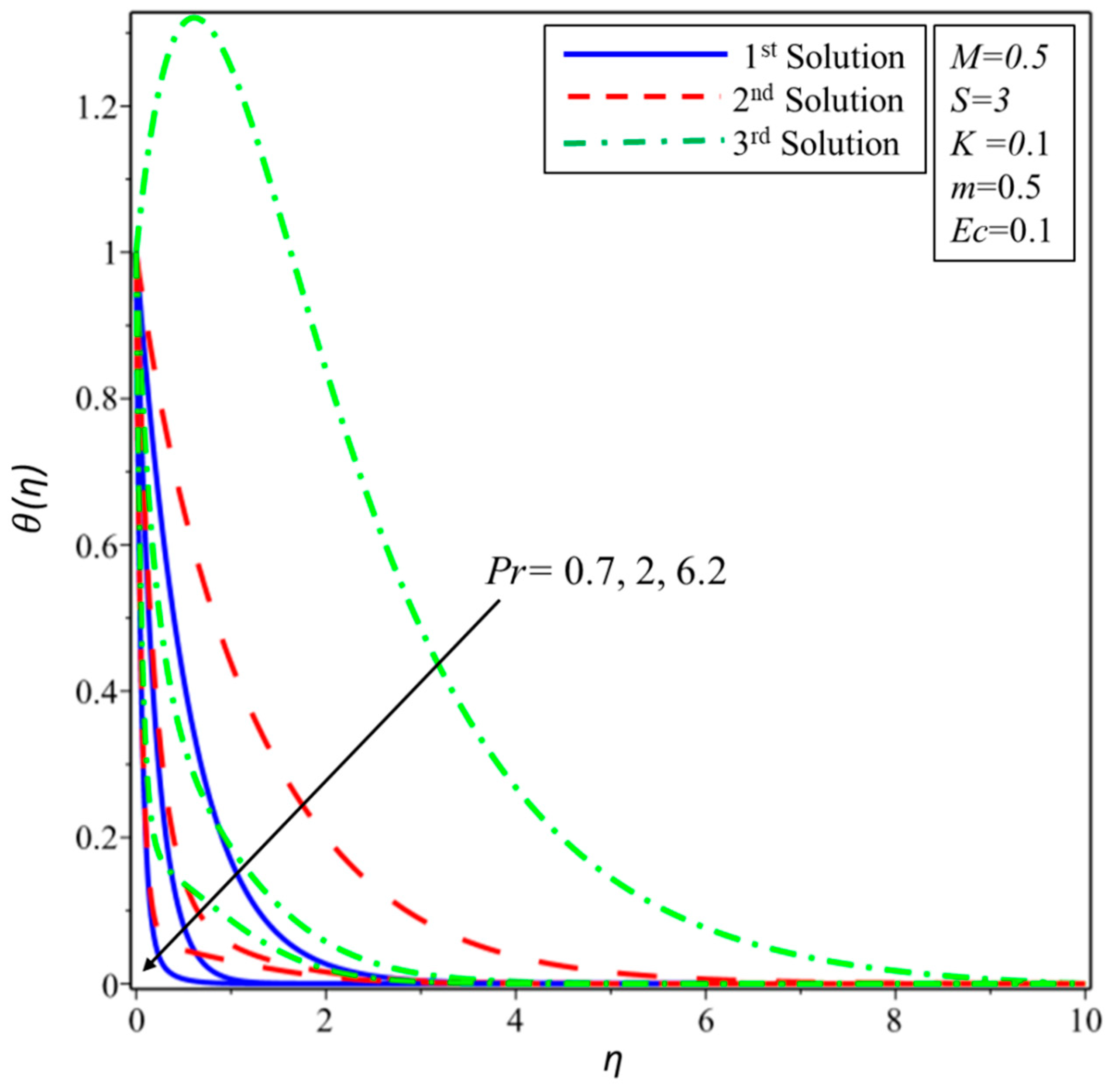
4. Results and Discussion
5. Conclusions
- Two solutions exist for the case of Newtonian fluid.
- Three solutions exist for the case of no-Newtonian fluid in the specific values of the suction parameter.
- Ranges of single and multiple solutions are dependent on the suction parameter.
- Results of the stability analysis of solutions indicate that only the first solution is stable.
- The thickness of the momentum boundary layer enhances in all solutions when the slip parameter is increased.
- The thickness of the thermal boundary layer is directly proportional to the values of the Eckert number. As the Eckert number increases, the temperature of fluid also rises due to the high impact of the kinetic energy.
- The occurrence of a higher velocity of the fluid is possible for unstable solutions when the magnetic parameter increases.
- The thermal field has been noted as lower corresponding to a larger Prandtl number in all solutions.
- The angular velocity of the micropolar fluid increased in the first and third solutions for the higher values of material and slip parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dero, S.; Rohni, A.M.; Saaban, A. MHD micropolar nanofluid flow over an exponentially stretching/shrinking surface: Triple solutions. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 56, 165–174. [Google Scholar]
- Raza, J.; Liyanage, J.P.; Al Atat, H.; Lee, J. A comparative study of maintenance data classification based on neural networks, logistic regression and support vector machines. J. Qual. Maint. Eng. 2010, 16, 303–318. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. Rheology of micropolar fluid in a channel with changing walls: Investigation of multiple solutions. J. Mol. Liq. 2016, 223, 890–902. [Google Scholar] [CrossRef]
- Khan, I.; Fatima, S.; Malik, M.Y.; Salahuddin, T. Exponentially varying viscosity of magnetohydrodynamic mixed convection Eyring-Powell nanofluid flow over an inclined surface. Results Phys. 2018, 8, 1194–1203. [Google Scholar] [CrossRef]
- Jafarimoghaddam, A. On the Homotopy Analysis Method (HAM) and Homotopy Perturbation Method (HPM) for a nonlinearly stretching sheet flow of Eyring-Powell fluids. Eng. Sci. Technol. 2019, 22, 439–451. [Google Scholar] [CrossRef]
- Kamran, M.; Wiwatanapataphee, B. Chemical reaction and Newtonian heating effects on steady convection flow of a micropolar fluid with second order slip at the boundary. Eur. J. Mech.-B/Fluids 2018, 71, 138–150. [Google Scholar] [CrossRef]
- Beneš, M.; Pažanin, I.; Radulović, M. Rigorous derivation of the asymptotic model describing a nonsteady micropolar fluid flow through a thin pipe. Comput. Math. Appl. 2018, 76, 2035–2060. [Google Scholar] [CrossRef]
- Kumar, M.S.; Sandeep, N.; Kumar, B.R. Three-dimensional magnetohydrodynamic rotating flow past a stretched surface with cross diffusion. Chin. J. Phys. 2017, 55, 2407–2421. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative heat and mass transfer analysis of micropolar nanofluid flow of Casson fluid between two rotating parallel plates with effects of Hall current. J. Heat Transf. 2019, 141, 022401. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Md Arifin, N.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N.; Pop, I. Mixed Convective Flow and Heat Transfer of a Dual Stratified Micropolar Fluid Induced by a Permeable Stretching/Shrinking Sheet. Entropy 2019, 21, 1162. [Google Scholar] [CrossRef]
- Bhattacharjee, B.; Chakraborti, P.; Choudhuri, K. Evaluation of the performance characteristics of double-layered porous micropolar fluid lubricated journal bearing. Tribol. Int. 2019, 138, 415–423. [Google Scholar] [CrossRef]
- Lakshmi, R.V.; Sarojamma, G.; Sreelakshmi, K.; Vajravelu, K. Heat Transfer Analysis in a Micropolar Fluid with Non-Linear Thermal Radiation and Second-Order Velocity Slip. In Applied Mathematics and Scientific Computing; Birkhäuser: Cham, Switzerland, 2019; pp. 385–395. [Google Scholar]
- Lund, L.A.; Omar, Z.; Khan, I. Mathematical analysis of magnetohydrodynamic (MHD) flow of micropolar nanofluid under buoyancy effects past a vertical shrinking surface: Dual solutions. Heliyon 2019, 5, e02432. [Google Scholar] [CrossRef] [PubMed]
- Lund, L.A.; Omar, Z.; Khan, I. Steady incompressible magnetohydrodynamics Casson boundary layer flow past a permeable vertical and exponentially shrinking sheet: A stability analysis. Heat Transf. 2019, 48, 3538–3556. [Google Scholar] [CrossRef]
- Uddin, M.S.; Bhattacharyya, K.; Shafie, S. Micropolar fluid flow and heat transfer over an exponentially permeable shrinking sheet. Propuls. Power Res. 2016, 5, 310–317. [Google Scholar]
- Lund, L.A.; Ching, D.L.C.; Omar, Z.; Khan, I.; Nisar, K.S. Triple local similarity solutions of Darcy-Forchheimer Magnetohydrodynamic (MHD) flow of micropolar nanofluid over an exponential shrinking surface: Stability analysis. Coatings 2019, 9, 527. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Lorenzini, G.; Oudina, F.M.; Animasaun, I.L. Significance of exponential space-and thermal-dependent heat source effects on nanofluid flow due to radially elongated disk with Coriolis and Lorentz forces. J. Therm. Anal. Calorim. 2019, 1–8. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Dero, S. Multiple solutions of Cu-C6H9NaO7 and Ag-C6H9NaO7 nanofluids flow over nonlinear shrinking surface. J. Cent. South Univ. 2019, 26, 1283–1293. [Google Scholar] [CrossRef]
- Ghosh, S.; Mukhopadhyay, S.; Vajravelu, K. Dual solutions of slip flow past a nonlinearly shrinking permeable sheet. Alex. Eng. J. 2016, 55, 1835–1840. [Google Scholar] [CrossRef]
- Dero, S.; Uddin, M.J.; Rohni, A.M. Stefan blowing and slip effects on unsteady nanofluid transport past a shrinking sheet: Multiple solutions. Heat Transf. 2019, 48, 2047–2066. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A.; Khan, I. Dual Solutions and Stability Analysis of Micropolar Nanofluid Flow with Slip Effect on Stretching/Shrinking Surfaces. Energies 2019, 12, 4529. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Kadry, S.; Rho, S.; Mari, I.A.; Nisar, K.S. Effect of Viscous Dissipation in Heat Transfer of MHD Flow of Micropolar Fluid Partial Slip Conditions: Dual Solutions and Stability Analysis. Energies 2019, 12, 4617. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z.; Awais, M. Rheology of the Cu-H2O nanofluid in porous channel with heat transfer: Multiple solutions. Physica E 2017, 86, 248–252. [Google Scholar] [CrossRef]
- Mohanty, B.; Mishra, S.R.; Pattanayak, H.B. Numerical investigation on heat and mass transfer effect of micropolar fluid over a stretching sheet through porous media. Alex. Eng. J. 2015, 54, 223–232. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Khan, Z.H.; Bég, O.A. A numerical study of magnetohydrodynamic transport of nanofluids over a vertical stretching sheet with exponential temperature-dependent viscosity and buoyancy effects. Chem. Phys. Lett. 2016, 661, 20–30. [Google Scholar] [CrossRef]
- Reddy, P.B.; Suneetha, S.; Reddy, N.B. Numerical study of magnetohydrodynamics (MHD) boundary layer slip flow of a Maxwell nanofluid over an exponentially stretching surface with convective boundary condition. Propuls. Power Res. 2017, 6, 259–268. [Google Scholar] [CrossRef]
- Pal, D.; Biswas, S. Perturbation analysis of magnetohydrodynamics oscillatory flow on convective-radiative heat and mass transfer of micropolar fluid in a porous medium with chemical reaction. Eng. Sci. Technol. 2016, 19, 444–462. [Google Scholar] [CrossRef]
- Salman Ahmed, N.J.; Khaleed, H.M.T.; Baig, M.A.A.; Khan, T.M.; Kamangar, S. Effect of viscous dissipation on aiding flow heat and mass transfer in porous cavity. In American Institute of Physics Conference Series; AIP: College Park, MD, USA, 2019; Volume 2104. [Google Scholar]
- Rasool, G.; Zhang, T.; Shafiq, A.; Durur, H. Influence of chemical reaction on Marangoni convective flow of nanoliquid in the presence of Lorentz forces and thermal radiation: A numerical investigation. J. Adv. Nanotechnol. 2019, 1, 32. [Google Scholar] [CrossRef]
- Hor, C.H.; Tso, C.P.; Chen, G.M. 4. Viscous Dissipation Effects in A Microchannel Caused by Oscillation of One Surface. J. Eng. Technol. Appl. Phys. 2019, 1, 13–17. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Shafiq, A. Second grade nanofluidic flow past a convectively heated vertical Riga plate. Phys. Scr. 2019, 94, 125212. [Google Scholar] [CrossRef]
- Raju, S.S.; Kumar, K.G.; Rahimi-Gorji, M.; Khan, I. Darcy–Forchheimer flow and heat transfer augmentation of a viscoelastic fluid over an incessant moving needle in the presence of viscous dissipation. Microsyst. Technol. 2019, 25, 3399–3405. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability Analysis of Darcy-Forchheimer Flow of Casson Type Nanofluid Over an Exponential Sheet: Investigation of Critical Points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Adegbie, S.K.; Kọrikọ, O.K.; Animasaun, I.L. Melting heat transfer effects on stagnation point flow of micropolar fluid with variable dynamic viscosity and thermal conductivity at constant vortex viscosity. J. Niger. Math. Soc. 2016, 35, 34–47. [Google Scholar] [CrossRef]
- Waqas, M.; Farooq, M.; Khan, M.I.; Alsaedi, A.; Hayat, T.; Yasmeen, T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transf. 2016, 102, 766–772. [Google Scholar] [CrossRef]
- Nadeem, U.S.; Khan, A.U. Stability analysis of Cu–H2O nanofluid over a curved stretching–shrinking sheet: Existence of dual solutions. Can. J. Phys. 2019, 97, 911–922. [Google Scholar]
- Lund, L.A.; Omar, Z.; Khan, I. Quadruple solutions of mixed convection flow of magnetohydrodynamic nanofluid over exponentially vertical shrinking and stretching surfaces: Stability analysis. Comput. Methods Programs Biomed. 2019, 182, 105044. [Google Scholar] [CrossRef]
- Rahman, M.M.; Rosca, A.V.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking surface with convective boundary condition using Buongiorno’s model. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 299–319. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Seikh, A.H.; Sherif ES, M.; Nisar, K.S. Stability analysis and multiple solution of Cu–Al2O3/H2O nanofluid contains hybrid nanomaterials over a shrinking surface in the presence of viscous dissipation. J. Mater. Res. Technol. 2019. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Transpiration effects on hybrid nanofluid flow and heat transfer over a stretching/shrinking sheet with uniform shear flow. Alex. Eng. J. 2019. [Google Scholar] [CrossRef]

| 1st Solution | 2nd Solution | 3rd Solution | ||
|---|---|---|---|---|
| 0.1 | 3 | 0.96439 | −0.78535 | −0.84652 |
| 2.5 | 0.86425 | −0.60258 | −0.64035 | |
| 0.2 | 3 | 0.88162 | −0.69025 | −0.72184 |
| 3.7 | 0.61582 | −0.46325 | −0.52287 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Sherif, E.-S.M.; Seikh, A.H. Magnetohydrodynamic (MHD) Flow of Micropolar Fluid with Effects of Viscous Dissipation and Joule Heating Over an Exponential Shrinking Sheet: Triple Solutions and Stability Analysis. Symmetry 2020, 12, 142. https://doi.org/10.3390/sym12010142
Lund LA, Omar Z, Khan I, Raza J, Sherif E-SM, Seikh AH. Magnetohydrodynamic (MHD) Flow of Micropolar Fluid with Effects of Viscous Dissipation and Joule Heating Over an Exponential Shrinking Sheet: Triple Solutions and Stability Analysis. Symmetry. 2020; 12(1):142. https://doi.org/10.3390/sym12010142
Chicago/Turabian StyleLund, Liaquat Ali, Zurni Omar, Ilyas Khan, Jawad Raza, El-Sayed M. Sherif, and Asiful H. Seikh. 2020. "Magnetohydrodynamic (MHD) Flow of Micropolar Fluid with Effects of Viscous Dissipation and Joule Heating Over an Exponential Shrinking Sheet: Triple Solutions and Stability Analysis" Symmetry 12, no. 1: 142. https://doi.org/10.3390/sym12010142
APA StyleLund, L. A., Omar, Z., Khan, I., Raza, J., Sherif, E.-S. M., & Seikh, A. H. (2020). Magnetohydrodynamic (MHD) Flow of Micropolar Fluid with Effects of Viscous Dissipation and Joule Heating Over an Exponential Shrinking Sheet: Triple Solutions and Stability Analysis. Symmetry, 12(1), 142. https://doi.org/10.3390/sym12010142







