Numerical Analysis of Fluid Forces for Flow Past a Square Rod with Detached Dual Control Rods at Various Gap Spacing
Abstract
1. Introduction
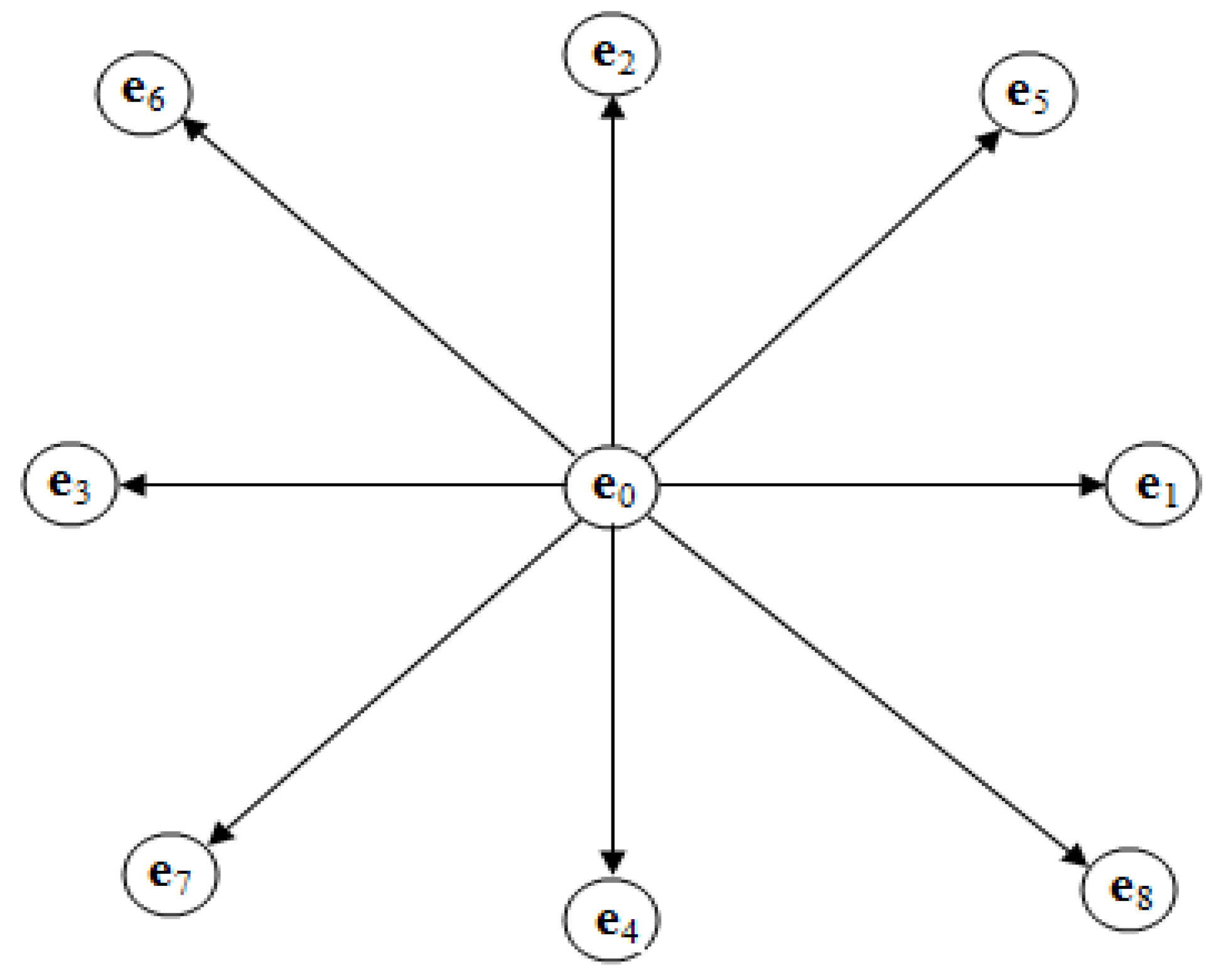
2. The Lattice Boltzmann Method
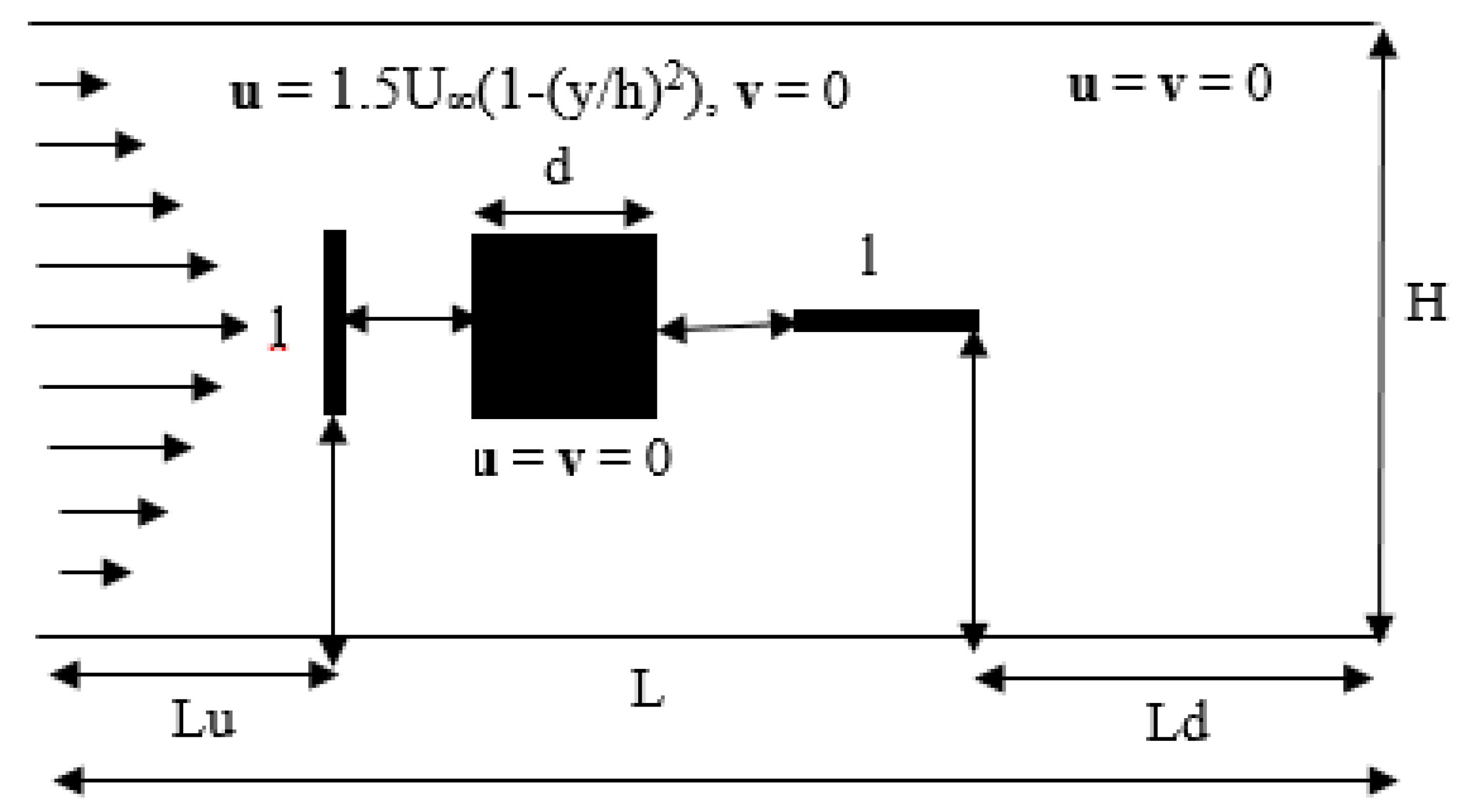
3. Problem Statements and Boundary Conditions
4. Computational Domain, Grid Independence and Code Validation Study
5. Results and Discussion
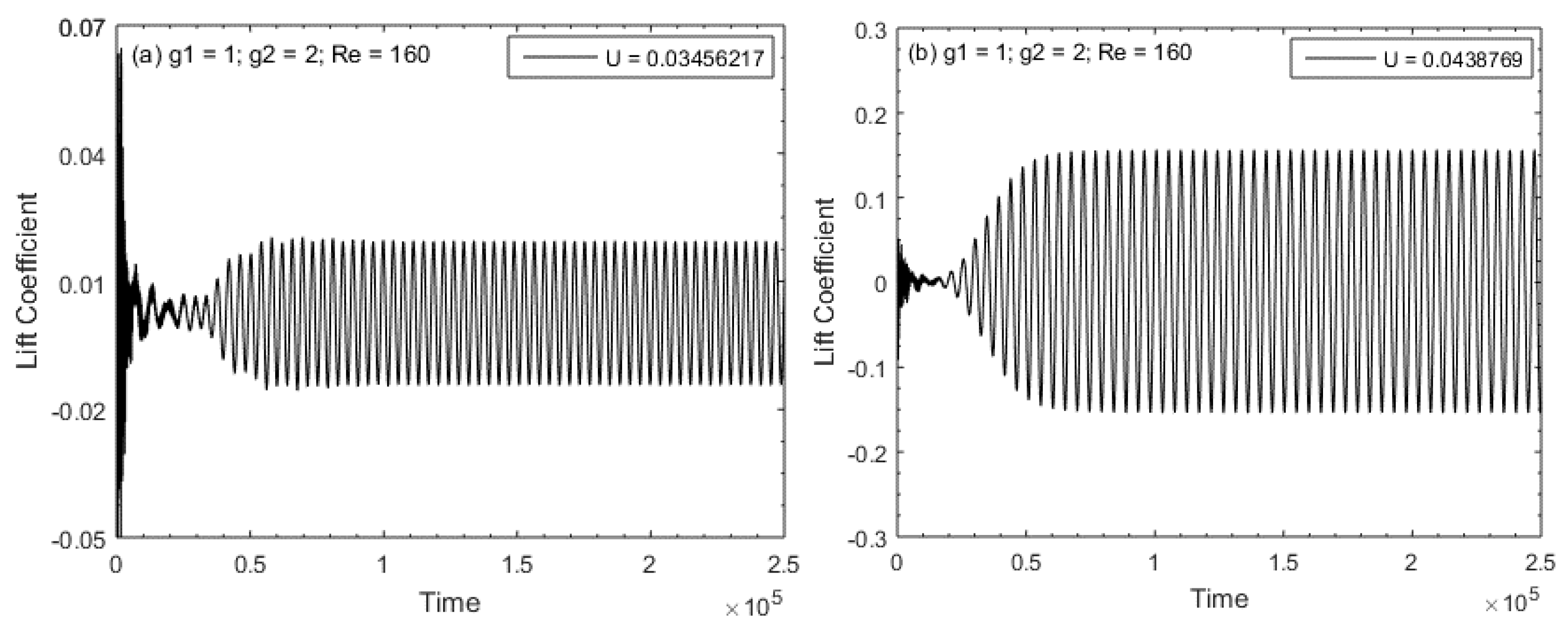
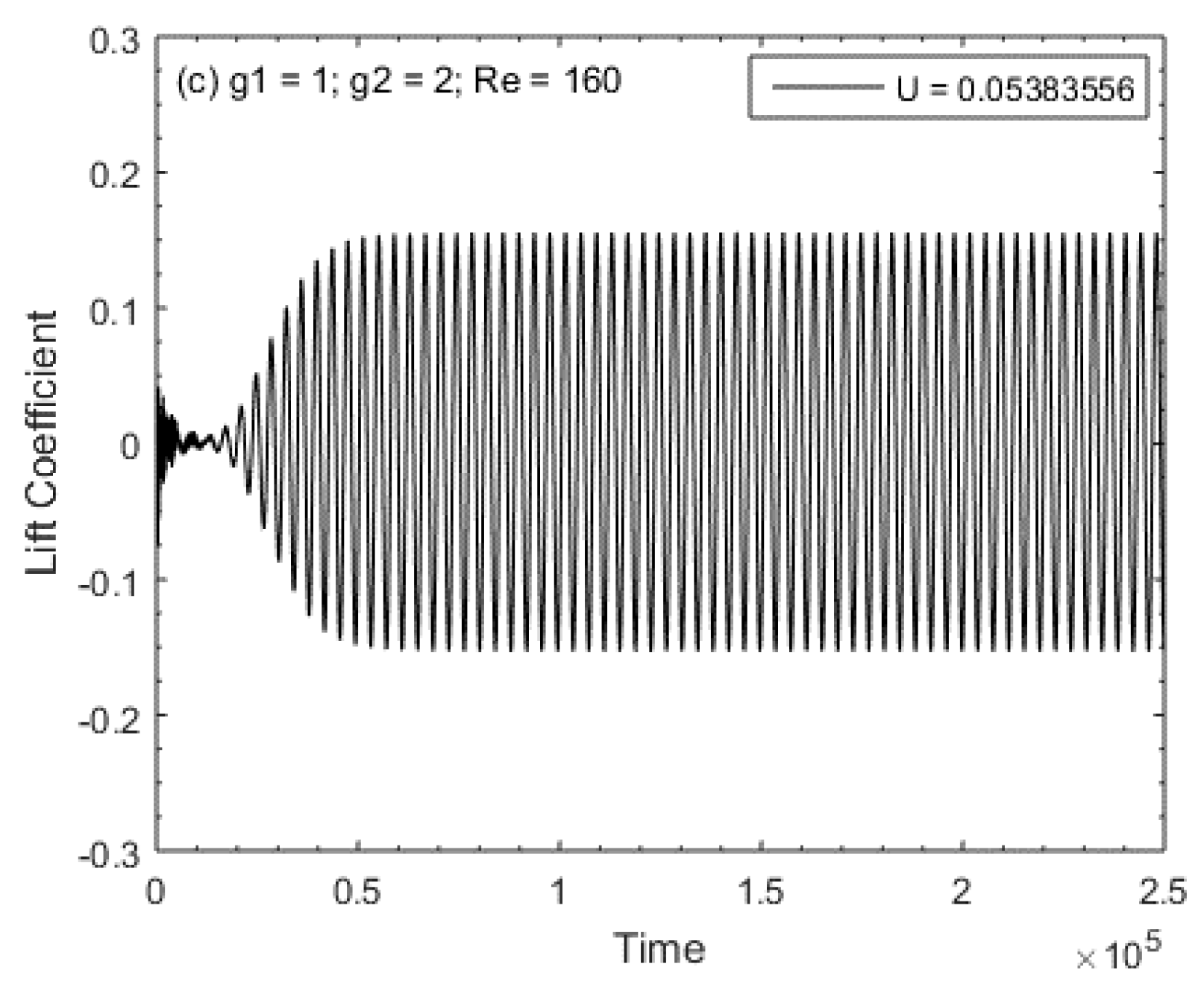
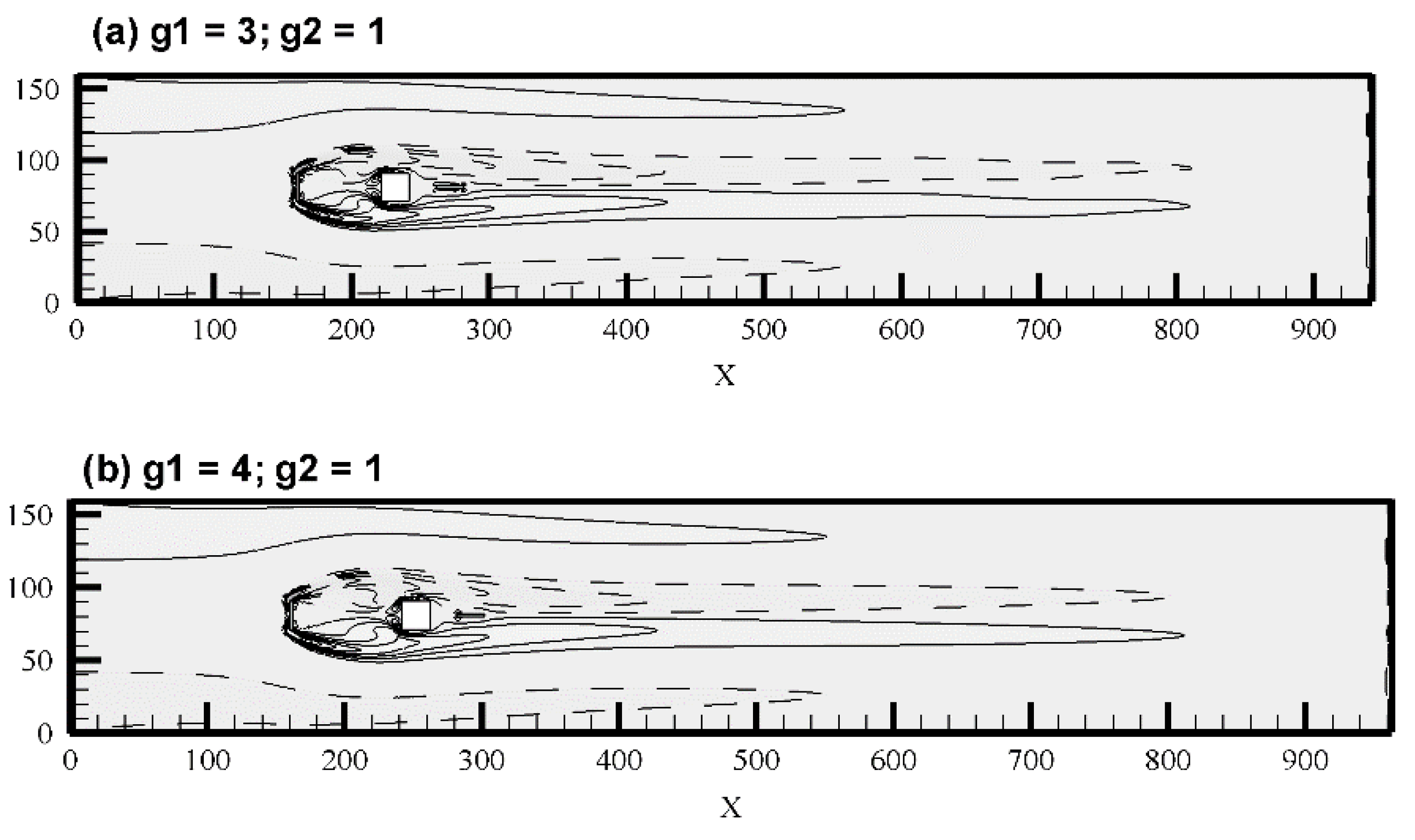
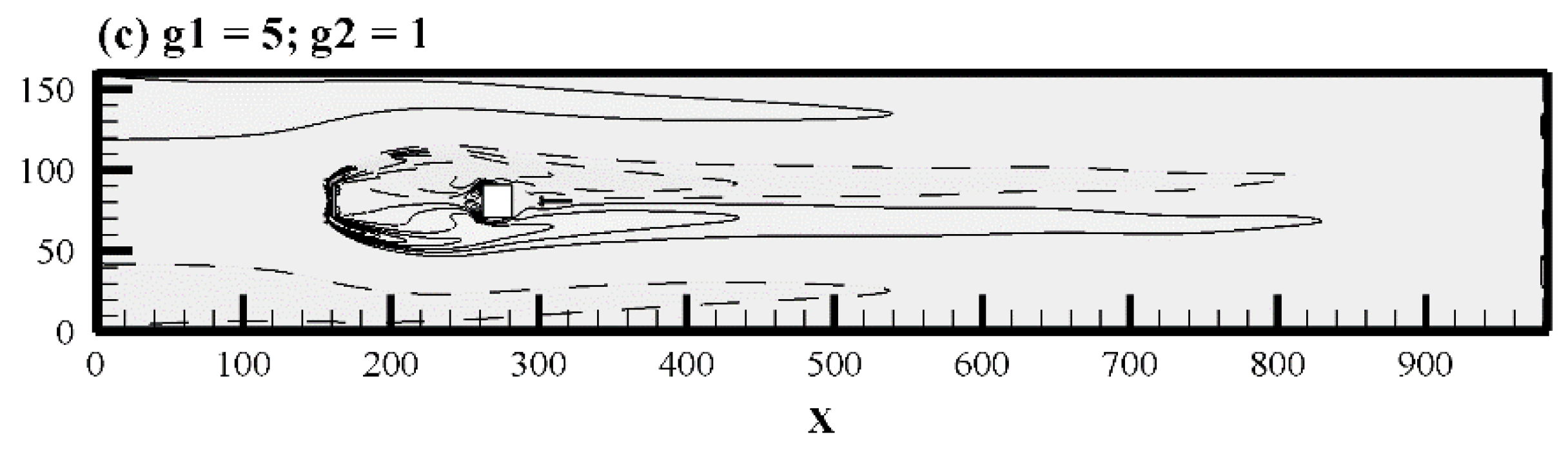
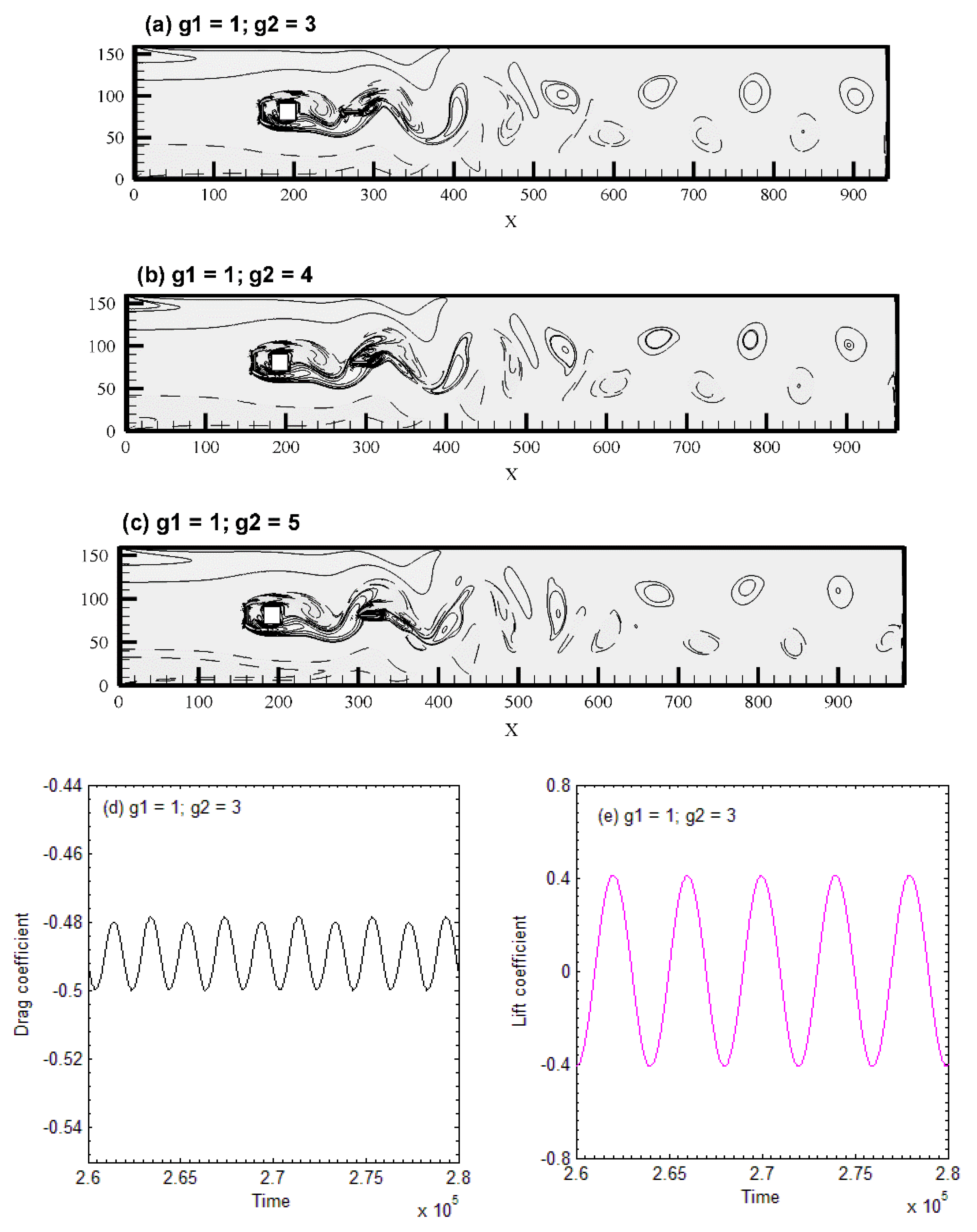
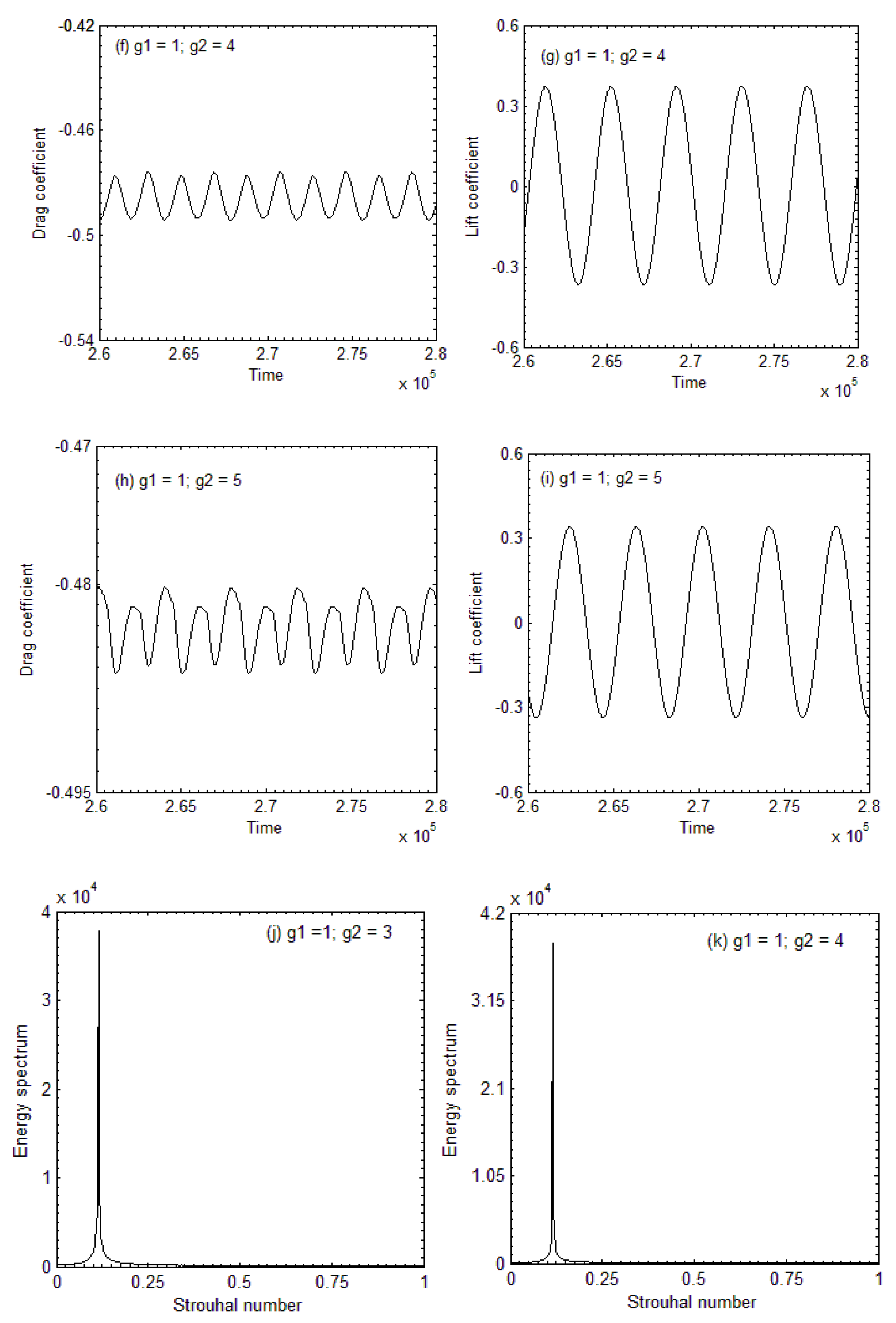
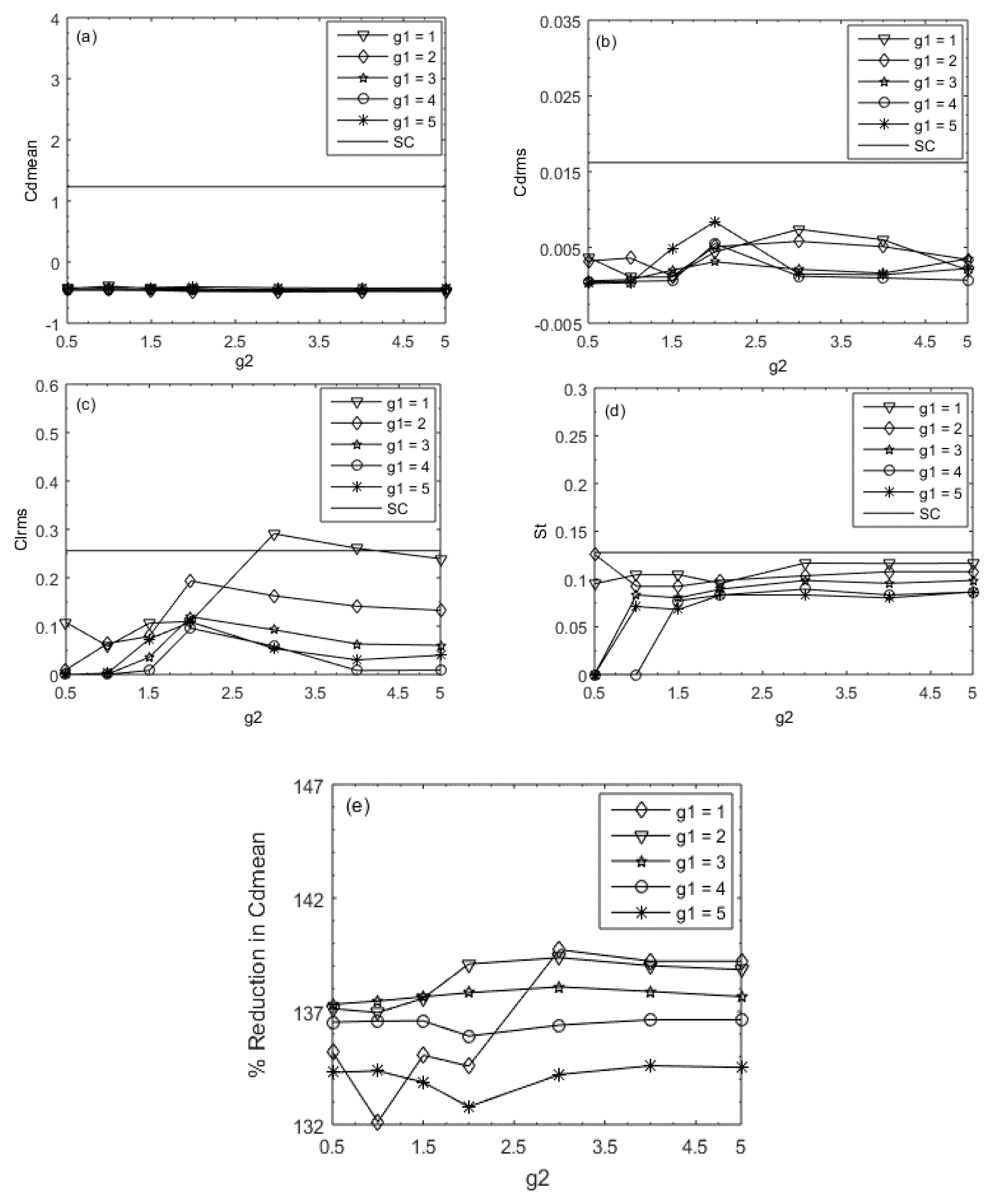
5.1. Vorticity Contours Visualization, Time-History Analysis of Drag and Lift Coefficients, and Energy Spectra Analysis of the Lift Coefficient
5.2. Physical Parameters
6. Conclusions
- (i)
- Three different types of flow modes were found and were named (a) shear layer reattachment (SLR), (b) steady flow mode (SF), and (c) semi-developed vortex shedding (SDVS).
- (ii)
- The values were negative for all selected combinations of and due to the effect of trust.
- (iii)
- The values of decreased by increasing the gap spacing. The maximum value of was obtained at
- (iv)
- The values of and increased by increasing the value of at fixed values of The maximum values of and were obtained at 0.0084 and 0.2910, respectively.
- (v)
- The greatest reduction in was obtained at and this value was 139.72%.
- (vi)
- The minimum reduction was acquired at , and this value was 132.1%.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Cd | Drag |
| Cl | Lift |
| Mean drag force | |
| Root-mean-square value of drag force | |
| Root-mean-square value of lift force | |
| Speed of sound | |
| Height of the control rods | |
| Size of the main rod | |
| Length of the control rods | |
| Velocities direction | |
| Horizontal component of force | |
| Transverse component of force | |
| fs | Vortex shedding |
| Density distribution function | |
| Equilibrium distribution function | |
| Upstream position | |
| Downstream position | |
| Number of particles | |
| Reynolds number | |
| Strouhal number | |
| Uniform inflow velocity | |
| SF | Steady flow |
| SLR | Shear layer reattachment |
| SDVS | Semi developed vortex shedding |
| SR | Single rod |
| Greek Symbols | |
| Kinematic viscosity | |
| Fluid density | |
| Weighting coefficients | |
References
- Darekar, R.M.; Sherwin, S.J. Flow past a bluff body with a wavy stagnation face. J. Fluid Struct. 2001, 15, 587–596. [Google Scholar] [CrossRef]
- Hwang, J.; Yang, K. Drag reduction on a circular cylinder using dual detached control rods. J. Wind Eng. Ind. Aerodyn. 2007, 95, 551–564. [Google Scholar] [CrossRef]
- Lee, S.; Lee, S.; Park, C. Reducing the drag on a circular cylinder by upstream Installation of a small control rod. Fluid Dyn. Res. 2004, 34, 233–250. [Google Scholar] [CrossRef]
- Roshko, A. On the Drag and Shedding Frequency of 2D Bluff Bodies; Tech Rept TN 3169; NACA: Washington, DC, USA, 1954. [Google Scholar]
- Apelt, C.; West, G. The Effects of Wake Control rods on Bluff-Body Flow in the Range 104 < Re < 5 × 104. J. Fluid Mech. 1975, 71, 145–160. [Google Scholar]
- Anderson, E.; Szewczyk, A. Effects of a Control rod on the Near Wake of a Circular Cylinder in 2D and 3D Flow Configurations. In Experimental on Fluids; Springer London: London, UK, 1997. [Google Scholar]
- Mittal, S.; Raghuvanshi, A. Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. Int. J. Numer. Methods Fluids 2001, 35, 421–447. [Google Scholar] [CrossRef]
- Kuo, C.H.; Chen, C.C. Passive control of wake flow by two small control cylinders at Reynolds number 80. J. Fluids Struct. 2009, 25, 1021–1028. [Google Scholar] [CrossRef]
- Alam, M.M.; Moriya, M.; Takai, K.; Sakamoto, H. Suppression of fluid forces acting on two square prisms in a tandem arrangement by passive control of flow. J. Fluids Struct. 2002, 16, 1073–1092. [Google Scholar] [CrossRef]
- Tsutsui, T.; Igrashi, T. Drag Reduction of a Circular Cylinder in an Air-Stream. J. Wind Eng. Ind. Aerodyn. 2002, 4, 527–541. [Google Scholar] [CrossRef]
- Turki, S. Numerical simulation of passive control on vortex shedding behind square rod using control rod. Eng. Appl. Comput. Fluid Mech. 2008, 2, 514–524. [Google Scholar]
- Malekzadeh, S.; Sohankar, A. Reduction of fluid forces and heat transfer on a square rod in a laminar flow regime using a control rod. Int. J. Heat Fluid Flow 2012, 34, 15–27. [Google Scholar] [CrossRef]
- Islam, S.U.; Rahman, H.; Abbasi, W.S.; Noreen, U.; Khan, A. Suppression of fluid force on flow past a square rod with a detached flat plate at low Reynolds number for various spacing ratios. J. Mech. Sci. Technol. 2014, 28, 4969–4978. [Google Scholar] [CrossRef]
- Vamsee, G.R.; De Tena, M.L.; Tiwari, S. Effect of arrangement of inline control rod on flow past square rod. Prog. Comput. Fluid. Dyn. 2014, 14, 277–293. [Google Scholar] [CrossRef]
- Islam, S.U.; Manzoor, R.; Tareen, A. Numerical investigation of flow around square rod with an upstream control rod at low Reynolds numbers in tandem. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1201–1223. [Google Scholar] [CrossRef]
- De Araujo, L.A.; Schettini, E.B.C.; Silvestrini, J.H. Direct numerical simulation of turbulent flow past a cylinder with control rod. In Proceedings of the 10th ABCM Spring School on Transition and Turbulence, São José dos Campos, Brazil, 19–23 September 2016. [Google Scholar]
- Vu, H.C.; Ahn, J.; Hwang, J.H. Numerical investigation of flow around circular cylinder with control rod. KSCE J. Civ. Eng. 2016, 20, 2559–2568. [Google Scholar] [CrossRef]
- Yuan, M.; Rashidi, M.M.; Yang, Z.G. Numerical Simulation of Flow past a Square rod with a Circular Bar Upstream and a Control rod downstream. J. Hydrodyn. 2018. [Google Scholar] [CrossRef]
- Gupta, A. Suppression of Vortex Shedding in Flow around Square Cylinder Using Control Cylinder; Department of Mechanical Engineering Indian Institute of Technology: Kanpur, India, 2013. [Google Scholar]
- Shadloo, M.S.; Zainali, A.; Yildziz, M.; Suleman, A. A robust weakly compressible SPH method and its comparison with an incompressible SPH. Int. J. Numer. Methods Eng. 2012, 89, 939–956. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Zainli, A.; Sadek, S.H.; Yildziz, M. Improved Incompressible Smoothed Particle Hydrodynamics method for simulating flow around bluff bodies. Comput. Methods Appl. Mech. Eng. 2011, 200, 1008–1020. [Google Scholar] [CrossRef]
- D’Orazio, A.; Nikkah, Z.; Karimipour, A. Simulation of copper–water nano fluid in a micro channel in slip flow regime using the lattice Boltzmann method with heat flux boundary condition. J. Phys. Conf. Ser. 2015, 655, 012029. [Google Scholar] [CrossRef]
- Goodarzi, M.; D’Orazio, A.; Keshavarzi, A.; Mousavi, S.; Karimipour, A. Develop the nano scale method of lattice Boltzmann to predict the fluid flow and heat transfer of air in the inclined lid driven cavity with a large heat source inside, Two case studies: Pure natural convection & mixed convection. Phys. A Stat. Mech. Its Appl. 2018, 509, 210–233. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Mohammad, A.A. Lattice Boltzmann Method: Fundamentals and Engineering Applications with Computer Codes; Springer London: London, UK, 2011. [Google Scholar]
- Rossi, N.; Ubertini, S.; Bella, G.; Succi, S. Unstructured lattice Boltzmann method in three dimensions. Int. J. Numer. Methods Fluids 2005, 49, 619–633. [Google Scholar] [CrossRef]
- Cornubert, R.; D’Humières, D.; Levermore, D. A Knudsen number theory for lattice gases. Physica D 1991, 47, 241–259. [Google Scholar] [CrossRef]
- Qian, Y.; D’Humieres, D.; Lallemand, P. Lattice BGK models for Navier-Stokes Equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Succi, S. Lattice Boltzmann Method for Fluid Dynamics and Beyond; Oxford Univ. Press: Oxford, UK, 2001. [Google Scholar]
- Wolf-Gladrow, D.A. Lattice-Gas Cellular Automata and Lattice Boltzmann Models an Introduction; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Sukop, M.C.; Thorne, D.T. Lattice Boltzmann Modeling: An Introduction for Geoscientists and Engineers; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Guo, Z.; Liu, H.; Luo, L.S.; Xu, K. A comparative study of the LBE and GKS method for 2D near incompressible laminar flows. J. Comput. Phys. 2008, 22, 4955–4976. [Google Scholar] [CrossRef]
- Saha, A.K.; Biswas, G.; Muralidhar, K. Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Int. J. Heat Fluid Flow. 2003, ED-24, 54–66. [Google Scholar] [CrossRef]
- Sohankar, A.; Davidson, L.; Norberg, C. Numerical simulation of unsteady flow around a square two-dimensional cylinder. In Proceedings of the Twelfth Australian Fluid Mechanics Conference, Sydney, Australia, 10–15 December 1995; pp. 517–520. [Google Scholar]
- Okajima, A. Strouhal numbers of rectangular cylinders. J. Fluid Mech Digit. Arch. 2006, 123, 379–398. [Google Scholar] [CrossRef]
- Norberg, C. Flow around rectangular cylinders: Pressure forces and wake frequencies. J. Wind Eng. Ind. Aerodyn. 1993, 49, 187–196. [Google Scholar] [CrossRef]
- Abograis, A.S.; Alshayji, A.E. Reduction of fluid forces on a square cylinder in a laminar flow using passive control methods. In Proceedings of the COMSOL Conference, Boston, MA, USA, 9–11 October 2013. [Google Scholar]
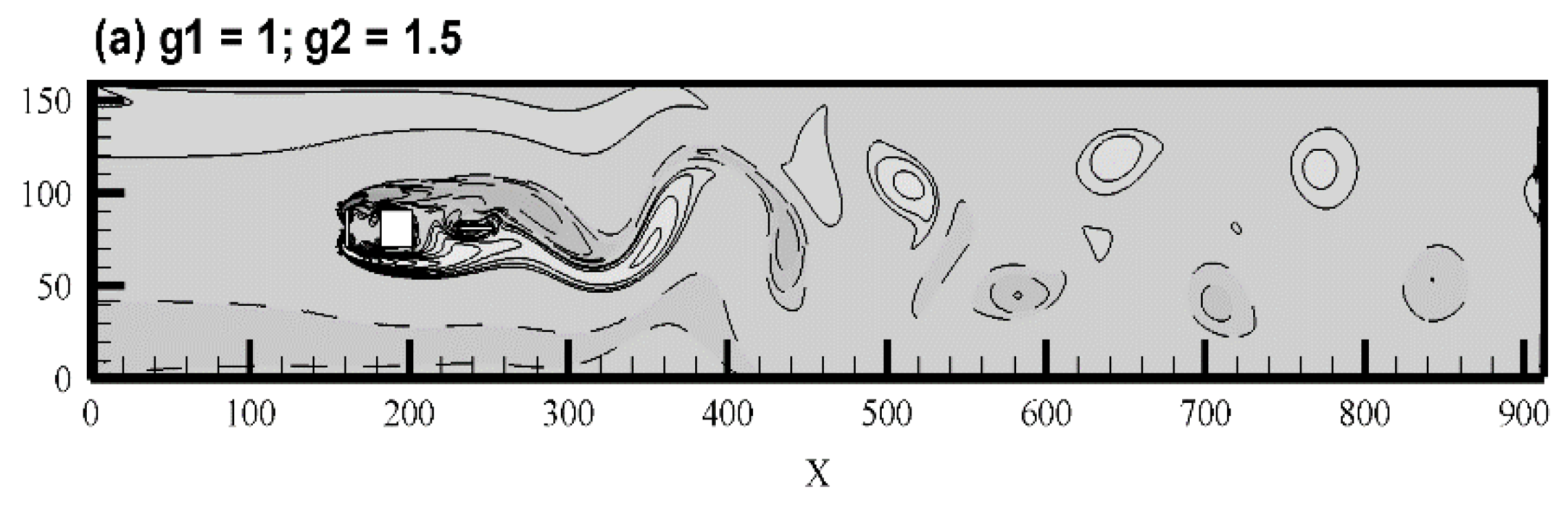
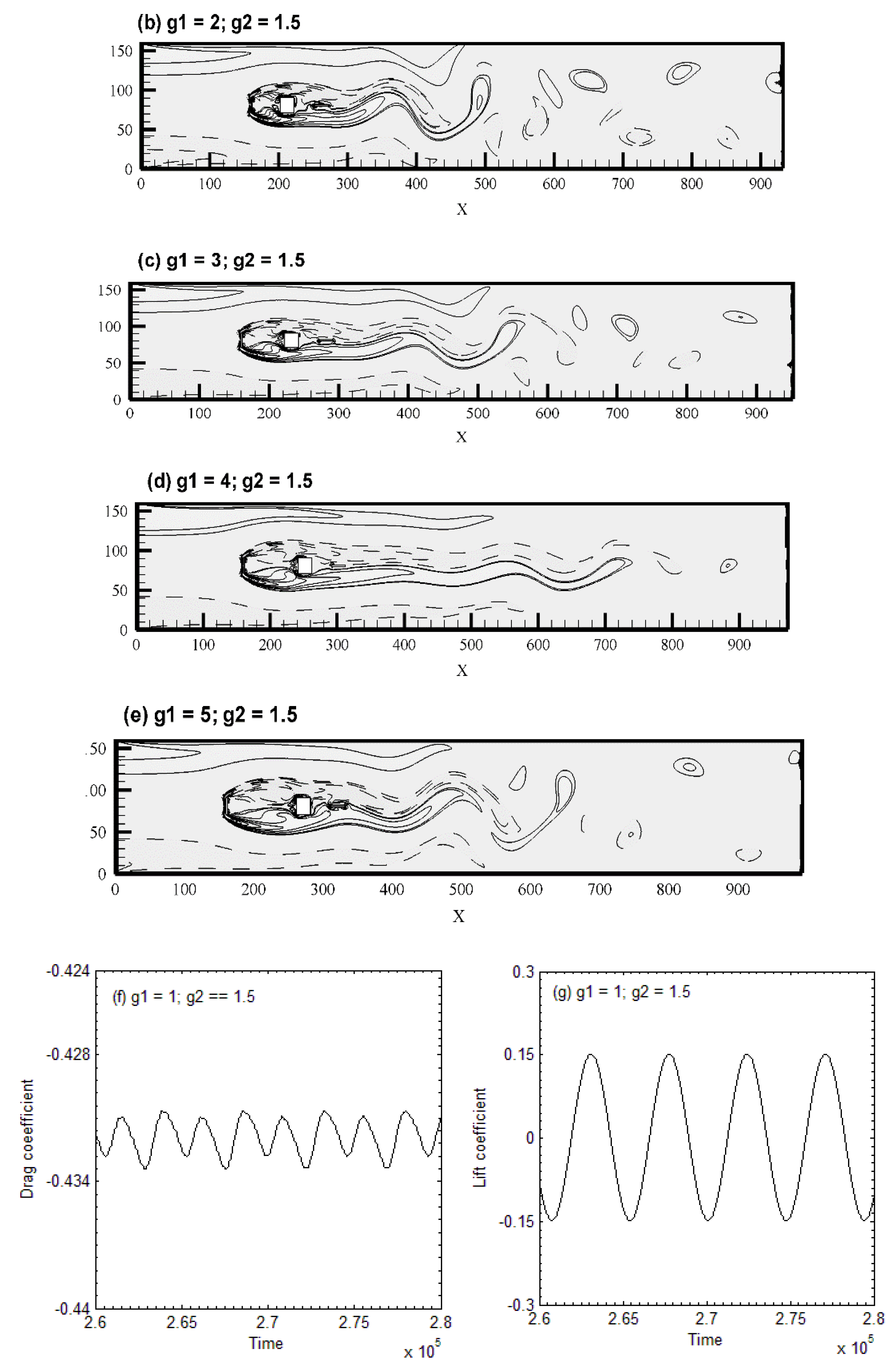
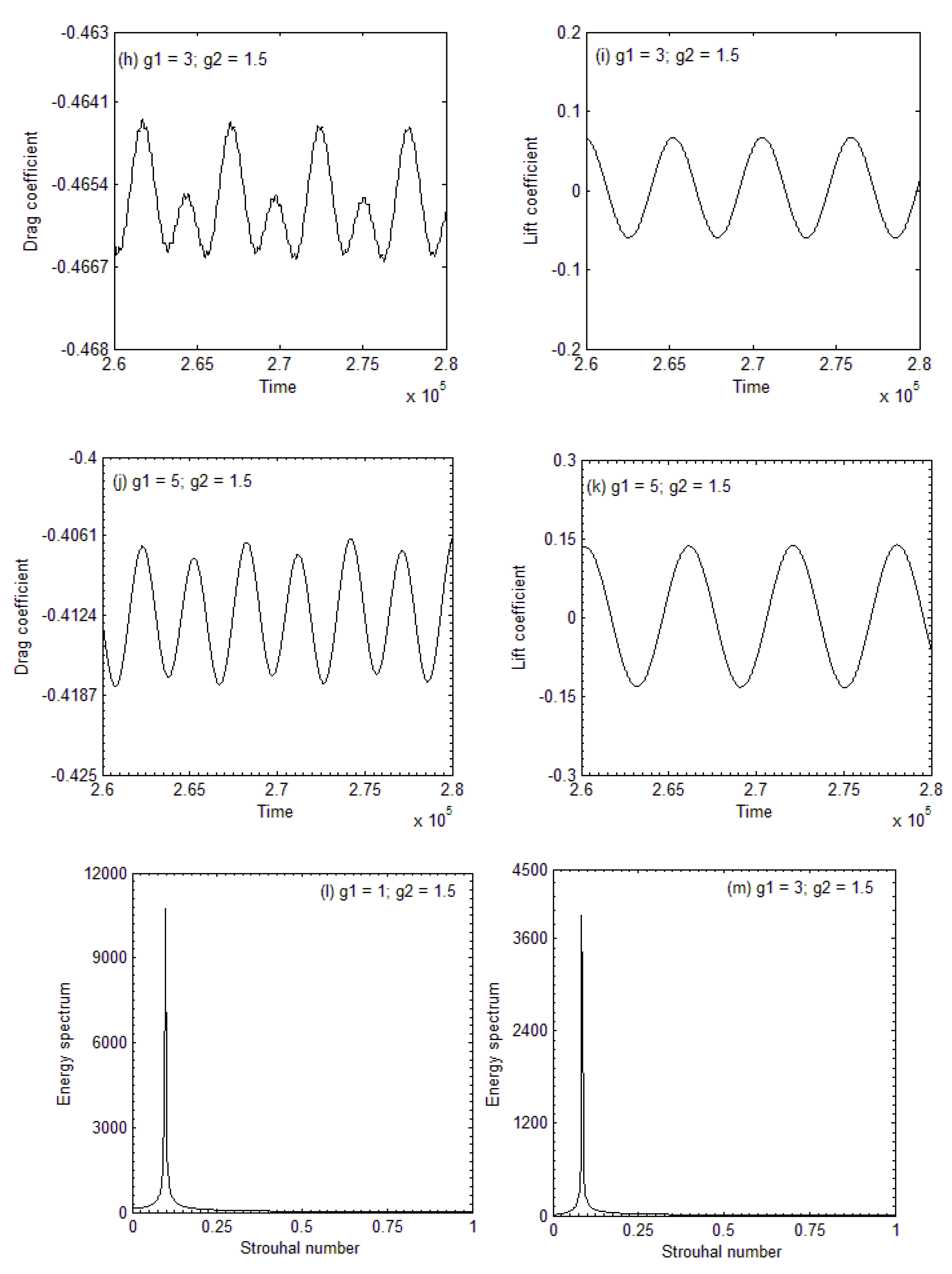
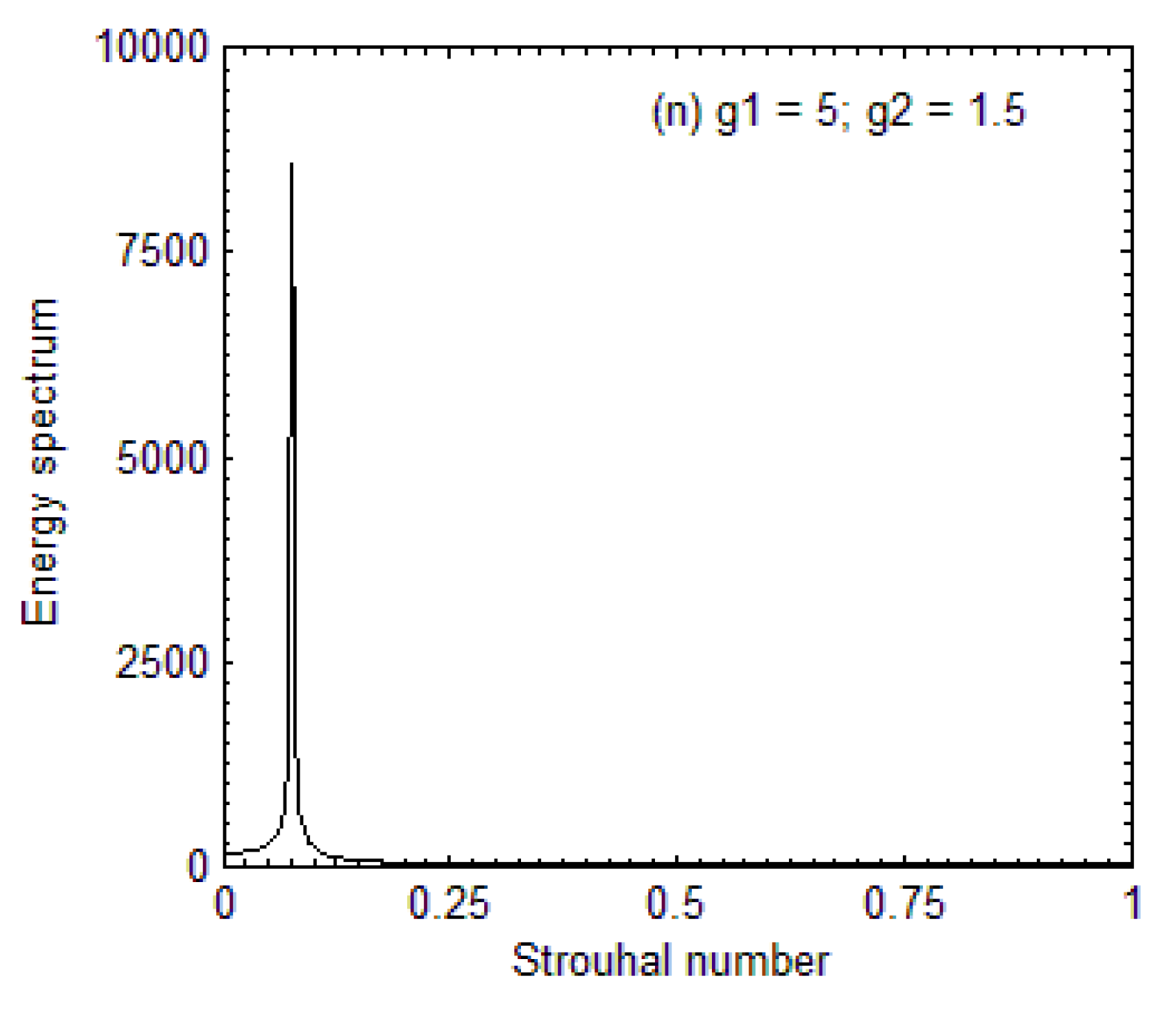

| Cases | Cdmean | Clrms | St | |
|---|---|---|---|---|
| (I) | Lu = 7.0 d; Ld = 33.0 d; H = 8.0 d | −0.425 | 0.1099 | 0.102 |
| (II) | Lu = 8.0 d; Ld = 33.0 d; H = 8.0 d | −0.426 | 0.1095 | 0.096 |
| (III) | Lu = 9.0 d; Ld = 33.0 d; H = 11.0 d | −0.427 | 0.1091 | 0.096 |
| (IV) | Lu = 8.0 d; Ld = 30.0 d; H = 8.0 d | −0.426 | 0.1097 | 0.099 |
| (V) | Lu = 8.0 d; Ld = 35.0 d; H = 8.0 d | −0.426 | 0.1096 | 0.102 |
| (VI) | Lu = 8.0 d; Ld = 33.0 d; H = 7.0 d | −0.422 | 0.0609 | 0.099 |
| (VII) | Lu = 8.0 d; Ld = 33.0 d; H = 9.0 d | −0.492 | 0.3623 | 0.108 |
| Cases | Cdmean | Cdrms | Clrms | St |
|---|---|---|---|---|
| d = 10.0 | 1.5932 | 0.0285 | 0.3688 | 0.3197 |
| d = 20.0 | 1.5272 | 0.0229 | 0.3152 | 0.1712 |
| d = 30.0 | 1.5458 | 0.0428 | 0.3033 | 0.2106 |
| d = 40.0 | 1.5528 | 0.5921 | 0.3104 | 0.2193 |
| Re = 200 | Cdmean | St |
|---|---|---|
| Saha et al. [33] | 1.670 | 0.163 |
| Sohankar et al. [34] | 1.424 | 0.165 |
| Okajima [35] | 1.480 | 0.138 |
| Norberg [36] | 1.450 | 0.152 |
| Abograis and Alshayji [37] | 1.488 | 0.153 |
| Present | 1.519 | 0.155 |
| Re = 200 | Cdrms | Clrms |
| Sohankar et al. [34] | 0.012 | 0.012 |
| Abograis and Alshayji [37] | 0.027 | 0.027 |
| Present | 0.038 | 0.038 |
| Flow Modes | (g1, g2) |
|---|---|
| Shear Layer Reattachment | (1, 0.5), (1, 1), (1, 1.5), (1, 2), (2, 0), (2, 0.5), (2, 1), (2, 1.5), (2, 2), (2, 3), (2, 4), (2, 5), (3, 0), (3, 1.5), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1.5), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1.5), (5, 2), (5, 3), (5, 4), (5, 5) |
| Steady | (3, 0.5), (3, 1), (4, 0), (4, 0.5), (4, 1), (5, 0), (5, 0.5), (5, 1) |
| Semi-Developed Vortex Shedding | (1, 3), (1, 4), (1, 5) |
| % Reduction Cdmean | g2 = 0.5 | g2 = 1 | g2 = 1.5 | g2 = 2 | g2 = 3 | g2 = 4 | g2 = 5 |
|---|---|---|---|---|---|---|---|
| g1 = 1 | 135.21 | 132.11 | 135.06 | 134.58 | 139.72 | 139.22 | 139.22 |
| g1 = 2 | 137.11 | 136.94 | 137.58 | 139.09 | 139.37 | 139.03 | 138.85 |
| g1 = 3 | 137.31 | 137.45 | 137.64 | 137.82 | 138.08 | 137.88 | 137.65 |
| g1 = 4 | 136.52 | 136.57 | 136.58 | 135.91 | 136.39 | 136.62 | 136.63 |
| g1 = 5 | 134.30 | 134.36 | 133.87 | 132.79 | 134.21 | 134.60 | 134.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzoor, R.; Ghaffar, A.; Baleanu, D.; Nisar, K.S. Numerical Analysis of Fluid Forces for Flow Past a Square Rod with Detached Dual Control Rods at Various Gap Spacing. Symmetry 2020, 12, 159. https://doi.org/10.3390/sym12010159
Manzoor R, Ghaffar A, Baleanu D, Nisar KS. Numerical Analysis of Fluid Forces for Flow Past a Square Rod with Detached Dual Control Rods at Various Gap Spacing. Symmetry. 2020; 12(1):159. https://doi.org/10.3390/sym12010159
Chicago/Turabian StyleManzoor, Raheela, Abdul Ghaffar, Dumitru Baleanu, and Kottakkaran Sooppy Nisar. 2020. "Numerical Analysis of Fluid Forces for Flow Past a Square Rod with Detached Dual Control Rods at Various Gap Spacing" Symmetry 12, no. 1: 159. https://doi.org/10.3390/sym12010159
APA StyleManzoor, R., Ghaffar, A., Baleanu, D., & Nisar, K. S. (2020). Numerical Analysis of Fluid Forces for Flow Past a Square Rod with Detached Dual Control Rods at Various Gap Spacing. Symmetry, 12(1), 159. https://doi.org/10.3390/sym12010159








