A Secure Authentication and Key Agreement Scheme for IoT-Based Cloud Computing Environment
Abstract
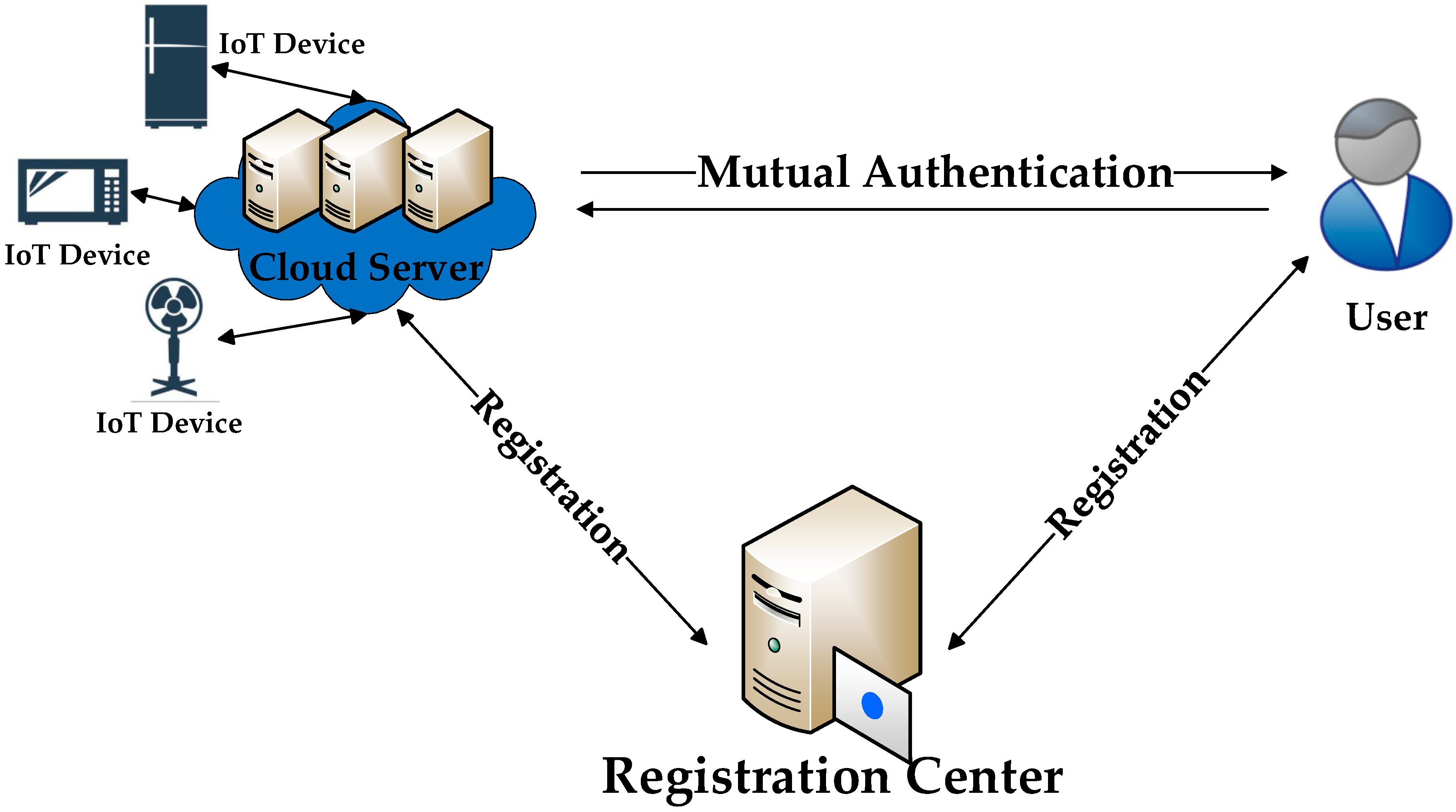
1. Introduction
Contributions
2. Preliminaries
2.1. Bilinear Pairing
2.2. Related Mathematical Problems
2.2.1. Discrete Logarithm Problem
2.2.2. Computational Diffie–Hellman Problem
2.3. Adversary Model
3. Review of He et al.’s Scheme
3.1. Setup Phase
3.2. User Registration Phase
- 1.
- chooses , and a random number freely. Then, computers . Finally, sends the registration message towards RC.
- 2.
- RC selects freely and computes , , , , . Then, RC transmits towards .
- 3.
- writes into .
3.3. Cloud Server Registration Phase
- 1.
- transmits to RC.
- 2.
- RC calculates and responses to via a private channel.
- 3.
- receives and stores safely.
3.4. Login and Authentication Phase
- 1.
- inserts to a reader, and inputs and . verifies the equality check for . If it holds true, ensures that and are correct. Then, randomly generates a number and calculates , . Finally, transmits a login request towards .
- 2.
- receives and calculates . Then, randomly chooses a number and calculates , . Finally, responds towards .
- 3.
- receives and checks the equality for . If , terminates the session. Otherwise, calculates , , , the session key and . Finally, transmits towards cloud server .
- 4.
- receives and recovers , , via computing . Furthermore, calculates , and checks the equality for . If it holds true, gets the session key .
3.5. Password Modification Phase
- 1.
- inputs , . checks the equality .
- 2.
- If , rejects the modification request. Otherwise, inputs . chooses a new random number , calculates , . Finally, SC replaces with and the new password is .
4. Cryptanalysis of He et al.’s Scheme
4.1. Insider Attack
4.1.1. Offline Password Guessing
- 1.
- guesses a candidate password .
- 2.
- calculates .
- 3.
- checks whether holds. If not, repeats Steps 1–3 until he acquires a true password. Otherwise, has already succeeded in getting the true password. The attack is finished.
4.1.2. User Impersonation
- 1.
- randomly generates a number and calculates , . Afterwards, transmits the request to server .
- 2.
- Upon receiving from , computes , , where and were obtained before. Subsequently, calculates , and gets the session key . Finally, sends to .The information generated by is legal. The cloud server considers as the user .
4.2. Possible DoS Attack
5. Our Improved Scheme
5.1. Setup Phase
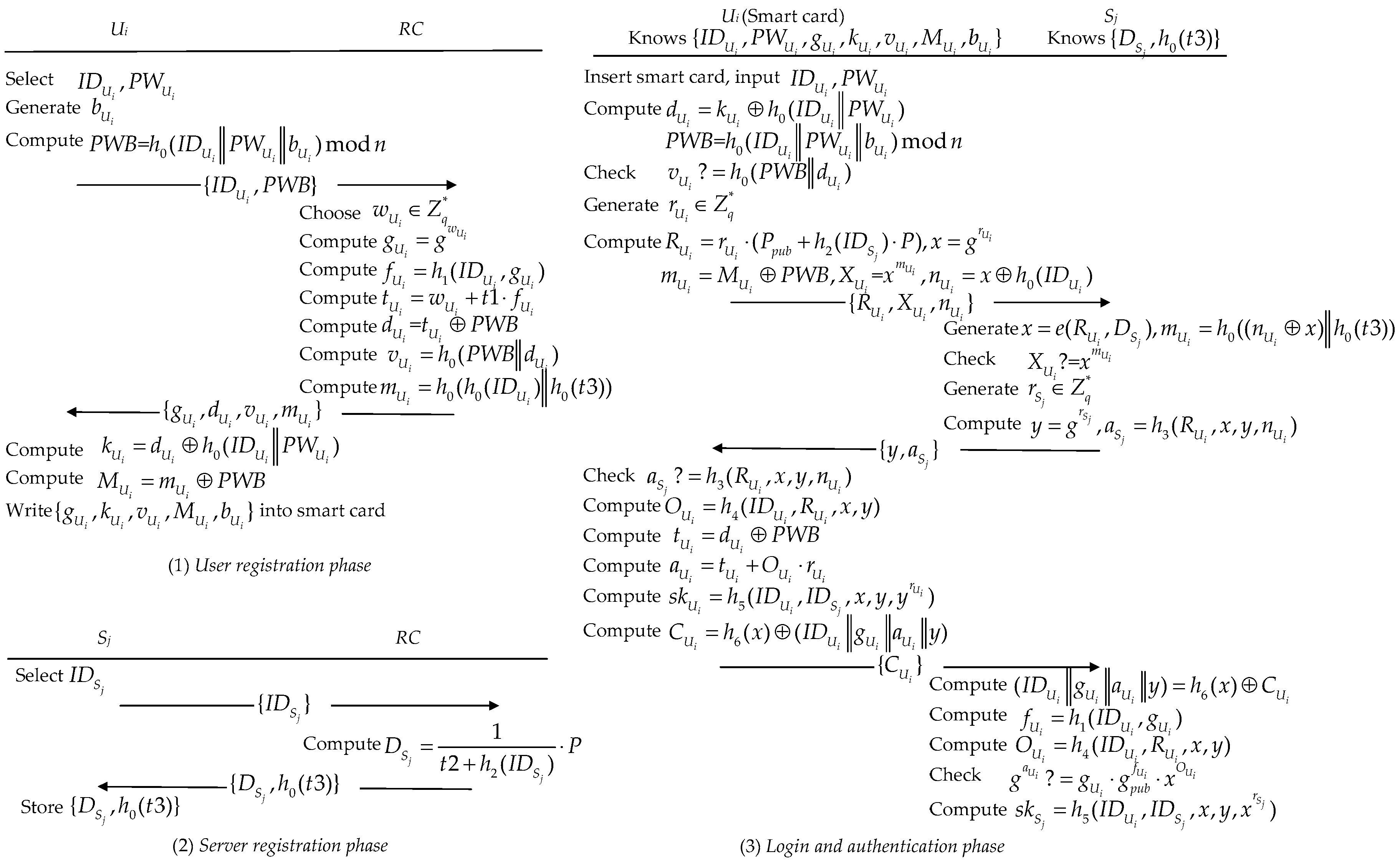
5.2. User Registration Phase
- 1.
- chooses , and a number freely. Then, computers . Note that is an integer that determines the capacity of . Then, it transmits the registration message towards RC.
- 2.
- RC selects freely and computes , , , , , . Then, RC responses to via a private secure channel.
- 3.
- receives and computes , . Finally, writes into .
5.3. Cloud Server Registration Phase
- 1.
- sends to RC.
- 2.
- Upon reception of , RC calculates and sends to via a private channel.
- 3.
- stores in secret.
5.4. Login and Authentication Phase
- 1.
- inserts to the reader and inputs and . calculates , and verifies the equality check for . If , rejects the login request. Otherwise, it randomly chooses and calculates , , , , . Finally, transmits login request towards .
- 2.
- receives and calculates , . Then, verifies the equality check . If , terminates the session. Otherwise, randomly selects and calculates , . Finally, transmits towards .
- 3.
- Upon reception of from , verifies the equality check . If , terminates the session. Otherwise, calculates , , , the session key and . Finally, transmits towards .
- 4.
- receives and recovers , and via computing . Furthermore, calculates , and checks the equality for . If it holds true, gets the session key .
5.5. Password Modification Phase
- 1.
- inputs , . computes , and checks the equality .
- 2.
- If , rejects the request. Otherwise, inputs . randomly generates and calculates , . Finally, replaces with .
6. Security Analysis
6.1. Security Verification Using ProVerif
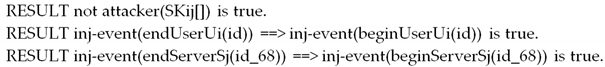
6.2. Formal Security Analysis Using BAN-Logic
6.2.1. Idealized Form
6.2.2. Verification Purposes
6.2.3. Assumptions about Initial State
6.2.4. Proofs
- 1.
- According to Message 2, we get the following: .
- 2.
- According to Assumption 3 and the message-meaning rule, we get the following: .
- 3.
- Based on Assumption 1 and the freshness–conjuncatenation rule, we can prove: .
- 4.
- From Step 2, Step 3, and the nonce-verification rule, we obtain the following: .
- 5.
- According to Step 4 and believe rule, .
- 6.
- According to Step 5, Assumption 3 and , we prove that: (Purpose 2).
- 7.
- Based on Step 6, Assumption 6, and jurisdiction rule, we prove that: (Purpose 1).
- 8.
- From Message 3, we get: .
- 9.
- Based on Assumption 4 and the message-meaning rule, we obtain the following: .
- 10.
- From Assumption 2 and the freshness-conjuncatenation rule, we can obtain: .
- 11.
- Based on Step 9, Step 10, and the nonce-verification rule, we obtain the following: .
- 12.
- According to Assumption 5, Step 11, , and the believe rule, we obtain the following: .
- 13.
- According to Step 12, Assumption 4, and , we prove that: (Purpose 4).
- 14.
- According to Step 13, Assumption 7, and jurisdiction rule, we prove that: (Purpose 3).
6.3. Informal Security Analysis
6.3.1. Anonymity and Untraceability
6.3.2. Forward Secrecy
6.3.3. Two-Factor Security
6.3.4. Session Key Agreement
6.3.5. Resistance of Other Attacks
7. The Comparisons of Security and Performance
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, H.; Kumara, S.; Bukkapatnam, S.T.S.; Tsung, F. The internet of things for smart manufacturing: A review. IISE Trans. 2019, 51, 1190–1216. [Google Scholar] [CrossRef]
- Dang, L.M.; Piran, M.; Han, D.; Min, K.; Moon, H. A Survey on Internet of Things and Cloud Computing for Healthcare. Electronics 2019, 8, 768. [Google Scholar] [CrossRef]
- Grobauer, B.; Walloschek, T.; Stocker, E. Understanding cloud computing vulnerabilities. IEEE Secur. Priv. 2010, 9, 50–57. [Google Scholar] [CrossRef]
- Lamport, L. Password authentication with insecure communication. Commun. ACM 1981, 24, 770–772. [Google Scholar] [CrossRef]
- Wang, B.; Ma, M. A smart card based efficient and secured multi-server authentication scheme. Wirel. Pers. Commun. 2013, 68, 361–378. [Google Scholar] [CrossRef]
- Sahoo, J.; Das, A.K.; Goswami, A. An efficient approach for mining association rules from high utility itemsets. Expert Syst. Appl. 2015, 42, 5754–5778. [Google Scholar] [CrossRef]
- Lu, Y.; Li, L.; Yang, X.; Yang, Y. Robust biometrics based authentication and key agreement scheme for multi-server environments using smart cards. PLoS ONE 2015, 10, e0126323. [Google Scholar] [CrossRef]
- Zhou, L.; Li, X.; Yeh, K.H.; Su, C.; Chiu, W. Lightweight IoT-based authentication scheme in cloud computing circumstance. Future Gener. Comput. Syst. 2019, 91, 244–251. [Google Scholar] [CrossRef]
- Li, X.; Wen, Q.; Li, W.; Zhang, H.; Jin, Z. A biometric-based password authentication with key exchange scheme using mobile device for multi-server environment. Appl. Math. Inf. Sci. 2015, 9, 1123. [Google Scholar]
- Amin, R.; Islam, S.K.H.; Gope, P.; Choo, K.K.R.; Tapas, N. Anonymity preserving and lightweight multi-medical server authentication protocol for telecare medical information system. IEEE J. Biomed. Health Inform. 2018, 23, 1749–1759. [Google Scholar] [CrossRef]
- Lwamo, N.M.R.; Zhu, L.; Xu, C.; Sharif, K.; Liu, X.; Zhang, C. SUAA: A Secure User Authentication Scheme with Anonymity for the Single & Multi-server Environments. Inf. Sci. 2019, 477, 369–385. [Google Scholar]
- Cui, J.; Zhang, X.; Cao, N.; Zhang, D.; Ding, J.; Li, G. An improved authentication protocol–based dynamic identity for multi-server environments. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718777654. [Google Scholar] [CrossRef]
- Renuka, K.; Kumar, S.; Kumari, S.; Chen, C.M. Cryptanalysis and Improvement of a Privacy-Preserving Three-Factor Authentication Protocol for Wireless Sensor Networks. Sensors 2019, 19, 4625. [Google Scholar] [CrossRef] [PubMed]
- Amin, R.; Islam, S.K.H.; Kumar, N.; Choo, K.K.R. An untraceable and anonymous password authentication protocol for heterogeneous wireless sensor networks. J. Netw. Comput. Appl. 2018, 104, 133–144. [Google Scholar] [CrossRef]
- Mohit, P.; Amin, R.; Karati, A.; Biswas, G.P.; Khan, M.K. A standard mutual authentication protocol for cloud computing based health care system. J. Med. Syst. 2017, 41, 50. [Google Scholar] [CrossRef]
- Xu, G.; Qiu, S.; Ahmad, H.; Xu, G.; Guo, Y.; Zhang, M.; Xu, H. A multi-server two-factor authentication scheme with un-traceability using elliptic curve cryptography. Sensors 2018, 18, 2394. [Google Scholar] [CrossRef]
- Chandrakar, P.; Om, H. A secure and robust anonymous three-factor remote user authentication scheme for multi-server environment using ECC. Comput. Commun. 2017, 110, 26–34. [Google Scholar] [CrossRef]
- Ying, B.; Nayak, A. Lightweight remote user authentication protocol for multi-server 5G networks using self-certified public key cryptography. J. Netw. Comput. Appl. 2019, 131, 66–74. [Google Scholar] [CrossRef]
- Hou, J.L.; Yeh, K.H. Novel authentication schemes for IoT based healthcare systems. Int. J. Distrib. Sens. Netw. 2015, 11, 183659. [Google Scholar] [CrossRef]
- Tomar, A.; Dhar, J. An ECC Based Secure Authentication and Key Exchange Scheme in Multi-server Environment. Wirel. Pers. Commun. 2019, 107, 351–372. [Google Scholar] [CrossRef]
- Qi, M.; Chen, J. Anonymous biometrics-based authentication with key agreement scheme for multi-server environment using ECC. Multimed. Tools Appl. 2019, 78, 27553–27568. [Google Scholar] [CrossRef]
- Tseng, Y.M.; Huang, S.S.; Tsai, T.T.; Ke, J.H. List-free ID-based mutual authentication and key agreement protocol for multiserver architectures. IEEE Trans. Emerg. Top. Comput. 2015, 4, 102–112. [Google Scholar] [CrossRef]
- Wang, H.; Guo, D.; Zhang, H.; Wen, Q. Robust Multiple Servers Architecture Based Authentication Scheme Preserving Anonymity. Sensors 2019, 19, 3144. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Zeadally, S.; Kumar, N.; Wu, W. Efficient and anonymous mobile user authentication protocol using self-certified public key cryptography for multi-server architectures. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2052–2064. [Google Scholar] [CrossRef]
- Blanchet, B.; Smyth, B.; Cheval, V.; Sylvestre, M. ProVerif 2.00: Automatic Cryptographic Protocol Verifier, User Manual and Tutorial. 2018. Available online: https://prosecco.gforge.inria.fr/personal/bblanche/proverif (accessed on 9 January 2020).
- Burrows, M.; Abadi, M.; Needham, R.M. A logic of authentication. Proc. R. Soc. Lond. A Math. Phys. Sci. 1989, 426, 233–271. [Google Scholar] [CrossRef]
- Dolev, D.; Yao, A. On the security of public key protocols. IEEE Trans. Inf. Theory 1983, 29, 198–208. [Google Scholar] [CrossRef]
- Veyrat-Charvillon, N.; Standaert, F.X. Generic side-channel distinguishers: Improvements and limitations. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 354–372. [Google Scholar]
- Wang, D.; He, D.; Wang, P.; Chu, C.H. Anonymous two-factor authentication in distributed systems: Certain goals are beyond attainment. IEEE Trans. Dependable Secur. Comput. 2014, 12, 428–442. [Google Scholar] [CrossRef]
- Huang, X.; Xiang, Y.; Chonka, A.; Zhou, J.; Deng, R.H. A generic framework for three-factor authentication: Preserving security and privacy in distributed systems. IEEE Trans. Parallel Distrib. Syst. 2010, 22, 1390–1397. [Google Scholar] [CrossRef]
- Das, M.L.; Saxena, A.; Gulati, V.P. A dynamic ID-based remote user authentication scheme. IEEE Trans. Consum. Electron. 2004, 50, 629–631. [Google Scholar] [CrossRef]
- Das, M.L. Two-factor user authentication in wireless sensor networks. IEEE Trans. Wirel. Commun. 2009, 8, 1086–1090. [Google Scholar] [CrossRef]
- Wang, D.; Gu, Q.; Cheng, H.; Wang, P. The request for better measurement: A comparative evaluation of two-factor authentication schemes. In Proceedings of the 11th ACM on Asia Conference on Computer and Communications Security, Xi’an, China, 30 May–3 June 2016; ACM: New York, NY, USA, 2016; pp. 475–486. [Google Scholar]
| Symbol | Description |
|---|---|
| . | The adversary can enumerate all elements of offline. |
| . | The adversary can obtain user ID (The user ID should be assumed to be sensitive information when evaluating the anonymity of the protocol). |
| . | The adversary can eavesdrop, intercept, insert, delete, or block messages flowing through the public channel. |
| . | For the n-factor protocol, the adversary can obtain n-1 of the n authentication factors simultaneously. |
| . | The adversary has a chance to capture an expired session key. |
| . | The adversary can obtain the long-term private keys of participants. (when evaluating forward secrecy). |
| . | An insider adversary can obtain user’s registration information and capture user’s smartcard (when evaluating insider attack). |
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| Registration Center | User | ||
| Private key of | Identification of | ||
| Large prime | Password of | ||
| prime order | Smart card of | ||
| Additive group | Cloud Server | ||
| Multiplicative group | Identification of | ||
| Public key of | Private key of | ||
| Bilinear pairing | XOR operation | ||
| Hash function | Session key of and |
| Symbol | Description |
|---|---|
| believes . | |
| sees . | |
| sends . | |
| has jurisdiction over . | |
| is fresh. | |
| or is part of . | |
| Use key to compute . | |
| and achieve the shared key for communication. |
| Rule | Description |
|---|---|
| Message-meaning rule | |
| Freshness-conjuncatenation rule | |
| Nonce-verification rule | |
| Jurisdiction rule | |
| Believe rule |
| Security Features and Defensible Attacks | He et al.’s | Ours |
|---|---|---|
| Anonymity | ||
| Un-traceability | ||
| Two-factor security | ||
| Forward Secrecy | ||
| Session key agreement | ||
| Insider attack | ||
| Cloud server spoofing attack | ||
| Replay attack | ||
| DoS attack | ||
| User impersonation attack | ||
| Offline password guessing attack | ||
| Smart card stolen attack |
| User | Cloud Server | |
|---|---|---|
| 13.405 ms | 2.165 ms | |
| 0.081 ms | 0.013 ms | |
| 2.249 ms | 0.339 ms | |
| 0.056 ms | 0.007 ms | |
| 32.713 ms | 5.427 ms |
| He et al.’s | Ours | |
|---|---|---|
| User | ||
| Cloud server |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Hu, L.; Chu, J. A Secure Authentication and Key Agreement Scheme for IoT-Based Cloud Computing Environment. Symmetry 2020, 12, 150. https://doi.org/10.3390/sym12010150
Yu Y, Hu L, Chu J. A Secure Authentication and Key Agreement Scheme for IoT-Based Cloud Computing Environment. Symmetry. 2020; 12(1):150. https://doi.org/10.3390/sym12010150
Chicago/Turabian StyleYu, Yicheng, Liang Hu, and Jianfeng Chu. 2020. "A Secure Authentication and Key Agreement Scheme for IoT-Based Cloud Computing Environment" Symmetry 12, no. 1: 150. https://doi.org/10.3390/sym12010150
APA StyleYu, Y., Hu, L., & Chu, J. (2020). A Secure Authentication and Key Agreement Scheme for IoT-Based Cloud Computing Environment. Symmetry, 12(1), 150. https://doi.org/10.3390/sym12010150




