Towards an Efficient Privacy-Preserving Decision Tree Evaluation Service in the Internet of Things
Abstract
1. Introduction
1.1. Motivation
1.2. Our Contributions
- We newly design a secure comparison protocol that can return additive shares of the comparison result on additively secret shared inputs. Compared with the Huang et al.’s work [21] and Zheng et al.’s work [20], the number of additive multiplications required can be reduced from and to l respectively, where l is the bit-length of a feature vector’s element. Compared with Liu et al.’s work [22], which is based on additive secret sharing and additively homomorphic cryptosystem, the proposed work is more secure and efficient.
- With the additive secret sharing technology and an asymmetrically homomorphic cryptosystem, i.e., Paillier cryptosystem [23], the privacy-preserving decision tree scheme based on the two-cloud model is proposed in this work. The scheme is tested on several widely used real-world datasets. The experimental results show that compared with the most recent work, i.e., Zheng et al.’s work [20], our scheme is more efficient when dealing with deeper trees. Particularly, the communication cost of our scheme is just 1/709 of Zheng et al.’s work [20].
- We show that our scheme can fully protect the privacy of the client. At the same time, during the evaluation process, the client also learns nothing of the decision tree. Additionally, since there are two clouds involved, we can also prove the model is not leaked to the other cloud except the number of the decision node.
1.3. Organization
2. Preliminaries
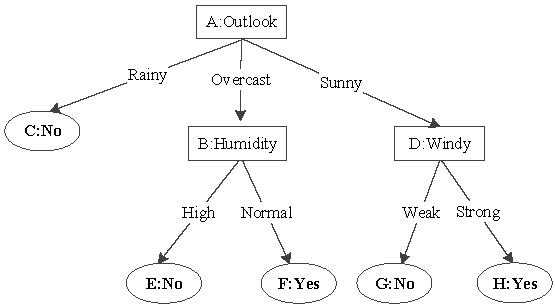
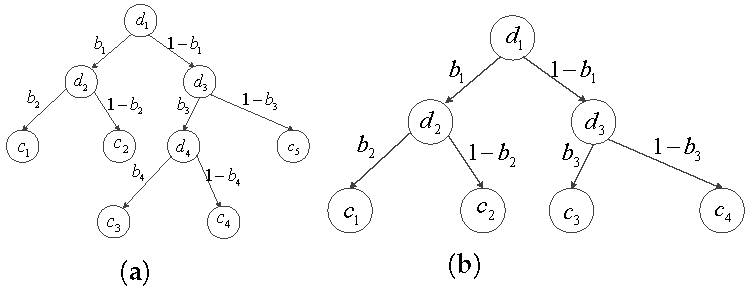
2.1. Decision Tree
2.2. Additive Secret Sharing
2.2.1. Addition of Additive Shares
2.2.2. Multiplication of Additive Shares
2.3. Paillier Cryptosystem
- Homomorphic Addition: If we have two ciphertext, e.g., , , encrypted by the same public key, we can easily compute .
- Scalar Multiplication: If given the ciphertext and a constant integer c, we could easily compute . Particularly, if c is , we can easily obtain that , where .
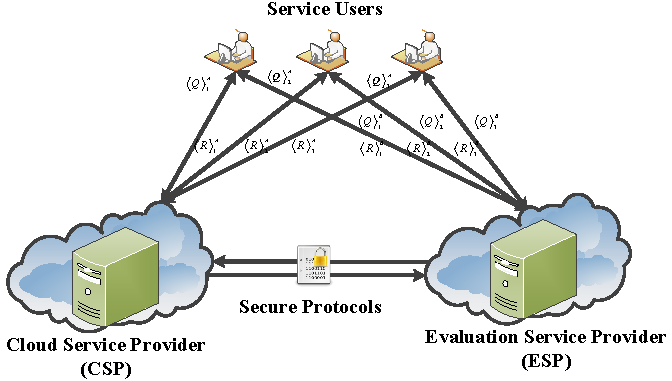
3. System Model and Design Goals
3.1. System Model
- Service Users: The Service User (SU) in our system wants to use a decision tree evaluation service in a privacy-preserving way. The SU splits the query vector into two additive shares before sending them to two clouds respectively.
- Cloud Service Provider: Assume that a trained decision tree model belongs to Cloud Service Provider. The CSP provides a decision tree classification service to SU. Since only one of the shares is sent to it, CSP needs to cooperate with the Evaluation Service Provider to fulfill the evaluation.
- Evaluation Service Provider: In our system, the ESP’s mission is to cooperate with the CSP to give the SU the evaluation result of the decision tree model in a privacy-preserving way. Besides, ESP generates the public/private key pair of the Paillier cryptosystem and reveals the public key to CSP.
3.2. Threat Model
- may eavesdrop the communication channel between CSP and ESP.
- may compromise ESP.
3.3. Design Goals
- Data Protection. For this decision tree evaluation scheme, data security and privacy issues are the most important ones to be solved. As we know, the outsourced data and the calculated classification result contain sensitive information that should be kept secret to the cloud, including CSP and ESP. Besides, for the CSP, the decision tree model is its assert, which also should not be leaked to ESP and the SUs. Moreover, all such information should be confidential to the active adversary .
- Classification Result’s Accuracy. The classification result should be the same as the non-privacy- preserving one.
- Efficiency. In this scheme, we insist that the two clouds should finish the evaluation process as fast as they can and return the classification labels to SUs quickly. Thus, the computation and communication costs of the clouds should be small enough.
- Offline SUs. As we know, SUs in the IoT usually do not have strong computation power and large storage space. Therefore, we should minimize the computation and communication burdens for the SUs. Thus, once sending the query to CSP and ESP, SUs should stay offline until obtaining results. We also should note that many clients are using this decision tree evaluation service. Thus, for the scalability of the system, this scheme is supposed to support offline SUs.
4. Privacy-Preserving Decision Tree Evaluation
4.1. Secure Comparison Algorithm
| Algorithm 1 Secure Comparison (SC) |
|
4.2. Privacy-Preserving Decision Tree Evaluation
4.2.1. Query Request Issuing
4.2.2. Secure Decision Tree Evaluation
5. Security Analysis
5.1. Security of Cryptographic Blocks
5.2. Security of Privacy-Preserving Decision Tree Evaluation Scheme
6. Performance Analysis and Comparison
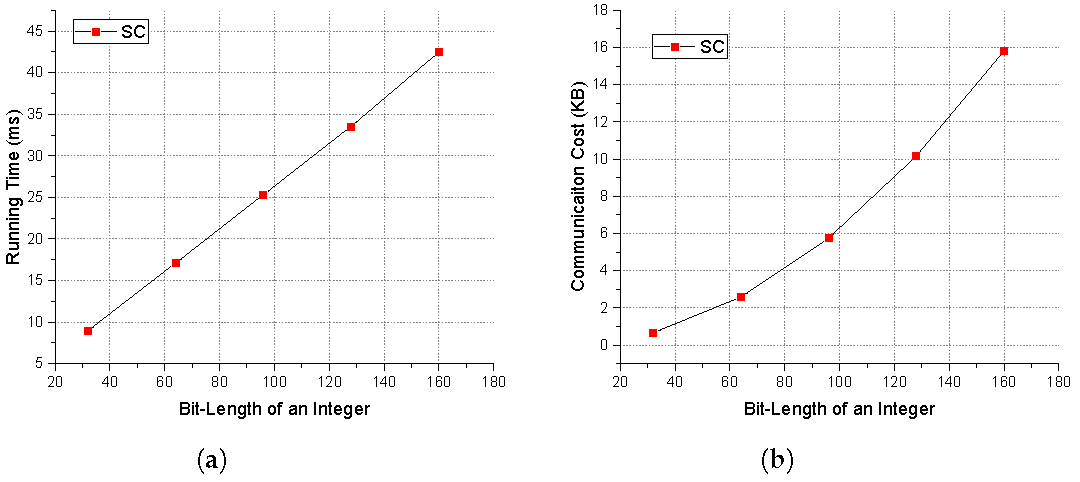
6.1. Experiment Analysis
6.2. Performance Comparison and Analysis
6.3. Comparative Analysis
7. Related Work
8. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Mahdavinejad, M.S.; Rezvan, M.; Barekatain, M.; Adibi, P.; Barnaghi, P.; Sheth, A.P. Machine learning for Internet of Things data analysis: A survey. Digit. Commun. Netw. 2018, 4, 161–175. [Google Scholar] [CrossRef]
- Amazon Machine Learning Service. Available online: https://aws.amazon.com/cn/machine-learning/ (accessed on 16 December 2019).
- Google Cloud, A.I. Available online: https://cloud.google.com/products/ai/ (accessed on 16 December 2019).
- Microsoft AI Service. Available online: https://www.microsoft.com/en-us/ai/ai-platform (accessed on 16 December 2019).
- Li, J.; Chen, R.; Su, J.; Huang, X.; Wang, X. ME-TLS: Middlebox-Enhanced TLS for Internet-of-things Devices. IEEE Internet Things J. 2019. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, P.; Wang, X.; You, I. Toward efficient authentication for space-air-ground integrated Internet of things. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, R.; Li, C.; Qu, L.; Yang, G. On the Security of LWE Cryptosystem against Subversion Attacks. Comput. J. 2019. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, R.; Liu, C.; Wang, B.; Wang, Y. Available online: https://doi.org/10.1007/s00779-018-01193-x (accessed on 02 January 2019).
- Rago, A.; Marcos, C.; Diazpace, J.A. Using semantic roles to improve text classification in the requirements domain. Lang. Resour. Eval. 2018, 52, 801–837. [Google Scholar] [CrossRef]
- Singh, A.; Guttag, J.V. A comparison of non-symmetric entropy-based classification trees and support vector machine for cardiovascular risk stratification. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 79–82. [Google Scholar]
- Azar, A.T.; Elmetwally, S.M. Decision tree classifiers for automated medical diagnosis. Neural Comput. Appl. 2013, 23, 2387–2403. [Google Scholar] [CrossRef]
- Koh, H.C.; Tan, W.C.; Goh, C.P. Available online: https://ijbi.org/ijbi/article/view/5 (accessed on 12 November 2019).
- Lindell, Y.; Pinkas, B. Privacy preserving data mining. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 2000; pp. 36–54. [Google Scholar]
- Agrawal, R.; Srikant, R. Privacy-preserving data mining. In ACM Sigmod Record; ACM: New York, NY, USA, 2000; Volume 29, pp. 439–450. [Google Scholar]
- Bost, R.; Popa, R.A.; Tu, S.; Goldwasser, S. Machine learning classification over encrypted data. In Proceedings of the NDSS, San Diego, CA, USA, 8–11 February 2015; Volume 4324, p. 4325. [Google Scholar]
- Wu, D.J.; Feng, T.; Naehrig, M.; Lauter, K. Privately evaluating decision trees and random forests. Proc. Priv. Enhancing Technol. 2016, 2016, 335–355. [Google Scholar] [CrossRef]
- Tai, R.K.; Ma, J.P.; Zhao, Y.; Chow, S.S. Privacy-Preserving Decision Trees Evaluation via Linear Functions. In Proceedings of the European Symposium on Research in Computer Security, Oslo, Norway, 11–15 September 2017; pp. 494–512. [Google Scholar]
- Tueno, A.; Kerschbaum, F.; Katzenbeisser, S. Private evaluation of decision trees using sublinear cost. Proc. Priv. Enhancing Technol. 2019, 2019, 266–286. [Google Scholar] [CrossRef]
- Liang, J.; Qin, Z.; Xiao, S.; Ou, L.; Lin, X. Efficient and Secure Decision Tree Classification for Cloud-Assisted Online Diagnosis Services. IEEE Trans. Dependable Secur. Comput. 2019. [Google Scholar] [CrossRef]
- Zheng, Y.; Duan, H.; Wang, C. Towards Secure and Efficient Outsourcing of Machine Learning Classification. In Proceedings of the European Symposium on Research in Computer Security, Luxembourg, 23–27 September 2019; pp. 22–40. [Google Scholar]
- Huang, K.; Liu, X.; Fu, S.; Guo, D.; Xu, M. A Lightweight Privacy-Preserving CNN Feature Extraction Framework for Mobile Sensing. IEEE Trans. Dependable Secur. Comput. 2019. [Google Scholar] [CrossRef]
- Liu, L.; Su, J.; Chen, R.; Chen, J.; Sun, G.; Li, J. Secure and Fast Decision Tree Evaluation on Outsourced Cloud Data. In Proceedings of the Second International Conference on Machine Learning for Cyber Security, Xi’an, China, 19–21 September 2019; pp. 1–17. [Google Scholar]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1999; Volume 99, pp. 223–238. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (sfcs 1986), Toronto, ON, Canada, 27–29 October 1986; pp. 162–167. [Google Scholar]
- Beaver, D. Efficient multiparty protocols using circuit randomization. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1991; pp. 420–432. [Google Scholar]
- Ohrimenko, O.; Schuster, F.; Fournet, C.; Mehta, A.; Nowozin, S.; Vaswani, K.; Costa, M. Oblivious Multi-Party Machine Learning on Trusted Processors. In Proceedings of the USENIX Security Symposium, Austin, TX, USA, 10–12 August 2016; pp. 619–636. [Google Scholar]
- Liu, L.; Su, J.; Liu, X.; Chen, R.; Huang, K.; Deng, R.H.; Wang, X. Towards Highly Secure Yet Efficient KNN Classification Scheme on Outsourced Cloud Data. IEEE Internet Things J. 2019, 6, 9841–9852. [Google Scholar] [CrossRef]
- Liu, X.; Choo, R.; Deng, R.; Lu, R.; Weng, J. Efficient and privacy-preserving outsourced calculation of rational numbers. IEEE Trans. Dependable Secur. Comput. 2016, 15, 27–39. [Google Scholar] [CrossRef]
- Liu, L.; Su, J.; Chen, R.; Liu, X.; Wang, X.; Chen, S.; Leung, H. Privacy-preserving mining of association rule on outsourced cloud data from multiple parties. In Proceedings of the Australasian Conference on Information Security and Privacy, Wollongong, NSW, Australia, 11–13 July 2018; pp. 431–451. [Google Scholar]
- Luo, Y.; Jia, X.; Fu, S.; Xu, M. pRide: Privacy-Preserving Ride Matching Over Road Networks for Online Ride-Hailing Service. IEEE Trans. Inf. Forensics Secur. 2018, 14, 1791–1802. [Google Scholar] [CrossRef]
- Damgård, I.; Fitzi, M.; Kiltz, E.; Nielsen, J.B.; Toft, T. Unconditionally secure constant-rounds multi-party computation for equality, comparison, bits and exponentiation. In Proceedings of the Theory of Cryptography Conference, New York, NY, USA, 4–7 March 2006; pp. 285–304. [Google Scholar]
- Hazay, C.; Mikkelsen, G.L.; Rabin, T.; Toft, T.; Nicolosi, A.A. Efficient RSA Key Generation and Threshold Paillier in the Two-Party Setting. J. Cryptol. 2019, 32, 265–323. [Google Scholar] [CrossRef]
- Veugen, T. Improving the DGK comparison protocol. In Proceedings of the 2012 IEEE International Workshop on Information Forensics and Security (WIFS), Tenerife, Spain, 2–5 December 2012; pp. 49–54. [Google Scholar]
- Goldreich, O. Foundations of Cryptography: Volume 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- GNU MP Library. Available online: https://gmplib.org/ (accessed on 16 December 2016).
- UC Irvine Machine Learning Respository. Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 16 December 2019).
- Joye, M.; Salehi, F. Private yet efficient decision tree evaluation. In Proceedings of the IFIP Annual Conference on Data and Applications Security and Privacy, Bergamo, Italy, 16–18 July 2018; pp. 243–259. [Google Scholar]
- De Cock, M.; Dowsley, R.; Horst, C.; Katti, R.; Nascimento, A.; Poon, W.S.; Truex, S. Efficient and private scoring of decision trees, support vector machines and logistic regression models based on pre-computation. IEEE Trans. Dependable Secur. Comput. 2017, 16, 217–230. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, M.; Huang, K.; Wang, D.; Fu, S. Efficient auditing for shared data in the cloud with secure user revocation and computations outsourcing. Comput. Secur. 2018, 73, 492–506. [Google Scholar] [CrossRef]
- Karapiperis, D.; Verykios, V.S. An LSH-based blocking approach with a homomorphic matching technique for privacy-preserving record linkage. IEEE Trans. Knowl. Data Eng. 2014, 27, 909–921. [Google Scholar] [CrossRef]
- Dritsas, E.; Kanavos, A.; Trigka, M.; Sioutas, S.; Tsakalidis, A. Storage Efficient Trajectory Clustering and k-NN for Robust Privacy Preservation Spatio-Temporal Databases. Algorithms 2019, 12, 266. [Google Scholar] [CrossRef]
- Brickell, J.; Porter, D.E.; Shmatikov, V.; Witchel, E. Privacy-preserving remote diagnostics. In Proceedings of the 14th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 28–31 October 2007; pp. 498–507. [Google Scholar]
| Notations | Definition |
|---|---|
| Additive secret share of x belongs to A/B | |
| The bit length of x | |
| The ciphertext of x encrypted by Paillier | |
| Add(·) | Addition on additive shares |
| Mul(·) | Multiplication on additive shares |
| Rec() | x’s value’s reconstruction |
| SC | Secure Comparison |
| SDTE | Secure Decision Tree Evaluation |
| Dataset | n | d | m | Time | Comm. Cost | Time [16] | Comm. Cost [16] | Time [20] | Comm. Cost [20] |
|---|---|---|---|---|---|---|---|---|---|
| breast-cancer | 9 | 8 | 12 | 0.256 s | 40.59 KB | 0.545 s | 132.0 KB | 0.0081 s | 73.22 KB |
| heat-disease | 13 | 3 | 5 | 0.103 s | 17.35 KB | 0.370 s | 43.9 KB | 0.0003 s | 2.66 KB |
| housing | 13 | 13 | 92 | 1.867 s | 306.19 KB | 4.081 s | 1795.2 KB | 0.3052 s | 2855 KB |
| credit-screening | 15 | 4 | 5 | 0.109 s | 17.45 KB | 0.551 s | 45.0 KB | 0.0007 s | 5.93 KB |
| spambase | 57 | 17 | 58 | 1.283 s | 191.31 KB | 16.595 s | 17363.3 KB | 14.639 s | 135807 KB |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Su, J.; Zhao, B.; Wang, Q.; Chen, J.; Luo, Y. Towards an Efficient Privacy-Preserving Decision Tree Evaluation Service in the Internet of Things. Symmetry 2020, 12, 103. https://doi.org/10.3390/sym12010103
Liu L, Su J, Zhao B, Wang Q, Chen J, Luo Y. Towards an Efficient Privacy-Preserving Decision Tree Evaluation Service in the Internet of Things. Symmetry. 2020; 12(1):103. https://doi.org/10.3390/sym12010103
Chicago/Turabian StyleLiu, Lin, Jinshu Su, Baokang Zhao, Qiong Wang, Jinrong Chen, and Yuchuan Luo. 2020. "Towards an Efficient Privacy-Preserving Decision Tree Evaluation Service in the Internet of Things" Symmetry 12, no. 1: 103. https://doi.org/10.3390/sym12010103
APA StyleLiu, L., Su, J., Zhao, B., Wang, Q., Chen, J., & Luo, Y. (2020). Towards an Efficient Privacy-Preserving Decision Tree Evaluation Service in the Internet of Things. Symmetry, 12(1), 103. https://doi.org/10.3390/sym12010103





