A Secure Authentication and Key Agreement Scheme for IoT-Based Cloud Computing Environment

Abstract

The integration of Internet of things (IoT) and cloud computing technology has made our life more convenient in recent years. Cooperating with cloud computing, Internet of things can provide more efficient and practical services. People can accept IoT services via cloud servers anytime and anywhere in the IoT-based cloud computing environment. However, plenty of possible network attacks threaten the security of users and cloud servers. To implement effective access control and secure communication in the IoT-based cloud computing environment, identity authentication is essential. In 2016, He et al. put forward an anonymous authentication scheme, which is based on asymmetric cryptography. It is claimed that their scheme is capable of withstanding all kinds of known attacks and has good performance. However, their scheme has serious security weaknesses according to our cryptanalysis. The scheme is vulnerable to insider attack and DoS attack. For overcoming these weaknesses, we present an improved authentication and key agreement scheme for IoT-based cloud computing environment. The automated security verification (ProVerif), BAN-logic verification, and informal security analysis were performed. The results show that our proposed scheme is secure and can effectively resist all kinds of known attacks. Furthermore, compared with the original scheme in terms of security features and performance, our proposed scheme is feasible.

1. Introduction

Internet of things (IoT) takes advantage of massive sensors, intelligent terminals, global positioning system, and other technologies to establish connections between people and things whenever and wherever, and realize intelligent control and management [1]. For example, users can use smartphones to remotely control lamps, TVs, and refrigerators at home through the Internet of things. Internet of things makes people’s lives more convenient, and also makes the social economy develop faster. However, limited by the low power and computation ability of embedded devices, applying the IoT in the real applications is still a critical issue. To settle the matter, researchers apply cloud computing to the Internet of things.

Cloud computing makes plentiful computing and storage resources accessible to all of the servers and users through the Internet. A cloud server has more resources and more powerful computation ability. Cooperating with the cloud server, IoT devices can provide a better quality of services for users [2]. In a typical scenario of the IoT-based cloud computing environment as shown in Figure 1, IoT devices and sensors submit the IoT-releated data they collected to a cloud server via a wired/wireless network. Users can access the cloud servers to get the IoT-releated data from anywhere at any time. Furthermore, Users can send commands to the IoT devices through the cloud server for productive remote control. The IoT-based cloud computing environment combines the advantages of IoT and cloud computing, making the Internet of things more efficient and practical.

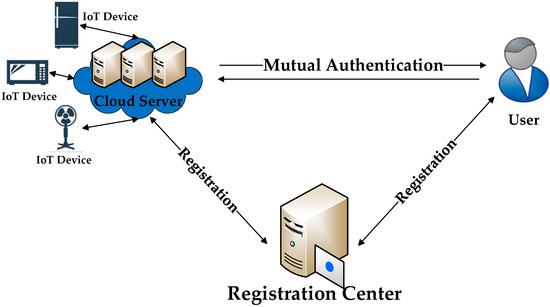
Figure 1. Proposed model of an IoT-based cloud computing environment.

As the cloud servers provide IoT services for users over an insecure public channel, the communications between users and cloud servers must be confidential [3]. It is essential to authenticate each other in an IoT-based cloud computing environment. Only authorized users can access the cloud server to obtain the services of IoT devices. Figure 1 shows the assumed architecture for an IoT-based cloud computing environment. As a trusted third party, the registration center (RC) provides registration services for users and cloud servers. After that, users and cloud servers establish secure communication through mutual authentication.

Authentication and key agreement protocols are playing a crucial part in the security of an IoT-based cloud computing environment. Since the first authentication scheme was put forward by Lamport in 1980 [4], the research on the authentication protocol has not stopped. Numerous schemes were proposed based on different cryptography technologies. Generally, the scheme using symmetric key cryptography [5,6,7,8,9,10,11,12,13,14] has better performance while it cannot achieve forward security. For the scheme using asymmetric cryptography [15,16,17,18,19,20,21,22,23], the balance between security and performance is a crucial problem.

In 2016, He et al. presented an anonymous authentication protocol [24], which is based on asymmetric cryptography. They declared that their scheme is capable of withstanding various known attacks and has good performance. However, we found that their scheme is vulnerable to DoS attack and insider attack under our proposed adversary model.

Contributions

The main contributions of this article include: (1) we propose a new adversary model in Section 2.3. (2) In Section 4, we show that He et al.’s scheme is unable to defend against insider attack and DoS attack under our proposed adversary model. (3) In Section 5, we present an improved authentication and key agreement scheme for the IoT-based cloud computing environment. The proposed scheme modifies the registration and authentication phases, uses ‘fuzzy verifier’, and adds the validation in the side of cloud servers, so as to effectively resist insider attack and DoS attack. (4) It is proven that our proposed scheme is secure via an automated security verification tool ProVerif [25] in Section 6.1. Meanwhile, we present the proofs of BAN logic [26] verification in Section 6.2. Furthermore, informal security analysis is put forward in Section 6.3. (5) In Section 7, we compare the proposed scheme with He et al.’s scheme in terms of security features and performance.

2. Preliminaries

2.1. Bilinear Pairing

Let $G_1$ be a cyclic additive group with a large prime order $q$ and $G_2$ a cyclic multiplicative group of the same order $q$. Let $P$ and $g$ be generators of $G_1$ and $G_2$ separately. A bilinear pairing is a map ${e: G}_1{\times G}_1 \to { G}_2$ and satisfies the following properties:

(1) Bilinear: Give $e (a·P,b·{Q) = e(P, Q)}^{ab}$ for all $P, Q \in { G}_1, a, b \in { Z}_q^{*}$.

(2) Non-degenerate: There exists $P, Q \in { G}_1$ such that $e (P, Q) \ne 1$.

(3) Computable: There exists an efficient algorithm to calculate $e (P, Q)$ for all $P, Q \in { G}_1$ in polynomial time.

2.2. Related Mathematical Problems

The mathematical problems for designing authentication protocols are as follows.

2.2.1. Discrete Logarithm Problem

Given $X = \tau ·{P (x = g}^{\tau })$, where $X \in { G}_1(x \in { G}_2)$, it is relatively easy to calculate $X\left(x\right)$ given τ and P ($\tau$ and g), while it is relatively hard to determine $\tau$ given X and P (x and g).

2.2.2. Computational Diffie–Hellman Problem

For $a,b \in { Z}_q^{*}$, given $a·P,b·P\in G_1{(g}^a{,g}^b\in G_2)$, it is hard to find $(a·b)·P \in { G}_1{(g}^{ab} \in { G}_2)$.

2.3. Adversary Model

The adversary model makes clear assumptions about the adversary’s ability in advance. The adversary model of remote authentication protocol always follows the classic Dolev–Yao model [27]. Recently, Side-channel technology [28] enables attackers to extract information from smart cards, and the ability of the adversary is enhanced. In this paper, we improve the adversary models in literature [29] and literature [30], and propose a more rigorous (but practical) multi-factor authentication protocol adversary model (see Table 1).

Table 1. The capabilities of adversaries.

Symbol	Description
$\mathrm{Capability} 1$.	The adversary can enumerate all elements of $|D_{ID}|\ast |D_{PW}|$ offline.
$\mathrm{Capability} 2$.	The adversary can obtain user ID (The user ID should be assumed to be sensitive information when evaluating the anonymity of the protocol).
$\mathrm{Capability} 3$.	The adversary can eavesdrop, intercept, insert, delete, or block messages flowing through the public channel.
$\mathrm{Capability} 4$.	For the n-factor protocol, the adversary can obtain n-1 of the n authentication factors simultaneously.
$\mathrm{Capability} 5$.	The adversary has a chance to capture an expired session key.
$\mathrm{Capability} 6$.	The adversary can obtain the long-term private keys of participants. (when evaluating forward secrecy).
$\mathrm{Capability} 7$.	An insider adversary can obtain user’s registration information and capture user’s smartcard (when evaluating insider attack).

In real life, when someone finds the lost smart card and the owner cannot be found, usually, the person who finds the smart card will give it to the insider to find the owner. Therefore, it is possible for insiders to obtain users’ smart cards. Meanwhile, the insiders have the opportunity to obtain the user’s registration information. Thus,$\mathrm{Capability} 7$ is realistic.

3. Review of He et al.’s Scheme

This section briefly reviews the authentication scheme proposed by He et al. There are the following phases in their scheme. Table 2 shows the notations used herein.

Table 2. Notations.

Symbol	Description	Symbol	Description
$RC$	Registration Center	$U_i$	User
$\tau ,\hat{\tau }$	Private key of $RC$	${ID}_{U_i}$	Identification of $U_i$
$P$	Large prime	${PW}_{U_i}$	Password of $U_i$
$q$	prime order	${SC}_{U_i}$	Smart card of $U_i$
$G_1$	Additive group	$S_j$	Cloud Server
$G_2$	Multiplicative group	${ID}_{S_j}$	Identification of $S_j$
$g_{pub},P_{pub}$	Public key of $RC$	$D_{S_j}$	Private key of $S_j$
$e(*,*)$	Bilinear pairing	$⨁$	XOR operation
$h_0{-h}_6$	Hash function	${sk}_{U_i},{sk}_{S_j}$	Session key of $U_i$ and $S_j$

3.1. Setup Phase

RC selects $G_1,G_2, e(*,*)$ and chooses his private keys $\tau ,\hat{\tau }\in { Z}_q^{*}$. Then, it calculates $g = e(P,P)$, $g_{pub}{ = g}^{\tau }$, $P_{pub}=\hat{\tau }·P$ as public keys. Furthermore, RC selects seven secure hash functions $\left\{h_i\right\}, i = 0–6$ and publishes all public parameters.

3.2. User Registration Phase

1.

$U_i$ chooses ${ID}_{U_i}$, ${PW}_{U_i},$ and a random number $b_{U_i}$ freely. Then, $U_i$ computers $h_{0 }{(\mathrm{ID}}_{U_i}{, PW}_{U_i}{, b}_{U_i})$. Finally, $U_i$ sends the registration message ${\{ID}_{U_i}{, h}_0{ (ID}_{U_i}{, PW}_{U_i}{, b}_{U_i}\left)\right\}$ towards RC.

2.

RC selects ${\omega }_{U_i} \in { Z}_q^{*}$ freely and computes $g_{U_i}{ = g}^{{\omega }_{U_i}}$, ${\xi }_{U_i}{ = h}_1\left({ID}_{U_i}{, g}_{U_i}\right)$, ${\tau }_{U_i}{ = \omega }_{U_i} + \tau ·{\xi }_{U_i}$, ${\phi }_{U_i}{ = \tau }_{U_i}⨁h_{0 }{(ID}_{U_i}{, PW}_{U_i}{, b}_{U_i})$, ${\vartheta }_{U_i}{ = h}_0{(h}_0\left({ID}_{U_i}{, PW}_{U_i}{, b}_{U_i}\right){, \phi }_{U_i})$. Then, RC transmits ${\{g}_{U_i}{, \phi }_{U_i}, {\vartheta }_{U_i}\}$ towards $U_i$.

3.

$U_i$ writes ${\{g}_{U_i}{,\phi }_{U_i},{\vartheta }_{U_i}{,b}_{U_i}\}$ into ${SC}_{U_i}$.

3.3. Cloud Server Registration Phase

1.

$S_j$ transmits ${ID}_{S_j}$ to RC.

2.

RC calculates $D_{S_j}=\frac{1}{\hat{\tau }+h_2\left({ID}_{S_j}\right)}$ and responses $\left\{D_{S_j}\right\}$ to $S_j$ via a private channel.

3.

$S_j$ receives and stores $D_{S_j}$ safely.

3.4. Login and Authentication Phase

1.

$U_i$ inserts ${SC}_{U_i}$ to a reader, and inputs ${ID}_{U_i}$ and ${PW}_{U_i}$. ${SC}_{U_i}$ verifies the equality check for ${\vartheta }_{U_i}{? = h}_{0 }{(h}_0 \left({ID}_{U_i}{, PW}_{U_i}{, b}_{U_i}\right){, \phi }_{U_i})$. If it holds true, ${SC}_{U_i}$ ensures that ${ID}_{U_i}$ and ${PW}_{U_i}$ are correct. Then, ${SC}_{U_i}$ randomly generates a number $r_{U_i} \in { Z}_q^{*}$ and calculates $R_{U_i}{ = r}_{U_i}·{(P}_{pub}{ + h}_{2 }{(ID}_{S_j})·P)$, ${x = g}^{r_{U_i}}$. Finally, $U_i$ transmits a login request $\left\{R_{U_i}\right\}$ towards $S_j$.

2.

$S_j$ receives $R_{U_i}$ and calculates ${x = e (R}_{U_i}{, D}_{S_j})$. Then, $S_j$ randomly chooses a number $r_{S_j} \in { Z}_q^{*}$ and calculates ${y = g}^{r_{S_j}}$, ${\alpha }_{S_j}{ = h}_3{(R}_{U_i},x,y)$. Finally, $S_j$ responds $\{y, {\alpha }_{S_j}\}$ towards $U_i$.

3.

$U_i$ receives ${\{y, \alpha }_{S_j}\}$ and checks the equality for ${\alpha }_{S_j}{? = h}_3{ (R}_{U_i}, x, y)$. If ${\alpha }_{S_j}\ne h_3{ (R}_{U_i}, x, y)$, $U_i$ terminates the session. Otherwise, $U_i$ calculates ${\theta }_{U_i}{ = h}_{4 }{(ID}_{U_i}{, R}_{U_i}, x, y)$, ${\tau }_{U_i}{ = \phi }_{U_i}⨁h_0{(ID}_{U_i}{,PW}_{U_i}{,b}_{U_i})$, ${\alpha }_{U_i}{ = \tau }_{U_i}{+\theta }_{U_i}·r_{U_i}$, the session key ${sk}_{U_i}{ = h}_5{ (ID}_{U_i}{, ID}_{S_j}{, x, y, y}^{r_{U_i}}),$ and $C_{U_i}{ = h}_6\left(x\right)⨁{(ID}_{U_i}{, g}_{U_i}{, \alpha }_{U_i})$. Finally, $U_i$ transmits $C_{U_i}$ towards cloud server $S_j$.

4.

$S_j$ receives $C_{U_i}$ and recovers ${ID}_{U_i}$, $g_{U_i}$, ${\alpha }_{U_i}$ via computing ${(ID}_{U_i}{, g}_{U_i}{, \alpha }_{U_i}{) = h}_6\left(x\right)⨁C_{U_i}$. Furthermore, $S_j$ calculates ${\xi }_{U_i}{ = h}_1{(ID}_{U_i}{, g}_{U_i})$, ${\theta }_{U_i}{ = h}_4{(ID}_{U_i}{, R}_{U_i}, x, y)$ and checks the equality for $g^{{\alpha }_{U_i}}{? = g}_{U_i}·g_{pub}^{{\xi }_{U_i}}·x^{{\theta }_{U_i}}$. If it holds true, $S_j$ gets the session key ${sk}_{S_j}{ = h}_5{ (ID}_{U_i}{, ID}_{S_j}{, x, y, x}^{r_{S_j}})$.

3.5. Password Modification Phase

1.

$U_i$ inputs ${ID}_{U_i}$, ${PW}_{U_i}$. ${SC}_{U_i}$ checks the equality ${\vartheta }_{U_i}{? = h}_0{(h}_0 \left({ID}_{U_i}{, PW}_{U_i}{, b}_{U_i}\right){, \phi }_{U_i})$.

2.

If ${\vartheta }_{U_i}\ne h_0{(h}_0 \left({ID}_{U_i}{, PW}_{U_i}{, b}_{U_i}\right){, \phi }_{U_i})$, ${SC}_{U_i}$ rejects the modification request. Otherwise, $U_i$ inputs ${PW}_{U_i}^{*}$. ${SC}_{U_i}$ chooses a new random number $b_{U_i}^{*}$, calculates ${\phi }_{U_i}^{*}{ = \phi }_{U_i}⨁h_{0 }{(ID}_{U_i}{, PW}_{U_i}{, b}_{U_i})⨁h_0{(ID}_{U_i}{, PW}_{U_i}^{*}{, b}_{U_i}^{*})$, ${\vartheta }_{U_i}^{*}{ = h}_{0 }{(h}_0 \left({ID}_{U_i}{, PW}_{U_i}^{*}{, b}_{U_i}^{*}\right){, \phi }_{U_i}^{*})$. Finally, SC replaces ${\{g}_{U_i}{, \phi }_{U_i}, {\vartheta }_{U_i}{, b}_{U_i}\}$ with $\{g_{U_i},{ \phi }_{U_i}^{*}, {\vartheta }_{U_i}^{*}, b_{U_i}^{*}\}$ and the new password is ${PW}_{U_i}^{*}$.

4. Cryptanalysis of He et al.’s Scheme

4.1. Insider Attack

In our proposed adversary model, an insider adversary is able to acquire the user’s registration information and smart card. Suppose an insider adversary $A$ acquires the registration information ${\{ID}_{U_i}{,h}_0{(ID}_{U_i}{,PW}_{U_i}{,b}_{U_i}\left)\right\}$ of $U_i$. Furthermore, $A$ gets $U_i$’s smart card and extracts the values $g_{U_i}$, ${\phi }_{U_i}$, ${\vartheta }_{U_i}$ and $b_{U_i}$. Using this information, $A$ can launch the following attacks through the following procedure.

4.1.1. Offline Password Guessing

Suppose an insider being an adversary $A$ knows the registration information ${\{ID}_{U_i}{,h}_0{(ID}_{U_i}{,PW}_{U_i}{,b}_{U_i}\left)\right\}$ of $U_i$. Furthermore, $A$ gets $U_i$’s smart card and extracts the values $g_{U_i}$, ${\phi }_{U_i}$, ${\vartheta }_{U_i}$ and $b_{U_i}$. Using this information, $A$ is able to launch an offline password guessing attack through following these steps:

1.

$A$ guesses a candidate password ${PW}_i^{*}$.

2.

$A$ calculates ${x = h}_0\left({ID}_{U_i}{,PW}_i^{*}{,b}_{U_i}\right)$.

3.

$A$ checks whether ${x? = h}_0\left({ID}_{U_i}{,PW}_{U_i}{,b}_{U_i}\right)$ holds. If not, $A$ repeats Steps 1–3 until he acquires a true password. Otherwise, $A$ has already succeeded in getting the true password. The attack is finished.

The computational overhead of this offline password attack is $T_h*|D_{id}|*|D_{pw}|$, where $T_h$ is the running time of one-way hash function, and $D_{iD}$ and $D_{pw}$ are the spaces of user identity and password, respectively. According to [31,32], we have $|D_{iD}|\le |D_{pw}|\le {10}^6$. According to experiment data in [33], we have $T_h\approx 0.591\mu s$. The adversary can obtain the true password in seven days. If using a high-performance cloud computing platform, the attack can be completed in a few hours.

4.1.2. User Impersonation

1.

$A$ randomly generates a number $r_{U_i} \in { Z}_q^{*}$ and calculates $R_{U_i}{ = r}_{U_i}·{(P}_{pub}{+h}_2{(ID}_{S_j})·P)$, ${x = g}^{r_{U_i}}$. Afterwards, $A$ transmits the request $R_{U_i}$ to server $S_j$.

2.

Upon receiving ${\{y,\alpha }_{S_j}\}$ from $S_j$, $A$ computes ${\theta }_{U_i}{ = h}_4{(ID}_{U_i}{,R}_{U_i},x,y)$, ${\tau }_{U_i}{ = \phi }_{U_i}⨁h_0{(ID}_{U_i}{,PW}_{U_i}{,b}_{U_i})$, where ${\phi }_{U_i}$ and $h_0{(ID}_{U_i}{,PW}_{U_i}{,b}_{U_i})$ were obtained before. Subsequently, $A$ calculates ${\alpha }_{U_i}{ = \tau }_{U_i}{+\theta }_{U_i}·r_{U_i}$, and gets the session key ${sk}_{U_i}{ = h}_5{(ID}_{U_i}{,ID}_{S_j}{,x,y,y}^{r_{U_i}})$. Finally, $A$ sends $C_{U_i}{ = h}_6\left(x\right)⨁{(ID}_{U_i}{,g}_{U_i}{,\alpha }_{U_i})$ to $S_j$.

The information generated by $A$ is legal. The cloud server $S_j$ considers $A$ as the user $U_i$.

4.2. Possible DoS Attack

In the authentication phase, $S_j$ doesn’t validate the login request information until formula $g^{{\alpha }_{U_i}}{? = g}_{U_i}·g_{pub}^{{\xi }_{U_i}}·x^{{\theta }_{U_i}}$ is validated. Even if the adversary sends illegal information, the cloud server still responds and completes the relevant calculations. This results in unnecessary communication costs and time costs and leads a possible DoS attack.

5. Our Improved Scheme

For overcoming the weaknesses above, we put forward an enhanced authentication and key agreement protocol. Figure 2 depicts our proposed scheme.

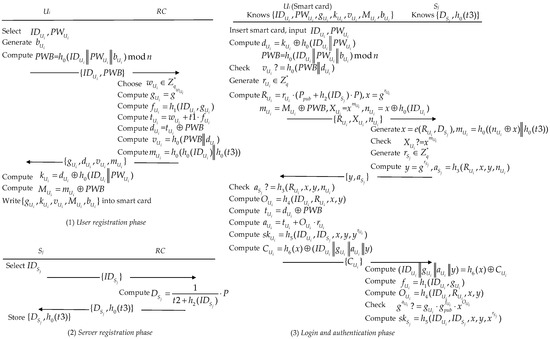
Figure 2. The conceptual architecture of our proposed protocol.

5.1. Setup Phase

RC selects $G_1,G_2, e(*,*)$ and chooses his private keys ${ t}_1{,t}_2{,t}_3 \in { Z}_q^{*}$. Then, RC calculates $g = e(P,P)$, $g_{pub}{ = g}^{t_1}$, $P_{pub}{ = t}_2·P$ as public keys. Furthermore, RC selects seven secure hash functions $\left\{h_i\right\},i = 0–6$. Finally, RC publishes all public parameters $\{\left(h_i\right), {i = 0–6,G}_1{, G}_2{, e, q, P, g, P}_{pub}\}$.

5.2. User Registration Phase

1.

$U_i$ chooses ${ID}_{U_i}$, ${PW}_{U_i}$ and a number $b_{U_i}$ freely. Then, $U_i$ computers ${PWB = h}_0{(ID}_{U_i}{||PW}_{U_i}||b_{U_i}{)mod n, 2}^4\le n \le 2^6$. Note that $n$ is an integer that determines the capacity of $(ID, PW)$. Then, it transmits the registration message ${\{ID}_{U_i},PWB\}$ towards RC.

2.

RC selects $w_{U_i} \in { Z}_q^{*}$ freely and computes $g_{U_i}{ = g}^{w_{U_i}}$, $f_{U_i}{ = h}_1\left({ID}_{U_i}{,g}_{U_i}\right)$, $t_{U_i}{ = w}_{U_i}{+t}_1·f_{U_i}$, $d_{U_i}{ = t}_{U_i}⨁PWB$, $v_{U_i}{ = h}_0{(PWB||d}_{U_i})mod n$, $m_{U_i}{ = h}_0{(h}_0{(ID}_{U_i}{)||h}_0{(t}_3\left)\right)$. Then, RC responses ${\{g}_{U_i}{,d}_{U_i}{,v}_{U_i}{,m}_{U_i}\}$ to $U_i$ via a private secure channel.

3.

$U_i$ receives ${\{g}_{U_i}{,d}_{U_i}{,v}_{U_i}\}$ and computes $k_{U_i}{ = d}_{U_i}⨁h_0{(ID}_{U_i}{,PW}_{U_i})$, $M_{U_i}{ = m}_{U_i}⨁PWB$. Finally, $U_i$ writes ${\{g}_{U_i}{,k}_{U_i}{,v}_{U_i}{,M}_{U_i}{,b}_{U_i}\}$ into ${SC}_{U_i}$.

5.3. Cloud Server Registration Phase

1.

$S_j$ sends ${ID}_{S_j}$ to RC.

2.

Upon reception of ${ID}_{S_j}$, RC calculates $D_{S_j} = \frac{1}{t_2+h_2{(ID}_{S_j})}·P$ and sends ${\{D}_{S_j}{, h}_0{ (t}_3\left)\right\}$ to $S_j$ via a private channel.

3.

$S_j$ stores ${\{D}_{S_j}{, h}_0{ (t}_3\left)\right\}$ in secret.

5.4. Login and Authentication Phase

1.

$U_i$ inserts ${SC}_{U_i}$ to the reader and inputs ${ID}_{U_i}$ and ${PW}_{U_i}$. ${SC}_{U_i}$ calculates $d_{U_i}{ = k}_{U_i}⨁h_0{(ID}_{U_i}{||PW}_{U_i})$, ${PWB = h}_0{(ID}_{U_i}{||PW}_{U_i}{||b}_{U_i})mod n$ and verifies the equality check for $v_{U_i}{? = h}_0{(PWB||d}_{U_i})mod n$. If $v_{U_i} \ne { h}_0{(PWB||d}_{U_i})mod n$, ${SC}_{U_i}$ rejects the login request. Otherwise, it randomly chooses $r_{U_i} \in { Z}_q^{*}$ and calculates $R_{U_i}{ = r}_{U_i}·{(P}_{pub}{+h}_2{(ID}_{S_j})·P)$, ${x = g}^{r_{U_i}}$, $m_{U_i}{ = M}_{U_i}⨁PWB$, $X_{U_i}{ = x}^{m_{U_i}}$, $n_{U_i} = x·h_0{(ID}_{U_i})$. Finally, $U_i$ transmits login request ${\{R}_{U_i}{,X}_{U_i}{,n}_{U_i}\}$ towards $S_j$.

2.

$S_j$ receives ${\{R}_{U_i}{,X}_{U_i}{,n}_{U_i}\}$ and calculates ${x = e(R}_{U_i}{,D}_{S_j})$, $m_{U_i}{ = h}_0{\left(\right(n}_{U_i}⨁{x)||h}_0{(t}_3\left)\right)$. Then, $S_j$ verifies the equality check $X_{U_i}{? = x}^{m_{U_i}}$. If $X_{U_i}\ne x^{m_{U_i}}$, $S_j$ terminates the session. Otherwise, $S_j$ randomly selects $r_{S_j} \in { Z}_q^{*}$ and calculates ${y = g}^{r_{S_j}}$, $a_{S_j}{ = h}_{3 }{(R}_{U_i}{, x, y, n}_{U_i})$. Finally, $S_j$ transmits ${\{y, a}_{S_j}\}$ towards $U_i$.

3.

Upon reception of ${\{y,a}_{S_j}\}$ from $S_j$, $U_i$ verifies the equality check $a_{S_j}{? = h}_3{(R}_{U_i}{, x, y, n}_{U_i})$. If $a_{S_j} \ne { h}_3{(R}_{U_i}{, x, y, n}_{U_i})$, $U_i$ terminates the session. Otherwise, $U_i$ calculates $O_{U_i}{ = h}_4{ (ID}_{U_i}{, R}_{U_i}, x, y)$, $t_{U_i}{ = d}_{U_i}⨁PWB$, $a_{U_i}{ = t}_{U_i}{+O}_{U_i}·r_{U_i}$, the session key ${sk}_{U_i}{ = h}_{5 }{(ID}_{U_i}{,ID}_{S_j}{, x, y, y}^{r_{U_i}})$ and $C_{U_i}{ = h}_{6 }\left(x\right)⨁{(ID}_{U_i}{||g}_{U_i}{||a}_{U_i}||y)$. Finally, $U_i$ transmits $C_{U_i}$ towards $S_j$.

4.

$S_j$ receives $C_{U_i}$ and recovers ${ID}_{U_i}$, $g_{U_i}$ and $a_{U_i}$ via computing ${(ID}_{U_i}{||g}_{U_i}{||a}_{U_i}{||y) = h}_6 \left(x\right)⨁C_{U_i}$. Furthermore, $S_j$ calculates $f_{U_i}{ = h}_{1 }{(ID}_{U_i}{, g}_{U_i})$, $O_{U_i}{ = h}_4{ (ID}_{U_i}{, R}_{U_i}, x, y)$ and checks the equality for $g^{a_{U_i}}{? = g}_{U_i}·g_{pub}^{f_{U_i}}·x^{O_{U_i}}$. If it holds true, $S_j$ gets the session key ${sk}_{S_j}{ = h}_{5 }{(ID}_{U_i}{, ID}_{S_j}{, x, y, x}^{r_{S_j}})$.

5.5. Password Modification Phase

1.

$U_i$ inputs ${ID}_{U_i}$, ${PW}_{U_i}$. ${SC}_{U_i}$ computes $d_{U_i}{ = k}_{U_i}⨁h_0{(ID}_{U_i}{||PW}_{U_i})$, ${PWB = h}_0{(ID}_{U_i}{||PW}_{U_i}{||b}_{U_i})mod n$ and checks the equality $v_{U_i}{? = h}_0{(PWB||d}_{U_i})mod n$.

2.

If $v_{U_i}\ne h_0{(PWB||d}_{U_i})mod n$, ${SC}_{U_i}$ rejects the request. Otherwise, $U_i$ inputs ${PW}_{U_i}^{new}$. ${SC}_{U_i}$ randomly generates $b_{U_i}^{*}$ and calculates $k_{U_i}^{new}{ = k}_{U_i}⨁h_0{(ID}_{U_i}{||PW}_{U_i})⨁h_0{(ID}_{U_i}{||PW}_{U_i}{||b}_{U_i})⨁h_0{(ID}_{U_i}{||PW}_{U_i}^{new}{||b}_{U_i}^{new})⨁h_0{(ID}_{U_i}{||PW}_{U_i}^{new})$, $v_{U_i}^{new}{ = h}_0{(h}_0\left({ID}_{U_i}{||PW}_{U_i}^{new}{||b}_{U_i}^{new}\right){,k}_{U_i}^{new}⨁h_0{(ID}_{U_i}{||PW}_{U_i}^{new}\left)\right)$. Finally, ${SC}_{U_i}$ replaces ${\{g}_{U_i}{, k}_{U_i}{, v}_{U_i}{, b}_{U_i}\}$ with ${\{g}_{U_i}{, k}_{U_i}^{new}{, v}_{U_i}^{new}{, b}_{U_i}^{new}\}$.

6. Security Analysis

6.1. Security Verification Using ProVerif

ProVerif [25] is one of the most widely used automated security verification tools. The security validation of ProVerif works on applied π calculus, and ProVerif can verify the authentication and confidentiality of authentication protocol. We elaborate the design process and results of security validation using ProVerif in this section.

First, we define two channels for communication between participants, an insecure channel Pch and a secure channel SEch.

(*--Channels--*)

free SEch:channel [private]. (* Secure Channel *)

free Pch:channel. (*Insecure Channel *)

Then, public and private parameters and constructors are defined as follows:

(*----------------Variable and constants---------------------*)

const P: bitstring.

const g: bitstring.

const q: bitstring.

const n: bitstring.

free Uid: bitstring. (* User ID *)

free PWi: bitstring [private]. (* Password of user *)

free bUi:bitstring. (* Random number of user in registration phase *)

free Sid: bitstring. (* Server ID *)

free t1, t2, t3: bitstring [private]. (* Private key of RC *)

free Ppub: bitstring. (* Ppub = t2. P *)

free gpub: bitstring. (* gpub = Exp (g, t1) *)

(*----------------Constructor---------------------*)

fun CONCAT (bitstring, bitstring): bitstring. (* CONCAT operation *)

fun Div1 (bitstring): bitstring. (* Division operation and get the first part *)

fun Div2 (bitstring): bitstring. (* Division operation and get the second part *)

fun h0 (bitstring): bitstring. (* Hash operation h0 *)

fun h1 (bitstring,bitstring): bitstring. (* Hash operation h1 *)

fun h2 (bitstring): bitstring. (* Hash operation h2 *)

fun h3 (bitstring,bitstring,bitstring,bitstring):bitstring. (* Hash operation h3 *)

fun h4 (bitstring,bitstring,bitstring,bitstring):bitstring. (* Hash operation h4 *)

fun h5 (bitstring,bitstring,bitstring,bitstring,bitstring): bitstring. (* Hash operation h5 *)

fun h6 (bitstring): bitstring. (* Hash operation h6 *)

fun Xor (bitstring, bitstring): bitstring. (* XOR operation *)

fun Smul (bitstring, bitstring): bitstring. (* Scalar multiplication operation *)

fun Padd (bitstring, bitstring): bitstring. (* Point addition operation *)

fun BPL (bitstring, bitstring): bitstring. (* Bilinear paring operation *)

fun Exp (bitstring, bitstring): bitstring. (* Exponentiation operation *)

fun Mod (bitstring, bitstring): bitstring. (* Mod operation *)

fun Mul (bitstring, bitstring): bitstring. (* multiplication operation *)

fun Add (bitstring, bitstring): bitstring. (* Addition operation *)

fun Inverse (bitstring): bitstring. (* inverse operation *)

The following four events are specified to check authentication between the user and server:

(*----------------Events---------------------*)

event beginUserUi (bitstring).

event endUserUi (bitstring).

event beginServerSj (bitstring).

event endServerSj (bitstring).

The processes UserUi, ServerSj, and RC represent $U_i$, $S_j$ and RC, respectively.

(*----------------Processes---------------------*)

(*----------------User Ui---------------------*)

let UserUi =

(* Registration Phase *)

let PWB = Mod (h0 (CONCAT (CONCAT (Uid, PWi), bUi)), n) in

out (SEch, (Uid, PWB));

in (SEch, (gUi: bitstring, dUi:bitstring, vUi:bitstring, mUi:bitstring));

let kUi = Xor (dUi, h0(CONCAT (Uid, PWi))) in

let MUi = Xor (mUi, PWB) in

(*Login and Authentication Phase *)

event beginUserUi (Uid);

let PWB = Mod (h0 (CONCAT (CONCAT (Uid, PWi), bUi)), n) in

let dUi = Xor (kUi, h0 (CONCAT (Uid, PWi))) in

let vUi’ = h0 (CONCAT (PWB, dUi)) in

if vUi’ = vUi then

new rUi:bitstring;

let RUi = Smul (rUi, Padd (Ppub, Smul (h2 (Sid), P))) in

let x = Exp (g, rUi) in

let mUi = Xor (MUi, PWB) in

let XUi = Exp (x, mUi) in

let nUi = Xor (x, h0 (Uid)) in

out (Pch, (RUi, XUi, nUi));

in (Pch, (y:bitstring, aSj:bitstring ));

let aSj’ = h3 (RUi, x, y, nUi) in

if (aSj = aSj’) then

let oUi = h4 (Uid,RUi, x, y) in

let tUi = Xor (dUi, PWB) in

let aUi = Add (tUi, Mul (oUi, rUi)) in

let SKij = h5 (Uid,Sid, x, y, Exp (y, rUi)) in

let CUi = Xor (h6 (x), CONCAT (CONCAT (CONCAT (Uid, gUi), aUi), y)) in

out (Pch, CUi);

event endUserUi (Uid)

else

0.

(*----------------Server Sj---------------------*)

let ServerSj =

(* Registration Phase *)

out (SEch, Sid);

in (SEch, (DSj: bitstring, ht3: bitstring));

(* Login and Authentication Phase *)

event beginServerSj (Sid);

in (Pch, (RUi: bitstring, XUi:bitstring, nUi:bitstring));

let x = BPL (RUi, DSj) in

let mUi = h0 (CONCAT (Xor (nUi, x), ht3)) in

let XUi’ = Exp (x, mUi) in

if XUi’ = XUi then

new rSj: bitstring;

let y = Exp (g, rSj) in

let aSj = h3 (RUi, x, y, nUi) in

out (Pch, (y, aSj));

in (Pch, CUi:bitstring);

let aUi = Div2 (Div1 (Xor (h6 (x), CUi))) in

let gUi = Div2 (Div1 (Div1 (Xor (h6 (x), CUi)))) in

let Uid = Div1 (Div1 (Div1 (Xor (h6 (x), CUi)))) in

let fUi = h1 (Uid, gUi) in

let oUi = h4 (Uid, RUi, x, y) in

let gaUi = Exp (g, aUi) in

let gaUi’ = Mul (Mul (gUi, Exp (gpub, fUi)), Exp (x,oUi)) in

if gaUi = gaUi’ then

let SKij = h5 (Uid, Sid, x, y, Exp (x, rSj)) in

event endServerSj (Sid)

else

0.

(*----------------Registration Centre RC---------------------*)

let RC =

(* Registration with User *)

in (SEch, (Uid: bitstring, PWB: bitstring));

new wUi: bitstring;

let gUi = Exp (g, wUi) in

let fUi = h1 (Uid, gUi) in

let tUi = Add (wUi, Mul (t1, fUi)) in

let dUi = Xor (tUi, PWB) in

let vUi = Mod (h0 (CONCAT (PWB, dUi)), n) in

let mUi = h0 (CONCAT (h0 (Uid), h0(t3))) in

out (SEch, (gUi, dUi, vUi, mUi));

(*Registration with Servers*)

in (SEch, Sid: bitstring);

let DSj = Inverse (Add (t2, h2(Sid))) in

let ht3 = h0(t3) in

out (SEch, (DSj, ht3));

0.

We simulate our proposed protocol as unbounded parallel execution of the three processes mentioned:

process

((! UserUi) | (! RC) | (! ServerSj))

The following queries are used to test mutual authentication and session key security of the improved protocol.

(*-------------Queries-----------------*)

free SKij: bitstring [private].

query attacker (SKij).

query id: bitstring; inj-event (endUserUi (id)) = = > inj-event (beginUserUi (id)).

query id: bitstring; inj-event (endServerSj (id)) = = > inj-event (beginServerSj (id)).

At last, we get the simulation result:

According to RESULT 2 and RESULT 3, mutual authentication between $U_i$ and $S_j$ succeeded. Furthermore, RESULT 1 indicates that no adversary is capable of exposing the session key.

6.2. Formal Security Analysis Using BAN-Logic

Burrows–Abadi–Needham logic [26] is a modal logic based on belief, which is proposed by Burrows et al. We use BAN-logic to prove that user $U_i$ and server $S_j$ have succeeded in session key agreement. Table 3 is the BAN-logic notations and the basic BAN-logic rules are shown in Table 4.

Table 3. BAN logic notations.

Symbol	Description
$P|\equiv X$	$P$ believes $X$.
$P◁X$	$P$ sees $X$.
$P|~X$	$P$ sends $X$.
$P\Rightarrow X$	$P$ has jurisdiction over $X$.
$⋕\left(X\right)$	$X$ is fresh.
$(X,Y)$	$X$ or $Y$ is part of $(X,Y)$.
${\left(X\right)}_K$	Use key $K$ to compute $X$.
$P\stackrel{K}{\leftrightarrow }Q$	$P$ and $Q$ achieve the shared key $K$ for communication.

Table 4. Basic BAN-logic rules.

Rule	Description
Message-meaning rule	$\frac{P|\equiv (P\stackrel{K}{\leftrightarrow }Q),P◁{\left(X\right)}_K}{P|\equiv Q|~X}$
Freshness-conjuncatenation rule	$\frac{P|\equiv ⋕\left(X\right)}{P|\equiv ⋕\left(X,Y\right)}$
Nonce-verification rule	$\frac{P|\equiv ⋕\left(X\right),P|\equiv Q|~X}{P|\equiv Q|\equiv X}$
Jurisdiction rule	$\frac{P|\equiv Q|\Rightarrow X,P|\equiv Q|\equiv X}{P|\equiv X}$
Believe rule	$\frac{P|\equiv Q|\equiv \left(X,Y\right)}{P|\equiv Q|\equiv X},\frac{P|\equiv X,P|\equiv Y}{P|\equiv \left(X,Y\right)}$

6.2.1. Idealized Form

Message 1: $U_i\to S_j: R_{U_i},X_{U_i},{\left({ID}_{U_i}\right)}_{U_i\stackrel{x}{\leftrightarrow }{S}_j}$

Message 2: $S_j\to U_i:y,{\left(R_{U_i},y,n_{U_i}\right)}_{U_i\stackrel{x}{\leftrightarrow }{S}_j}$

Message 3: $U_i\to S_j:{\left({ID}_{U_i},g_{U_i},a_{U_i},y\right)}_{U_i\stackrel{x}{\leftrightarrow }{S}_j}$

6.2.2. Verification Purposes

Purpose 1: $U_i|\equiv {(U}_i\stackrel{sk}{\leftrightarrow }{S}_j)$.

Purpose 2: $U_i|\equiv S_j|\equiv {(U}_i\stackrel{sk}{\leftrightarrow }{S}_j)$.

Purpose 3: $S_j|\equiv {(U}_i\stackrel{sk}{\leftrightarrow }{S}_j)$.

Purpose 4: $S_j|\equiv U_i|\equiv {(U}_i\stackrel{sk}{\leftrightarrow }{S}_j)$.

6.2.3. Assumptions about Initial State

Assumption 1: $U_i|\equiv ⋕\left(r_{U_i}\right)$.

Assumption 2: $S_j|\equiv ⋕\left(r_{S_j}\right)$.

Assumption 3: $U_i|\equiv {(U}_i\stackrel{x}{\leftrightarrow }{S}_j)$.

Assumption 4: $S_j|\equiv {(U}_i\stackrel{x}{\leftrightarrow }{S}_j)$.

Assumption 5: $S_j|\equiv U_i|\equiv {(ID}_{S_j})$

Assumption 6: $U_i|\equiv S_j\Rightarrow {(U}_i\stackrel{Sx}{\leftrightarrow }{S}_j)$.

Assumption 7: $S_j|\equiv U_i\Rightarrow {(U}_i\stackrel{Sx}{\leftrightarrow }{S}_j)$

6.2.4. Proofs

1.

According to Message 2, we get the following: $U_i◁(y,{\left(R_{U_i}, y,n_{U_i}\right)}_{U_i\stackrel{x}{\leftrightarrow }{S}_j})$.

2.

According to Assumption 3 and the message-meaning rule, we get the following: $U_i|\equiv S_j|~(R_{U_i}, y,n_{U_i})$.

3.

Based on Assumption 1 and the freshness–conjuncatenation rule, we can prove: $U_i|\equiv ⋕\left(R_{U_i}, y,n_{U_i}\right)$.

4.

From Step 2, Step 3, and the nonce-verification rule, we obtain the following: $U_i|\equiv S_j|\equiv \left(R_{U_i}, y,n_{U_i}\right)$.

5.

According to Step 4 and believe rule, $U_i|\equiv S_j|\equiv \left({ID}_{U_i},{ID}_{S_j}, y,r_{U_i}\right)$.

6.

According to Step 5, Assumption 3 and ${sk = h}_5{ (ID}_{U_i}{, ID}_{S_j}{, x, y, y}^{r_{U_i}})$, we prove that: $U_i|\equiv S_j|\equiv {(U}_i\stackrel{sk}{\leftrightarrow }{S}_j)$ (Purpose 2).

7.

Based on Step 6, Assumption 6, and jurisdiction rule, we prove that: $U_i|\equiv {(U}_i\stackrel{sk}{\leftrightarrow }{S}_j)$ (Purpose 1).

8.

From Message 3, we get: $S_j◁ {\left({ID}_{U_i},g_{U_i},a_{U_i}, y\right)}_{U_i\stackrel{x}{\leftrightarrow }{S}_j}$.

9.

Based on Assumption 4 and the message-meaning rule, we obtain the following: $S_j|\equiv U_i|~\left({ID}_{U_i},g_{U_i},a_{U_i},y\right)$.

10.

From Assumption 2 and the freshness-conjuncatenation rule, we can obtain: $S_j|\equiv ⋕\left({ID}_{U_i},g_{U_i},a_{U_i},y\right)$.

11.

Based on Step 9, Step 10, and the nonce-verification rule, we obtain the following: $S_j|\equiv U_i|\equiv \left({ID}_{U_i},g_{U_i},a_{U_i},y\right)$.

12.

According to Assumption 5, Step 11, ${y = g}^{r_{S_j}}$, and the believe rule, we obtain the following: $S_j|\equiv U_i|\equiv \left({ID}_{U_i},{ID}_{S_j},r_{S_j}, y\right)$.

13.

According to Step 12, Assumption 4, and ${sk = h}_5{ (ID}_{U_i}{, ID}_{S_j}{, x, y, x}^{r_{S_j}})$, we prove that: $S_j|\equiv U_i|\equiv {(U}_i\stackrel{sk}{\leftrightarrow }{S}_j)$ (Purpose 4).

14.

According to Step 13, Assumption 7, and jurisdiction rule, we prove that: $S_j|\equiv {(U}_i\stackrel{sk}{\leftrightarrow }{S}_j)$ (Purpose 3).

From Purposes 1–4, $U_i$ and $S_j$ believe that the session key has been established between them successfully.

6.3. Informal Security Analysis

6.3.1. Anonymity and Untraceability

In authentication phase, the adversary can intercept the login request information from users and the response information from cloud servers. The constructions of $C_{U_i}$, $X_{U_i}$ and $n_{U_i}$ are related to ${ID}_{U_i}$, $C_{U_i}{ = h}_6\left(x\right)⨁{(ID}_{U_i}{||g}_{U_i}{||a}_{U_i}||y)$, $X_{U_i}{ = x}^{m_{U_i}}$, $n_{U_i} = x ⨁{ h}_{0 }{(ID}_{U_i})$. Obviously, under the protection of shared secret $x$ and hash function, the adversary is unable to obtain ${ID}_{U_i}$. On the other hand, the generation of $x$ is affected by random number $r_{U_i}$, so the parameters $C_{U_i}$, $X_{U_i}$ and $n_{U_i}$ generated by $U_i$ in each session changes. Even if an adversary intercepts $\left\{C_{U_i},X_{U_i},n_{U_i}\right\}$ and other information, he can’t judge whether two sessions come from the same user, and can’t track the user’s access behavior effectively.

6.3.2. Forward Secrecy

Suppose the adversary captured the private keys $t1, t2, t3$ and intercepts ${(R}_{U_i}{, X}_{U_i}{, n}_{U_i}{, y, a}_{S_j}, C_{U_i})$ propagated in the public channel. The adversary can calculate $x$ through the private key, but he can’t calculate $y^{r_{U_i}}$ and $x^{r_{S_j}}$ in polynomial time, so the adversary is unable to capture session key ${sk}_{U_i}{ = h}_{5 }{(ID}_{U_i}{, ID}_{S_j}{, x, y, y}^{r_{U_i}}) {= h}_5{ (ID}_{U_i}{, ID}_{S_j}{, x, y, x}^{r_{S_j}}{) = sk}_{S_j}$.

6.3.3. Two-Factor Security

It is obviously less difficult for adversary to break through the user’s password than for smart cards. In the proposed scheme, the process of ${SC}_{U_i}$ verification is a fuzzy verification process, $v_{U_i}{? = h}_0{ \left(\right(h}_0{ (ID}_{U_i}{||PW}_{U_i}{||b}_{U_i}{)\mathrm{mod} n)||(k}_{U_i}⨁h_0{ (ID}_{U_i}{||PW}_{U_i}\left)\right))\mathrm{mod} n$. Even if ${(ID}_{U_i}^{*}{, PW}_{U_i}^{*})$ guessed by the adversary has passed the verification of the smart card, it still needs to go through the online login authentication process to determine whether it is correct. Specifically, an adversary needs to log in online $|D_{id}|·|D_{pw}|/2^6$ times to get the correct password, about $2^{34}$ times, the cloud server can easily resist this attack.

6.3.4. Session Key Agreement

In the proposed scheme, $U_i$ and $S_j$ reach a session key for future communication after the login and authentication phase is completed, ${sk}_{U_i}{ = h}_5{(ID}_{U_i}{, ID}_{S_j}{, x, y, y}^{r_{U_i}}) {= h}_{5 }{(ID}_{U_i}{, ID}_{S_j}{, x, y, x}^{r_{S_j}}{) = sk}_{S_j}$.

6.3.5. Resistance of Other Attacks

Insider attack: In our proposed adversary model, an insider can acquire user’s registration information ${\{ID}_{U_i}, PWB\}$ and smart card parameter ${\{g}_{U_i}{, k}_{U_i}{, v}_{U_i}{, b}_{U_i}\}$. Since PWB is generated by modulo operation, the insider adversary cannot directly acquire ${PW}_{U_i}$ via offline password guessing. On the other hand, when the insider adversary wants to authenticate with the cloud server $S_j$ as $U_i$, he cannot compute $d_{U_i}{ = k}_{U_i}⨁h_0{(ID}_{U_i}{||PW}_{U_i})$. Therefore, no effective attack can be launched.

Cloud Server Spoofing Attack: If the adversary wants to complete authentication with user $U_i$ as cloud server $S_j$, he needs to generate legal response information; however, only when the adversary gets $D_{S_j}$ can he generate legal login request information. Therefore, the attack is unfeasible.

Replay attack: In the improved scheme, the change of random number $r_{U_i}$ and $r_{S_j}$ will affect the login request information and cloud server response information. As a result, the replay attack cannot be launched.

DoS attack: Different from He et al.’s scheme, $S_j$ verifies $U_i$’s login request before subsequent operations in the improved scheme $X_{U_i}{? = x}^{m_{U_i}}$. Only legitimate users could generate legitimate login information, so the improved scheme is capable of withstanding DoS attack.

According to the above analysis, we know that an insider adversary cannot guess the user’s password offline and impersonate a user, even if he obtains the user’s smart card and registration information. As a result, offline password guessing attack, stolen smart card attack, and user impersonation attack are unfeasible.

7. The Comparisons of Security and Performance

We compare the proposed protocol with [24] in terms of security features. The comparisons are demonstrated in Table 5.

Table 5. Comparison of security features.

Security Features and Defensible Attacks	He et al.’s	Ours
Anonymity	$\surd$	$\surd$
Un-traceability	$\surd$	$\surd$
Two-factor security	$\surd$	$\surd$
Forward Secrecy	$\surd$	$\surd$
Session key agreement	$\surd$	$\surd$
Insider attack	$⨁$	$\surd$
Cloud server spoofing attack	$\surd$	$\surd$
Replay attack	$\surd$	$\surd$
DoS attack	$⨁$	$\surd$
User impersonation attack	$\surd$	$\surd$
Offline password guessing attack	$⨁$	$\surd$
Smart card stolen attack	$\surd$	$\surd$

We compare the proposed protocol with [24] in terms of time complexity. Since RC is usually regarded as a powerful device, our efficiency analysis focuses on users and servers. For the sake of convenience, we define $T_{bp},T_{pm},T_{pa},T_{exp},T_h$ to represent time of bilinear paring operation, point scalar multiplication operation, point addition operation, exponentiation operation, and hash function respectively.

The XOR operation, concatenate operation, the modular multiplication, and modular operation are neglected while comparing with the related operation mentioned above. Based on the experiments conducted on a Quad-core 2.45G processor with 2 GB memory and an I5-4460S 2.90GHz processor with 4 GB memory in [24], we get the running time of above operations in Table 6.

Table 6. The running time of related operations based on [24].

	User	Cloud Server
$T_{pm}$	13.405 ms	2.165 ms
$T_{pa}$	0.081 ms	0.013 ms
$T_{exp}$	2.249 ms	0.339 ms
$T_h$	0.056 ms	0.007 ms
$T_{bp}$	32.713 ms	5.427 ms

All participants register with RC only once, and users do not change their passwords frequently. Therefore, the computation cost of registration phase and password modification phase is not discussed. Table 7 summarizes the results of efficiency comparison.

Table 7. Comparison of computation cost.

	He et al.’s	Ours
User	${2 \times T}_{pm}{ + T}_{pa}{ + 2 \times T}_{exp}{ + 7 \times T}_h\approx 31.781ms$	${2 \times T}_{pm}{ + T}_{pa}{ + 3 \times T}_{exp}{ + 9 \times T}_h\approx 34.142ms$
Cloud server	$T_{bp}{ + 5 \times T}_{exp }{+ 5 \times T}_h\approx 7.157ms$	$T_{bp}{ + 6 \times T}_{exp}{ + 6 \times T}_h\approx 7.503ms$

8. Conclusions

Numerous research efforts on authentication and key agreement scheme can be witnessed in recent years. In 2016, He et al. proposed an anonymous authentication protocol using asymmetric cryptography, which is looking promising. However, we discovered vulnerabilities of their scheme under our proposed adversary model. Furthermore, we propose an improved authentication and key agreement scheme for IoT-based cloud computing environment, and provide ProVerif tool verification and formal security analysis via BAN-logic. The comparisons of security and performance show that the computational cost of our proposed scheme is slightly higher but is much safer than the original scheme.