User Embedding for Rating Prediction in SVD++-Based Collaborative Filtering
Abstract
1. Introduction
2. Related Work
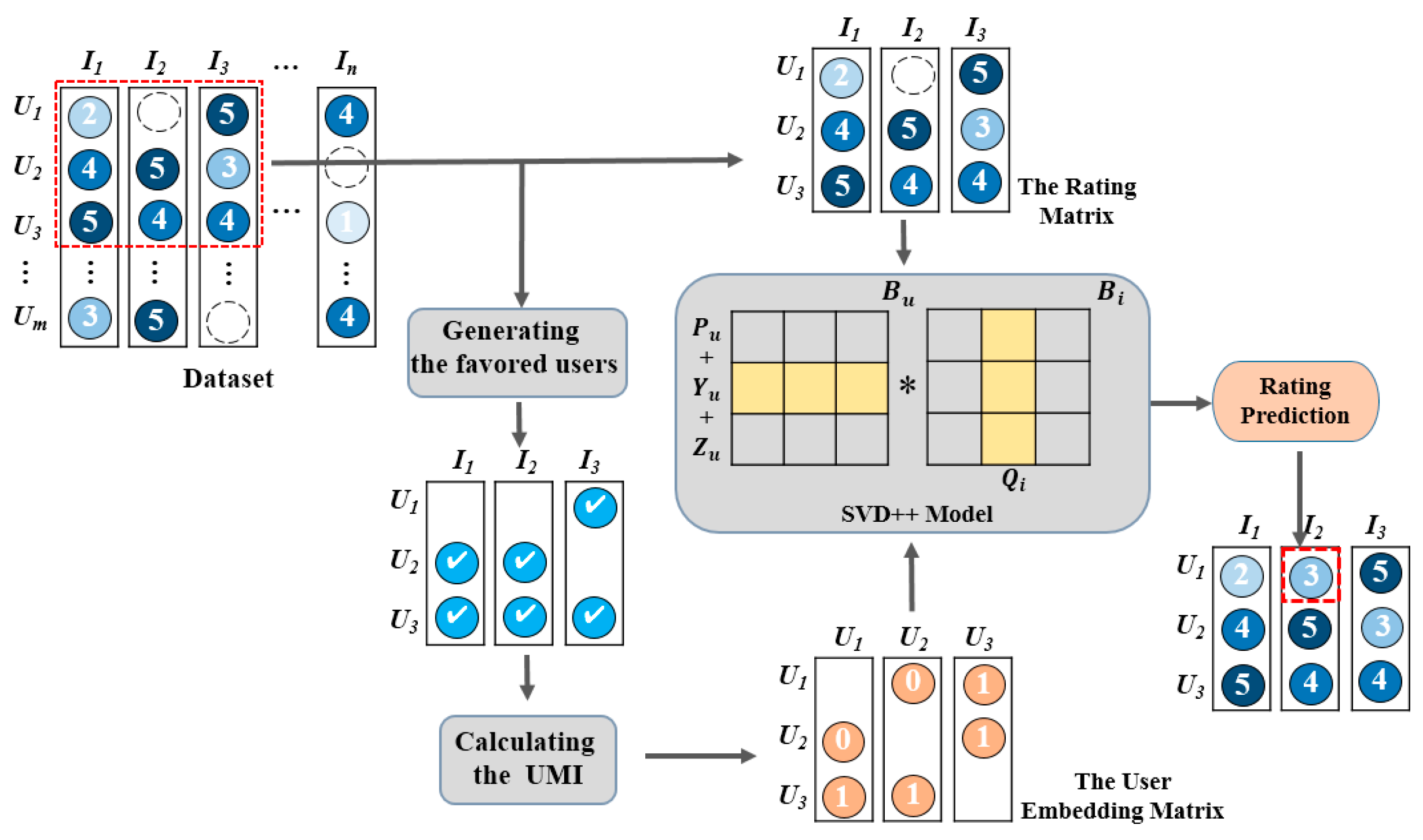
3. Proposed UE-SVD++ Model
3.1. Fundamental Theory
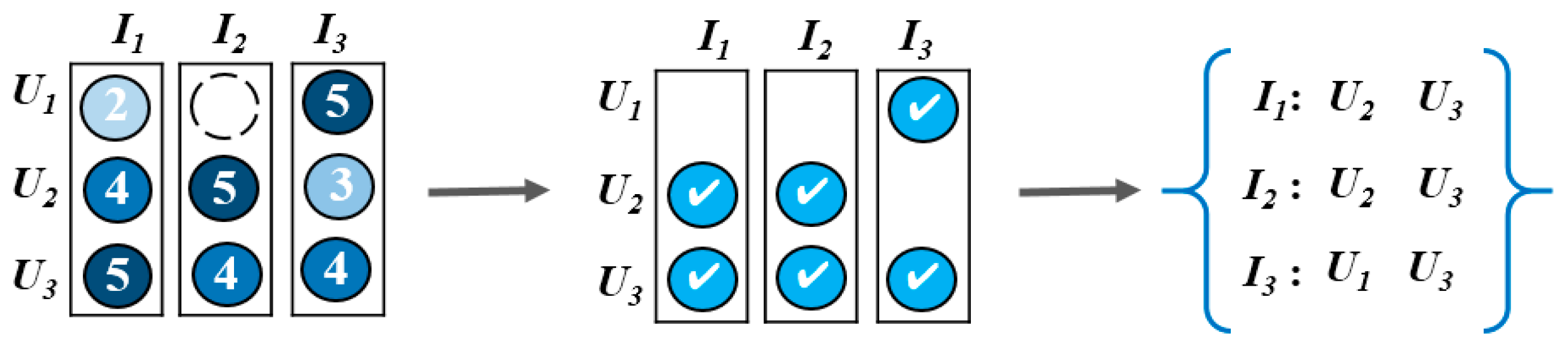
3.2. User Embedding Matrix
| Algorithm 1: The process of computing the user embedding matrix. | |
| Input: the rating matrix Output: the user embedding matrix | |
| 1. | Count all user collections that rated on the item based on the rating matrix. |
| 2. | Calculate the number of the favored users for a particular item. The users who rated for an item with a rating greater than 70% of the highest rating are the favored user data. |
| 3. | Compute the user-wise mutual information (UMI) value of specific and using Equations (1)–(4). |
| 4. | Filter the UMI values using Equation (6). |
| 5. | Generate the user embedding matrix. |
3.3. Proposed UE-SVD++ Model
| Algorithm 2: The Proposed UE-SVD++ algorithm. | |
| Input: the rating matrix, the user embedding matrix Output: the predicted rating matrix | |
| 1. | Calculate the mean rating based on the rating matrix. |
| 2. | Initialize the “bias information” and . Initialize the user vector and the item vector . Initialize the user embedding hidden feature . Initialize the implicit parameters . |
| 3. | Calculate the inner product of the user vector and the item vector using Equation (9). User ratings are predicted. |
| 4. | Calculate the prediction error based on the real rating and the predicted rating. The stochastic gradient descent (SGD) method is utilized to complete optimization, as shown in Equations (12)–(18). |
| 5. | Repeat the third step and fourth step to get the prediction rating . Update the predicted rating matrix. |
4. Experiment
4.1. Experimental Datasets and Evaluations
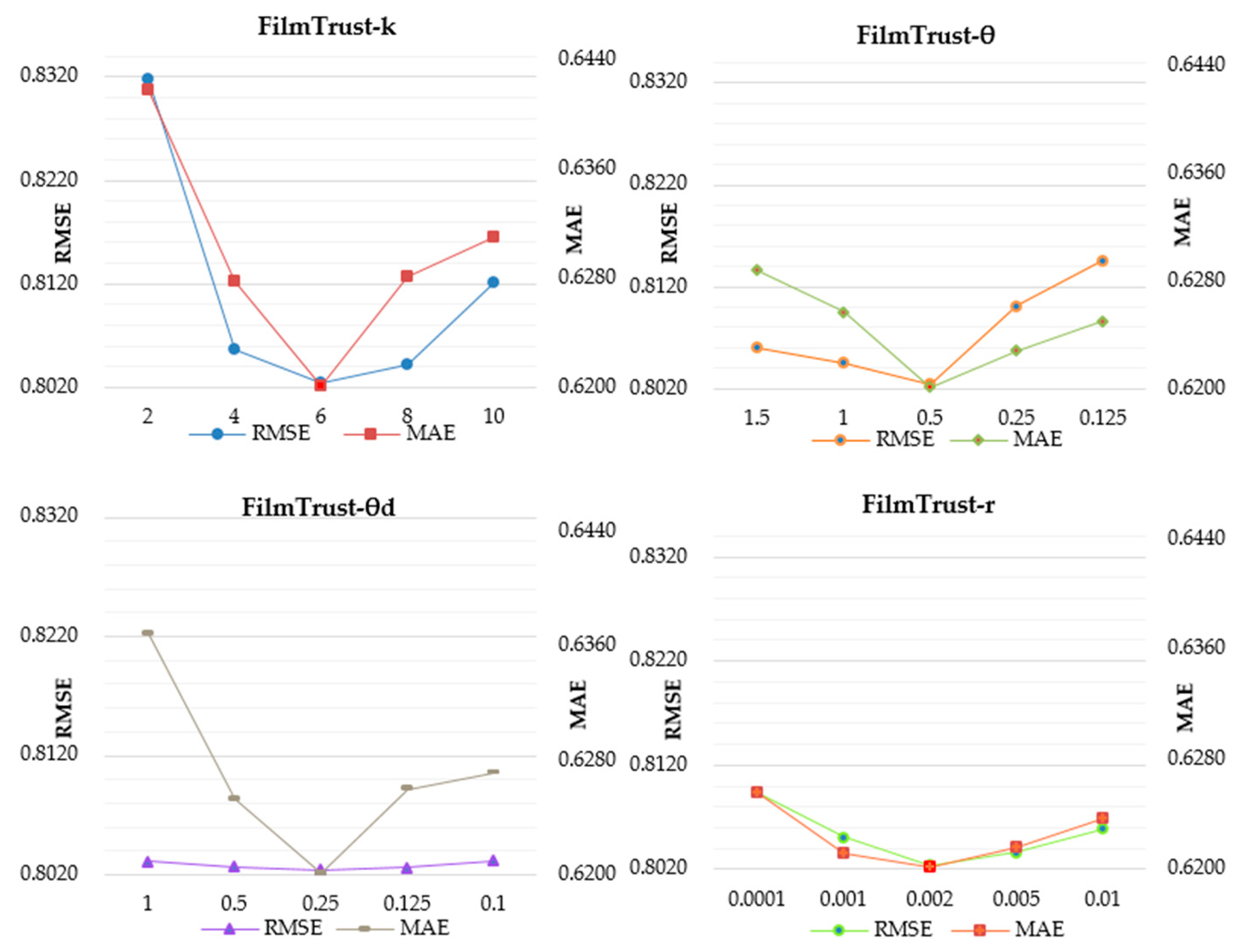
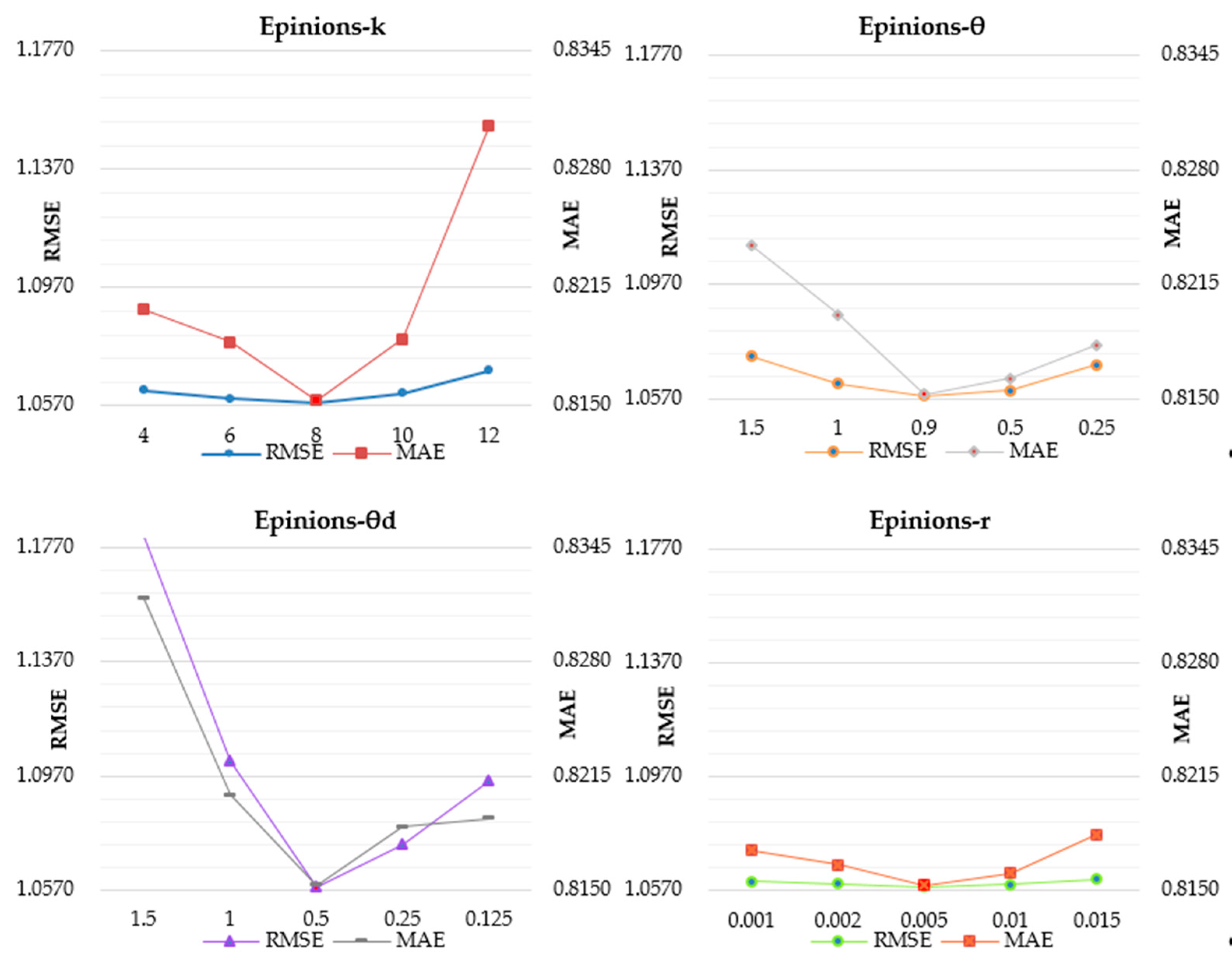
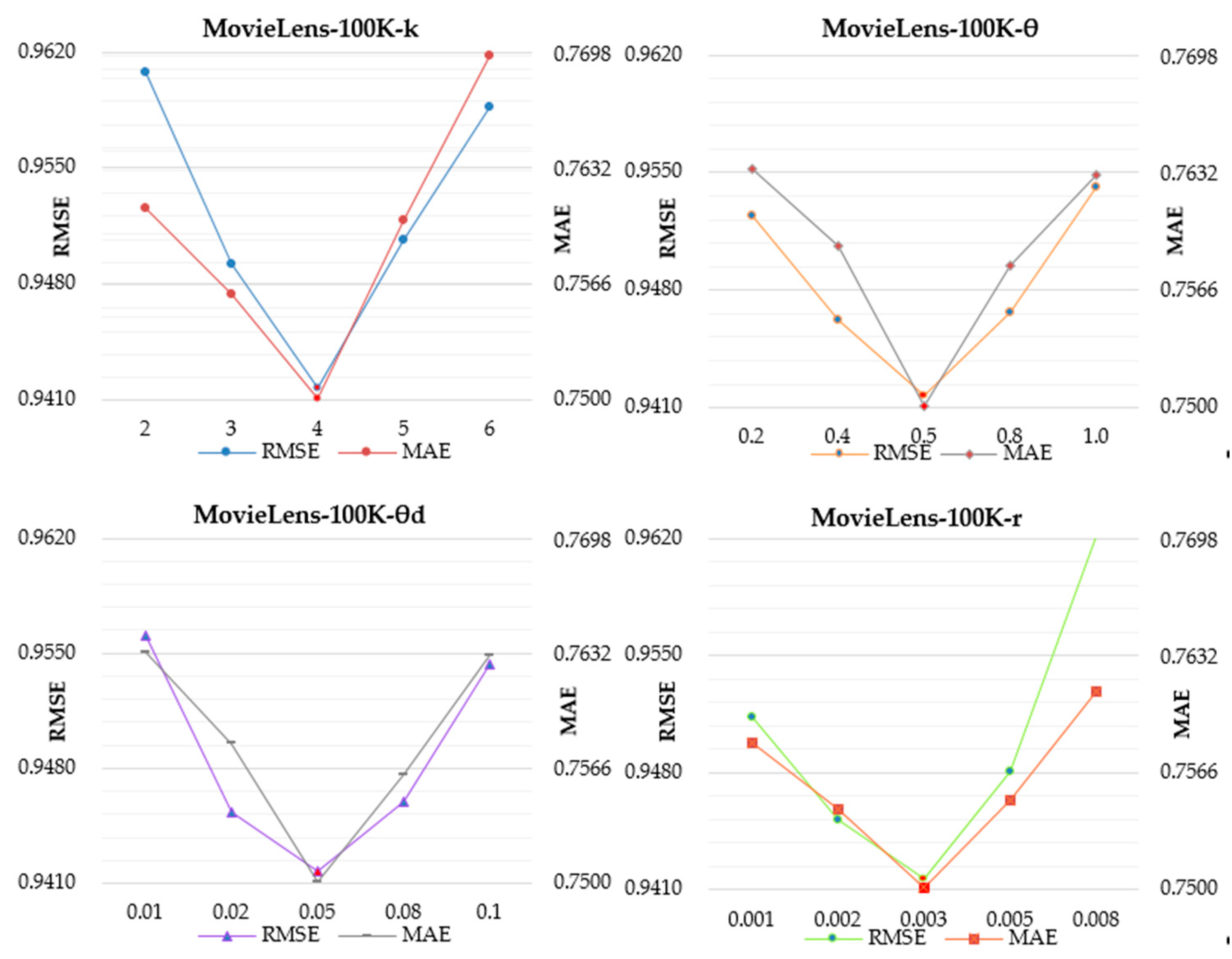
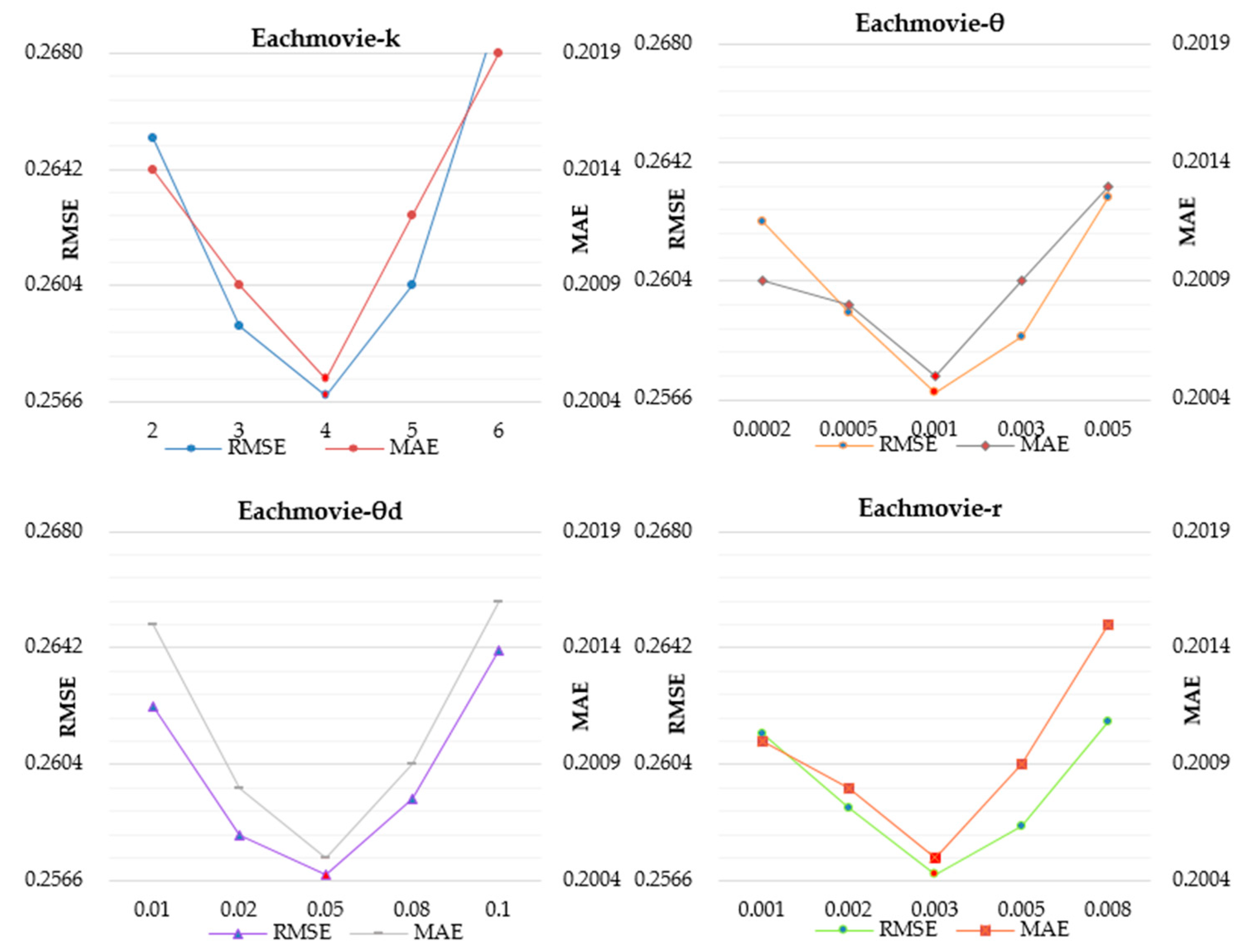
4.2. Model Parameter Selection
4.3. Compared Models
4.4. Performance Comparison
4.5. The Influence of the Training Data Volume on Model Performance and the Execution Time
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 2009, 30–38. [Google Scholar] [CrossRef]
- Resnick, P.; Iacovou, N.; Suchak, M.; Bergstrom, P.; Riedl, J. GroupLens: An Open Architecture for Collaborative Filtering of Netnews. 1994. Available online: https://dl.acm.org/doi/10.1145/192844.192905 (accessed on 11 December 2019).
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009, 1–19. [Google Scholar] [CrossRef]
- Deshpande, M.; Karypis, G. Item-Based top-n, recommendation algorithms. ACM Trans. Inf. Syst. 2004, 22, 143–177. [Google Scholar] [CrossRef]
- Linden, G.; Smith, B.; York, J. Amazon.com recommendations: Item-to-Item collaborative filtering. IEEE Internet Comput. 2003, 7, 76–80. [Google Scholar] [CrossRef]
- Koren, Y. Factor in the neighbors: Scalable and accurate collaborative filtering. ACM Trans. Knowl. Discov. Data 2010, 4, 1. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, J.; Yorke-Smith, N. TrustSVD: Collaborative filtering with both the explicit and implicit influence of user trust and of item ratings. In Proceedings of the 29th AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–29 January 2015; AAAI Press: Menlo Park, CA, USA, 2015; pp. 123–129. [Google Scholar]
- Adomavicius, G.; Kwon, Y.O. Overcoming accuracy-diversity tradeoff in recommender systems: A variance-based approach. In Proceedings of the WITS, Paris, France, 1 January 2008; p. 8. [Google Scholar]
- Adomavicius, G.; Kwon, Y. Improving recommendation diversity using ranking-based techniques. IEEE Trans. Knowl. Data Eng. 2009, 896–911. [Google Scholar] [CrossRef]
- Levy, O.; Goldberg, Y. Neural Word Embedding as Implicit Matrix Factorization. 2014. Available online: http://papers.nips.cc/paper/5477-neural-word-embedding-as (accessed on 11 December 2019).
- Chae, D.K.; Shin, J.A.; Kim, S.W. Collaborative Adversarial Autoencoders: An Effective Collaborative Filtering Model under the GAN Framework. IEEE Access 2019, 7, 37650–37663. [Google Scholar] [CrossRef]
- Mnih, A.; Salakhutdinov, R. Probabilistic Matrix Factorization. 2008. Available online: http://papers.nips.cc/paper/3208-probabilistic-matrix-factorization.pdf (accessed on 11 December 2019).
- Salakhutdinov, R.; Mnih, A. Bayesian Probabilistic Matrix Factorization Using Markov Chain Monte Carlo. 2008. Available online: https://dl.acm.org/doi/10.1145/1390156.1390267 (accessed on 11 December 2019).
- Koren, Y.; Bell, R. Advances in collaborative filtering. In Recommender Systems Handbook; Springer: Boston, MA, USA, 2015; pp. 77–118. [Google Scholar]
- Kim, K.S.; Chang, D.S.; Choi, Y.S. Boosting Memory-Based Collaborative Filtering Using Content-Metadata. Symmetry 2019, 11, 561. [Google Scholar] [CrossRef]
- Koren, Y. Collaborative Filtering with Temporal Dynamics. 2009. Available online: https://dl.acm.org/doi/10.1145/1557019.1557072 (accessed on 11 December 2019).
- Devooght, R.; Kourtellis, N.; Mantrach, A. Dynamic Matrix Factorization with Priors on Unknown Values. 2015. Available online: https://dl.acm.org/doi/10.1145/2783258.2783346 (accessed on 11 December 2019).
- Jamali, M.; Ester, M. A Matrix Factorization Technique with Trust Propagation for Recommendation in Social Networks. 2010. Available online: https://dl.acm.org/doi/10.1145/1864708.1864736 (accessed on 11 December 2019).
- Ma, H.; Yang, H.; Lyu, M.R.; King, I. SoRec: Social Recommendation Using Probabilistic Matrix Factorization. 2008. Available online: https://dl.acm.org/doi/10.1145/1458082.1458205 (accessed on 11 December 2019).
- Yang, B.; Lei, Y.; Liu, D.Y.; Liu, J.M. Social Collaborative Filtering by Trust. 2013. Available online: https://ieeexplore.ieee.org/abstract/document/7558226/ (accessed on 11 December 2019).
- Tang, J.; Hu, X.; Gao, H.; Liu, H. Exploiting Local and Global Social Context for Recommendation. 2013. Available online: https://www.aaai.org/ocs/index.php/IJCAI/IJCAI13/paper/viewPaper/6936 (accessed on 11 December 2019).
- Wang, H.; Song, Y.; Mi, P.; Duan, J. The Collaborative Filtering Method Based on Social Information Fusion. Math. Probl. Eng. 2019. Available online: https://www.hindawi.com/journals/mpe/2019/9387989/abs/ (accessed on 11 December 2019).
- Koren, Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge discovery and data mining, Las Vegas, NV, USA, 24–27 August 2008; ACM Press: New York, NY, USA, 2008; pp. 426–434. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed Representations of Words and Phrases and Their Compositionality. 2013. Available online: http://papers.nips.cc/paper/5021-distributed-representations-of-words-andphrases (accessed on 11 December 2019).
- Guàrdia-Sebaoun, E.; Guigue, V.; Gallinari, P. Latent Trajectory Modeling: A Light and Efficient Way to Introduce Time in Recommender Systems. 2015. Available online: https://dl.acm.org/doi/10.1145/2792838.2799676 (accessed on 11 December 2019).
- Barkan, O.; Koenigstein, N. Item2vec: Neural Item Embedding for Collaborative Filtering. 2016. Available online: https://ieeexplore.ieee.org/abstract/document/7738886/ (accessed on 11 December 2019).
- Yang, X.; Steck, H.; Liu, Y. Circle-Based Recommendation in Online Social Networks. 2012. Available online: https://dl.acm.org/doi/10.1145/2339530.2339728 (accessed on 11 December 2019).
- Li, H.; Wu, D.; Tang, W.; Mamoulis, N. Overlapping Community Regularization for Rating Prediction in Social Recommender Systems. 2015. Available online: https://dl.acm.org/doi/10.1145/2792838.2800171 (accessed on 11 December 2019).
| Users | Items | Ratings | Ratings Range | Density | |
|---|---|---|---|---|---|
| FilmTrust | 1508 | 2071 | 35,497 | {0.5, …, 4.0} | 1.136% |
| Epinions | 49,289 | 139,738 | 664,823 | {1.0, …, 5.0} | 0.051% |
| MovieLens-100K | 943 | 1682 | 100,000 | {1.0, …, 5.0} | 6.304% |
| EachMovie | 29,520 | 1648 | 1,048,575 | {0.2, …, 1.0} | 2.155% |
| Datasets | FilmTrust | Epinions | MovieLens-100K | EachMovie | ||||
|---|---|---|---|---|---|---|---|---|
| Metrics Models | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE |
| ITEM-MF | 0.9274 | 0.7138 | 1.2001 | 0.9134 | 1.0872 | 0.8717 | 0.2842 | 0.2228 |
| USER-MF | 0.8960 | 0.6646 | 1.1894 | 0.9128 | 1.0946 | 0.8648 | 0.2847 | 0.2296 |
| PMF | 0.8541 | 0.6554 | 1.1152 | 0.8426 | 0.9573 | 0.7602 | 0.2627 | 0.2058 |
| BIAS-SVD | 0.8199 | 0.6311 * | 1.0809 * | 0.8342 | 0.9629 | 0.7587 * | 0.2597 | 0.2029 * |
| FUNK-SVD | 0.8487 | 0.6546 | 1.0970 | 0.8331 | 0.9587 | 0.7594 | 0.2615 | 0.2054 |
| SVD++ | 0.8340 | 0.6315 | 1.1194 | 0.8315 | 0.9521 * | 0.7624 | 0.2594 * | 0.2035 |
| LOCABAL | 0.8297 | 0.6519 | 1.1316 | 0.8477 | ||||
| SOCIAL-MF | 0.8506 | 0.659 | 1.0823 | 0.8314 | ||||
| MFC | 0.8198 | 0.6496 | 1.1263 | 0.836 | ||||
| TRUST-SVD | 0.8197 * | 0.6349 | 1.0908 | 0.8258 * | ||||
| UE-SVD++ | 0.8024 | 0.6201 | 1.0583 | 0.8153 | 0.9417 | 0.7501 | 0.2568 | 0.2005 |
| Improve | 2.110% | 1.742% | 2.091% | 1.271% | 1.092% | 1.133% | 1.002% | 1.182% |
| 30% Training | 40% Training | 50% Training | 60% Training | 70% Training | 80% Training | |
|---|---|---|---|---|---|---|
| RMSE | 0.8634 | 0.8406 | 0.8291 | 0.8196 | 0.8109 | 0.8024 |
| MAE | 0.6742 | 0.6684 | 0.6521 | 0.6324 | 0.6259 | 0.6201 |
| Time (s) | 1394.2 | 1420.6 | 1482.4 | 1549.7 | 1636.4 | 1719.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Wang, L.; Qin, J. User Embedding for Rating Prediction in SVD++-Based Collaborative Filtering. Symmetry 2020, 12, 121. https://doi.org/10.3390/sym12010121
Shi W, Wang L, Qin J. User Embedding for Rating Prediction in SVD++-Based Collaborative Filtering. Symmetry. 2020; 12(1):121. https://doi.org/10.3390/sym12010121
Chicago/Turabian StyleShi, Wenchuan, Liejun Wang, and Jiwei Qin. 2020. "User Embedding for Rating Prediction in SVD++-Based Collaborative Filtering" Symmetry 12, no. 1: 121. https://doi.org/10.3390/sym12010121
APA StyleShi, W., Wang, L., & Qin, J. (2020). User Embedding for Rating Prediction in SVD++-Based Collaborative Filtering. Symmetry, 12(1), 121. https://doi.org/10.3390/sym12010121




