Effects of Nanoparticle Enhanced Lubricant Films in Thermal Design of Plain Journal Bearings at High Reynolds Numbers
Abstract
1. Introduction
2. Mathematical Problem
2.1. Governing Equations
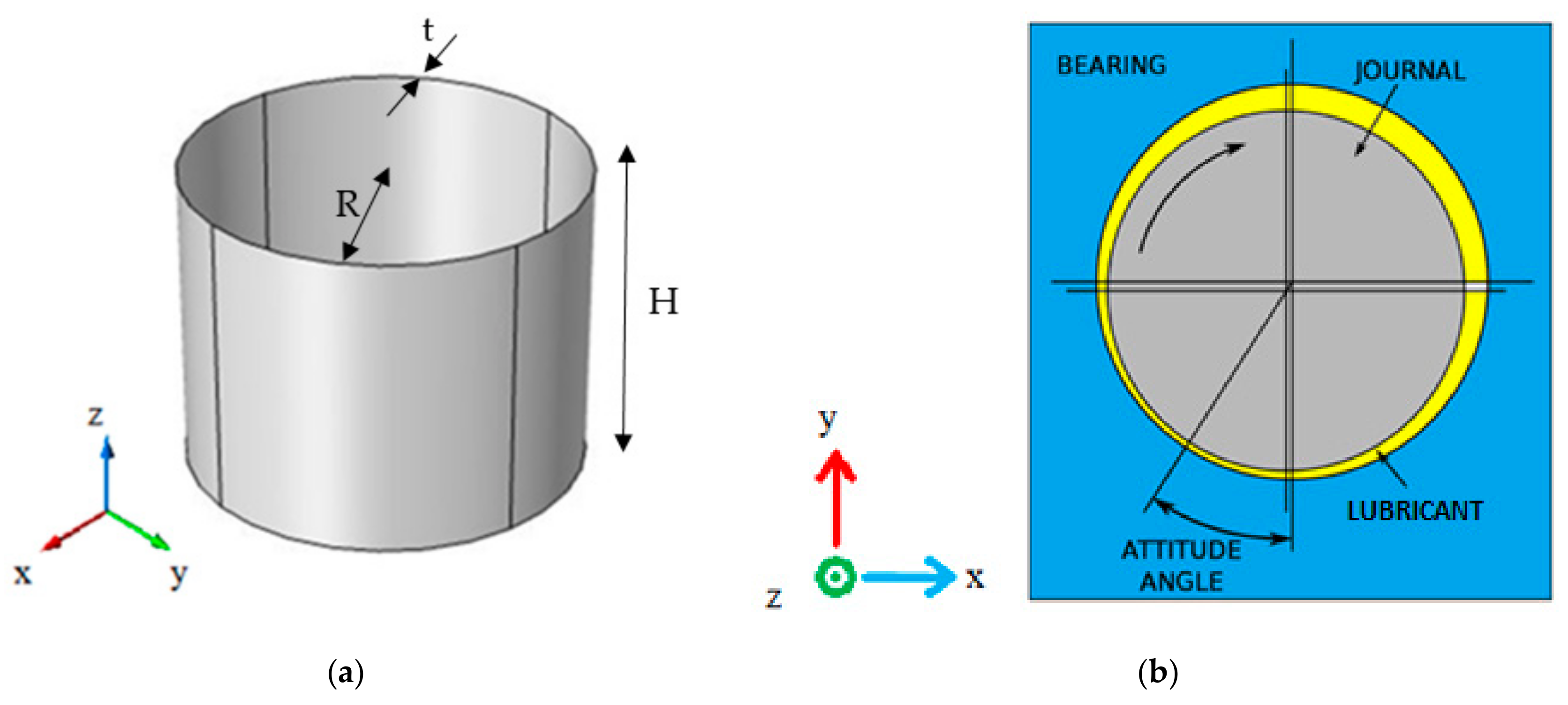
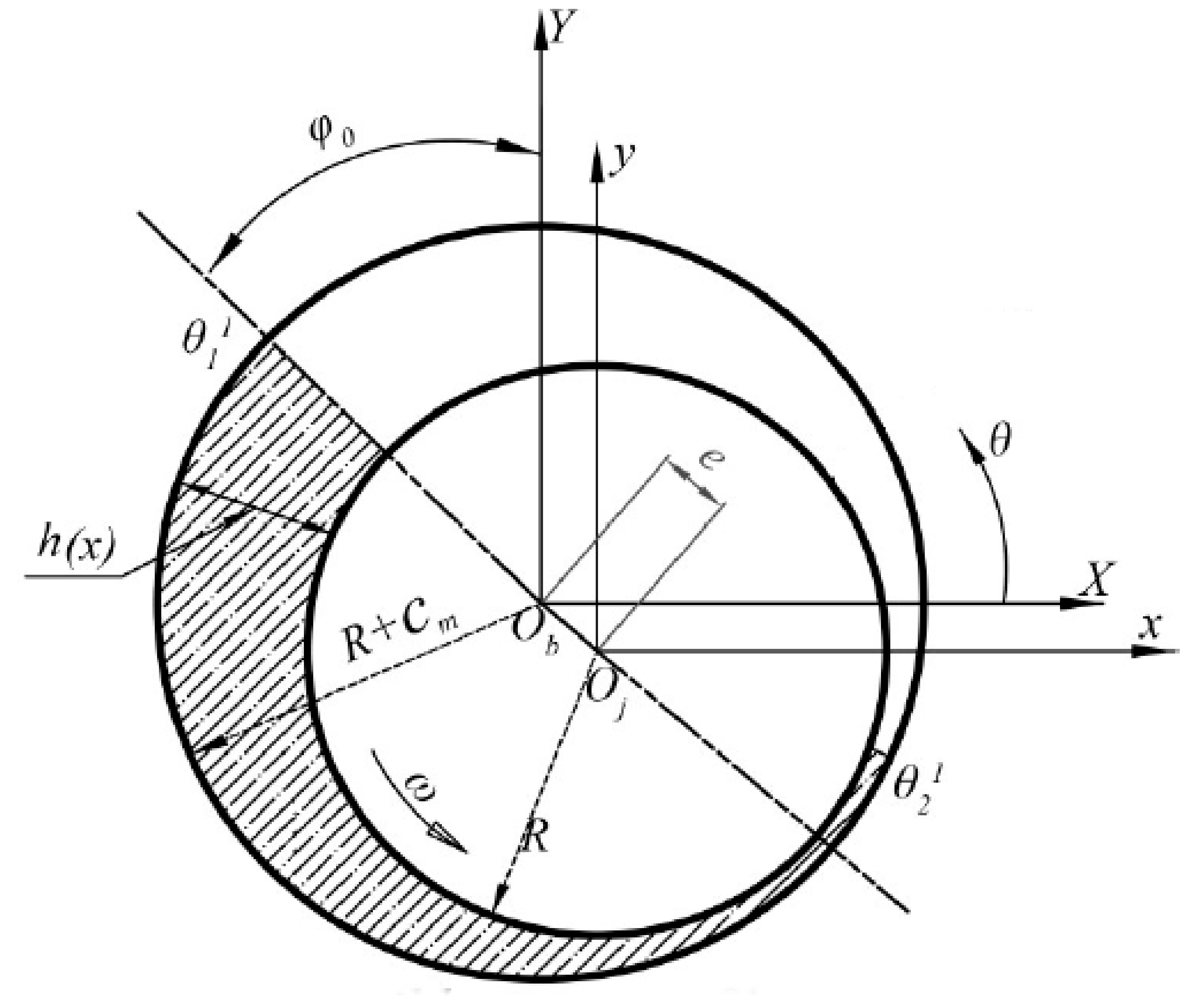
2.2. Lubricant Film Thickness in Bearings
2.3. Reynolds Equation
2.4. Thermophysical Properties
2.5. Energy Equation
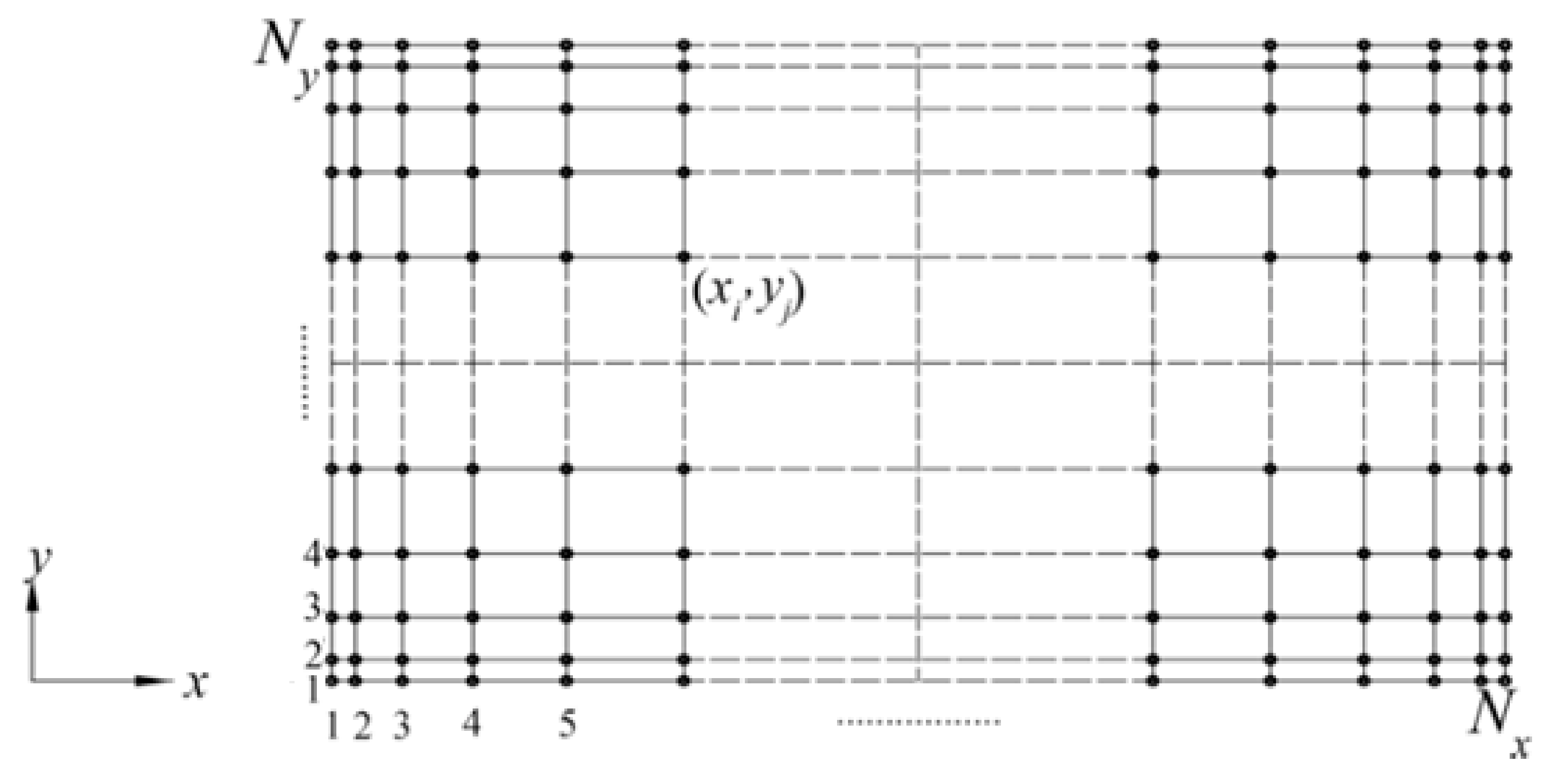
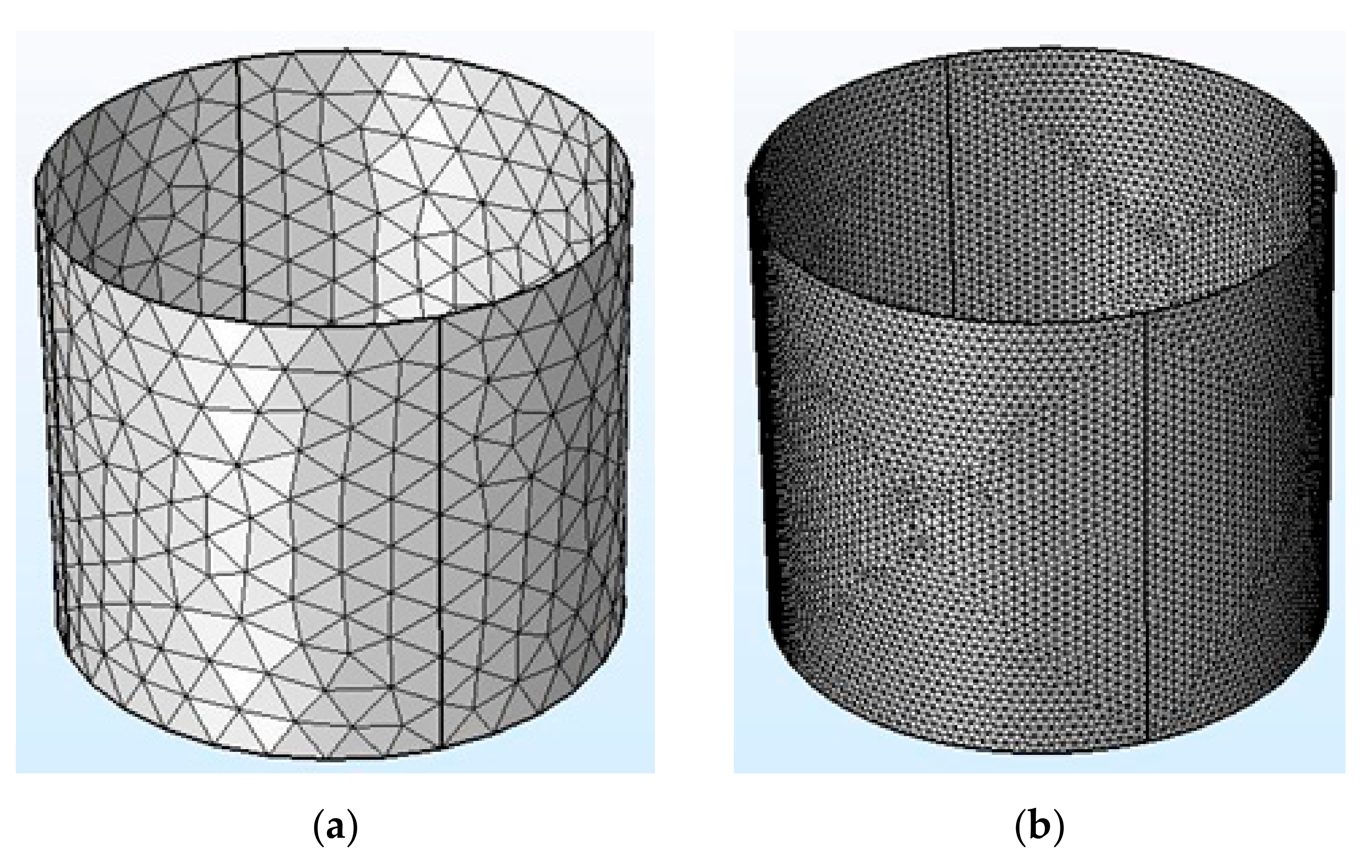
3. Numerical Algorithm
4. Results and Discussions
5. Conclusions
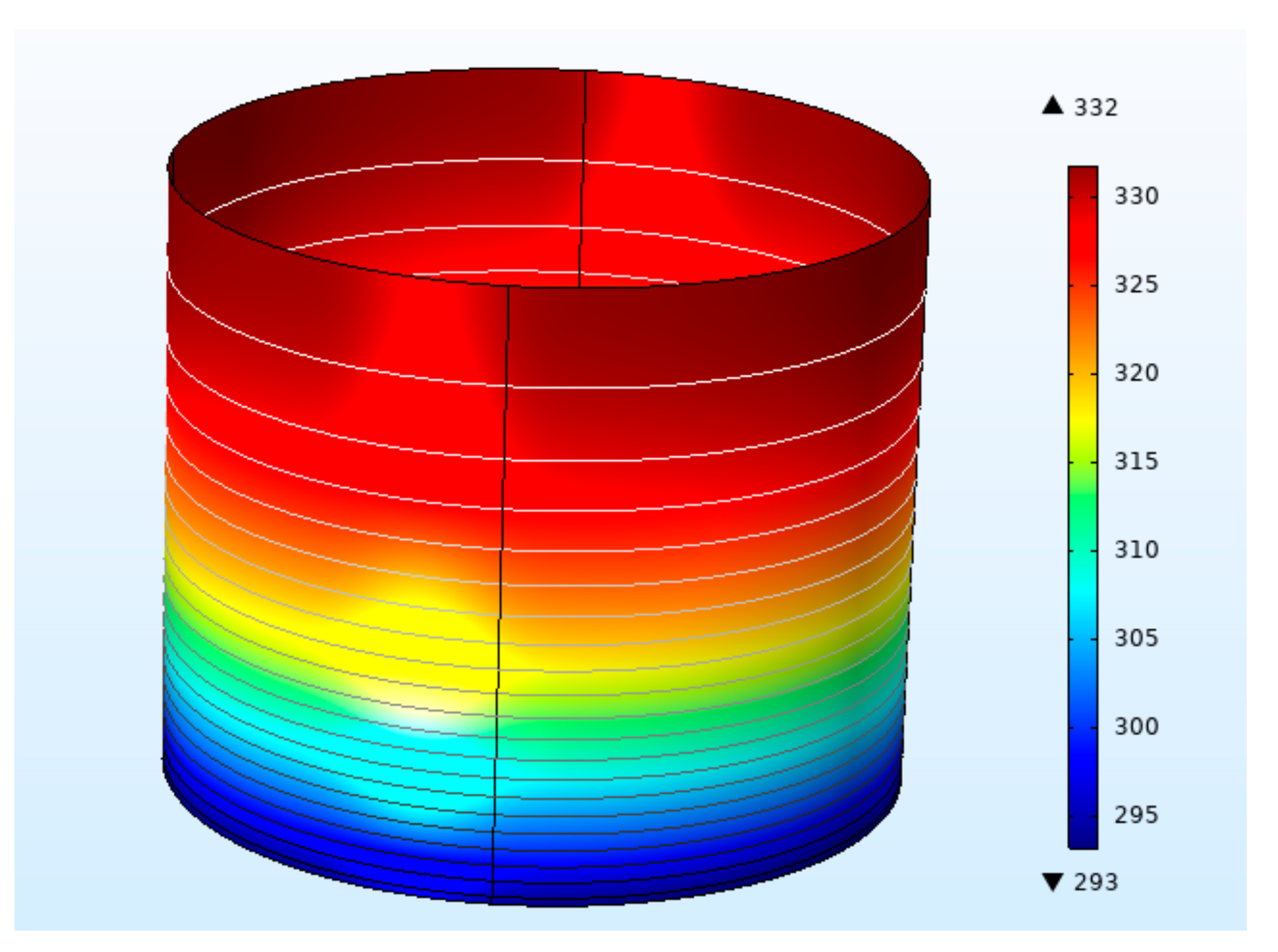
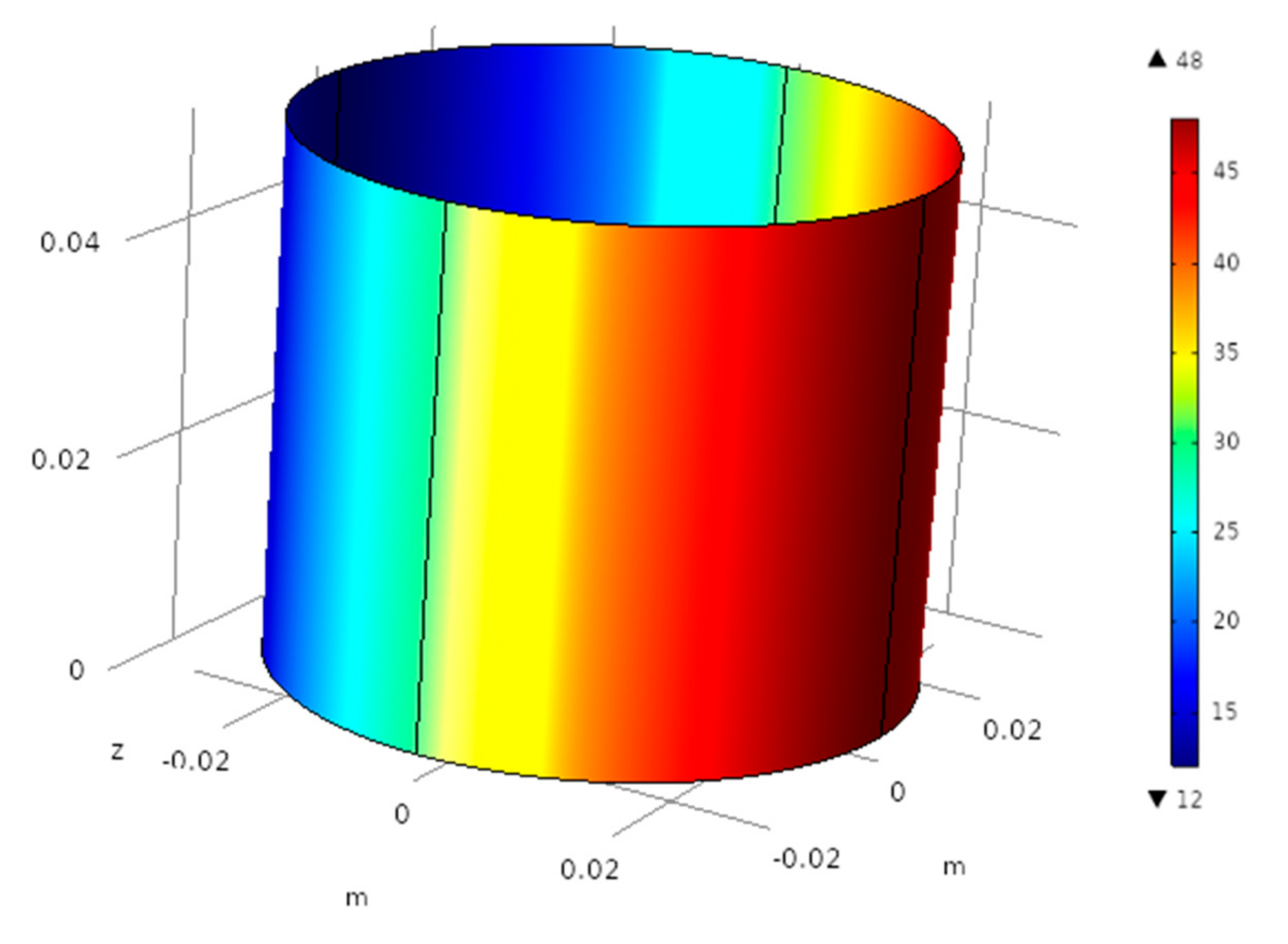
- Temperature on the bearing surface increases monotonically along the z coordinate under specific loading.
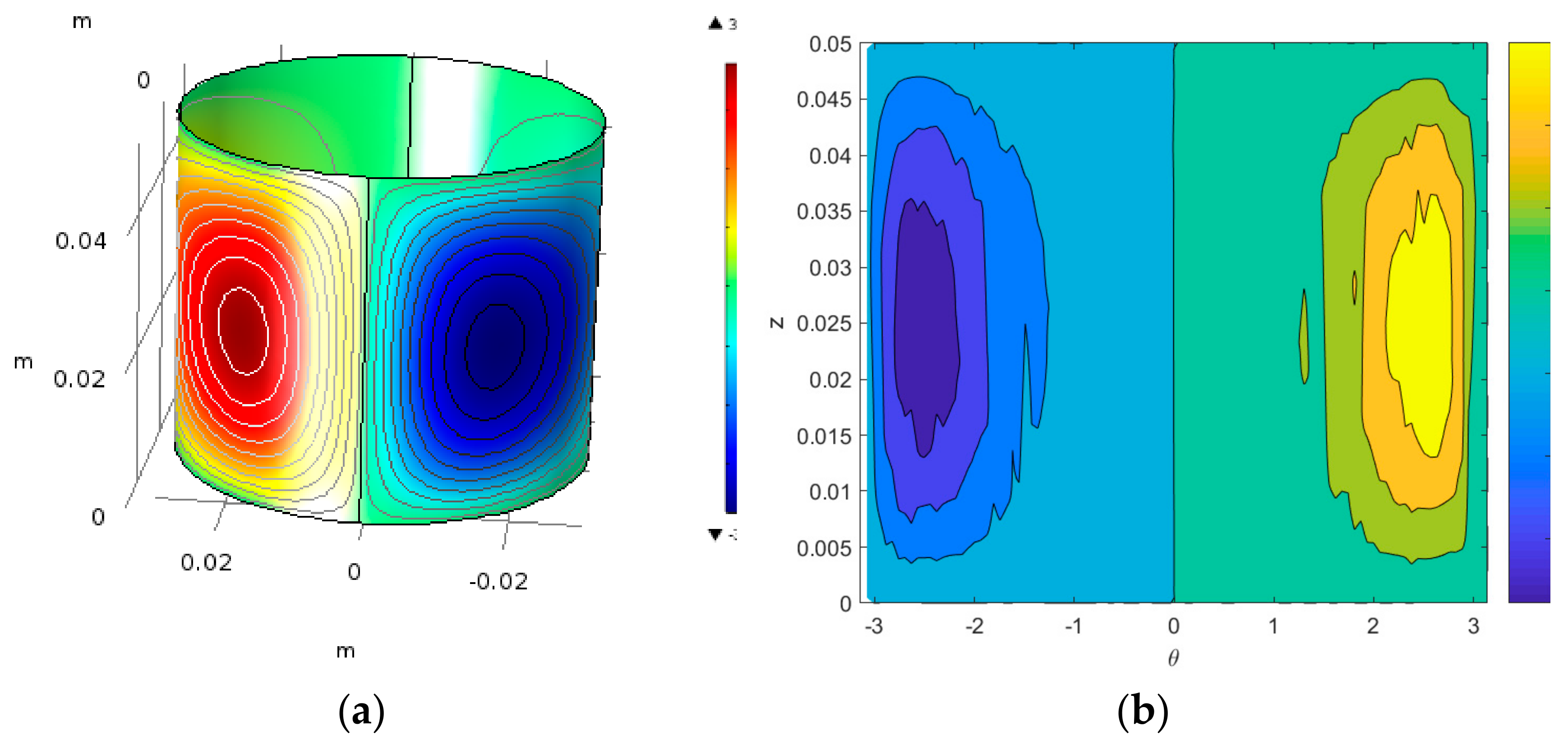
- Maximum and minimum pressure on the bearing surface under specific loading is occurred at the middle cylinder. Moreover, these maximum and minimum pressure points are adjacent to each other.
- Distribution of velocity vectors under specific loading is uniform both in magnitude and direction while the rotation is on the counter clock-wise direction.
- Total gap height between the bearing and journal surface is constant along the z coordinate for a specific position on the cylindrical coordinate due to uniform distribution of specific load.
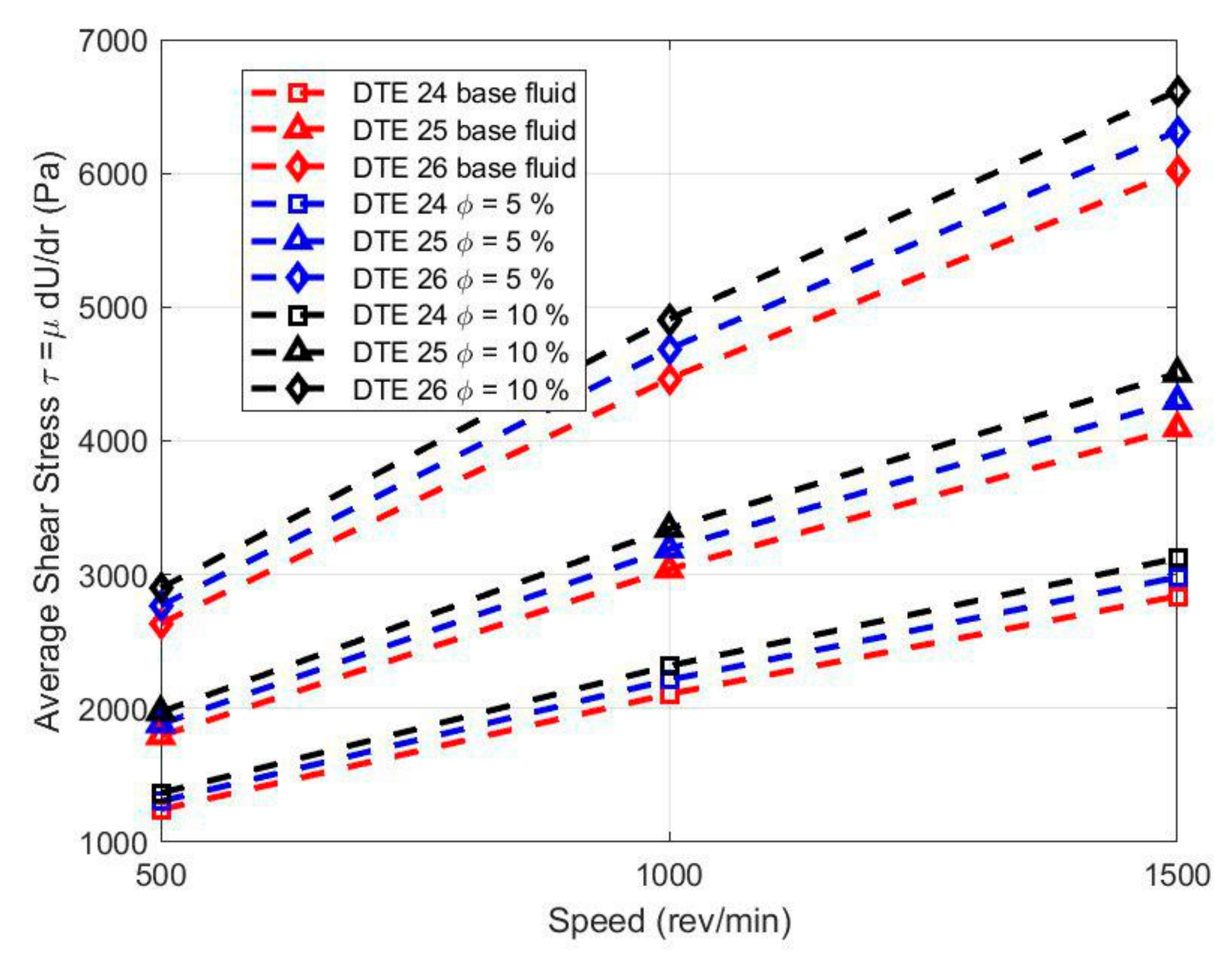
- For all different lubricant types, the rotational speed has a direct relationship with the increase of the average shear stress. By increasing the rotational speed from 500 to 1500 rpm, the average shear stress increases by more than 100%, 120%, and 130% for DTE 26, DTE 25, and DTE 24 lubricant types, respectively. Increasing nanoparticles enhances the average shear rate by approximately 10% for all cases.
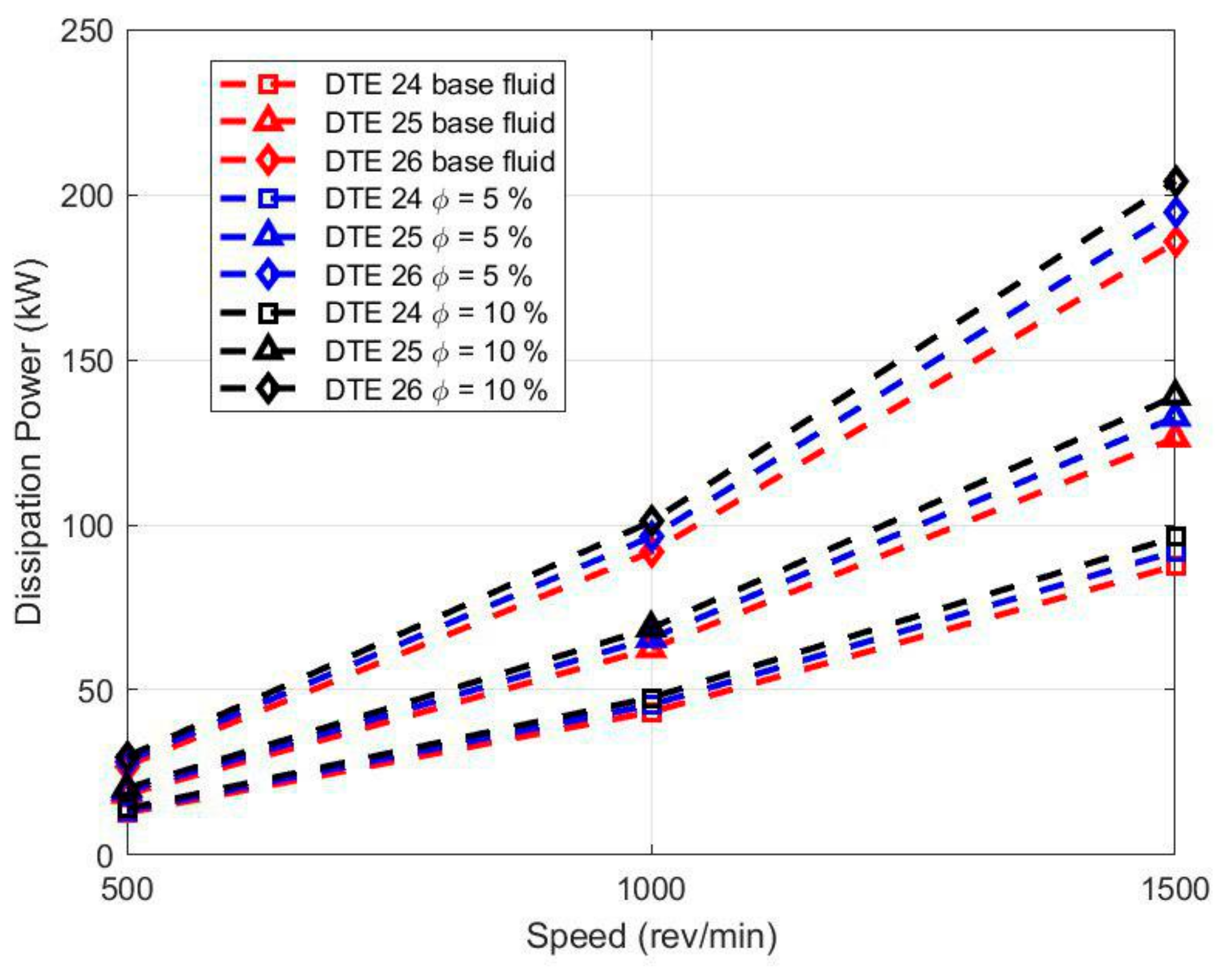
- Dissipation power increases with the rotational speed. By increasing the rotational speed from 500 to 1500 rpm, average shear stress increases around 600% for all lubricant types. Increasing nanoparticles volume fraction increases the average shear rate by approximately 10% for all lubricant types and in all rotational speeds.
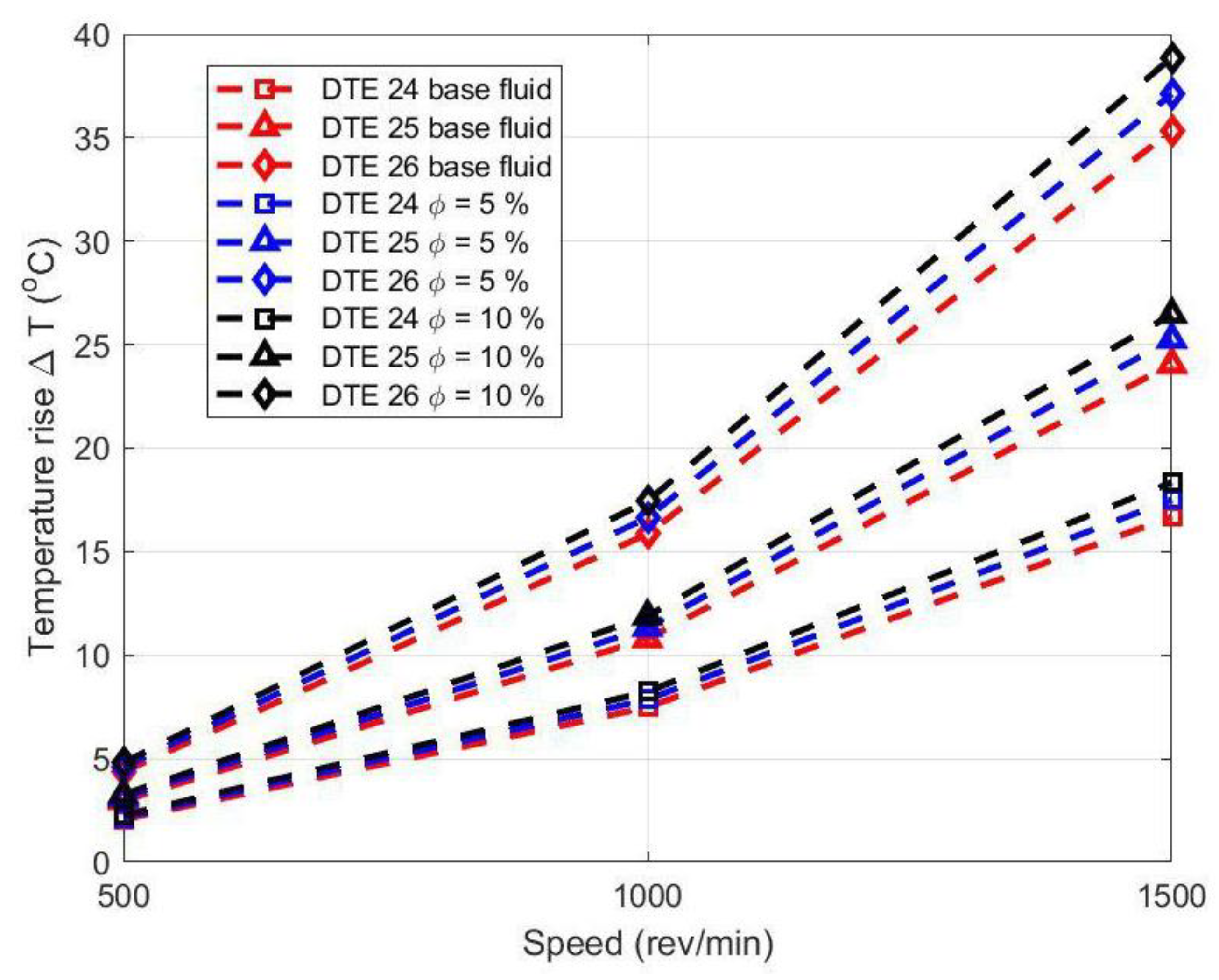
- By increasing the rotational speed from 500 to 1500 rpm, the temperature rise increases around 800% for almost all lubricant types.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| R | Journal radius, | Number of sampling points in the x direction | |
| t | Solid thickness, | Number of sampling points in the y direction | |
| H | Journal height, | Flow rate, | |
| c | Clearance between the journal and the bearing, | Slip velocity, | |
| Nanoparticle volume fraction | Thermal conductivity, | ||
| Fluid velocity vector, | Kinematic viscosity, | ||
| Pressure, | Temperature, K | ||
| Dynamic viscosity, | Viscous stress tensor, | ||
| Gap function, | Convection coefficient, | ||
| Minimum radial clearance | Ambient temperature, K | ||
| Position of the journal center in the static equilibrium state | Subscripts | ||
| Position of the journal center in the static equilibrium state | Base fluid | ||
| Specific heat capacity, | Solid nanoparticles, | ||
| Rotor angular velocity, | Fluid (oil) | ||
| Linear velocity of the rigid rotor, | s | Solid (pad and rotor) | |
| Weight coefficients matrices for the first-order derivatives of the pressure distribution | Feeding oil | ||
| Weight coefficients matrices for the first-order derivatives of the pressure distribution | Inner bearing surface | ||
| Second-order weight coefficients matrices for the pressure distribution | Outer bearing surface | ||
| Second-order weight coefficients matrices for the pressure distribution | Outflow bearing surface | ||
| Density, | Outer radius of the groove region | ||
| Specific heat capacity, | Inlet | ||
| Slip length, | Critical |
References
- Nguyen, T.; Tran, T.; de Boer, H.; van den Berg, A.; Eijkel, J.C.T. Rotary-Atomizer Electric Power Generator. Phys. Rev. Appl. 2015, 3, 034005. [Google Scholar] [CrossRef]
- Nguyen, M.Q.; Shadloo, M.S.; Hadjadj, A.; Lebon, B.; Peixinho, J. Perturbation threshold and hysteresis associated with the transition to turbulence in sudden expansion pipe flow. Int. J. Heat Fluid Flow 2019, 76, 187–196. [Google Scholar] [CrossRef]
- Shadloo, M.; Hadjadj, A. Laminar-turbulent transition in supersonic boundary layers with surface heat transfer: A numerical study. Numer. Heat Transf. A 2017, 72, 40–53. [Google Scholar] [CrossRef]
- Crosby, W. Thermal considerations in the solution of finite journal bearings. Wear 1980, 64, 15–32. [Google Scholar] [CrossRef]
- Nagaraju, Y.; Joy, M.; Nair, K.P. Thermohydrodynamic analysis of a two-lobe journal bearing. Int. J. Mech. Sci. 1994, 36, 209–217. [Google Scholar] [CrossRef]
- Ma, M.T.; Taylor, C.M. An experimental investigation of thermal effects in circular and elliptical plain journal bearings. Tribol. Int. 1996, 29, 19–26. [Google Scholar] [CrossRef]
- Banwait, S.; Chandrawat, H. Effect of misalignment on thermohydrodynamic analysis of elliptical journal bearings. J. Inst. Eng. India Mech. Eng. Div. 2000, 93–101. [Google Scholar]
- Singh, D.; Majumdar, B. Computer-aided design of hydrodynamic journal bearings considering thermal effects. Proc. Inst. Mech. Eng. J 2005, 219, 133–139. [Google Scholar] [CrossRef]
- Mishra, P.; Pandey, R.; Athre, K. Temperature profile of an elliptic bore journal bearing. Tribol. Int. 2007, 40, 453–458. [Google Scholar] [CrossRef]
- Chauhan, A.; Sehgal, R.; Sharma, R.K. Thermohydrodynamic analysis of elliptical journal bearing with different grade oils. Tribol. Int. 2010, 43, 1970–1977. [Google Scholar] [CrossRef]
- Prasad, E.S.; Nagaraju, T.; Sagar, J.P. Thermohydrodynamic performance of a journal bearing with 3D-surface roughness and fluid inertia effects. Int. J. Appl. Res. Mech. Eng. 2012, 2, 18–24. [Google Scholar]
- Singla, A.; Kumar, A.; Bala, S.; Singh, P.; Chauhan, A. Thermo-hydrodynamic Analysis on Temperature Profile of Circular Journal Bearing Using Computational Fluid Dynamics. In Proceedings of the 2014 Recent Advances in Engineering and Computational Sciences, Chandigarh, India, 6–8 March 2014; pp. 1–6. [Google Scholar]
- Baskar, S.; Sriram, G.; Arumugam, S. The Use of D-optimal Design for Modeling and Analyzing the Tribological Characteristics of Journal Bearing Materials Lubricated by Nano-Based Biolubricants. Tribol. Trans. 2016, 59, 44–54. [Google Scholar] [CrossRef]
- Solghar, A.A. Investigation of nanoparticle additive impacts on thermohydrodynamic characteristics of journal bearings. Proc. Inst. Mech. Eng. J 2015, 229, 1176–1186. [Google Scholar] [CrossRef]
- Li, X.; Zhu, D.; Wang, X. Experimental investigation on viscosity of Cu-H2O nanofluids. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2009, 24, 48–52. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y.; Ghasemi, M.; Alamian, R.; Wongwises, S.; Afrand, M.; Shadloo, M.S. Modeling of Subcooled Flow Boiling with Nanoparticles under the Influence of a Magnetic Field. Symmetry 2019, 11, 1275. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S.; Afrand, M.; Mahmoudi, B.; Mahian, O.; Wongwises, S. An updated review on application of nanofluids in heat exchangers for saving energy. Energy Convers. Manag. 2019, 198, 111886. [Google Scholar] [CrossRef]
- Rejvani, M.; Saedodin, S.; Vahedi, S.M.; Wongwises, S.; Chamkha, A.J. Experimental investigation of hybrid nano-lubricant for rheological and thermal engineering applications. J. Therm. Anal. Calorim. 2019, 138, 1823–1839. [Google Scholar] [CrossRef]
- Asadi, A.; Aberoumand, S.; Moradikazerouni, A.; Pourfattah, F.; Żyła, G.; Estelle, P.; Mahian, O.; Wongwises, S.; Nguyen, H.M.; Arabkoohsar, A. Recent advances in preparation methods and thermophysical properties of oil-based nanofluids: A state-of-the-art review. Powder Technol. 2019, 352, 209–226. [Google Scholar] [CrossRef]
- Suryawanshi, S.; Pattiwar, J. Effect of TiO2 Nanoparticles Blended with Lubricating Oil on the Tribological Performance of the Journal Bearing. Tribol. Ind. 2018, 40, 370–391. [Google Scholar] [CrossRef]
- Lee, C.-G.; Hwang, Y.-J.; Choi, Y.-M.; Lee, J.-K.; Choi, C.; Oh, J.-M. A study on the tribological characteristics of graphite nano lubricants. Int. J. Precis. Eng. Manuf. 2009, 10, 85–90. [Google Scholar] [CrossRef]
- Tao, Y.; Tao, Y.; Wang, B.; Tai, Y. Preparation and investigation of nano-AlN lubricant with high performance. Mater. Chem. Phys. 2014, 147, 28–34. [Google Scholar] [CrossRef]
- Binu, K.; Shenoy, B.; Rao, D.; Pai, R. A variable viscosity approach for the evaluation of load carrying capacity of oil lubricated journal bearing with TiO2 nanoparticles as lubricant additives. Procedia Mater. Sci. 2014, 6, 1051–1067. [Google Scholar] [CrossRef]
- Binu, K.; Shenoy, B.; Rao, D.; Pai, R. Static characteristics of a fluid film bearing with TiO2 based nanolubricant using the modified Krieger–Dougherty viscosity model and couple stress model. Tribol. Int. 2014, 75, 69–79. [Google Scholar] [CrossRef]
- Babu, K.S.; Nair, K.P.; Rajendrakumar, P. Computational analysis of journal bearing operating under lubricant containing Al 2 O 3 and ZnO nanoparticles. Int. J. Eng. Sci. Technol. 2014, 6, 34–42. [Google Scholar] [CrossRef]
- Jatti, V.S.; Singh, T. Copper oxide nano-particles as friction-reduction and anti-wear additives in lubricating oil. J. Mech. Sci. Technol. 2015, 29, 793–798. [Google Scholar] [CrossRef]
- Papadopoulos, C.; Kaiktsis, L.; Fillon, M. CFD thermohydrodynamic analysis of 3-D sector-pad thrust bearings with rectangular dimples. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Jamalabadi, M.Y.A. Effects of Nanoparticle Enhanced Lubricant Films in Dynamic Properties of Plain Journal Bearings at High Reynolds Numbers. Int. J. Eng. Technol. 2017, 13, 1–23. [Google Scholar] [CrossRef]
- Hatami, M.; Ganji, D.D.; Sheikholeslami, M. Chapter 3—DTM for Heat Transfer Problems. In Differential Transformation Method for Mechanical Engineering Problems; Hatami, M., Ganji, D.D., Sheikholeslami, M., Eds.; Academic Press: London, UK, 2017; pp. 103–151. [Google Scholar]
- Nguyen, T.; van der Meer, D.; van den Berg, A.; Eijkel, J.C. Investigation of the effects of time periodic pressure and potential gradients on viscoelastic fluid flow in circular narrow confinements. Microfluid. Nanofluid. 2017, 21, 37. [Google Scholar] [CrossRef]
- Rahmatabadi, A.; Mehrjardi, M.Z.; Fazel, M. Performance analysis of micropolar lubricated journal bearings using GDQ method. Tribol. Int. 2010, 43, 2000–2009. [Google Scholar] [CrossRef]
- Frene, J.; Nicolas, D.; Degueurce, B.; Berthe, D.; Godet, M. Hydrodynamic Lubrication: Bearings and Thrust Bearings; Elsevier: Amsterdam, The Netherlands, 1997; Volume 33. [Google Scholar]
- Spikes, H.; Granick, S. Equation for slip of simple liquids at smooth solid surfaces. Langmuir 2003, 19, 5065–5071. [Google Scholar] [CrossRef]
- Shadloo, M.S. Numerical Simulation of Compressible Flows by Lattice Boltzmann Method. Numer. Heat Transf. A 2019, 75, 167–182. [Google Scholar] [CrossRef]

| Parameter | Value | Unit | Description |
|---|---|---|---|
| Number of pads | 6 | - | Number of pads |
| R | 0.03 | M | Journal radius |
| T | 0.051 | M | Solid thickness |
| H | 0.05 | M | Journal height |
| c | 0.00003 | M | Clearance between the journal and the bearing |
| Lubricant | 855 | |
| 0.13 | ||
| 2035 | ||
| Solid | 7800 | |
| 47 | ||
| 434 |
| Domain | Position | Boundary Condition |
|---|---|---|
| Pad | ||
| Top (Fluid-Solid interface) | Continuity of heat flux and temperature | |
| Bottom/ Outer surface/ Inner surface | ||
| Inlet Side/Outlet Side | Adiabatic | |
| Fluid | ||
| Inlet/Inner side | Zero relative pressure, | |
| Outer side/Outlet | Zero relative pressure, |
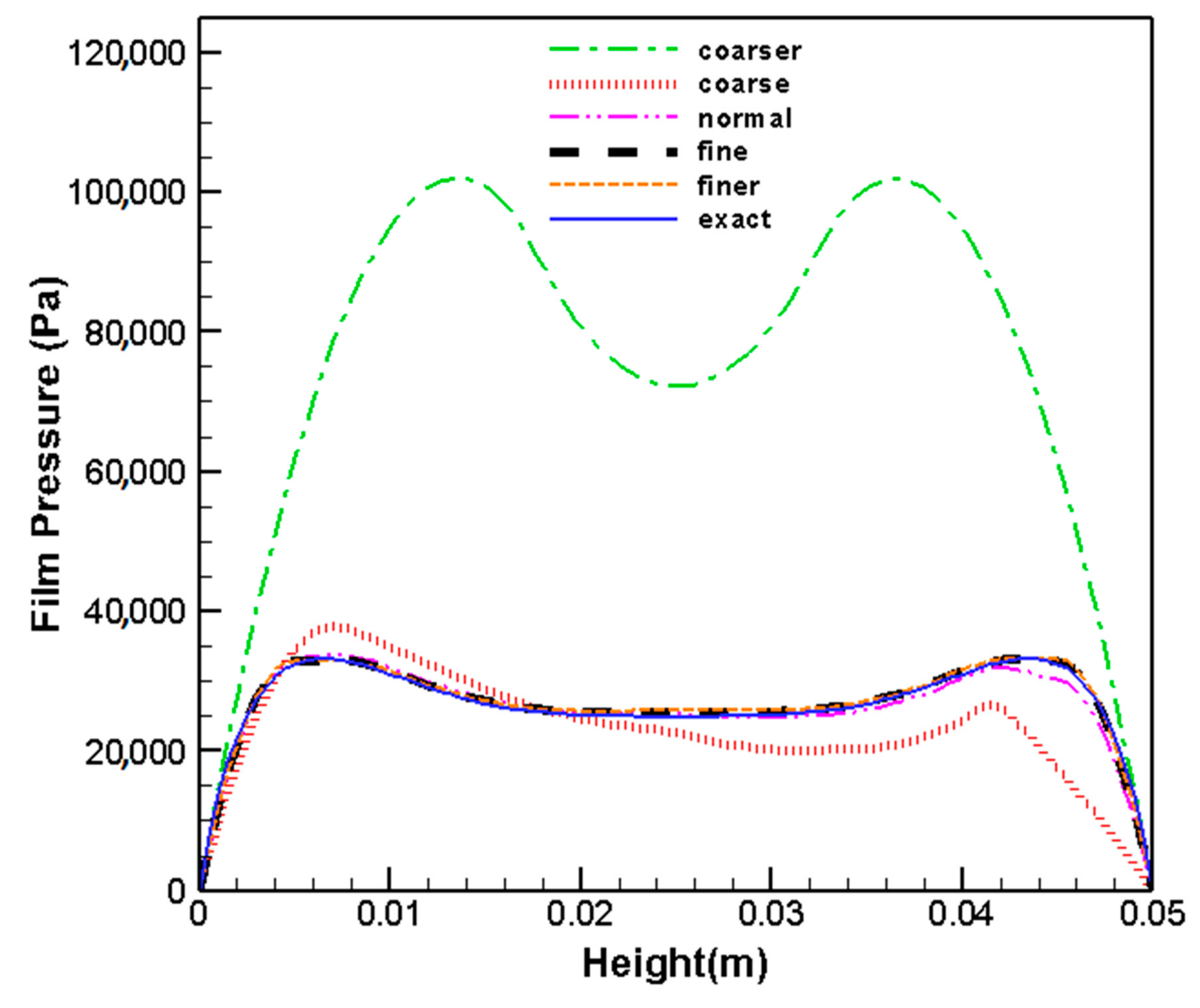
| Mesh Resolution | Number of Elements | Relative Percent Error in Pressure Calculation |
|---|---|---|
| Coarser | 64 | 183.22 |
| Coarse | 276 | 78.4 |
| Normal | 812 | 18.66 |
| Fine | 1180 | 2.17 |
| Finer | 5724 | 0.53 |
| Extremely fine (Exact) | 16,212 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdollahzadeh Jamalabadi, M.Y.; Alamian, R.; Yan, W.-M.; Li, L.K.B.; Leveneur, S.; Safdari Shadloo, M. Effects of Nanoparticle Enhanced Lubricant Films in Thermal Design of Plain Journal Bearings at High Reynolds Numbers. Symmetry 2019, 11, 1353. https://doi.org/10.3390/sym11111353
Abdollahzadeh Jamalabadi MY, Alamian R, Yan W-M, Li LKB, Leveneur S, Safdari Shadloo M. Effects of Nanoparticle Enhanced Lubricant Films in Thermal Design of Plain Journal Bearings at High Reynolds Numbers. Symmetry. 2019; 11(11):1353. https://doi.org/10.3390/sym11111353
Chicago/Turabian StyleAbdollahzadeh Jamalabadi, Mohammad Yaghoub, Rezvan Alamian, Wei-Mon Yan, Larry K. B. Li, Sébastien Leveneur, and Mostafa Safdari Shadloo. 2019. "Effects of Nanoparticle Enhanced Lubricant Films in Thermal Design of Plain Journal Bearings at High Reynolds Numbers" Symmetry 11, no. 11: 1353. https://doi.org/10.3390/sym11111353
APA StyleAbdollahzadeh Jamalabadi, M. Y., Alamian, R., Yan, W.-M., Li, L. K. B., Leveneur, S., & Safdari Shadloo, M. (2019). Effects of Nanoparticle Enhanced Lubricant Films in Thermal Design of Plain Journal Bearings at High Reynolds Numbers. Symmetry, 11(11), 1353. https://doi.org/10.3390/sym11111353







