Abstract
Security is a main concern for the Internet of Things (IoT) infrastructure as large volumes of data are collected and processed in the systems. Due to the limited resources of interconnected sensors and devices in the IoT systems, efficiency is one of the key considerations when deploying security solutions (e.g., symmetric/asymmetric encryption, authentication, etc.) in IoT. In this paper, we present an efficient Hierarchical Identity-Based Encryption (HIBE) system with short parameters for protecting data confidentiality in distributed IoT infrastructure. Our proposed HIBE system has the public parameters, private key, and ciphertext, each consisting of a constant number of group elements. We prove the full security of the HIBE system in the standard model using the dual system encryption technique. We also implement the proposed scheme and compare the performance with the original Lewko–Waters HIBE. To the best of our knowledge, our construction is the first HIBE system that achieves both full security in the standard model and short parameters in terms of the public parameters, private key, and ciphertext.
1. Introduction
Encryption is a security solution used for data confidentiality protection. There are two types of encryption systems, namely symmetric and asymmetric. A symmetric encryption system uses the same key for encryption and decryption. In an asymmetric encryption (also known as public-key encryption) system, a public key of the data recipient is used for encryption, and the private key is used for decryption. In 1984, Shamir [1] proposed the idea of identity-based cryptography where the identity (ID) of a user is used as a public key, and a third party, called the Private Key Generator (PKG), is responsible for generating a private key for the user. This approach simplifies the problem of managing digital certificates in traditional public key systems. It was only in 2001 that Boneh and Franklin [2] constructed the first Identity-Based Encryption (IBE) scheme from the Weil pairing with chosen ciphertext security in the random oracle model. Many IBE schemes [3,4,5] were then proposed and proven secure in the standard model. Horwitz and Lynn [6] introduced the notion of Hierarchical Identity-Based Encryption (HIBE), which gives more flexibility for users to share and manage sensitive data. In an HIBE scheme, private keys at a lower level of PKG can be issued by a higher level of PKG. This reduces the burden for a single PKG setting of IBE.
One of the main design issues for the HIBE system is to obtain an efficient scheme with short parameters (e.g., public parameters, private key, ciphertext). It is desirable to design an HIBE scheme with parameters that are independent of the maximum hierarchy depth or the depth of user identity. Otherwise, it is not practical to be implemented in the application due to high computation and communication cost. In terms of security, it is desirable to have an HIBE system with full security as compared to selective-identity security. Many previous HIBE schemes have been designed in the direction of achieving the above properties. However, most previous realizations of HIBE systems [7] only provided the above features partially, i.e., achieving constant-size ciphertext (resp. private key), but the private key (resp. ciphertext) still depends on the hierarchy depth.
1.1. Applications
The hierarchical structure and the key delegation property of HIBE make it an ideal security solution for protecting data confidentiality in the emerging computing and network environments, such as cloud storage, smart home systems, mobile networks, and the Internet of Things (IoT) [8,9,10,11,12]. The advantage of an HIBE system is that it provides the scalability of IBE system in a distributed network environment by reducing the workload of a root PKG. This can be achieved by delegating lower-level sub-PKGs for key generation.
Consider the applications in IoT where many sensors and devices are interconnected. HIBE can be deployed in the IoT system such as the unit IoT and Ubiquitous IoT (U2IoT) architecture [13,14] to support secure data storage and exchange. In the U2IoT architecture, multiple interconnected sensors or devices form a unit IoT. A local IoT and industrial IoT comprise multiple unit IoT within a region or an industry, respectively. The local IoT and industrial IoT in a country are integrated by a national IoT to form the ubiquitous IoT. Data collected and exchanged by each IoT system in this architecture are managed by a Unit Data Center (UDC), Local Data Center (LDC), Industry Data Center (IDC), and National Data Center (NDC), respectively.
The root PKG of HIBE can be deployed in NDC, which delegates LDC and IDC as the sub-PKGs. The delegations follow the paths in the hierarchical structure as shown in Figure 1, where the lowest level is formed by the sensors. The NDC is responsible for generating the public parameters of the whole system. It also generates the private keys used by LDC and IDC, respectively. Subsequently, the task of key generation can be delegated to LDC and IDC for generating private keys of the UDC under their management. The private keys used by the sensors at the lowest level can be obtained from their respective UDC. Due to the constraint of the computation capability and power supply of the sensors in the IoT system, it is desirable to implement an efficient and secure HIBE system with short public parameters, private key, or ciphertext.
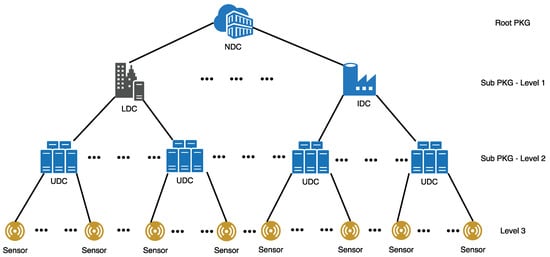
Figure 1.
Hierarchical Identity-Based Encryption (HIBE) application scenario. NDC, National Data Center; LDC, Local Data Center; IDC, Industry Data Center; UDC, Unit Data Center; PKG, Private Key Generator.
1.2. Our Contributions
We present an efficient HIBE system with a constant size of public parameters, private key, and ciphertext based on the composite order group. In particular, both the private key and ciphertext of our proposed HIBE system contain only three group elements, respectively. Our improved HIBE system is constructed by tweaking the HIBE system of Lewko and Waters [7]. The proposed HIBE construction is more efficient than [7] in terms of the runtime for key generation and encryption, as well as the size of public parameters and the private key. We apply the dual system encryption technique to prove the full security under three static assumptions. We believe that our system is the first one that achieves both full security and a constant size of public parameters, private key, and ciphertext.
1.3. Related Work
Horwitz and Lynn [6] first presented the concept of HIBE. In 2002, Gentry and Silverberg [15] constructed the first HIBE scheme, which was proven secure in the random oracle model. An efficient selective-ID secure HIBE without the random oracle was proposed by Boneh and Boyen [16]. Since then, some fully-secure HIBE schemes [17,18] without the random oracle were presented. The security of the above schemes was proven using a partitioning strategy [19], which divided the identity space into identities that were used in the key query phase and challenge phase, respectively. IBE systems that were proven secure using this technique generally had large public parameters, which make them impractical. The partitioning approach is also inadequate to use for proving the security of HIBE systems.
These limitations were highlighted by Waters [19] and solved with his dual-system encryption approach. Waters realized a fully-secure HIBE system with linear-sized ciphertext based on the proof technique in [19]. Lewko and Waters [7] proposed a new technique for dual-system encryption in composite order bilinear groups. They constructed the HIBE system with constant-size ciphertexts without tags. Angelo, Vincenzo, and Giuseppe [20] modified the HIBE construction of [7] to achieve anonymity. Some other recent fully-secure HIBE systems, which were proven using the dual-system encryption technique, include [21,22]. Chen and Wee [21] proposed a compact HIBE scheme in prime-order groups, but the scheme had a linear-sized private key and ciphertext. In [22], a fully-secure and anonymous HIBE scheme with short ciphertexts in prime order (asymmetric) bilinear groups was proposed. However, the size of public parameters and the private key of their HIBE scheme grew linearly with the hierarchy depth.
Park and Lee [23] constructed the first anonymous HIBE with constant-size ciphertext over prime-order groups, which was proven secure without random oracles. The anonymous HIBE scheme proposed in [24] had a constant size of the private key and ciphertext. However, we note that their HIBE construction was only secure against selective-identity-chosen plaintext attack. Hu et al. [25] also proposed an HIBE system that achieved a constant-size ciphertext and private key without random oracle, but the size of the public parameters depended on the hierarchy depth. Since the proposed Revocable Hierarchical Identity-Based Encryption (RHIBE) by Seo and Emura [26], there have been many studies on the construction of more efficient RHIBE in terms of shorter public parameters, private key, update key, or ciphertext [27,28,29,30,31,32].
1.4. Paper Organization
Definitions of the HIBE system and complexity assumptions are briefly reviewed in Section 2. Our improved HIBE scheme is described in Section 3. The security proof is shown in Section 4. Section 5 compares the performance of our construction with the HIBE system in [7]. Section 6 gives the conclusions and an open problem of our improved scheme.
2. Preliminaries
2.1. Bilinear Groups
Let be distinct primes and and be cyclic groups of order . To define composite order bilinear groups [33], we use a group generating algorithm , which takes a security parameter k as input and outputs a tuple , where is a map with the following properties:
- (Bilinear) .
- (Non-degenerate) such that has order N in .
Here, we let , , and denote the subgroups of order , , and in , respectively. Given and for , we have (i.e., the identity element in ). This is known as the orthogonality property, and it will be used in our construction.
2.2. Complexity Assumptions
We use the complexity assumptions introduced in [7] to prove the security of our HIBE system. In the assumptions below, we let denote the subgroup of order in and denote the subgroup of order in .
Assumption 1.
The following distribution is defined based on a group generator :
For an adversary , we define the advantage as follows:
Definition 1.
We say that a group generator satisfies Assumption 1 if for all polynomial time adversaries , we have that is negligible.
Assumption 2.
The following distribution is defined based on a group generator :
For an adversary , we define the advantage as follows:
Definition 2.
We say that a group generator satisfies Assumption 2 if for all polynomial time adversaries , we have that is negligible.
Assumption 3.
The following distribution is defined based on a group generator :
For an adversary , we define the advantage as follows:
Definition 3.
We say that a group generator satisfies Assumption 3 if for all polynomial time adversaries , we have that is negligible.
2.3. Hierarchical Identity-Based Encryption
An HIBE scheme is defined as the following five algorithms:
- GlobalSetup (): On input where k is a security parameter, it returns the public parameters and a master secret key .
- KeyGen (): On input and an identity of depth j, it returns a private key of .
- Delegate: On input , a private key for , and an identity , it returns a private key for =().
- Encrypt (): On input message M, , and identity , it returns a ciphertext C.
- Decrypt: On input and C, it returns the message M.
2.4. Security Definition
The security of HIBE [34] is defined in term of the following game between a challenger and an adversary .
Setup: The challenger runs the GlobalSetup algorithm and obtains the public parameters. also maintains a set S for private keys it has created. Initially, . gives the public parameters to .
Phase 1: issues the following queries:
- Create: The identity vector of depth j is given to by . runs the KeyGen algorithm to generate the key for this identity vector. The key is then added in the set S. A reference of this key is returned to .
- Delegate: specifies a private key in S and gives an identity to . runs the Delegate algorithm to generate a new private key for =( and adds this key to S. It returns a reference of this key to .
- Reveal: specifies an element of the set S. gives this private key to and removes it from S. At this point, no longer needs to make delegation queries for this private key, as it can run the Delegate algorithm by itself.
Challenge: gives two equal-length messages and , as well as a challenge identity to . The restriction is that no revealed identity in Phase 1 is a prefix of this challenge identity. flips a coin and encrypts under . It gives the resulting ciphertext to .
Phase 2: This phase is identical to Phase 1 with the restriction that any revealed identity must not be a prefix of the challenge identity .
Guess. outputs a guess .
If , then wins the game. We define the advantage of an adversary in this game to be:
Definition 4.
A hierarchical identity-based encryption scheme is secure if all polynomial time adversaries have at most a negligible advantage in the above security game.
3. Our Improved HIBE System
Our improved HIBE system achieves short parameters with a constant size of ciphertext, private key, and public parameter. The idea of the HIBE construction is to tweak the original Lewko and Waters HIBE system [7] by reducing the parameters without sacrificing its security. We find out that the aim of adding to the original HIBE [7] is to make the key random in key delegation. We replace with , and the randomness is still the same as the original HIBE where the key has a random in the exponent. Therefore, even when we take out , the key remains fully randomized, and thus, our improved HIBE system also achieves full security.
3.1. Construction
Suppose and denote bilinear groups of order , where are distinct primes. Let be the subgroup of order in and be the bilinear map. The HIBE system is constructed as follows.
- GlobalSetup (): Let k be the security parameter, , and . The public parameters and master secret key are generated as:
- KeyGen (): The key generation algorithm first selects a random and random elements of . It then generates the private key for an identity of depth j by computing:It outputs the private key as .
- Delegate: Given a private key for (), a new key for () is created as follows. The delegation algorithm selects a random and random elements . The new key is computed as: It outputs the private key for as . We fully rerandomize this new key, i.e., the new key is only related to the values of the previous key.
- Encrypt (): To encrypt a message M under the public key , the encryption algorithm selects a random . It computes:
- Decrypt: Given an identity and a ciphertext , it decrypts the ciphertext with the private key by first computing:Based on the orthogonality property, we have and .The message is then recovered by computing:
3.2. Semi-Functional Algorithms
The security of our HIBE system is proven by using the dual system encryption [7,19] methodology. With this proof technique, it is required to define an additional ciphertext and key, namely a semi-functional ciphertext and key. We only use them in the security proof of the HIBE system, but not in the real system.
We denote as a generator of . The semi-functional key is created based on the normal private key that was generated by the key generation algorithm. We then select exponents and generate the semi-functional key as:
The semi-functional ciphertext is created based on the normal ciphertext generated by the encryption algorithm. We then select exponents and generate the semi-functional ciphertext as:
The decryption of a semi-functional ciphertext under a semi-functional key is computed by multiplying the blinding factor with . We will obtain a correct decryption if .
4. Security Analysis
The security proof of our HIBE system is shown with a sequence of games from – that are played between an adversary and a challenger . We will show that no polynomial-time adversary can distinguish one game from the next under a complexity assumption.
: The first game is the usual security game used for defining HIBE security. In this game, normal private keys and the challenge ciphertext are used between and .
: This game is the same as with the exception that all key queries will be answered by fresh calls to the key generation algorithm (the challenger will not be asked to delegate keys in a particular way).
: This game is almost identical to except that the adversary is restricted from making key queries for identities, which are prefixes of the challenge identity modulo .
: is similar to , except the following changes: 1. The first k keys are semi-functional for k from 0–w, where w denotes the number of key queries made by . The rest of the keys are normal. 2. The ciphertext given to is semi-functional. In , all of the keys are normal. and a semi-functional challenge ciphertext is given to . In , all the keys and challenge ciphertext given to are semi-functional.
: This game is the same as , except that the challenger gives a semi-functional encryption of a random message to as the challenge ciphertext. The random message is independent of the messages provided by .
Lemma 1.
For any adversary , .
Proof.
Keys that are returned to ’s queries are identically distributed whether they are generated by the Delegate algorithm from a previous key or from a fresh call to the KeyGen algorithm. ’s view in is identical to its view in . □
Lemma 2.
Suppose there exists an adversary such that . Then, we can build an algorithm with advantage in breaking Assumption 2.
Proof.
Suppose has a probability of producing identities and such that modulo N and divides . can then determine a nontrivial factor of N by computing . Let . We consider the following three cases:
- one of is , and the other is ;
- one of is , and the other is ;
- one of is , and the other is .
Given and T, where or , can simulate the security games with and determine which of the above cases has occurred as follows:
- Case 1: first tests whether or . If either one of these equalities holds, then Case 1 occurs. subsequently tests whether (we assume without loss of generality that and ). If the equality holds, determines that . Otherwise, .
- Case 2: first tests whether or . If neither of these holds and the test for Case 1 fails, then Case 2 occurs. Next, can determine which of a, b is equal to by testing which of , is the identity. Without loss of generality, we assume that and . subsequently tests whether . If the equality holds, determines that . Otherwise, .
- Case 3: If the tests for Cases 1 and 2 fail, then Case 3 occurs. can then determine which of a, b is equal to by testing which of , is the identity. We assume without loss of generality that . subsequently tests whether . If the equality holds, determines that . Otherwise, .
□
Lemma 3.
Suppose there exists an adversary such that . Then, we can build an algorithm with advantage in breaking Assumption 1.
Proof.
Given and T, where or , or is simulated as follows. first selects random exponents . It then sets . keeps the master secret key . It sends the public parameters = {} to .
’s queries for the private key of identity are answered by as follows: selects random exponents and and sets:
At some point, receives a challenge identity and two messages , from . chooses a random and returns the challenge ciphertext as follows:
If , the simulated semi-functional ciphertexts could match the primary semi-functional ciphertexts as follows:
The ciphertext is semi-functional with T implicitly set as and in . This is properly distributed as is not correlated with and . If , then the ciphertext is normal in with T implicitly set as . Therefore, these possibilities for T can be distinguished by using the output of . □
Lemma 4.
Suppose there exists an adversary such that . Then, we can build an algorithm with advantage in breaking Assumption 2.
Proof.
Given and T, where or , or is simulated as follows. selects random exponents and sets . sends the public parameters = {} to and keeps the master secret key .
answers ’s key query for identity as follows:
- For , selects random exponents first and then creates a semi-functional key as:The semi-functional key is properly distributed with . We note that values of t and zmodulo and modulo are uncorrelated by the Chinese remainder theorem.
- For , runs the KeyGen algorithm to generate a normal key.
- For , sets first and then creates the following key by choosing random exponents :If , it means that T is implicitly set as and the key is normal. If , it means that T is implicitly set as and we have a semi-functional key.
At some point, receives a challenge identity and two messages , from . chooses a random and returns the challenge ciphertext as follows:
This means that and are implicitly set in the challenge ciphertext. Since is not a prefix of the challenge , and are independent and randomly distributed.
If generates a semi-functional ciphertext for and attempts to test whether the key is semi-functional by trying the decryption, then we will have , which makes the decryption always work regardless.
If , then has properly simulated . If , then has properly simulated . Therefore, these possibilities for T can be distinguished by using the output of . □
Lemma 5.
Suppose there exists an adversary such that . Then, we can build an algorithm with advantage in breaking Assumption 3.
Proof.
Given and T, where or T is a random element of , simulates or with as follows. It chooses random exponents and sets . sends the public parameters = {} to .
’s queries for the private key of identity are answered by as follows: randomly selects exponents , and sets a semi-functional key as:
This means that it implicitly sets . At some point, receives a challenge identity and two messages , from . chooses a random and returns the challenge ciphertext as follows:
This implicitly sets . We note that and are elements of , so when a and b are randomly chosen from , the values of and and the value are random and independent.
If , then we have a properly-distributed semi-functional ciphertext under the message in . If T is a random element of , then we have a semi-functional ciphertext under a random message in . Therefore, these possibilities for T can be distinguished by using the output of . □
Theorem 1.
If Assumptions 1–3 hold, then the proposed HIBE system is secure.
Proof.
If Assumptions 1–3 hold, then we have shown by the previous lemmas that the real security game is indistinguishable from , in which the value of is information-theoretically hidden from the adversary. Hence, the adversary can obtain no advantage in breaking the HIBE system. □
5. Performance Comparison
We provide a performance comparison of our improved HIBE system with other HIBE systems proposed in [7,19,22,25]. The efficiency comparison is summarized in Table 1. Let n be the maximum depth of the HIBE and d be the depth of identity vector. “ size”, “ size”, and “ size” denote the length of public parameters, private key, and ciphertext, respectively. We use P, E, and to represent the computational cost of a bilinear pairing, a -exponentiation, and a -exponentiation operation respectively for the KeyGen, Encrypt, and Decrypt algorithms.

Table 1.
Efficiency comparison between existing and our improved HIBE system.
The public parameters size of [19] contains group elements. The private key size of [19] is . The public parameters and private key of [7] contain and group elements, respectively. The public parameters size of [25] is , where b is the bit length of an identity. However, the private key size of [25] is . In [22], the public parameters size is and the private key contains group elements. In contrast, our improved HIBE system only requires constant-size public parameters and private key (i.e., independent of the depth of the hierarchy). In particular, public parameters and private key in our HIBE system contain only four and three group elements, respectively. All the HIBE systems in this comparison have constant-size ciphertext except [19] with of ciphertext size.
All of the three computational costs for [19] grow linearly with the depth of the identity vector. The computational costs of the Decrypt algorithm for [7,22,25] and our improved HIBE systems are all independent of the hierarchy depth. However, our improved HIBE system achieves better computation efficiency for the KeyGen and Encrypt algorithms as they are independent of the depth of the hierarchy and identity vector, respectively.
We implemented our improved HIBE system on a Windows 10 PC with a CPU of Intel Core i7-7700 (3.60 GHz) and memory of 16GB. We ran the KeyGen and Encrypt algorithms for different hierarchy depths () and recorded the run time as shown in Table 2 and Table 3, respectively. As shown in Figure 2 and Figure 3, the run times of the KeyGen and Encrypt algorithms for our improved HIBE system were much faster than the original HIBE system in [7].

Table 2.
The private key generation time of [7] and our improved HIBE system.

Table 3.
The encryption time of [7] and our improved HIBE system.
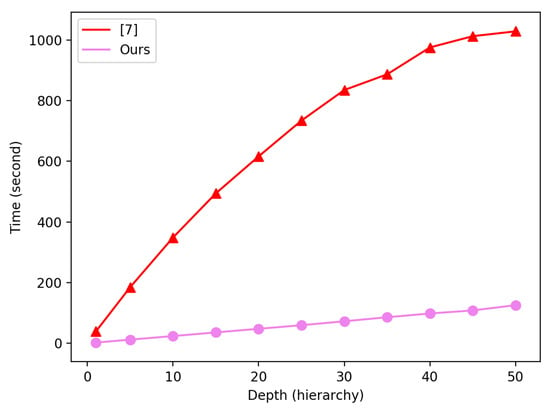
Figure 2.
Run time of the KeyGen algorithm for [7] and our improved HIBE system.
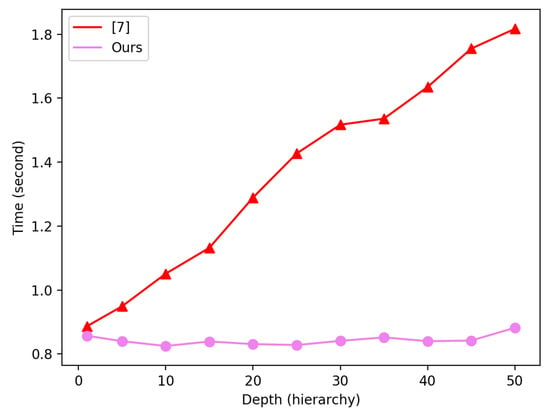
Figure 3.
Run time of the Encrypt algorithm for [7] and our improved HIBE system.
6. Conclusions and Future Work
Deploying efficient data protection mechanisms are the main challenges for a complex and heterogeneous Internet of Things infrastructure. We proposed an efficient HIBE system with short parameters where the public parameters, private key, and ciphertext are all independent of the hierarchy or identity depth. We proved the security of the improved system using the dual-system encryption technique. This is the only HIBE system simultaneously achieving full security in the standard model and providing -sized public parameters, private key, and ciphertext. Our improved HIBE construction is based on composite order groups. In general, an HIBE construction in prime order groups can achieve similar security levels with a smaller size of group elements. This may result in shorter ciphertexts, and the decryption is more efficient as compared to an HIBE system constructed over composite order groups [23]. Therefore, it would be interesting to explore the construction of an HIBE system based on prime order groups that can achieve all these properties simultaneously.
Author Contributions
Writing, original draft preparation, L.G. and J.W.; writing, review and editing, W.-C.Y.
Funding
Lifeng Guo was supported by National Science Foundation of China (Grant No. 61202365), Project for Returned Overseas of Shanxi Province (2015-015), Natural Science Foundation of Shanxi Province, China (Grant No. 201701D12052), and National Natural Science Foundation of China (Grant No. 61872226).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
References
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Advances in Cryptology; Springer: Berlin/Heidelberg, Germany, 1984; pp. 47–53. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-Based Encryption from the Weil Pairing. In Advances in Cryptology-CRYPTO 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Boneh, D.; Boyen, X. Secure Identity Based Encryption Without Random Oracles. In Advances in Cryptology—CRYPTO 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 443–459. [Google Scholar]
- Gentry, C. Practical Identity-Based Encryption Without Random Oracles. In Advances in Cryptology—EUROCRYPT 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 445–464. [Google Scholar]
- Waters, B. Efficient Identity-Based Encryption Without Random Oracles. In Advances in Cryptology—EUROCRYPT 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 114–127. [Google Scholar]
- Horwitz, J.; Lynn, B. Towards Hierarchical Identity-Based Encryption. In Advances in Cryptology—EUROCRYPT 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 466–481. [Google Scholar]
- Lewko, A.; Waters, B. New Techniques for Dual System Encryption and Fully Secure HIBE with Short Ciphertexts. In Theory of Cryptography—TCC2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 455–479. [Google Scholar]
- Daniel, R.M.; Rajsingh, E.B.; Silas, S. Analysis of Hierarchical Identity Based Encryption Schemes and Its Applicability to Computing Environments. J. Inf. Secur. Appl. 2017, 36, 20–31. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Zhang, Y. SecHome: A Secure Large-Scale Smart Home System Using Hierarchical Identity Based Encryption. In Information and Communications Security; Springer: Cham, Switzerland, 2018; pp. 339–351. [Google Scholar]
- Sha, K.; Wei, W.; Yang, T.A.; Wang, Z.; Shi, W. On Security Challenges and Open Issues in Internet of Things. Future Gener. Comput. Syst. 2018, 83, 326–337. [Google Scholar] [CrossRef]
- Trnka, M.; Cerny, T.; Stickney, N. Survey of Authentication and Authorization for the Internet of Things. Secur. Commun. Netw. 2018, 2018, 4351603. [Google Scholar] [CrossRef]
- Yu, F.R.; Tang, H.; Mason, P.C.; Wang, F. A Hierarchical Identity Based Key Management Scheme in Tactical Mobile Ad Hoc Networks. IEEE Trans. Netw. Serv. Manag. 2010, 7, 258–267. [Google Scholar] [CrossRef]
- Ning, H.; Liu, H.; Yang, L.T. Aggregated-Proof Based Hierarchical Authentication Scheme for the Internet of Things. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 657–667. [Google Scholar] [CrossRef]
- Yang, L.T.; Liu, H.; Ning, H. Cyberentity Security in the Internet of Things. Computer 2013, 46, 46–53. [Google Scholar]
- Gentry, C.; Silverberg, A. Hierarchical ID-Based Cryptography. In Advances in Cryptology—ASIACRYPT 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 548–566. [Google Scholar]
- Boneh, D.; Boyen, X. Efficient Selective-ID Secure Identity-Based Encryption Without Random Oracles. In Advances in Cryptology—EUROCRYPT 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 223–238. [Google Scholar]
- Chatterjee, S.; Sarkar, P. HIBE With Short Public Parameters Without Random Oracle. In Advances in Cryptology—ASIACRYPT 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 145–160. [Google Scholar]
- Sarkar, P.; Chatterjee, S. Construction of a Hybrid HIBE Protocol Secure against Adaptive Attacks: without Random Oracle. In First International Conference on Provable Security—ProvSec 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 51–67. [Google Scholar]
- Waters, B. Dual System Encryption: Realizing Fully Secure IBE and HIBE under Simple Assumptions. In Advances in Cryptology—CRYPTO 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 619–636. [Google Scholar]
- De Caro, A.; Iovino, V.; Persiano, G. Fully Secure Anonymous HIBE and Secret-Key Anonymous IBE with Short Ciphertexts. In Pairing-Based Cryptography—Pairing 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 347–366. [Google Scholar]
- Chen, J.; Wee, H. Dual System Groups and its Applications—Compact HIBE and More. 2014. Available online: https://eprint.iacr.org/2014/265.pdf (accessed on 18 June 2019).
- Lee, K.; Park, J.H.; Lee, D.H. Anonymous HIBE with Short Ciphertexts: Full Security in Prime Order Groups. Designs Codes Cryptogr. 2015, 74, 395–425. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, D.H. Anonymous HIBE: Compact Construction Over Prime-Order Groups. IEEE Trans. Inf. Theory 2013, 59, 2531–2541. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, Y.; Wu, Q. Compact Anonymous Hierarchical Identity-Based Encryption with Constant Size Private Keys. Comput. J. 2016, 59, 452–461. [Google Scholar] [CrossRef][Green Version]
- Hu, X.; Wang, J.; Xu, H.; Yang, Y. Constant Size Ciphertext and Private Key HIBE without Random Oracles. J. Inf. Sci. Eng. 2014, 30, 333–345. [Google Scholar]
- Seo, J.H.; Emura, K. Revocable Hierarchical Identity-based Encryption. Theor. Comput. Sci. 2014, 542, 44–62. [Google Scholar] [CrossRef]
- Jia, H.; Chen, Y.; Lan, J.; Huang, K.; Wang, J. Efficient Revocable Hierarchical Identity-Based Encryption using Cryptographic Accumulators. Int. J. Inf. Secur. 2018, 17, 477–490. [Google Scholar] [CrossRef]
- Lee, K.; Park, S. Revocable Hierarchical Identity-Based Encryption with Shorter Private Keys and Update Keys. Designs Codes Cryptogr. 2018, 86, 2407–2440. [Google Scholar] [CrossRef]
- Park, S.; Lee, D.H.; Lee, K. Revocable Hierarchical Identity-Based Encryption from Multilinear Maps. arXiv 2016, arXiv:1610.07948. [Google Scholar]
- Wang, C.; Li, Y.; Jiang, S.; Wu, J. An Efficient Adaptive-ID Secure Revocable Hierarchical Identity-Based Encryption Scheme. In Proceedings of the International Conference on Smart Computing and Communication (SmartCom 2016), Shenzhen, China, 17–19 December 2019; pp. 506–515. [Google Scholar]
- Xing, Q.; Wang, B.; Wang, X.; Chen, P. Unbounded Revocable Hierarchical Identity-Based Encryption with Adaptive-ID Security. In Proceedings of the IEEE 18th International Conference on High Performance Computing and Communications, Sydney, Austrilia, 12–14 Decmber 2016; pp. 430–437. [Google Scholar]
- Xing, Q.; Wang, B.; Wang, X.; Tao, J. Unbounded and Revocable Hierarchical Identity-Based Encryption with Adaptive Security, Decryption Key Exposure Resistant, and Short Public Parameters. PLoS ONE 2018, 13, e0195204. [Google Scholar] [CrossRef] [PubMed]
- Boneh, D.; Goh, E.-J.; Nissim, K. Evaluating 2-DNF Formulas on Ciphertexts. In Theory of Cryptography—TCC2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 325–341. [Google Scholar]
- Shi, E.; Waters, B. Delegating Capabilities in Predicate Encryption Systems. In Automata, Languages and Programming—ICALP2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 560–578. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).