Abstract
Pool hopping attack is the result of miners leaving the pool when it offers fewer financial rewards and joining back when the rewards of mining yield higher rewards in blockchain networks. This act of leaving and rejoining the pool only during the good times results in the miner receiving more rewards than the computational power they contribute. Miners exiting the pool deprive it of its collective hash power, which leaves the pool unable to mine the block successfully. This results in its competitors mining the block before they can finish mining. Existing research shows pool hopping resistant measures and detection strategies; however, they do not offer any robust preventive solution to discourage miners from leaving the mining pool. To prevent pool hopping attacks, a smart contract-based pool hopping attack prevention model is proposed. The main objective of our research is maintaining the symmetrical relationship between the miners by requiring them all to continually contribute their computational power to successfully mine a block. We implement a ledger containing records of all miners, in the form of a miner certificate, which tracks the history of the miner’s earlier behavior. The certificate enables a pool manager to better initiate terms of the smart contract, which safeguards the interests of existing mining pool members. The model prevents frequent mine hoppers from pool hopping as they submit coins in the form of an escrow and risk losing them if they abandon the pool before completing mining of the block. The key critical factors that every pool hopping attack prevention solution must address and a study of comparative analysis with existing solutions are presented in the paper.
1. Introduction
Blockchain is a distributed data redundant storage mechanism that ensures integrity. It was unveiled to the world as a key concept of bitcoin cryptocurrency, including the proof-of-work (POW) consensus algorithm, for mining blocks in the blockchain-based cryptocurrency network, and it can prevent double spending attack [1]. The initial blockchain design was for individual mining. However, individual mining resulted in only a few major miners receiving rewards, and profits for mining are unpredictable [2]. A miner is unable to solve the block puzzle individually, while a group of miners are collectively able to successfully mine the block. Therefore, miners created collaboration amongst each other called a Mining Pool to earn steady rewards and reduce the individual requirement of resources to mine the blocks [3]. The perfect symmetry between the miners collectively contributing their hash power enables them to complete mining of the block before other competing mining pools. It also impacts a positive change, where miners are now able to receive mining rewards periodically. In the mining pool, if mining is successful, the miners in the pool share mining rewards according to a specific criterion. These are pay per share (PPS), pay per last n shares (PPLNS), and predictable [4].
Predictable solo mining (PSM) as the criteria for sharing rewards is where each pool adopts different rules and regulations [5,6]. Such mining pools account for 65.8% of Bitcoin’s total mining rate and 76.9% of Ethereum’s overall mining rate, which significantly affect blockchain maintenance [7].
There are multiple attacks that target mining pools known as pool hopping, block withholding attack (BWH) [8], and fork after withholding (FAW) attack [9]. Among these attacks, principally, pool hopping attacks are known to be fatal to the blockchain mining pools. Pool hopping attacks operate when a miner hops across different mining pools and participates only when the expected income of the pool is high and leaves when the predicted income is low. These malicious miners can still be rewarded even after leaving or participating in the pool, which places the honest miner at a disadvantage who continually participates in the mining pool. If the mining pool hopping attack is left unchecked, there is no reason for an honest miner to stay in a pool. Consequently, if everyone does pool hopping, then only individual miners will remain, and the honest miner will lose money and leave the blockchain mining pool. If only individual miners remain, they will not participate in mining blockchain blocks, as individual mining requires very high computational resources, which many cannot afford. If few miners remain, then they cannot guarantee the integrity of the blockchain and make it unmanageable to maintain the Blockchain [10,11]. Therefore, a pool hopping attack must be prevented to maintain the blockchain network.
However, existing research proposes methods for detecting pool hopping attacks using the presence of return transaction ordering based deanonymization technology, time-based and reputation-based detection methods, and pool-resistant measures whose goal is only to detect the attack. The detection of pool hopping is not only a chief requirement but also important to prevent it from taking place in future [12].
The system proposed in this paper introduces the concepts of Hop_Count and coins submitted as an escrow. Hop_Count is the number that increases when the miner leaves the mining pool, and this determines how many coins must be submitted as an escrow [13]. The miner submits coins as escrow and will be deprived of them when they abandon the mining pool. In other words, the coin stored in the escrow serves as a deposit and allows the miner to stay in only one pool so as not to lose the deposited money.
In this paper, the problem of mining pools experiencing the lack of a solution to prevent pool hopping attacks is addressed. Miners leave the mining pool for personal financial benefits, reducing the computational power of the mining pool. The loss of hash power results in the mining pool losing the block rewards to their competitors.
The paper addresses the described problem and contributes in the following manner:
- Pool hopping attacks and existing studies to mitigate these attacks are described in detail.
- To prevent future pool hoping attacks, we describe a smart contract-based pool hopping attack prevention model.
- A detailed numerical equation is provided to evaluate the miner risk to the mining pool and how to calculate the escrow amount a miner will submit as part of the smart contract agreement.
- Three key consideration factors, computational power, miner risk, and accountability, are analyzed to demonstrate the effectiveness of our proposed model.
- A practical case study based on an Internet of Things smart home network is presented, which illustrates how the proposed model’s methodology will function in a real-world scenario.
- A comparative analysis with existing solutions and the proposed model is presented.
- The limitations of the proposed model and future directions of the research are discussed.
This paper is organized as follows: Section 2 describes related works on pool hopping attacks and key considerations to implement the proposed model solution. In Section 3, the proposed framework and methodology for smart contract-based pool hopping attack prevention is introduced for blockchain networks. In Section 4, a detailed practical case study based on an IoT smart home network is presented to evaluate our proposed model along with a comparative analysis with existing studies. The limitations of the research and future directions are also discussed. Finally, we conclude our paper in Section 5.
2. Related Work
In this section, various related studies done to address pool hopping attacks are explained in detail. These attacks discuss detection strategies and pool hopping resistant measures. Furthermore, we also discuss the key factors that must be considered when providing any pool hopping attack-based prevention solution. These key considerations lay the foundation based on which, if fulfilled, ensures that the pool hopping attack-based prevention model is effective and feasible to practically implement in a mining pool.
2.1. Pool Hopping Attack
Many researchers have studied and discussed protocols and methods regarding mining pool-based pool hopping attacks. Belotti et al. [14] proposed a methodology to analyze pool hopping and focused primarily on detection of pool hoppers in mining. They present a detection strategy based on an epoch system, which refers to a specific time period, to determine if a miner received rewards from different mining pools. They analyzed those bitcoin transactions in the Coinbase wallet where mining pools send rewards to its participants. Based on their proposed model, it is possible to determine the time epoch where miners worked. Slush’s method [15] proposed a scoring system that is used to give rewards to miners at the end of every round. Salimitari et al. [16] proposed a prospect theory to predict the profit for a specific miner by giving his hash rate power and electricity costs. It primarily focused on Bitcoin cryptocurrency and its mining pools. Rosenfeld et al. [17] described a scoring system that is used to calculate rewards of participants when mining a bitcoin cryptocurrency-based pool. They proposed a geometric algorithm based on the scoring system like Slush’s method for resisting pool hopping, with the exception that the score assigned for any current or future share remained the same. Luu et al. [18] proposed a smart pool based novel protocol for a decentralized mining pool using smart contracts in an autonomous blockchain program for decentralized cryptocurrency mining.
Existing studies are unable to prevent the formation of an asymmetrical relationship between the miners as they suggest solutions which either only detect pool hoppers or calculate an individual miner’s rewards. They do not prevent a miner from leaving the mining pool, resulting in loss of collective computational power. Each miner expects other miners to contribute the maximum amount of their computational power to mine the block before other competing mining pools.
2.2. Key Considerations
There are three key factors that must be considered for an effective pool hopping prevention measure. They are computational power, security, and accountability. The importance of the identified key considerations is as below:
- Computational power: Miners require a certain amount of computational power to solve cryptographic puzzles to block a mine successfully [19,20]. To increase their chances of success, they join with other miners to mine collectively. If the miner or a group of miners abandon the mining pool, the collective computational power will be reduced severely. Mining pools compete with other pools to block the mine first. The first one to successfully block receives the rewards. Hence, a loss of computational power jeopardizes the primary objective of solving the block puzzle first.
- Miner risk: Mining pools face varying hash powers, and there are delays in mining the block (i.e., the mining needs more than the average time required to mine the block). It is important to ensure that a new miner who joins the mining pool is not a risk in the future. A miner with a record of abandoning pools and joining back later should either not be allowed to join or be asked to agree to terms that prevent them from leaving. A pool manager must be able to determine the risk factor of allowing a miner to join the mining network [21].
- Accountability: There is a need for an accountability measure for each miner that abandons the mining pool to achieve greater financial rewards for their personal economic growth. The need for this consideration is to perform as a preventive method ensuring the miner determining to leave the pool is at a significant disadvantage and the existing miners in the mining pool get adequately and evenly rewarded during such an event.
Based on the analysis of the research mentioned above, there are currently no existing prevention measures to prevent pool hoppers from leaving the mining pool prematurely. While they can successfully detect mine hoppers or offer a pool hopping resistant solution, there is no proposed methodology to deter them from repeating the same behavior.
3. Smart Contract-Based Mining Pool Hopping Prevention Model
In this section, the prevention model using smart contracts is proposed, which places a severe penalty on the miner and gives economic benefits to the mining pool in the event the miner leaves the mining pool before solving the block puzzle.
In the proposed model we prevent serial pool hopping attacks from occurring in a blockchain-based network for cryptocurrency. Malicious miners take advantage of the reward distribution method of successfully mining a block, which results in revenue reduction to honest and successful miners. To counter this, a smart contract-based pool hopping attack prevention model is proposed. The benefits of the proposed model are (1) the pool manager keeps a record of the behavior of each miner before allowing them to join the mining pool, (2) it prevents the most frequent of mine hoppers from abandoning the mining pool as they are required to submit coins as escrow, which are seized as punishment if they commit a pool hopping attack, and (3) a detailed numerical model is presented, which helps to calculate the exact escrow amount for each miner.
3.1. Design Overview
The proposed smart contract-based pool hopping attack prevention model illustrated in Figure 1 comprises the following four steps. Firstly, the miner requests to join a mining pool. Secondly, the pool manager requests the miner to submit the miner address, which is linked with the block address stored on a local database by the pool manager. The pool manager using the block address locates the miner certificate from the blockchain network. Thirdly, in the event the miner has a high hop count and previous smart contracts violated (i.e., has repeatedly hopped mining pools and has a high count of previous smart contracts violated), they will be asked to agree to terms of a smart contract enforcing them to submit coins as escrow to protect the mining pool. Finally, the pool manager will update the mining certificate and return or take hold of the submitted coins based on the miner’s behavior. The proposed model preserves the symmetry of the mining pool by preventing miners from leaving and withdrawing their computational power. Existing methods present detection strategies; however, they do not present a robust solution that helps prevent any future pool hopping attacks.
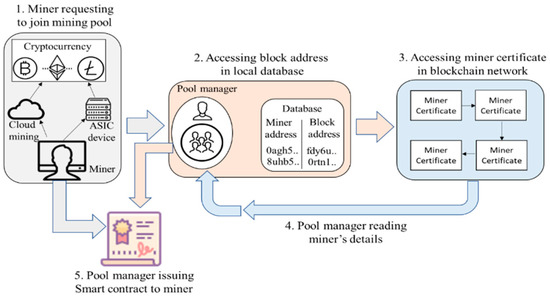
Figure 1.
Design overview of the proposed model.
This model operates on the basis that the pool managers have a ledger that allows them to find a miner’s certificate using the miner’s address. Using the example of Ethpool wallet, a popular Ethereum-based blockchain wallet, the miner’s address would be where they receive block rewards. This is the address based on which they receive coins as a reward for successfully mining a block or through other transactions with other users. The miner’s address is unique to each miner’s certificate, and no two certificates contain the same miner’s address.
When the miner leaves a mining pool, the pool manager will update the certificate based on the behavioral outcome of the miner. The updated certificate will be submitted to the blockchain network, and the block address is stored on the local database managed by the pool manager. The miner’s certificate contains the following details: miner’s address, hop count, previous smart contracts upheld, and previous smart contracts violated.
If a miner requests to join a new mining pool, the pool manager requests the miner to submit their miner address. Using the address, the pool manager looks up the local database for the hash value to the block which contains the miner certificate on the blockchain network. Based on the miner certificate details, the pool manager will issue a new smart contract.
If the miner is a new miner in the cryptocurrency network and wishes to join a mining pool, they will be issued a new certificate after they complete the mining process or abandon it. The pool manager will update the certificate and submit it as a transaction on the blockchain network. The block address containing the miner certificate is stored on the local database linked with the miner’s address. This ensures that no other entity can modify the details of the miner’s certificate.
A pool manager may allow a miner who has frequently hopped many mining pools to join their pool network. This is based on the condition that the miner agrees to accept the terms of a smart contract where they will submit coins as an escrow. The contract requires that the miner is to remain with the mining pool network until the block is not mined. Upon successful mining of the block, the coins submitted are returned to the miner, including the rewards for mining the pool. In the event the miner does not honor the contract, they will lose all their coins. The coins are then distributed to all existing miners within the network.
3.2. Methodological Flow of the Proposed Model
In this subsection, the methodological flow of the proposed model consists of three separate modules and addresses three major concerns. The modules are: (1) evaluation, which defines how the pool manager assesses miner risk to the mining pool, (2) terms, which specifies the escrow value to be calculated for the miner, and (3) update, which specifies the method to revise the miner certificate based on two different scenarios, as shown in Figure 2. In our suggested model, a ledger is maintained by and is accessible by only pool managers for accessing a miner’s certificate with read/write access. The pool manager accesses the miner’s details based on the miner address given by the miner. The miner’s certificate contains the following details:
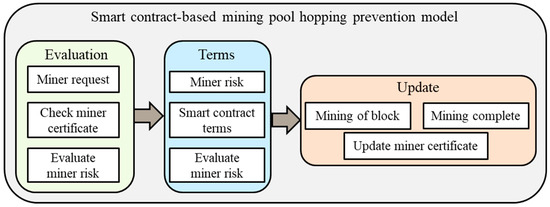
Figure 2.
Methodological overview of the proposed model.
- Miner’s Address: This address is based on the certificate that will be identified as belonging to the miner. Each certificate is bound to a single miner address, and one miner address cannot be associated with a second certificate. This ensures that a serial pool hopping miner cannot request for a new certificate by the pool manager to mask their malicious behavior.
- Hop_Count: The hop-count shows the number of times a miner has hopped a mining pool in their entire history. It is a reputation-based count that is updated by the pool manager to reflect the miner’s behavior. If the miner hops the pool, the count increases by one, and if the miner does not leave the pool until the mining process is complete, the Hop_Count will reduce by one. If the miner has no Hop_Count (i.e., it is zero), the count will remain at zero if the mining process is complete.
- Smart contract upheld (SCupheld): This shows the count of how many times the miner has fulfilled previous smart contracts signed with previous pool managers. If the count of contracts fulfilled is high, then the current pool manager will keep the escrow amount low, as the miner appears trustworthy.
- Smart contract violated (SCviolated): This shows the times the miner has violated the terms of the smart contract by hopping the mining pool. If the count is high, then the pool manager may increase the escrow amount to safeguard the interests of the mining pool.
The methodology, as shown in Figure 3, Figure 4 and Figure 5 for the proposed model, is a multistep process based on three modules. The modules describe the point from when the pool manager evaluates the miner requesting to join the mining pool, the conditions to be established for the smart contract, and the updating of the miner certificate based on the miner’s contribution to the mining pool and Miner risk, Escrow deposit, Mner attack, Self miner are notify in Table 1. We now discuss the three modules (1) evaluation, (2) terms, and (3) update as follows:
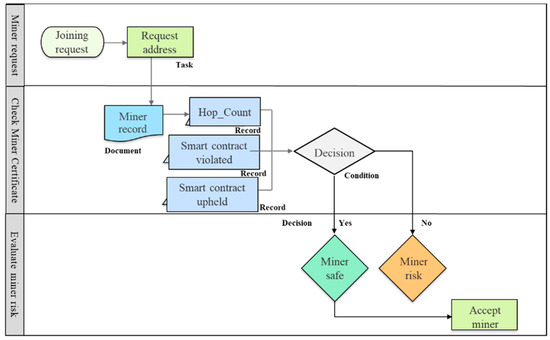
Figure 3.
Evaluation of the miner in the proposed model.
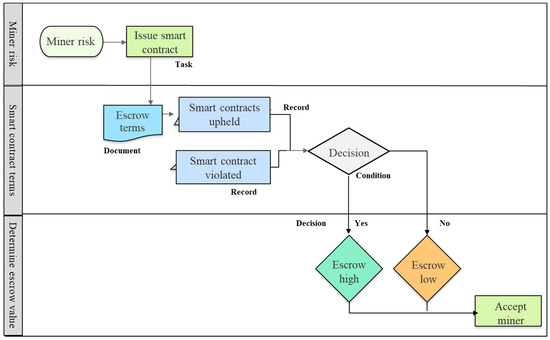
Figure 4.
Terms of the smart contract for the miner in the proposed model.
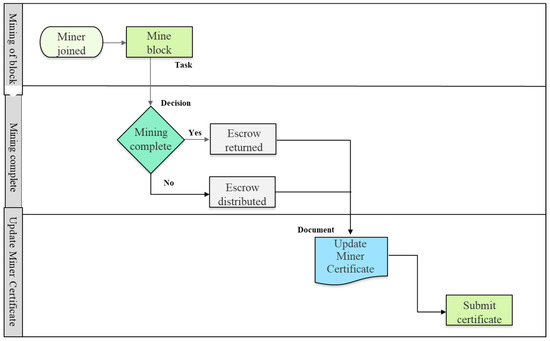
Figure 5.
Updating the miner’s certificate in the proposed model.

Table 1.
Notation table.
- Evaluation. When a miner requests to join the mining pool, as shown in Figure 3, the pool manager is required to evaluate the risk factors of allowing the miner to join. The manager will determine the trustworthiness of the miner to remain as part of the mining process until block mining is complete. This module is based on a three-step process, which is as follows:
- Miner request. The miner will request the pool manager to join the network. If the miner has a past mining record, it will have a pre-issued miner certificate that will present past behavior of the miner. If, however, the miner is a first-time miner, the pool manager will issue a new miner certificate. The pool manager will request the miner to submit their miner’s address in order to locate the miner’s certificate from the ledger. This ledger is stored locally on the database by the pool manager. Each miner certificate is unique to each miner’s address. A request to the miner’s address does not violate the privacy of the miner as this address is essential for the miner to receive the rewards for successfully mining a block.
- Check miner certificate. The pool manager accesses the ledger stored in the local database using the miner’s address to locate the block address. Using the block address, the pool manager locates the miner’s certificate stored as data on the blockchain network. The pool manager will primarily check the Hop_Count of the miner, count of previous SCupheld and count of SCviolated. The pool manager decides about the miner based on the value of the Hop_Count and SCviolated to determine if the miner is safe or a risk to the entire mining pool.
- Evaluate miner risk. The pool manager will evaluate if the miner is a risk to the mining pool. The manager will check the count of two elements, Hop_Count (α) and SCviolated (β). If both values α and β are zero, the miner is evaluated as safe and joins the mining pool. If, however, the miner certificate displays α and β as one or above, the miner is assessed as a risk to the mining pool. Miner risk is calculated using the following Equation (1):Mrsk = α + β.
Miner risk is denoted by Mrsk and is evaluated based on two conditions: (1) the miner is safe and (2) the miner is a risk to the mining pool. Two different case studies are presented to explain both conditions. To satisfy the first condition, we assume that the miner is joining the mining pool for the first time. The α and β values are presumed zero, and Mrsk is calculated as zero. The miner is safe to join the mining pool.
To fulfil the second condition, we assume that the miner has previously abandoned the mining pool at least once. The α and β values are one; thus, Mrsk is calculated as two. The miner is evaluated as a high risk to the mining pool.
- Terms. In this module, as shown in Figure 4, the terms of the smart contract are decided for the miner, who is evaluated as a risk to the mining pool because of a high Hop_Count value. The miner is required to submit coins as an escrow, which serves as a means of enforcing a financial penalty if the miner leaves the mining pool without completing the mining of the block. An escrow is a condition in the smart contract that is enforced if the terms of the smart contract are fulfilled. The coins are stored in the smart contract digital agreement as a safety measure to protect the interests of the existing members of the mining pool. The miner risks losing the coins if they leave the mining pool early. This module is based on a three-step process, which is as follows:
- Miner risk. The Hop_Count of the miner is determined to be at one or above, and such they are a risk to the mining pool. The miner exhibits behavior that could potentially hop the mining pool when it is not suitable for them and return when the rewards are high. The pool manager will issue a smart contract, based on which the miner must agree to a set of terms, to be allowed to join the mining pool.
- Smart contract terms. The primary requirement of a smart contract between the mining pool and the new miner is the need for escrow. To present a reliable defensive measure against pool hopping attacks, a miner with a high Hop_Count value must submit a certain amount of coins in the smart contract. The risk of losing the coins acts as a discouraging measure for the miner to hop or abandon the mining pool. The pool manager will observe the number of previous smart contracts upheld and broken by the miner. The count of previous honored smart contracts demonstrates that even if the miner has a record of a high Hop_Count, their behavior from the last mining pools is that of a trustworthy miner.
- Determine escrow value. The primary requirement in a smart contract between the mining pool and the new miner is the need for an escrow. The miner submits coins as a means of a security deposit where if the miner abandons the mining pool, they will forfeit the coins in escrow. A miner with a Hop_Count and SCviolated value of one and above is required to submit coins as an escrow. In our proposed method, the value of SCviolated cannot go below one. If a miner abandons the mining pool once, they are required to submit at least one coin in escrow. The escrow amount is calculated using the following Equation (2):
Escrow value is denoted by Es_dep, and it is based on three conditions: (1) the miner pays zero coins as escrow, defined as Mrsk = 0, (2) the escrow amount for a high-risk miner is two or greater, defined as Mrsk being two or above, and (3) the miner is a low-risk miner and is required to pay one coin as escrow, defined as Mrsk = 1.
To satisfy the first condition, the miner joined the mining pool for the first time and has a Hop_Count value (α), SCviolated value (β), and SCupheld value (μ) of zero. Using Equation (2), we determine that the miner is not required to pay any coins.
In the second scenario, we assume that the miner has abandoned the mining pool once previously. The Hop_Count value (α) and SCviolated value (β) are both one, and SCupheld (μ) is zero. Using Equation (1), Mrsk is calculated as two, and the miner is evaluated as a high-risk miner. Using Equation (2), we determine the escrow amount the miner is required to pay, which is two coins.
To fulfil the third condition, we suppose the values of α is 0, β is 1, and μ is 1. Using Equation (1), Mrsk is calculated as a low-risk miner. Mathematically, using Equation (2), the miner is not required to pay any coins. However, in our proposed model, as a condition, if the miner abandons the pool even once, the value of (β) always remains one or above. Therefore, using Equation (2), the miner is required to pay one coin as escrow.
- Update. Once the miner joins the mining pool, as shown in Figure 5, they usually leave once the mining of the block is complete. However, a miner may leave early and commit a pool hopping attack. The pool manager will update the miner’s certificate based on the miner’s behavior. In this module, the smart contract issued will determine if the agreed terms are fulfilled or not. If the block is mined, the miner receives their coins submitted in escrow, and the new miner certificate will show the Hop_count value reduced by one. If the miner left before mining the block, they lose all coins deposited in escrow, and their Hop_count value will be increased by one. This module is based on a three-step process, which is as follows:
- Mining of block. The miner in agreement to the terms of the smart contract joins and becomes a member of the mining pool. The miner will continue to mine the block and be part of the reward sharing system adopted by the pool. Upon successful completion of the mining, all miners receive the reward for solving the cryptographic puzzle of the block.
- Mining complete. The pool manager will determine if the miner who submitted coins as escrow will receive them back or not. The decision at this stage is made if the smart contract was fulfilled or broken. If the terms of the smart contract are fulfilled, the miner will receive all the coins submitted in escrow. If the conditions are not fulfilled, the miner will lose all coins offered in escrow. These coins will be divided equally to all other miners of the mining pool to make up for the loss of computational power as the result of pool hopping attack. The financial consequences of not fulfilling the terms of the contract are a necessary measure to discourage the miner from abandoning the mining pool. Miners leaving the pool for their financial gains and losing coins to the mining pool breaks that objective.
- Update miner certificate. The pool manager will update the miner certificate based on the outcome of the smart contract. The smart contract is updated based on two conditions: (1) the miner committed a pool hopping attack (Matt)and abandoned the mining pool, and (2) the miner is safe (Msf) and completed the mining process. (Matt)and (Msf) are used to help explain the updating process of the miner certificate. The final values of α, β, and μ are important and are updated in the miner’s certificate to help evaluate the miner risk (Mrsk) using Equation (1) and escrow amount using Equation (2). If the miner abandoned the mining pool, the Hop_Count (α) and the SCviolated (β) value increases by one and the SCupheld (μ) value decreases by one. The pool hopping attack-based update of the miner certificate is expressed in the following Equation (3):
In the first condition we assume that the miner abandoned the mining pool for the first time (Matt), so the values of α and β are now one. Since the miner has committed a pool hopping attack for the first time, their μ remains at zero. The miner now has a miner risk (Mrsk) value of one. The values of α and μ in the proposed model cannot decrease more than zero. The value for β will not go below one.
To fulfill the second condition, the miner is safe (Msf) and completed the mining process. The Hop_Count (α) value decreases by one and the SCupheld (μ) value increases by one. However, the SCviolated (β) count remains constant, and the value does not decrease. The update of the miner certificate upon successful completion of mining of the block is expressed in the following Equation (4):
We expand the previous case study used for Equation (3) and assume that the miner with a previous record of abandoning the mining pool completed the mining process. Their α value is now zero, β remains constant at one since it cannot go below one, and the value of μ is one. In the future, if the miner requests to join the same mining pool to mine other blocks, using Equation (1) we determine the miner is a low risk. The miner is required to submit one coin as an escrow using Equation (2).
The value of SCviolated is kept constant in the case of the miner completing the block in order to solve the following scenario when the miner requests to join the mining pool. The example scenario using Equation (1) is as follows:
If the miner has zero Hop_Count and SCviolated values, then the miner is perceived as safe to join. The miner may leave the mining pool when it offers fewer financial rewards (Mrsk = 1 + 1) and join back when the rewards are greater. The miner will pay the escrow of two coins and complete the mining process. The escrow amount is returned, and the Hop_Count is set to zero. If the SCviolated count value is decreased by one, the miner can repeat the process of leaving the pool and returning later when the rewards are higher. However, if the SCviolated is kept constant (Mrsk = 0 + 1), then the miner cannot join the pool without paying one coin as an escrow. The pool hopping behavior of the miner is recorded, and the pool manager is aware of the miner’s past behavior.
The proposed smart contract-based pool hopping attack prevention model promotes the use of smart contracts and miner certificates to ensure that pool hopping attacks which frequently occur on mining pools can be deterred. Miner certificate ledgers ensure that a record is kept at all times of each miner so that different pool managers can access them and take necessary actions to safeguard their mining pools from such attacks. The use of smart contracts along with an escrow of coins submitted by repeat pool offenders ensures that, in the event of the attack, all honest miners benefit in the form of coins. There are many pool hopping detection solutions; however, none of the existing studies for the mining pool network perform as a pool hopping attack prevention model.
4. Evaluation of the Proposed Model
In this section, the proposed model using a practical case study is based on two different scenarios: when a miner finishes mining of the block and when the miner abandons the mining pool. The two different scenarios are evaluated according to the proposed methodology. Loss of computational power is simulated by comparing existing studies with our proposed model. A comparative analysis of our proposed model is presented with related studies. The proposed method’s limitations and its implications are discussed.
4.1. Practical Case Study
The practical case study is based on two scenarios: (1) the miner commits a pool hopping attack and (2) the miner remains as part of the mining pool and completes mining of the block. In a blockchain-based IoT, a pool manager oversees a mining pool for a single IoT-based blockchain network for smart homes. The mining pool runs on the Ethereum-based public blockchain network. Geth is used as the command line tool to set up the Ethereum nodes and connect with the blockchain network, Mainnet. Mist application operates as a user interface tool to communicate with Geth. Remix web browser Integrated Development Environment is used with Solidity language to build smart contracts. Web3 Ethereum JavaScript Application Programming Interface provides the necessary collection of libraries to interact with the Ethereum node. The mining pool used to evaluate the proposed model is Ethpool. The two scenarios are as below:
Scenario 1: If a miner determines that another Ethereum mining pool based on a smart building provides more financial rewards, they leave the current mining pool and join another pool. The miner transfers all his computational power to the smart building-based mining pool network. The miner benefits from more financial rewards and only returns to the previous smart home-based mining pool if it offers better profits in the future. This strategy of abandoning the mining pool and returning when it is economically beneficial for the miner is called pool hopping attack. In the following scenario, a miner presumed to work for an Ethereum-based mining pool for a smart home blockchain network abandons the mining pool. A practical user case study based on the proposed methodological flow is as follows:
- Evaluation. In this module, the pool manager (PM) manages the mining pool, Ethpool, in the Ethereum-based mining pool for a smart home blockchain network.
- Miner request. A new miner M1 decides to join the mining pool to contribute their hashing power to mine the block and earn rewards. PM will request the miner to submit their miner address linking to MyEtherWallet built for Ethereum networks.
- Check miner certificate. PM manages a local MySQL-based database, which stores each existing and past miner addresses. Each miner address is associated with a hash value of transaction data previously stored in the blockchain network by the PM. The transaction in the blockchain network refers to the data stored in the blockchain containing the miner certificate. The PM retrieves the hash value of the transaction in the database using the MySQL ‘SELECT’ search command. Using the Web3 JavaScript API for Ethereum blockchain network, the PM will retrieve block details that contain the miner’s certificate using the “web3.eth.getBlock(block_hash_value)” command. The block data provides the miner’s record shown as below:“Hop_Count”: 4“SCupheld”: 2“SCviolated”: 3
- Evaluate miner risk. The PM determines the miner risk from the miner certificate using Equation (1),Mrsk = α + β.
The miner has a high Hop_Count value of four and is a potential risk to the entire Ethpool mining pool.
- Terms. In this module, the PM has evaluated that M1 may abandon the pool if it requires additional days to mine the block. As more days are required to mine the block, the miner has to spend more electricity than expected.
- Miner risk. M1 has a Hop_Count value of four and exhibits dishonest behavior. The miner’s abandoning of the mining pool reduces the total hash power and decreases the chances for the mining pool to finish mining the block.
- Smart contract terms. The PM issues a smart contract to safeguard the economic interests of the Ethpool mining members. The smart contract lists a condition that M1 must submit coins as escrow to prevent them from leaving.
- Determine escrow value. PM observes Hop_Count (4), SCupheld (2), and SCviolated (3) count values to determine the escrow amount. Using Equation (2),Es_dep = α + β − μ.
The PM determines that M1 should submit 5 ETHcoins as escrow. The escrow calculation method is defined in Section 3.2. M1 agrees to submit coins as escrow and joins the Ethpool mining pool.
- Update. In this module, M1 joins the Ethpool, begins mining the block, and observes the percentage required to mine the block fully. M1 will decide if it is profitable to continue mining the block or abandon the pool based on the hash rate of the mining pool. If the hash rate goes lower over time, M1 leaves Ethpool and joins another smart building based Ethereum mining pool that has more hash power. The second mining pool will require less time and electricity to complete mining, and M1 will benefit more as an individual.
- Mining of block. The Ethpool dashboard displays the current hash rate in 176 MH/s. Average time to complete mining of the block is five weeks. After a week of mining, the Ethpool dashboard displays the hash rate of 140 MH/s. The mining time required has increased by another week, and M1 is expected to spend more time and electricity to mine the block than earlier expected.
- Mining complete. M1 abandons the Ethpool and joins another smart building based Ethereum mining pool that offers quicker mining of the block and more significant rewards. The second mining pool has a hash rate of 200 MH/s and takes three weeks to complete mining of the block. M1 incurs fewer costs on electricity and earns more than the smart home based Ethpool mining pool. PM determines that M1 has abandoned the pool and committed a pool hopping attack. The smart contract terms require that M1 forfeits the escrow amount of 5 ETH coins. These coins are evenly distributed among all existing miners.
- Update miner certificate. Using Equation (3), PM updates the miner certificate, increments the Hop_Count and SCviolated value by one and decreases the SCupheld count by one. The certificate data is stored in the blockchain network as a transaction, and the block address is noted. The PM updates the mining pool’s MySQL-based database using the MySQL ‘UPDATE’ command and associates the miner address with the new block address.
Scenario 2: The miner in this scenario decides not to abandon the Ethpool mining pool and commit a pool hopping attack. In the practical user case study based on the proposed methodological flow, the first two modules, evaluation and terms, are the same as mentioned in scenario 1. However, there are changes in the third module, update, for scenario 2, which are as follows:
- Update. M1 joins the Ethpool and determines the profitability of remaining in the mining pool. The profitability is based on the time taken to complete the mining of the block, which is determined by the total hash rate of the mining pool. If the time taken to mine the block fully is more than other mining pools, such as the smart building based Ethereum mining pool, M1 will consider joining the other mining pool. However, M1 risks losing his 5 ETH coins submitted in escrow, which will have a severe financial impact.
- Mining of block. The Ethpool dashboard displays the current hash rate as 176 MH/s. Average time to complete mining of the block is five weeks. After a week of mining, the Ethpool dashboard displays the hash rate of 140 MH/s. The mining time required has increased by another week, and M1 is expected to spend more time and electricity to mine the block than earlier expected.
- Mining complete. The other smart building based Ethereum mining pool has a hash rate of 200 MH/s, which requires three weeks less than Ethpool with a hash rate of 140 MH/s to complete the mining. It also incurs less cost on the electricity bill by finishing the mining in two weeks less than Ethpool, which requires five weeks. M1 evaluates how much money he saves on electricity in three weeks. The electricity cost per week is 136 USD, and for three weeks it is 408 USD. Abandoning the Ethpool requires M1 to forfeit the 5 ETH coins submitted as an escrow. A single ETH coin is 272 USD, and 5 ETH coins are 1360 USD. The miner will lose 952 USD if they abandon Ethpool, so they decide to continue mining. Upon completion of the mining, PM returns the escrow amount of 5 ETH coins along with block rewards.
- Update miner certificate. Using Equation (4), PM updates the miner’s certificate, decrements the Hop_Count by one, and increments the SCupheld count by one. The certificate data is stored in the blockchain network as a transaction, and the block address is noted. The PM updates the mining pool’s MySQL-based database using the MySQL ‘UPDATE’ command and associates the miner address with the new block address.
Using a practical case study and numerical equations to evaluate the performance of the proposed model, real-world experimental results are provided and discussed in detail.
4.2. Comparative Analysis
The proposed pool hopping attack prevention model is compared based on three critical factors, as defined in Section 2. In the following comparative analysis, a summary of which is presented in Table 2, we observe our suggested model outperforms other proposed models based on three critical factors: computational power, security, and accountability.

Table 2.
Comparative analysis of the proposed model with existing research.
- Computational power: We compare other methods with the proposed model based on numerical equations to determine how they prevent the loss of computational power when a miner leaves the mining pool.
- Proposed model: Our proposed model suggests the use of smart contracts to ensure that a miner with a high Hop_Count value does not leave the mining pool, jeopardizing the collective computational power. Equation (2) calculates the escrow value as follows:Es_dep = α + β − μThe equation presents that a miner with high values of Hop_Count (α), SCviolated (β), and SCupheld (μ) is enforced to submit a higher escrow value of coins. The higher the escrow amount, the lower the risk the miner leaves the pool, as they risk losing a large value of their coins. Financial loss is a strong motivation for the miner to not leave, which in turn preserves the computational power of the mining pool.
- Epoch system: Belotti et al. [14] proposed a detection method to detect potential mine hoppers. They have a detection strategy where they implemented an epoch system, which refers to a specific period, to determine if a miner receives rewards from multiple mining pools in a coin base wallet. In the event there are two rewarding transactions from two different mining pools, the miner is detected as a pool hopper. This model provides no defensive measure to protect the mining pool’s computational power. There are questions unanswered such as if a pool hopper is detected, will the miner be removed/allowed to mine? Or, are there any safeguards or incentives to keep a potential mine hopper from not leaving the pool for better economic gains? The means to safeguard the mining pool’s collective computational power are not addressed.
- Slush’s method: The slush mining pool [15,16] proposed using a scoring system to give rewards to miners at the end of each round. The higher the time elapsed, the higher the score. The weakness in the proposed method is that there is little to no incentive in mining the pool in the early period, as there are insufficient prior shares to share the reward with miners. A miner will choose to hop the mining pool and return later when it is more profitable. They provide an equation to calculate the share award system as follows:The block rewards score (s) is distributed according to the score miners received for each submitted share for each round in time (t0). The equation defines the score at a time (t0) for each share (s) at time (ts). Here, Λ is defined as a constant value that represents the speed at which the score decreases over time. An exponentially decreasing scoring is better because of its invariance to time shift. The slush pool equation, unlike the proposed Equation (2), does not present a means to prevent a miner from abandoning the pool but provides a means to calculate the share of rewards an individual miner receives. A pool hopper will only get rewards from the mining pool according to their share of work contributed. However, the equation does not provide a means to prevent a miner from leaving. The miner will leave the mining pool and reduce the collective computational power of the slush pool.
- Geometric method: Rosenfeld et al. [17] proposed the geometric method, which principally addresses the flaws of Slush’s method for resisting pool hopping in mining pools. It implements the related score-based solution as Slush’s method, with the difference that the score assigned for each new share, whether it is the score of an existing or a future share, will remain the same. They proposed an equation logarithmic scale to calculate pay per share for each miner when the mining round ends as follows:
The fixed fee (f) is a parameter value, out of every block a fee is kept by the operator, and (1–f) is distributed to the miners according to their score. The miner reward sharing depends on the decaying rate (r) and is updated based on the varying difficulty of the block puzzle. If the difficulty is fixed, then r remains constant. The counter for keeping track of the score (s) grows exponentially as the round progresses. The logarithmic representation of each worker (k) to keep track of their score is represented by lSk. The logarithmic representation of each score (s) is represented by ls. The next round’s average score for each miner to earn rewards is represented by p. As each round continues, the score (s) grows significantly, and the value of older shares decreases. The value obtained from the equation implemented in the geometric method enables each miner to keep track of their block rewards. The method implements a variable fee for each starting round and increases if the round is short. As the score of each miner decays, the variable fee also decays. This ensures that the score for each new share and future shares remains equal. A miner has no advantage to join the mining pool in the beginning or later rounds of mining the block. The value of the equation provides a miner the means to keep track of their earnings. While a miner will receive rewards for their time share of mining, it does not prevent a miner from leaving the pool. A miner will abandon and return when rewards are higher. While the geometric method is resistant to pool hopping like Slush’s method, they both do not offer any solution to prevent a pool hopper from leaving the pool.
- Miner risk: We compare other methods with the proposed model based on numerical equations to determine the risk that a miner commits a pool hopping attack before they join the mining pool.
- Proposed model: The proposed model determines the risk factor of a new miner using the following Equation (1):The equation presents that a miner with high values of Hop_Count (α) and SCviolated (β) is evaluated as a risk to the mining pool. The higher the values of α and β, the higher the risk the miner is to the mining pool. The pool manager can either decide not to allow the miner to join or issue terms using a smart contract to reduce the risk of the miner of leaving the mining pool.
- Epoch system: To determine miner risk, Belotti et al. [14] suggested the use of the mapping-based procedure by studying the transactions in the bitcoin network. Their approach studies the transactions processed in the wallet using transaction addresses, which determines that the miner receives rewards from multiple pools in a single period called an epoch. However, this is a relatively complicated and time-consuming approach as it requires the pool manager to do a manual, in-depth analysis of each miner before allowing them to join the mining pool. The real-world implementation of the epoch system is not feasible.
- Slush’s method: Slush’s method [15,16] does not provide the means to determine miner risk. They focus on providing the share-based reward system for each miner and allow any miner to join their mining pool.
- Geometric method: Rosenfeld et al. [17] proposed a geometric method that focuses on improving the share-based reward system proposed by Slush pool. Their research allows all miners to join the mining pool. There is no means to calculate the miner risk to the mining pool.
- Accountability: We compare other methods with the proposed model based on numerical equations.
- Proposed model: In our proposed model, the miner that abandons the mining pool has their behavior recorded on the mining certificate by the pool manager. Miner accountability evaluates by The Equation (3):The miner’s Hop_Count (α) and SCviolated (β) are incremented by one, and the SCupheld (μ) value is decremented by one in the miner certificate. When the miner applies to rejoin the mining pool, the pool manager observes the past behavior of the miner in the miner certificate and issues a smart contract.
- Epoch system: Belotti et al.’s research [14] did not discuss measures to record a miner’s past behavior with the mining pool. A miner may leave and rejoin, and the pool manager cannot determine if the miner has committed a pool hopping attack earlier on their mining pool.
- Slush’s method: Slush’s method [15,16] did not present a solution to record if a miner has previously abandoned their mining pool. A pool manager will add a miner with high probability that they may leave the mining pool again in the future.
- Geometric method: Rosenfeld et al.’s [17] proposed geometric method only addresses the miner per share reward system and does not discuss how to maintain a record of a miner’s prior performance in the mining pool. A miner may repeatedly abandon the mining pool and return whenever the financial rewards are higher.
The discussed pool hopping resistant and detection measures, unlike our proposed idea, offer no preventive solutions to ensure that the miner does not leave the pool, affecting the overall computational power of the mining pool. A pool with less computational power is unable to complete solving the block puzzle before its competing mining pools. This results in loss of block rewards for all miners. We observe that Belotti et al.’s [14] proposed solution provides a means to detect pool hoppers; however, it is a very complex solution, and it is not feasible to implement in a practical environment. Slush’s method [15] and Rosenfeld et al. [17] do not provide any prevention measures for pool hopping attacks.
4.3. Discussion and Implications
In this paper, we mainly focused on preventing pool hopping attacks on mining pools and presented numerical models to calculate the miner risk before a pool manager includes them in the mining pool. A detailed equation is implemented to calculate the number of coins a miner submits as an escrow. An equation is suggested to implement the changes required to be made to the miner’s certificate based on two scenarios: (1) the miner completes mining of the block, and (2) the miner leaves the mining pool before completing the mining process. The proposed methodology is discussed based on three modules:
- Evaluation
- Terms
- Update
Each module presents the methodology step by step from when the miner requests to join the mining pool, the assessment of miner risk, the issuance of the smart contract with an escrow amount calculated, and the updating of the miner certificate. We performed a practical user case study based on an IoT smart home blockchain network using the equations presented in the proposed methodology. The implications of the proposed model nearly eliminate the pool hopping attack scenario unless the miner is willing to pay substantial penalties as punishment through the escrow. The model is inexpensive to implement and requires no specialized technical knowledge.
Existing research focuses on either detecting pool hopping attacks or calculating the pay per share for each miner based on a score method. The calculation of pay per share is to ensure that no miner is rewarded more than their contribution to the mining pool. A pool hopper does not receive rewards for the time they have been absent from the mining pool when they rejoin. However, existing methods do not prevent pool hopping attacks against mining pools. We introduce the concept of evaluation of miner risk and escrow value using mathematical models in Equations (1) and (2), respectively. Existing research does not provide any practical implementation or mathematical model to prevent pool hopping attacks. The idea of a miner certificate is presented to maintain a miner’s previous behavior with the mining pool, and the method to update using numerical equations is presented. Our proposed model’s results did not comply with existing research, as existing research has not evaluated miner risk before a miner joins the mining pool. There is no means to assess the escrow amount to ensure a miner does not leave. We introduced the concept of a miner certificate to track each miner’s past engagement with the mining pool, which helps in evaluating miner risk. Existing studies do not prevent a miner from leaving the mining pool but focus on calculating miner reward shares and detecting pool hoppers.
There are limitations in the proposed model as follows:
- Conflict. The miner certificate is managed solely by the pool manager. In the event there is a conflict between the miner and the pool manager, the pool manager may wrongly update the miner certificate.
- Database security. The block addresses are stored on a local database managed by the pool manager, and these address link to the miner’s certificate stored on the blockchain network. Database security against cyber-attacks is essential to maintain records of all current and past miners interacting with the mining pool. If the database records are deleted, the pool manager cannot evaluate the miner’s risk to the mining pool.
Future work should address the limitations of our proposed method by mitigating possible conflicts between the miner and the pool manager. Verification of miner data submitted to the miner’s certificate in the blockchain network is possible by allowing all existing members of the mining pool to approve the data before the pool manager updates the miner’s certificate. The proposed research allows future research to focus on automating the proposed model, where the miner’s risk and escrow amount are evaluated automatically, and miner certificates are updated without pool manager intervention.
5. Conclusions
The problem of effectively preventing pool hopping attacks is discussed in the paper, and a smart contract-based pool hopping attack prevention for blockchain networks is introduced. The novelty of our work lies in the following aspects: (1) miner risk is evaluated before they join the mining pool, (2) the conditions for issuing a smart contract and calculating the escrow amount are presented, and (3) the concept of a miner certificate to maintain miner records and its updating are presented with a mathematical equation. A practical case study is implemented to demonstrate the working of the proposed model in the real world for an IoT smart home based Ethereum blockchain network. The proposed model enforces a heavy punishment on miners that abandon the mining pool by distributing the submitted escrow coins equally to the existing pool members.
There are two limitations in the proposed model: (1) inaccurate updating of the miner certificate due to a conflict between the miner and the pool manager and (2) database security of the local database maintained by the pool manager. In future research, we will address the limitations by ensuring miner certificates are updated with the consent of all existing miners in the mining pool.
Author Contributions
Supervision, S.K.S.; Writing—review & editing, S.K.S.; Writing—original draft, M.M.S.; Methodology, M.M.S.; Validation, M.M.S. and J.C.; Resources, M.C.; Visualization, M.C.; Formal analysis, J.C.; Supervision, J.H.P.; Project administration, J.H.P.; Funding acquisition, Y.P. and J.H.P.
Funding
This study was supported by the Advanced Research Project funded by the SeoulTech (Seoul National University of Science and Technology).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 8 May 2019).
- Ferreira, M.; Rodrigues, S.; Reis, C.; Maximiano, M. Blockchain: A Tale of Two Applications. Appl. Sci. 2018, 8, 1506. [Google Scholar] [CrossRef]
- Nguyen, G.T.; Kim, K. A Survey about Consensus Algorithms Used in Blockchain. J. Inf. Process. Syst. 2018, 14, 101–128. [Google Scholar]
- Johnson, B.; Laszka, A.; Grossklags, J.; Vasek, M.; Moore, T. Game-theoretic analysis of DDoS attacks against Bitcoin mining pools. In Proceedings of the International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 3–7 March 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 72–86. [Google Scholar]
- Fisch, B.; Pass, R.; Shelat, A. Socially optimal mining pools. In Proceedings of the International Conference on Web and Internet Economics, Bangalore, India, 17–20 December 2017; Springer: Cham, Germany, 2017; pp. 205–218. [Google Scholar]
- Haghighat, A.T.; Shajari, M. Block withholding game among bitcoin mining pools. Future Gener. Comput. Syst. 2019, 97, 482–491. [Google Scholar] [CrossRef]
- Mining Pool Starts. Available online: https://miningpoolstats.stream/bitcoin (accessed on 8 May 2019).
- Liang, X.; Shetty, S.; Tosh, D. Exploring the Attack Surfaces in Blockchain Enabled Smart Cities. In Proceedings of the 2018 IEEE International Smart Cities Conference (ISC2), Kansas City, MO, USA, 16–19 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Kwon, Y.; Kim, D.; Son, Y.; Vasserman, E.; Kim, Y. Be selfish and avoid dilemmas: Fork after withholding (faw) attacks on bitcoin. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; ACM: New York, NY, USA, 2017; pp. 195–209. [Google Scholar]
- Park, J.; Park, J. Blockchain security in cloud computing: Use cases, challenges, and solutions. Symmetry 2017, 9, 164. [Google Scholar] [CrossRef]
- Rahouti, M.; Xiong, K.; Ghani, N. Bitcoin concepts, threats, and machine-learning security solutions. IEEE Access 2018, 6, 67189–67205. [Google Scholar] [CrossRef]
- Zhu, S.; Li, W.; Li, H.; Tian, L.; Luo, G.; Cai, Z. Coin Hopping Attack in Blockchain-based IoT. IEEE Internet Things J. 2019, 6, 4614–4626. [Google Scholar] [CrossRef]
- Chávez, J.J.G.; da Silva Rodrigues, C.K. Automatic hopping among pools and distributed applications in the Bitcoin network. In Proceedings of the 2016 XXI Symposium on Signal. Processing, Images and Artificial Vision (STSIVA), Bucaramanga, DC, USA, 31 August–2 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–7. [Google Scholar]
- Belotti, M.; Kirati, S.; Secci, S. Bitcoin Pool-Hopping Detection. In Proceedings of the 2018 IEEE 4th International Forum on Research and Technology for Society and Industry (RTSI), Palermo, Italy, 10–13 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- SLUSH POOL: Stratum Mining Protocol. Available online: https://slushpool.com/help/#!/manual/stratum-protocol (accessed on 16 May 2019).
- Salimitari, M.; Chatterjee, M.; Yuksel, M.; Pasiliao, E. Profit maximization for bitcoin pool mining: A prospect theoretic approach. In Proceedings of the 2017 IEEE 3rd International Conference on Collaboration and Internet Computing (CIC), San Jose, CA, USA, 15–17 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 267–274. [Google Scholar]
- Rosenfeld, M. Analysis of bitcoin pooled mining reward systems. Distributed, Parallel, and Cluster Computing. arXiv 2011, arXiv:1112.4980. [Google Scholar]
- Luu, L.; Velner, Y.; Teutsch, J.; Saxena, P. Smartpool: Practical decentralized pooled mining. In Proceedings of the 26th USENIX Security Symposium (USENIX Security 17), Vancouver, BC, Canada, 16–18 August 2017; pp. 1409–1426. [Google Scholar]
- Rajput, U.; Abbas, F.; Oh, H. A Solution towards Eliminating Transaction Malleability in Bitcoin. J. Inf. Process. Syst. 2018, 14, 837–850. [Google Scholar]
- Zamyatin, A.; Wolter, K.; Werner, S.; Harrison, P.G.; Mulligan, C.E.; Knottenbelt, W.J. Swimming with Fishes and Sharks: Beneath the Surface of Queue-based Ethereum Mining Pools. In Proceedings of the 2017 IEEE 25th International Symposium on Modeling, Analysis, and Simulation of Computer and Telecommunication Systems (MASCOTS), Banff, AB, Canada, 20–22 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 99–109. [Google Scholar]
- Kim, H.W.; Jeong, Y.S. Secure authentication-management human-centric scheme for trusting personal resource information on mobile cloud computing with blockchain. Hum.-Cent. Comput. Inf. Sci. 2018, 8, 11. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).