A New Method for MAGDM Based on Improved TOPSIS and a Novel Pythagorean Fuzzy Soft Entropy
Abstract
:1. Introduction
2. Preliminaries
3. Pythagorean Fuzzy Entropy and Pythagorean Fuzzy Soft (PFS) Entropy
- (D1)
- (D2)
- iff
- (D3)
- (D4)
- (P1)
- (P2)
- (P3)
- (P4)
4. Integrated Weight of Attributes Based on the PFS Entropy
5. Multiple-Attribute Group Decision Making (MAGDM) Method Based on the Novel Pythagorean Fuzzy Soft Entropy
- Step 1.
- Suppose that there are experts whose weight vector is giving evaluation values under jth attribute. By the formula (8), we now obtain the overall evaluation value as follows.
- Step 2.
- Let be the universe of discourse and be a set of parameters. We can establish a binary table form of PFSSs as Table 1.
- Step 3.
- Calculate fuzzy entropy of different attributes on Pythagorean fuzzy soft sets by utilizing Equation (12).
- Step 4.
- Obtain the objective weight and integrated weight of attribute by utilizing Equation (13) and Equation (14).
- Step 5.
- Determine alternatives’ positive ideal solution (PIS) and negative ideal solution (NIS) in Pythagorean fuzzy model for synthetic judgement as follows:For benefit attributes: whereFor cost attributes: whereZhang [25] determine PIS and NIS for each attribute according to score function of each element (). But their score function are pointed out that the comparison result is sometimes unreasonable [10,30]. And our method also has another advantage which possesses higher distinguish degree. Because the distance between alternatives and PIS or NIS will be larger with our method in same distance measure. It is obvious that any elements in our PIS will be better than [25] under several laws of comparing PFNs [9,25,30].
- Step 6.
- Calculate the weighted Pythagorean fuzzy distance between alternative and positive ideal solution(PIS) and the weighted Pythagorean fuzzy distance between alternative and negative ideal solution (NIS) . We think the four parameters are equal here.
- Step 7.
- Calculate the relative closeness coefficient [34] to the Pythagorean ideal solution.
- Step 8.
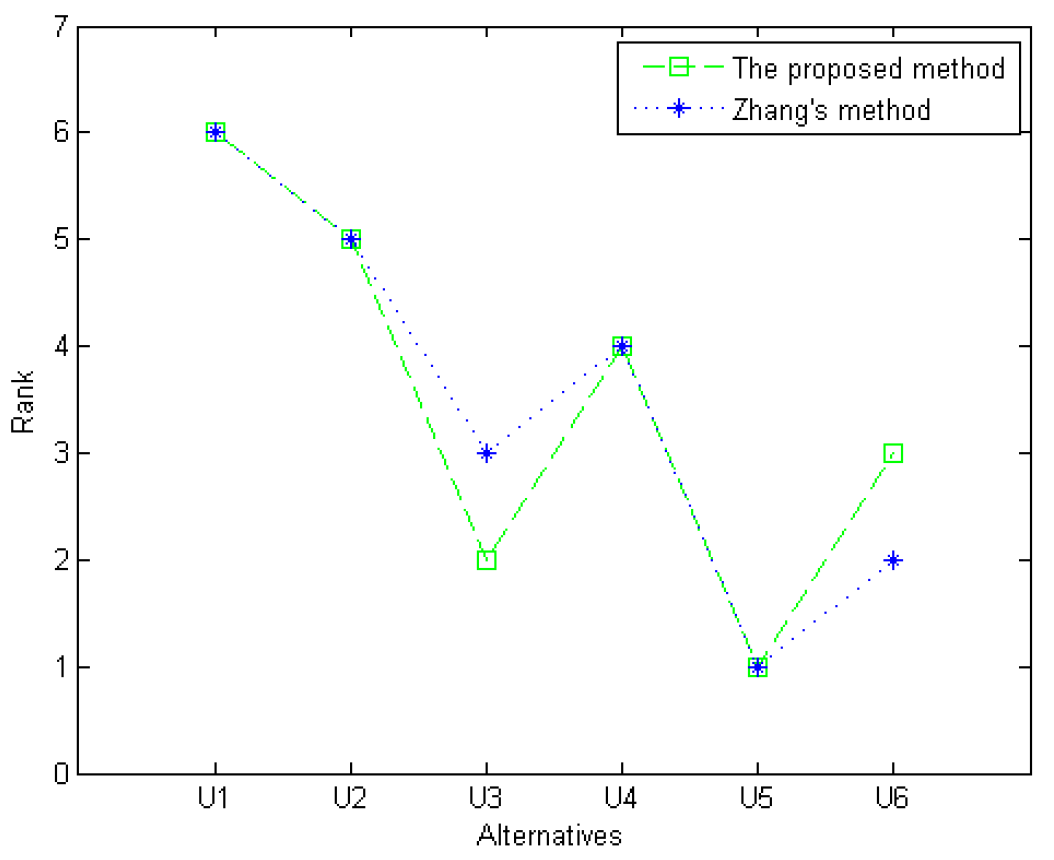
- Rank the alternatives according to the above relative closeness coefficient . The lager the is, the better the alternative is.
6. Illustrative Example
- Step 1.
- Now we consider a simple condition. The three experts’ weight vector is equal. By the Formula (8), we can obtain the overall evaluation values.
- Step 2.
- We establish a binary table form of PFSSs as Table 3 according to the overall evaluation values.
- Step 3.
- Calculate fuzzy entropy by utilizing Equation (12)
- Step 4.
- Experts give their subjective weights vector after careful consideration and discussion. Calculate the objective weight and integrated weight of the attribute by utilizing Equations (13) and (14). The results of calculating are shown in Table 4.
- Step 5.
- Determine the alternatives’ positive ideal solution and negative ideal solution by utilizing Equations (15) and (16).
- Step 6.
- Calculate the weighted distance and by utilizing Equations (17) and (18).
- Step 7.
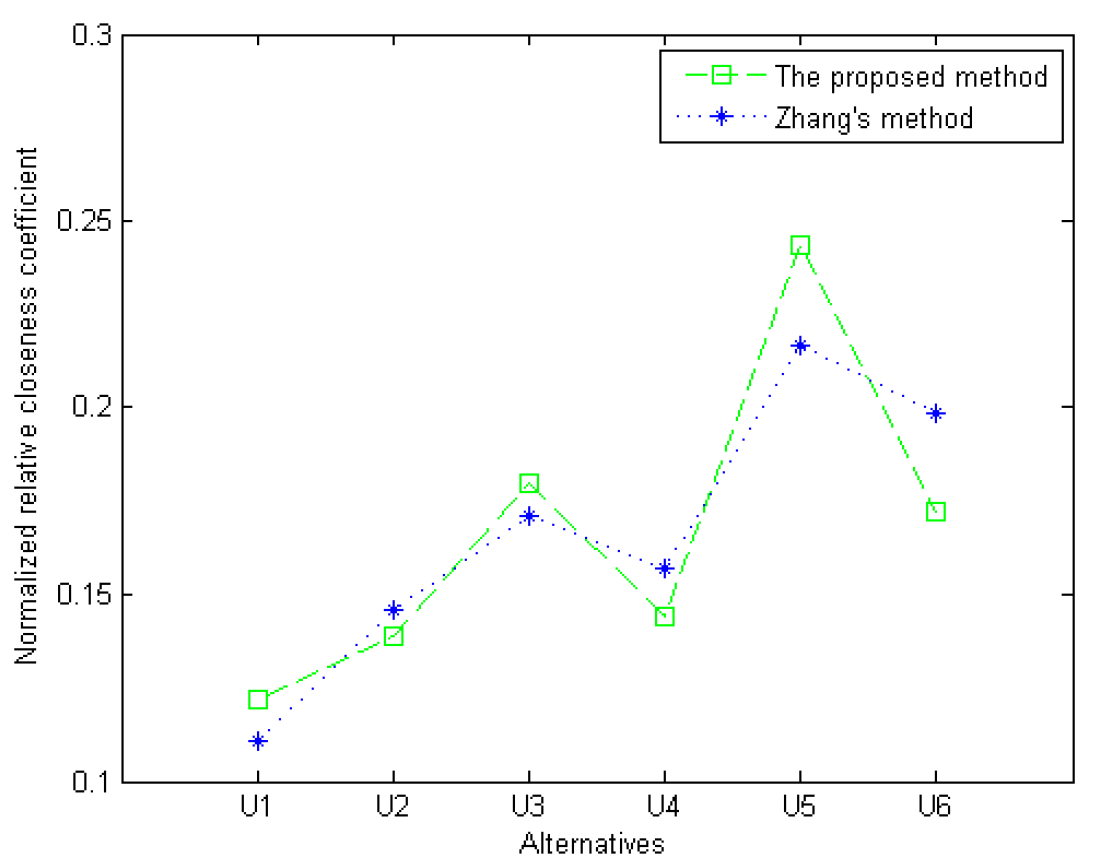
- Calculate the relative closeness coefficient to the Pythagorean ideal solution by utilizing Equation (19).
7. Conclusions
- (1)
- We combined PFSs and soft sets which have advantages in handling vague and uncertain information.
- (2)
- In most cases, experts may only be familiar with some particular attributes. We considered this situation and introduced a method to aggregate evaluation information.
- (3)
- We redefined PF entropy and proposed novel PF and PFS entropy measures which are more reasonable and valid.
- (4)
- To better determine the weights of attributes, we used PFS entropy to obtain objective weights. Then we combined objective weights and experts’ subjective weights which includes decision makers’ subjective intention to obtain integrated weights.
- (5)
- To better apply the TOPSIS method in PFSSs, we introduced more reasonable ways of determining positive ideal solutions, negative ideal solutions and calculating distances between PFNs, etc.
Author Contributions
Funding
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Wen, Q.; Huang, W. A new approach to construct similarity measure for intuitionistic fuzzy sets. Soft Comput. 2017. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Zhu, J.; Lei, L. Sensor dynamic reliability evaluation based on evidence theory and intuitionistic fuzzy sets. Appl. Intell. 2018. [Google Scholar] [CrossRef]
- Luo, X.; Li, W.; Zhao, W. Intuitive distance for intuitionistic fuzzy sets with applications in pattern recognition. Appl. Intell. 2018. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory—First results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Liu, Z.; Qin, K.; Pei, Z. A method for fuzzy Soft sets in decision-making based on an ideal solution. Symmetry 2017, 9, 246. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean Membership Grades, Complex Numbers, and Decision Making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Li, D.; Zeng, W. Distance Measure of Pythagorean Fuzzy Sets. Int. J. Intell. Syst. 2017. [Google Scholar] [CrossRef]
- Xue, W.; Xu, Z.; Zhang, X.; Tian, X. Pythagorean Fuzzy LINMAP Method Based on the Entropy Theory for Railway Project Investment Decision Making. Int. J. Intell. Syst. 2017. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K.S. Multiple Attribute Decision Methods and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Chen, C.T.; Lin, C.T.; Huang, S.F. A fuzzy approach for supplier evaluation and selection in supply chain management. Int. J. Prod. Econ. 2006, 102, 289–301. [Google Scholar] [CrossRef]
- Pawel, Z.; Jaroslaw, J.; Jaroslaw, W. Online Comparison System with Certain and Uncertain Criteria Based on Multi-criteria Decision Analysis Method. In Proceedings of the Conference on Computational Collective Intelligence Technologies & Applications, Nicosia, Cyprus, 27–29 September 2017; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Chen, S.M.; Cheng, S.H.; Lan, T.C. Multicriteria decision making based on the TOPSIS method and similarity measures between intuitionistic fuzzy values. Inf. Sci. 2016. [Google Scholar] [CrossRef]
- Muthukumar, P.; Krishnan, G.S.S. A Similarity Measure of Intuitionistic Fuzzy Soft Sets and its Application in Medical Diagnosis. Appl. Soft Comput. 2015, 41. [Google Scholar] [CrossRef]
- Meng, F.; Chen, X. Entropy and similarity measure of Atanassov’s intuitionistic fuzzy sets and their application to pattern recognition based on fuzzy measures. Pattern Anal. Appl. 2016, 19, 11–20. [Google Scholar] [CrossRef]
- Liu, M.F.; Ren, H.P. A study of multi-attribute decision making based on a new intuitionistic fuzzy entropy measure. Syst. Eng. Theory Pract. 2015, 35, 2909–2916. (In Chinese) [Google Scholar]
- Wang, G.; Zhang, J.; Song, Y.; Li, Q. An entropy-based knowledge measure for Atanassov’s intuitionistic fuzzy Sets and its Application to multiple attribute decision making. Entropy 2018, 20, 981. [Google Scholar] [CrossRef]
- James, A.R. QuantumIS: A Qualia Consciousness Awareness and Information Theory Quale Approach to Reducing Strategic Decision-Making Entropy. Entropy 2019, 21, 125. [Google Scholar] [CrossRef]
- Garg, H. Generalized Intuitionistic Fuzzy Entropy-Based Approach for Solving Multi-attribute Decision-Making Problems with Unknown Attribute Weights. Natl. Acad. Sci. India Sect. A Phys. Sci. 2017. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Zeng, S.; Chen, J.; Li, X. A Hybrid Method for Pythagorean Fuzzy Multiple-Criteria Decision Making. Int. J. Inf. Tech. Decis. Mak. (IJITDM) 2016, 15. [Google Scholar] [CrossRef]
- Li, Z.; Wei, G.; Lu, M. Pythagorean fuzzy Hamy mean operators in multiple attribute group decision making and their application to supplier selection. Symmetry 2018, 10, 505. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z. Extension of TOPSIS to Multiple Criteria Decision Making with Pythagorean Fuzzy Sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Lei, L.; Xue, A. A novel similarity measure on intuitionistic fuzzy sets with its applications. Appl. Intell. 2015, 42, 252–261. [Google Scholar] [CrossRef]
- Maji, P.K.; Roy, A.R.; Biswas, R. Fuzzy soft sets. J. Fuzzy Math. 2001, 9, 589–602. [Google Scholar]
- Kumar, M.P.; Roy, A.R.; Biswas, R. On Intuitionistic Fuzzy Soft Sets. J. Fuzzy Math. 2004, 20, 669–684. [Google Scholar]
- Jiang, Y.; Tang, Y.; Liu, H.; Chen, Z. Entropy on intuitionistic fuzzy soft sets and on interval-valued fuzzy soft sets. Inf. Sci. 2013, 240, 95–114. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Some Results for Pythagorean Fuzzy Sets. Int. J. Intell. Syst. 2015, 30, 1133–1160. [Google Scholar] [CrossRef]
- Mao, J.; Yao, D.; Wang, C. A novel cross-entropy and entropy measures of IFSs and their applications. Knowl. Based Syst. 2013, 48, 37–45. [Google Scholar] [CrossRef]
- Yang, N.D.; Wu, J.J. Emergency Rescue Decision-Making Method for Coal Mine Based on Intuitionistic Fuzzy Soft Sets. Oper. Res. Manag. Sci. 2019, 28, 54–60. (In Chinese) [Google Scholar]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Boran, F.E.; Genç, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
| e1 | e2 | … | en | |
|---|---|---|---|---|
| … | ||||
| … | ||||
| … | … | … | … | … |
| … |
| 2.1. The PFNs evaluation values of expert A | ||||||
| <0.5, 0.8> | <0.7, 0.6> | <0.6, 0.3> | <0.4, 0.7> | <0.5, 0.2> | <0.8, 0.6> | |
| <0.2, 0.3> | <0.5, 0.3> | <0.8, 0.4> | <0.7, 0.5> | <0.6, 0.2> | <0.7, 0.4> | |
| <0.7, 0.2> | <0.8, 0.2> | <0.6, 0.6> | <0.8, 0.4> | <0.7, 0.6> | <0.4, 0.5> | |
| 2.2. The PFNs evaluation values of expert B | ||||||
| <0.3, 0.6> | <0.7, 0.6> | <0.6, 0.3> | <0.8, 0.4> | <0.7, 0.3> | <0.4, 0.2> | |
| <0.2, 0.7> | <0.6, 0.3> | <0.7, 0.6> | <0.6, 0.6> | <0.8, 0.1> | <0.7, 0.4> | |
| <0.6, 0.5> | <0.3, 0.8> | <0.5, 0.7> | <0.5, 0.3> | <0.9, 0.2> | <0.7, 0.6> | |
| 2.3. The PFNs evaluation values of expert C | ||||||
| <0.2, 0.8> | <0.7, 0.4> | <0.8, 0.2> | <0.6, 0.3> | <0.6, 0.5> | <0.8, 0.2> | |
| <0.3, 0.6> | <0.1, 0.9> | <0.4, 0.6> | <0.3, 0.8> | <0.7, 0.2> | <0.9, 0.0> | |
| <0.8, 0.3> | <0.6, 0.3> | <0.7, 0.6> | <0.6, 0.4> | <0.8, 0.4> | <0.3, 0.7> | |
| <0.5, 0.8> | <0.25, 0.45> | <0.37, 0.57> | <0.45, 0.55> | <0.8, 0.3> | |
| <0.7, 0.6> | <0.6, 0.45> | <0.7, 0.3> | <0.2, 0.85> | <0.6, 0.3> | |
| <0.6, 0.3> | <0.7, 0.35> | <0.7, 0.47> | <0.45, 0.65> | <0.7, 0.6> | |
| <0.4, 0.7> | <0.7, 0.5> | <0.67, 0.43> | <0.4, 0.55> | <0.6, 0.4> | |
| <0.5, 0.2> | <0.75, 0.25> | <0.7, 0.4> | <0.8, 0.2> | <0.8, 0.4> | |
| <0.8, 0.6> | <0.55, 0.3> | <0.63, 0.37> | <0.8, 0.3> | <0.3, 0.7> |
| 0.24 | 0.2027 | 0.2449 | |
| 0.17 | 0.1855 | 0.1588 | |
| 0.18 | 0.1964 | 0.1780 | |
| 0.23 | 0.2077 | 0.2347 | |
| 0.18 | 0.2077 | 0.1837 |
| Zhang’s method | 0.1110 | 0.1457 | 0.1711 | 0.1573 | 0.2165 | 0.1985 |
| The proposed method | 0.1218 | 0.1390 | 0.1797 | 0.1439 | 0.2438 | 0.1720 |
| Mean Value | ||||||
|---|---|---|---|---|---|---|
| Zhang’s method | 20.85 | 15.21 | 8.29 | 35.52 | 10.80 | 18.13 |
| The proposed method | 10.31 | 24.42 | 21.47 | 59.93 | 43.08 | 31.84 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Q.; Li, W.; Song, Y.; Zhang, T.; Wang, R. A New Method for MAGDM Based on Improved TOPSIS and a Novel Pythagorean Fuzzy Soft Entropy. Symmetry 2019, 11, 905. https://doi.org/10.3390/sym11070905
Han Q, Li W, Song Y, Zhang T, Wang R. A New Method for MAGDM Based on Improved TOPSIS and a Novel Pythagorean Fuzzy Soft Entropy. Symmetry. 2019; 11(7):905. https://doi.org/10.3390/sym11070905
Chicago/Turabian StyleHan, Qi, Weimin Li, Yafei Song, Tao Zhang, and Rugen Wang. 2019. "A New Method for MAGDM Based on Improved TOPSIS and a Novel Pythagorean Fuzzy Soft Entropy" Symmetry 11, no. 7: 905. https://doi.org/10.3390/sym11070905
APA StyleHan, Q., Li, W., Song, Y., Zhang, T., & Wang, R. (2019). A New Method for MAGDM Based on Improved TOPSIS and a Novel Pythagorean Fuzzy Soft Entropy. Symmetry, 11(7), 905. https://doi.org/10.3390/sym11070905





