Abstract
Three-way decisions, as a decision-making mode which is consistent with human cognition, have been widely used in various fields. In this paper, we fuse the theory of reliability into the three-way decisions method, replace the conditional probability in the three-way decisions method with reliability, and then propose a novel three-way decisions method. We also describe the loss functions with single-valued triangular neutrosophic numbers (SVTNNs) and propose an operator to calculate the score function of triangular neutrosophic numbers. Then, the result of decision is attained according to the principle of minimizing loss. Finally, we apply this method to the overhaul of machines in a factory, which proves the practicability and effectiveness of the proposed methods.
1. Introduction
When people make a decision about project selection, they are faced with three choices: accepting the project, rejecting the project or delaying the decision. Research on three-way decisions problems has drawn much attention. In 1982, the rough set theory [1,2] was proposed by Pawlak, which uses lower and upper approximations to divide the universal set into three pair-wise disjoint regions: the positive region, negative region and boundary region. After that, three-way decisions were proposed by Yao et al. [3,4], which link the three regions to the three choices of the decision. With the development of three-way decisions theory, three-way decisions have been applied in various fields, such as risk decision-making [5,6], cluster analysis [7,8], credit scoring [9], etc. Based on all the above papers, conditional probability [10] and loss function [11,12,13] have always been the two main points of three-way decisions methods. Then the question arises: How should the loss functions occurred by the decisions be described? In real decision making, due to the lack of information and uncertainty of people’s cognition, it is often difficult for decision-makers to evaluate the alternatives by real numbers. Therefore, Zadeh [14] firstly proposed the fuzzy set (FS) theory, which is a useful analysis tool to deal with fuzzy information. Since then, many research achievements on FS have been made [15,16,17,18]. Nevertheless, there is a disadvantage in FS that it only has a membership and cannot express non-membership. To solve this problem, Atanassov [19] proposed the intuitionstic fuzzy set (IFS) by adding a non-membership. Since then, IFS has been favored by many scholars for a long time and developed rapidly [20,21]. However, FS and IFS can only process incomplete information but not the indeterminate information and inconsistent information, which exist commonly in belief systems [22]. Therefore, Smarandache [23] proposed the concept of the neutrosophic set (NS) by adding an independent indeterminacy-membership on the basis of IFS. Wang et al. [24] developed an instance of the NS, called the single-valued neutrosophic set (SVNS). Liu and Wang [25] presented the concept of single valued triangular neutrosophic numbers, which is appropriate to describe the degree of losses and the assessor’s belief.
The three-way decisions method can also be applied to the engineering fields. With the development of our industry, more and more factories are set up. Each factory needs a large number of machines to operate, thus deciding whether to overhaul the machines has become a necessary problem to solve. As everyone knows, the mathematical theory of reliability [26,27,28,29] was first studied in the field of machines’s maintenance [30]. In this paper, we are committed to fusing the theory of reliability into three-way decisions method, and we replace conditional probability in three-way decisions method with reliability. Next, based on the multiple attributes of the machines, all machines are classified into three types, and then a novel three-way decisions method is proposed. Finally, the method of three-way decisions is applied to the overhaul of machines in factories.
Based on the above analysis, the highlights of this paper mainly include the following points: (1) We fuse the theory of reliability into the three-way decisions method, replace the conditional probability in the three-way decisions method with reliability, and then apply the novel three-way decisions method to the overhaul of machines in factories. (2) We describe the loss function with single-valued triangular neutrosophic numbers (SVTNNs) and propose an operator to calculate the score function of triangular neutrosophic numbers. (3) These machines are classified into different equivalence classes according to their importance and their stages of life. (4) When the machines of different importance fail, they will cause different losses. Therefore, we propose different loss function matrices for them. Such a design is in line with the practical application of engineering.
The remainder of this paper is organized as follows. In Section 2, we provide the basic concepts of three-way decisions theory, SVTNNs and reliability theory. In Section 3, we develop a novel three-way decision model based on the reliability theory. In Section 4, we elaborate the specific decision-making processes of the three-way method. In Section 5, we give a case study of the overhaul of the factory’s machines to demonstrate our proposed method. In Section 6, we conclude the importance of our research.
2. Preliminaries
In this part, we carry out a brief introduction to some basic concepts of the three-way decisions [3], single-valued triangular neutrosophic numbers(SVTNNs) [25] and theory of reliability [29].
2.1. Three-Way Decisions
Let U be a finite nonempty set, the theory of three-way decisions aim at dividing U into three disjoint regions. There are two states and three actions in the decision-making process. = denotes the set of states which indicates that an element is in X or not in X. In terms of the three regions, = denotes the set of actions, where the three actions are used to classify an object x. The three actions actually correspond to three regions of rough sets [1], i.e., deciding , and , respectively. In different states, the loss function regarding the risk of actions is denoted by Table 1.

Table 1.
The risk of actions in different states.
In Table 1, the losses incurred for taking actions P, B and N are given by , , and , respectively, when an object x belongs to X. Namely, the losses incurred for taking actions are given by , , and when the object x does not belong to X. denotes the conditional probability of an object x belonging to X given that the object is described by its equivalence class [x]. In terms of an object x, we can express the expected loss incurred for taking the different action as follows:
Based on the results given in [3], we can construct the following minimum-cost decision rules:
() If ≤ and ≤, decide x∈;
() If ≤ and ≤, decide x∈; and
() If ≤ and ≤, decide x∈.
Since +1, the rules can be simplified based only on the probability and the loss function. According to the semantics of DTRSs [3], we consider a reasonable kind of losses satisfying the conditions:
Then, we can express the decision-making rules briefly as follows:
() If and , decide x∈;
() If and , decide x∈; and
() If and , decide x∈.
The threshold values , , could be deduced in the form:
When , could be deduced, the decision-making rules could be described as follows:
() If ≥, decide x∈;
() If , decide x∈; and
() If , decide x∈.
2.2. Single-Valued Triangular Neutrosophic Numbers
The single-valued triangular neutrosophic number (SVTNN) is composed of triangular fuzzy number, truth-membership, indeterminacy-membership, and falsity-membership. It overcomes the limitation of traditional fuzzy set [14] and intuitionistic fuzzy set [19], which is a very useful tool to character the information of evaluation by decision makers on alternatives under the indeterminate or inconsistent conditions.
Definition 1.
[23] Let X be a space of points and , be a neutrosophic set, where the functions denote the truth-membership function, an indeterminacy-membership function and a falsity-membership function of the element to the set A, respectively. Therefore, .
Definition 2.
[24] Let be a single valued neutrosophic set, where the functions with .
Definition 3.
[25] Let be a single valued triangular neutrosophic number, which is a neutrosophic set on the real line set R, with , denotes a triangular fuzzy number, , and . Then, we could define the truth-membership, the indeterminacy-membership and the falsity-membership functions of this neutrosophic number as follows:
where , and denote the maximum degree of truth-membership, the minimum degree of indeterminacy and the falsity-membership, respectively. A single valued triangular neutrosophic number may express an indeterminate quantity about a, which is approximately equal to a.
Liu and Wang [25] defined the SVTNNs, but did not give the method to calculate the score function of SVTNNs. Therefore, we propose a novel operator for calculating the score function as follows:
Definition 4.
Let be a single valued triangular neutrosophic number. Then, the score function of a SVTNN is defined as follows:
Example 1.
Assuming is a single valued triangular neutrosophic number, we can calculate its score function as follows:
2.3. Theory of Reliability
Reliability theory is a science that takes the life characteristics of products as the main research object. It has important value to reduce the loss cased by equipment’s malfunction in engineering.
Definition 5.
[29] The loss of a specified function of a product is called malfunction. We usually describe a product’s life with a nonnegative random variable T, the corresponding distribution function of T is
Then, denotes the probability of occurring malfunction before the time t.
Definition 6.
[29] Let be reliability of product, which represents the probability of a product performing a specified function under specified conditions and within a specified time. Then, could be expressed as follows:
Then, denotes the probability of working normally before the time t.
Definition 7.
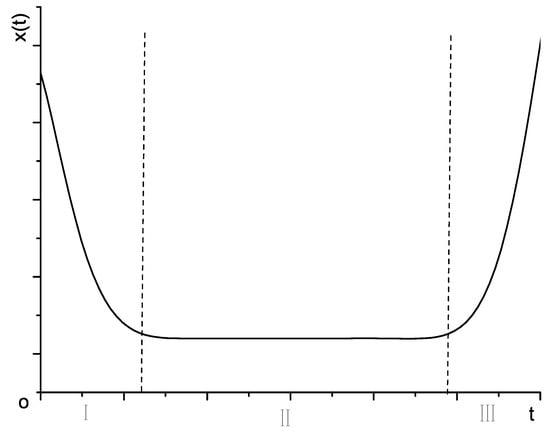
[29] For a product, the typical function of malfunction’s rate is shown in Figure 1. It takes on the shape of a bathtub, thus we call it a bathtub curve. As shown in Figure 1, when the product is in the period of Stage I, it shows a downward trend, which is the period of early malfunction. Besides, it is also a stage for the new product to blend in with the working environment. When the product is in the period of Stage , it basically stays constant, and this is the period of accidental malfunction, which is the best time for the product to work. When the product is in the period of Stage , it has a rising trend, which is the period of wear malfunction. Because of aging, wear and so on, the product performance gradually becomes worse.

Figure 1.
The typical function of malfunction’s rate.
3. Three-Way Decisions Based on the Theory of Reliability
In this section, we fuse the theory of reliability into the three-way decisions method, and then we replace conditional probability in three-way decisions method with reliability. Afterwards, the loss function of three-way decision is described by a SVTNN. In the end, a new model of three-way decision is proposed by us. Based on the decision-making procedure of three-way decisions, the new model of three-way decisions conclude three main steps: (a) constructing loss function matrix with SVTNNs; (b) calculating its thresholds according to the Bayesian decision-making procedure; and (c) forming decision-making rules.
3.1. Loss Function Matrix with SVTNNs
There are two states and three actions in the decision-making process, and then a corresponding loss will be incurred when you take an action in a state. To ensure the integrity of the information, a decision maker evaluates these losses with its SVTNN value, which is given in Table 2.

Table 2.
Loss function with SVTNNs in different states.
In Table 2,
where denotes the losses degrees that is incurred to take actions of , , and , respectively, when an object belong to X. denotes the indeterminacy-membership function of . denotes the truth-membership function of . denotes the falsity-membership function of .
where denotes the losses degrees that is incurred to take actions of , , and , respectively, when an object belong to . denotes the indeterminacy-membership function of . denotes the truth-membership function of . denotes the falsity-membership function of .
Example 2.
denotes the loss of keep working when there is no fault with the machines, which is measured by a SVTNN, e.g. . represents the loss of not making an immediate decision when there is no fault with the machines, e.g. . denotes the loss of choosing to overhaul the machine when there is no fault with the machines, which is measured by a SVTNN, e.g. . denotes the loss of keep working when there is fault with the machines, which is measured by a SVTNN, e.g. . represents the loss of not making an immediate decision when there is fault with the machines, e.g. . denotes the loss of choosing to overhaul the machines when there is fault with the machines, which is measured by a SVTNN, e.g. .
Based on Equations (4) and (5), a reasonable relationship for the losses could be obtained as follows:
Definition 8.
denotes reliability of machines, which represents the probability of machines performing a specified function under specified conditions and within a specified time. denotes the probability of occurring malfunction before the time t. Then, based on Equations (1)–(3), we replace the conditional probability with reliability, and the expected loss based on reliability could be defined as follows:
For a shipment of machines , denotes the expected loss when you decide to keep working without overhaul, denotes the expected loss when you decide to delay the decision, and denotes the expected loss when you decide to overhaul the machines.
3.2. The Calculation of Three Threshold Values with SVTNNs
Calculating the threshold values is an important step of decision making in three-way decision method. The score function is a useful tool during aggregating the SVTNNs information, which maps the SVTNNs into real numbers.
Based on Equations (6)–(8), we can calculate the threshold values , , and with SVTNNs as follows:
3.3. Decision-Making Rules Based on Theory of Reliability
According to the decision-making rules , the corresponding decision-making rules based on reliability can be deduced as follows:
() If ≥ and ≥, decide x∈, that is we decide to keep working without overhaul;
() If ≤ and ≥, decide x∈, that is we decide to delay the decision; and
() If ≤ and ≤, decide x∈, that is we decide to overhaul the machines.
4. Applications in the Overhaul of Factory’s Machines
With the development of our industry, more and more factories are set up. Each factory needs a large number of machines to be operated. Every time we start work, we have to make an important decision: whether to overhaul the machines or not. If we decide to keep working without overhaul when there is fault with the machines, once they break down in the working process, the working process of the whole factory will be delayed, the raw materials will be wasted, all workers in the factory will stop working, and it will cause great loss to the factory. If we decide to overhaul the machines when there is no fault with the machines, it will cause a waste of human resources and time. Therefore, to minimize the loss of each factory, deciding whether to overhaul the machines becomes a problem that we have to solve.
The Decision-Making Process of Three-Way Decisions
According to the above-studied result, a new method of three-way decisions based on the reliability in the SVTNNs environment is developed by us. The detailed steps of our proposed method are as follows:
Step 1: Based on the attributes of substitutability, quantity and the difficulty of maintenance, all machines are classified into three types. : important, their substitutability is very low, they are few in number and their difficulty of maintenance is very high; : medium, their substitutability is medium, they are medium in number and their difficulty of maintenance is medium; and : general, their substitutability is high, there are a lot of them and their difficulty of maintenance is very low.
Step 2: For three different types of machines, different loss function matrices with SVTNNs are given by decision maker, respectively. The importance of three different types of machines is different, thus the loss cased by the same action in the same state is not the same.
(1) Machines : They are important types of machines, and their substitutability is very low, in the working process. Once they break down, the working process of the whole factory will be delayed, the raw materials will be wasted, and then they are not easy to repair. Therefore, the loss functions of them will be large.
(2) Machines : They are medium types of machines, and their substitutability is medium, therefore the loss functions of them will be medium.
(3) Machines : They are general types of machines, and their substitutability is very high. In the working process, if they break down, we could use other machines to replace them, and they are easy to repair. Therefore, the loss functions of them will be small.
Step 3: According to the stages of their life, we continue to subdivide the three types of machines further. In Definition 7, we define Stages I, , and based on the malfunction’s rate of products. Therefore, we could divide Machines into three types, namely , , and . refers to the important machines which are in the period of Stage I. Similarly, Machines could be divided into three types: , , and . Machines could also be divided into three types: , , and .
Step 4: Based on the historical data of the such machines, the function of malfunction’s rate of such machines is fitted. Then, we calculate the reliability of each machines based on Equations (14) and (15). The reliability of a type of machines could be calculated as follows:
where is the element of , is the reliability of Machines , is the reliability of machine , and denotes the number of elements in Machines .
Step 5: Based on the loss function matrices gained from Step 2 and Equation (12), we convert the loss function matrices with SVTNNs to the loss function matrices with real numbers. Then, we could calculate the threshold values , , and of three types of Machines – based on Equation (18).
Step 6: Based on the decision rules , we can determine the decision-making result for each object by comparing the reliability with the threshold values.
With the aid of Steps 1–6, the decision result for each object can be determined by us. Next, we apply this method to the following case to prove its practicability.
5. A Case Study about the Overhaul of the Factory’s Machines
With the rise of the construction industry, many factories producing building materials have been set up. There is a glazed tile factory which has one blank extruder, two slurry agitators, four ball grinding mills and eight tile pressing machines. We need to decide whether to overhaul the machines before they start working in the factory. If we decide to keep working without overhaul when there is fault with the machines, once they break down in the working process, the working process of the whole factory will be delayed, the raw materials will be wasted, all the workers in the factory will stop working, and it will cause great loss to the factory. If we decide to overhaul the machines when there is no fault with the machines, it will cause a waste of human resources and time. Therefore, to minimize the loss of factory, in this section, our proposed method (see Section 4) is adopt to make decisions. For the sake of clarity, the decision-making process for factory is shown in Figure 2.
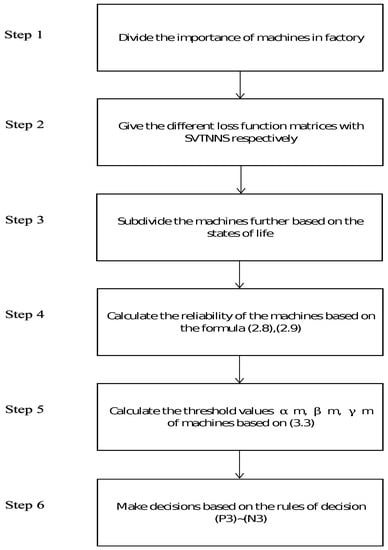
Figure 2.
The decision-making process for factory.
Step 1: There are four kinds of machines in this glazed tile factory: blank extruder, slurry agitator, ball grinding mill and tile pressing machine. The blank extruder is the most important; all materials must be processed to form by it. It is the core machine for the production of glazed tiles, with a small number. Next, the ball grinding mill and the slurry agitator are the initial tools for processing raw materials; their substitutability is medium. Finally, the number of tile pressing machines is a little large, and we can replace these machines with manual operation. Therefore, we could divide the machines into three types:
- : blank extruder;
- : ball grinding mill, slurry agitator; and
- : tile press.
Step 2: For three different types of machines, different loss function matrices with SVTNNs are given in the form of Table 2 by decision maker, respectively.
For Machines (Table 3):

Table 3.
Loss function with SVTNNs for .
For Machines (Table 4):

Table 4.
Loss function with SVTNNs for .
For Machines (Table 5):

Table 5.
Loss function with SVTNNs for .
Step 3: In Machine , the blank extruder is in the period of Stage , therefore we put it in the category. In Machines , the ball grinding mills are in the period of Stage I, while the slurry agitators are in the period of Stage , therefore we put the ball grinding mills in the category, and the slurry agitators in the category. In Machines , four tile press machines are in the period of Stage , while four tile press machines are in the period of Stage , therefore we put four tile press machines in the category, and the others in the category.
Step 4: Based on Step 4 of the decision-making process in Section 4, we can attain the reliability of equivalence classes shown as Table 6.

Table 6.
Loss function with SVTNNs for .
Step 5: Based on Equation (12) and the loss functions attained from Step 2, we convert the loss function matrices with SVTNNs to the loss function matrices with real numbers. For Machines :
The transformed result is shown in Table 7.

Table 7.
Loss function with real numbers for .
Then, we could calculate the threshold values , , and of three types of Machines – based on Equation (18). The result of threshold values is shown in Table 8.

Table 8.
The threshold values of three-way decision.
Step 6: At last, according to the decision rules , we can compare the value of reliability to the threshold values. Then, the following results can be deduced: , , and . The results we attain imply that we should decide to make Machines keep working without overhaul and overhaul Machines , while Machines need to be further investigated for their judgements.
6. Conclusions
In this paper, we fuse the theory of reliability into the three-way decisions method, replace the conditional probability in the three-way decisions method with reliability, and then propose a novel three-way decisions method. We also describe the loss function with single-valued triangular neutrosophic numbers (SVTNNs) and propose an operator to calculate the score function of triangular neutrosophic numbers. Finally, the results of decisions are attained according to the principle of minimizing loss. According to the existing literature, no scholar has applied three-way decisions into the maintenance strategy of factory equipment, thus the research in this paper has a certain degree of innovation. The method proposed in this paper belongs to the maintenance based on status in the common maintenance mode. Compared with the traditional post-fault maintenance mode in the factory, it can help the factory to reduce losses. Compared with periodic preventive maintenance mode, it is more efficient and can save time and resources. Therefore, the method proposed in this paper has relatively high application value.
Author Contributions
All authors contributed equally.
Funding
This work was supported by the National Natural Science Foundation of China (11461043 and 11661053), the Provincial Natural Science Foundation of Jiangxi, China (20161BAB201009), and the outstanding youth scientist foundation plan of Jiangxi (20171BCB23004).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pawlak, Z.; Grzymala-Busse, J.; Slowinski, R.; Ziarko, W. Rough sets. Int. J. Comput. Inform. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Pawlak, Z.; Skowron, A. Rudiments of rough sets. Inform. Sci. 2006, 177, 3–27. [Google Scholar] [CrossRef]
- Yao, Y.Y.; Wong, S.K. A decision theoretic framework for approximating concepts. Int. J. Man-Mach. Stud. 1992, 37, 793–809. [Google Scholar] [CrossRef]
- Yao, Y.Y. Decision-Theoretic Rough Set Models, International Conference on Rough Sets and Knowledge Technology; Springer-Verlag: Berlin, Germany, 2007. [Google Scholar]
- Li, H.X.; Zhou, X.Z. Risk decision making based on decision-theoretic rough set: A three-way view decision model. Int. J. Comput. Intell. Syst. 2011, 4, 1–11. [Google Scholar] [CrossRef]
- Liang, D.C.; Liu, D.; Pedrycz, W.; Hu, P. Triangular fuzzy decision-theoretic rough sets. Int. J. Approximate Reason. 2013, 54, 1087–1106. [Google Scholar] [CrossRef]
- Lingras, P.; Chen, M.; Miao, D.Q. Rough cluster quality index based on decision theory. IEEE Trans. Knowl. Data Eng. 2009, 21, 1014–1026. [Google Scholar] [CrossRef]
- Yu, H.; Liu, Z.G.; Wang, G.Y. Automatically determining the number of clusters using decision-theoretic rough set. In Proceedings of the Rough Sets and Knowledge Technology-International Conference (DBLP); Springer: Heidelberg/Berlin, Germany, 2011; Volume 6954, pp. 504–513. [Google Scholar]
- Sebastin, M.; Georg, P.; Richard, W. Credit Scoring using Three-Way Decisions with Probabilistic Rough Sets. Inform. Sci. 2018, 1–15. [Google Scholar] [CrossRef]
- Liang, D.C.; Xu, Z.S. Method for three-way decisions using ideal TOPSIS solutions at Pythagorean fuzzy information. Inform. Sci. 2018, 435, 282–295. [Google Scholar] [CrossRef]
- Liang, D.C.; Xu, Z.S.; Liu, D. Three-way decisions with intuitionistic fuzzy decision-theoretic rough sets based on point operators. Inform. Sci. 2017, 375, 183–201. [Google Scholar] [CrossRef]
- Agbodah, K. The determination of three-way decisions with decision-theoretic rough sets considering the loss function evaluated by multiple experts. Granul. Comput. 2019, 4, 285–297. [Google Scholar] [CrossRef]
- Mandal, P.; Ranadive, A.S. Decision-theoretic rough sets under Pythagorean fuzzy information. Int. J. Intell. Syst. 2018, 33, 818–835. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Chu, T.C. A fuzzy number interval arithmetic based fuzzy MCDM algorithm. Int. J. Fuzzy Syst. 2002, 4, 867–872. [Google Scholar]
- Liu, P.D. Some Hamacher aggregation operators based onthe interval-valued intuitionistic fuzzy numbers and their application to Group Decision Making. Appl. Math. Model. 2014, 37, 2430–2444. [Google Scholar] [CrossRef]
- Xu, Z.S. Study on method for triangular fuzzy number based multi-attribute decision making with preference information on alternatives. Syst. Eng. Electron. 2002, 24, 9–12. [Google Scholar]
- Liu, P.D.; Jin, F. Methods for aggregating intuitionistic uncertain linguistic variables and their application to group decision making. Inform. Sci. 2012, 205, 58–71. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Li, D.F. The GOWA operator based approach to multi-attribute decision making using intuitionistic fuzzy sets. Math. Comput. Model. 2011, 53, 1182–1196. [Google Scholar] [CrossRef]
- Wei, G.W. Some induced geometric aggregation operators with intuitionistic fuzzy information and their application to group decision making. Appl. Soft Comput. 2010, 10, 423–431. [Google Scholar] [CrossRef]
- Capraro, V.; Perc, M. Grand Challenges in Social Physics: In Pursuit of Moral Behavior. Front. Phys. 2018, 6, 107. [Google Scholar] [CrossRef]
- Smarandache, F. A geometric interpretation of the neutrosophic set A generalization of the intuitionistic fuzzy set. In Proceedings of the 2011 IEEE International Conference on Granular Computing, Kaohsiung, Taiwan, 8–10 November 2011. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. In Proceedings of the 10th 476 International Conference on Fuzzy Theory and Technology, Salt Lake City, UT, USA, 21–26 July 2005. [Google Scholar]
- Liu, P.; Wang, Y. Multiple attribute decision-making method based on single-valued neutrosophic normalized weighted Bonferroni mean. Neural Comput. Appl. 2014, 25, 2001–2010. [Google Scholar] [CrossRef]
- Amstadter, B.L. Reliability Mathematics; Science Press: Beijing, China, 1978. [Google Scholar]
- Barlow, R.E.; Proschan, F. Mathematical Theory of Realiability; Wiley: New York, NY, USA, 1965. [Google Scholar]
- Cheng, K. Mathematical Theory of Life Distribution Classes and Reliability; Science Press: Beijing, China, 1999. [Google Scholar]
- Cao, J.H.; Cheng, K. Introduction to Reliability Mathematics, 2nd ed.; Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Palm, C. Arbetskraftens fordelning vid betjaning av automatckiner. Ind. Norden 1947, 75, 75–80. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).