Abstract
This research paper adds to the theory of the generalized neutrosophic number from a distinctive frame of reference. It is universally known that the concept of a neutrosophic number is generally associated with and strongly related to the concept of positive, indeterminacy and non-belongingness membership functions. Currently, all membership functions always lie within the range of 0 to 1. However, we have generated bipolar concept in this paper where the membership contains both positive and negative parts within the range −1 to 0 and 0 to 1. We describe different structures of generalized triangular bipolar neutrosophic numbers, such as category-1, category-2, and category-3, in relation to the membership functions containing dependency or independency with each other. Researchers from different fields always want to observe the co-relationship and interdependence between fuzzy numbers and crisp numbers. In this platform, we also created the perception of de-bipolarization for a triangular bipolar rneutrosophic number with the help of well-known techniques so that any bipolar neutrosophic fuzzy number of any type can be smoothly converted into a real number instantly. Creating a problem using bipolar neutrosophic perception is a more reliable, accurate, and trustworthy method than others. In this paper, we have also taken into account a multi-criteria decision-making problem (MCDM) for different users in the bipolar neutrosophic domain.
1. Introduction
Fuzzy set theory, which deals with the concept of vagueness and uncertainty theory, was first presented by Zadeh in his paper [1] (1965). Vagueness theory plays a key role in solving problems related to engineering and statistical computation. It is widely used in social science, networking, and decision-making problems or any kind of real-life problem. Based on Zadeh’s paper, Atanassov [2] presented in 1986 the legerdemain idea of an intuitionistic fuzzy set in the field of mathematics where he considered the concept of membership function as well as non-membership function in the case of an intuitionistic fuzzy set. Subsequently, in 2007, Liu and Yuan [3] invented the concept of triangular intuitionistic fuzzy set, which in reality is the mixture of triangular fuzzy set and intuitionistic fuzzy set. Later, Ye [4] introduced the elementary idea of trapezoidal intuitionistic fuzzy set where both truth function and falsity function are a trapezoidal number in nature instead of triangular. Uncertainty theory plays an influential role in creating interesting models in various fields having scientific and technological problems. However, an elementary question arises: how can we develop or utilize the uncertainty concepts in our mathematical modeling with respect to daily life? Researchers everywhere have invented many approaches and methods to define those concepts and have offered different recommendations for using uncertainty philosophy. The literature presents different types of suggestions to classify some of the basic ambiguous parameters. It should be noted that there is no exclusive representation of the vagueness parameter. For solving a problem, the decision maker’s choice can be variously conferred in different applications.
In 1995, Smarandache (published in 1998) [5] put forward the idea of a neutrosophic set having three different components, namely, (i) truthiness, (ii) indeterminacies, and (iii) falseness. All aspects of the neutrosophic set are very relevant to our real-life systems. The neutrosophic concept is a very effective and exciting idea in real life. Later, Wang et al. [6] advanced the perception of a single typed neutrosophic set, which is very useful in solving any complex problem. Chakraborty et al. [7] introduced the concept of triangular neutrosophic as well as its classification. Chakraborty et al. [8] presented the perception of defuzzification using the removal area method. Maity et al. [9] also developed the idea of ranking and defuzzification in a new way.
To tackle human decision making based on positive and negative parts, Boscand Pivert [10] put forth the idea of bipolarity. They introduced the idea of the positive part of a membership function as well as the negative part of a membership function. Subsequently, Lee [11,12] defined the concept of bipolar fuzzy set in their research articles. Later, Kang and Kang [13] extended this idea into semi-groups and group structures. As research continued, Deli et al. [14] generated the idea of a bipolar neutrosophic set and tried to apply it to a decision-making problem. Broumi et al. [15] developed the concept of bipolar neutrosophic graph theory and, afterward, Ali and Smarandache [16] introduced the concept of the uncertain complex neutrosophic set. Molodtsov [17] introduced the concept of the soft bipolar set and, afterward, Aslam et al. [18] used it in an application-based problem. Vakkas et al. [19] invented the idea of similar measure on a bipolar set. Later, Wang et al. [20] also introduced the idea of operators in a bipolar neutrosophic set and used it in a decision-making problem. Recently, Raja et al. [21] developed a hope function in a bipolar neutrosophic set. We can find many applications of neutrosophic theory and development of multi criteria decision making problem in the literature surveys presented in [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. The development of fuzzy set theory continues [41,42,43,44,45,46,47,48,49].
In this research article, we developed the concept of a different bipolar neutrosophic number in the triangular aspect. We invented both linear and nonlinear forms of a single typed triangular bipolar neutrosophic number for different categories. There are three categories of numbers when the three membership functions are maybe dependent or independent among each other. We introduced the concept of a category-1, -2, or -3 triangular bipolar neutrosophic numbers and also a generalized linear and nonlinear bipolar neutrosophic number. Researchers from everywhere are very interested in defuzzification techniques. As research goes on, they continually develop many techniques to solve the defuzzification problem. We introduced the removal area methods and built up the de-bipolarization technique concept in the case of a linear triangular bipolar fuzzy number. Using that particular result, we converted a triangular bipolar neutrosophic set into a crisp one.
Currently, researchers from around the globe are very interested in solving multi-criteria decision-making problems. For that type of problem, we considered a finite number of alternatives as well as a finite number of attributes with different types of weight function for different numbers of decision makers. The goal of this method was to find a comparison between the alternatives and the attributes while maintaining the weight of the decision makers so that we could easily discover the best alternatives and the worst one. Many researchers have already proposed ideas about multi-criteria decision-making (MCDM) problems, but in this new triangular bipolar neutrosophic arena, we considered a MCDM problem and we focused and analyzed this problem using our developed de-polarization technique.
1.1. Motivation
The concept of vagueness plays a key role in mathematical modeling, engineering problem solving and medical diagnosis problem solving, among others. An important issue then arises if one considers a triangular bipolar neutrosophic number: what will be the linear and nonlinear forms and what will be the geometrical figure? How should we specify a category-1, -2, or -3 bipolar neutrosophic number when the membership functions are related to each other? Based on this perspective, we developed the subject of this research article. We succeeded in producing certain interesting results on de-bipolarization techniques and other applications.
1.2. Novelties
Numerous works have already been published in this bipolar fuzzy set context. Researchers have already developed several formulations and applications in various fields. However, many interesting results are still unknown. Our work aimed to develop ideas for those unknown aspects:
(i) Introduction of a distinctive form of triangular bipolar neutrosophic fuzzy number and its definition for different cases.
(ii) Graphical representation of a triangular bipolar neutrosophic fuzzy number.
(iii) Development of a de-bipolarization technique.
(iv) Application in an MCDM problem.
1.3. Verbal Phrasesin theNeutrosophic Arena
With respect to daily life, an interesting question often arises about how we can connect the concept of vagueness and neutrosophic theory to real life and, in that case, what are the verbal phrases that can be used.
Example 1.

Let us consider a problem of vote casting. Suppose, in an election, that one must select a candidate among a finite number of candidates. People have different emotions, feelings, demands, ethics, dreams, etc. Therefore, according to their viewpoint, the result can be any kind of fuzzy number, such as an interval number, triangular fuzzy number, intuitionistic number, or neutrosophic fuzzy number. Let us check the verbal phrases in each different case for the given problem in Table 1.

Table 1.
Verbal phrases.
1.4. Logical Relationship between the Objective and the Subjective Partsof this Paper
The objective part of this paper is to invent the disjunctive form of a triangular bipolar fuzzy number and the geometrical representation of it for different cases. The subjective part is to apply the linear form of the bipolar neutrosophic number to a real-life multi-criteria decision-making problem. To do so, we invented the logical removal area technique to compute the de-bipolarized value of the defined number. Using this de-bipolarization technique, we were able to relate a crisp number and a triangular bipolar neutrosophic number very easily. For the multi-criteria decision-making problem, we considered the weighted mean approach and the normalized approach as well as the de-bipolarization method to compute the best alternatives.
1.5. Structure of this Paper
In this research article, Section 1 contains the introduction presenting the basic concepts and the literature survey. It also includes the novelties, the motivation for this work, and verbal phrase perceptions on the neutrosophic domain. Section 2 presents the preliminary portion, some established definitions, and other elements. Section 3 contains the concept and development of disjunctive forms of a linear triangular bipolar fuzzy number. Section 4 presents its nonlinear and generalized form. In Section 5, we present the developed de-bipolarization technique of a linear bipolar fuzzy number (with disjunctive figures), using the concept of a removal area technique presented in Section 6. We consider a multi-criteria decision-making (MCDM) problem in a bipolar neutrosophic environment and solve it using the results from the previous sections with a real-life example accompanied by a sensitivity analysis. Lastly, Section 7 contains the conclusions reached about the research undertaken.
2. Preliminaries
Definition 1.
Fuzzy Set: [1] A set, defined asand generally denoted by the pair,belongs to the crisp setandbelongs to the interval, then setis called a fuzzy set.
Definition 2.
Neutrosophic Set: [5] A setin the universal discoursegenerally specified byis called a neutrosophic set if, whererepresents the degree of confidence,represents the degree of hesitation andrepresents the degree of falseness of the decision. Where,satisfies the relation
Definition 3.
Single Typed Neutrosophic Number: [10] Single Typed Neutrosophic Numberis specified aswhere, where,andis given as:
Definition 4.
Bipolar Neutrosophic Set: [11] A bipolar neutrosophic set is specified as,
Whererepresents the degree of confidence, represents the degree of hesitation andrepresents the degree of falseness of the decision.
3. Single Typed Linear Triangular Bipolar Neutrosophic Number
In this section, we define different types of a single typed linear bipolar neutrosophic number. To help researchers, we present the following block diagram as in Figure 1:
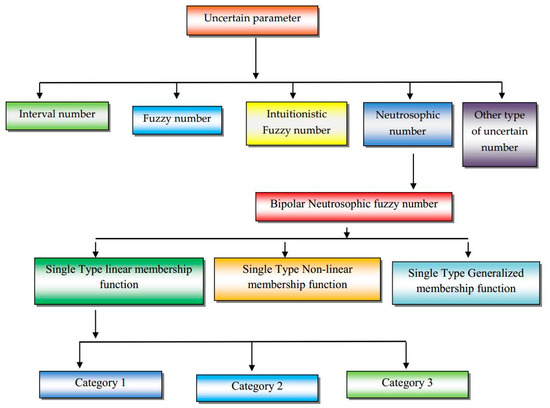
Figure 1.
Block diagram for different types of a single typed linear triangular bipolar neutrosophic number.
3.1. Triangular Single Typed Bipolar NeutrosophicNumber of Category-1: The Portion of the Authenticity, Hesitation, and Untrue Are Independent
This case may arise with the following problem: one must select one member or one party in the election system of a country. Suppose there is a finite number of candidates, and one of them is X. A certain percentage of the people will surely cast their vote in favor of X, which is the authenticity function. A certain percentage of them will surely cast their vote against X, which is the untrue function. Apart from these two groups of people, a few people will hesitate to give their vote. Here, all components are independent.
A triangular single typed neutrosophic number of category-1 is specified as and whose authenticity membership, hesitation, and untrue membership are specified as follows:
and
and
where .
The parametric representation of the above category-1 number is defined as follows:
where
Here, ,, and .
3.2. Triangular Single TypedBipolar Neutrosophic Number of Category-2: The Portion of Hesitation and Untrue Are Dependent
This case may arise with the following problem: one must select one member or one party in the election system of a country. Suppose there is a finite number of candidates, and one of them is X. A certain percentage of the people will surely cast their vote in favor of X, which is the authenticity function. However, a certain percentage of the people will surely cast their vote against X, while they hesitate to cast their vote for the other candidates in this election. In this case, the hesitation membership function and the untrue portion are dependent on each other.
A triangular single typed bipolar neutrosophic number of Category-2 is specified as and whose authenticity membership, hesitation, and untrue membership are specified as follows:
and
and
where , .
The parametric representation of the above category-2 number is defined as follows:
where
Here, , , and and .
3.3. Triangular Single TypedBipolar Neutrosophic Number of Category-3: The Portion of the Authenticity, Hesitation, and Untrue Are Dependent
This case may arise with the following problem: suppose a company manufactures some useful products and they have launched them into the market. They do not know whether they will be accepted in the market (hesitant function). After product launching, people can either accept then (authenticity function) or reject them (untrue function). Here, all three components are dependent on each other.
A triangular single typed bipolar neutrosophic number of Category-3 is specified as and whose authenticity membership, hesitation, and untrue membership are specified as follows:
and
and
where , .
The parametric representation of the above category-3 number is defined as follows:
where
Here, ,, and
4. Single Typed Nonlinear Triangular Bipolar Neutrosophic Number
4.1. Single Typed Nonlinear Triangular Bipolar Neutrosophic Number
A single typed nonlinear triangular bipolar neutrosophic number is specified as and whose positive membership, hesitation, and negative membership are specified as follows and graphically in Figure 2.
and
and
where
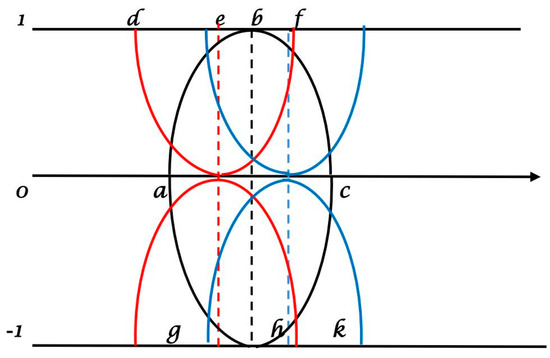
Figure 2.
Nonlinear triangular bipolar neutrosophic number.
4.2. Single Typed Generalized Triangular Bipolar Neutrosophic Number
A single typed triangular bipolar generalized neutrosophic number is specified as and whose positive membership, hesitation and negative membership are specified as follows:
and
and
where
4.3. Single Typed Generalized Non Linear Triangular Bipolar Neutrosophic Number
A single typed nonlinear triangular generalized bipolar neutrosophic number with nine components is specified as and whose authenticity membership, hesitation and untrue membership are defined as follows:
and
and
where
5. De-Bipolarization of a Linear Neutrosophic Triangular Bipolar Fuzzy Number
De-bipolarization is a process of creating a logical result in a crisp system corresponding to the bipolar neutrosophic fuzzy number and its membership function. Researchers from different countries of the world are interested in this question: if there is a bipolar neutrosophic fuzzy number having its membership function, what will be the crisp value associated with the number? As research goes on, they continually consider useful methods to convert a fuzzy number into a crisp number.
Some of the well-known methods are as follows:
- BADD (basic defuzzification distributions)
- BOA (bisector of area)
- CDD (constraint decision defuzzification)
- COA (center of area)
- COG (center of gravity)
- ECOA (extended center of area)
- EQM (extended quality method)
- FCD (fuzzy clustering defuzzification), etc.
In our triangular bipolar neutrosophic environment, researchers are very interested in finding out which conversion process will be applicable and logical to convert a triangular bipolar neutrosophic number into a crisp number. In the case of a triangular bipolar neutrosophic fuzzy number, three different kinds of membership functions are present. Lastly, we propose the “removal area method” to convert a triangular bipolar neutrosophic fuzzy number into a crisp number.
5.1. De-Bipolarization Using the Removal Area Method
Let us consider a linear bipolar neutrosophic triangular fuzzy number as follows:
The graphical representation of a triangular bipolar neutrosophic fuzzy number is presented in Figure 3:
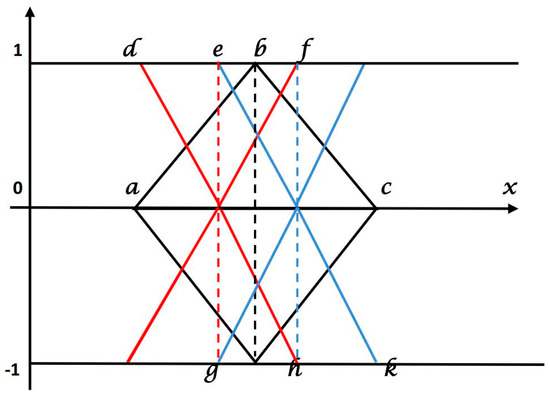
Figure 3.
Linear triangular bipolar neutrosophic number.
We assume areal number and an uncertain number for black line indicated triangles, the left portion area of w.r.t is is specified as the region enclosed by and the left portion of the fuzzy number Using the same concept, the right portion area of w.r.t is now consider a real number together with a fuzzy number for the left most top and lower triangles , then the left portion area of w.r.t is and is specified as the region enclosed by and the left portion of the fuzzy number Again, the right portion area of w.r.t is , a fuzzy number for the right most top and lower triangle , then the left portion removal of w.r.t is and is specified as the region enclosed by and the left portion of the fuzzy number Similarly, the right portion removal of w.r.t is
Mean is defined as , ,
Then, we specified the de-bipolarization of a linear bipolar neutrosophic triangular fuzzy as follows:
For , ,,
Then,
We take .
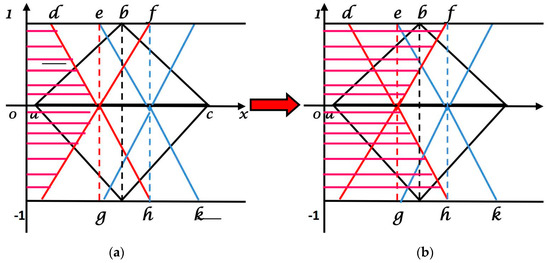
Figure 4.
(a) Shaded Region of falsity portion (Step I); (b) Shaded Region of falsity portion (Step II).
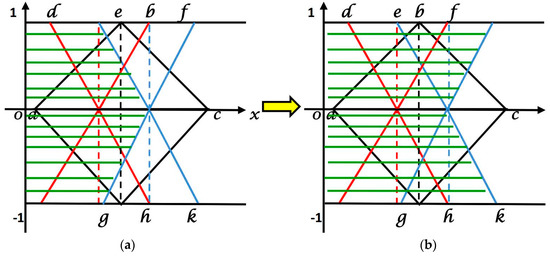
Figure 5.
(a) Shaded Region of hesitant portion (Step I); (b) Shaded Region of hesitant portion (Step II).
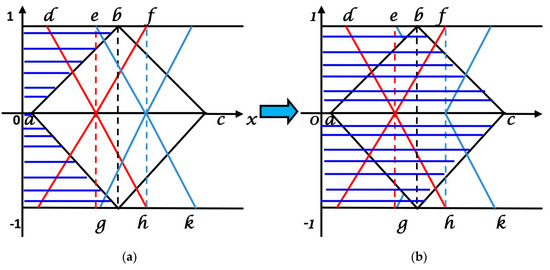
Figure 6.
(a) Shaded Region of truth portion (Step I); (b) Shaded Region of truth portion (Step II).
Hence,
So,
6. Multi-Criteria Decision-Making in a Triangular Bipolar Neutrosophic Fuzzy Set Environment
In this process, we tried to find the best alternatives on the basis of the attribute values defined by the decision makers. It is not an easy task to evaluate the attribute value in terms of a crisp number due to the presence of impreciseness. The information of the attribute values are of triangular bipolar neutrosophic number in nature.
In our daily lives, we often face multi-criteria decision-making problems. Suppose someone wants to buy a good mobile phone within their financial range. Many companies and products are available in the market and, additionally, the products have different types of features like camera quality, long-lasting, type of processor, RAM, etc. Moreover, for the same features, different companies fix different prices. The buyer therefore faces a problem about which one will be the best mobile phone. Their mind is in a dilemma about buying the product. Thus, hesitation appears in the mind, so the problem belongs to the bipolar neutrosophic fuzzy environment domain. The person will accept some suggestions from friends or from other persons to form an opinion about the product. They will give their own opinion according to their choice after giving some weight to the features. This problem now becomes a multi -criteria decision-making problem and the person wants to find the best alternatives.
In this section, we consider a multi-criteria decision-making problem where a finite number of different decision makers is available and according to their viewpoint, we must find the best alternative. To do so, we constructed an algorithm based on the weighted mean and normalization approach so that we could solve the uncertainty problem very easily. Then, using the result of the de-bipolarization value, we were able to choose the best alternative among all of them.
6.1. Illustration of the MCDM Problem
We consider the problem as follows:
Let be the distinct alternative set and be the distinct attribute set, respectively. Let be the weight set associated with the attributes Q, where each 0 and also satisfies the relation . We also consider the set of decision makers associated with alternatives whose weight vector is defined as , where each 0 and also satisfies the relation ; this weight vector will be selected according to the decision maker’s quality of judgment, knowledge, thinking power, etc.
6.2. Weighted Mean and Normalisation Algorithm of the MCDM Problem
Step 1: Creation of decision matrices
First, we create the decision matrices for each decision maker’s choice associated with alternatives versus attribute functions. We consider the member of the matrices in the bipolar neutrosophic environment, so all are a member of the bipolar neutrosophic set. The associated matrix is defined as follows:
Step 2: Creation of weighted single-decision matrix
To obtain a single group decision matrix, we use the operation for each individual decision matrix , and thus we get the new matrix as follows:
Step 3: Creation of weighted priority matrix using weight vector
To obtain single-column decision matrix, we use the operation for each individual column, and thus we get the decision matrix as follows:
Step 4: Ranking
Now, we consider the de-bipolarization value and convert the matrix (3) into crisp form so that we can evaluate the best alternative corresponding to the best attributes. We consider the score values according to the increasing order and choose the best fit result. The highest value gives us the best result and lowest one, the worst one.
Flowchart: The flowchart is given in Figure 7:
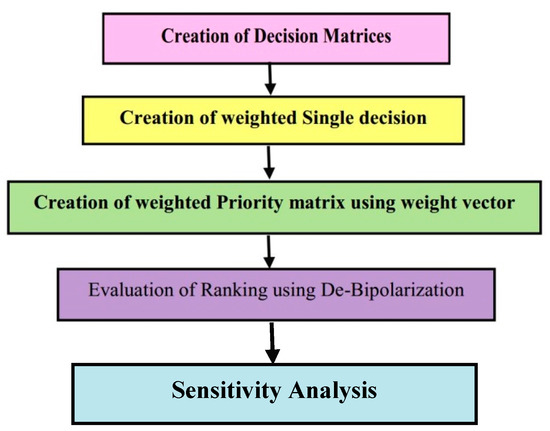
Figure 7.
The flowchart.
6.3. Illustrative Example
Let us consider a problem related to three different products and their distinctive attributes. We know that many products are available in the market and they have different components with different qualities and features. Therefore, this is multi-criteria decision-making problem with different types of decision makers. We define the problem as follows: , , are the alternatives; , , are the attributes.
We consider there are three types of decision makers: having weight function and we also consider the weight vector associated with the attribute function A verbal matrix is created by the designer to assist the decision maker in the creation of their decision matrix. The verbal phrases for all the different attributes are listed in Table 2.

Table 2.
List of verbal phrases.
Step 1:
We consider the matrices according to each decision maker’s choice related to alternatives and attribute functions (See Table 3). All the members of the matrices are of a spherical neutrosophic nature. Therefore, the decision matrices are as follows:

Table 3.
Verbal matrix.
Step 2: Creation of weighted mean single-decision matrix
Step 3: Creation of weighted Priority matrix using weight vector
Step 4: Ranking
Now, we consider the De-Bipolarization value defined in Section 5.1 and converts the triangular bipolar neutrosophic numbers into a crisp one. Thus, we obtain the final ideal decision matrix as follows:
Now, after arranging the numbers in ascending order, we obtain . Thus, the ranking of the priority alternatives is .
6.4. Results and Sensitivity Analysis
A sensitivity analysis was done to understand how the attribute weights of each criterion affected the relative matrix and their ranking. The main idea of a sensitivity analysis is to interchange weights of the attribute values while keeping the rest of the terms fixed. Table 4 shows the sensitivity results. Also input data is in Figure 8 and output result shown in Figure 9.

Table 4.
Sensitivity analysis chart.
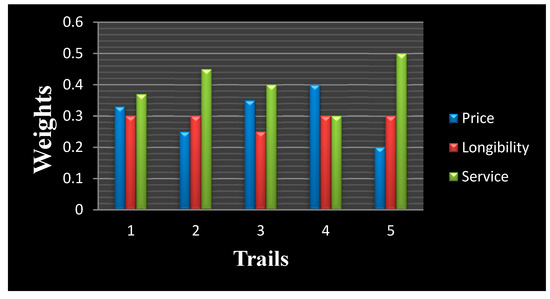
Figure 8.
Input table with the associated weight of the different parameters.
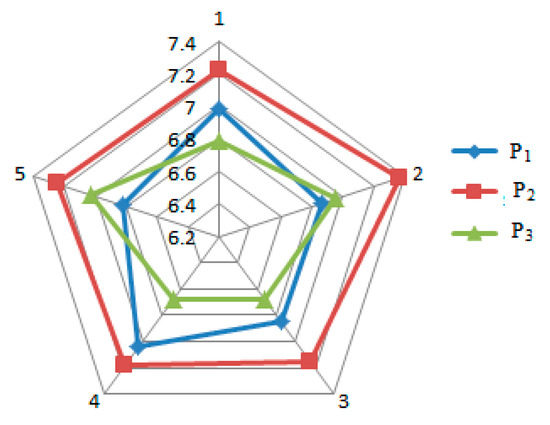
Figure 9.
Output table of the preferred priority alternatives.
6.5. Comparison with Other Established Work:
We compare our work with other previous work described by the authors [11,18,49] for finding the best alternatives we observed that in each cases becomes the best alternative (see Table 5).

Table 5.
Comparison table.
Remark 1.
The novelty of this paper is to understand the behavior of the weights of different criteria on the ranking of the alternatives. For this reason, a sensitivity analysis was performed by interchanging the weights of the criteria. Using a sensitivity analysis, we observe a certain level of change in the attribute values and that, ultimately, is the best alternative, whereas the other alternatives change their ordering.
7. Conclusions and Future Research Scope
The concept of a triangular bipolar neutrosophic number is interesting and pragmatic and has a practical use in the current research arena. The formulation of a distinctive type of triangular bipolar neutrosophic number of category-1, -2, or -3 and of a de-polarization technique is essential for researchers who deal with the ideas of uncertainty and vagueness. To solve any kind of multi-criteria decision-making problem, one can also apply the current method discussed above. In this paper, we adopted the concept of a bipolar neutrosophic number from different viewpoints and perspectives. We also used the idea of linear as well as nonlinear form with truth, false, and hesitant functions in the case of a triangular bipolar neutrosophic number when the membership functions were related to each other. The concept of de-bipolarization was very helpful when we wanted to find the best result in the case of different decision-making problems, in which the number of alternatives and attributes was finite and different decision makers were involved. Finally in the example portion we also consider a sensitivity analysis and also did comparison with the other paper’s result to tally our proposed work and we can conclude that our result is more suitable as we consider the updated De-Bipolarized value in the problem to tackle the multi criteria decision making problem. Furthermore, researchers can apply this concept of a bipolar number in various fields, such as engineering problems, diagnosis problems, mathematical modeling, among others.
Author Contributions
All authors have contributed equally to this paper.
Funding
This research was financially supported by the Ministry of Education, Malaysia under FRGS Grant (Project No.: 01-01-18-2031FR).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzysets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, X.H. Fuzzy number intuitionistic fuzzy set. Fuzzy Syst. Math. 2007, 21, 88–91. [Google Scholar]
- Ye, J. Prioritized aggregation operators of trapezoidal intuitionistic fuzzy sets and their application to multi criteria decision making. Neural Comput. Appl. 2014, 25, 1447–1454. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, Delaware, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Q.; Sunderraman, R. Single valued neutrosophic sets. MultiSpace and Multistructure 2010, 4, 410–413. [Google Scholar]
- Chakraborty, A.; Mondal, S.P.; Ahmadian, A.; Senu, N.; Alam, S.; Salahshour, S. Different forms of triangular neutrosophic numbers, de-Neutrosophication techniques, and their applications. Symmetry 2018, 10, 327. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mondal, S.P.; Ahmadian, A.; Senu, N.; Dey, D.; Alam, S.; Salahshour, S. The pentagonal fuzzy number: Its different representations, properties, ranking, defuzzificationand applicationin game problem. Symmetry 2019, 11, 248. [Google Scholar] [CrossRef]
- Maity, S.; Chakraborty, A.; De, S.K.; Mondal, S.P.; Alam, S. A Comprehensive Study of A Backlogging EOQ Model with Non Linear Heptagonal Dense Fuzzy Environment. Available online: https://doi.org/10.1051/ro/2018114 (accessed on 3 April 2019).
- Bosc, P.; Pivert, O. On a fuzzy bipolar relational algebra. Inf. Sci. 2013, 219, 1–16. [Google Scholar] [CrossRef]
- Lee, K.M. Bipolar-valued fuzzy sets and their operations. In Proceedings of the International Confernceon Intelligent Technologies, Bangkok, Thailand, 28–30 May 2000; pp. 307–312. [Google Scholar]
- Lee, K.J. Bipolar fuzzy sub algebras and bipolar fuzzy ideals of BCK/BCI-algebras. Bull. Malays Math. Sci. Soc. 2009, 32, 361–373. [Google Scholar]
- Kang, M.K.; Kang, J.G. Bipolar fuzzy set theory applied to sub-semi groups with operators in semi groups. J. Korean Soc. Math. Educ. Ser. B Pure Appl. Math. 2012, 19, 23–35. [Google Scholar]
- Deli, I.; Ali, M.; Smarandache, F. Bipolar neutrosophic sets and their application based on multi-criteria decision making problems. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems, Beijing, China, 22–24 August 2015. [Google Scholar]
- Broumi, S.; Smarandache, F.; Talea, M.; Bakali, A. An introduction to bipolar single valued neutrosophic graph theory. Appl. Mech. Mater. 2016, 841, 184–191. [Google Scholar] [CrossRef]
- Ali, M.; Smarandache, F. Complex neutrosophic set. Neural Comput. Appl. 2016, 25, 1–18. [Google Scholar] [CrossRef]
- Molodtsov, D.A. Soft set theory-first results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Aslam, M.; Abdullah, S.; Ullah, K. Bipolar fuzzy soft sets and its applications in decision making problem. arXiv 2013, arXiv:1303.6932v1. [Google Scholar]
- Ulucay, V.; Deli, I.; Sahin, M. Similarity measures of bipolar neutrosophic sets and their application to multiple criteria decision making. Neural Comput. Appl. 2018, 29, 739–748. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Wang, J. Frank choquet bonferroni mean operators of bipolar neutrosophic sets and their application to multi-criteria decision-making problems. Int. J. Fuzzy Syst. 2018, 20, 13–28. [Google Scholar] [CrossRef]
- Hashim, R.M.; Gulistan, M.; Smarandache, F. Applications of neutrosophic bipolar fuzzy sets in HOPE Foundation for planning to build a children hospital with different types of similarity measures. Symmetry 2018, 10, 331. [Google Scholar] [CrossRef]
- Zhang, W.R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multi agent decision analysis. In Proceedings of the First International Joint Conference of The North American Fuzzy Information Processing Society Biannual Conference, San Antonio, TX, USA, 18–21 December 1994; pp. 305–309. [Google Scholar]
- Zhang, W.R. Bipolar fuzzy sets. In Proceedings of the 1998 IEEE International Conference on Fuzzy Systems, Anchorage, AK, USA, 4–9 May 1998; pp. 835–840. [Google Scholar]
- Deli, I.; Broumi, S.; Smarandache, S.F. On neutrosophic refined sets and their applications in medical diagnosis. J. New Theory 2015, 6, 88–98. [Google Scholar]
- Broumi, S.; Deli, I.; Smarandache, F. Relations on interval valued neutrosophic soft sets. J. New Results Sci. 2014, 5, 1–20. [Google Scholar]
- Broumi, S.; Alkhazaleh, S.; Hazaymeh, A. N-valued refined neutrosophic soft sets and their applications in decision making problems and medical diagnosis. J. Artif. Int. Soft Comput. Res. 2018, 8, 79–86. [Google Scholar] [CrossRef]
- Ali, M.; Smarandache, F. The theory of neutrosophic cubic sets and their applications in pattern recognition. J. Intell. Fuzzy Syst. 2016, 30, 1957–1963. [Google Scholar] [CrossRef]
- Broumi, S.; Bakali, A.; Talea, M. Smarandache F Isolated single valued neutrosophic graphs. Neutrosophic Sets Syst. 2016, 11, 74–78. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, X.H. Simplified neutrosophic sets and their applications in multi-criteria group decision making problems. Int. J. Syst. Sci. 2015, 47, 2342–2358. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Zhang, H.Y.; Chen, X.H. The fuzzy cross-entropy for intuitionistic hesitant fuzzy sets and their application in multi-criteria decision-making. Int. J. Syst. Sci. 2014, 46, 2335–2350. [Google Scholar] [CrossRef]
- Wang, J.Q.; Peng, J.J.; Zhang, H.Y.; Liu, T.; Chen, X.H. An uncertain linguistic multi-criteria group decision-making method based on a cloud model. Group Decis. Negot. 2015, 24, 171–192. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Wang, J.; Chen, X.H. Multi valued neutrosophic sets and power aggregation operators with their applications in multi-criteria group decision-making problems. Int. J. Comput. Intell. Syst. 2015, 8, 345–363. [Google Scholar] [CrossRef]
- Wang, J.Q.; Li, X.E. The TODIM method with multi-valued neutrosophic sets. Control Decis. 2015, 30, 1139–1142. [Google Scholar]
- Garg, H. A linear programming method based on an improved score function for interval-valued pythagorean fuzzy numbers and its application to decision-making. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2018, 26, 67–80. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lee, H.S. The revised method of ranking fuzzy numbers with an area between the centroid and original points. Comput. Math. Appl. 2008, 55, 2033–2042. [Google Scholar] [CrossRef]
- Halgamuge, S.; Runkler, T.; Glesner, M. On the neural defuzzification methods. In Proceedings of the 5th IEEE International Conference on Fuzzy Systems, New Orleans, LA, USA, 8–11 September 1996; pp. 463–469. [Google Scholar]
- Song, Q.; Leland, R.P. Adaptive learning defuzzification techniques and applications. Comput. Math. Appl. 1996, 81, 321–329. [Google Scholar] [CrossRef]
- Yager, R.R. Knowledge-based defuzzification. Fuzzy Sets Syst. 1996, 80, 177–185. [Google Scholar] [CrossRef]
- Filev, D.P.; Yager, R.R. A generalized defuzzification method via BADD distributions. Int. J. Intell. Syst. 1991, 6, 687–697. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y. Generalized defuzzification strategies and their parameter learning procedure. IEEE Trans. Fuzzy Syst. 1996, 4, 64–71. [Google Scholar] [CrossRef]
- Ali, M.; Son, l.; Deli, I.; Tien, N.D. Bipolar neutrosophic soft sets and applications in decision making. J. Intell. Fuzzy Syst. 2017, 33, 4077–4087. [Google Scholar] [CrossRef]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Ali, M. Shortest path problem under bipolar neutrosphic setting. Appl. Mech. Mater. 2016, 859, 59–66. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Geng, Y. Multi-criteria decision-making method based on single-valued neutrosophic schweizer–sklar muirhead mean aggregation operators. Symmetry 2019, 11, 152. [Google Scholar] [CrossRef]
- Qamar, M.A.; Hassan, N. An approach toward a Q-neutrosophic soft set and its application in decision making. Symmetry 2019, 11, 139. [Google Scholar] [CrossRef]
- Grzegorzewski, P. On separability of fuzzy relations. Int. J. Fuzzy Logic Intell. Syst. 2017, 17, 137–144. [Google Scholar] [CrossRef]
- Saber, Y.M.; Alsharari, F. Generalized fuzzy ideal closed setson fuzzy topological spaces in sostak sense. Int. J. Fuzzy Logic Intell. Syst. 2018, 18, 161–166. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Group decision making using intuitionistic hesitant fuzzy sets. Int. J. Fuzzy Logic Intell. Syst. 2014, 14, 181–187. [Google Scholar] [CrossRef]
- Tourad, M.C.; Abdal, A. An Intelligent Similarity Model between Generalized Trapezoidal Fuzzy Numbers in Large Scale. Int. J. Fuzzy LogicIntell. Syst. 2018, 18, 303–315. [Google Scholar] [CrossRef]
- Garg, H. A novel accuracy function under interval-valued Pythagorean fuzzy environment for solving multi criteria decision making problem. J. Intell. Fuzzy Syst. 2016, 31, 529–540. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).