Abstract
Supply chain sustainability has become one of the most attractive decision management topics. There are many articles that have focused on this field presenting many different points of view. This research is centred on the evaluation of supply chain sustainability based on two critical dimensions. The first is the importance of evaluation metrics based on economic, environmental and social aspects, and the second is the degree of difficulty of information gathering. This paper aims to increase the accuracy of the evaluation. The proposed method is a combination of quality function deployment (QFD) with plithogenic aggregation operations. The aggregation operation is applied to aggregate: Firstly, the decision maker’s opinions of requirements that are needed to evaluate the supply chain sustainability; secondly, the evaluation metrics based on the requirements; and lastly, the evaluation of information gathering difficulty. To validate the proposed model, this study presented a real world case study of Thailand’s sugar industry. The results showed the most preferred and the lowest preferred metrics in order to evaluate the sustainability of the supply chain strategy.
1. Introduction
Supply chain sustainability has been one of the most attractive and dynamic research topics in the domain of supply chain management for a long time. The influence of manufacturing activities to global warming and the consumption of natural resources assisted the researchers in considering the importance of the supply chain operation’s sustainability []. As a result of increasing competition, globalization, technological growth and huge customer expectations, the sustainable supply chain is a significant goal to each supply chain in every field. The supply chain sustainability can be described as the capability of operating the business with the long term goal of preserving economic, environment and societal welfare []. A more general definition of sustainable supply chain could be the management of supply chain activities in order to improve the profitability by taking into consideration the environmental impacts and social aspects. Therefore, supply chain sustainability guarantees success and achievements of the whole supply chain management in the long term. Under the uncertainty component, supply chain sustainability became a more important goal for companies. This explains why measuring supply chain sustainability means to identify possible strategic decisions under various situations [].
The evaluation of supply chain sustainability is an interesting topic based on metrics in economic, environmental and social scopes. Measuring sustainability of the supply chain guides firms in the direction of risk elimination and standards/guidelines following []. Moreover, the advantages of evaluating supply chain (SC) sustainability are reducing costs, increasing competence, supporting competitive advantages and improving operational performance []. The challenges of measuring supply chain sustainability are []: The managerial and organizational absence of the inter-organizational metrics; the variety of the organization’s goals and objectives producing different measures; and the difficulty in non-traditional data gathering that reduce the SC performance.
There are several studies in supply chain sustainability assessment including supply chain sustainability risk and assessment [], literature reviews [], multi-objective mathematical models for sustainable supply chain management [] and decision making models for a sustainable supply chain []. Evaluating supply chain sustainability is a multi-criteria decision making (MCDM) problem, therefore the evaluation metrics may be the criteria, and the alternatives may be selected based on these sets of metrics. There are some limitations of SC sustainability studies, such as the fact that the researchers do not consider the difficulty of collecting the information for the metrics that will measure the sustainability. In addition, only a few studies use the linguistic variables to evaluate the metrics, leading to less consideration on the uncertainty or lack of information []. Also, there is the matter of the decision maker’s priorities and contradiction degree between metrics which leads to less accuracy of results. In the comical industry, Rajeev (2019) proposed a framework to describe the evolution of a sustainable supply chain [].
In this research, most of these limitations were processed by the proposed MCDM model that assists in metrics selection and the weighting of sustainable supply chain. The proposed model is based on a combination of plithogenic aggregation operations with quality function deployment (QFD). The details of the model have been explained in Section 3.
QFD is one of the most popular techniques to improve quality in order to meet customer expectations. This tool combines all customer needs in every aspect of the product, transforming them into technical requirements so they can meet their expectations []. QFD records great results in many fields, such as rating engineering characteristics [], the design of building structures [], service level measurements [], industry development [], product development [], or supplier selection problems [].
Plithogeny refers to the creation, development and progression of new entities from composition of contradictory or non-contradictory multiple old entities []. It was introduced by Smarandache in 2017 as a generalization of neutrosophy. A plithogenic set (as a generalization of crisp, fuzzy, intuitionistic fuzzy, and neutrosophic sets) is a set whose elements are characterised by the attribute values. Each attribute value has its contradiction degree values c(vj,vD) between vj and the dominant (most important) attribute value vD. The contradiction degree between attributes assists the model to gain more accurate results. The plithogenic set, logic, probability and statistics that were also introduced by Smarandache in 2017, are obtained from plithogeny, and they are generalizations of neutrosophic sets, logic, probability and statistics respectively.
The rest of this papers is organized as follows: In Section 2, there is a literature review of sustainable supply chain, quality function deployment, clarification of plithogenic sets, and a recapitulation of neutrosophic sets. Section 3 presents the proposed model to evaluate the sustainable supply chain. In Section 4, a real world case is studied in order to evaluate the proposed model. Section 5 discusses the results of this case. Finally, the conclusion and suggestions for future works end Section 6.
2. Literature Review
2.1. Supply Chain Sustainability
In the supply chain management field, there are many considerations that need to be taken into account to minimize the negative influence of business production to environment and social effects. These considerations pushed for the strategic developments plans for sustainability []. Three dimensions of sustainability are considered in the supply chain, derived from customer and stakeholder desires, which are economic, environmental and social aspects to manage raw materials, information and finance flows []. Other definitions of supply chain sustainability is the integration of an organization’s economic, social and environmental dimensions by coordinating the business process in order to improve the organization’s performance in the long term []. A more focused definition could be supply chain management strategies and activities concerning social and environmental aspects, correlated to the production, distribution, design and supply of products and services []. The evaluation of supply chain sustainability metrics are attributes and requirements used to measure the supply chain performance considering economic, social and environmental features []. Table 1 summarizes some of the studies on supply chain sustainability metrics and frameworks.

Table 1.
Studies about supply chain sustainability metrics.
2.2. Quality Function Deployment (QFD)
Quality function deployment (QFD) originated in Japan in the 1960s. QFD establishes quality measurement for the improvement and design, rather than just quality control in manufacturing processes []. The QFD method is the link that connects the customer voice to the design requirement in order to respond these expectations effectively. As illustrated in Figure 1, the components of QFD are as follows []:
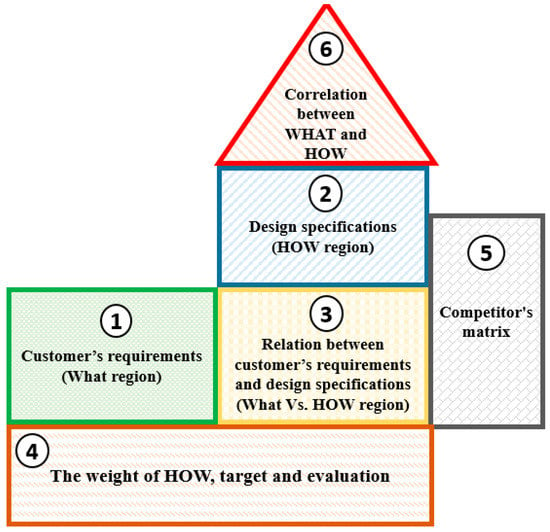
Figure 1.
QFD structure.
- Area (1): The customers’ requirements (what region) that consists of two indicators: The customers’ requirements and the importance of each of them .
- Area (2): The quality characteristics or design specifications (how region), composed of two parts: The design specifications and the way of development.
- Area (3): The relationship between customer requirements and design specifications (what versus how region) by score .
- Area (4): This area is a combination of the value of the design specification, the acceptance level of it, and the score
- Area (5): The comparison of the product and competitors, and how much it satisfies customer needs.
- Area (6): The comparison between each design specification, and how much their improvement may affect each other.
There are several studies that combine QFD with other techniques to evaluate supply chain sustainability, such as: A hybrid QFD–ANP approach to design a sustainable maritime supply chain []; integration of QFD and grey relational analysis (GRA) in order to solve compound decision making complications []; QFD and MCDM techniques in supplier selection problems []. Dursun et al. (2018) considered the competition factor in the process of new product development using QFD []. A combination of best-worst method (BWM) and QFD was proposed in order to determine the relation between customer requirements and engineering characteristics in Mei et al. (2018) [].
2.3. Plithogenic Set Characteristics
Plithogeny is the formation, construction, development, germination, and evolution of new entities from combinations of contradictory (dissimilar) or non-contradictory multiple old entities []. A plithogenic set (P, A, V, d, c) is a set that includes numerous elements described by a number of attributes A = {α1, α2, …, αm}, m ≥ 1, which has a values V = {v1, v2, …, vn}, for n ≥ 1. There are two main features of each attribute’s value, V. The first is the appurtenance degree function d(x,v) of the element x, with respect to some given criteria []. The contradiction (dissimilarity) degree function c(v,D) is the second one, which is realized between each attribute value and the most important (dominant) one. The contradiction degree function is mainly the key element of the plithogenic aggregation operations (intersection, union, complement, inclusion, and equality) that increase the accuracy of aggregation.
Let A be a non-empty set of uni-dimensional attributes A = {α1, α2, …, αm}, m ≥ 1, and let α ∊ A be an attribute with its value spectrum the set S, where S can be defined as a finite discrete set, S = {s1, s2, …, sl}, 1 ≤ l <∞, or infinitely countable set S = {s1, s2, …, s∞}, or infinitely uncountable (continuum) set S = ]a,b[, a < b, where ]…[ is any open, semi-open, or closed interval from the set of real numbers or from other general sets [].
Let V be a non-empty subset of S, where V is the range of all attributes of α’s values defined by the experts based on the application, V = {v1, v2, …, vn} for n ≥ 1. In the set V, there is a dominant attribute value which is determined by the experts based on preferences and the nature of the application.
Each attribute value in V has its appurtenance degree d(x,v) with respect to some criteria. The degree of appurtenance may be a fuzzy, or intuitionistic fuzzy, or neutrosophic degree of appurtenance to the plithogenic set. Therefore, the appurtenance degree d(x,v) of attribute value v is:
∀x ∈ P, d: P × V → P ([0, 1]z),
Therefore, d(x, v) is a subset of [0, 1]z, and P([0, 1]z) is the power set of [0, 1]z, where z = 1, 2, 3, for fuzzy, intuitionistic fuzzy, and neutrosophic degrees of appurtenance respectively [].
Let c: V × V → [0, 1] be the attribute value contradiction degree function c(v1, v2), representing the dissimilarity between two attribute values v1 and v2, and satisfying the following axioms:
c(v1, v1) = 0, contradiction degree between the attribute values and itself is zero.
c(v1, v2) = c(v2, v1), contradiction degree function can be fuzzy CF, intuitionistic attribute value contradiction function (CIF: V × V → [0, 1]2), or a neutrosophic attribute value contradiction function (CN: V × V → [0, 1]3).
2.4. Neutrosophic Set
Neutrosophy is a new branch of philosophy (generalization of dialectics and Yin Yang Chinese philosophy), introduced by Florentin Smarandache in 1980, which studies the origin, nature, and scope of neutralities, as well as their interactions with different ideational spectra. Neutrosophy is the foundation of neutrosophic logic, neutrosophic probability, neutrosophic sets, and neutrosophic statistics. Neutrosophic set definitions are clearly stated in the following:
Definition 1.
[] Let X be a universal set of objects, consisting of non-specific elements defined as x. A neutrosophic set N ⊂ X reflects a set such that each element x from N is characterized by TN(x)–the truth-membership function, IN(x)–the indeterminacy-membership function, and FN(x)–the falsity-membership function. TN(x), IN(x) and FN(x) are subsets of [0−, 1+], so the three neutrosophic components are TN(x) ∊ [0−, 1+], IN(x) ∊ [0−, 1+] and FN(x) ∊ [0−, 1+]. IN(x) is depicts uncertainty, indeterminate, unidentified, or error values. The sum of the three components is 0− ≤ TN(x) + IN(x) + FN(x) ≤ 3+.
Definition 2.
[] Let X be a space of points and x ∈ X. A neutrosophic set N in X is recognized by a truth-membership function TN(x), an indeterminacy-membership function IN(x) and a falsity-membership function FN(x), where TN(x), IN(x) and FN(x) are subsets of ]-0, 1+[. TN(x):X → ]-0, 1+[, IN(x):X → ]-0, 1+[ and FN(x):X → ]-0,1+[. There is no restriction on the summation of membership functions. Therefore, 0− ≤ sup TN(x) + sup IN(x) + sup FN(x) ≤ 3+.
Definition 3.
[] Let be a single valued triangular neutrosophic set, with truth membership Ta(x), indeterminate membership Ia(x), and falsity membership function Fa(x) as follows:
where,,∈ [0,1]. They represent the highest truth membership degree, the lowest indeterminacy membership degree, and the lowest falsity membership degree, respectively.
3. Proposed Model
In this paper, the authors proposed a model to evaluate the supply chain sustainability metrics based on a combination of quality function deployment and plithogenic aggregation operations. This model combines the benefits of the QFD method to link customer needs with design requirements and plithogenic aggregation operator features. The usefulness of this model derives from the plithogenic aggregation operation, because this technique ensures more accurate results and takes into consideration the degree of uncertainty, which is defective in other studies of the same problem. The steps of the proposed model have been explained in detail in this section and it is shown in Figure 2.

Figure 2.
Steps of the proposed model.
- ❖
- Step 1: First of all, decision makers (DM) identify a series of requirements to appraise the supply chain sustainability. The most popular requirements of supply chain sustainability evaluation are summarized in Table 2 or the DM can identify other requirements based on their strategy. These requirements must reflect economic, social and environmental features which is called triple bottom line (TPL).
 Table 2. Popular requirements of supply chain sustainability evaluations.
Table 2. Popular requirements of supply chain sustainability evaluations.- -
- The decision makers measure the importance of each requirement based on the supply chain strategy using linguistic terms.
- -
- The linguistic scale is defined to describe the assessment of each requirement by the DM. In this model, the scale is suggested as a triangular neutrosophic scale, as shown in Table 3.
 Table 3. Linguistic scale.
Table 3. Linguistic scale.
- ❖
- Step 2: Using plithogenic aggregation operations, the decision maker’s opinions are aggregated based on the contradiction degree of each requirement. This step increases the accuracy of results.
- -
- Define contradiction degree c of each requirement with respect to the dominant.
- -
- Plithogenic neutrosophic set intersection is defined as following:where and are fuzzy t-norm and t-conorm respectively.
- -
- The neutrosophic number is transformed into a crisp number using the following equation:
- ❖
- Step 3: In order to find the best requirement considering the set of criteria, the distance of each requirement is found from the best and worst solutions.
- -
- The best (positive) ideal solution S+ and worst (negative) ideal solution S− require definition.
- -
- For example, in price requirements, the lowest value is desired (best ideal solution); on the other side, the maximum value is the worst ideal solution. In the opposite of that, in profit requirements, the maximum value is positive and the lowest value is negative.
- -
- The formula of Euclidean distance is used to find the distance of each requirement to the ideal positive and ideal negative solutions, as shown in Equations (8) and (9) [].
- -
- The superior alternative has the smallest distance from the positive ideal solution S+ and the worst alternative has a larger distance from the negative ideal solution S−.
- ❖
- Step 4: The performance score of each requirement is found in order to weight each of them based on Equation (10).- The performance score is normalized to find the weight of each requirement that satisfies two constraints which are 0 ≤ ≤ 1 and .
- ❖
- Step 5: The decision makers define a combination of metrics by considering the requirements selected previously in step 1 and the TPL.Some of the economic metrics are cost reduction, transaction costs, environmental costs, service level, or sales. The environmental metrics are environmental policies, recycling of waste, air pollution emission, solid waste, water consumption, and so on. Finally, the social diminution consists of working conditions, employee satisfaction, government relationships, employee training, and reputation, among others.- The DMs define the relation between each metric and explain each requirement using linguistic terms as in Table 3.
- ❖
- Step 6: Steps 2–4 are repeated on the evaluation metrics. As in Step 2, the plithogenic aggregation operation is used to combine all decision makers’ judgments about defined metrics. Then, Equations (8) and (9) are used to establish the distance of every metric from the best and worst solutions. The importance of each metric is determined using the performance score as in Equation (10).
- ❖
- Step 7: As proposed in Osiro, Lauro et al. 2018 [], the limitations of other studies that do not consider the hardness of data gathering of each metric need to be addressed. In this step, the difficulty in regards to three dimensions are evaluated in relation to information accessibility, human resources and time needed for assessment, and other required resources [].
- -
- The difficulty of assessment metrics data collecting based on three dimensions explained by linguistic variables are evaluated.
- -
- The assessment based on the contradiction degree to obtain accuracy of results are aggregated, and thenits crisp value is found.
- -
- Their performance score of data collecting difficulty based on the distance of best and worst solutions are found.
- ❖
- Step 8: In this final step, the goal is to categorize the set of supply chain sustainability metrics.
- -
- The performance degree found in Step 4 (the importance of each metric) and Step 7 (the difficulty of data gathering) using Equation (11) are normalized as proposed in (Osiro, Lauro et al. 2018) [].where is the normalized value, is the difference between the value and the mean, and is the standard deviation.
- -
- This is the result if supply chain sustainability evaluation metrics are categorized according to Figure 3 based on the importance of each metric and its difficulty of data gathering.
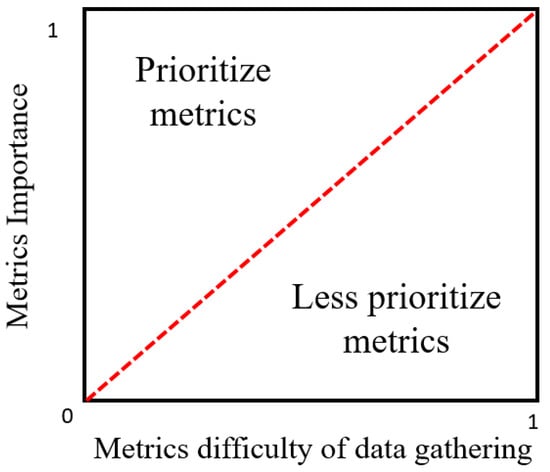 Figure 3. Two dimentions model categorization.
Figure 3. Two dimentions model categorization.
4. Real World Case Study
In this paper, the proposed model has been illustrated in an application on Thailand’s sugar industry in order to measure the overall sustainability of this supply chain (Figure 4). The sugar industry in Thailand is considered one of the most important economic pillars. Thailand is the fourth largest sugar producer and second largest exporter in the world. In this application, four decision makers (DMs) were assisted by their experience in solving such cases to evaluate the sustainability of Thailand’s sugar industry. They are experienced in manufacturing (DM1), quality control (DM2), finance and purchasing (DM3), and environmental expert (DM4). The main goal of this case is to evaluate Thailand’s sugar industry supply chain sustainability metrics based on their significance and difficulty degree of data gathering. Initially, the four experts identified a group of seven requirements for Thailand’s sugar industry supply chain sustainability evaluation. They are: Profit (R1), costs (R2), delivery reliability (R3), product development (R4), environmental aspects (R5), product quality (R6), health and security (R7).
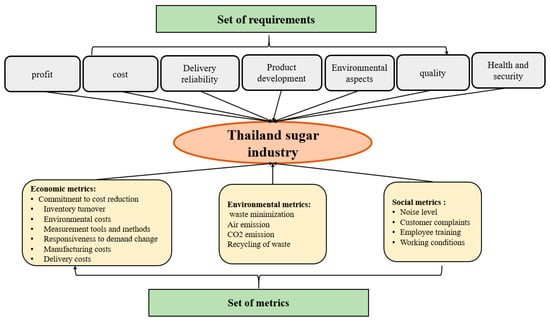
Figure 4.
Thailand’s sugar industry sustainability requirements and metrics.
- ➢
- The requirements by the DMs based on linguistic variables in Table 3 are evaluated as a triangular neutrosophic value. The evaluation is shown in Table 4.
 Table 4. The evaluation of the requirements by four DMs.
Table 4. The evaluation of the requirements by four DMs. - ➢
- As explained in Step 2, the plithogenic aggregation operation is used to combine all decision makers judgments about the requirements based on the contradiction degree of each one as in Table 5.
 Table 5. The requirements contradiction degree.
Table 5. The requirements contradiction degree. - ➢
- Using Equation (6), the aggregation results are shown in Table 6 and then their crisp value is found using Equation (7).
 Table 6. The aggregation results of requirements.
Table 6. The aggregation results of requirements. - ➢
- In Steps 3 and 4, the distance of positive and negative ideal solutions are found using the Euclidean distance as in Equations (8) and (9). Then, the performance degree is measured as mentioned in Equation (10) to find the weight vector of the seven requirements as shown in Table 7.
 Table 7. The weights of requirements based on positive and negative distances.
Table 7. The weights of requirements based on positive and negative distances. - ➢
- The decision makers define a set of supply chain sustainability metrics with respect to economic, environmental, and social dimensions (Table 8). Then, based on linguistic variables in Table 3, the DMs evaluate them as specified in Table 9.
 Table 8. Economic, environmental and social metrics.
Table 8. Economic, environmental and social metrics. Table 9. The evaluation of metrics.
Table 9. The evaluation of metrics. - ➢
- Table 10 shows the metrics aggregation using a plithogenic aggregation operator according to each requirement and based on the contradiction degree in Table 11. Then, their crisp values can be found.
 Table 10. The aggregation results of the metrics.
Table 10. The aggregation results of the metrics. Table 11. Contradiction degree of metrics.
Table 11. Contradiction degree of metrics. - ➢
- As in Steps 3 and 4, using the Euclidean distance as in Equations (8) and (9), the distance of positive and negative ideal solutions are found. Then, as mentioned in Equation (10), the performance degree is measured to find the weight vector of the metrics. Their results are shown in Table 12.
 Table 12. The performance score based on positive and negative distances.
Table 12. The performance score based on positive and negative distances. - ➢
- As proposed in Osiro, Lauro et al. 2018 [], the limitations of neglecting the difficulty of data gathering of every metric is addressed. In this step, the decision makers evaluate the difficulty in regards to three dimensions: Information accessibility, human resources and time needed for assessments, and other required resources, as shown in Table 13.
 Table 13. The evaluation of information gathering difficulty.
Table 13. The evaluation of information gathering difficulty. - ➢
- Then, the decision makers evaluations were aggregated using a plithogenic aggregation equation as shown in Table 14:
 Table 14. The aggregation results of information gathering difficulty.
Table 14. The aggregation results of information gathering difficulty. - ➢
- Equations (8) and (9) were used to find the distance of every metric from the positive ideal solution and negative ideal solution. Then, Equation (10) was used to calculate the performance degree, as shown in the fourth column in Table 15.
 Table 15. The performance score of information gathering difficulty.
Table 15. The performance score of information gathering difficulty. - ➢
- Finally, the performance score was normalized using Equation (11) that relates to metrics importance and difficulty of data gathering. The normalization results are shown in Table 16.
 Table 16. Normalization of importance and data gathering difficulty.
Table 16. Normalization of importance and data gathering difficulty. - ➢
- Figure 5 shows the Thailand sugar industry supply chain sustainability metrics distribution categorized in two regions which are the prioritized metrics and less prioritized metrics based on the four decision maker’s evaluation.
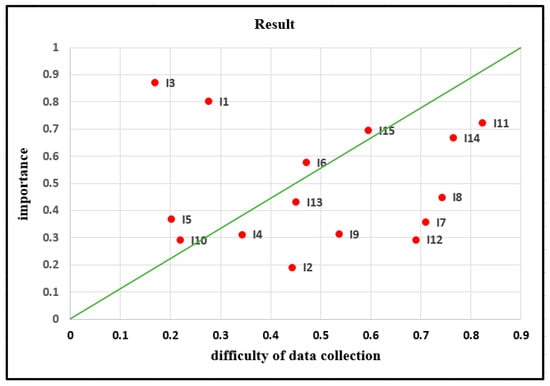 Figure 5. The categorization of Thailand’s sugar industry sustainability.
Figure 5. The categorization of Thailand’s sugar industry sustainability.
5. Results and Discussion
Based on the decision makers evaluations, the prioritize metrics to evaluate Thailand’s sugar industry sustainability are: Commitment to cost reduction (I1), environmental costs (I3), responsiveness to demand change (I5), manufacturing costs (I6), working conditions (I15) and CO2 emission (I10). In this case, the decision makers were considering the economic aspects more than social or environmental dimensions. The importance of commitment to cost reduction (I1), environmental costs (I3) and recycling of wastes (I11) gained the highest importance in value compared to other metrics, as shown in Figure 6. On the other side, recycling of the waste (I11), employee training (I14) and waste minimization (I8) were the most difficult gathering information metrics. However, the CO2 emission (I10), environmental costs (I3) and responsiveness to demand changes (I5) were the most available information that had the lowest difficulty of data gathering degree as in Figure 7.
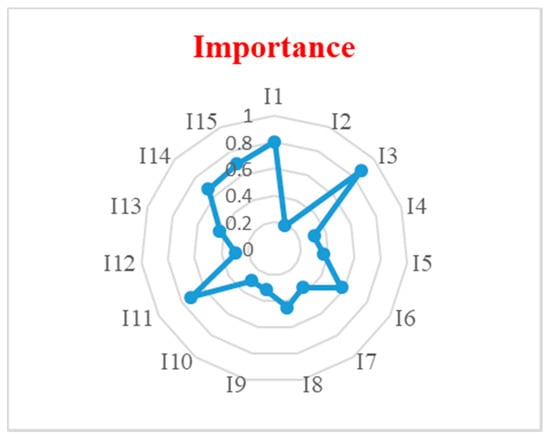
Figure 6.
Metrics evaluation based on their importance.
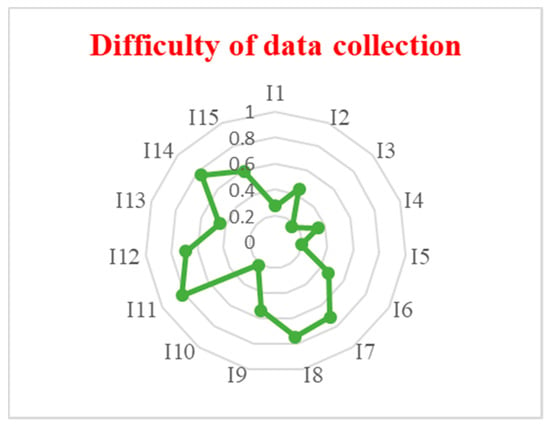
Figure 7.
Metrics evaluation based on difficulty of data collection.
As the results of distribution of the Thailand sugar industry sustainability metrics were categorized based on the significance and difficulty of data gathering, this study found that the most preferred metrics were: Environmental cost (I3), commitment to cost reduction (I1) and realization to demand change (I5), respectively, which were all economic metrics. It can be concluded that the economic metrics were more critical than the environmental and social metrics. These results are based on the evaluation of four decision makers, which means that it is not a general result for similar applications.
The main point in this paper is the plithogenic aggregation operation to group the decision maker’s opinions in a more accurate manner. The plithogenic aggregation is taking into consideration the contradiction degree that mainly increases the accuracy of the aggregation. This study aggregated the decision maker’s assessment of supply chain sustainability requirements, the evaluation of metrics importance, and measuring the difficulty of information gathering. Also, the difficulty of data gathering was not considered in many articles, but the authors found it to be a critical diminution to be measured.
Similar studies on this topic differ based on the model and the nature of the problem. As Ignatius, Joshua, et al. [] proposed, the ANP-QFD approach which mainly considered environmental indicators in order to ensure a green building structure. On the other hand, Jamalnia, Aboozar, et al. [] considered economic metrics such as costs, raw material and labour availability to solve a facility location problem using the QFD method. Khodakarami, Mohsen, et al. [] and Izadikhah, et al. [] used data envelopment analysis (DEA) for the evaluation of supply chain sustainability by taking into account mostly economic and environmental metrics. Ahmadi, et al. [] used the best worst method (BWM) to evaluate the social sustainability of supply chain by considering social indicators rather than economic or environmental aspects.
6. Conclusions and Future Works
Due to strict government requests and the huge stress from the public, the consideration of supply chain sustainability was increased []. Sustainable development is one of the most significant conditions of saving resources and keeping the supply chain phases operating efficiently []. This explains why SSCM became one of the most important competitive strategies in organizations []. This study proposed an efficient combination of plithogenic aggregation operations with the quality function deployment method. The advantage of this combination is the improvement of the accuracy of the results while aggregating the assessments of the decision makers. QFD produced great results in supply chain sustainability evaluation. However, it does not consider the depth of data gathering difficulty which loosen the accuracy of the results. The supply chain sustainability evaluation is a critical topic that needs to be studied with high accuracy by considering economic, environmental and social dimensions.
This study observed the proposed combined model in a major real world case study, which was Thailand’s sugar industry. Based on the nature of this supply chain strategy, its sustainability requirements was defined and measured by four decision makers. Their opinions were aggregated using plithogenic aggregation operator based on the contradiction degree to maximize the accuracy of the aggregation. In the same way, the measurement metrics was defined based on the previous requirement and included economic, social and environmental dimensions evaluated by the DMs. The results showed that the importance of commitment to cost reduction (I1), environmental costs (I3) and recycling of wastes (I11) gained the most important metrics compared to the rest of metrics. Finally, the difficulty of data gathering of these metrics was measured and aggregated. For each dimension of evaluation, the distance of the metrics to the best and worst ideal solutions was calculated to find the importance and the degree of information gathering difficulty. The result of this point was recycling of the waste (I11), employee training (I14) and waste minimization (I8) were the most difficult gathering information metrics. Moreover, the performance degree of the metrics was intended and normalized to distribute the metrics based on the two defined dimensions. It can be concluded that the most preferred metrics based in both dimensions are environmental cost (I3), commitment to cost reduction (I1) and realization to demand change (I5).
Real contributions of this proposed methodology:
- The main contribution of this proposed model lies in providing accurate results of the decision makers assessments based on the contradiction degree while applying the aggregation.
- The plithogenic aggregation operation allows the DMs to consider several experts opinions in order to maximize the efficiency of the decision making.
- Also, it measures the supply chain sustainability based on two major aspects, the significance of the metrics and its level of difficulty of data gathering, which is really a critical point that affects the evaluations.
- Using a triangular neutrosophic linguistic scale to evaluate the requirement, metrics and information availability improved the level of consideration to uncertainty, because it confirms the best representation by using the three membership degrees positive, negative and boundary areas of decision making.
- The proposed methodology is efficient and has a high accuracy degree in decision making problems, Therefore, it is a great tool that may help firms in their estimation of customer needs in addition to evaluating the supply chain sustainability requirements.
In future research directions, this model may be used in assessment of other supply chain strategies to evaluate their sustainability. In addition, the plithogenic aggregation operators could be combined with other techniques to evaluate the supply chain sustainability. Finally, more evaluation dimensions could be added to the importance and difficulty of information gathering to measure supply chain sustainability.
Author Contributions
All authors have contributed equally to this paper. The individual responsibilities and contribution of all authors can be described as follows: The idea of this whole paper was put forward by M.A.-B. and R.M., A.E.-N.H.Z. completed the preparatory work of the paper. F.S. analyzed the existing work. The revision and submission of this paper was completed by M.A.-B.
Funding
“This research received no external funding”.
Acknowledgments
The authors would like to thank the anonymous referees, Chief-Editor, and support Editors for their constructive suspensions and propositions that have helped to improve the quality of this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ageron, B.; Gunasekaran, A.; Spalanzani, A. Sustainable supply management: An empirical study. Int. J. Prod. Econ. 2012, 140, 168–182. [Google Scholar] [CrossRef]
- Hassini, E.; Surti, C.; Searcy, C. A literature review and a case study of sustainable supply chains with a focus on metrics. Int. J. Prod. Econ. 2012, 140, 69–82. [Google Scholar] [CrossRef]
- Fera, M.; Fruggiero, F.; Lambiase, A.; Macchiaroli, R.; Miranda, S. The role of uncertainty in supply chains under dynamic modeling. Int. J. Ind. Eng. Comput. 2017, 8, 119–140. [Google Scholar] [CrossRef]
- Taticchi, P.; Tonelli, F.; Pasqualino, R. Performance measurement of sustainable supply chains: A literature review and a research agenda. Int. J. Product. Perform. Manag. 2013, 62, 782–804. [Google Scholar] [CrossRef]
- Chithambaranathan, P.; Subramanian, N.; Gunasekaran, A.; Palaniappan, P.K. Service supply chain environmental performance evaluation using grey based hybrid MCDM approach. Int. J. Prod. Econ. 2015, 166, 163–176. [Google Scholar] [CrossRef]
- Hervani, A.A.; Helms, M.M.; Sarkis, J. Performance measurement for green supply chain management. Benchmarking Int. J. 2004, 14, 330–353. [Google Scholar] [CrossRef]
- Xu, M.; Cui, Y.; Hu, M.; Xu, X.; Zhang, Z.; Liang, S.; Qu, S. Supply chain sustainability risk and assessment. J. Clean. Prod. 2018, 225, 857–867. [Google Scholar] [CrossRef]
- Martins, C.L.; Pato, M.V. Supply chain sustainability: A tertiary literature review. J. Clean. Prod. 2019. [Google Scholar] [CrossRef]
- Vafaeenezhad, T.; Tavakkoli-Moghaddam, R.; Cheikhrouhou, N. Multi-objective mathematical modeling for sustainable supply chain management in the paper industry. Comput. Ind. Eng. 2019. [Google Scholar] [CrossRef]
- Tseng, M.L.; Wu, K.J.; Hu, J.; Wang, C.H. Decision-making model for sustainable supply chain finance under uncertainties. Int. J. Prod. Econ. 2018, 205, 30–36. [Google Scholar] [CrossRef]
- Osiro, L.; Lima-Junior, F.R.; Carpinetti, L.C. A group decision model based on quality function deployment and hesitant fuzzy for selecting supply chain sustainability metrics. J. Clean. Prod. 2018, 183, 964–978. [Google Scholar] [CrossRef]
- Rajeev, A.; Pati, R.K.; Padhi, S.S. Sustainable supply chain management in the chemical industry: Evolution, opportunities, and challenges. Resour. Conserv. Recycl. 2019, 149, 275–291. [Google Scholar]
- Akkawuttiwanich, P.; Yenradee, P. Fuzzy QFD approach for managing SCOR performance indicators. Comput. Ind. Eng. 2018, 122, 189–201. [Google Scholar] [CrossRef]
- Li, S.; Tang, D.; Wang, Q. Rating engineering characteristics in open design using a probabilistic language method based on fuzzy QFD. Comput. Ind. Eng. 2019. [Google Scholar] [CrossRef]
- Eleftheriadis, S.; Duffour, P.; Mumovic, D. Participatory decision-support model in the context of building structural design embedding BIM with QFD. Adv. Eng. Inform. 2018, 38, 695–711. [Google Scholar] [CrossRef]
- Lee, C.K.; Ru, C.T.; Yeung, C.L.; Choy, K.L.; Ip, W.H. Analyze the healthcare service requirement using fuzzy QFD. Comput. Ind. 2015, 74, 1–15. [Google Scholar] [CrossRef]
- Eldermann, M.; Siirde, A.; Gusca, J. QFD framework for selection of industry development scenarios. Energy Procedia 2017, 128, 230–233. [Google Scholar] [CrossRef]
- Zaim, S.; Sevkli, M.; Camgöz-Akdağ, H.; Demirel, O.F.; Yayla, A.Y.; Delen, D. Use of ANP weighted crisp and fuzzy QFD for product development. Expert Syst. Appl. 2014, 41, 4464–4474. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Mohamed, M.; Chilamkurti, N. Three-way decisions based on neutrosophic sets and AHP-QFD framework for supplier selection problem. Future Gener. Comput. Syst. 2018, 89, 19–30. [Google Scholar] [CrossRef]
- Smarandache, F. Plithogeny, Plithogenic Set, Logic, Probability, and Statistics; Infinite Study, 2017; p. 141. [Google Scholar]
- Ahi, P.; Searcy, C. Assessing sustainability in the supply chain: A triple bottom line approach. Appl. Math. Model. 2015, 39, 2882–2896. [Google Scholar] [CrossRef]
- Closs, D.J.; Speier, C.; Meacham, N. Sustainability to support end-to-end value chains: The role of supply chain management. J. Acad. Mark. Sci. 2011, 39, 101–116. [Google Scholar] [CrossRef]
- Haake, H.; Seuring, S. Sustainable procurement of minor items–exploring limits to sustainability. Sustain. Dev. 2009, 17, 284–294. [Google Scholar] [CrossRef]
- Linton, J.D.; Klassen, R.; Jayaraman, V. Sustainable supply chains: An introduction. J. Oper. Manag. 2007, 25, 1075–1082. [Google Scholar] [CrossRef]
- Jadhav, A.; Orr, S.; Malik, M. The role of supply chain orientation in achieving supply chain sustainability. Int. J. Prod. Econ. 2008. [Google Scholar] [CrossRef]
- Yazdani, M.; Kahraman, C.; Zarate, P.; Onar, S.C. A fuzzy multi attribute decision framework with integration of QFD and grey relational analysis. Expert Syst. Appl. 2019, 115, 474–485. [Google Scholar] [CrossRef]
- Qorri, A.; Mujkić, Z.; Kraslawski, A. A conceptual framework for measuring sustainability performance of supply chains. J. Clean. Prod. 2018, 189, 570–584. [Google Scholar] [CrossRef]
- Searcy, C.; Dixon, S.M.; Neumann, W.P. The use of work environment performance indicators in corporate social responsibility reporting. J. Clean. Prod. 2016, 112, 2907–2921. [Google Scholar] [CrossRef]
- Chen, R.H.; Lin, Y.; Tseng, M.L. Multicriteria analysis of sustainable development indicators in the construction minerals industry in China. Resour. Policy 2015, 46, 123–133. [Google Scholar] [CrossRef]
- Haghighi, S.M.; Torabi, S.A.; Ghasemi, R. An integrated approach for performance evaluation in sustainable supply chain networks (with a case study). J. Clean. Prod. 2016, 137, 579–597. [Google Scholar] [CrossRef]
- Akao, Y.; Mazur, G.H. The leading edge in QFD: Past, present and future. Int. J. Qual. Reliab. Manag. 2003, 20, 20–35. [Google Scholar] [CrossRef]
- Moubachir, Y.; Bouami, D. A new approach for the transition between QFD phases. Procedia CIRP 2015, 26, 82–86. [Google Scholar] [CrossRef][Green Version]
- Lam, J.S. Designing a sustainable maritime supply chain: A hybrid QFD-ANP approach. Transp. Res. Part E: Logist. Transp. Rev. 2015, 78, 70–81. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P.; Zavadskas, E.K.; Zolfani, S.H. Integrated QFD-MCDM framework for green supplier selection. J. Clean. Prod. 2017, 142, 3728–3740. [Google Scholar] [CrossRef]
- Dursun, M.; Arslan, Ö. An Integrated Decision Framework for Material Selection Procedure: A Case Study in a Detergent Manufacturer. Symmetry 2018, 10, 657. [Google Scholar] [CrossRef]
- Meksavang, P.; Shi, H.; Lin, S.M.; Liu, H.C. An Extended Picture Fuzzy VIKOR Approach for Sustainable Supplier Management and Its Application in the Beef Industry. Symmetry 2019, 11, 468. [Google Scholar] [CrossRef]
- Smarandache, F. Plithogenic Set, an Extension of Crisp, Fuzzy, Intuitionistic Fuzzy, and Neutrosophic Sets–Revisited. Neutrosophic Sets Syst. 2018, 21, 153–166. [Google Scholar]
- Smarandache, F. Physical Plithogenic Set. APS Meeting Abstracts. 2018.
- Smarandache, F. Extension of Soft Set to Hypersoft Set, and then to Plithogenic Hypersoft Set. Neutrosophic Sets Syst. 2018, 24, 168–170. [Google Scholar]
- Liu, P.; Wang, Y. Multiple attribute decision-making method based on single-valued neutrosophic normalized weighted Bonferroni mean. Neural Comput. Appl. 2014, 25, 2001–2010. [Google Scholar] [CrossRef]
- Abdel-Baset, M.; Hezam, I.M.; Smarandache, F. Neutrosophic goal programming. Neutrosophic Sets Syst. 2016, 11. [Google Scholar]
- Rivieccio, U. Neutrosophic logics: Prospects and problems. Fuzzy Sets Syst. 2008, 159, 1860–1868. [Google Scholar] [CrossRef]
- Govindan, K.; Khodaverdi, R.; Jafarian, A. A fuzzy multi criteria approach for measuring sustainability performance of a supplier based on triple bottom line approach. J. Clean. Prod. 2003, 47, 345–354. [Google Scholar] [CrossRef]
- Osiro, L.; Lima-Junior, F.R.; Carpinetti, L.C. A fuzzy logic approach to supplier evaluation for development. Int. J. Prod. Econ. 2014, 153, 95–112. [Google Scholar] [CrossRef]
- Kannan, D.; Khodaverdi, R.; Olfat, L.; Jafarian, A.; Diabat, A. Integrated fuzzy multi criteria decision making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain. J. Clean. Prod. 2013, 47, 355–367. [Google Scholar] [CrossRef]
- Huang, S.H.; Keskar, H. Comprehensive and configurable metrics for supplier selection. Int. J. Prod. Econ. 2007, 105, 510–523. [Google Scholar] [CrossRef]
- Katsikeas, C.S.; Paparoidamis, N.G.; Katsikea, E. Supply source selection criteria: The impact of supplier performance on distributor performance. Ind. Mark. Manag. 2004, 33, 755–764. [Google Scholar] [CrossRef]
- Mani, V.; Agrawal, R.; Sharma, V. Supplier selection using social sustainability: AHP based approach in India. Int. Strateg. Manag. Rev. 2014, 2, 98–112. [Google Scholar] [CrossRef]
- Chang, B.; Chang, C.W.; Wu, C.H. Fuzzy DEMATEL method for developing supplier selection criteria. Expert Syst. Appl. 2011, 38, 1850–1858. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making. Inf. Sci. 2014, 271, 125–142. [Google Scholar] [CrossRef]
- Lima-Junior, F.R.; Carpinetti, L.C. A multicriteria approach based on fuzzy QFD for choosing criteria for supplier selection. Comput. Ind. Eng. 2016, 101, 269–285. [Google Scholar] [CrossRef]
- Ignatius, J.; Rahman, A.; Yazdani, M.; Šaparauskas, J.; Haron, S.H. An integrated fuzzy ANP–QFD approach for green building assessment. J. Civ. Eng. Manag. 2016, 22, 551–563. [Google Scholar] [CrossRef]
- Jamalnia, A.; Mahdiraji, H.A.; Sadeghi, M.R.; Hajiagha, S.H.; Feili, A. An integrated fuzzy QFD and fuzzy goal programming approach for global facility location-allocation problem. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 263–290. [Google Scholar] [CrossRef]
- Khodakarami, M.; Shabani, A.; Saen, R.F.; Azadi, M. Developing distinctive two-stage data envelopment analysis models: An application in evaluating the sustainability of supply chain management. Measurement 2015, 70, 62–74. [Google Scholar] [CrossRef]
- Izadikhah, M.; Saen, R.F. Evaluating sustainability of supply chains by two-stage range directional measure in the presence of negative data. Transp. Res. Part D Transp. Environ. 2016, 49, 110–126. [Google Scholar] [CrossRef]
- Ahmadi, H.B.; Kusi-Sarpong, S.; Rezaei, J. Assessing the social sustainability of supply chains using Best Worst Method. Resour. Conserv. Recycl. 2017, 126, 99–106. [Google Scholar] [CrossRef]
- Matić, B.; Jovanović, S.; Das, D.K.; Zavadskas, E.K.; Stević, Ž.; Sremac, S.; Marinković, M. A New Hybrid MCDM Model: Sustainable Supplier Selection in a Construction Company. Symmetry 2019, 11, 353. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, M.; Smarandache, F. A hybrid neutrosophic group ANP-TOPSIS framework for supplier selection problems. Symmetry 2018, 10, 226. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).