Abstract
Multi-attribute decision-making (MADM) is a part of management decision-making and an important branch of the modern decision theory and method. MADM focuses on the decision problem of discrete and finite decision schemes. Uncertain MADM is an extension and development of classical multi-attribute decision making theory. When the attribute value of MADM is shown by neutrosophic number, that is, the attribute value is complex data and needs three values to express, it is called the MADM problem in which the attribute values are neutrosophic numbers. However, in practical MADM problems, to minimize errors in individual decision making, we need to consider the ideas of many people and synthesize their opinions. Therefore, it is of great significance to study the method of attribute information aggregation. In this paper, we proposed a new theory—non-dual multi-granulation neutrosophic rough set (MS)—to aggregate multiple attribute information and solve a multi-attribute group decision-making (MGDM) problem where the attribute values are neutrosophic numbers. First, we defined two kinds of non-dual MS models, intersection-type MS and union-type MS. Additionally, their properties are studied. Then the relationships between MS, non-dual MS, neutrosophic rough set (NRS) based on neutrosophic intersection (union) relationship, and NRS based on neutrosophic transitive closure relation of union relationship are outlined, and a figure is given to show them directly. Finally, the definition of non-dual MS on two universes is given and we use it to solve a MGDM problem with a neutrosophic number as the attribute value.
1. Introduction
Fuzzy sets and rough sets are widely used to solve uncertain problems [1,2,3,4]. However, all these theories have their own deficiency, such as in a voting, you may support, not support, be neutral, or abstain from voting, so Smarandache present the definition of the neutrosophic set (NS) [5]. NS is an extensional model of the fuzzy set and intuitionistic fuzzy set. But the original definition of NS is not convenient to solve real-world problems, thus Wang et al. proposed a single-valued neutrosophic set (SVNS) [6]. After that, SVNS was extended and used in many fields. Peng et al. [7] defined simplified NS and obtained some properties. Peng et al. [8] proposed the definition of probability multi-valued NS and studied its properties. Deli et al. [9] defined bipolar NS and studied its properties. Zhang et al. [10] analyzed new inclusion relationships of SVNS and discussed its lattice structure. As an extension of fuzzy sets and rough sets, many scholars combined them and got some results [11,12,13]. Yang et al. [14] combined SVNS and rough set, then produced a single-valued neutrosophic rough set and discussed its properties. Now NSs and NRSs have been used widely in decision-making problems [15,16,17,18,19].
From the perspective of particle computing, the above rough set theories are essentially defined in a single particle space, and the lower and upper approximations (ULA) of the target concept is shown by the information particles in the particle space induced by a single binary relationship. However, Qian et al. think that, in decision analysis problems, the relationship between the multiple decision makers may be independent of each other, so multiple binary relations are needed to approximate the target. Therefore, they put forward the concept of a multi-granularity rough set (MRS) model [20], and define the optimistic MRS model and pessimistic MRS model, respectively. The biggest difference between MRS and classical rough sets is that MRS can use the knowledge in a multi-granular space to approximate the target. Additionally, because it analyzes the problem from multiple angles and levels, it can obtain a more reasonable and satisfactory solution for the problem, so it has a better application prospect in many practical decision-making problems. Yao et al. [21] studied the rough set models under the multi-granulation approximation space. Now the MRS model has been used widely and has produced some interesting results [22,23,24,25,26,27,28].
The ULA operator of most MRS models is dual, there are few articles studying the non-dual MRS model or hybrid MRS model [29,30]. Zhang et al. [31] put forward non-dual MRS (union-type MRS and intersection-type MRS) models and outline the relationships between MRSs. In this paper, we put forward non-dual MS (intersection-type MS and union-type MS) models and study their properties. Then we show the relationships between MS, non-dual MS, NRS-based neutrosophic union relation, and NRS-based neutrosophic intersection relation. Finally, we propose non-dual MS models on two universes and use it to solve MGDM problems with neutrosophic numbers as the attribute values.
The structure of this article is as follows. In Section 2, some basic notions and operations of NRS and MS are introduced. In Section 3, the concepts of non-dual MS are put forward and their qualities are investigated. In Section 4, the relationships between MS, non-dual MS, neutrosophic rough set (NRS) based on neutrosophic intersection (union) relationship, and NRS based on neutrosophic transitive closure relation of union relationship are discussed. In Section 5, non-dual MS models on two universes are proposed and an application to solve the MGDM problem where the attribute values are neutrosophic numbers is outlined. Finally, Section 6 provides our conclusions and outlook.
2. Preliminary
In this section, we look at several basic concepts of NRS and MS.
Definition 1
([6]).A SVNS A is denoted by
where TA(x) represents truth-membership function, IA(x) represents indeterminacy-membership function, FA(x) represenst falsity-membership function and TA(x), IA(x), FA(x) ∈ [0, 1]. Additionally, they satisfy the condition 0 ≤ TA(x) + IA(x) + FA(x) ≤ 3.
In this paper, “SVNS” is abbreviated to “NS” and we use the symbol NS(U) to denote the set of all NSs in U.
Definition 2
([6]).For any two NSs A and B, the inclusion relation, union, intersection, and complement operations are defined:
- (1)
- A ⊆ B iff ∀ x ∈ U, TA(x) ≤ TB(x), IA(x) ≥ IB(x), FA(x) ≥ FB(x);
- (2)
- A ∪ B = {(x, TA(x) ∨ TB(x), IA(x) ∧ IB(x), FA(x) ∧ FB(x)) | x ∈ U};
- (3)
- A ∩ B = {(x, TA(x) ∧ TB(x), IA(x) ∨ IB(x), FA(x) ∨ FB(x)) | x ∈ U};
- (4)
- Ac = {(x, FA(x), 1‒IA(x), TA(x)) | x ∈ U}.
Definition 3
[14]).Suppose (U, R) is a neutrosophic approximation space (NAS). ∀ A ∈ NS(U), the LUA of A, denoted by and , are defined as: ∀ x ∈ U,
The pairis called the SVNRS of A.
Definition 4
([28]).Suppose (U, Ri) is a multi-granulation neutrosophic approximation space (MAS). A ∈ NS(U), the optimistic ULA of A, represented by and , are defined:
Then the pairis called an optimistic MS when .
Definition 5
([28]).Suppose (U, Ri) is a MAS. ∀A ∈ NS(U), the pessimistic ULA of A, represented by and , are defined:
Then the pairis called a pessimistic MS when .
Proposition 1
([28]).Suppose (U, Ri) be a MAS. ∀ A, B ∈ NS(U), then
- (1)
- ,.
- (2)
- ,.
- (3)
- ,.
- (4)
- ,.
- (5)
- .
- (6)
- .
- (7)
- ,.
- (8)
- ,.
Definition 6
([14]).If A and B are two neutrosophic numbers in U, the operation of A and B is defined as follows:
Definition 7
([10]).Let (t, i, f) be a neutrosophic number, the type-3 score function and type-3 accuracy function are defined:
Definition 8
([10]).Let (t1, i1, f1) and (t2, i2, f2) be two neutrosophic numbers. Then
- (1)
- If, then.
- (2)
- If, then.
- (3)
- If,,, then; if, then.
3. Non-Dual Multi-Granulation Neutrosophic Rough Set
In this section, we introduce non-dual MS (intersection-type MS and union-type MS) models and study their properties.
Definition 9.
Let tuple ordered set (U, Ri) (1 ≤ i ≤ m) be a MAS. For any A ∈ NS(U), the intersection-type ULA and in (U, Ri) are defined:
Obviously,andare two NSs of U. Furthermore, A is called a definable NS on (U, Ri) when. Otherwise, the pairis called intersection-type MS.
Definition 10.
Let tuple ordered set (U, Ri) (1 ≤ i ≤ m) be a MAS. For any A ∈ NS(U), the union-type ULA and in (U, Ri) are defined:
Obviously,andare two NSs of U. Furthermore, A is called a definable NS on (U, Ri) when. Otherwise, the pairis called union-type MS.
Proposition 2.
Let (U, Ri) be a MAS, Ri (1 ≤ i ≤ m) be the neutrosophic relations on U. For any A, B ∈ NS(U), we have
- (1)
- ,;
- (2)
- ,;
- (3)
- ,;
- (4)
- ,;
- (5)
- ,;
- (6)
- ,.
Proof.
(1) By Definition 9, we have
Similarly, by Definition 9, we can get
(2) By Definition 10, we have
Similarly, by Definition 10, we can get
(3) Suppose A ⊆B, then TA(x) ≤ TB(x), IA(x) ≥ IB(x), FA(x) ≥ FB(x),
Hence, .
Similarly, we can get .
(4) The proof is similar with (3).
(5) According to Definition 9, we have
Hence, .
Additionally, we have
Hence, .
(6) According to Definition 10, we have
Hence, .
Additionally, we have
Hence, . □
4. The Relationships between Multi-Granulation Neutrosophic Rough Set Models
In this section, we discuss the relationships between MS, non-dual MS, neutrosophic rough set (NRS) based on neutrosophic intersection (union) relationship, and NRS based on neutrosophic transitive closure relation of union relationship and show it by a relational graph.
Definition 11.
Suppose U is a non-empty finite universe, and Ri (1 ≤ i ≤ m) is the binary NR on U. The ULA based on neutrosophic union relationship, represented by and , are defined:
Definition 12.
Suppose U is a non-empty finite universe, and Ri (1 ≤ i ≤ m) is the binary NR on U. The ULA based on neutrosophic intersection relationship, represented by and , are defined:
Definition 13
([32]).Suppose R is a neutrosophic relation in U. The minimal transitive neutrosophic relation containing R is called transitive closure of R, denoted by t(R).
Proposition 3.
Suppose R is a neutrosophic relation in U. Then . Where Rk = R●R●R● ⋯, .
Definition 14.
Suppose (U, R) is neutrosophic approximation space. Suppose U is a non-empty finite universe, Ri (1 ≤ i ≤ m) is neutrosophic relations on U, and t(R) denotes the transitive closure of the union of neutrosophic relations Ri on U.∀A ∈ NS(U), the ULA of A, denoted by and , are defined as: ∀ x ∈ U,
Proposition 4.
Let (U, Ri) be a MAS, Ri (1 ≤ i≤ m) be neutrosophic relations on U. For any A ∈ NS (U), we have
- (1)
- ;
- (2)
- .
Proof.
(1) According to Definition 4, Definition 5, Definition 9, and Definition 10, we can get , . Let R = R1 ∪ R2 ∪ ⋯ ∪ Rm, t(R) = R ∪ R2 ∪ ⋯, then (t(R))c = Rc ∩ (R2)c ∩ ⋯, so (t(R))c ⊆ Rc, thus
Additionally, we have
Then we get the proof.
(2) According to Definition 4, Definition 5, Definition 9, and Definition 10, we can get , . Let R = R1 ∪ R2 ∪ ⋯ ∪ Rm, t(R) = R ∪ R2 ∪ ⋯, then R ⊆ t(R), thus
Additionally, we have
Then we get the proof. □
The above results show that the four kinds of lower and upper approximations equipped with the inclusion relation ⊆ can construct a lattice. This fact can be described by Figure 1, where i ≠ j, each node denotes an approximation or a concept, and each diagonal line connects two approximations, the lower node is a subset of the upper node.
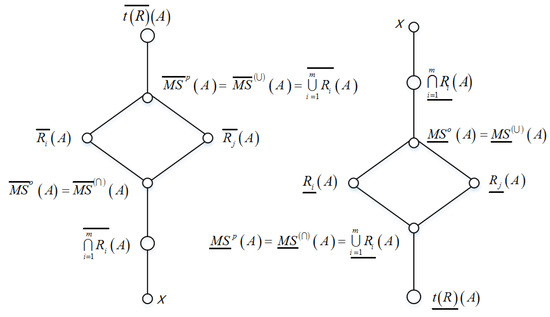
Figure 1.
The relationships between neutrosophic rough lower and upper approximations.
5. The Application of Non-Dual Multi-Granulation Neutrosophic Rough Set on Two Universes in MGDM
In this section, we propose the concept of non-dual MS on two universes and we talk about the relationship between non-dual MS on two universes and non-dual MS on a single universe. Additionally, we used non-dual MS on two universes to deal with a MGDM problem where the attribute values are neutrosophic numbers.
Definition 14
([28]).Suppose U, V are two non-empty finite universes, and Ri ∈ NS (U × V) (1 ≤ i ≤ m) is binary NR. We call (U, V, Ri) the MAS on two universes.
Definition 15.
Let tuple ordered set (U, V, Ri) (1 ≤ i ≤ m) be a MAS on two universes. For any A ∈ NS(U), the intersection-type ULA and in (U, V, Ri) are defined:
Obviously,andare two NSs. Furthermore, A is called a definable NS on (U, V, Ri) when. Otherwise, the pairare called intersection-type MS on two universes.
Definition 16.
Let tuple ordered set (U, V, Ri) (1 ≤ i ≤ m) be a MAS on two universes. For any A ∈ NS(U), the union-type ULA and in (U, V, Ri) are defined:
Obviously,andare two NSs. Furthermore, A is called a definable NS on (U, V, Ri) when. Otherwise, the pairare called union-type MS on two universes.
Proposition 5.
Let (U, V, Ri) be a MAS on two universes. For any A, B ∈ NS(U), we have
- (1)
- ,;
- (2)
- ,;
- (3)
- ,;
- (4)
- ,;
- (5)
- ,;
- (6)
- ,.
Proof.
The proof is similar with Proposition 2. □
Remark 1.
Note that if the two universes are the same, then the intersection-type (union-type) MS on two universes degenerates into the intersection-type (union-type) MS on a single universe in Section 3.
Next, we will use the non-dual MSs to solve the MGDM problems where the attribute values are neutrosophic numbers. For a multiple attribute group decision making problem, let U = {x1, x2, …, xn} be the decision set and V = {y1, y2, …, ym} be the criteria set, Rl represent l evaluation experts. Here, Rl ∈ NR (U × V) is NRs from U to V, where ∀(xi, yj) ∈ U × V, Rl(xi, yj) denotes the degree of membership about criteria set yj (yj ∈ V) with respect to xi (xi ∈ U). In the following, we show the process about the non-dual MSs on two universes to solve MGDM problems with neutrosophic numbers as attribute values.
Step 1 Calculate non-dual multi-granulation neutrosophic rough ULA , , , and .
Step 2 Calculate the sum of non-dual multi-granulation neutrosophic rough ULA , , λ ∈ [0, 1] according to Definition 6.
Step 3 Make a descending order according to Definitions 7 and 8 for the multi-granulation neutrosophic rough sets in step 2 and use the Borda number scoring method in reference [33] to make a total rank.
In practice, the parameter λ represents a decision maker’s preference for risk. In general, the higher the parameter λ is, the more likely the decision maker is to be risk-prone. The smaller the parameter λ is, the less risk the decision maker prefers. Therefore, the value of the parameter λ is determined by the decision maker’s preference or by an advance empirical study.
Next, we show the algorithm to calculate the ULA of a union-type multi-granulation neutrosophic rough set.
| Algorithm 1 The lower approximation of a union-type multi-granulation neutrosophic rough set |
| Define the method to acquire a complement for a matrix A: each neutrosophic number in matrix A do complement the operator according to the following Formula: . Return matrix C. Define the method for two matrixes to do union operator: the union of B and C is the neutrosophic number of each row in C to do union operator with the corresponding neutrosophic number in B according to the Formula (22) Return matrix D. Define the method for one matrix to do intersection operator: the neutrosophic numbers of each row in D do intersection operator according to the Formula (23) Return matrix E. Define the method for one matrix to do union operator: the neutrosophic numbers of each row in E do union operator according to the Formula (22). Return matrix F. For the number of iterations is h, Transfer the method of acquire complement, assign X. Get Y. Transfer the method for two matrixes to do union operator, assign Y, Z. Get M. Transfer the method to do intersection operator, assign M. Get N. End for. Combine h matrixes N. Get P. Transfer the method for one matrix to do union operator, assign P. Get Q. |
X, Y, M are matrixes which line numbers are m, column number is n, and every membership is a neutrosophic number. Z is a matrix which line number is 1, column number is n, and every membership is a neutrosophic number. N and Q are matrixes which line numbers are m, column number is 1, and every membership is a neutrosophic number. P is a matrix which line number is m, column number is h, and every membership is a neutrosophic number.
The lower approximation of a union-type multi-granulation neutrosophic rough set is the transpose of matrix Q.
| Algorithm 2 The upper approximation of a union-type multi-granulation neutrosophic rough set |
| Define the method for two matrixes to do intersection operator: the intersection of B and C is the neutrosophic number of each row in C to do intersection operator with the corresponding neutrosophic number in B according to the Formula (23). Return matrix D. Define the method for one matrix to do union operator: the neutrosophic numbers of each row in D do union operator according to the Formula (22). Return matrix E. For the number of iterations is h, Transfer the method for two matrixes to do intersection operator, assign Y, Z. Get M. Transfer the method for one matrix to do union operator, assign M. Get N. End for. Combine h matrixes N. Get P. Transfer the method for one matrix to do intersection operator, assign P. Get Q. |
Y, M are matrixes which line numbers are m, column number is n, and every membership is a neutrosophic number. Z is a matrix which line number is 1, column number is n, and every membership is a neutrosophic number. N and Q are matrixes which line numbers are m, column number is 1, and every membership is a neutrosophic number. P is a matrix which line number is m, column number is h, and every membership is a neutrosophic number.
The upper approximation of a union-type multi-granulation neutrosophic rough set is the transpose of matrix Q.
With the same method we can get the ULA of an intersection-type multi-granulation neutrosophic rough set. Then, to decide the value of λ, we calculate the sum of ULA of the union-type MS and intersection-type MS according to Formula (6) and (7), and rank them according to Definition 7.
Next, we show an example.
Example 1.
We consider the decision making problem adapted from reference [34]. Suppose U = {x1, x2, x3} is a criterion set, where x1 represents the ability of salesman, x2 represents the overall condition of the stable supplier, and x3 represents the position of high flow. Let V = {y1, y2, y3, y4, y5} be the decision set, where y1 represents shop 1, y2 represents shop 2, y3 represents shop 3, y4 represents shop 4, and y5 represents shop 5.
Assume there are three experts. They provide their evaluations shown in Table 1, Table 2 and Table 3 based on their knowledge and experience. The data of the three tables were adapted from Table 2 in reference [34]. We take the first positive membership and negative membership of the intuitionistic fuzzy set of interval values y1–y5 in Table 2 as the true membership and false membership of the neutrosophic set, respectively, and the second negative membership as the uncertain membership of the neutrosophic set. Let A = {(0.9, 0.1, 0.2), (0.7, 0.7, 0.3), (0.5, 0.8, 0.6)}.

Table 1.
Neutrosophic relation R1.

Table 2.
Neutrosophic relation R2.

Table 3.
Neutrosophic relation R3.
By Definitions 15 and 16, we can compute
Let λ = 0.3, then
Then, according to Definition 6, we can get
s(∪) (y1) = 0.5259, s(∪) (y2) = 0.6814, s(∪) (y3) = 0.6963, s(∪) (y4) = 0.6930, s(∪) (y5) = 0.6319.
So, the ranking result for union-type MS is: y1 ≺ y5 ≺ y2 ≺ y4 ≺ y3.
s(∩) (y1) = 0.6903, s(∩)(y2) = 0.5726, s(∩)(y3) = 0.6592, s(∩)(y4) = 0.6201, s(∩)(y5) = 0.5432.
So, the ranking result for intersection-type MS is: y5 ≺ y2 ≺ y4 ≺ y3 ≺ y1.
Using the Borda counting method, score 4, 3, 2, 1, and 0 for the first, second, third, fourth, and fifth place, respectively, then we can get
B(x1) = 4, B(x2) =3, B(x3) = 7, B(x4) = 5, B(x5) = 1.
So, when λ = 0.3, the best choice, shop 3, is chosen.
6. Conclusions
The multi-granulation neutrosophic rough set is a useful tool for MGDM problems. In this paper, we proposed non-dual MSs and study their operators and properties. Then we discussed the relationship between NRS, optimistic (pessimistic) MS, non-dual MS, NRS based on intersection (union) NRs, and NRS based on transitive closure relationship of union NRs, we used Figure 1 to show the relationship. Furthermore, we proposed a non-dual MS on two universes and talk about the relationship between non-dual MS on two universes and non-dual MS on a single universe, and we used non-dual MS on two universes to solve a MGDM problem where the attribute values were neutrosophic numbers.
For future orientation, we will research other types of fusions of MRSs and NSs. Additionally, we will study the applications of the concepts in this paper to totally-dependent neutrosophic sets and some algebraic systems and discuss in relation to other algorithms [35,36,37,38,39,40,41,42,43,44].
Author Contributions
X.Z. and C.B. initiated the research and wrote the paper, S.S. participated in some of the research work.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 61573240).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Atanassov, K.T. Type-1 Fuzzy Sets and Intuitionistic Fuzzy Sets. Algorithms 2017, 10, 106. [Google Scholar] [CrossRef]
- Bisht, K.; Joshi, D.K.; Kumar, S. Dual Hesitant Fuzzy Set-Based Intuitionistic Fuzzy Time Series Forecasting. In Ambient Communication and Computer Systems; Springer: Singapore, 2018; pp. 317–329. [Google Scholar]
- Kumar, K.; Garg, H. TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment. Comput. Appl. Math. 2018, 37, 1319–1329. [Google Scholar] [CrossRef]
- Maji, P. Advances in Rough Set Based Hybrid Approaches for Medical Image Analysis. In International Joint Conference on Rough Sets; Springer: Cham, Germany, 2017; pp. 25–33. [Google Scholar]
- Smarandache, F. Neutrosophic set—A generialization of theintuitionistics fuzzy sets. Int. J. Pure Appl. Math. 2005, 24, 287–297. [Google Scholar]
- Wang, H.B.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistruct. 2010, 4, 410–413. [Google Scholar]
- Peng, J.; Wang, J.; Wang, J.; Zhang, H.; Chen, H. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, H.; Wang, J. Probability multi-valued neutrosophic sets and its application in multi-criteria group decision-making problems. Neural Compt. Appl. 2018, 30, 563–583. [Google Scholar] [CrossRef]
- Deli, I.; Ali, M.; Smarandache, F. Bipolarneutrosophic sets and their application based on multi-criteria decision making problems. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems, Beijing, China, 22–24 August 2015; pp. 249–254. [Google Scholar]
- Zhang, X.; Bo, C.X.; Smarandache, F.; Dai, J.H. New inclusion relation of neutrosophic sets withapplications and related lattice structure. Int. J. Mach. Learn. Cybern. 2018, 9, 1753–1763. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 1990, 17, 191–209. [Google Scholar] [CrossRef]
- Cornelis, C.; De Cock, M.; Kerre, E.E. Intuitionistic fuzzy rough sets: At the crossroads of imperfect knowledge. Expert Syst. 2003, 20, 260–270. [Google Scholar] [CrossRef]
- Zhan, J.; Ali, M.I.; Mehmood, N. On a novel uncertain soft set model: Z-soft fuzzy rough set model and corresponding decision making methods. Appl. Soft Comput. 2017, 56, 446–457. [Google Scholar] [CrossRef]
- Yang, H.L.; Zhang, C.L.; Guo, Z.L.; Liu, Y.L.; Liao, X. A hybrid model of single valued neutrosophic sets and rough sets: Single valued neutrosophic rough set model. Soft Comput. 2017, 21, 6253–6267. [Google Scholar] [CrossRef]
- Garg, H. An improved score function for ranking neutrosophic sets and its application to decision-making process. Int. J. Uncertain. Quantif. 2016, 6, 377–385. [Google Scholar]
- Li, Y.Y.; Zhang, H.; Wang, J.Q. Linguistic neutrosophic sets and their application in multicriteria decision-making problems. Int. J. Uncertain. Quantif. 2017, 7, 135–154. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, M. The role of single valued neutrosophic sets and rough sets in smart city: Imperfect and incomplete information systems. Measurement 2018, 124, 47–55. [Google Scholar] [CrossRef]
- Yang, H.L.; Bao, Y.L.; Guo, Z.L. Generalized Interval Neutrosophic Rough Sets and its Application in Multi-Attribute Decision Making. Filomate 2018, 32, 11–33. [Google Scholar] [CrossRef]
- Zhang, C.; Zhai, Y.; Li, D.; Mu, Y. Steam turbine fault diagnosis based on single-valued neutrosophicmultigranulation rough sets over two universes. J. Intell. Fuzzy Syst. 2016, 31, 2829–2837. [Google Scholar] [CrossRef]
- Qian, Y.H.; Liang, J.Y.; Yao, Y.Y.; Dang, C.Y. MGRS: A multi-granulation rough set. Inf. Sci. 2010, 180, 949–970. [Google Scholar] [CrossRef]
- Yao, Y.; She, Y. Rough set models in multigranulation spaces. Inf. Sci. 2016, 327, 40–56. [Google Scholar] [CrossRef]
- Kumar, S.S.; Inbarani, H.H. Optimistic multi-granulation rough set based classification for medical diagnosis. Procedia. Comput. Sci. 2015, 47, 374–382. [Google Scholar] [CrossRef]
- Majumdar, P.; Samanta, S.K. On similarity and entropy of neutrosophic sets. J. Int. Fuzzy Syst. 2014, 26, 1245–1252. [Google Scholar]
- Kang, Y.; Wu, S.; Li, Y.; Liu, J.; Chen, B. A variable precision grey-based multi-granulation rough set model and attribute reduction. Knowl. Based Syst. 2018, 148, 131–145. [Google Scholar] [CrossRef]
- Sun, B.Z.; Ma, W.M.; Qian, Y.H. Multigranulation fuzzy rough set over two universes and its application to decision making. Knowl. Based Syst. 2017, 123, 61–74. [Google Scholar] [CrossRef]
- Pan, W.; She, K.; Wei, P. Multi-granulation fuzzy preference relation rough set for ordinal decision system. Fuzzy Sets Syst. 2017, 312, 87–108. [Google Scholar] [CrossRef]
- Huang, B.; Guo, C.; Zhuang, Y.; Li, H.; Zhou, X. Intuitionistic fuzzy multi-granulation rough sets. Inf. Sci. 2014, 277, 299–320. [Google Scholar] [CrossRef]
- Bo, C.X.; Zhang, X.; Shao, S.T.; Smarandache, F. New multi-granulation neutrosophic rough set with applications. Symmetry 2018, 10, 578. [Google Scholar] [CrossRef]
- Xu, W.; Li, W.; Zhang, X. Generalized multigranulation rough sets and optimal granularity selection. Granul. Comput. 2017, 2, 271–288. [Google Scholar] [CrossRef]
- Lin, H.; Wang, Q.; Lu, X.; Li, H. Hybrid multi-granulation rough sets of variable precision based on tolerance. J. Int. Fuzzy Syst. 2016, 31, 717–725. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, D.; Liu, C.; Le, M. Constructive methods of rough approximation operators and multi-granulation rough sets. Knowl. Based Syst. 2016, 91, 114–125. [Google Scholar] [CrossRef]
- Yang, H.L.; Guo, Z.L.; Liao, X. On single valued neutrosophic relations. J. Intell. Fuzzy Syst. 2016, 30, 1045–1056. [Google Scholar] [CrossRef]
- Zarghami, M. Soft computing of the Borda count by fuzzy linguistic quantifiers. Appl. Soft Comput. 2011, 11, 1067–1073. [Google Scholar] [CrossRef]
- Chai, J.; Liu, J.N.K.; Xu, Z. A rule-based group decision model for warehouse evaluation under interval-valued Intuitionistic fuzzy environments. Expert Syst. Appl. 2013, 40, 1959–1970. [Google Scholar] [CrossRef]
- Zhang, X.H.; Bo, C.X.; Smarandache, F.; Park, C. New operations of totally dependent-neutrosophic sets and totally dependent-neutrosophic soft sets. Symmetry 2018, 10, 187. [Google Scholar] [CrossRef]
- Zhang, X.H.; Mao, X.Y.; Wu, Y.T.; Zhai, X.H. Neutrosophic filters in pseudo-BCI algebras. Int. J. Uncertain. Quantif. 2018, 8, 511–526. [Google Scholar] [CrossRef]
- Ma, Y.C.; Zhang, X.H.; Yang, X.F.; Zhou, X. Generalized neutrosophic extended triplet group. Symmetry 2019, 11, 327. [Google Scholar] [CrossRef]
- Wu, X.Y.; Zhang, X.H. The decomposition theorems of AG-neutrosophic extended triplet loops and strong AG-(l, l)-loops. Mathematics 2019, 7, 268. [Google Scholar] [CrossRef]
- Zhang, X.H.; Borzooei, R.A.; Jun, Y.B. Q-filters of quantum B-algebras and basic implication algebras. Symmetry 2018, 10, 573. [Google Scholar] [CrossRef]
- Abu Qamar, M.; Hassan, N. An Approach toward a Q-Neutrosophic Soft Set and Its Application in Decision Making. Symmetry 2019, 11, 139. [Google Scholar] [CrossRef]
- Badamchizadeh, M.A.; Nikdel, A.; Kouzehgar, M. Comparison of genetic algorithm and particle swarm optimization for data fusion method based on Kalman filter. Int. J. Artifi. Intell. 2010, 5, 67–78. [Google Scholar]
- Pozna, C.; Precup, R.E.; Tar, J.K.; Skrjanc, L.; Preitle, S. New results in modelling derived from Bayesian filtering. Knowl. Based Syst. 2010, 23, 182–194. [Google Scholar] [CrossRef]
- Jankowski, J.; Kazienko, P.; Wątróbski, J.; Lewandowska, A.; Zimba, P.; Zioło, M. Fuzzy multi-objective modeling of effectiveness and user experience in online advertising. Expert Syst. Appl. 2016, 65, 315–331. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wang, X.J.; Smarandache, F.; Jaiyeola, T.G.; Lian, T.Y. Singular neutrosophic extended triplet groups and generalized groups. Cognitive Systems Research 2019, 57, 32–40. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).