Peristaltic Pumping of Nanofluids through a Tapered Channel in a Porous Environment: Applications in Blood Flow

Abstract

In this study, we present an analytical study on blood flow analysis through with a tapered porous channel. The blood flow was driven by the peristaltic pumping. Thermal radiation effects were also taken into account. The convective and slip boundary conditions were also applied in this formulation. These conditions are very helpful to carry out the behavior of particle movement which may be utilized for cardiac surgery. The tapered porous channel had an unvarying wave speed with dissimilar amplitudes and phase. The non-dimensional analysis was utilized for some approximations such as the proposed mathematical modelling equations were modified by using a lubrication approach and the analytical solutions for stream function, nanoparticle temperature and volumetric concentration profiles were obtained. The impacts of various emerging parameters on the thermal characteristics and nanoparticles concentration were analyzed with the help of computational results. The trapping phenomenon was also examined for relevant parameters. It was also observed that the geometric parameters, like amplitudes, non-uniform parameters and phase difference, play an important role in controlling the nanofluids transport phenomena. The outcomes of the present model may be applicable in the smart nanofluid peristaltic pump which may be utilized in hemodialysis.

1. Introduction

Peristaltic motion [1,2,3,4,5,6] is a fundamental physiological mechanism which has many applications in bio-mechanical and engineering sciences where transport phenomena at micro/macro level occur. This mechanism is also applicable in transporting the nanofluids without any contaminations. The nanofluid term was first invented by Choi and Eastman [7] with reference to a conventional heat transfer liquid retention distribution of a nanosized particle. The behavior of nanoliquid in thermal conductivity enhancement has been observed by Masuda et al. [8] and experimental results of nanoparticle into pure fluid may conduct to reduce in heat transfer. The closed form model for convective transport in nanofluids studying the thermophoresis and Brownian diffusion has been studied by Buongiorno and Hu [9] and Buongiorno [10].

In the peristaltic pumping models, nanoliquid was introduced by Akbar and Nadeem [11]. They investigated endoscopic influences on the peristaltic motion of a nanofluid. Akbar [12] further presented the peristaltic transport of a Sisko nanoliquid in an asymmetric channel. It was noticed that enhances in the Sisko nanoliquid parameter axial pressure rise in the peristaltic pumping region. The effect of nanoliquid features on peristaltic heat transfer in a two-dimensional axisymmetric channel was discussed by Tripathi and Beg [13]. They examined that the nanoliquids incline to suppress backflow equated with Newtonian fluids. Akbar et al. [14] discussed the magnetohydrodynamic (MHD) peristaltic motion of a Carreau nanoliquid in an asymmetric channel. Furthermore, Beg and Tripathi [15] introduced the double diffusion process in peristaltic pumping. They discussed the salute and nanoparticle concentrations in their analysis. The effects of nanoparticle geometry on peristaltic motion has been analyzed by Akbar et al. [16]. MHD peristaltic pumping with viscoelastic nanofluids have been studied by Reddy and Makinde [17]. The velocity and slip influences on peristaltic pumping of nanoliquids have been examined by the Akbar et al. [18]. Heat and mass transfer analysis on peristaltic pumping through the rectangular duct was presented by Nadeem et al. [19]. Peristaltic transport of Prandtl nanofluid through the rectangular duct was studied by Ellahi et al. [20] and with magnetic field [21]. Hyperbolic tangent nanofluid with peristaltic pumping was implemented by Kothandapani and Prakash [22] in the presence of a radiation parameter and inclined magnetic field. Peristaltic pumping by eccentric cylinders has been discussed by the Nadeem et al. [23]. In similar directions, many more investigations [24,25,26,27,28,29,30,31,32,33,34,35,36,37] on peristaltic pumping, nanofluids and non-Newtonian nanofluids with various physical constraints and various flow geometries had been described in the literature.

The analysis of fluid flow through porous channels or tubes had gained attention recently because of its several applications in biomedical engineering and many other engineering areas like the flow of blood oxygenators, gall bladder with stones, in small blood vessels, the design of filters, in transpiration cooling boundary layer control, the flow of blood in the capillaries, the dialysis of blood in artificial kidney, gaseous diffusion in the spreading of fatty cholesterol and artery-clogging blood clots in the lumen of a coronary artery [38,39,40,41,42,43,44,45,46,47]. The steady laminar incompressible free convective flow of a nanofluid over a permeable upward facing horizontal plate located in a porous medium in an existence of thermal convective boundary condition was considered numerically by Uddin et al. [48]. Chamkha et al. [49] studied the mixed convection boundary layer flow in the existence of laminar and isothermal vertical porous medium. The onset of convection in a horizontal layer of a porous medium by a nanofluid was analytically studied by Kuznetsov and Nield [50]. Akbar [51] investigated the double-diffusive peristaltic transport of Jeffrey nanoliquids in a porous region in the presence of natural convective. Double-diffusive natural convective peristaltic flow of a Jeffrey nanofluid in a porous channel has been analyzed by Nadeem et al. [52] and investigated the peristaltic flow of nanofluid eccentric tubes which comprises a porous medium. Two-phase flow driven by the peristaltic pumping through porous medium was studied by Bhatti et al. [53]. Perturbation solutions have been obtained and it is observed that chemical reaction and Soret numbers oppose the particle concentration. The applications of porosity can be deeply studied by using nanofluid model in [54,55].

Moreover, the no-slip condition is inadequate when a fluid revealing macroscopic wall slip is considered and that, in general, is governed by the relation between the slip velocity and grip. The slip condition plays significant role in shear skin, spurt and hysteresis belongings. The nanofluids that exhibit boundary slip have vital technological purposes such as in shining valves of the artificial heart and internal holes. The proposed mathematical geometry is very similar to the blood vessel models. The blood vessels can be classified into three types: the largest vessels, small vessels and intermediate blood vessels. The largest vessels are identified in the aorta and vena cava and also experience very little heat transfer with the tissue. In addition, there are also more blood vessels that fall into this category. The smallest vessels are noticed in place of arterioles, capillaries and venules which basically experience ideal heat transfer with the blood departure at tissue temperature. The intermediate blood vessels fall in a relatively narrow band with uniformly distributed temperature. These classifications are dependent on the amplitude of vessels and width of channel. Hence, the main purpose of this paper is to study a theoretical analysis of peristaltic transport of a Newtonian nanofluid with slip through a porous medium in the tapered wavy channel subject to convective boundary conditions. The long wavelength and low Reynolds number assumptions are considered. The exact solutions are found in the form of axial velocity from which temperature and volumetric concentration are deduced. Computational results are illustrated and discussed in detail.

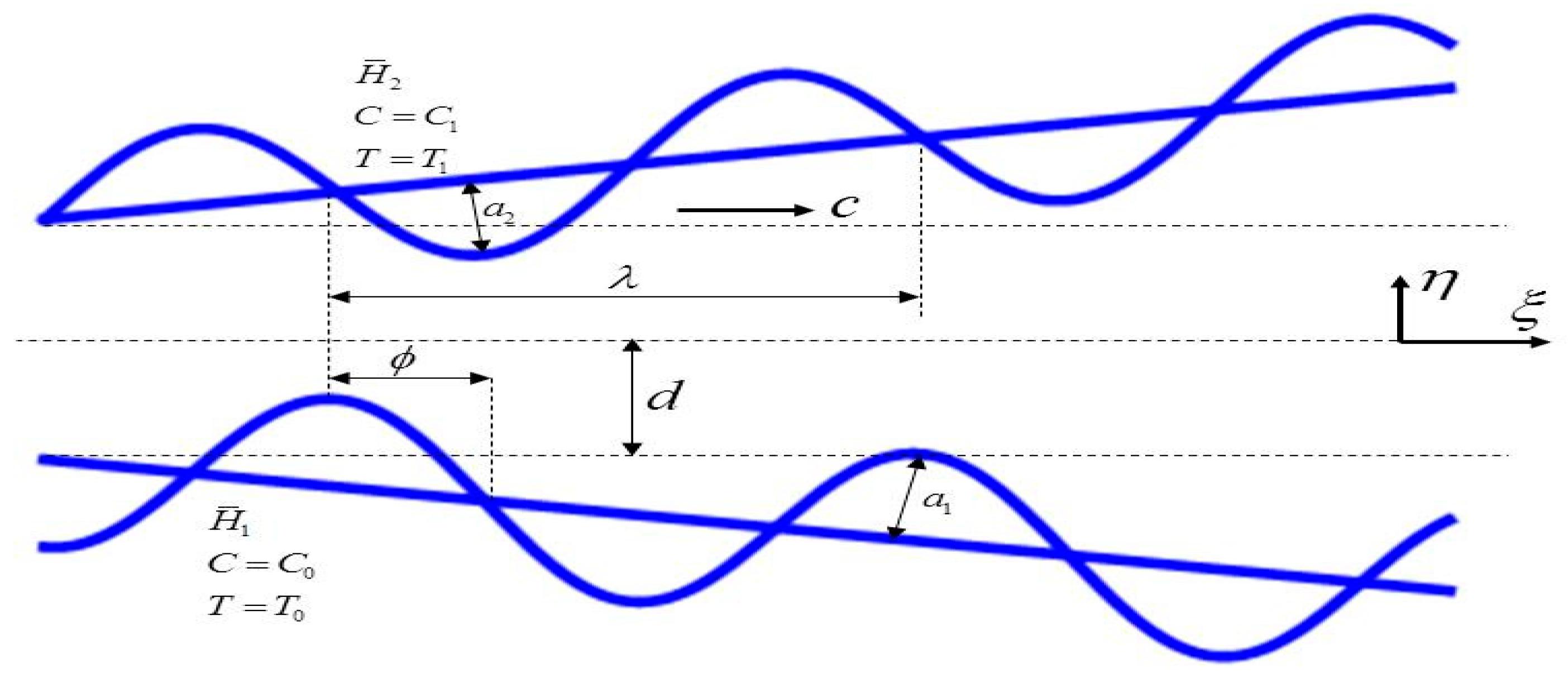
2. Mathematical Formulation

Consider an incompressible viscous nanofluid filling the porous space in the tapered wavy channel. The heat transfer between the blood network and living tissues which passes through the channel depends on the geometry of the blood vessel and it is important to understand the behavior of the blood flow and the neighboring tissue nature. Let $\overline{\eta }={\overline{H}}_1$ and $\overline{\eta }={\overline{H}}_2$ be, correspondingly, the lower and upper blood vessel boundaries of the channel. The sinusoidal waves propagating along the wavy walls of the tapered channel are demonstrated in Figure 1 and mathematically shown as:

$$\begin{array}{c}{\overline{H}}_2(\overline{\xi },t^{\prime })=\overline{d}+\overline{m}\overline{\xi }+a_2\sin \left[\frac{\pi }{\lambda }\left(\overline{\xi }-c{t}^{\prime }\right)\right]\cos \left[\frac{\pi }{\lambda }\left(\overline{\xi }-c{t}^{\prime }\right)\right],\\ {\overline{H}}_1(\overline{\xi },t^{\prime })=-\overline{d}-\overline{m}\overline{\xi }-a_1\sin \left[\frac{\pi }{\lambda }\left(\overline{\xi }-c{t}^{\prime }\right)+\varphi \right]\cos \left[\frac{\pi }{\lambda }\left(\overline{\xi }-c{t}^{\prime }\right)+\varphi \right]\end{array}$$

(1)

here $2\overline{d}$, $a_1$, $a_2$, $\overline{m}\left(<<1\right)$, $\lambda$, $c$, $\varphi$, are the width of the channel at the inlet, amplitudes of lower wavy wall, amplitude of upper wavy wall, dimensional non–uniform parameter, wave length, phase speed of the wave and phase difference varies in the range $0\le \varphi \le \pi$, $\varphi =0$ which corresponds to tapered symmetric channel i.e., together walls move towards inward or outward concurrently.

For an incompressible viscous nanofluid the balance of mass, momentum, nanoparticle temperature and volumetric concentration are presented as [56,57,58,59]:

$$\frac{\partial \overline{U}}{\partial \overline{\xi }}+\frac{\partial \overline{V}}{\partial \overline{\eta }}=0,$$

(2)

$${\rho }_f\left[\frac{\partial }{\partial t^{\prime }}+\overline{U}\frac{\partial }{\partial \overline{\xi }}+\overline{V}\frac{\partial }{\partial \overline{\eta }}\right]\overline{U}=-\frac{\partial \overline{P}}{\partial \overline{\xi }}+\mu \left[\frac{{\partial }^2}{\partial {\overline{\xi }}^2}+\frac{{\partial }^2}{\partial {\overline{\eta }}^2}\right]\overline{U}-\frac{\mu }{k}\overline{U},$$

(3)

$${\rho }_f\left[\frac{\partial }{\partial t^{\prime }}+\overline{U}\frac{\partial }{\partial \overline{\xi }}+\overline{V}\frac{\partial }{\partial \overline{\eta }}\right]\overline{V}=-\frac{\partial \overline{P}}{\partial \overline{\eta }}+\mu \left[\frac{{\partial }^2}{\partial {\overline{\xi }}^2}+\frac{{\partial }^2}{\partial {\overline{\eta }}^2}\right]\overline{V}-\frac{\mu }{k}\overline{V},$$

(4)

$$\begin{array}{r}{(\rho c^{\prime })}_f\left[\frac{\partial }{\partial t^{\prime }}+\overline{U}\frac{\partial }{\partial \overline{\xi }}+\overline{V}\frac{\partial }{\partial \overline{\eta }}\right]\overline{T}=\kappa \left[\frac{{\partial }^2}{\partial {\overline{\xi }}^2}+\frac{{\partial }^2}{\partial {\overline{\eta }}^2}\right]\overline{T}-\frac{\partial {\overline{q}}_r}{\partial \overline{\eta }}+\mu \left[4{\left(\frac{\partial \overline{U}}{\partial \overline{\xi }}\right)}^2+{\left(\frac{\partial \overline{V}}{\partial \overline{\xi }}+\frac{\partial \overline{U}}{\partial \overline{\eta }}\right)}^2\right]\\ +{(\rho c^{\prime })}_p\left[D_B\left(\frac{\partial \overline{C}}{\partial \overline{\xi }}\frac{\partial \overline{T}}{\partial \overline{\xi }}+\frac{\partial \overline{C}}{\partial \overline{\eta }}\frac{\partial \overline{T}}{\partial \overline{\eta }}\right)+\frac{D_T}{T_m}\left[{\left(\frac{\partial \overline{T}}{\partial \overline{\xi }}\right)}^2+{\left(\frac{\partial \overline{T}}{\partial \overline{\eta }}\right)}^2\right]\right],\end{array}$$

(5)

$$\left[\frac{\partial }{\partial t^{\prime }}+\overline{U}\frac{\partial }{\partial \overline{\xi }}+\overline{V}\frac{\partial }{\partial \overline{\eta }}\right]\overline{C}=D_B\left[\frac{{\partial }^2}{\partial {\overline{\xi }}^2}+\frac{{\partial }^2}{\partial {\overline{\eta }}^2}\right]\overline{C}+\frac{D_T}{T_m}\left[\frac{{\partial }^2}{\partial {\overline{\xi }}^2}+\frac{{\partial }^2}{\partial {\overline{\eta }}^2}\right]\overline{T},$$

(6)

in which $\overline{U}$, $\overline{V}$ are the components of axial velocity along $\overline{\xi }$ and $\overline{\eta }$ directions correspondingly, $t^{\prime }$, ${d/dt}^{\prime }$, $\overline{P}$, ${\rho }_f$, ${\rho }_p$, $\overline{T}$, $\kappa$, $k$, $D_B$, $D_T$, $T_m$, $\overline{C}$ and $\tau \left(=\frac{{(\rho c^{\prime })}_p}{{(\rho c^{\prime })}_f}\right)$ are the dimensional time, material time derivative, dimensional pressure, density of the fluid, density of the particle, nanoparticle temperature, thermal conductivity, permeability of porous medium, Brownian diffusion coefficient, themophoretic diffusion coefficient, mean temperature, nanoparticle volumetric volume fraction and the ratio of the effective heat capacity of nanoparticle material and heat capacity of the fluid with $\rho$ being the density. Additionally, $T_0,T_1,C_0$ and $C_1$ are the temperature and nanoparticle volume fraction at the lower and upper walls.

3. Convective Boundary Conditions

The convective boundary conditions [60,61] are utilized using Newton’s cooling law as:

$$\overline{U}=\frac{\sqrt{\overline{k}}}{\overline{\alpha }}\frac{\partial \overline{U}}{\partial \overline{\eta }},-{\overline{k}}_h\frac{\partial \overline{T}}{\partial \overline{\eta }}={\overline{h}}_h\left(T_0-\overline{T}\right)\mathrm{and}-{\overline{k}}_m\frac{\partial \overline{C}}{\partial \overline{\eta }}={\overline{h}}_m\left(C_0-\overline{C}\right)\mathrm{at}\overline{\eta }={\overline{H}}_1,$$

(7)

$$\overline{U}=-\frac{\sqrt{\overline{k}}}{\overline{\alpha }}\frac{\partial \overline{U}}{\partial \overline{\eta }},-{\overline{k}}_h\frac{\partial \overline{T}}{\partial \overline{\eta }}={\overline{h}}_h\left(\overline{T}-T_1\right)\mathrm{and}-{\overline{k}}_m\frac{\partial \overline{C}}{\partial \overline{\eta }}={\overline{h}}_m\left(\overline{C}-C_1\right)\mathrm{at}\overline{\eta }={\overline{H}}_2,$$

(8)

where $\overline{k}$, $\overline{\alpha }$, ${\overline{h}}_h$, ${\overline{h}}_m$, ${\overline{k}}_h$ and ${\overline{k}}_m$ are the permeability of the porous walls (Darcy number), slip coefficient at the surface of the porous walls, the heat transfer coefficients, mass transfer coefficients respectively, the thermal conductivity and the mass conductivity.

4. Non-Dimensional Analysis

In order to depict the nanoliquid flow in the following non-dimensional measures are introduced in Equations (1)–(8). $\left(u=\frac{\overline{U}}{c},u=\frac{\partial \psi }{\partial y},v=\frac{\overline{V}}{c},v=-\delta \frac{\partial \psi }{\partial y}\right)$ are the velocity components in direction of $\left(x=\frac{\overline{\xi }}{\lambda },y=\frac{\overline{\eta }}{\overline{d}}\right)$, $\psi$ is the stream function, $t=\frac{c{t}^{\prime }}{\lambda }$ is the dimensionless time, $h_1=\frac{{\overline{H}}_1}{\overline{d}}$ and $h_2=\frac{{\overline{H}}_2}{\overline{d}}$ represent the dimensionless form of the lower and upper channel, and $R=\frac{{\rho }_{f}c\overline{d}}{\mu }$ is the Reynolds number, $p=\frac{{\overline{d}}^2\overline{P}}{c\lambda \mu }$ is the dimensionless pressure, $a=\frac{a_1}{\overline{d}}$ is the amplitude of lower wavy wall, $b=\frac{a_2}{\overline{d}}$ is the amplitude of upper wavy wall, $m=\frac{\lambda \overline{m}}{\overline{d}}$ is the dimensionless non-uniform parameter, $\delta =\frac{\overline{d}}{\lambda }$ is the wave number, $Sc=\frac{v}{D_B}$ is the Schmidt number, $K=\frac{k}{{\overline{d}}^2}$ is the Permeability parameter, $\theta =\frac{\overline{T}-T_0}{T_1-T_0}$ is the dimensionless nanoparticle temperature, $\sigma =\frac{\overline{C}-C_0}{C_1-C_0}$ is the nanoparticle volumetric concentration or dimensionless rescaled nanoparticle volume fraction, $\mathrm{Pr}=\frac{\mu c_f}{\kappa }$ is the Prandtl number, $N_b=\frac{\tau D_B(C_1-C_0)}{\nu }$ is the Brownian motion parameter $N_t=\frac{\tau D_T(T_1-T_0)}{T_m\nu }$ is the thermophoresis parameter, $Ec=\frac{c^2}{c_f{T}_m}$ is the Eckert number, $Br=\mathrm{Pr}Ec$ is the Brinkman number, and $R_n=\frac{16\overline{\sigma }{T}_0^3}{3\overline{k}\mu c_f}$ is the thermal radiation parameter and also, applying the long wavelength and low Reynolds number approximations, we attain:

$$\frac{\partial p}{\partial x}=\frac{{\partial }^3\psi }{\partial y^3}-\left(\frac{1}{K}\right)\frac{\partial \psi }{\partial y},$$

(9)

$$\frac{\partial p}{\partial y}=0,$$

(10)

$$\left(1+Rn\mathrm{Pr}\right)\frac{{\partial }^2\theta }{\partial y^2}+Br{\left(\frac{{\partial }^2\psi }{\partial y^2}\right)}^2+\left(Nb\mathrm{Pr}\right)\left(\frac{\partial \sigma }{\partial y}\frac{\partial \theta }{\partial y}\right)+\left(Nt\mathrm{Pr}\right){\left(\frac{\partial \theta }{\partial y}\right)}^2=0,$$

(11)

$$\frac{{\partial }^2\sigma }{\partial y^2}+\left(\frac{Nt}{Nb}\right)\frac{{\partial }^2\theta }{\partial y^2}=0.$$

(12)

Equation (10) shows that p is not dependent on x. Reducing the pressure gradient term from Equations (9) and (10), it yields:

$$\frac{{\partial }^4\psi }{\partial y^4}-\left(\frac{1}{K}\right)\frac{{\partial }^2\psi }{\partial y^2}=0.$$

(13)

Additionally, it is noticed that the continuity equation is routinely fulfilled.

$$\begin{array}{c}{h}_1=-1-mx-a\cos (\pi (x-t)+\varphi )\sin (\pi (x-t)+\varphi )\mathrm{and}\\ h_2=1+mx+b\cos (\pi (x-t))\sin (\pi (x-t))\end{array}$$

$$\begin{array}{c}\psi =-\frac{F}{2},\frac{\partial \psi }{\partial y}=L\frac{{\partial }^2\psi }{\partial y^2},\frac{\partial \theta }{\partial y}=B_h\theta \mathrm{and}\frac{\partial \sigma }{\partial y}=B_m\sigma \mathrm{at}y=h_1,\\ \psi =\frac{F}{2},\frac{\partial \psi }{\partial y}=-L\frac{{\partial }^2\psi }{\partial y^2},\frac{\partial \theta }{\partial y}=B_h(1-\theta )\mathrm{and}\frac{\partial \sigma }{\partial y}=B_m(1-\sigma )\mathrm{at}y=h_2.\end{array}$$

(14)

where $L=\frac{\sqrt{\overline{k}}}{\overline{d}\overline{\alpha }}$ is the velocity slip parameter, $B_h=\frac{{\overline{h}}_h\overline{d}}{{\overline{k}}_h}$ is the heat transfer Biot number and $B_m=\frac{{\overline{h}}_m\overline{d}}{{\overline{k}}_m}$ is the mass transfer Biot number.

5. Analytical Solution

The solution of the Equation (13) subject to the conditions in Equation (14) is obtained as:

$$\begin{array}{cc}\hfill \psi (y)=& -(F\left(\cosh Ny-\sinh Ny\right)(2\left(\cosh 2Ny-\sinh 2Ny\right)-2\left(\cosh (N(h_1+h_2))+\sinh (N(h_1+h_2))\right)\hfill \\ & +\left(h_1+h_2-2y\right)N\left(\cosh Ny+\sinh Ny\right)\left(\cosh N{h}_1+\sinh N{h}_1+\cosh N{h}_2+\sinh N{h}_2\right)\hfill \\ & -L{N}^2\left(\cosh Ny+\sinh Ny\right)(h_1+h_2-2y)\left(\cosh N{h}_1+\sinh N{h}_1-\cosh N{h}_2-\sinh N{h}_2\right)))\hfill \\ & /\left(2\left(\begin{array}{l}\left(2+L{N}^2{h}_1-L{N}^2{h}_2\right)\left(\cosh N{h}_1+\sinh N{h}_1-\cosh N{h}_2-\sinh N{h}_2\right)\\ -\left(N{h}_1-N{h}_2\right)\left(\cosh N{h}_1+\sinh N{h}_1+\cosh N{h}_2+\sinh N{h}_2\right)\end{array}\right)\right)\hfill \end{array}$$

(15)

The integration of Equation (12) with respect to $y$, we obtain

$$\frac{\partial \sigma }{\partial y}+\frac{Nt}{Nb}\frac{\partial \theta }{\partial y}=f(x).$$

(16)

Solving Equations (11) and (12) and substituting in Equation (16) subject to boundary conditions of Equations (14), the dimensionless nanoparticle temperature field is attained as

$$\begin{array}{cc}\hfill \theta (y)=& A_8+A_9\left(\cosh (A_1{A}_5{N}_{b}y)-\sinh (A_1{A}_5{N}_{b}y)\right)-\frac{A_2^3{A}_4\left(\cosh (2Ny)+\sinh (2Ny)\right)}{4N^2+\left(\cosh (2A_1{A}_5{N}_{b}N)+\sinh (2A_1{A}_5{N}_{b}N)\right)}\hfill \\ & -\frac{A_3^2{A}_4\left(\cosh (2Ny)-\sinh (2Ny)\right)}{4N^2-\left(\cosh (2A_1{A}_5{N}_{b}N)+\sinh (2A_1{A}_5{N}_{b}N)\right)}-\frac{\left(A_6\beta +2A_2{A}_3{A}_4\right)y}{A_1{A}_5{N}_b},\hfill \end{array}$$

(17)

and the nanoparticle volumetric concentration is obtained as:

$$\begin{array}{ll}\hfill \sigma (y)=& A_{10}+A_{11}y-\frac{A_9{N}_t\left(\cosh (A_1{A}_5{N}_{b}y)-\sinh (A_1{A}_5{N}_{b}y)\right)e^{-A_1{A}_5{N}_{b}y}}{N_b}\hfill \\ & +\frac{A_4{A}_3^2{N}_t(\cosh (2Ny)-\sinh (2Ny))}{4N^2{N}_b-2A_1{A}_{5}N{N}_b^2}+\frac{A_4{A}_2^2{N}_t(\cosh (2Ny)+\sinh (2Ny))}{4N^2{N}_b+2A_1{A}_{5}N{N}_b^2}.\hfill \end{array}$$

(18)

The coefficient of nanoparticle heat transfer at the lower wall is specified by

$$Z=h_{1x}{\theta }_y.$$

(19)

The above mentioned constants are elaborated in the Appendix A.

6. Computational Results and Discussion

In general, exact solutions for temperature, nanoparticle volumetric concentrations and coefficient of nanoparticle temperature depend on the value of $f(x).$ First of all, $f(x)$ can be influenced by hiring for $\theta$ and $\sigma$ from Equation (16). It ought to be noticed that observing the value of $f(x)$ analytically from Equation (16) in terms of the other parameters set is a very difficult task and it may be impossible. Nevertheless, with the help of MATHEMATICA/MATLAB software, the numerical solutions are still available. The numerical value of $f(x)$ plays an important role in plotting the graphs for variation of the streamlines, nanoparticle temperature distribution, nanoparticle volumetric concentration and coefficient of nanoparticle temperature.

To analyze the results, instantaneous volume rate $F(x,t)$ is considered as varying exponentially with the relation (Kikuchi [62])

$$F=\Theta e^{-At},$$

(20)

where $\Theta$ is the mean flow rate or flow constant, A is the blood flow constant. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 were plotted to examine the stream function $\left(\psi (x,y)\right)$, nanoparticle temperature $\left(\theta (y)\right)$, nanoparticle concentration $\left(\sigma (y)\right)$ and heat transfer coefficient $\left(Z(x)\right)$. Additionally, it is noticed that the flow rate for the non-positive and positive flow rate $F<0$ or $F>0$ may be according to $\Theta <0$ or $\Theta >0$. It was detected through an experiment performed by Kikuchi [62] that the flow rate decreases exponentially with time however mean flow rate does not depend on the structural details of the channel.

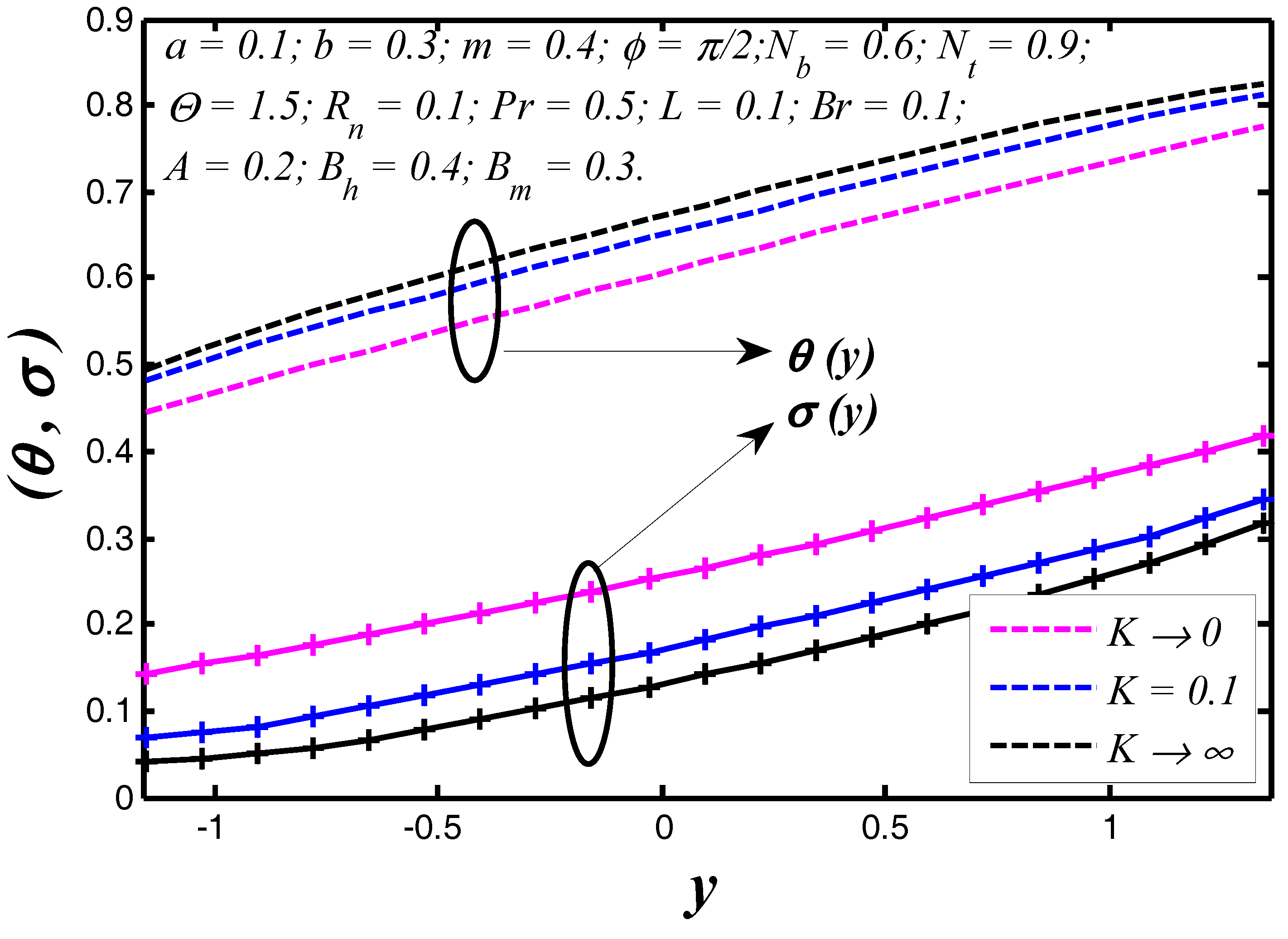
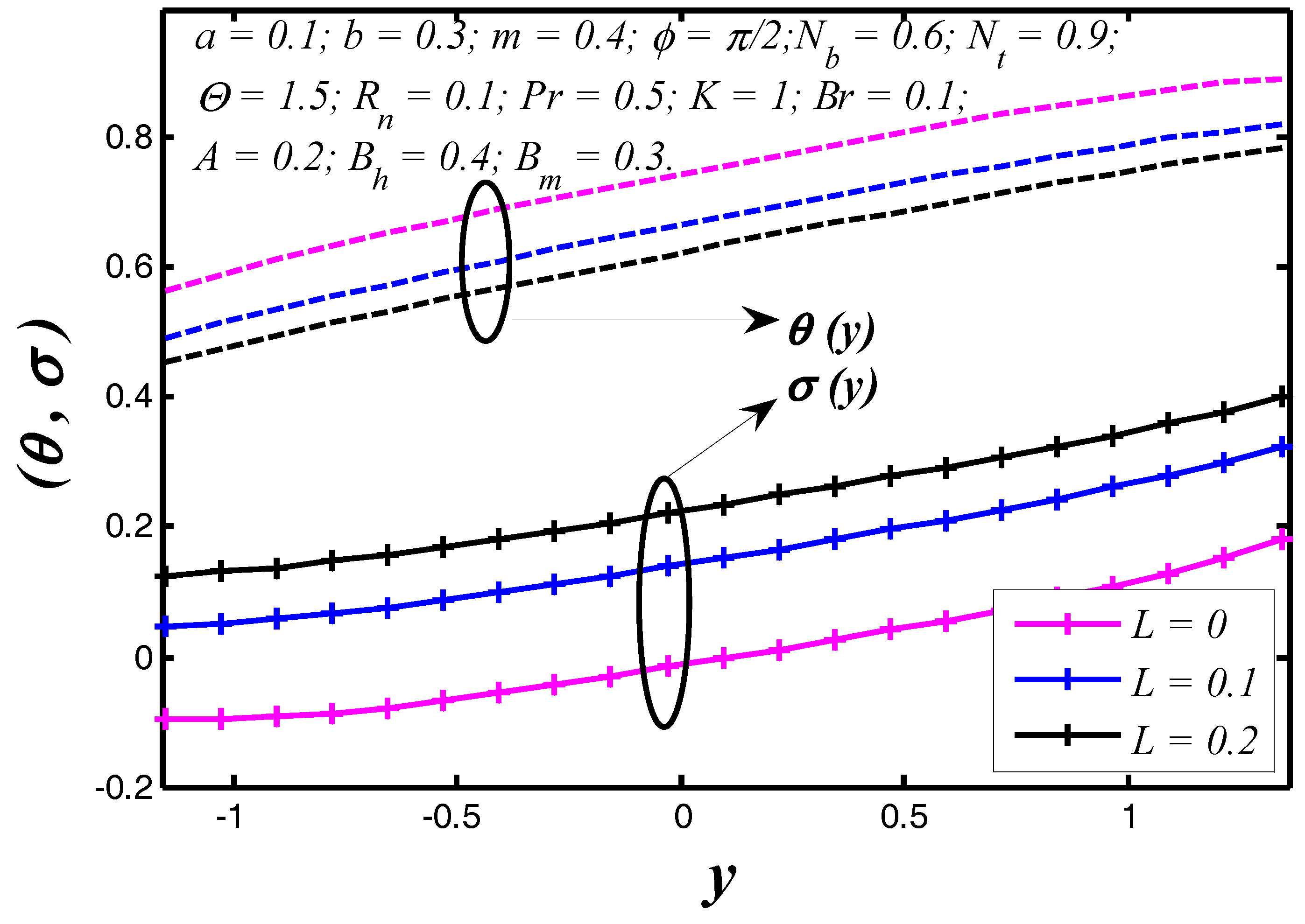
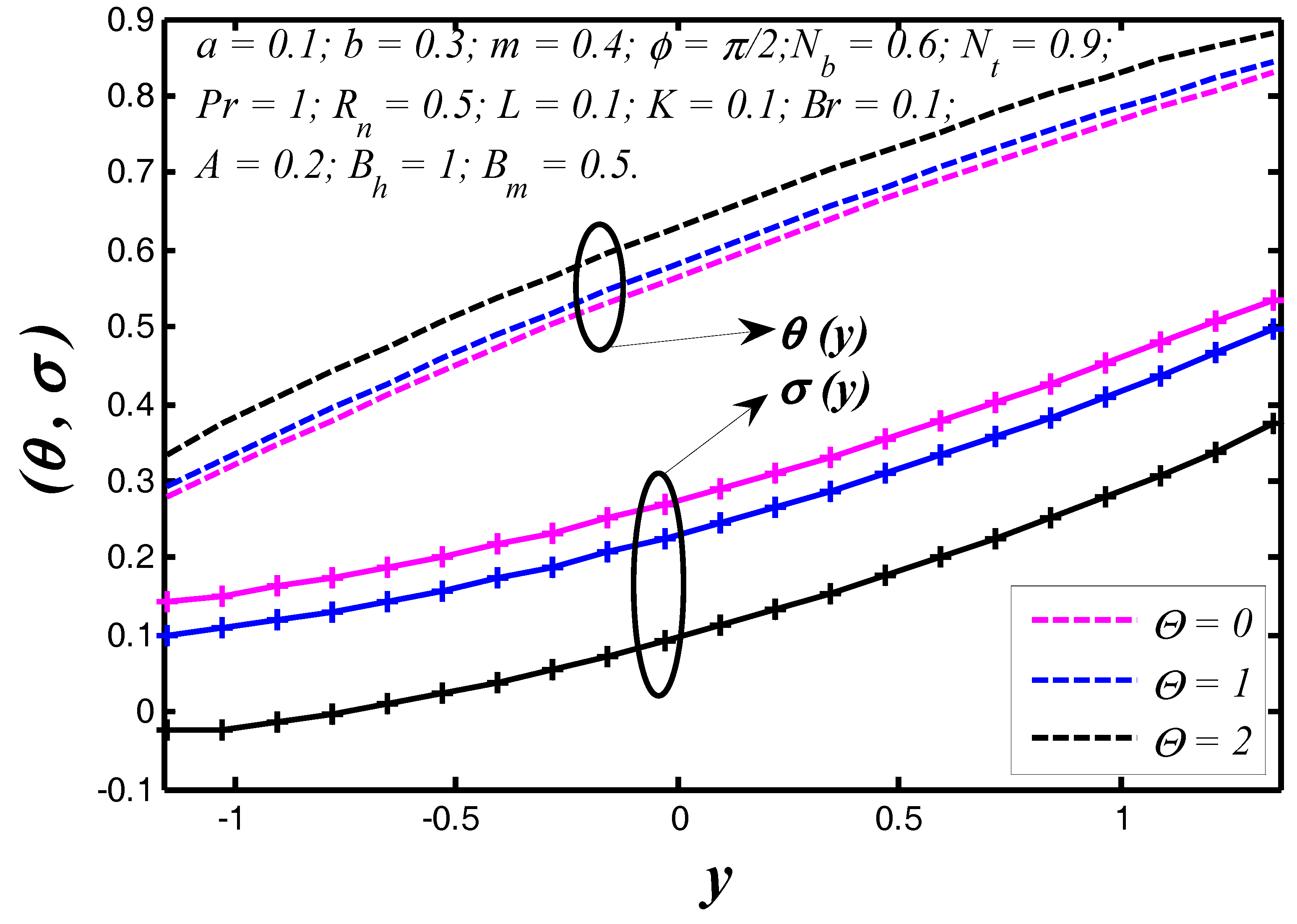
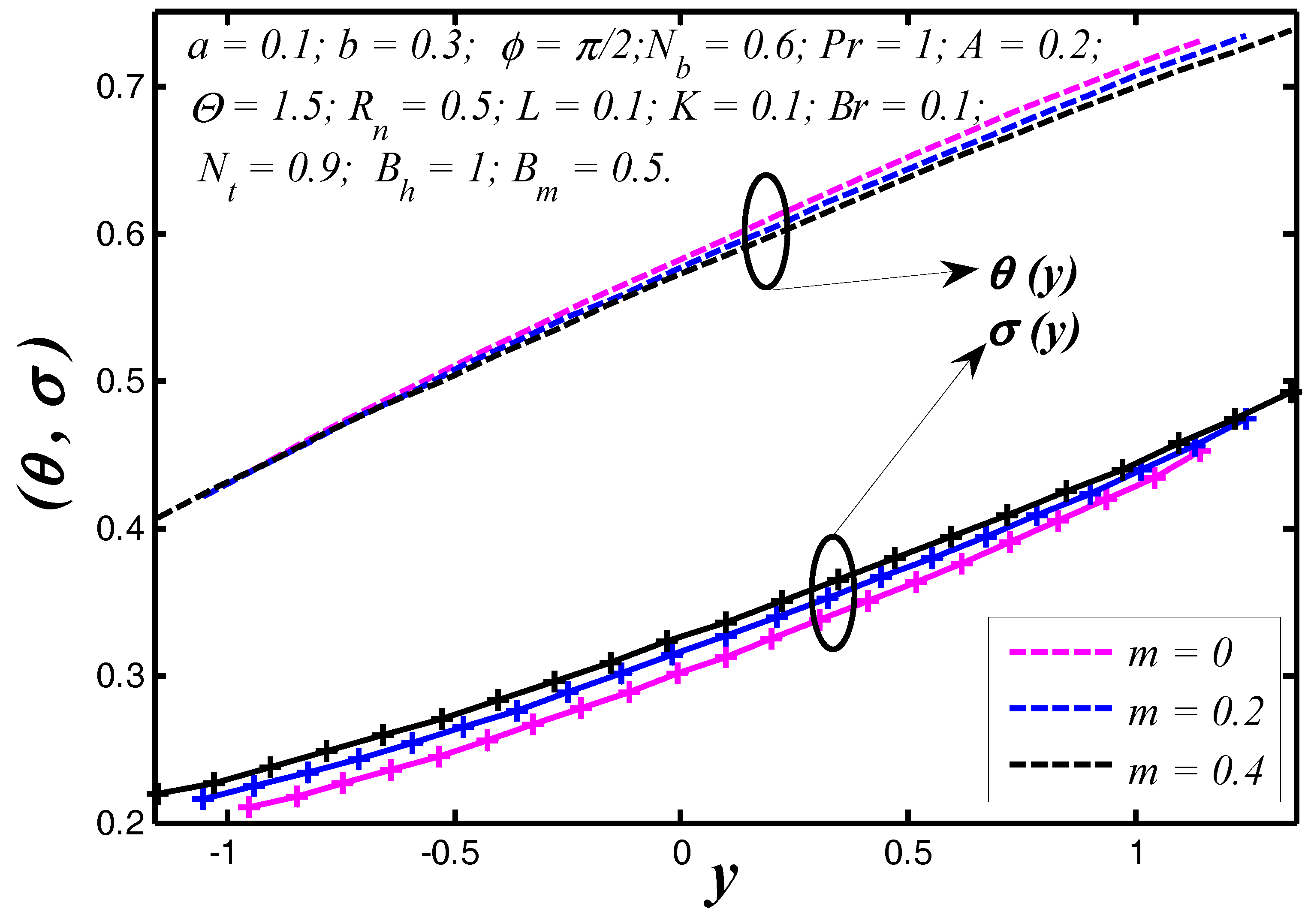
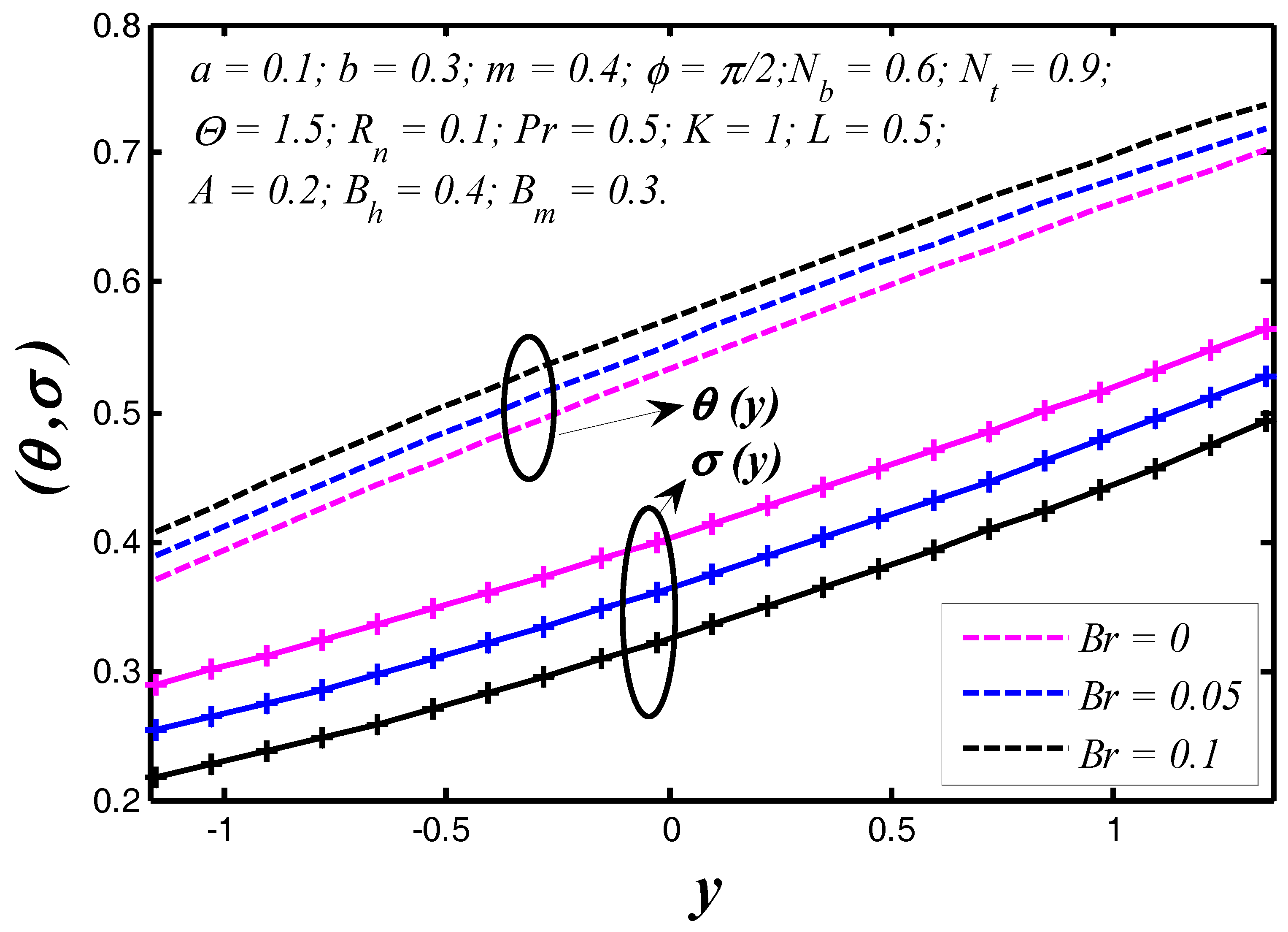
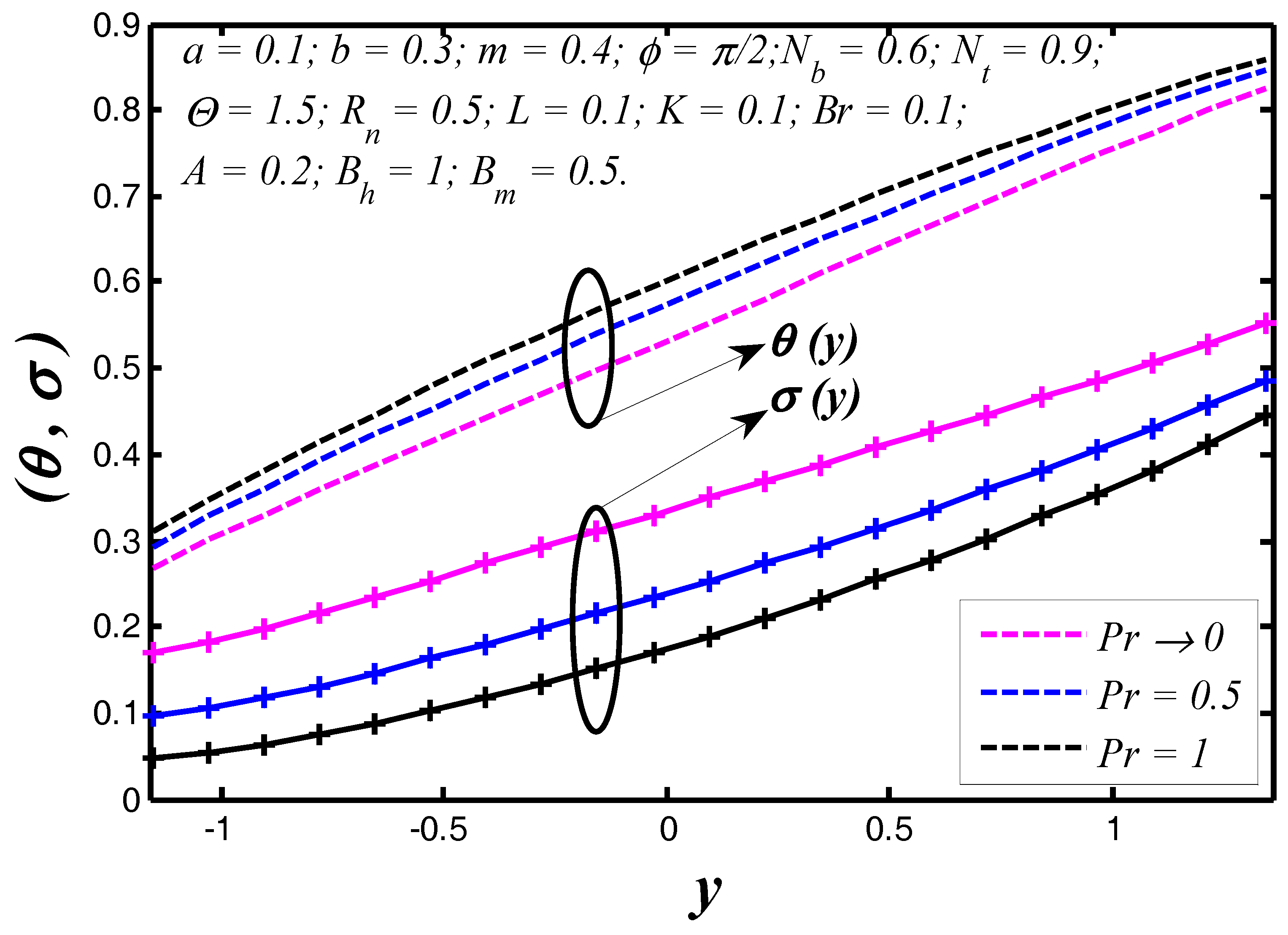
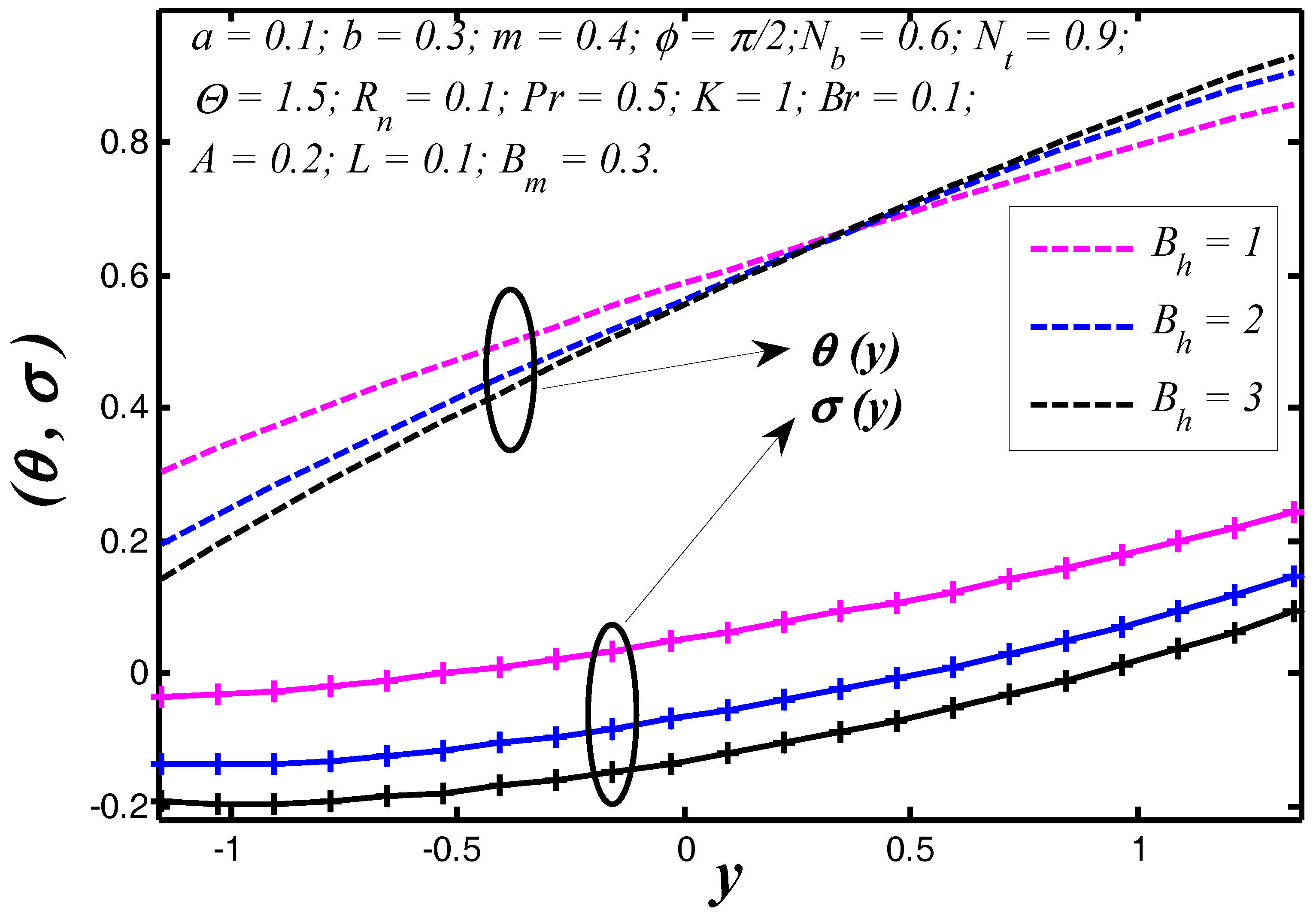
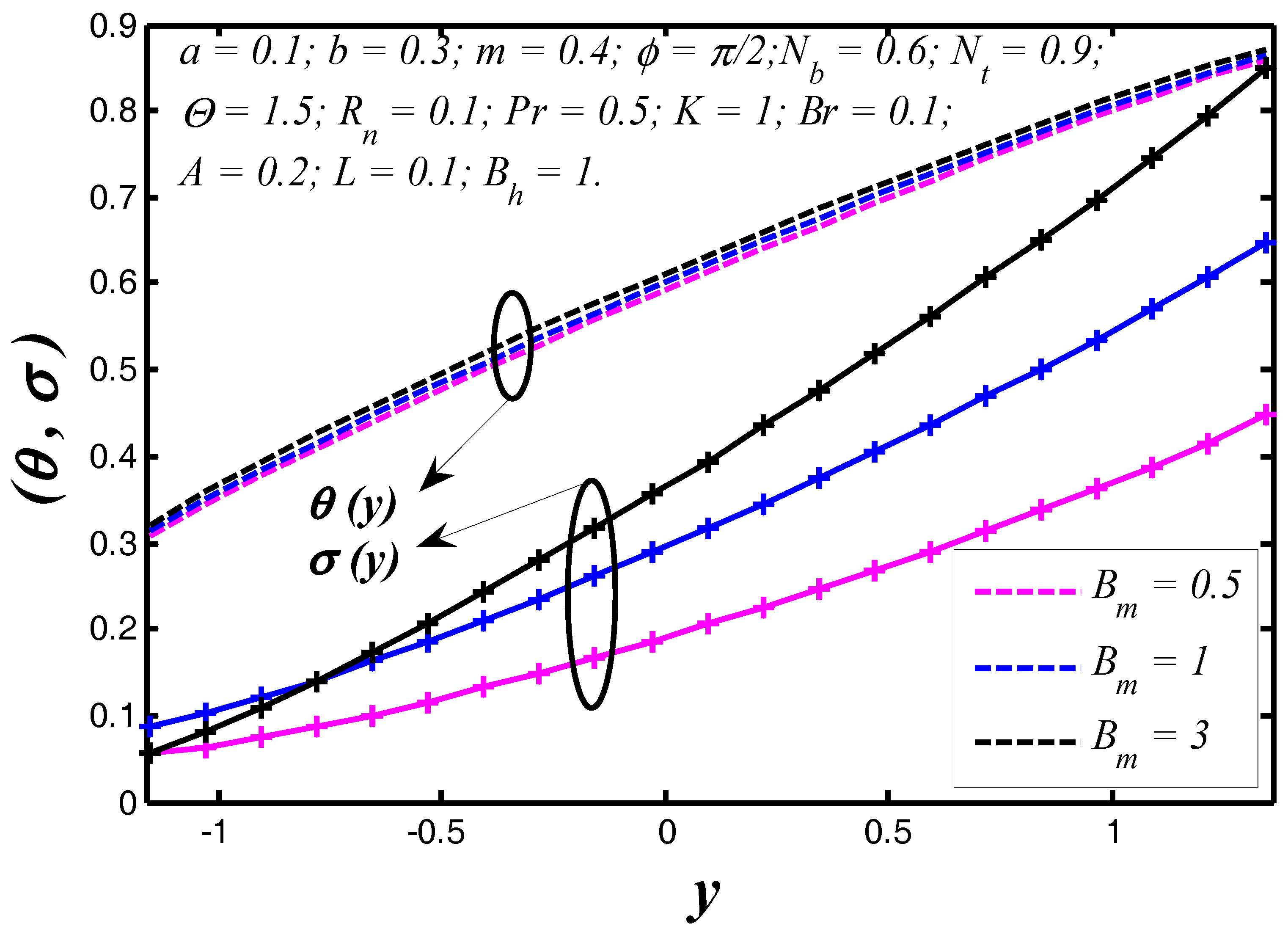
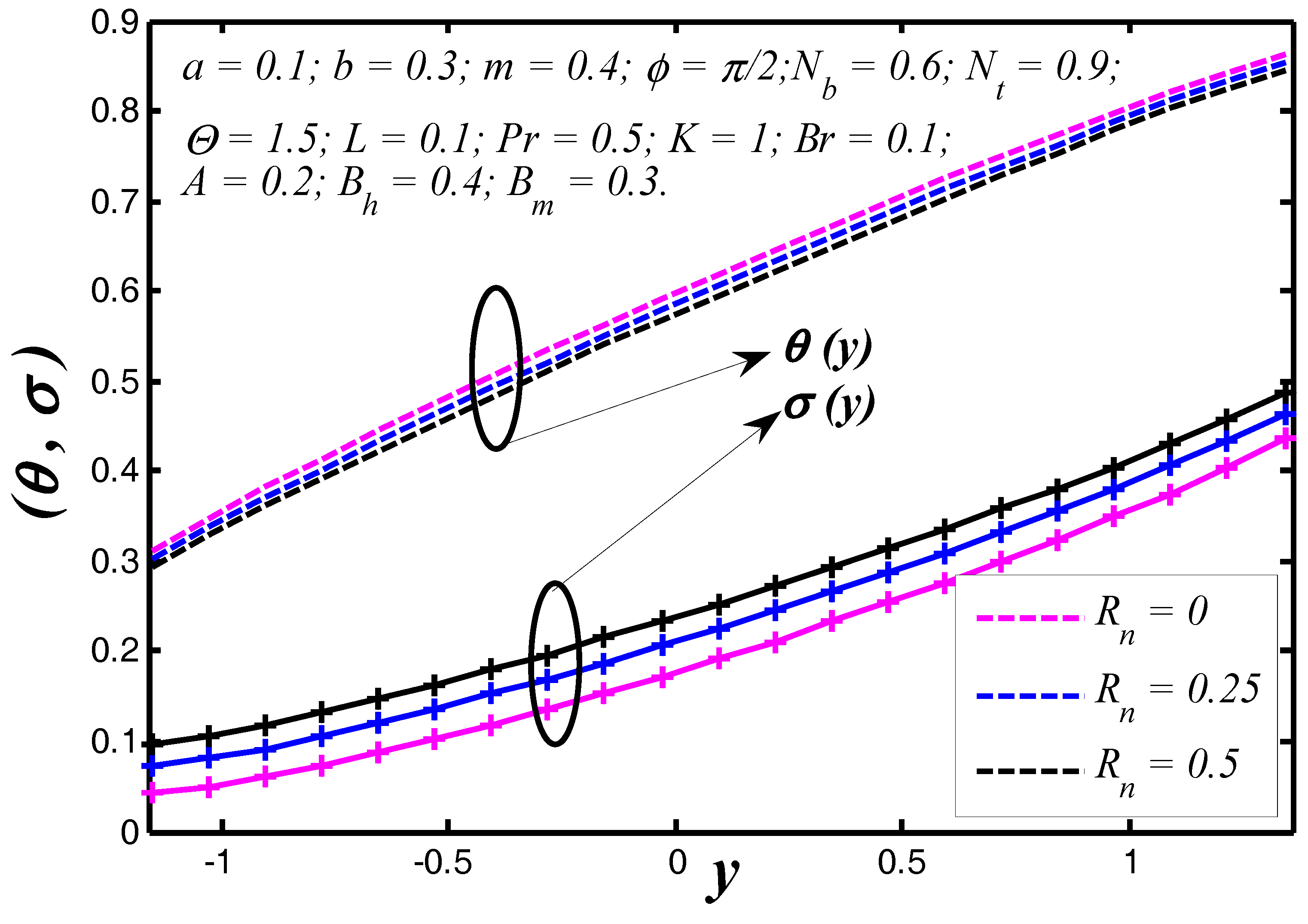
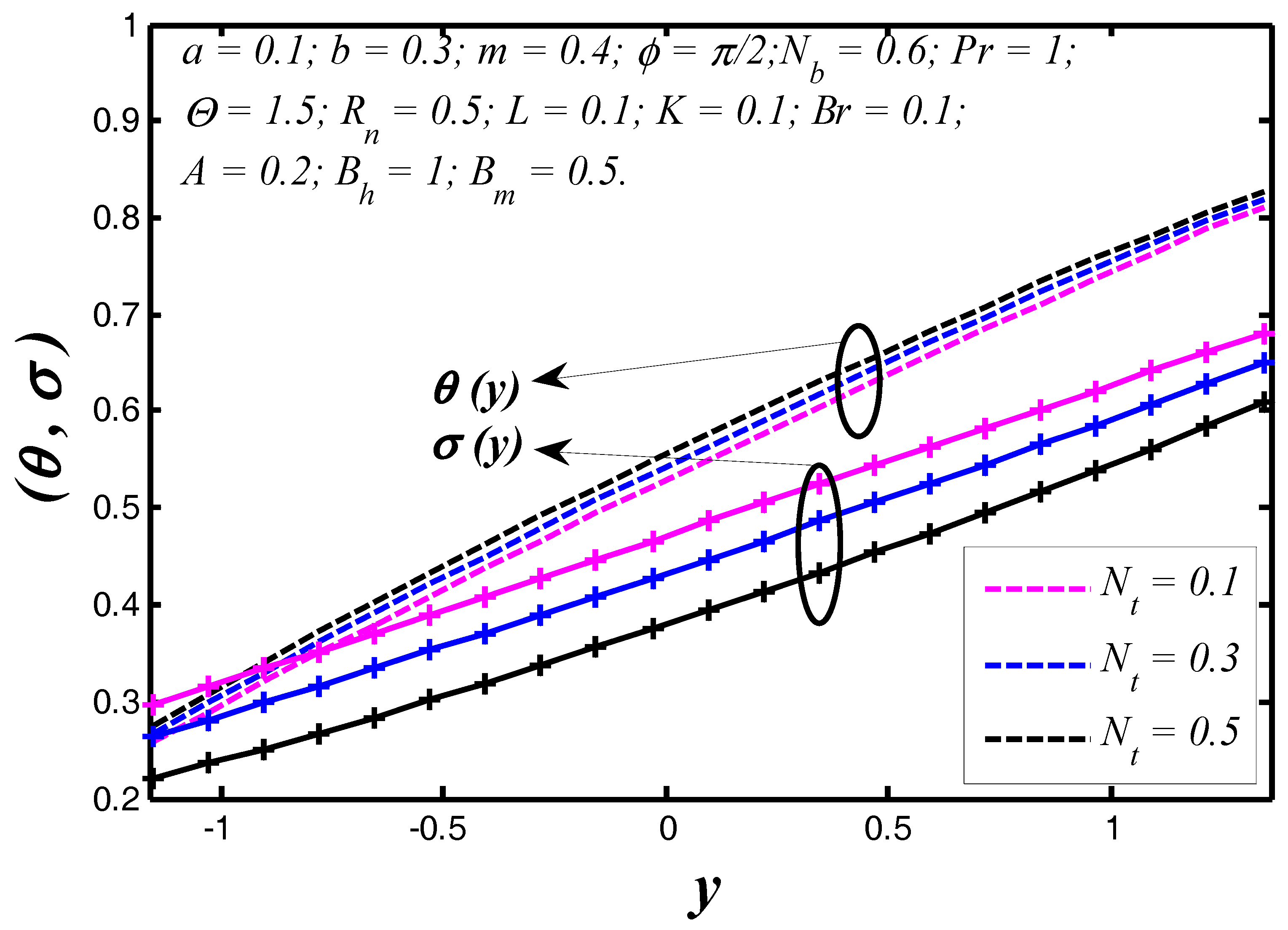
6.1. Thermal and Concentration Profiles

Effects of permeability parameter $\left(K\right),$ slip parameter $\left(L\right),$ mean flow rate $(\Theta )$, non-uniform parameter $\left(m\right),$ Brinkman number $\left(Br\right),$ Prandtl number $\left(Pr\right),$ heat transfer Biot number $\left(B_h\right),$ mass transfer Biot number $\left(B_m\right),$ thermal radiation $\left(R_n\right)$ and thermophoresis parameter $\left(N_t\right)$ on temperature profile are analyzed through Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. In accordance with physical laws, the energy fluency requires to destroy cancer cells greatly depends on the number of nanoparticles temperature within the cell. Additionally, the role of this study is to improve correlations and estimation methods for calculating magnitudes of upper and lower tapered wavy wall boundaries of heat transfer in and around the individual blood vessels. The analysis did not consider vessel size and any experimental values because flow oscillations due to the heartbeat are not present in these small vessels. The aim of this study is to improve correlations and estimation methods for scheming magnitudes and upper and lower limits of heat and mass transfer in and around individual blood vessels.

The nanoparticle temperature and concentration profiles resulted in the vessel exit are shown in Figure 2 for three different permeability parameter values such as $\left(K\to 0,K=0.2,K\to \infty \right)$. It is noticed, theoretically, the absence of a permeability parameter shows very few heat exchanges in the blood vessel, but the particles movement is raised in the blood vessel. In Figure 3, we noticed the effects of slip parameter $(L)$ on the nanoparticle temperature and concentration profiles for fixed values of other parameters. Three different slip parameters are used in the nanoparticle temperature and concentration distribution such as $L=0,L=0.1$ and $L=0.2$. It is important to note with the enhancement in the velocity slip parameter, the nanoparticle temperature and concentration at any point in the flow medium enhances, but the behavior of temperature profile decreases and at the same time nanoparticle concentration increases when the velocity slip parameter rises. The effects of flow constant $(\Theta )$ on nanoparticle temperature and concentration profiles are shown in Figure 4. It is noticed that presence of a flow constant increases the nanoparticle temperature and also enhances uniformly in the boundaries of the channel. However, the nanoparticle concentration shows the revised behavior in nature of temperature distribution. From Figure 5, which elucidates the effect of the non-uniform parameter $\left(m\right)$ on the nanoparticle temperature and concentration profiles, it is exposed that when the non-uniform parameter increases, the nanoparticle temperature of blood flow consistently reduces with the flow medium. The nanoparticle displacement increases with increasing of the non-uniform parameter. These physical changes play crucial roles in the treatment of thermotherapy. In Figure 6, the causes of Brinkman number $\left(Br\right)$ on nanoparticle temperature and concentration are captured. It is noticed that the temperature of the fluid increases with the increase of Brinkman number. It is well known about nanofluids that when the nanoparticle temperature rises, the distance between molecules increases due to cohesive force decreases. Therefore, viscosity of nanofluids decreases when the nanoparticle temperature increases. On the flip side, absence of Brinkman number shows the maximum displacement of the particles. The effect of the Prandtl number $\left(\mathrm{Pr}\right)$ on nanoparticle temperature and concentration are depicted in Figure 7. It is observed that with an increase in $\mathrm{Pr}$, the temperature of the fluid increases. It indicates that nanofluids can have significantly better heat transfer characteristics than the base fluids. Additionally, it is noticed that the nanoparticle concentration decreases with increasing the Prandtl number. This indicates that enhances in Prandtl number is accompanied by an enrichment of the heat transfer rate at the tapered wavy wall of the blood vessel. The fundamental physics behind this can be depicted as follows. When the blood achieves a higher Prandtl number, its thermal conductivity is dropped down and so its heat conduction capacity is reduced. Simultaneously, the heat transfer rate at the vessel wall is enhanced. We noticed from Figure 8 that the temperature enhances with rise of heat transfer Biot number $(B_h)$ at the upper portion of the channel, but the influence is reversed at the lower portion of the channel. Further, it can be noted that the temperature at the upper wall is maximum and it reduces slowly towards the lower wall. The small value of heat transfer Biot number shows the conduction nature, while high values of heat transfer Biot number indicates that the convection is the main heat transfer mechanism. Any rate of nanoparticle concentration reduces with increase of the heat transfer Biot number. Figure 9 reveals that the nanoparticle temperature and concentration enhance as mass transfer Biot number increases. Figure 10 illuminates the influence of the thermal radiation on nanoparticle temperature and concentration distribution. This figure highlights that thermal radiation enhances during blood flow in the channel, thereby the nanoparticle temperature of the tapered asymmetric wavy channel is reduced by increase of thermal radiation. Additionally, the converse situation occurred in the nanoparticle concentration profile. It shows that the external radiation dilutes the temperature, and at the same time movement of the particle increases. This concept may be very useful in the treatment of heart transfer mechanism. Figure 11 illuminates a very significant influence of the thermophoresis parameter on the nanoparticle temperature and concentration profiles. It is well known that the strength of thermophoresis rises due to temperature gradient enhancement, which increases the blood flow in the channel. At the same time, the nanoparticle concentration of the particle displacement reduces with increases of the thermophoresis parameter.

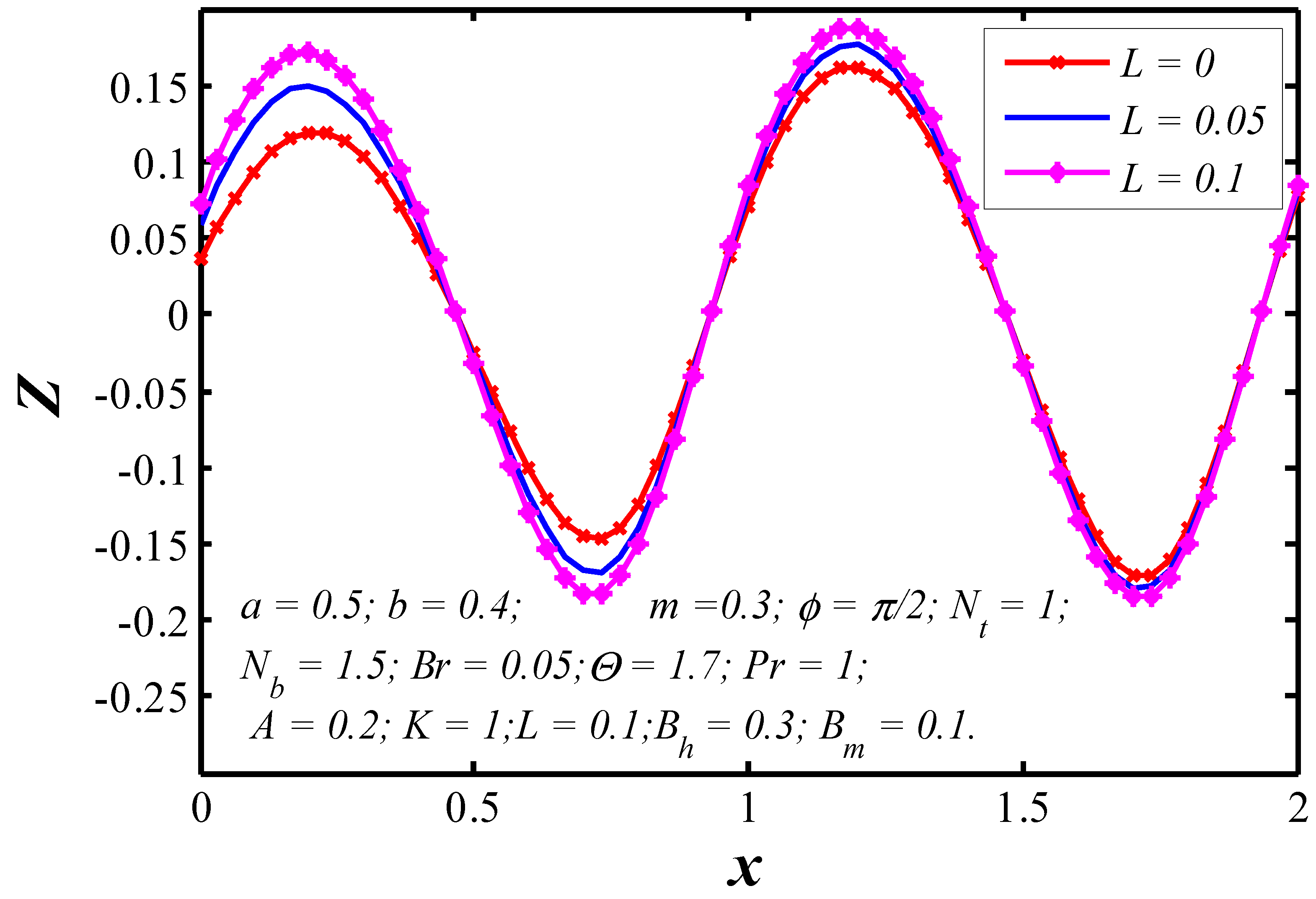
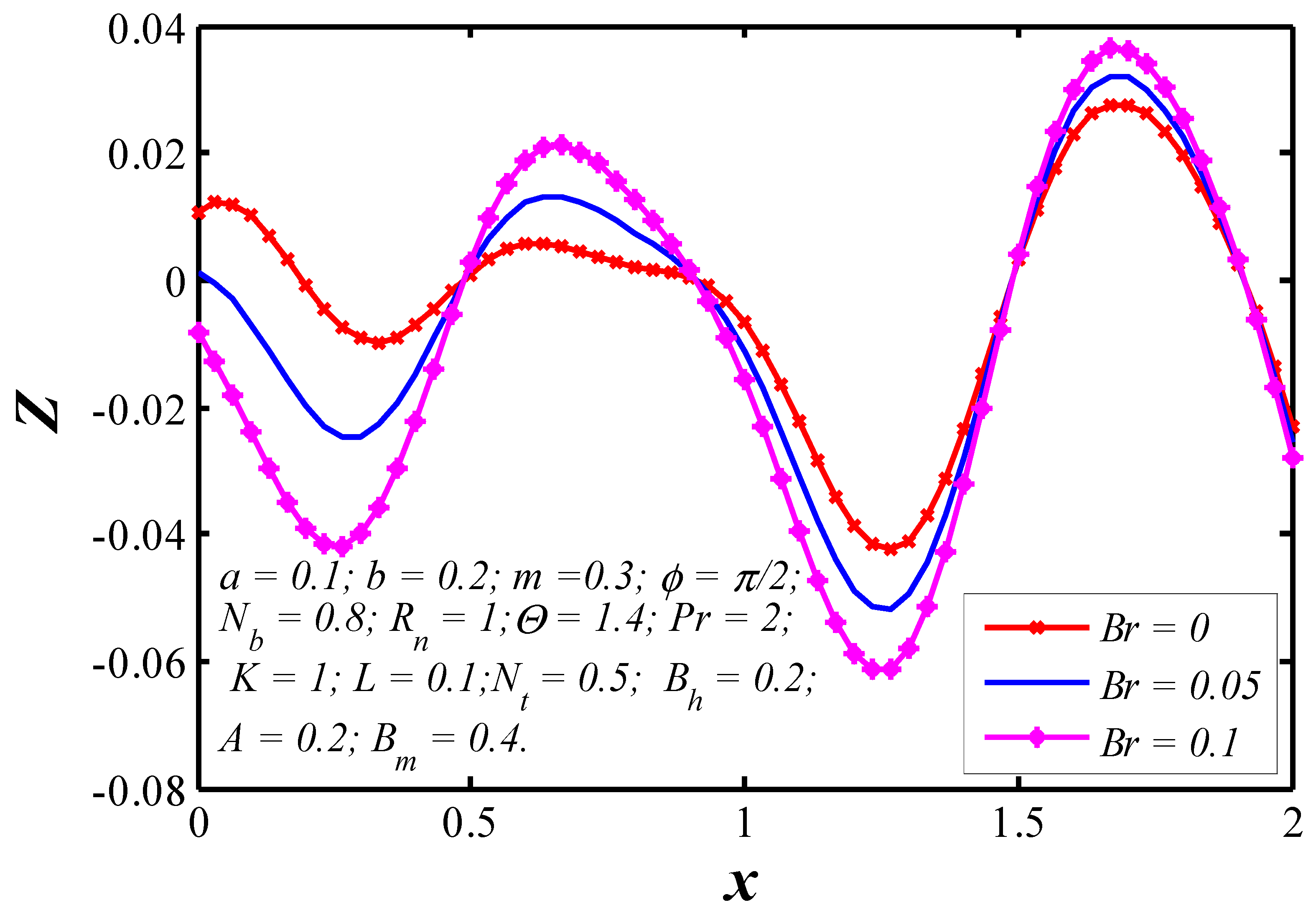
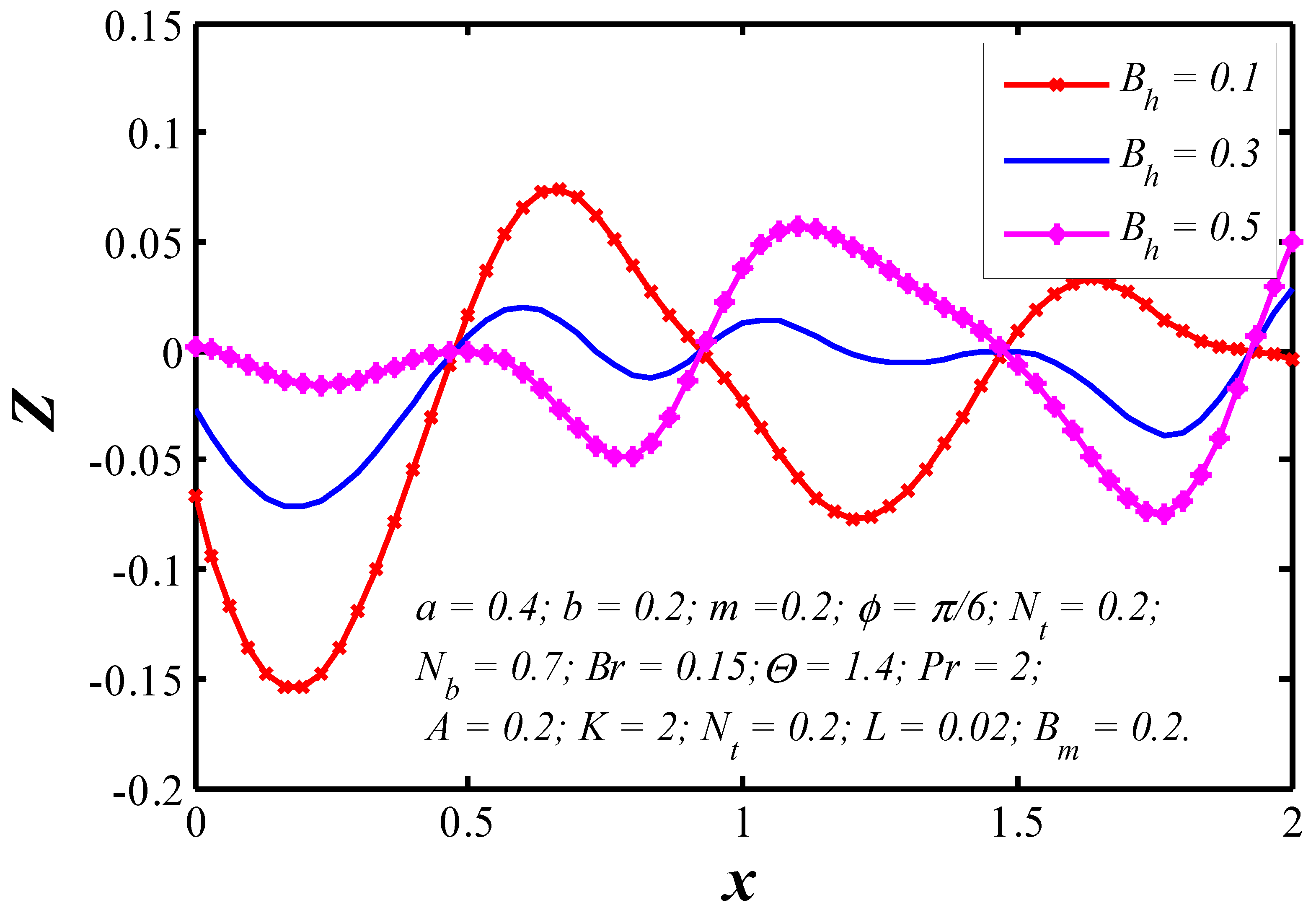
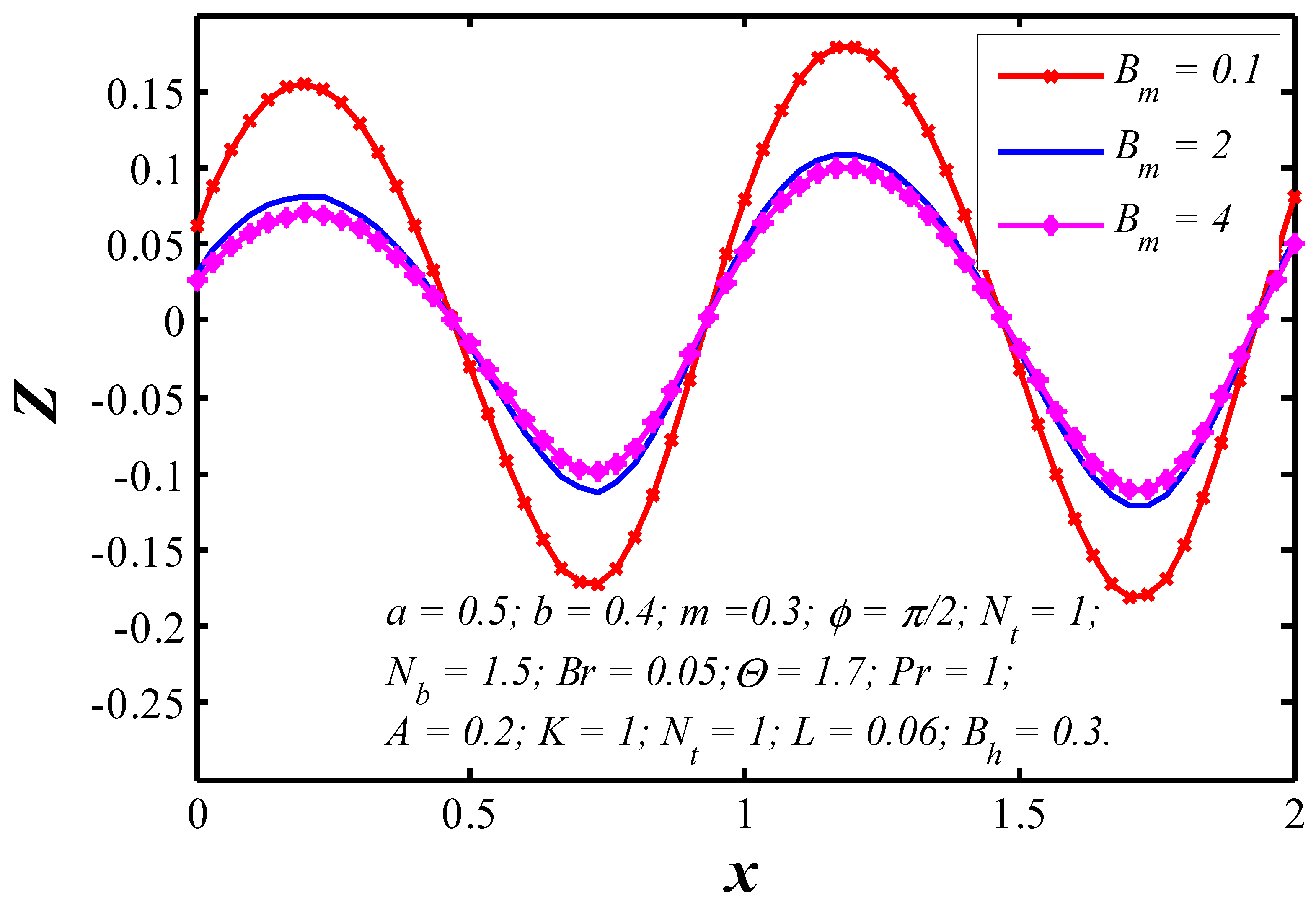
6.2. Nanoparticle Heat Transfer Coefficient

The effects of various parameters on the nanoparticle heat transfer coefficient at the upper wall are represented in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18. The nanoparticle heat transfer coefficients for a viscous nanofluid in the tapered wavy channel depends on many physical quantities related to the fluid or the geometry of the system through which the fluid is flowing. It is observed that the heat transfer coefficient is in oscillatory behavior which may be due to contraction and equation of walls. The absolute value of heat transfer coefficient increases with the increase of $L$ and $Br$ while it decreases with increasing $m,B_h,B_m,N_b$ and $R_n$.

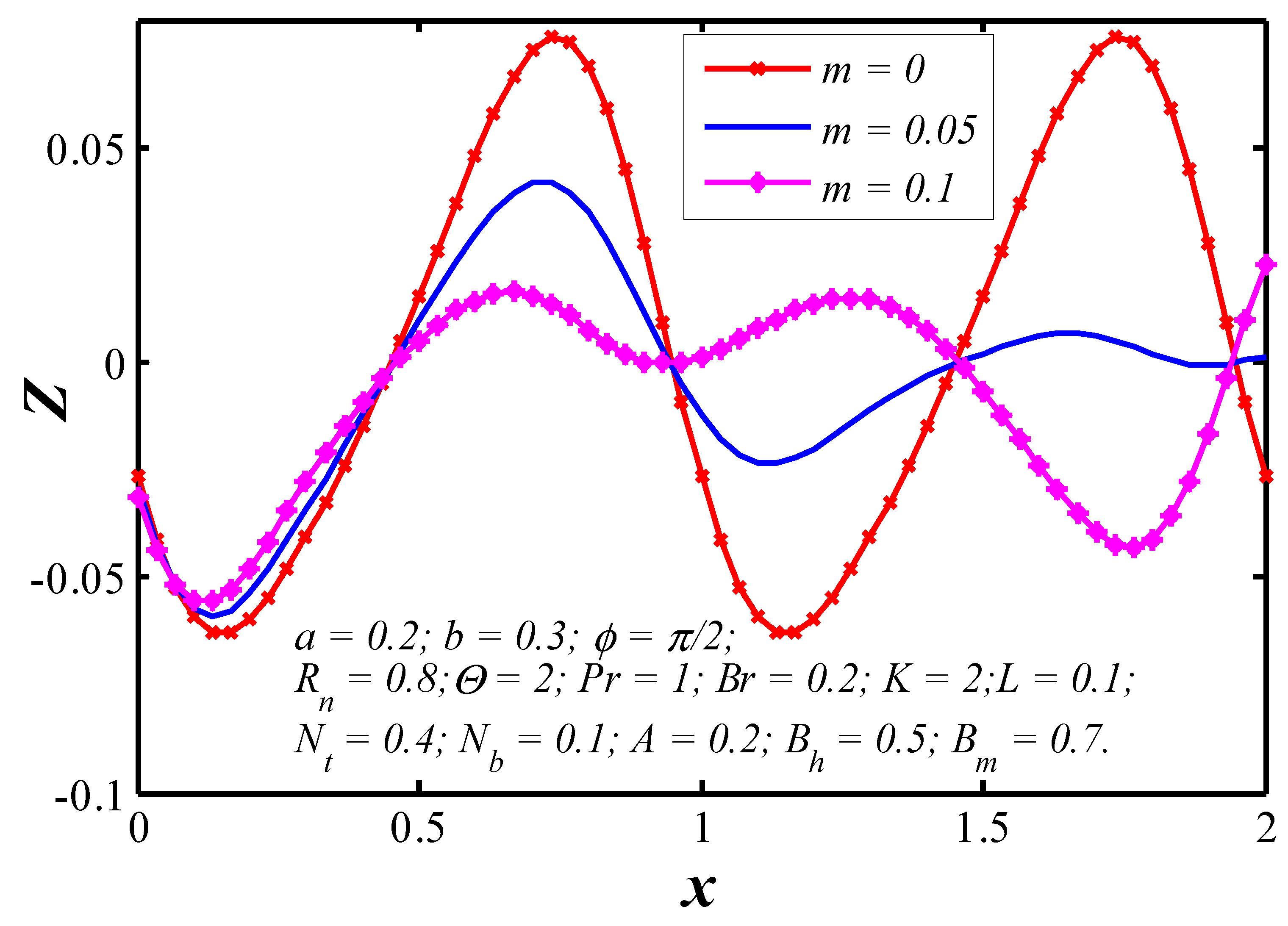
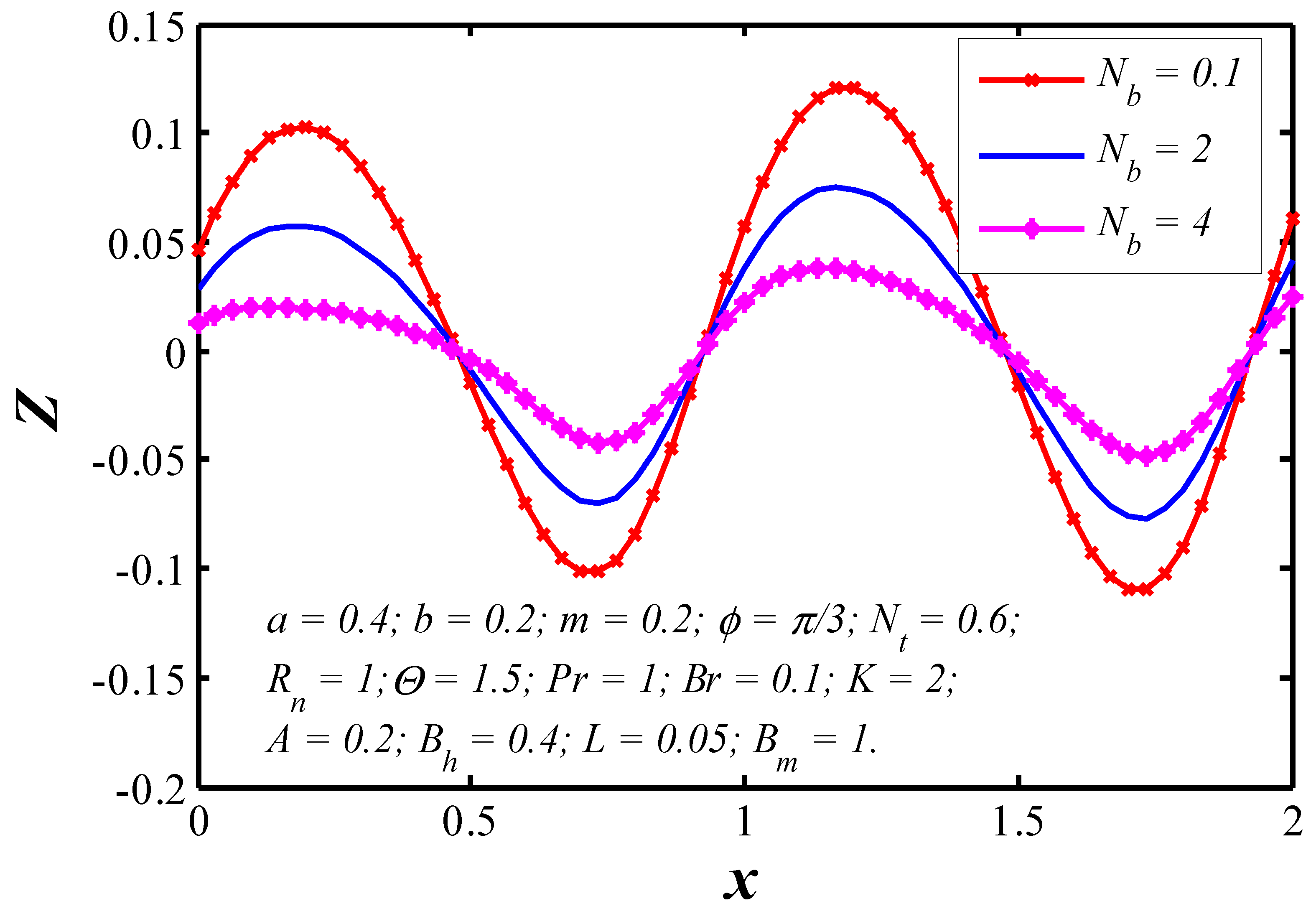
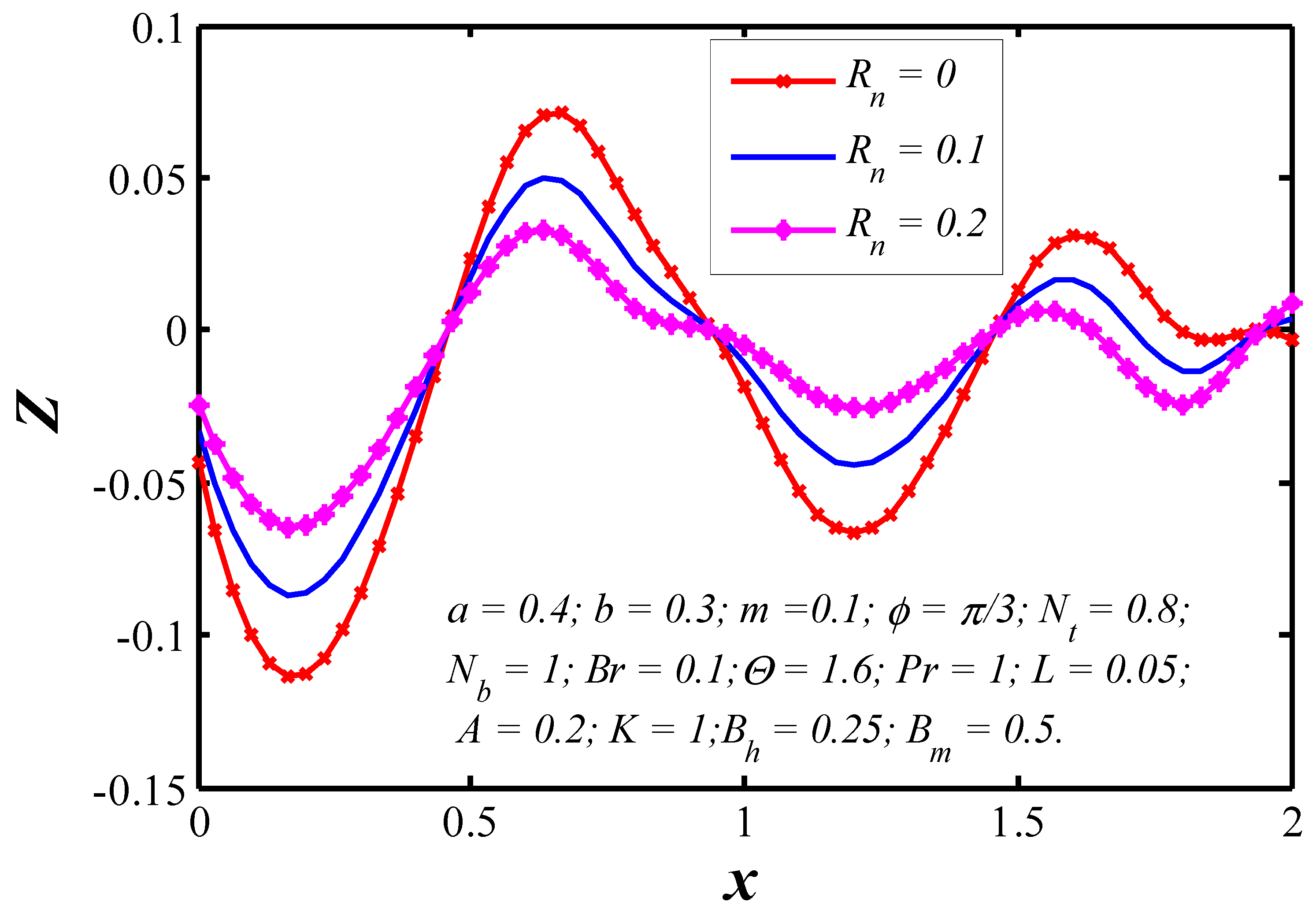
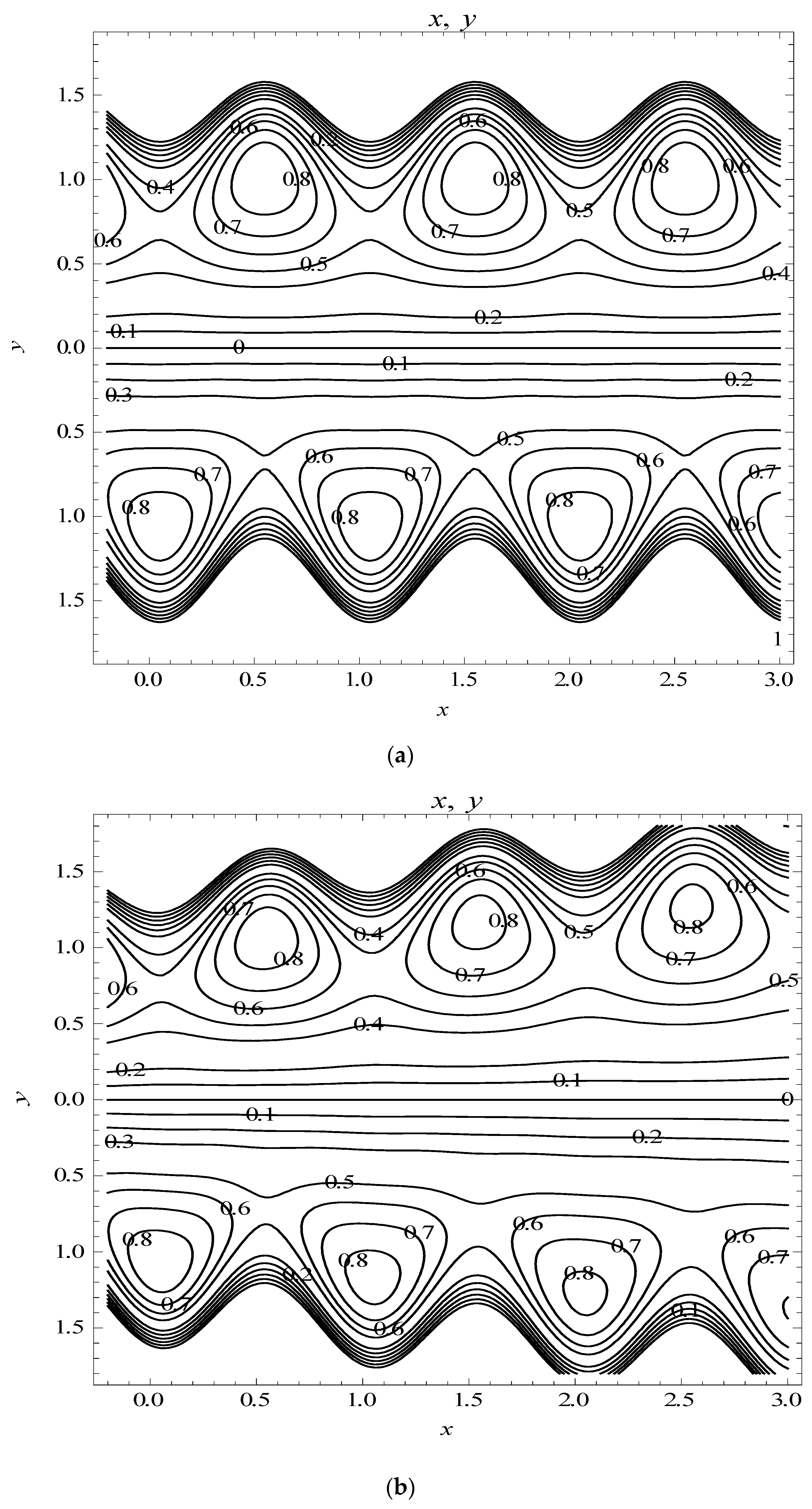
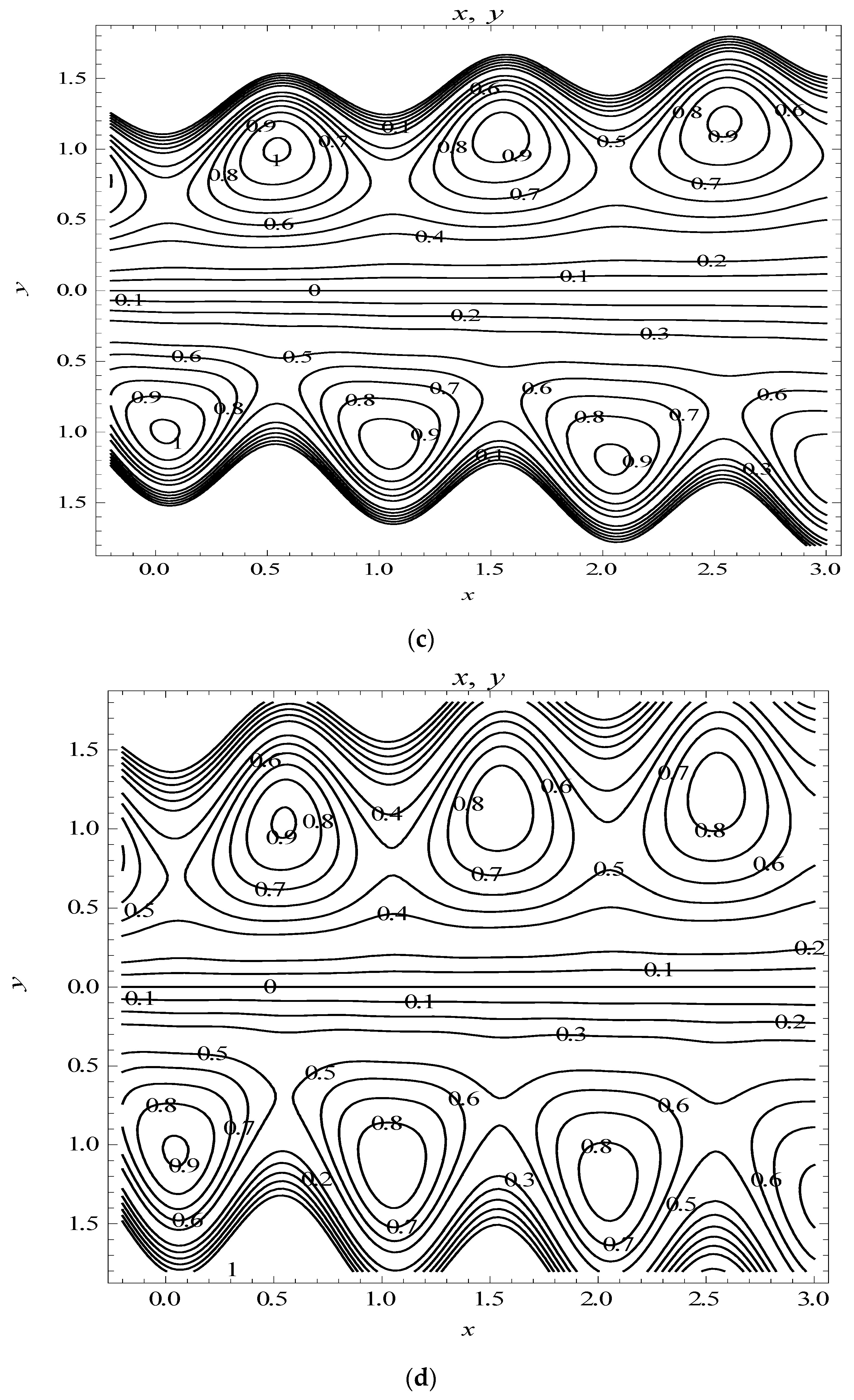
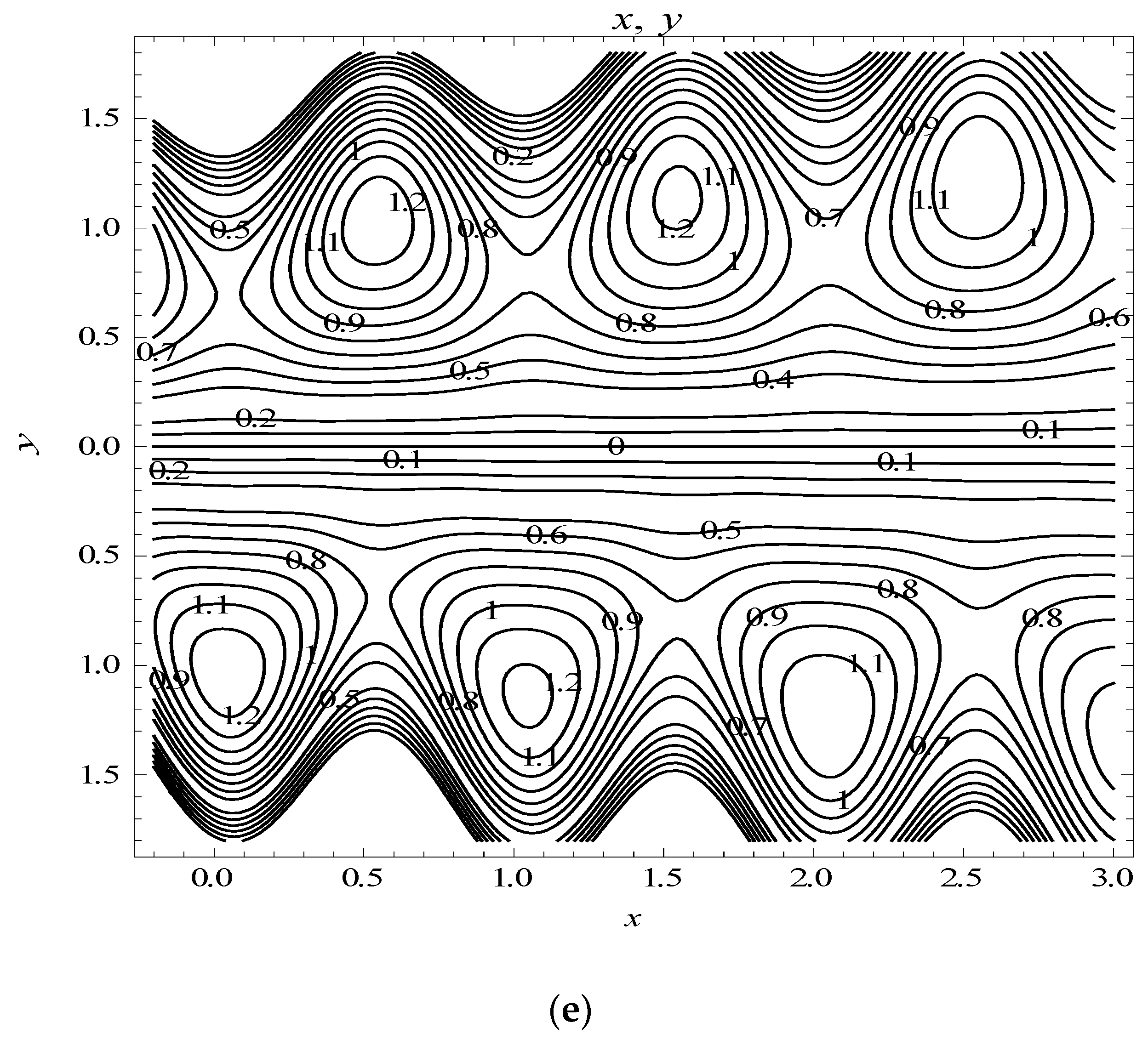
6.3. Trapping

In this subsection, the streamlines for the tapered asymmetry channels are shown in Figure 19. The effects of the non-uniform parameter $m$ on trapping are presented in Figure 19a,b. One can observe that the size of the trapped bolus increases with an increase in $m$. The effect of slip parameter L on trapping can be seen in Figure 19b,c. It is observed that by increasing the value of velocity slip parameter L, the circulation of trapped bolus increases, at the same time size of the bolus is reduced. To see the effects of permeability parameter $K$ on trapping, Figure 19c,d was illustrated. It is noted that an increase in the permeability parameter increases the size of channel, but the size of the trapped bolus decreases. The streamline patterns in the wave frame for viscous nanofluid for different values of Blood flow rate parameter $\Theta$ are shown in Figure 19d,e. It is observed that for small values of $\Theta$ only one trapped bolus is formed. It is also observed that the bolus near the upper and lower wavy walls increase eventually with the tapered micro channel.

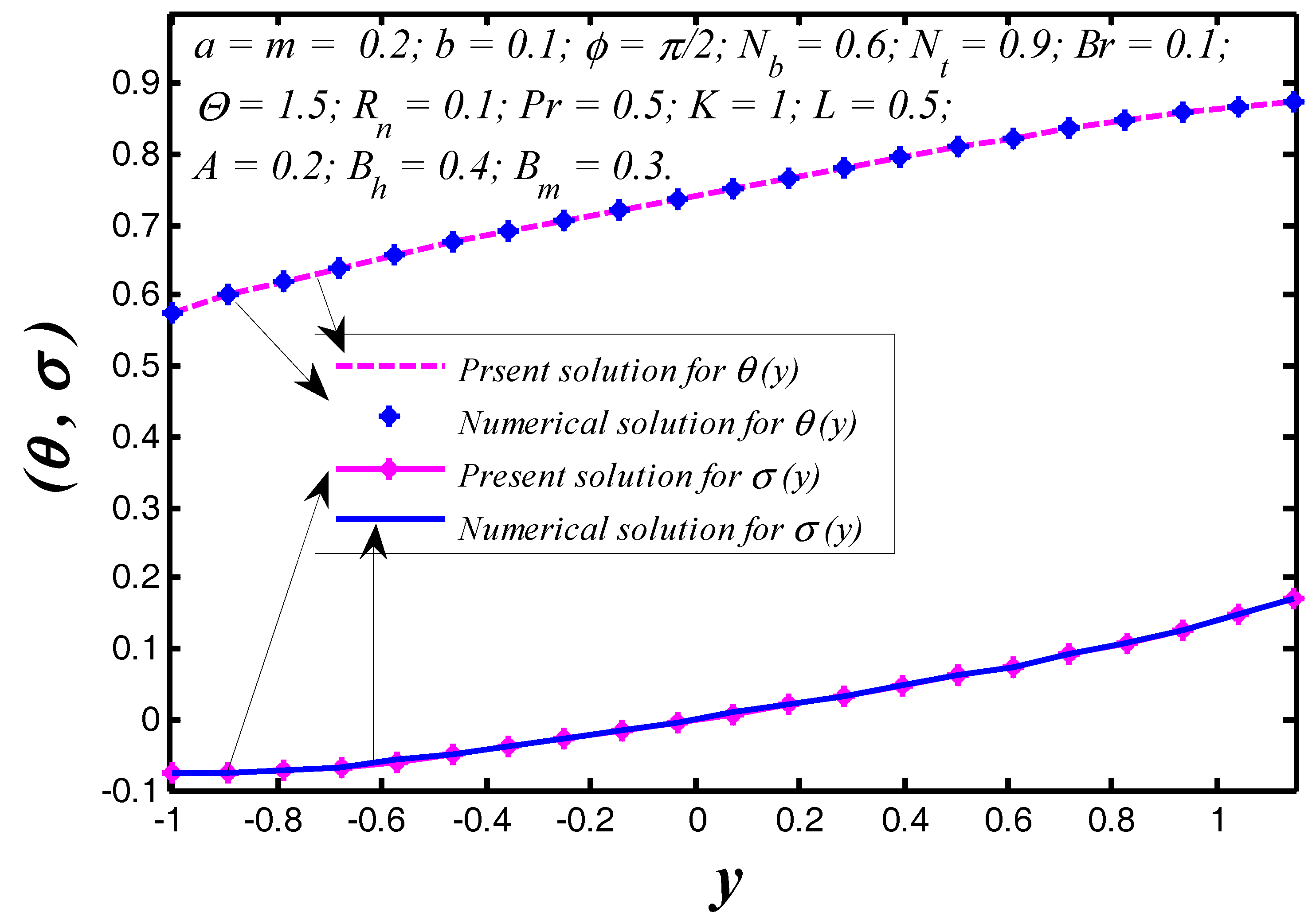
6.4. Validation

The results of present mathematical model obtained by direct analytical approach were authenticated with the numerical solutions computed by MATLAB through BVP4c command. A validation was completed in Figure 20 and it is portrayed for nanoparticle temperature and concentration distribution at fixed values of pertinent parameters. Additionally, it is noticed that the analytical solution for the entire values of the tapered wavy channel width has a good correlation with the numerical solution computed by the MATLAB. The proposed mathematical formulation has very good correlation in axial velocity with Mishra and Rao [63] in the absence of $a=0,$$b=0$ and $K\to \infty$.

7. Conclusions

The analytical and numerical solutions of Equations (9)–(12) were estimated for stream function, nanoparticle temperature and concentration distribution. The expressions for nanoparticle temperature, volumetric fraction, heat transfer coefficient profile and stream function were discussed graphically. The following observations were noticed.

• Nanoparticle heat transfer between the tapered walls strongly depends on Brinkman number because the tissue presents the chief resistance to heat flow.
• Thermal radiation contains the potential to contribute a significant change in the nanoparticle temperature distribution.
• With increasing the radiation parameter, the nanoparticle temperature and heat transfer coefficient enhance.
• The nanoparticle temperature reduces with enhancing the Prandtl number, however, reverse behavior is noticed for nanoparticle concentration.
• Heat transfer coefficient depends on the flow, thermal and geometrical nature of flow regime.
• The trapping phenomenon also alters with changing the magnitude of slip and permeability parameters.
• The findings of the present models can be utilized to engineer smart peristaltic pumps which can be applicable for transporting drugs and delivery of nanoparticles.