Integer and Non-Integer Order Study of the GO-W/GO-EG Nanofluids Flow by Means of Marangoni Convection
Abstract
1. Introduction
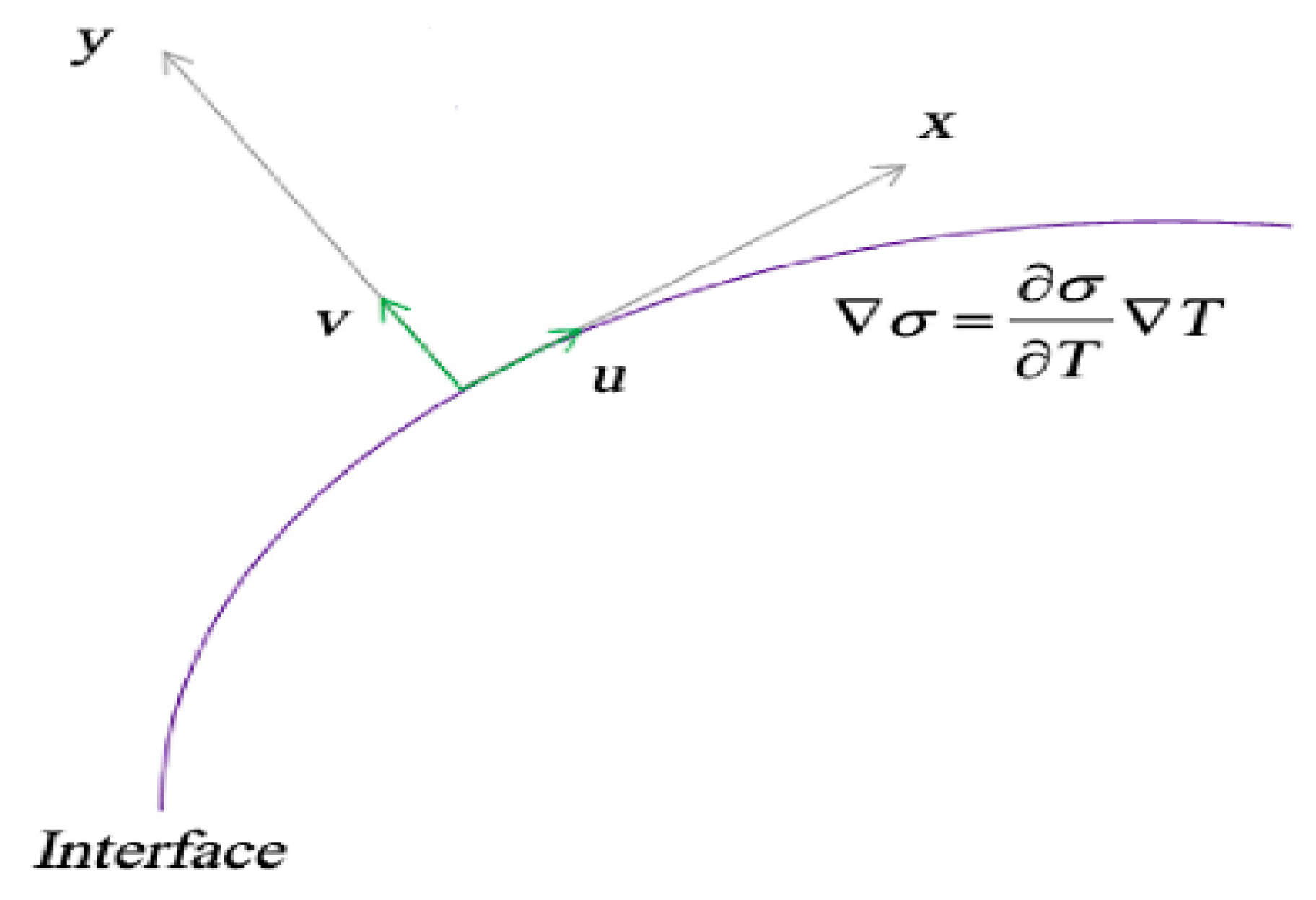
2. Problem Formulation
3. Preliminaries on the Caputo Fractional Derivatives
3.1. Definition 1
3.2. Property 1
3.3. Property 2
4. Solution Methodology
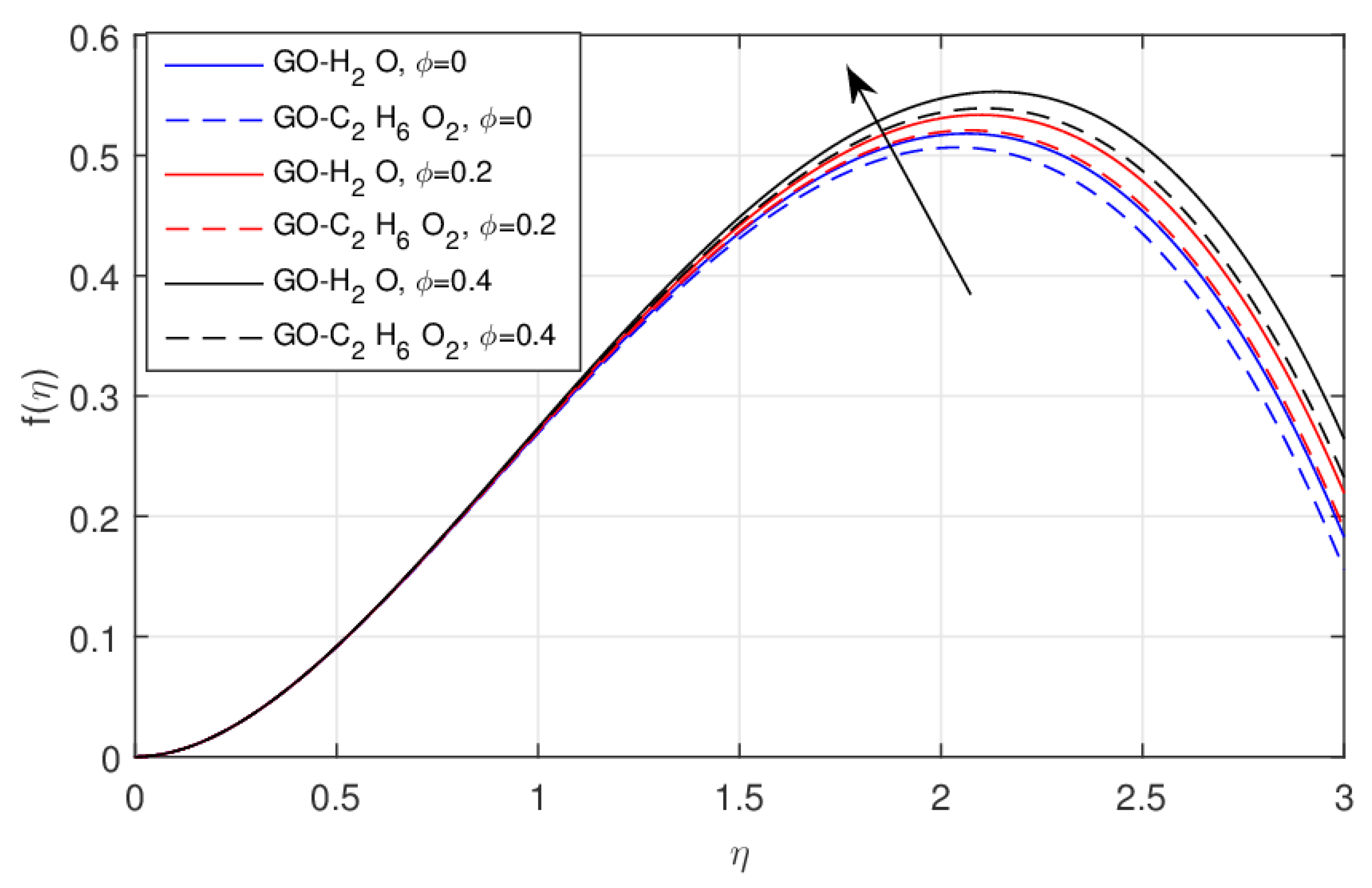
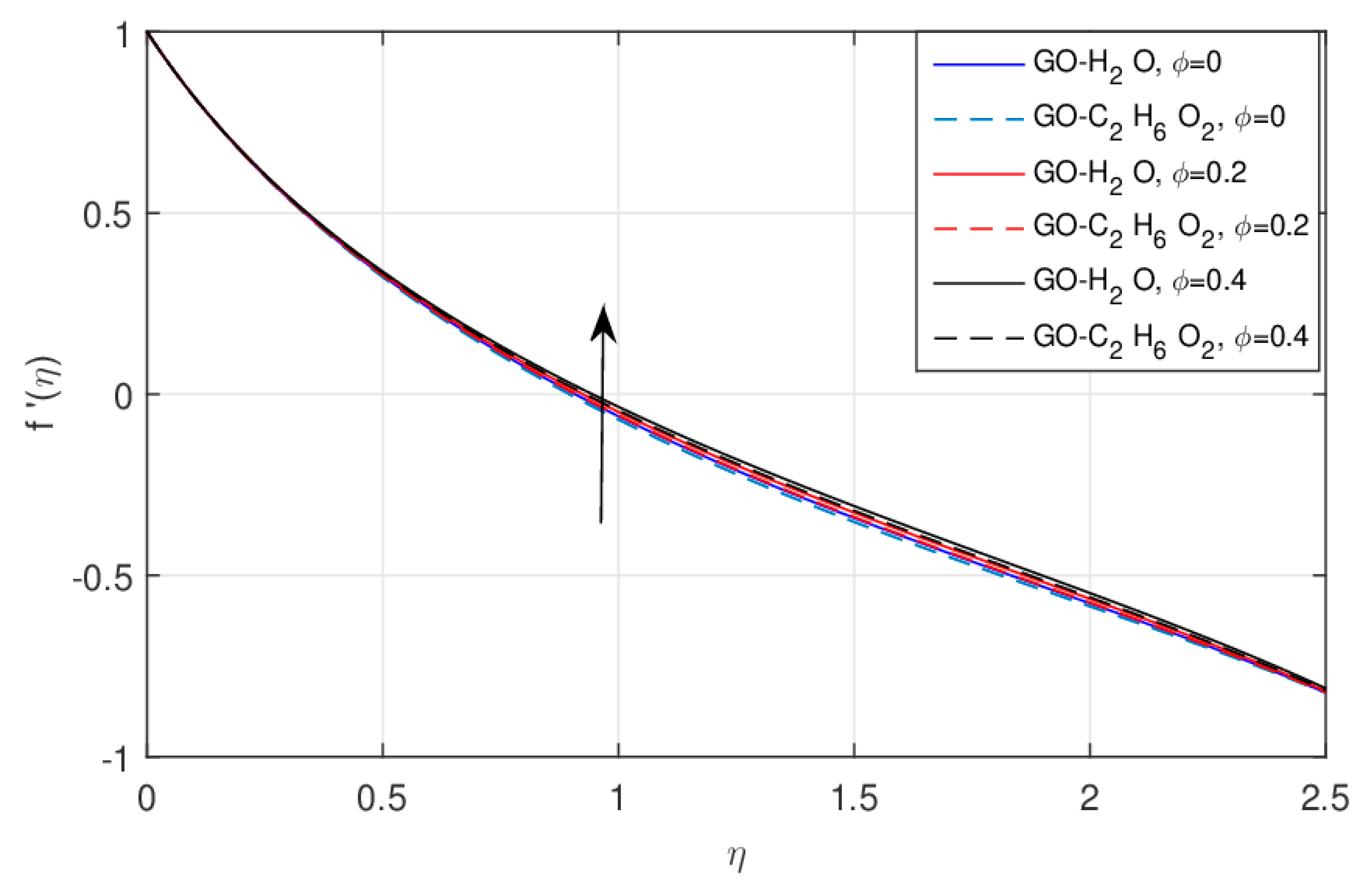
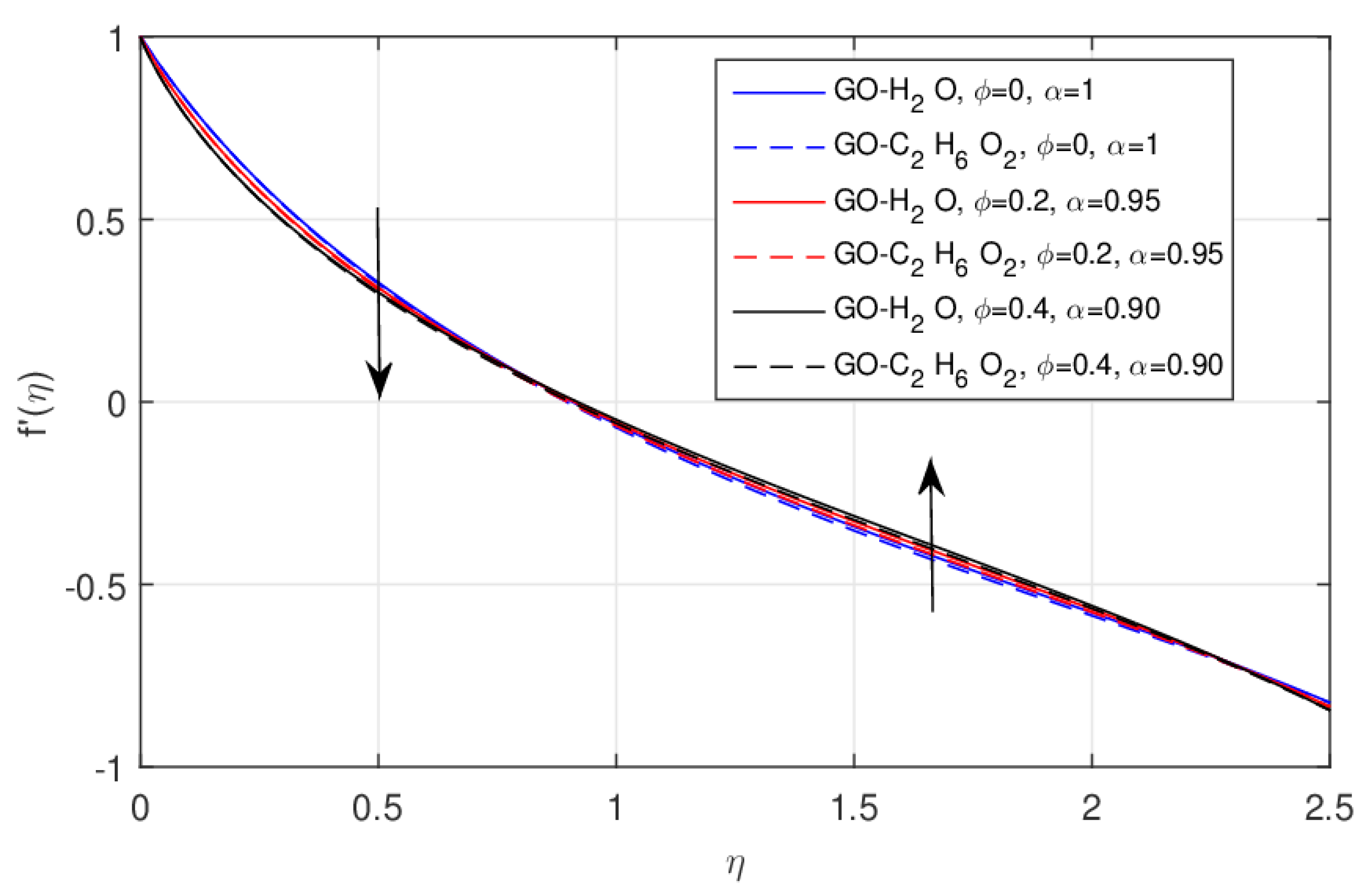
5. Results and Discussions
6. Conclusions
- The rising values of lead to the linear enhancement of the velocity field, which was observed more clearly in the non-integer case compared with the classical model.
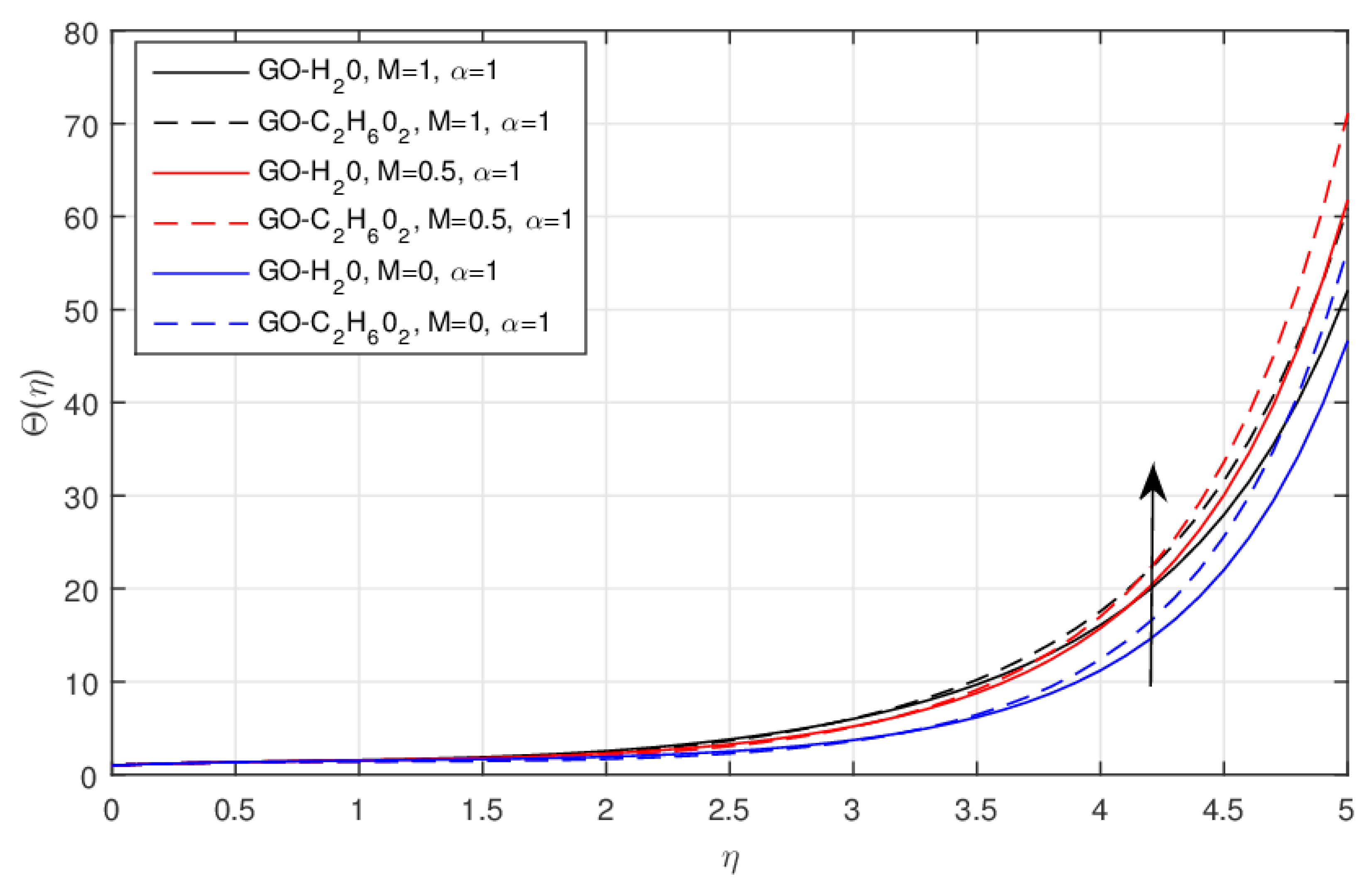
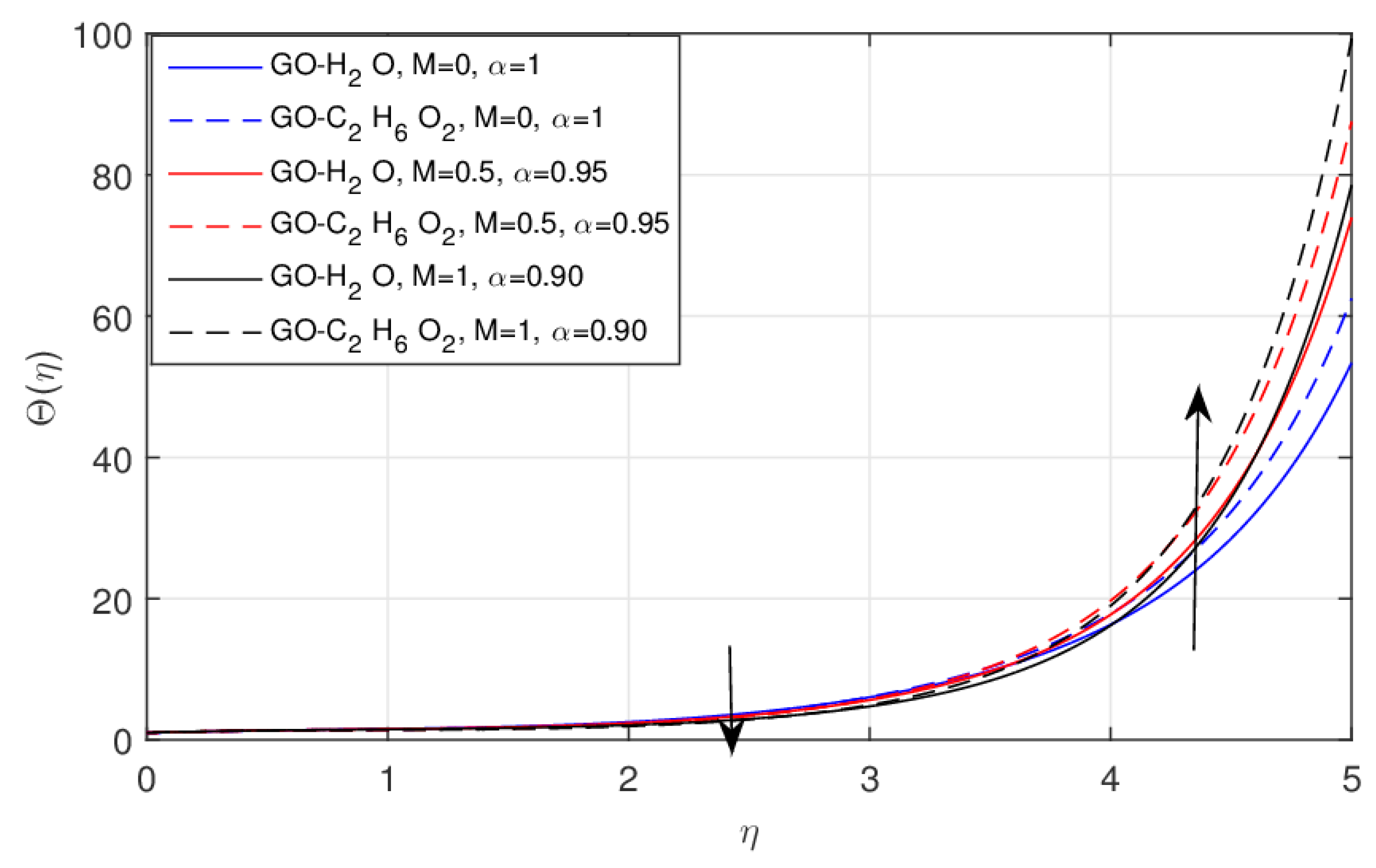
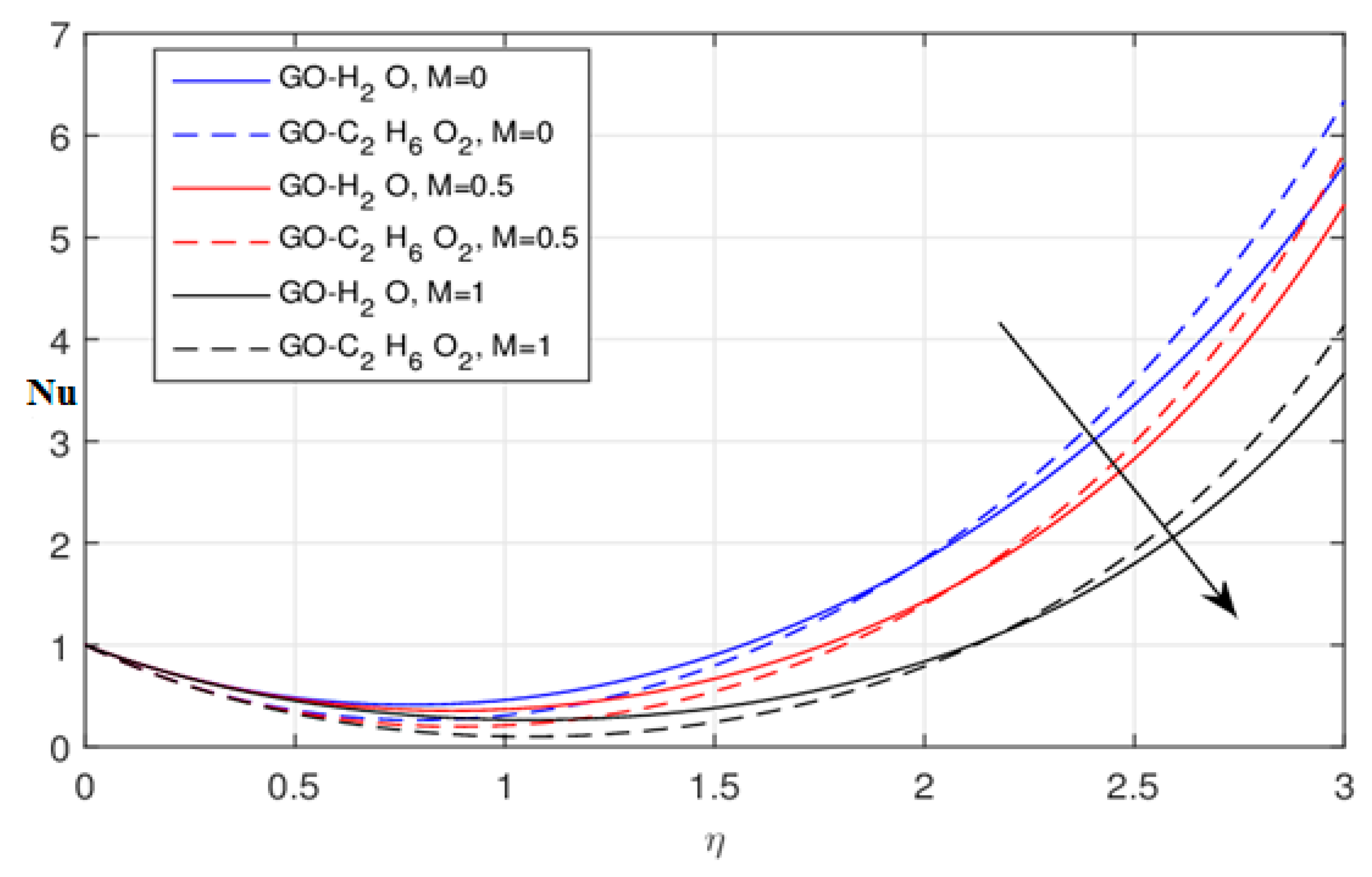
- The increasing values of the magnetic parameter increase the temperature field and decrease the Nusselt number. This effect is somewhat better in the fractional case compared to the integer model.
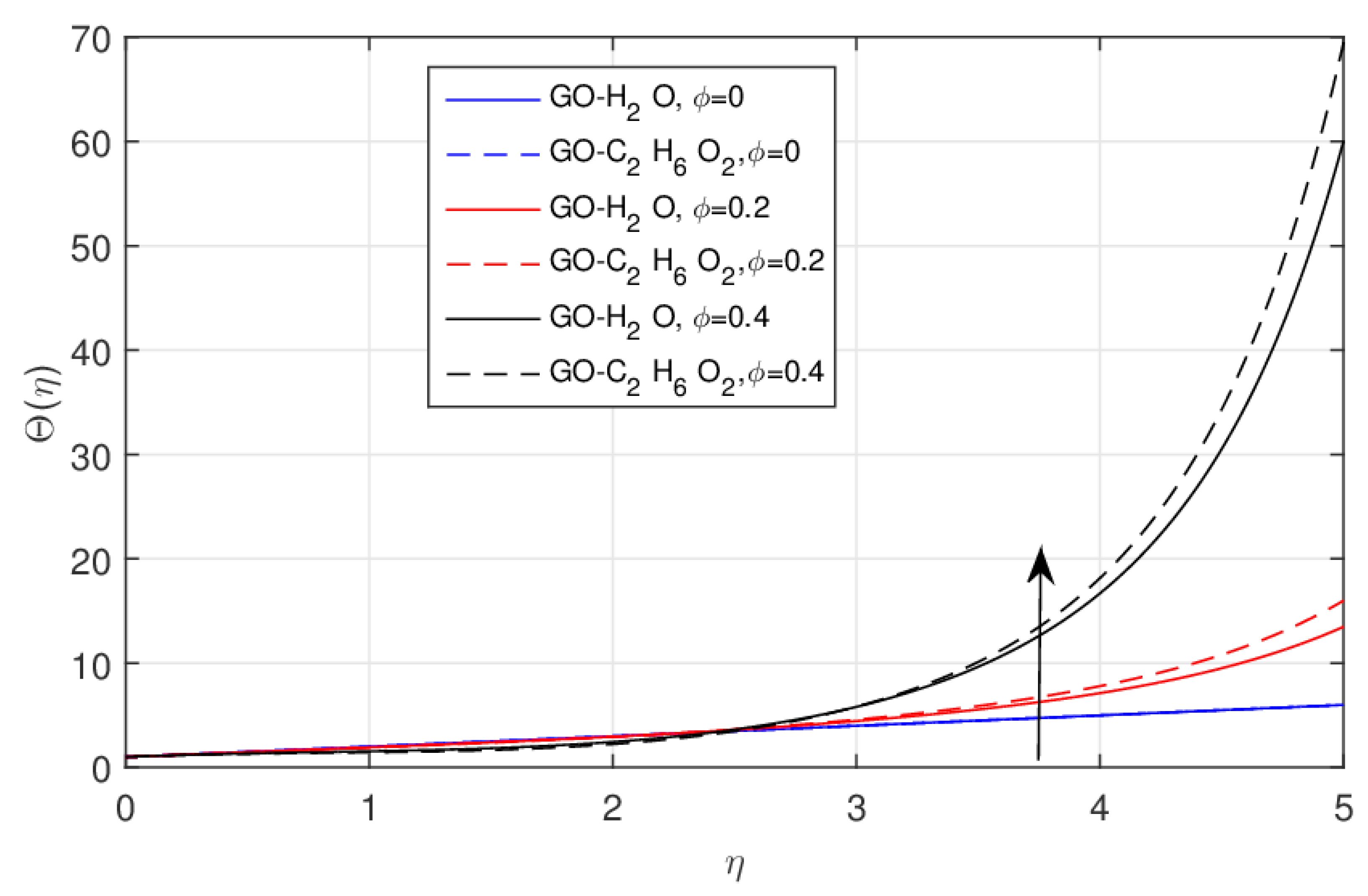
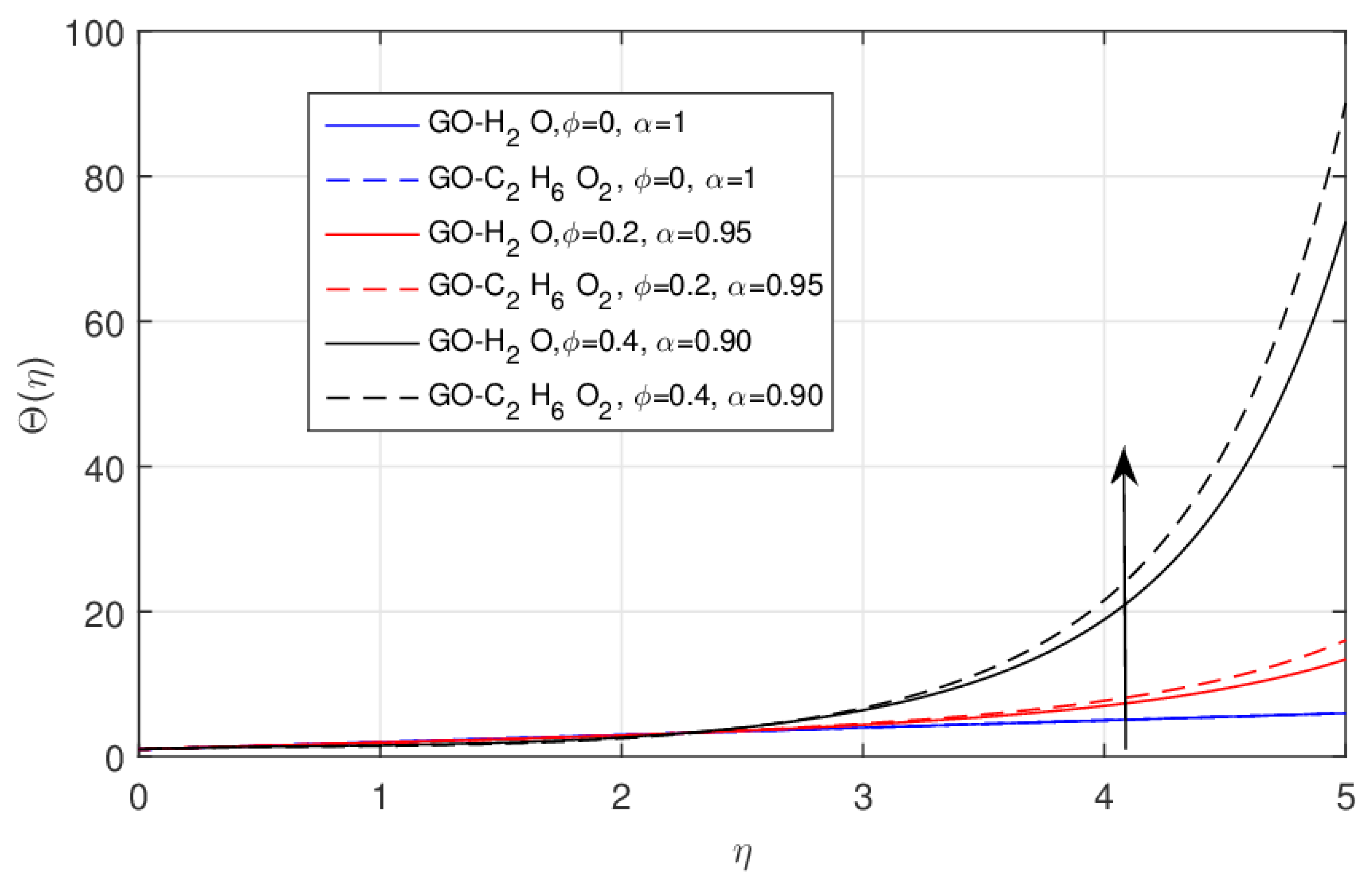
- Due to the rising values of , the thermal boundary layer increases and this effect is somewhat better in the GO-EG nanofluid rather than the GO-W nanofluid.
- The cooling efficiency and heat transfer of the GO-EG nanofluid is far better than that of the GO-W nanofluid.
- With the Lorentz force, resistance arises in the transport phenomenon. This particular phenomenon controls the GO-W and GO-EG nanofluid velocities. Also, this effect is more visible in GO-EG than in GO-W.
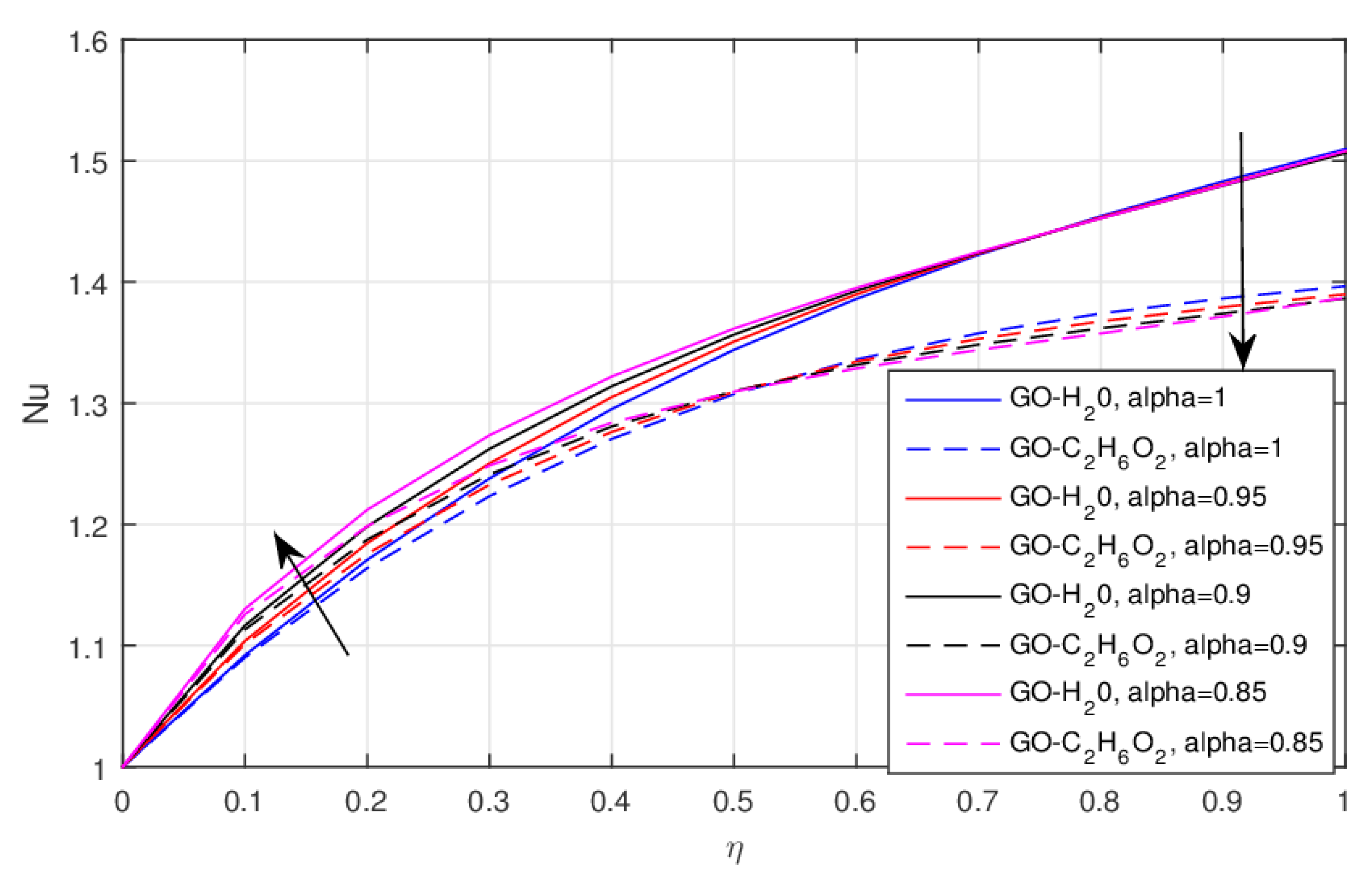
- Due to the fractional order the heat transfer rate enhances in growing increments and this effect is far better in the GO-W nanofluid compared with the GO-EG nanofluid.
7. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Caputo, M. Models of flux in porous media with memory. Water Resour. Res. 2000, 36, 693–705. [Google Scholar] [CrossRef]
- El Amin, M.F.; Radwan, A.G.; Sun, S. Analytical solution for fractional derivative gas-flow equation in porous media. Results Phys. 2017, 7, 2432–2438. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. Numerical approximation of the space-time Caputo-Fabrizio fractional derivative and application to groundwater pollution equation. Adv. Differ. Equ. 2016, 2016, 156–169. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T.; Koca, I.; Atangan, A. A novel approach of variable order derivative: Theory and Methods. J. Nonlinear Sci. Appl. 2016, 9, 4867–4876. [Google Scholar] [CrossRef]
- Shang, Y. Finite-time consensus for multi-agent systems with fixed topologies. Int. J. Syst. Sci. 2012, 43, 499–506. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Y.; Wang, Q.; Sun, C. Fixed-time event-triggered consensus control for multi-agent systems with nonlinear uncertainties. Neurocomputing 2017, 260, 497–504. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. FED-231lMD 1995, 66, 99–105. [Google Scholar]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of Natural Convection MHD Nanofluid by Means of Single and Multi-Walled Carbon Nanotubes Suspended in a Salt-Water Solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Gul, T.; Nasir, S.; Islam, S.; Shah, Z.; Khan, M.A. Effective prandtl number model influences on the Al2O3-H2O and Al2O3-C2H6O2 nanofluids spray along a stretching cylinder. Arab. J. Sci. Eng. 2019, 2, 1601–1616. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of a non-Newtonian nanofluid in a pipe, Analytical solution. Appl. Math. Model. 2013, 37, 1451–1457. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Study of Shiny Film Coating on Multi-Fluid Flows of a Rotating Disk Suspended with Nano-Sized Silver and Gold Particles: A Comparative Analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Taza, G.; Waris, K.; Muhammad, S.; Muhammad, A.K.; Ebenezer, B. MWCNTs/SWCNTs Nanofluid Thin Film Flow over a Nonlinear Extending Disc: OHAM solution. J. Therm. Sci. 2019, 28, 115–122. [Google Scholar] [CrossRef]
- Hummers, W.S.; Offeman, R.E. Preparation of graphitic oxide. J. Am. Chem. Soc. 1958, 80, 1339. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Maxwell, J.C. Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1873. [Google Scholar]
- Wei, Y.; Huaqing, X.; Dan, B. Enhanced thermal conductivities of nanofluids containing graphene oxide nanosheets. Nanotechnology 2010, 21, 055705. [Google Scholar]
- Gul, T.; Ferdous, K. The experimental study to examine the stable dispersion of the graphene nanoparticles and to look at the GO–H2O nanofluid flow between two rotating disks. Appl. Nanosci. 2018, 8, 1711–1728. [Google Scholar] [CrossRef]
- Thomson, J. On certain curious motions observable at the surface of wine and other alcoholic liquors. Philos. Mag. 1855, 10, 330–333. [Google Scholar] [CrossRef]
- Marangoni, C. Ueber die Ausbreitung der Tropfeneiner Flussigkeit auf der Oberflache einer anderen. Ann. Phys. 1871, 143, 337–354. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Influence of magnetic field on CuOeH2O nanofluid flow considering Marangoni boundary layer. Int. J. Hydrog. Energy 2017, 42, 2748–2755. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Ellahi, R.; Sheikholeslami, T.F.; Behzadmehr, A. Numerical investigation of heat and mass transfer flow under the influence of silicon carbide by means of plasmaenhanced chemical vapor deposition vertical reactor. Neural Comput. Appl. 2018, 30, 3721–3731. [Google Scholar] [CrossRef]
- Barikbin, Z.; Ellahi, R.; Abbasbandy, S. The Ritz-Galerkin method for MHD Couette Fow of non-Newtonian fluid. Int. J. Ind. Math. 2014, 6, 235–243. [Google Scholar]
- Hayat, T.; Saif, R.S.; Ellahi, R.; Muhammad, T.; Ahmad, B. Numerical study of boundary-layer flow due to a nonlinear curved stretching sheet with convective heat and mass conditions. Results Phys. 2017, 7, 2601–2606. [Google Scholar] [CrossRef]
- Hayat, T.; Saif, R.S.; Ellahi, R.; Muhammad, T.; Ahmad, B. Numerical study for Darcy-Forchheimer flow due to a curved stretching surface with Cattaneo-Christov heat flux and homogeneous heterogeneous reactions. Results Phys. 2017, 7, 2886–2892. [Google Scholar] [CrossRef]
- Javeed, S.; Baleanu, D.; Waheed, A.; Khan, M.S.; Affan, H. Analysis of Homotopy Perturbation Method for Solving Fractional Order Differential Equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef]
- Srivastava, H.M.; El-Sayed, A.M.A.; Gaafar, F.M. A Class of Nonlinear Boundary Value Problems for an Arbitrary Fractional-Order Differential Equation with the Riemann-Stieltjes Functional Integral and Infinite-Point Boundary Conditions. Symmetry 2018, 10, 508. [Google Scholar] [CrossRef]
- Diethelm, K.; Freed, A.D. The Frac PECE subroutine for the numerical solution of differential equations of fractional order. In Forschung und Wissenschaftliches Rechnen; Heinzel, S., Plesser, T., Eds.; 1998 Gessellschaft fur Wissenschaftliche Datenverarbeitung: Gottingen, Germany, 1999; pp. 57–71. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Saifullah Khan, M.A.; Farooq, M. A fractional model for the dynamics of TB virus. Chaos Solitons Fractals 2018, 116, 63–71. [Google Scholar]
- Gul, T.; Khan, M.A.; Khan, A.; Shuaib, M. Fractional-order three-dimensional thin-film nanofluid flow on an inclined rotating disk. Eur. Phys. J. Plus 2018, 133, 500–5011. [Google Scholar] [CrossRef]
- Gul, T.; Khan, M.A.; Noman, W.; Khan, I.; Alkanhal, T.A.; Tlili, I. Fractional Order Forced Convection Carbon Nanotubes Nanofluid Flow Passing Over a Thin Needle. Symmetry 2019, 11, 312. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.A.; Farooq, M.; Gul, T.; Hussai, F. A fractional order HBV model with hospitalization. Discret. Contin. Dyn. Syst. 2019, 957–974. [Google Scholar] [CrossRef]
- Agarwal, R.; Hristova, S.; O’Regan, D. Global Mittag-Leffler Synchronization for Neural Networks Modeled by Impulsive Caputo Fractional Differential Equations with Distributed Delays. Symmetry 2018, 10, 473. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Saad, K.M.; Khan, M.A.; Agarwal, P. Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: A fractional calculus approach. Phys. A Stat. Mech. Its Appl. 2019, 523, 48–65. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, S.; Farhan, M. The dynamics of Zika virus with Caputo fractional derivative. AIMS Math. 2019, 4, 134–146. [Google Scholar] [CrossRef]


| Model | |||
|---|---|---|---|
| Water (W) | 997.1 | 4179 | 0.613 |
| Graphene oxide (GO) | 1800 | 717 | 5000 |
| Ethylene glycol (EG) | 1.115 | 0.58 | 0.1490 |
| 0.1 | 1.0921 | 1.0903 | 0.1 | 1.1039 | 1.1014 | 0.1 | 1.1167 | 1.1133 | 0.1 | 1.1304 | 1.1259 |
| 0.2 | 1.1708 | 1.1639 | 0.2 | 1.1845 | 1.1758 | 0.2 | 1.1983 | 1.1875 | 0.2 | 1.2121 | 1.1986 |
| 0.3 | 1.2380 | 1.2234 | 0.3 | 1.2504 | 1.2328 | 0.3 | 1.2624 | 1.2413 | 0.3 | 1.2736 | 1.2486 |
| 0.4 | 1.2953 | 1.2706 | 0.4 | 1.3051 | 1.2764 | 0.4 | 1.3141 | 1.2809 | 0.4 | 1.3221 | 1.2840 |
| 0.5 | 1.3442 | 1.3076 | 0.5 | 1.3509 | 1.3095 | 0.5 | 1.3567 | 1.3101 | 0.5 | 1.3617 | 1.3096 |
| 0.6 | 1.3862 | 1.3361 | 0.6 | 1.3899 | 1.3344 | 0.6 | 1.3928 | 1.3318 | 0.6 | 1.3952 | 1.3288 |
| 0.7 | 1.4225 | 1.3578 | 0.7 | 1.4235 | 1.3532 | 0.7 | 1.4242 | 1.3484 | 0.7 | 1.4250 | 1.3441 |
| 0.8 | 1.4544 | 1.3741 | 0.8 | 1.4534 | 1.3676 | 0.8 | 1.4527 | 1.3619 | 0.8 | 1.4527 | 1.3577 |
| 0.9 | 1.4832 | 1.3866 | 0.9 | 1.4809 | 1.3794 | 0.9 | 1.4796 | 1.3741 | 0.9 | 1.4800 | 1.3715 |
| 1.0 | 1.5098 | 1.3966 | 1.0 | 1.5072 | 1.3900 | 1. | 1.5064 | 1.3866 | 1.0 | 1.5083 | 1.3872 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gul, T.; Anwar, H.; Khan, M.A.; Khan, I.; Kumam, P. Integer and Non-Integer Order Study of the GO-W/GO-EG Nanofluids Flow by Means of Marangoni Convection. Symmetry 2019, 11, 640. https://doi.org/10.3390/sym11050640
Gul T, Anwar H, Khan MA, Khan I, Kumam P. Integer and Non-Integer Order Study of the GO-W/GO-EG Nanofluids Flow by Means of Marangoni Convection. Symmetry. 2019; 11(5):640. https://doi.org/10.3390/sym11050640
Chicago/Turabian StyleGul, Taza, Haris Anwar, Muhammad Altaf Khan, Ilyas Khan, and Poom Kumam. 2019. "Integer and Non-Integer Order Study of the GO-W/GO-EG Nanofluids Flow by Means of Marangoni Convection" Symmetry 11, no. 5: 640. https://doi.org/10.3390/sym11050640
APA StyleGul, T., Anwar, H., Khan, M. A., Khan, I., & Kumam, P. (2019). Integer and Non-Integer Order Study of the GO-W/GO-EG Nanofluids Flow by Means of Marangoni Convection. Symmetry, 11(5), 640. https://doi.org/10.3390/sym11050640






