Abstract
The Couette–Poiseuille flow of couple stress fluid with magnetic field between two parallel plates was investigated. The flow was driven due to axial pressure gradient and uniform motion of the upper plate. The influence of heating at the wall in the presence of spherical and homogeneous Hafnium particles was taken into account. The temperature dependent viscosity model, namely, Reynolds’ model was utilized. The Runge–Kutta scheme with shooting was used to tackle a non-linear system of equations. It was observed that the velocity decreased by increasing the values of the Hartman number, as heating of the wall reduced the effects of viscous forces, therefore, resistance of magnetic force reduced the velocity of fluid. However, due to shear thinning effects, the velocity was increased by increasing the values of the viscosity parameter, and as a result the temperature profile also declined. The suspension of inertial particles in an incompressible turbulent flow with Newtonian and non-Newtonian base fluids can be used to analyze the biphase flows through diverse geometries that could possibly be future perspectives of proposed model.
1. Introduction
Diverse forms of flow paths appear when fluid flow is diverted by debris blocking streams. Such multiphase flows take place naturally due to the various factors on plateaus. The physical occurrence of multiphase flows includes chemical processes, pharmaceutical, wastewater management, and power generation. Consequently, the multiphase flows have attracted the attention of scientists and engineers due to the frequently arising issues in industrial and mechanical problems. For instance, couple stress fluid flow under the influence of heat between two parallel walls was examined by Farooq et al. [1]. Mahabaleshwar et al. [2] have investigated the magnetohydrodynamics (MHD) couple stress fluid over the flat sheet affected by the radiation. Exact solutions for the velocity were derived using a power series method for two different models. The First case described the surface temperature while the second case dealt with heat flux. Saad and Ashmway [3] have studied the flow of an unsteady couple stress fluid between two plates. The fluid flows with constant motion of the upper plate which was initially at rest. Influence of lubrication on walls was pondered in such a way that the couple stresses on the boundaries had no impact at all. A suitable transform helps to obtain the velocity of fluid numerically. Akhtar and Shah [4] have presented the exact results for three different types of fundamental flows by taking couple stress fluid as a base fluid. Khan et al. [5] reported an incompressible flow of MHD couple stress in which thermally charged fluid was disturbed by transversely applied magnetic fields. The unsteady Couette flow of non-uniform magnetic field has been investigated by Asghar and Ahamd [6]. Shaowei and Mingyu [7] have devoted their efforts for the study of the Couette flow of Maxwell fluid. Integral and Weber transforms have been used to analyze the physical phenomenon. The Couette flow through a symmetric channel was numerically tackled by Eegunjobi et al. [8]. Few core investigations on Couette flow [9,10,11,12] and couple stress fluid [13,14,15] are listed for those working in the same regimes.
Moreover, Poply et al. [16] have examined the temperature-dependent fluid properties of MHD flow with heat transfer. Ellahi et al. [17] have considered two different viscosity models for their investigations of heated flow. They chose third-grade nanofluid flow through coaxial cylinders. Homotopy analysis method is used to produce a closed form solution. In Reference [18] authors have discussed a temperature dependent thick flow between two opposite walls of uneven configurations. The viscosity of two-dimensional flow was assumed to be decreasing exponentially subject to temperature rise. The study contained the simultaneous effects of radiation and a porous medium. A steady-state flow of fourth-grade fluid in a cylinder was analyzed by Nadeem and Ali [19] and offered a comparative analysis in it. Ellahi et al. [20] studied the thermally charged couple stress fluid suspended with spherically homogenous metallic Hafnium particles for bi-phase flow along slippery walls. The rough surfaces of the walls is tackled with the lubrication effects. Variation in the viscosity of viscoelastic fluid by the Runge–Kutta technique with the shooting technique can be seen in Reference [21]. Makinde [22] focused on the impact of viscosity on the steady fluid flow with gravitational effects. The overhead surface was assumed to be at a constant temperature while the adjunct surface of the plate was heated with some external source. A few core investigations for viscous dissipation can be found in References [23,24].
Furthermore, to enhance the thermal performance, different types of nanoparticles having sizes from 1–100 nm have been utilized in bi-phase fluids. For example, Karimipour et al. [25] have studied the role of miscellaneous nanoparticles for heat transfer flow with MHD. Hosseini et al. [26] repotted a unique model on thermal conductivity of nanofluids. Nasiri et al. [27] have proposed a particle hydrodynamics approach for nano-fluid flows. Safaei et al. [28] have examined nanoplatelets–silver/water nanofluids in fully developed turbulent flows of graphene. All said investigations including References [29,30,31,32,33] end up stating that the presence of nanoparticles always sped up the heat transfer rate.
In the current article, we aim to study the magnetized multiphase Couette-Poiseuille flow of non-Newtonian couple stress fluid suspended by metallic particles of Hafnium with temperature dependent viscosity. The viscosity of the base fluid is exponentially decreasing due to the heating effects at the lower wall of the channel which is at rest. However, the motion of the upper wall causes the multiphase (i.e., solid–liquid) transport. The contribution of the pressure gradient simultaneously distinguishes the investigation further. The humble effort will not only speak about the mechanical and industrial multi-phase flows but would also fill the gap yet not available in the existing literature on the topic under consideration.
2. Mathematical Analysis
Consider a plane Couette flow between two opposite flat plates at , as shown in Figure 1. Flow is investigated in plane in such a way that -axis lies in the middle and along the plates. It is a well-established fact [34] that when the flow is generated by the constantly moving upper plate, then only can the unidirectional disturbance in the -direction occur. The axial velocity was along the -direction, whereas lateral velocity was in the -direction is zero. When the metallic particles of Hafnium were suspended in couple stress fluid under the influence of higher temperature of the lower wall, then the governing equations in component form [35] can be expressed as:
Figure 1.
Configuration of the flow.
(i). For fluid phase
(ii). For particle phase
(iii). Energy equation
where, denotes concentration of the particles, is the viscosity of solid-liquid, viscosity of the base liquid, is a material constant associated with couple stress fluid, is the electric conductivity of the fluid, is the magnetic strength, is temperature, and is the thermal conductivity of the fluid whereas, are, respectively, axial and lateral coordinates. Moreover, denotes the drag coefficient of interaction for the force exerted by particle on the fluid, and is given by Tam [36]:
where, in Equation (6) the radius of the Hafnium particles is denoted by .
Boundary Conditions
The flow interaction at the surfaces of the parallel plates are denoted by the following:
By using the following appropriate quantities:
Equations (1)–(5), in non-dimensional form after neglecting asterisk can be written as
In which, is the Hartmann number, is the couple stress parameter, is the drag constant and is he Brinkman number.
3. Results and Discussion
3.1. Variable Viscosity
The Reynolds’ model for temperature dependent viscosity [37] can be defined as
In view of expression given in (10), the non-dimensional form of Equation (14), after dropping asterisk is obtained as
where .
Obviously, for the convergence of Equation (15), .
By Walter’ lemma, the Maclaurin’ series of Equation (15) can be linearized as
In view of Equations (12) and (16), Equations (11) and (13) provide the set of nonlinear coupled differential equations involving the viscosity of the fluid deeply affected by the presence of heat applied at the wall along with a constant pressure gradient at each point of the channel (i.e., ) as follows
On the same contrast, Equations (8) and (9), in view of (10), are acquired as
3.2. Numerical Procedure
The set of non-linear differential Equations (17) and (18) with the boundary conditions (19) and (20) are solved by employing the most efficient numerical procedure consist of Runge–Kutta method and the shooting scheme [38] using MATLAB software. It is an iterative scheme, in which each step possible error can be successively reduced by changing higher order derivatives.
Let:
be the velocity of the fluid phase, then the derivatives of , in terms of system of first ordinary differential equations (ODEs) can be expressed as:
here the sign of prime (′) at the top indicates the derivative with respect to “”. In view of Equations (22)–(26) the fluid phase differential equation is transformed as:
The transformed set of conditions are given as:
where can be easily determined during the routine numerical procedure.
3.3. Graphical Illustration
To see the effects of physical parameters for Reynolds model on velocity and temperature, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 have been displayed. The range of all physical parameters available in the existing literatures are as follows: the range of Hartmann number is [39], the Brinkman number varies from 0.5 to 2.0 [40], the range of couple stress parameter is 0.5 to 2.0 [41], the range of concentration of the metallic particles’ is 0 to 0.2 [42], and the range of viscous parameter lies between 0 to 1. The role of transversely applied magnetic fields can be sighted in Figure 2. It is found that the velocity of fluid decreases by increasing the values of Hartmann number. It is in accordance with the physical expectation, as increased in the Hartmann number, means to strengthen the magnetic field lines which result to impede the flow. Therefore, the obtained results validate the expected outcomes. In Figure 3, addition of some extra metallic particles to the system that expedites the flow is observed. It is found that velocity of fluid escalates for higher values of C. It is very much obvious as the constant movement of the upper wall does not allow the particle to exert an extra drag force to attenuate the base fluid motion. Thus, particle-to-particle interaction and fluid–particle interaction gets meager, which causes the frisky movement of the Hafnium particles in the base fluid. In Figure 4, we show that an increase in the couple stress parameter weakens the rotational field of couple stress fluid particles. It was revealed that the velocity profile increased by increasing the values of the couple stress parameter. It is because of friction force that fails to gain enough strength which can cause enough resistance to slow down the celerity of the flow. Similarly, the application of heat on the lower wall contributes in shear thinning effects which aids the fluid particles to get extra momentum. Hence, increase in the velocity of the fluid flow is vivid in display. Figure 5 shows the impact of decreasing viscous parameter on the flow dynamics. In Equation (14), it can be inferred that as the temperature difference mounts, the shear thinning effects on the viscosity of the base fluid aggravates. This attenuation of physical property results in the increase of the celerity of the fluid and particles movements. Figure 6 describes the role of Brinkman number on the temperature. It is seen that higher values of Brinkman heats up the fluid by surging the temperature. However, the quite opposite behavior was observed for the case of viscosity parameter as shown in Figure 7. It was revealed that the temperature of the fluid declines for the higher values of . This temperature decline was in fact due to the rapid movement of the couple stress fluid.
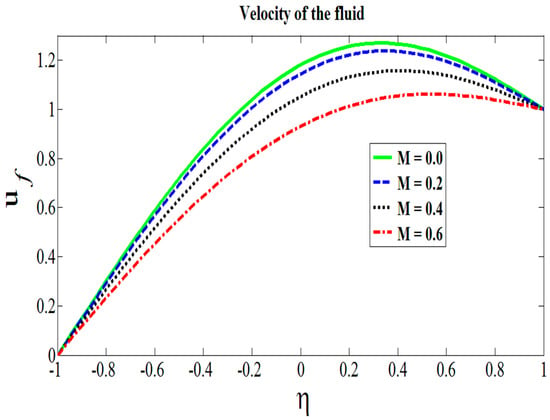
Figure 2.
Effects of Hartmann number on the flow.
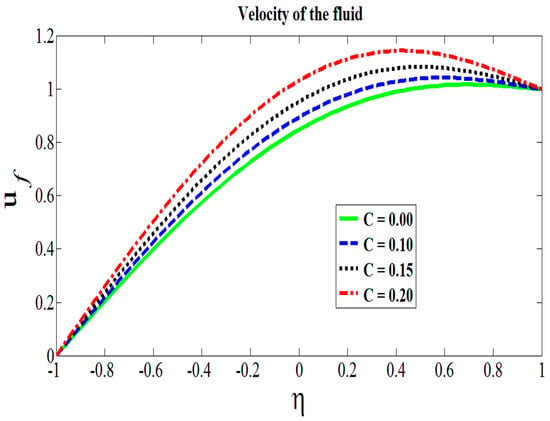
Figure 3.
Effects of metallic particle concentration on the flow.
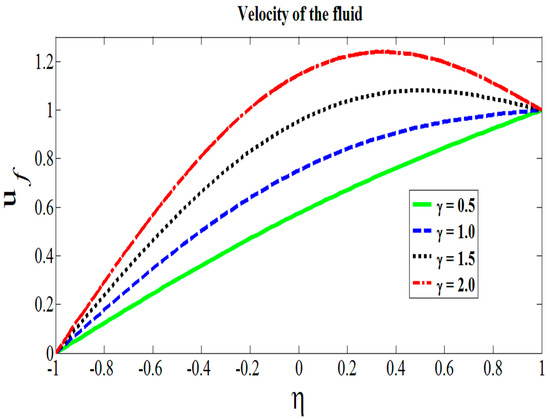
Figure 4.
Couples stress parameter affecting the flow.
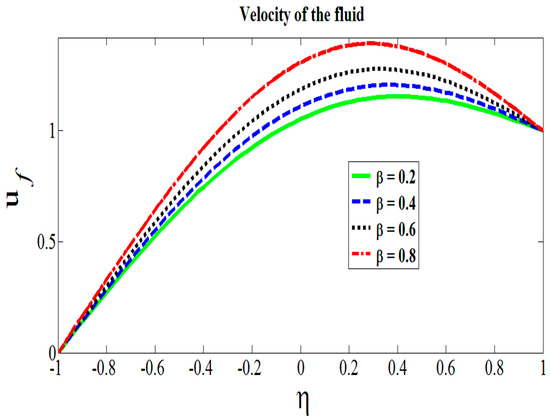
Figure 5.
Effects of viscous parameter on the flow.
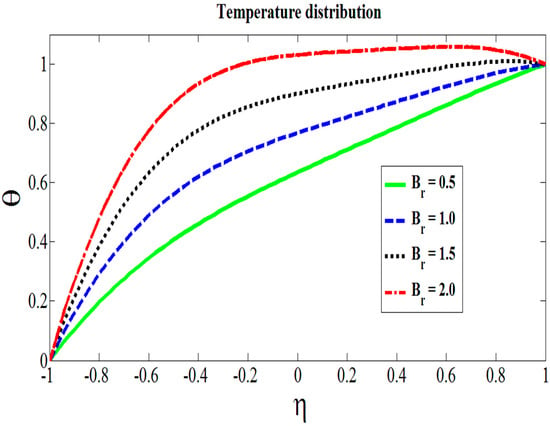
Figure 6.
Role of Brinkman number on the temperature.
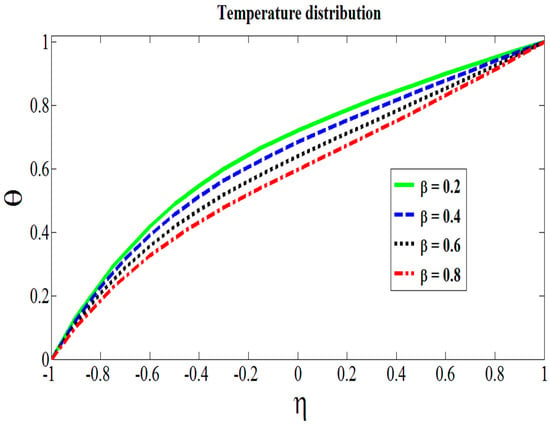
Figure 7.
Role of viscous parameter on the temperature.
3.4. Validation
The numerical results are being presented in Table 1, Table 2 and Table 3. The variation in the velocities of both phases against couple stress parameter when and are kept fixed are given in Table 1 whereas the variation in the velocities for single- and two-phase flows at different points of the domain when , and are specified in Table 2. The thermal variation at the different points of given domain when can be seen in Table 3. In all three table, one can conclude that temperature and velocities for both fluid and nanoparticles were an increasing function of metallic particles concentration , couple stress parameter , and the Brinkman number . The results extracted by numerical computation were found to be in excellent agreement with graphical illustrations and also satisfied all the subjected conditions. This provides a useful check that the presented solutions are correct.

Table 1.
Variation in the velocities of both phases for Newtonian case and couple stress fluid.

Table 2.
Variation in the velocities for single- and two-phase flows.

Table 3.
Thermal variation at the different points.
4. Conclusions
The Couette–Poiseuille flow of couple stress fluid in the presence of Hafnium particles was studied. The viscous dissipation effects were also reported. Exponentially decreasing viscosity of base fluid was presented by the Reynolds model. Transversely acting magnetic fields contributed by hindering the bi-phase flow. The key findings are described as:
- ⮚
- The flow of couple stress fluid resists for increasing values of Hartmann number.
- ⮚
- The temperature effectively variates the viscosity of the fluid to cause the shear thinning effects.
- ⮚
- The temperature of the flow mounts in response of higher values of Brinkman number.
- ⮚
- Attenuation of the viscosity results to expedite the flows.
- ⮚
- Viscosity parameter brings celerity in the velocity of bi-phase fluid due to high temperature difference.
- ⮚
- Molecules additives of base fluid reduce the force of friction and hence in both phases the velocity is galvanized.
- ⮚
- Due to the immense applications of multiphase flows in industrial and pharmaceutical, the proposed theoretical model is now available to vet relevant experimental investigations.
Author Contributions
Conceptualization, R.E.; Investigation, F.H.; Methodology, T.A.; Visualization, A.Z.
Funding
This research received no external funding.
Acknowledgments
R. Ellahi thanks to Sadiq M. Sait, the Director Office of Research Chair Professors, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia, to honor him with the Chair Professor at KFUPM. F. Hussain is also acknowledged Higher Education Commission Pakistan to provide him indigenous scholar for the pursuance of his Ph.D. studies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Farooq, M.; Rahim, M.T.; Islam, S.; Siddiqui, A.M. Steady Poiseuille flow and heat transfer of couple stress fluids between two parallel inclined plates with variable viscosity. J. Assoc. Arab Univ. Basic Appl. Sci. 2013, 14, 9–18. [Google Scholar] [CrossRef][Green Version]
- Mahabaleshwar, U.S.; Sarris, I.E.; Hill, A.; Lorenzini, G.; Pop, I. An MHD couple stress fluid due to a perforated sheet undergoing linear stretching with heat transfer. Int. J. Heat Mass. Transf. 2017, 105, 157–167. [Google Scholar] [CrossRef]
- Saad, H.; Ashmawy, E.A. Unsteady plane Couette flow of an incompressible couple stress fluid with slip boundary conditions. Int. J. Med. Health Sci. 2016, 3, 85–92. [Google Scholar] [CrossRef]
- Akhtar, S.; Shah, N.A. Exact solutions for some unsteady flows of a couple stress fluid between parallel plates. Ain Shams Eng. J. 2018, 9, 985–992. [Google Scholar] [CrossRef]
- Khan, N.A.; Khan, H.; Ali, S.A. Exact solutions for MHD flow of couple stress fluid with heat transfer. J. Egypt. Math. Soc. 2016, 24, 125–129. [Google Scholar] [CrossRef]
- Asghar, S.; Ahmad, A. Unsteady Couette flow of viscous fluid under a non-uniform magnetic field. Appl. Math. Lett. 2012, 25, 1953–1958. [Google Scholar] [CrossRef]
- Shaowei, W.; Mingyu, X. Exact solution on unsteady Couette flow of generalized Maxwell fluid with fractional derivative. Acta Mech. 2006, 187, 103–112. [Google Scholar] [CrossRef]
- Eegunjobi, A.S.; Makinde, O.D.; Tshehla, M.S.; Franks, O. Irreversibility analysis of unsteady Couette flow with variable viscosity. J. Hydrodyn. B 2015, 27, 304–310. [Google Scholar] [CrossRef]
- Ellahi, R.; Wang, X.; Hameed, M. Effects of heat transfer and nonlinear slip on the steady flow of Couette fluid by means of Chebyshev Spectral Method. Z. Naturforsch A. 2014, 69, 1–8. [Google Scholar] [CrossRef]
- Ellahi, R.; Shivanian, E.; Abbasbandy, S.; Hayat, T. Numerical study of magnetohydrodynamics generalized Couette flow of Eyring-Powell fluid with heat transfer and slip condition. Int. J. Numer. Method Heat Fluid Flow 2016, 26, 1433–1445. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Ellahi, R. Analysis of activation energy in Couette-Poiseuille flow of nanofluid in the presence of chemical reaction and convective boundary conditions. Results Phys. 2018, 8, 502–512. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R. Electroosmotic flow of MHD Power law Al2O3-PVC nanofluid in a horizontal channel: Couette-Poiseuille flow model. Commun. Theor. Phys. 2018, 69, 655–666. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A.; Vafai, K. Modelling study on heated couple stress fluid peristaltically conveying gold nanoparticles through coaxial tubes: A remedy for gland tumors and arthritis. J. Mol. Liq. 2018, 268, 149–155. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Asadollahi, A. Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy. Symmetry 2019, 11, 276. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhatti, M.M.; Fetecau, C.; Vafai, K. Peristaltic flow of couple stress fluid in a non-uniform rectangular duct having compliant walls. Commun. Theor. Phys. 2016, 65, 66–72. [Google Scholar] [CrossRef]
- Poply, V.; Singh, P.; Yadav, A.K. A study of Temperature-dependent fluid properties on MHD free stream flow and heat transfer over a non-linearly stretching sheet. Procedia Eng. 2015, 127, 391–397. [Google Scholar] [CrossRef]
- Ellahi, R.; Raza, M.; Vafai, K. Series solutions of non-Newtonian nanofluids with Reynolds model and Vogel’s model by means of the homotopy analysis method. Math. Comput. Model. 2012, 55, 1876–1891. [Google Scholar] [CrossRef]
- Disu, A.B.; Dada, M.S. Reynolds model viscosity on radiative MHD flow in a porous medium between two vertical wavy walls. J. Taibah Univ. Sci. 2017, 11, 548–565. [Google Scholar] [CrossRef][Green Version]
- Nadeem, S.; Ali, M. Analytical solutions for pipe flow of a fourth-grade fluid with Reynolds and Vogel’s models of viscosities. Commun. Nonlin. Sci. Numer. Simulat. 2009, 14, 2073–2090. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Thermally charged MHD bi-phase flow coatings with non-Newtonian nanofluid and Hafnium particles through slippery walls. Coatings 2019, 9, 300. [Google Scholar] [CrossRef]
- Mahmoud, M.A. Chemical reaction and variable viscosity effects on flow and mass transfer of a non-Newtonian visco-elastic fluid past a stretching surface embedded in a porous medium. Meccanica 2010, 45, 835–846. [Google Scholar] [CrossRef]
- Makinde, O.D. Laminar falling liquid film with variable viscosity along an inclined heated plate. Appl. Math. Comput. 2006, 175, 80–88. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Majdoubi, J.; Tlili, I.; Khan, W.; Khan, I. Impact of nonlinear thermal radiation and the viscous dissipation effect on the unsteady three-dimensional rotating flow of single-wall carbon nanotubes with aqueous suspensions. Symmetry 2019, 11, 207. [Google Scholar] [CrossRef]
- Ellahi, R. A study on the convergence of series solution of non-Newtonian third grade fluid with variable viscosity: By means of homotopy analysis method. Adv. Math. Phys. 2012, 2012, 634925. [Google Scholar] [CrossRef]
- Karimipour, A.; Orazio, A.D.; Shadloo, M.S. The effects of different nano particles of Al2O3 and Ag on the MHD nano fluid flow and heat transfer in a microchannel including slip velocity and temperature jump. Phys. E 2017, 86, 146–153. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Safaei, M.R.; Goodarzi, M.; Alrashed, A.A.A.A.; Nguyen, T.K. New temperature, interfacial shell dependent dimensionless model for thermal conductivity of nanofluids. Int. J. Heat Mass Transf. 2017, 114, 207–210. [Google Scholar] [CrossRef]
- Nasiri, H.; Jamalabadi, M.Y.A.; Sadeghi, R.; Safaei, M.R.; Nguyen, T.K.; Shadloo, M.S. A smoothed particle hydrodynamics approach for numerical simulation of nano-fluid flows. J. Therm. Anal. Calorim. 2018, 1–9. [Google Scholar] [CrossRef]
- Safaei, M.R.; Ahmadi, G.; Goodarzi, M.S.; Shadloo, M.S.; Goshayeshi, H.R.; Dahari, M. Heat transfer and pressure drop in fully developed turbulent flows of graphene nanoplatelets–silver/water nanofluids. Fluids 2016, 1, 20. [Google Scholar] [CrossRef]
- Sadiq, M.A. MHD stagnation point flow of nanofluid on a plate with anisotropic slip. Symmetry 2019, 11, 132. [Google Scholar] [CrossRef]
- Rashidi, S.; Esfahani, J.A.; Ellahi, R. Convective heat transfer and particle motion in an obstructed duct with two side by side obstacles by means of DPM model. Appl. Sci. 2017, 7, 431. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R.; Rashidid, S. Modelling study on internal energy loss due to entropy generation for non-Darcy Poiseuille flow of silver-water nanofluid: An application of purification. Entropy 2018, 20, 851. [Google Scholar] [CrossRef]
- Hassan, M.; Ellahi, R.; Bhatti, M.M.; Zeeshan, A. A comparative study of magnetic and non-magnetic particles in nanofluid propagating over a wedge. Can. J. Phys. 2019, 97, 277–285. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, A.; Ellahi, R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef]
- Ashrafi, N.; Khayat, R.E. A low-dimensional approach to nonlinear plane-Couette flow of viscoelastic fluids. Phys. Fluids. 2000, 12, 345–365. [Google Scholar] [CrossRef]
- Srivastava, L.M.; Srivastava, V.P. Peristaltic transport of a particle-fluid suspension. J. Biomech. Eng. 1989, 111, 157–165. [Google Scholar] [CrossRef]
- Tam, C.K.W. The drag on a cloud of spherical particles in a low Reynolds number flow. J. Fluid Mech. 1969, 38, 537–546. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1457. [Google Scholar] [CrossRef]
- Hossain, M.A.; Subba, R.; Gorla, R. Natural convection flow of non-Newtonian power-law fluid from a slotted vertical isothermal surface. Int. J Numer. Methods Heat Fluid Flow 2009, 19, 835–846. [Google Scholar] [CrossRef]
- Makinde, O.D.; Onyejekwe, O.O. A numerical study of MHD generalized Couette flow and heat transfer with variable viscosity and electrical conductivity. J. Magn. Magn. Mater. 2011, 323, 2757–2763. [Google Scholar] [CrossRef]
- Coelho, M.P.; Faria, J.S. On the generalized Brinkman number definition and its importance for Bingham fluids. J. Heat Transf. 2011, 133, 545051–545055. [Google Scholar] [CrossRef]
- Swarnalathamma, B.V.; Krishna, M.V. Peristaltic hemodynamic flow of couple stress fluid through a porous medium under the influence of magnetic field with slip effect. AIP Conf. Proc. 2016, 1728, 0206031–0206039. [Google Scholar] [CrossRef]
- Charm, S.E.; Kurland, G.S. Blood Flow and Microcirculation; Wiley: New York, NY, USA, 1974. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).